Unit -1 Relations and Functions

Chapter-1

Relations and Functions 

Cartesian Product , Relations and Types of Relations

Cartesian Product

Suppose there are two non-empty sets A and B.

Then the Cartesian product of A and B is the set of all ordered pairs of elements from A and B.

i.e., A × B = {(a , b) : a ∊ A, b ∊ B}

Example: Let A = {a_1,a_2,a₃,a₄} and B = {b₁,b₂}

Then, The Cartesian product of A and B will be;

A × B = {(a_1,b₁₎, (a_2,b₁),( a_3,b₁),( a_4,b₁).( a_1,b₂),( a_2,b₂),( a_3,b₂),( a_4,b₂ )}

Example: Let us say, A = {1,2} and B = { a,b,c}

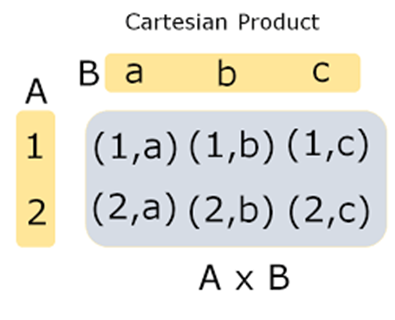
Therefore, A × B = {(1,a),(1,b),(1,c),(2,a),(2,b),(2,c)}.

This set has 8 ordered pairs. We can also represent it as in a tabular form.

Note: Two ordered pair X and Y are equal, if and only if the corresponding first elements and second elements are equal.

Example: Suppose, A = {cow, horse} B = {egg, juice}

 then, A×B = {(cow, egg), (horse, juice), (cow, juice), (horse, egg)}

If either of the two sets is a null set, i.e., either A = Φ or B = Φ, then, A × B = Φ i.e., A × B will also be a null set

Number of Ordered Pairs

For two non-empty sets, A and B. If the number of elements of A is p

 i.e., n(A) = p & that of B is q

 i.e., n(B) = q,

then the number of ordered pairs in Cartesian product will be n(A × B) = n(A) × n(B) = pq.

Properties

1. The Cartesian Product is non-commutative: A × B ≠ B × A.
2. The cardinality of the Cartesian Product is defined as the number of elements in A × B and is equal to the product of cardinality of both sets:

|A × B| = |A| * |B|

3. A × B = ∅, if either A = ∅ or B = ∅
4. If (x,y) = (a,b) ,then x=a , y=b
5. A×B=B×A, if only A=B
6. The Cartesian product is associative:

(A×B)×C=A×(B×C). It means the Cartesian product of the three-set is the same, i.e., it doesn’t depend upon which bracket is multiplied first as the final result will be the same.

7. Distributive property over a set intersection:

A×(B∩C)=(A×B)∩(A×C)

8. Distributive property over set union:

A×(B∪C)=(A×B)∪(A×C)

9. If A⊆B, then A×C⊆B×C for any set C.
10. AxBxC  = {(a,b,c) : aÎA, bÎ B ,cÎ C}

Here (a,b,c) is called ordered triplet.

Relation

Relation is association between two well-defined  objects.

Relations can be represented in different forms such as arrow representation, algebraic form, set-builder form, graphically, roster form, and tabular form. 

Definition

Let A and B be two non empty sets.

Then R  :  A ® B  is said to be a relation if R Í AxB .

The element of A (first element) of AxB in the relation is called Domain or Pre-image of relation R.

The element of B (second element) of AxB in the relation is called Range or image of relation R.

The whole B set of AxB in the relation is called Codomain of relation R.

Range Í Codomain

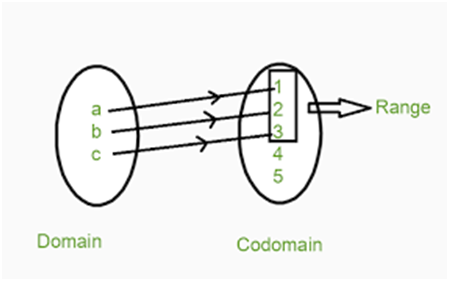
Example : Define a relation R from A to A = {1, 2, 3, 4, 5, 6} as R = {(x, y) : y = x + 1}. Determine the domain, codomain and range of R.

Answer: We can see that A = {1, 2, 3, 4, 5, 6} is the domain and codomain of R.

To determine the range, we determine the values of y for each value of x, that is, when x = 1, 2, 3, 4, 5, 6

• • x = 1, y = 1 + 1 = 2;
  • x = 2, y = 2 + 1 = 3;
  • x = 3, y = 3 + 1 = 4;
  • x = 4, y = 4 + 1 = 5;
  • x = 5, y = 5 + 1 = 6;
  • x = 6, y = 6 + 1 = 7.

Since 7 does not belong to A and the relation R is defined on A, hence, x = 6 has no image in A.

Therefore range of R = {2, 3, 4, 5, 6}

Answer: Domain = Codomain = {1, 2, 3, 4, 5, 6}, Range = {2, 3, 4, 5, 6}

Example :

Let A = {1, 2, 3, … , 14}. Define a relation R from A to A by R = {(x, y): 3x – y = 0, where x, y ∈ A}. Write down its domain, codomain and range.

ANSWER:

The relation R from A to A is given as

R = {(x, y): 3x – y = 0, where x, y ∈ A}

i.e., R = {(x, y): 3x = y, where x, y ∈ A}

∴R = {(1, 3), (2, 6), (3, 9), (4, 12)}

The domain of R is the set of all first elements of the ordered pairs in the relation.

∴Domain of R = {1, 2, 3, 4}

The whole set A is the codomainof the relation R.

∴Codomain of R = A = {1, 2, 3, …, 14}

The range of R is the set of all second elements of the ordered pairs in the relation.

∴Range of R = {3, 6, 9, 12}

Example:

The given figure shows a relationship between the sets P and Q. write this relation

(i) in set-builder form (ii) in roster form.

What is its domain and range?

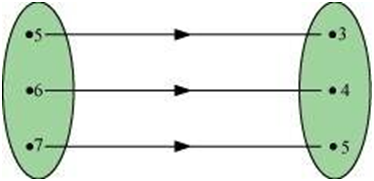
ANSWER:

According to the given figure, P = {5, 6, 7}, Q = {3, 4, 5}

(i) R = {(x, y): y = x – 2; x ∈ P} or R = {(x, y): y = x – 2 for x = 5, 6, 7}

(ii) R = {(5, 3), (6, 4), (7, 5)}

Domain of R = {5, 6, 7}

Range of R = {3, 4, 5}

Example:       

Let R be the relation on Z defined by R = {(a, b): a, b ∈ Z, a – b is an integer}. Find the domain and range of R.

ANSWER:

R = {(a, b): a, b ∈ Z, a – b is an integer}

It is known that the difference between any two integers is always an integer.

∴Domain of R = Z

Range of R = Z

Types of Relations

Given below is a list of different types of relations:

1. Empty Relation
2. Universal Relation
3. Identity Relation
4. Inverse Relation
5. Reflexive Relation
6. Symmetric Relation
7. Transitive Relation
8. Equivalence Relation

1) Empty Relation - A relation is an empty relation if it has no elements, that is, no element of set A is mapped or linked to any element of A. It is denoted by R = ∅.

For example, if set A = {1, 2, 3} then, one of the void relations can be R = {x, y} where, |x – y| = 8. For empty relation,

R = φ ⊂ A × A

2) Universal Relation - A relation R in a set A is a universal relation if each element of A is related to every element of A, i.e., R = A × A. It is called the full relation.

Consider set A = {a, b, c}. Now one of the universal relations will be R = {x, y} where, |x – y| ≥ 0. For universal relation,

R = A × A

3) Identity Relation - A relation R on A is said to be an identity relation if each element of A is related to itself, that is, R = {(a, a) : for all a ∈ A}

 For example, in a set A = {a, b, c}, the identity relation will be I = {a, a}, {b, b}, {c, c}. For identity relation,

I = {(a, a), a ∈ A}

4) Inverse Relation - Define R to be a relation from set P to set Q i.e., R ∈ P × Q. The relation R-1 is said to be an Inverse relation if R-1 from set Q to P is denoted by R^-1 = {(q, p): (p, q) ∈ R}.

For example if set A = {(a, b), (c, d)}, then inverse relation will be R^-1 = {(b, a), (d, c)}. So, for an inverse relation,

R^-1 = {(b, a): (a, b) ∈ R}

5) Reflexive Relation - A binary relation R defined on a set A is said to be reflexive if, for every element a ∈ A, we have aRa, that is, (a, a) ∈ R.

For example, consider a set A = {1, 2,}. Now an example of reflexive relation will be R = {(1, 1), (2, 2), (1, 2), (2, 1)}. The reflexive relation is given by-

(a, a) ∈ R

6) Symmetric Relation - A binary relation R defined on a set A is said to be symmetric if and only if, for elements a, b ∈ A, we have aRb, that is, (a, b) ∈ R, then we must have bRa, that is, (b, a) ∈ R.

 An example of symmetric relation will be R = {(1, 2), (2, 1)} for a set A = {1, 2}. So, for a symmetric relation,

aRb ⇒ bRa, ∀ a, b ∈ A

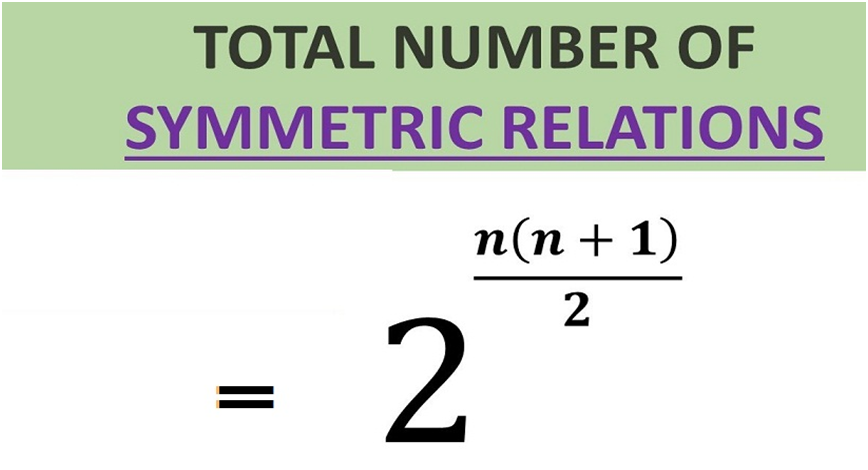
Example: For the set P={a,b}, the relation R={(a,b),(b,a)} is called symmetric relation, where a,b∈P.

7) Transitive Relation - A relation R is transitive if and only if (a, b) ∈ R and (b, c) ∈ R ⇒ (a, c) ∈ R for a, b, c ∈ A

Example: For the set A ={a,b,c}, the relation R={(a,b),(b,c),(a,c)} is called transitive relation, where a,b,c∈ A.

8) Equivalence Relation - A relation R defined on a set A is said to be an equivalence relation if and only if it is reflexive, symmetric and transitive.

Conditions:

1. If the relation (R) is reflexive, then all the elements of set A are mapped with itself, such that for every x∈ A , then (x,x)∈R.

2. The relation (R) is symmetric on set A, if (x,y)∈R, then (y,x)∈R, such that a,b∈ A.

3. The relation R on set A, if (x,y)∈R and (y,z)∈R, then (x,z)∈R, for all a,b,c∈ A is called transitive relation.

Example: Let A = {1, 2, 3, 4} and R = {(1, 1), (1, 3), (2, 2), (2, 4), (3, 1), (3, 3), (4, 2), (4, 4)}.

Show that R is an Equivalence Relation.

Solution:

Reflexive: Relation R is reflexive as (1, 1), (2, 2), (3, 3) and (4, 4) ∈ R.

Symmetric: Relation R is symmetric because whenever (a, b) ∈ R, (b, a) also belongs to R.

Example: (2, 4) ∈ R ⟹ (4, 2) ∈ R.

Transitive: Relation R is transitive because whenever (a, b) and (b, c) belongs to R, (a, c) also belongs to R.

Example: (3, 1) ∈ R and (1, 3) ∈ R ⟹ (3, 3) ∈ R.

So, as R is reflexive, symmetric and transitive, hence, R is an Equivalence Relation.

Question 1:

Let us assume that F is a relation on the set R real numbers defined by x F y if and only if x-y is an integer. Prove that F is an equivalence relation on R.

Solution:

Reflexive: Let  x belongs to R,then x – x = 0 which is an integer.

Therefore x F x.

So , F is reflexive.

Symmetric: Let  x and y belongs to R and x F y.

•  x – y is an integer.
• Thus, y – x = – ( x – y), y – x is also an integer.
•  Therefore yFx.

So , F is Symmetric.

 

Transitive: Let x and y belongs to R, xFy and yFz.

•  x-y and y-z are integers.
•  ( x – y ) + ( y – z ) = x – z is also an integer.
• So that xFz.

So , F is Transitive.

Thus, R is an equivalence relation on R.

Question 2:

Show that the relation R is an equivalence relation in the set A = { 1, 2, 3, 4, 5 } given by the relation R = { (a, b):|a-b| is even }.

Solution:

R = { (a, b):|a-b| is even }. Where a, b belongs to A

Reflexive Property :

Let a is belongs to A.

|a – a| = | 0 |=0

•  0 is always even.
• Thus, |a-a| is even
• Therefore, (a, a) belongs to R

Hence R is Reflexive

Symmetric Property :

Let  a, b belongs to A

|a – b| = |b – a|

Let a R b

We know that |a – b| = |-(b – a)|= |b – a|

•  |a – b| is even,
• |b – a| is also even.

Therefore, if (a, b) ∈ R, then (b, a) belongs to R

Hence R is symmetric.

Transitive Property :

Let a, b, c  belongs to A

Let a R b and b R c

• |b-c| is even and (b-c) is even

Since , If |a-b| is even, then (a-b) is even.

Sum of even number is also even

•  a-b+ b-c is even
• a – c is also even

Then, a R c

So,

|a – b| and |b – c| is even , then |a-c| is even.

Therefore, if (a, b) ∈ R and (b, c) ∈ R, then (a, c) also belongs to R

Hence R is transitive.

Therefore R is an equivalence relation.

Equivalence Class

Let R be an equivalence relation on set A.  For each a∈A, we denote the equivalence class of a as [a] defined as:

                       [a]={x ∈A ∣ x R a}                                          

Example:

Define a relation ∼ on Z by

a∼b⇔a mod 4=b mod 4

                              Find the equivalence classes of ∼

Answer

Two integers will be related by ∼ if they have the same remainder after dividing

by 4.  The possible remainders are 0, 1, 2, 3

 

[0]={...,−12,−8,−4,0,4,8,12,...}

[1]={...,−11,−7,−3,1,5,9,13,...}

[2]={...,−10,−6,−2,2,6,10,14,...}

[3]={...,−9,−5,−1,3,7,11,15,...}

Example:

Let S=P({1,2,3})={∅,{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}}.

For convenience, label

S0=∅,S1={1},S2={2},S3={3},S4={1,2},S5={1,3},S6={2,3},S7={1,2,3}.

Define this equivalence relation ∼ on S by

Si∼Sj⇔|Si|=|Sj|

 

Find the equivalence classes of ∼.

Answer

Two sets will be related by ∼ if they have the same number of elements.  

[S0]={S0}

[S2]={S1,S2,S3}

[S4]={S4,S5,S6}

[S7]={S7}

Example:

Consider set S={a,b,c,d} with this partition: {{a,b},{c},{d}}.

Find the ordered pairs for the relation R, induced by the partition.

Proof

R={(a,a),(a,b),(b,a),(b,b),(c,c),(d,d)}

Question :

Let R be a relation from N to N defined by R = {(a, b): a, b ∈ N and a = b²}. Are the following true?

(i) (a, a) ∈ R, for all a ∈ N

(ii) (a, b) ∈ R, implies (b, a) ∈ R

(iii) (a, b) ∈ R, (b, c) ∈ R implies (a, c) ∈ R.

Justify your answer in each case.

ANSWER:

R = {(a, b): a, b ∈ N and a = b²}

(i) It can be seen that 2 ∈ N;however, 2 ≠ 2² = 4.

Therefore, the statement “(a, a) ∈ R, for all a ∈ N” is not true.

(ii) It can be seen that (9, 3) ∈ N because 9, 3 ∈ N and 9 = 3².

Now, 3 ≠ 9² = 81; therefore, (3, 9) ∉ N

Therefore, the statement “(a, b) ∈ R, implies (b, a) ∈ R” is not true.

(iii) It can be seen that (16, 4) ∈ R, (4, 2) ∈ R because 16, 4, 2 ∈ N and 16 = 4² and 4 = 2².

Now, 16 ≠ 2² = 4; therefore, (16, 2) ∉ N

Therefore, the statement “(a, b) ∈ R, (b, c) ∈ R implies (a, c) ∈ R” is not true.

Example 5: Check whether the relation R defined in the set {1, 2, 3, 4, 5, 6} as R = {(a, b): b = a + 1} is reflexive, symmetric or transitive.

Solution:

Given R = {(a, b): b = a + 1}

Now for this relation we have to check whether it is reflexive, transitive and symmetric Reflexivity:

Let a be an arbitrary element of R.

Then, a = a + 1 cannot be true for all a ∈ A.

⇒ (a, a) ∉ R

So, R is not reflexive on A.

Symmetry:

Let (a, b) ∈ R

⇒ b = a + 1

⇒ −a = −b + 1

⇒ a = b − 1

Thus, (b, a) ∉ R

So, R is not symmetric on A.

Transitivity:

Let (1, 2) and (2, 3) ∈ R

⇒ 2 = 1 + 1 and 3

2 + 1  is true.

But 3 ≠ 1+1

⇒ (1, 3) ∉ R

So, R is not transitive on A.

Example 6:  Check whether the relation R on R defined as R = {(a, b): a ≤ b³} is reflexive, symmetric or transitive.

Solution:

Given R = {(a, b): a ≤ b³}

It is observed that (1/2, 1/2) in R as 1/2 > (1/2)³ = 1/8

∴ R is not reflexive.

Now,

(1, 2) ∈ R (as 1 < 2³ = 8)

But,

(2, 1) ∉ R (as 2 > 1³ = 1)

∴ R is not symmetric.

We have (3, 3/2), (3/2, 6/5) in “R as” 3 < (3/2)³ and 3/2 < (6/5)³

But (3, 6/5) ∉ R as 3 > (6/5)³

∴ R is not transitive.

Hence, R is neither reflexive, nor symmetric, nor transitive.

Example 7: Prove that every identity relation on a set is reflexive, but the converse is not necessarily true.

Solution:

Let A be a set.

Then, Identity relation IA=I_A is reflexive, since (a, a) ∈ A ∀a

The converse of it need not be necessarily true.

Consider the set A = {1, 2, 3}

Here,

Relation R = {(1, 1), (2, 2) , (3, 3), (2, 1), (1, 3)} is reflexive on A.

However, R is not an identity relation.

Example 8: If A = {1, 2, 3, 4} define relations on A which have properties of being

(i) Reflexive, transitive but not symmetric

(ii) Symmetric but neither reflexive nor transitive.

(iii) Reflexive, symmetric and transitive.

Solution:

(i) The relation on A having properties of being reflexive, transitive, but not symmetric is

R = {(1, 1), (2, 2), (3, 3), (4, 4), (2, 1)}

Relation R satisfies reflexivity and transitivity.

⇒ (1, 1), (2, 2), (3, 3) ∈ R

And (1, 1), (2, 1) ∈ R ⇒ (1, 1) ∈ R

However, (2, 1) ∈ R, but (1, 2) ∉ R

(ii)  The relation on A having properties of being reflexive, transitive, but not symmetric is

R = {(1, 1), (2, 2), (3, 3), (4, 4), (2, 1)}

Relation R satisfies reflexivity and transitivity.

⇒ (1, 1), (2, 2), (3, 3) ∈ R

And (1, 1), (2, 1) ∈ R ⇒ (1, 1) ∈ R

However, (2, 1) ∈ R, but (1, 2) ∉ R

(iii) The relation on A having properties of being symmetric, reflexive and transitive is

R = {(1, 1), (2, 2), (3, 3), (4, 4), (1, 2), (2, 1)}

The relation R is an equivalence relation on A.

Example 9:. Show that the relation R defined by R = {(a, b): a – b is divisible by 3; a, b ∈ Z} is an equivalence relation.

Solution:

Given R = {(a, b): a – b is divisible by 3; a, b ∈ Z} is a relation

To prove equivalence relation it is necessary that the given relation should be reflexive, symmetric and transitive.

Let us check these properties on R.

Reflexivity:

Let a be an arbitrary element of R.

Then, a – a = 0 = 0 × 3

⇒ a − a is divisible by 3

⇒ (a, a) ∈ R for all a ∈ Z

So, R is reflexive on Z.

Symmetry:

Let (a, b) ∈ R

⇒ a − b is divisible by 3

⇒ a − b = 3p for some p ∈ Z

⇒ b − a = 3 (−p)

Here, −p ∈ Z

⇒ b − a is divisible by 3

⇒ (b, a) ∈ R for all a, b ∈ Z

So, R is symmetric on Z.

Transitivity:

Let (a, b) and (b, c) ∈ R

⇒ a − b and b − c are divisible by 3

⇒ a – b = 3p for some p ∈ Z

And b − c = 3q for some q ∈ Z

Adding the above two equations, we get

a − b + b – c = 3p + 3q

⇒ a − c = 3 (p + q)

Here, p + q ∈ Z

⇒ a − c is divisible by 3

⇒ (a, c) ∈ R for all a, c ∈ Z

So, R is transitive on Z.

Therefore R is reflexive, symmetric and transitive.

Hence, R is an equivalence relation on Z.

Example 10: Show that the relation R on the set Z of integers, given by
R = {(a, b): 2 divides a – b}, is an equivalence relation.

Solution:

Given R = {(a, b): 2 divides a – b} is a relation defined on Z.

To prove equivalence relation it is necessary that the given relation should be reflexive, symmetric and transitive.

Let us check these properties on R.

Reflexivity:

Let a be an arbitrary element of the set Z.

Then, a ∈ R

⇒ a − a = 0 = 0 × 2

⇒ 2 divides a − a

⇒ (a, a) ∈ R for all a ∈ Z

So, R is reflexive on Z.

Symmetry:

Let (a, b) ∈ R

⇒ 2 divides a − b

⇒ (a-b)/2 = p for some p ∈ Z

⇒ (b-a)/2 = – p

Here, −p ∈ Z

⇒ 2 divides b − a

⇒ (b, a) ∈ R for all a, b ∈ Z

So, R is symmetric on Z

Transitivity:

Let (a, b) and (b, c) ∈ R

⇒ 2 divides a−b and 2 divides b−c

⇒ (a-b)/2 = p and (b-c)/2 = q for some p, q ∈ Z

Adding the above two equations, we get

(a – b)/2 + (b – c)/2 = p + q

⇒ (a – c)/2 = p +q

Here, p+ q ∈ Z

⇒ 2 divides a − c

⇒ (a, c) ∈ R for all a, c ∈ Z

So, R is transitive on Z.

Therefore R is reflexive, symmetric and transitive.

Hence, R is an equivalence relation on Z.

Example 11:. Prove that the relation R on Z defined by (a, b) ∈ R ⇔ a − b is divisible by 5 is an equivalence relation on Z.

Solution:

Given relation R on Z defined by (a, b) ∈ R ⇔ a − b is divisible by 5

To prove equivalence relation it is necessary that the given relation should be reflexive, symmetric and transitive.

Let us check these properties on R.

Reflexivity:

Let a be an arbitrary element of R. Then,

⇒ a − a = 0 = 0 × 5

⇒ a − a is divisible by 5

⇒ (a, a) ∈ R for all a ∈ Z

So, R is reflexive on Z.

Symmetry:

Let (a, b) ∈ R

⇒ a − b is divisible by 5

⇒ a − b = 5p for some p ∈ Z

⇒ b − a = 5 (−p)

Here, −p ∈ Z                      [Since p ∈ Z]

⇒ b − a is divisible by 5

⇒ (b, a) ∈ R for all a, b ∈ Z

So, R is symmetric on Z.

Transitivity:

Let (a, b) and (b, c) ∈ R

⇒ a − b is divisible by 5

⇒ a − b = 5p for some Z

Also, b − c is divisible by 5

⇒ b − c = 5q for some Z

Adding the above two equations, we get

a −b + b − c = 5p + 5q

⇒ a − c = 5 ( p + q )

⇒ a − c is divisible by 5

Here, p + q ∈ Z

⇒ (a, c) ∈ R for all a, c ∈ Z

So, R is transitive on Z.

Therefore R is reflexive, symmetric and transitive.

Hence, R is an equivalence relation on Z.

Example 12:. Let n be a fixed positive integer. Define a relation R on Z as follows:
(a, b) ∈ R ⇔ a − b is divisible by n.
Show that R is an equivalence relation on Z.

Solution:

Given (a, b) ∈ R ⇔ a − b is divisible by n is a relation R defined on Z.

To prove equivalence relation it is necessary that the given relation should be reflexive, symmetric and transitive.

Let us check these properties on R.

Reflexivity:

Let a ∈ N

Here, a − a = 0 = 0 × n

⇒ a − a is divisible by n

⇒ (a, a) ∈ R

⇒ (a, a) ∈ R for all a ∈ Z

So, R is reflexive on Z.

Symmetry:

Let (a, b) ∈ R

Here, a − b is divisible by n

⇒ a − b = n p for some p ∈ Z

⇒ b − a = n (−p)

⇒ b − a is divisible by n                     [ p ∈ Z⇒ − p ∈ Z]

⇒ (b, a) ∈ R

So, R is symmetric on Z.

Transitivity:

Let (a, b) and (b, c) ∈ R

Here, a − b is divisible by n and b − c is divisible by n.

⇒ a − b= n p for some p ∈ Z

And b−c = n q for some q ∈ Z

a – b + b − c = n p + n q

⇒ a − c = n (p + q)

⇒ (a, c) ∈ R for all a, c ∈ Z

So, R is transitive on Z.

Therefore R is reflexive, symmetric and transitive.

Hence, R is an equivalence relation on Z

FUNCTIONS

It is a special type of relation.

Defⁿ: A relation R:AàB is said to be a function if every element of a set A has only one image in set B.

Or                

A relation R:AàB is said to be a function if Domain(R)=A and One many relation is not present.

Or

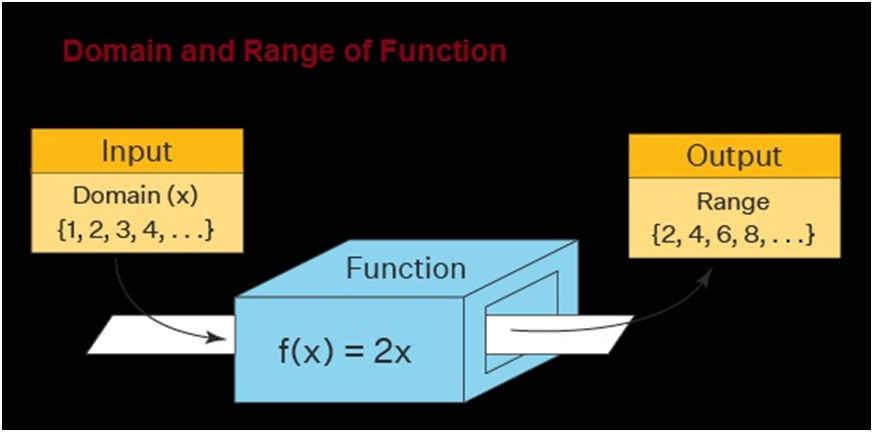
A special relationship where each input has a single output. It is often written as "f(x)" where x is the input value.

Example:

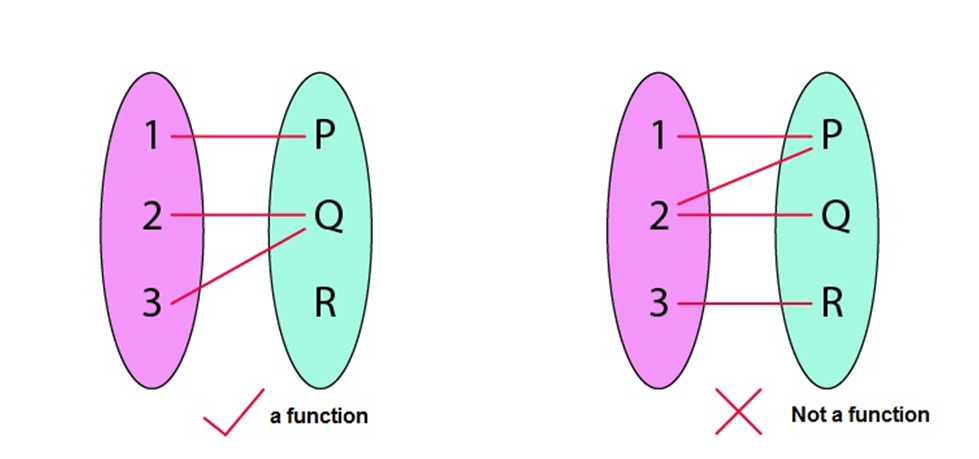
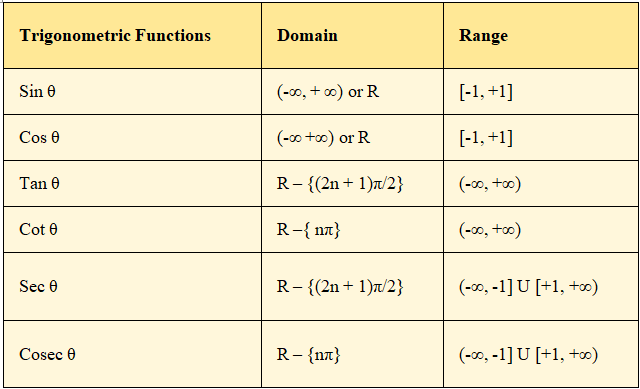
Different types of functions their domain and range

Types of Functions

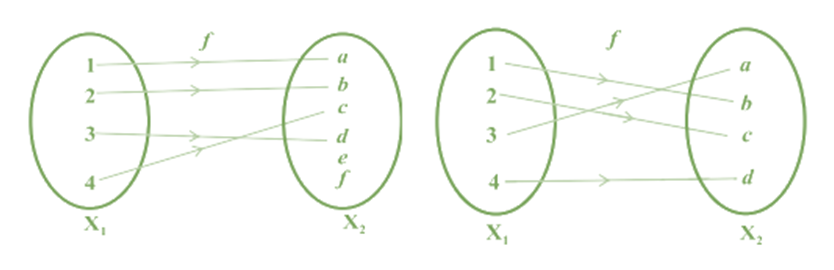
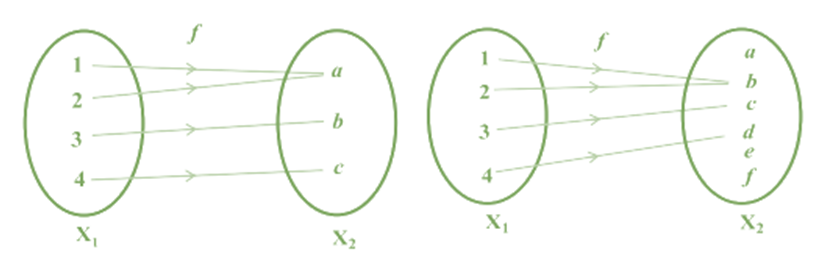
One to one Function: A function f : X → Y is defined to be one-one (or injective), if the images of distinct elements of X under f are distinct,

i.e., for every x₁ , x₂ ∈ X, f(x₁ ) = f(x₂ ) implies x₁ = x₂ . Otherwise, f is called many-one.

Examples

Examples of one-one / injective Function

• The identity function X → X is always one-one.
• If function f: R→ R, then f(x) = 2x is one-one.
• If function f: R→ R, then f(x) = 2x+1 is one-one.
• If function f: R→ R, then f(x) = x² is not an injective function, because here

if x = -1, then f(-1) = 1 = f(1). Hence, the element of co-domain is not discrete here.

• If function f: R→ R, then f(x) = x/2 is one-one.
• If function f: R→ R, then f(x) = x³ is one-one.
• If function f: R→ R, then f(x) = 4x+5 is one-one.

Properties of One-One Function

• If f and g are both one to one, then f ∘ g follows one-one.
• If g ∘ f is one to one, then function f is one to one, but function g may not be.
• f: X → Y is one-one, if and only if, given any functions g, h : P → X whenever f ∘ g = f ∘ h, then g = h..
• If f: X → Y is one-one and P is a subset of X, then f^-1 (f(A)) = P. Thus, P can be retrieved from its image f(P).
• If f: X → Y is one-one and P and Q are both subsets of X, then f(P ∩ Q) = f(P) ∩ f(Q).
• If both X and Y are limited with the same number of elements, then f: X → Y is one-one, if and only if f is surjective or onto function.

Example :

Show that f: R→ R defined as f(a) = 3x³ – 4 is one to one function?

Solution:

Let f ( x₁ ) = f ( x₂ ) for all a₁ , a₂ ∈ R

•  3x₁³ – 4 = 3x₂³ – 4
• x₁³ = x₂³ 
• x₁³ – x₂³ = 0
• (x₁ – x₂) (x₁ + x₁x₂ + x₂²) = 0
• x₁ = x₂ and (x₁² + x₁x₂ + x₂²) = 0 
• (x₁² + x₁x₂ + x₂²) = 0 is not considered because there are no real values of x₁ and x₂.

Therefore,  the given function f is one-one.

1. Onto Function: A function f: X → Y is said to be onto (or surjective), if every element of Y is the image of some element of X under f,(Codomain=Range)

i.e., for every y ∈ Y, there exists an element x in X such that f(x) = y.