7. Distance of a point from a plane and Distance between two planes

Distance of a Point from a Plane

The distance between point and plane is the length of the perpendicular to the plane passing through the given point.

If we want to determine the distance between the point P with coordinates (x_o, y_o, z_o) and the given plane with equation Ax + By + Cz = D, then the distance between point P and the given plane is given by d= |Ax_o + By_o+ Cz_o + D|/√(A² + B² + C²).

Example: Determine the distance between the point P = (1, 2, 5) and the plane π: 3x + 4y + z + 7 = 0

Solution: We know that the formula for distance between point and plane is: d = |Ax_o + By_o + Cz_o + D |/√(A² + B² + C²)

Here, A = 3, B = 4, C = 1, D = 7, x_o = 1, y_o = 2, z_o = 5

Substituting the values in the formula, we have

d = |Ax_o + By_o + Cz_o + D |/√(A² + B² + C²)

= |3 × 1 + 4 × 2 + 1 × 5 + 7|/√(3² + 4² + 1²)

= |3 + 8 + 5|/√(9 + 16 + 1)

= |16|/√26

= 8√26/13 units

Important Notes on Distance Between Point and Plane

• Distance Between Point and Plane Formula: |Ax_o + By_o + Cz_o + D |/√(A² + B² + C²)
• Distance Between Point and Plane is zero if the given point lies on the given plane.

Angle between a Line and a Plane:   

Let θ be the angle between the line and the normal to the plane. Its value can be given by the following equation:

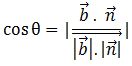
Φ is the angle between the line and the plane which is the complement of θ or 90 – θ. We know that cos θ is equal to sin (90 – θ). So Φ can be given by:

sin (90 – θ) = cos θ

or

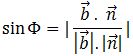
or

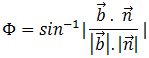
Problem: A line has an equation

The equation of a plane is 3x + 4y – 12z = 7. Find the angle between them.

Solution: Let θ be the angle between the line and the normal to the plane. In the vector form, the equations can be written as:

The equation of the plane in the vector form can be given by:

So we have

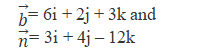
Finding the value of the Φ between the line and the plane:

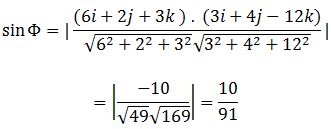
The value of Φ can be found by

Definition : The angle between a line and a plane is the complement of the angle between the line and normal to the plane