- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Geometrical interpretation and Some properties of indefinite integral
Comparison between differentiation and integration
1. Both are operations on functions.
2. Both satisfy the property of linearity, i.e.,
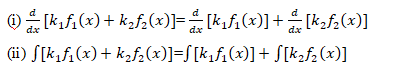
Here k1 and k2 are constants.
3. We have already seen that all functions are not differentiable. Similarly, all functions
are not integrable. We will learn more about nondifferentiable functions and
nonintegrable functions in higher classes.
4. The derivative of a function, when it exists, is a unique function. The integral of
a function is not so. However, they are unique upto an additive constant, i.e., any
two integrals of a function differ by a constant.
5. When a polynomial function P is differentiated, the result is a polynomial whose
degree is 1 less than the degree of P. When a polynomial function P is integrated,
the result is a polynomial whose degree is 1 more than that of P.
6. We can speak of the derivative at a point. We never speak of the integral at a
point, we speak of the integral of a function over an interval on which the integral
is defined .
7. The derivative of a function has a geometrical meaning, namely, the slope of the
tangent to the corresponding curve at a point. Similarly, the indefinite integral of a function represents geometrically, a family of curves placed parallel to each other having parallel tangents at the points of intersection of the curves of the family with the lines orthogonal (perpendicular) to the axis representing the variable
of integration.
8. The derivative is used for finding some physical quantities like the velocity of a
moving particle, when the distance traversed at any time t is known. Similarly,
the integral is used in calculating the distance traversed when the velocity at time
t is known.
9. Differentiation is a process involving limits. So is integration.
10.The process of differentiation and integration are inverses of each other .
Types of Integration Maths or the Integration Techniques:-
- Integration by Inspection.
- Integration by Substitution.
- Integration by Parts.
- Integration by Partial Fraction.
Integration by Inspection:
Example: Solve ![]()
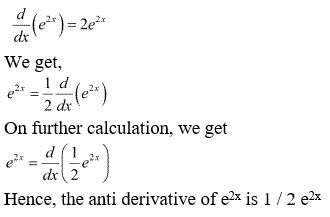
Example : Find the anti derivative F of f defined by f (x) = 4x3 – 6, where F (0) = 3
Solution: One anti derivative of f (x) is x4 – 6x since
![]()
Therefore, the anti derivative F is given by
F(x) = x4 – 6x + C, where C is constant.
Given that F(0) = 3, which gives,
3 = 0 – 6 0 + C or C = 3
Hence, the required anti derivative is the unique function F defined by
F(x) = x4 – 6x + 3.
Example:
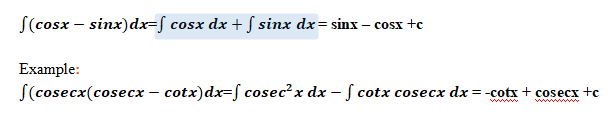

 KRISHNA PUBLICATIONS
KRISHNA PUBLICATIONS
