6. Binomial distribution , mean and variance of random variable

Binomial distribution , mean and variance of random variable

Mean of a random variable:

Definition : Let X be a random variable whose possible values x1, x2, x3, ..., xn occur with probabilities p1, p2, p3,..., pn, respectively. The mean of X, denoted by m, is the number

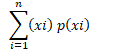
i.e. the mean of X is the weighted average of the possible values of X, The mean of a random variable X is also called the expectation of X, denoted by E(X).

Example : Let a pair of dice be thrown and the random variable X be the sum of the numbers that appear on the two dice. Find the mean or expectation of X.

Solution : The sample space of the experiment consists of 36 elementary events in the form of ordered pairs (xi, yi), where xi= 1, 2, 3, 4, 5, 6 and yi= 1, 2, 3, 4, 5, 6.

The random variable X i.e. the sum of the numbers on the two dice takes the values 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 or 12.

Thus, the mean of the sum of the numbers that appear on throwing two fair dice is 7.         

Variance of a random variable:     

Let X be a random variable whose possible values x1, x2,...,xn occur with

probabilities p(x1), p(x2),..., p(xn) respectively.

Let m= E (X) be the mean of X. The variance of X, denoted by Var (X) or s2_x is defined as.

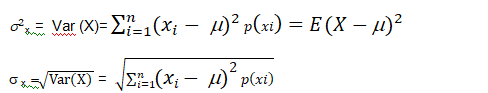
is called the standard deviation of the random variable X.

Bernoulli Trials and Binomial Distribution      

Bernoulli trials:

Definition : Trials of a random experiment are called Bernoulli trials, if they satisfy the following conditions :

(i) There should be a finite number of trials.

(ii) The trials should be independent.

(iii) Each trial has exactly two outcomes : success or failure.

(iv) The probability of success remains the same in each trial.

Example : Six balls are drawn successively from an urn containing 7 red and 9 black balls. Tell whether or not the trials of drawing balls are Bernoulli trials when after each draw the ball drawn is

(i) replaced (ii) not replaced in the urn.

Solution:

(i) The number of trials is finite. When the drawing is done with replacement, the probability of success (say, red ball) is p =7/16

which is same for all six trials (draws). Hence, the drawing of balls with replacements are Bernoulli trials.

(ii) When the drawing is done without replacement, the probability of success

(i.e., red ball) in first trial is 7/16  , in 2nd trial is  6/15

if the first ball drawn is red or  7/15

if the first ball drawn is black and so on. Clearly, the probability of success is not same for all trials, hence the trials are not Bernoulli trials.

Binomial distribution:

The binomial distribution formula is for any random variable X, given by;

Where,

n = the number of experiments

x = 0, 1, 2, 3, 4, …

p = Probability of Success in a single experiment

q = Probability of Failure in a single experiment = 1 – p

The binomial distribution formula can also be written in the form of n-Bernoulli trials, where ⁿC_x = n!/[x!(n-x)!]. Hence,

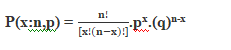
Binomial Distribution Mean and Variance

Binomial distribution, the mean, variance and standard deviation for the given number of success are represented using the formulas

Mean, μ = np

Variance, σ² = npq

Standard Deviation σ= √(npq)

Where p is the probability of success

q is the probability of failure, where q = 1-p

Properties of Binomial Distribution

The properties of the binomial distribution are:

• There are two possible outcomes: true or false, success or failure, yes or no.
• There is ‘n’ number of independent trials or a fixed number of n times repeated trials.
• The probability of success or failure varies for each trial.
• Only the number of success is calculated out of n independent trials.
• Every trial is an independent trial, which means the outcome of one trial does not affect the outcome of another trial.

Example 1: If a coin is tossed 5 times, find the probability of:

(a) Exactly 2 heads

(b) At least 4 heads.

Solution:

(a) The repeated tossing of the coin is an example of a Bernoulli trial. According to the problem:

Number of trials: n=5

Probability of head: p= 1/2 and hence the probability of tail, q =1/2

For exactly two heads:

x=2

P(x=2) = ⁵C2 p² q^5-2 = 5! / 2! 3! × (½)²× (½)³

P(x=2) = 5/16

(b) For at least four heads,

x ≥ 4, P(x ≥ 4) = P(x = 4) + P(x=5)

Hence,

P(x = 4) = ⁵C4 p⁴ q^5-4 = 5!/4! 1! × (½)⁴× (½)¹ = 5/32

P(x = 5) = ⁵C5 p⁵ q^5-5 = (½)⁵ = 1/32

Therefore,

P(x ≥ 4) = 5/32 + 1/32 = 6/32 = 3/16

Example 2: For the same question given above, find the probability of:

a) Getting at least 2 heads

Solution: P (at most 2 heads) = P(X ≤ 2) = P (X = 0) + P (X = 1)

P(X = 0) = (½)⁵ = 1/32

P(X=1) = ⁵C₁ (½)^5.= 5/32

Therefore,

P(X ≤ 2) = 1/32 + 5/32 = 3/16

Example 3:

A fair coin is tossed 10 times, what are the probability of getting exactly 6 heads and at least six heads.

Solution:

Let x denote the number of heads in an experiment.

Here, the number of times the coin tossed is 10. Hence, n=10.

The probability of getting head, p ½

The probability of getting a tail, q = 1-p = 1-(½) = ½.

The binomial distribution is given by the formula:

P(X= x) = ⁿC_xp^xq^n-x, where = 0, 1, 2, 3, …

Therefore, P(X = x) = ¹⁰C_x(½)^x(½)^10-x

(i) The probability of getting exactly 6 heads is:

P(X=6) = ¹⁰C₆(½)⁶(½)^10-6

P(X= 6) = ¹⁰C₆(½)¹⁰

P(X = 6) = 105/512.

Hence, the probability of getting exactly 6 heads is 105/512.

(ii) The probability of getting at least 6 heads is P(X ≥ 6)

P(X ≥ 6) = P(X=6) + P(X=7) + P(X= 8) + P(X = 9) + P(X=10)

P(X ≥ 6) = ¹⁰C₆(½)¹⁰ + ¹⁰C₇(½)¹⁰ + ¹⁰C₈(½)¹⁰ + ¹⁰C₉(½)¹⁰ + ¹⁰C₁₀(½)¹⁰

P(X ≥ 6) = 193/512.