6. Angle between two planes a line and a plane

Angle between Two Planes:

 The angle between normal to two planes is the angle between the two planes.

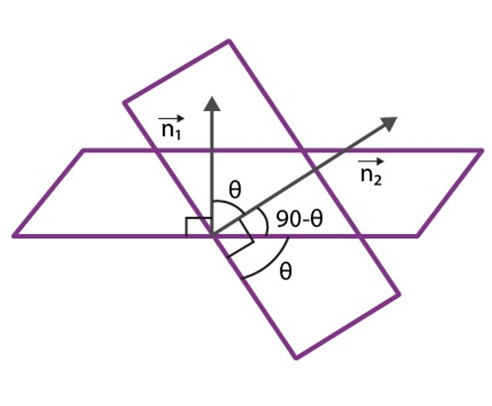
Cartesian form:

Let A₁ x + B₁ y + C₁z + D₁ = 0 and A₂x + B₂y + C₂ z + D₂ = 0  be the equation of two planes aligned to each other at an angle θ where A₁, B₁, C₁ and A₂, B₂, C₂ are the direction ratios of the normal to the planes, then the cosine of the angle between the two planes is given by:

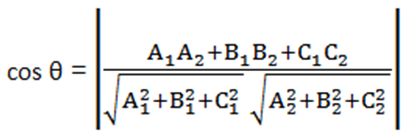
Example: Determine the angle between the two planes whose vector equations are given as r.(2i + 2j - 3k) = 4 and r.(3i - 3j + 5k) = 3.

Solution: The equations of the planes are given in vector form. Now to find the angle between the planes r.(2i + 2j - 3k) = 4 and r.(3i - 3j + 5k) = 3, we will use the formula cos θ = |(n₁ . n₂)|/(|n₁|.|n₂|). We have,

n₁ = 2i + 2j - 3k, n₂ = 3i - 3j + 5k

|n₁| = √(2² + 2² + (-3)²) = √(4 + 4 + 9) = √17

|n₂| = √(3² + (-3)² + 5²) = √(9 + 9 + 15) = √43

Scalar product of the normal vectors is given by, n₁ . n₂ = (2i + 2j - 3k) . (3i - 3j + 5k) = 2 × 3 + 2 × (-3) + (-3) × 5 = 6 - 6 - 15 = -15

Substituting these values into the formula, we have

cos θ = |(-15)|/(√17 . √43)

= 15/√731

⇒ θ = cos^-1(15/√731)

Example: Find the angle between two planes with equations 2x + y - 2z = 5 and 3x - 6y - 2z = 7.

Solution: Since the equations of the two planes are given in the cartesian form, we will determine the angle between two planes in cartesian form using the formula cos θ = |(A₁A₂ + B₁B₂ + C₁C₂)|/[√(A₁² + B₁² + C₁²)√(A₂² + B₂² + C₂²)]. The equations of the planes are 2x + y - 2z = 5 and 3x - 6y - 2z = 7. Here, A₁ = 2, B₁ = 1, C₁ = -2, A₂ = 3, B₂ = -6, C₂ = -2. Substituting these values into the formula, we have

cos θ = (2×3 + 1×(-6) + (-2)×(-2))/[√(2² + 1² + (-2)²)√(3² + (-6)² + (-2)²)]

= (6 + (-6) + 4)/[√(4 + 1 + 4)√(9 + 36 + 4)]

= 4/(√9 √49)

= 4/(3×7)

= 4/21

⇒ θ = cos^-1(4/21) 

 

Important Notes on Angle Between Two Planes

• The angle between two planes is equal to the angle between the normal vectors to the two planes and is called the dihedral angle.
• For planes, r.n₁ = d₁ and r.n₂ = d₂, the angle between them is given by, cos θ = |(n₁ . n₂)/(|n₁|.|n₂|)
• For planes, A₁x + B₁y + C₁z + D₁ = 0 and A₂x + B₂y + C₂z + D₂ = 0, the angle between two planes in cartesian form is given by, cos θ = |(A₁A₂ + B₁B₂ + C₁C₂)|/[√(A₁² + B₁² + C₁²)√(A₂² + B₂² + C₂²)]