3. Increasing and Decreasing Functions

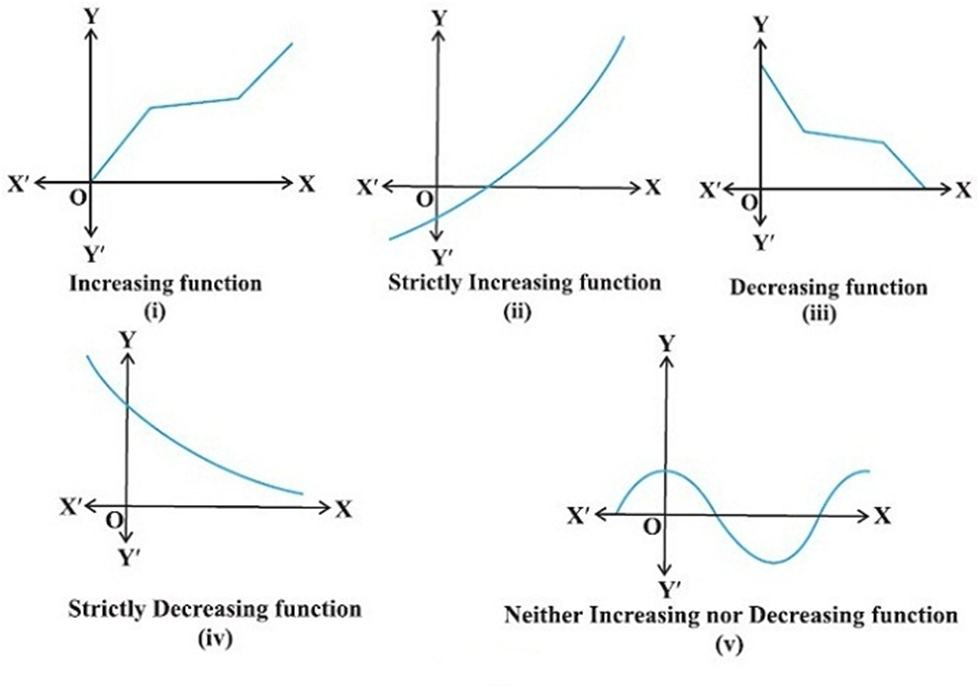
Increasing and Decreasing Functions:

Definition :  Let I be an interval contained in the domain of a real valued function f.

Then f is said to be

1. increasing on I if x1 < x2 in I ⇒f(x1 ) < f(x2 ) for all x1 , x2 ∈ I.

 (ii) decreasing on I, if x 1 , x 2 in I ⇒f(x 1 ) < f(x 2 ) for all x 1 , x 2 ∈ I.

3. constant on I, if f(x) = c for all x ∈ I, where c is a constant.

(iv) decreasing on I if x1 < x2 in I ⇒ f (x1 ) ≥ f(x2 ) for all x1 , x2 ∈ I.

4. strictly decreasing on I if x1 < x2 in I ⇒ f(x1 ) > f(x2 ) for all x1 , x2 ∈ I.

 

Definition :

 Let x ₀ be a point in the domain of definition of a real valued function f. Then f is said to be increasing, decreasing at x₀ if there exists an open interval I containing x ₀ such that f is increasing, decreasing, respectively, in I

Example :

 Show that the function given by f(x) = 7x – 3 is increasing on R.

 Solution:

 Let x₁ and x Î R. Then x₁ < x₂ ⇒ 7x₁ < 7x₂ ⇒ 7x₁ – 3 < 7x₂ – 3 ⇒ f(x₁ ) < f(x₂ ) Thus, by Definition ,

it follows that f is strictly increasing on R.

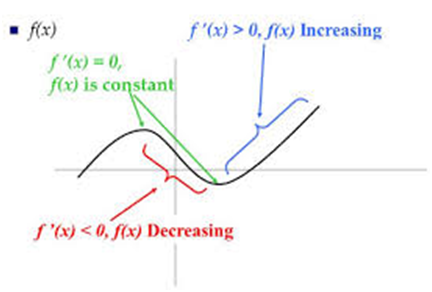
Theorem 1 :

Let f be continuous on [a, b] and differentiable on the open interval (a,b).

Then (a) f is increasing in [a,b] if f ′(x) > 0 for each x ∈ (a, b)

(b) f is decreasing in [a,b] if f ′(x) < 0 for each x ∈ (a, b)

(c) f is a constant function in [a,b] if f ′(x) = 0 for each x ∈ (a, b)

Proof :

1. Let x₁ , x₂ ∈ [a, b] be such that x₁ < x₂ . Then, by Mean Value Theorem ,

there exists a point c between x₁ and x₂

 such that f(x₂ ) – f(x₁ ) = f ′(c) (x₂ – x₁ )

 i.e. f(x₂ ) – f(x₁ ) > 0 (as f ′(c) > 0 (given))

i.e. f(x₂ ) > f(x₁ )

Thus, we have x₁< x₂ =>f (x₁ )<f (x₂ ), for all x₁,x_2Î [ a,b ]

Hence, f is an increasing function in [a,b].

The proofs of part (b) and (c) are similar

Example :

 Find the intervals in which the function f given by f(x) = x ² – 4x + 6 is

1. increasing (b) decreasing

Solution :

We have f (x) = x ² – 4x + 6

or f ′(x) = 2x – 4

Therefore, f ′(x) = 0 gives x = 2.

Now the point x = 2 divides the real line into two disjoint intervals namely, (– ∞, 2) and (2, ∞)

 In the interval (– ∞, 2), f ′(x) = 2x – 4 < 0.

Therefore, f is decreasing in this interval. Also, in the interval (2,  ∞) , f  ′(x )> 0

 and so the function f is increasing in this interval.

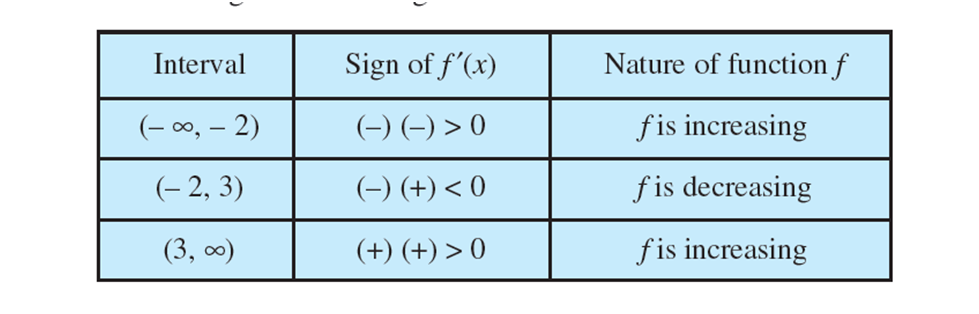
Example :

 Find the intervals in which the function f given by f (x) = 4x ³ – 6x ² – 72x + 30 is

1. increasing (b) decreasing.

 Solution:  We have f(x) = 4x ³ – 6x ² – 72x + 30

or f ′(x) = 12x ² – 12x – 72

 = 12(x ² – x – 6) = 12(x – 3) (x + 2)

Therefore, f ′(x) = 0 gives x = – 2, 3.

The points x = – 2 and x = 3 divides the real line into three disjoint intervals, namely,

 (– ∞, – 2), (– 2, 3)

and (3, ∞).

In the intervals (– ∞, – 2) and (3, ∞), f ′(x) is positive while in the interval (– 2, 3), f ′(x) is negative. Consequently, the function f is increasing in the intervals (– ∞, – 2) and (3, ∞) while the function is decreasing in the interval (– 2, 3).

 However, f is neither increasing nor decreasing in R.