4. Different Types of Linear Programming Problems

Different Types of Linear Programming Problems:

A few important types of  linear programming problems are:

 (i) Manufacturing problems

 (ii) Diet problems

 (iii) Transportation problems

(iv) Allocation Problems

The different types of linear programming problems are discussed below.

Manufacturing problems

These problems can be seen in the manufacturing sector in order to optimize production by maximising profits. The profits can be a function of the number of workers, working hours, materials required, the value of the product in the market, the demand for the product, the supply of the product etc.

Constraints – Factors such as labour hours, the cost of packing materials, and so on.

The production rate is the objective function.

Example:

A manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of Rs 17.50 per package on nuts and Rs 7.00 per package on bolts. How many packages of each should be produced each day so as to maximize his profit, if he operates his machines for at the most 12 hours a day?

Solution:

Let the manufacturer produce x package of nuts and y package of bolts. Hence,

x ≥ 0 and y ≥ 0

The given information can be compiled in a table as given below

The profit on a package of nuts is Rs 17.50 and on a package of bolts is Rs 7

Hence, the constraints are

x + 3y ≤ 12

3x + y ≤ 12

Then, total profit, Z = 17.5x + 7y

The mathematical formulation of the given problem can be written as follows

Maximize Z = 17.5x + 7y …………. (1)

Subject to the constraints,

x + 3y ≤ 12 …………. (2)

3x + y ≤ 12 ………… (3)

x, y ≥ 0 …………….. (4)

The feasible region determined by the system of constraints is given below

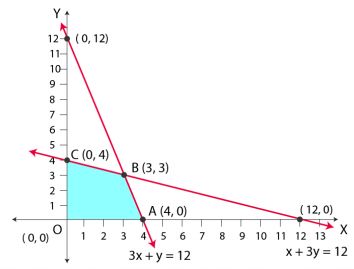
A (4, 0), B (3, 3) and C (0, 4) are the corner points

The values of Z at these corner points are given below

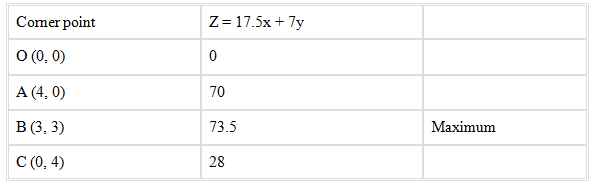
Therefore, Rs 73.50 at (3, 3) is the maximum value of Z

Hence, 3 packages of nuts and 3 packages of bolts should be produced each day to get the maximum profit of Rs 73.50

Diet problems

Such problems involve the optimisation of the amount of intake of different types of foods, which are required by the body to obtain necessary nutrients. The agenda of a diet problem will be selecting those foods with the required nutrient at a lesser cost.

Example:

.Reshma wishes to mix two types of food P and Q in such a way that the vitamin contents of the mixture contain at least 8 units of vitamin A and 11 units of vitamin B. Food P costs Rs 60/kg and Food Q costs Rs 80/kg. Food P contains 3 units /kg of vitamin A and 5 units /kg of vitamin B while food Q contains 4 units /kg of vitamin A and 2 units /kg of vitamin B. Determine the minimum cost of the mixture?

Solution:

Let the mixture contain x kg of food P and y kg of food Q.

Hence, x ≥ 0 and y ≥ 0

The given information can be compiled in a table as given

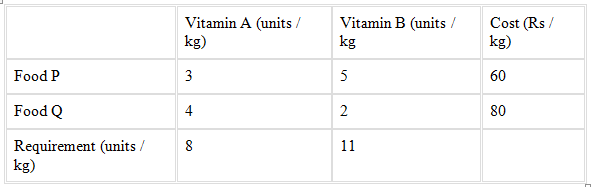
The mixture must contain at least 8 units of vitamin A and 11 units of vitamin B. Hence, the constraints are

3x + 4y ≥ 8

5x + 2y ≥ 11

Total cost of purchasing food is, Z = 60x + 80y

So, the mathematical formulation of the given problem can be written as

Minimise Z = 60x + 80y (i)

Now, subject to the constraints,

3x + 4y ≥ 8 … (2)

5x + 2y ≥ 11 … (3)

x, y ≥ 0 … (4)

The feasible region determined by the system of constraints is given below

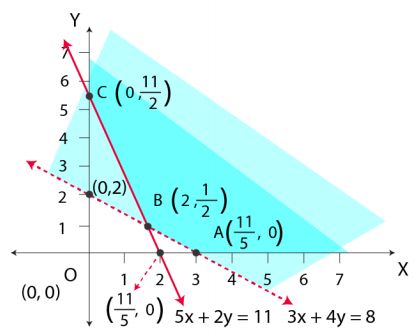
Clearly, we can see that the feasible region is unbounded

A (8 / 3, 0), B (2, 1 / 2) and C (0, 11 / 2)

The values of Z at these corner points are given below

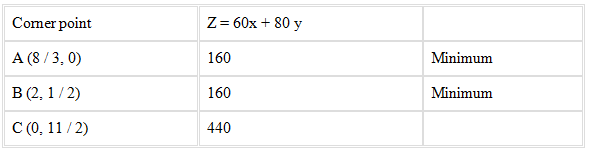
Here the feasible region is unbounded, therefore, 160 may or may not be the minimum value of Z.

For this purpose, we graph the inequality, 60x + 80y < 160 or 3x + 4y < 8, and check whether the resulting half plane has points in common with the feasible region or not

Here, it can be seen that the feasible region has no common point with 3x + 4y < 8

Hence, at the line segment joining the points (8 / 3, 0) and (2, 1 / 2), the minimum cost of the mixture will be Rs 160

 

Transportation problems

These problems involve the transportation of manufactured goods efficiently to different places such that the transportation cost is minimum. For big companies, the analysis of transportation cost is very much important as it caters to a widespread area.

Example: Two godowns A and B have grain capacity of 100 quintals and 50 quintals respectively. They supply to 3 ration shops, D, E and F whose requirements are 60, 50 and 40 quintals respectively. The cost of transportation per quintal from the godowns to the shops are given in the following table:

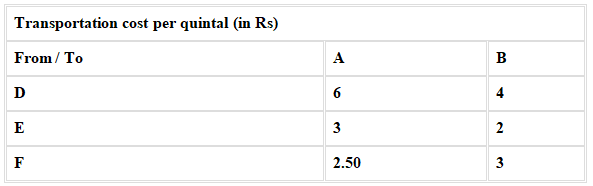
How should the supplies be transported in order that the transportation cost is minimum? What is the minimum cost?

Solution:

Let godown A supply x and y quintals of grain to the shops D and E

So, (100 – x – y) will be supplied to shop F.

Since, x quintals are transported from godown A, so the requirement at shop D is 60 quintals. Hence, the remaining (60 – x) quintals will be transported from godown B.

Similarly, (50 – y) quintals and 40 – (100 – x – y) = (x + y – 60) quintals will be transported from godown B to shop E and F

The given problem can be represented diagrammatically as given below

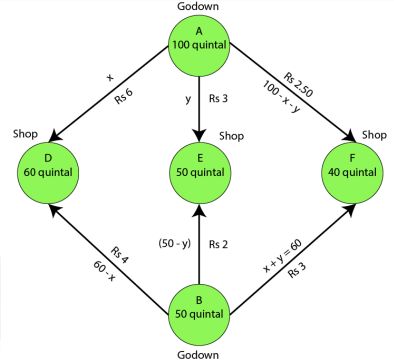
x ≥ 0, y ≥ 0, and 100 – x – y ≥ 0

Then, x ≥ 0, y ≥ 0, and x + y ≤ 100

60 – x ≥ 0, 50 – y ≥ 0, and x + y – 60 ≥ 0

Then, x ≤ 60, y ≤ 50, and x + y ≥ 60

Total transportation cost z is given by,

z = 6x + 3y + 2.5 (100 – x – y) + 4 (60 – x) + 2 (50 – y) + 3 (x + y – 60)

= 6x + 3y + 250 – 2.5x – 2.5y + 240 – 4x + 100 – 2y + 3x + 3y – 180

= 2.5x + 1.5y + 410

The given problem can be formulated as given below

Minimize z = 2.5x + 1.5y + 410 …………. (i)

Subject to the constraints,

x + y ≤ 100 ……….. (ii)

x ≤ 60 ……….. (iii)

y ≤ 50 ………. (iv)

x + y ≥ 60 ……… (v)

x, y ≥ 0 …………..(vi)

The feasible region determined by the system of constraints is given below

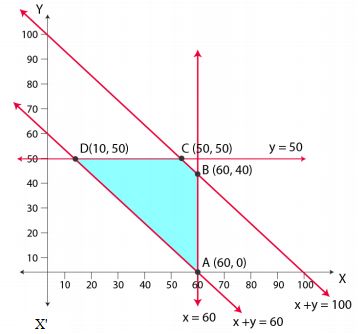
A (60, 0), B (60, 40), C (50, 50) and D (10, 50) are the corner points

The values of z at these corner points are given below

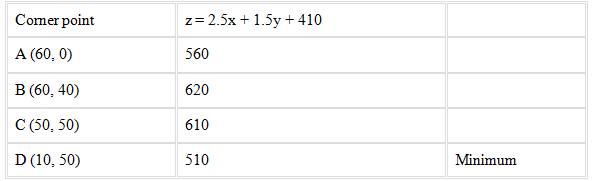
The minimum value of z is 510 at (10, 50)

Hence, the amount of grain transported from A to D, E and F is 10 quintals, 50 quintals and 40 quintals respectively and from B to D, E and F is 50 quintals, 0 quintals, 0 quintals respectively

Thus, the minimum cost is Rs 510

 

Example: A farmer mixes two brands P and Q of cattle feed. Brand P, costing Rs 250 per bag, contains 3 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand Q costing Rs 200 per bag contains 1.5 units of nutritional element A, 11.25 units of element B, and 3 units of element C. The minimum requirements of nutrients A, B and C are 18 units, 45 units and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag?

Solution:

Let the farmer mix x bags of brand P and y bags of brand Q respectively

The given information can be compiled in a table is given below

 

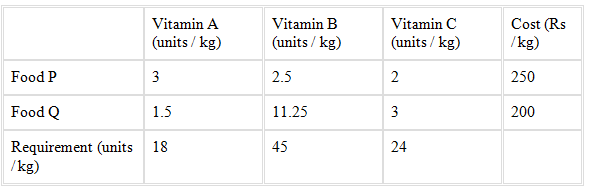
The given problem can be formulated as given below

Minimize z = 250x + 200y ………… (i)

3x + 1.5y ≥ 18 ………….. (ii)

2.5x + 11.25y ≥ 45 ……….. (iii)

2x + 3y ≥ 24 ………….. (iv)

x, y ≥ 0 ………. (v)

The feasible region determined by the system of constraints is given below

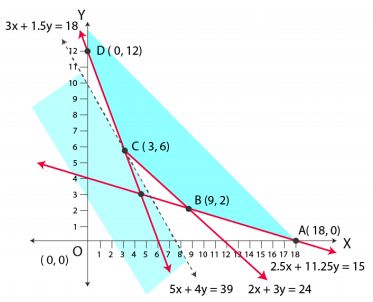
A (18, 0), B (9, 2), C (3, 6) and D (0, 12) are the corner points of the feasible region

The values of z at these corner points is given below

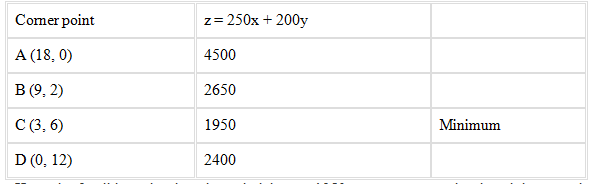
Here, the feasible region is unbounded, hence, 1950 may or may not be the minimum value of z

For this purpose, we draw a graph of the inequality, 250x + 200y < 1950 or 5x + 4y < 39, and check whether the resulting half plane has points in common with the feasible region or not

Here, it can be seen that the feasible region has no common point with 5x + 4y < 39

Hence, at point (3, 6) the minimum value of z is 1950

Therefore, 3 bags of brand P and 6 bags of brand Q should be used in the mixture to minimize the cost to Rs 1950

 

Allocation problems

The problem is to determine the optimum weekly production quantities for the products. The goal is to maximize total profit. In constructing a model, the first step is to define the decision variables; the next step is to write the constraints and objective function in terms of these variables and the problem data.

Example:

There are two types of fertilizers F₁ and F₂. F₁ consists of 10% nitrogen and 6% phosphoric acid and F₂ consists of 5% nitrogen and 10% phosphoric acid. After testing the soil conditions, a farmer finds that she needs atleast 14 kg of nitrogen and 14 kg of phosphoric acid for her crop. If F₁ costs Rs 6 / kg and F₂ costs Rs 5 / kg, determine how much of each type of fertilizer should be used so that nutrient requirements are met at a minimum cost. What is the minimum cost?

Solution:

Let the farmer buy x kg of fertilizer F₁ and y kg of fertilizer F₂. Hence,

x ≥ 0 and y ≥ 0

The given information can be compiled in a table is given below

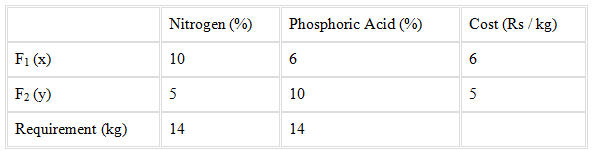
F₁ consists of 10% nitrogen and F₂ consists of 5% nitrogen.

However, the farmer requires at least 14 kg of nitrogen

So, 10% of x + 5% of y ≥ 14

x / 10 + y / 20 ≥ 14

By L.C.M we get

2x + y ≥ 280

F₁ consists of 6% phosphoric acid and F₂ consists of 10% phosphoric acid.

However, the farmer requires at least 14 kg of phosphoric acid

So, 6% of x + 10 % of y ≥ 14

6x / 100 + 10y / 100 ≥ 14

3x + 5y ≥ 700

Total cost of fertilizers, Z = 6x + 5y

The mathematical formulation of the given problem can be written as

Minimize Z = 6x + 5y ………….. (i)

Subject to the constraints,

2x + y ≥ 280 ……… (ii)

3x + 5y ≥ 700 ………. (iii)

x, y ≥ 0 …………. (iv)

The feasible region determined by the system of constraints is given below

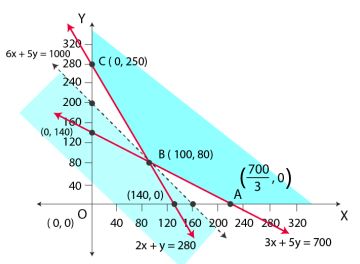
Here, we can see that the feasible region is unbounded.

A (700 / 3, 0), B (100, 80) and C (0, 280) are the corner points

The values of Z at these points are given below

Here, the feasible region is unbounded, hence, 1000 may or may not be the minimum value of Z.

For this purpose, we draw a graph of the inequality, 6x + 5y < 1000, and check whether the resulting half plane has points in common with the feasible region or not.

Here, it can be seen that the feasible region has no common point with 6x + 5y < 1000

Hence, 100 kg of fertilizer F₁ and 80 kg of fertilizer F₂ should be used to minimize the cost. The minimum cost is Rs 1000