6. Solutions of homogeneous differential equations of first order and first degree

Homogeneous differential equations

A function F(x, y) is said to be homogeneous function of degree n if

F(λx, λy) = λⁿF(x, y) for any nonzero constant λ   .

A differential equation of the form     is said to be homogenous if  F(x, y) is a homogenous function of degree zero. We make the substitution y = v . x

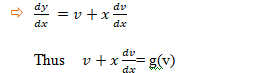
Separating the variables in equation , we get

Integrating both sides of equation (5), we get

Equation (6) gives general solution (primitive) of the differential equation (1) when

we replace v by y/x.

Example: Solve dy/dx = (x-y)/(x+y)

Solution: Given, dy/dx = (x-y)/(x+y)

It is homogeneous degree 0.

Then,

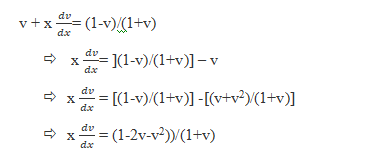
Now we can use the separation of variables method;

(1+v)/(1-2v-v²) dv = (1/x) dx

Integrating both the sides;

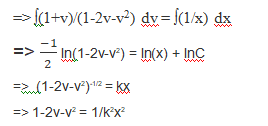
Again, putting v = y/x;

1-2(y/x)-(y/x)² = 1/k²x²

Eliminating x² term from denominator on both the sides, we get;

x²-2xy-y² = 1/k²

or

y²+2xy-x² = -1/k²

Now, put -/k² = c

Adding 2x² on both the sides;

y²+2xy+x² = c+2x²

Now factoring the above equation, we get;

(y+x)² = 2x²+c

y+x=√(2x²)+c

Or y = ±√(2x²+c) − x

This is the solution for the given equation.

Example: Find the equation of the curve passing through the point (1,-2) when the tangent at any point is given by  

Solution: The equation of tangent represents the slope of the curve i.e.

This equation is homogeneous in nature.

On cross-multiplication, we get- 

Solving the equation, we get

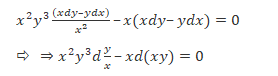
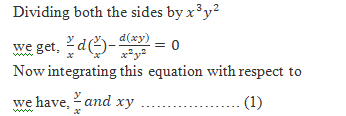
Now substituting the value of the given point in the above equation, we have

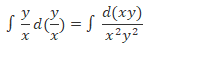
Put this value of the constant C in equation (1) we get

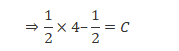
This is the required solution.