- Books Name
- ABCD CLASSES Mathmatics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 12
- Subject
- Mathmatics
Chapter-1
Relations and Functions
Cartesian Product , Relations and Types of Relations
Cartesian Product
Suppose there are two non-empty sets A and B.
Then the Cartesian product of A and B is the set of all ordered pairs of elements from A and B.
i.e., A × B = {(a , b) : a ∊ A, b ∊ B}
Example: Let A = {a1,a2,a3,a4} and B = {b1,b2}
Then, The Cartesian product of A and B will be;
A × B = {(a1,b1), (a2,b1),( a3,b1),( a4,b1).( a1,b2),( a2,b2),( a3,b2),( a4,b2 )}
Example: Let us say, A = {1,2} and B = { a,b,c}
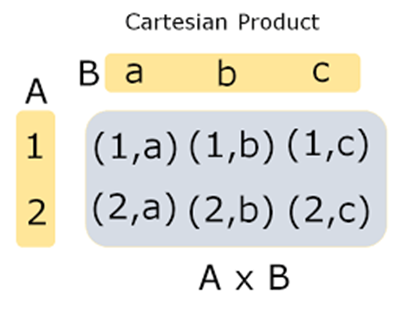
Therefore, A × B = {(1,a),(1,b),(1,c),(2,a),(2,b),(2,c)}.
This set has 8 ordered pairs. We can also represent it as in a tabular form.
Note: Two ordered pair X and Y are equal, if and only if the corresponding first elements and second elements are equal.
Example: Suppose, A = {cow, horse} B = {egg, juice}
then, A×B = {(cow, egg), (horse, juice), (cow, juice), (horse, egg)}
If either of the two sets is a null set, i.e., either A = Φ or B = Φ, then, A × B = Φ i.e., A × B will also be a null set
Number of Ordered Pairs
For two non-empty sets, A and B. If the number of elements of A is p
i.e., n(A) = p & that of B is q
i.e., n(B) = q,
then the number of ordered pairs in Cartesian product will be n(A × B) = n(A) × n(B) = pq.
Properties
- The Cartesian Product is non-commutative: A × B ≠ B × A.
- The cardinality of the Cartesian Product is defined as the number of elements in A × B and is equal to the product of cardinality of both sets:
|A × B| = |A| * |B|
- A × B = ∅, if either A = ∅ or B = ∅
- If (x,y) = (a,b) ,then x=a , y=b
- A×B=B×A, if only A=B
- The Cartesian product is associative:
(A×B)×C=A×(B×C). It means the Cartesian product of the three-set is the same, i.e., it doesn’t depend upon which bracket is multiplied first as the final result will be the same.
- Distributive property over a set intersection:
A×(B∩C)=(A×B)∩(A×C)
- Distributive property over set union:
A×(B∪C)=(A×B)∪(A×C)
- If A⊆B, then A×C⊆B×C for any set C.
- AxBxC = {(a,b,c) : aÎA, bÎ B ,cÎ C}
Here (a,b,c) is called ordered triplet.
Relation
Relation is association between two well-defined objects.
Relations can be represented in different forms such as arrow representation, algebraic form, set-builder form, graphically, roster form, and tabular form.
Definition
Let A and B be two non empty sets.
Then R : A ® B is said to be a relation if R Í AxB .
The element of A (first element) of AxB in the relation is called Domain or Pre-image of relation R.
The element of B (second element) of AxB in the relation is called Range or image of relation R.
The whole B set of AxB in the relation is called Codomain of relation R.
Range Í Codomain
Example : Define a relation R from A to A = {1, 2, 3, 4, 5, 6} as R = {(x, y) : y = x + 1}. Determine the domain, codomain and range of R.
Answer: We can see that A = {1, 2, 3, 4, 5, 6} is the domain and codomain of R.
To determine the range, we determine the values of y for each value of x, that is, when x = 1, 2, 3, 4, 5, 6
-
- x = 1, y = 1 + 1 = 2;
- x = 2, y = 2 + 1 = 3;
- x = 3, y = 3 + 1 = 4;
- x = 4, y = 4 + 1 = 5;
- x = 5, y = 5 + 1 = 6;
- x = 6, y = 6 + 1 = 7.
Since 7 does not belong to A and the relation R is defined on A, hence, x = 6 has no image in A.
Therefore range of R = {2, 3, 4, 5, 6}
Answer: Domain = Codomain = {1, 2, 3, 4, 5, 6}, Range = {2, 3, 4, 5, 6}
Example :
Let A = {1, 2, 3, … , 14}. Define a relation R from A to A by R = {(x, y): 3x – y = 0, where x, y ∈ A}. Write down its domain, codomain and range.
ANSWER:
The relation R from A to A is given as
R = {(x, y): 3x – y = 0, where x, y ∈ A}
i.e., R = {(x, y): 3x = y, where x, y ∈ A}
∴R = {(1, 3), (2, 6), (3, 9), (4, 12)}
The domain of R is the set of all first elements of the ordered pairs in the relation.
∴Domain of R = {1, 2, 3, 4}
The whole set A is the codomainof the relation R.
∴Codomain of R = A = {1, 2, 3, …, 14}
The range of R is the set of all second elements of the ordered pairs in the relation.
∴Range of R = {3, 6, 9, 12}
Example:
The given figure shows a relationship between the sets P and Q. write this relation
(i) in set-builder form (ii) in roster form.
What is its domain and range?
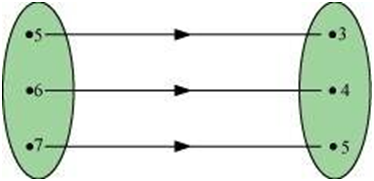
ANSWER:
According to the given figure, P = {5, 6, 7}, Q = {3, 4, 5}
(i) R = {(x, y): y = x – 2; x ∈ P} or R = {(x, y): y = x – 2 for x = 5, 6, 7}
(ii) R = {(5, 3), (6, 4), (7, 5)}
Domain of R = {5, 6, 7}
Range of R = {3, 4, 5}
Example:
Let R be the relation on Z defined by R = {(a, b): a, b ∈ Z, a – b is an integer}. Find the domain and range of R.
ANSWER:
R = {(a, b): a, b ∈ Z, a – b is an integer}
It is known that the difference between any two integers is always an integer.
∴Domain of R = Z
Range of R = Z

 Chintu
Chintu
