8. Scalar triple product and properties of scalar triple product

Scalar triple product and properties of scalar triple product

The scalar triple product of three vectors a, b, c is the scalar product of ector a with the 

cross product of the vectors b and c, i.e., a · (b × c). Symbolically, it is also written as [a b c] = [a, b, c] = a · (b × c). The scalar triple product [a b c] gives the volume of a parallelepiped with adjacent sides a, b, and c. If we are given three vectors a, b, c, then their scalar triple products [a b c] are:

a · (b × c)

• a · (c × b)
• b · (a × c)
• b · (c × a)
• c · (b × a)
• c · (a × b)

Now, before moving to the formula of the scalar triple product, we need to note that:

• [a, b, c] = a · (b × c) = b · (c × a) = c · (a × b)
• a · (b × c) = - a · (c × b)
• b · (c × a) = - b · (a × c)
• c · (a × b) = - c · (b × a)
• a · (b × c) = (a × b) · c

 

the scalar triple product of vectors means the product of three vectors. It means taking the dot product of one of the vectors with the cross product of the remaining two. It is denoted as

[a b c ] = ( a × b) . c

The following conclusions can be drawn, by looking into the above formula:

i) The resultant is always a scalar quantity.

ii) Cross product of the vectors is calculated first, followed by the dot product which gives the scalar triple product.

iii) The physical significance of the scalar triple product formula represents the volume of the parallelepiped whose three coterminous edges represent the three

vectors a, b and c. The figure will make this point more clear.

 

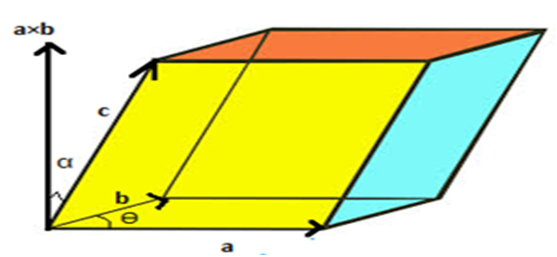
According to this figure, the three vectors are represented by the coterminous edges as shown. The cross product of vectors a and b  gives the area of the base, and also, the direction of the cross product of vectors is perpendicular to both the vectors. As volume is the product of area and height, the height, in this case, is given by the component of vector c along the direction of the cross product of a and b. The component is given by c cos α.

Thus, we can conclude that for a Parallelepiped, if the coterminous edges are denoted by three vectors and a, b and c then,

Volume of parallelepiped = ( a × b) c cos α =  ( a × b) . c

Where α is the angle between  ( a × b)  and c.

We are familiar with the expansion of cross products of vectors. Keeping that in mind,

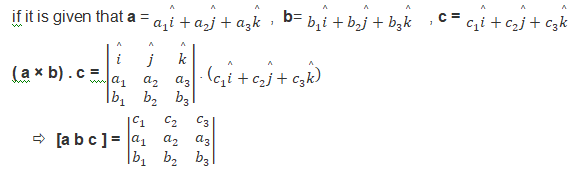
Properties of Scalar Triple Product:

i) If the vectors are cyclically calculated, then

 ( a × b) . c = a.( b × c) 

ii)  The product is cyclic in nature, i.e.,

a.(b × c) = b.(c × a) = c.(a × b)

Thus,

[ a b c ] = [ b c a ] = [ c a b ] = – [ b a c ] = – [ c b a ] = – [ a c b ] 

Example : Evaluate the volume of a parallelepiped whose coterminous edges are i - j + k, 2i + 3j - k, and -i - j + 5k.

Solution: To determine the volume of the parallelepiped with edges i - j + k, 2i + 3j - k, and -i - j + 5k, we will determine its scalar triple product.

[ i - j + k, 2i + 3j - k, -i - j + 5k] = 

= 1(15 - 1) + 1(10 - 1) + 1(-2 + 3)

= 14 + 9 + 1

= 24

Answer: The volume of the parallelepiped is 24 cubic units.