1. Concept of Matrices and Types of Matrices

Chapter-3

Matrices

Concept of Matrices and Types of Matrices

Matrices

Definition

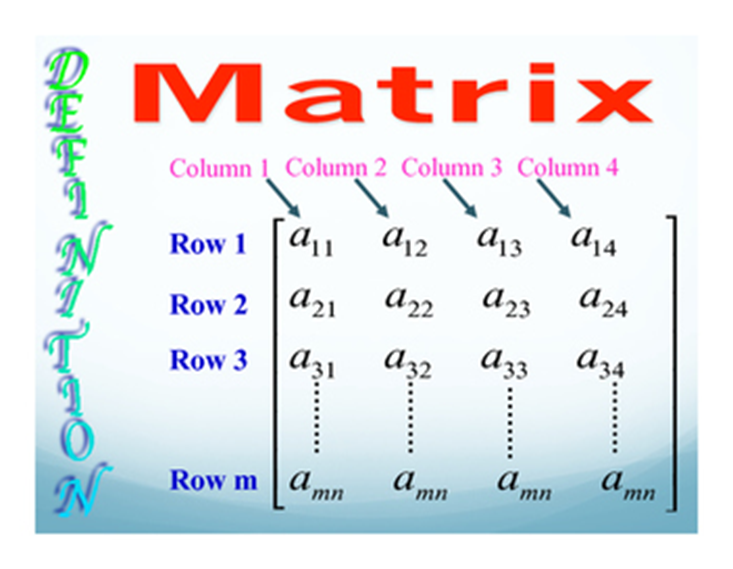
A matrix is a rectangular array of numbers or functions or objects  arranged in row and column.

The numbers or functions or objects in the array are called the entities or members or the elements of the matrix. The horizontal array of elements in the matrix is called rows, and the vertical array of elements are called the columns. If a matrix has m rows and n columns, then it is known as the matrix of order ‘m x n’ or ‘m by n’.

Symbol: ( ) or [ ]

i.e., A = [a_ij]_m×n  means m rows and n columns.

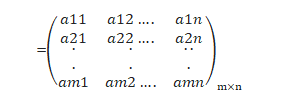
Note: If A = [a_ij] _n×n  is a square matrix of order n, then elements a₁₁, a₂₂, a₃₃,…, a_nn is said to constitute the diagonal of the matrix A. In general, A = [a_ij]_m×m is a diagonal matrix, if a_ij = 0, when i ≠ j.

Types of Matrices:

1. Column matrix
2. Row matrix
3. Square matrix
4. Diagonal matrix
5. Scalar matrix
6. Identity matrix
7. Zero matrix

 Equality of Matrices

Two matrices are said to be equal if-

(i) The order of both the matrices are the same

(ii) Each element of one matrix is equal to the corresponding element of the other matrix

i.e.,