- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Invertible Matrices and Inverse of a matrix by elementary operations
Elementary Operation (Transformation) of a Matrix
There are six operations (transformations) on a matrix, three of which are due to rows, and three are due to columns, known as elementary operations or transformations.
[1] The interchange of any two rows or two columns.
denoted by Ri ↔ Rj and interchange of i th and j th column is denoted by Ci ↔ Cj .
[2] The multiplication of the elements of any row or column by a non zero number.
denoted by Ri → kRi . The corresponding column operation is denoted by Ci → kCi
[3] The addition to the elements of any row or column, the corresponding elements of any other row or column are multiplied by any non zero number.
denoted by Ri → Ri + kRj . The corresponding column operation is denoted by Ci → Ci + kCj .
Elementary transformations are operations done on the rows and columns of matrices to change their shape so that the computations become easier. It is also used to discover the inverse of a matrix, the determinants of a matrix, and to solve a system of linear equations. A square matrix is always an elementary matrix.
Invertible Matrices
Suppose a square matrix A of order m, and if there exists another square matrix B of the same order m, such that AB = BA = I, then B is called the inverse matrix of A, and it is denoted by A-1. Also, matrix A is said to be an invertible matrix here.
Note:-
[1] A rectangular matrix does not possess inverse matrix, since for products BA and AB to be defined and to be equal, it is necessary that matrices A and B should be square matrices of the same order.
[2] If B is the inverse of A, then A is also the inverse of B.
Theorem 4: If A and B are invertible matrices of the same order,
then (AB)–1 = B–1 A–1
Proof : From the definition of inverse of a matrix,
we have (AB) (AB)–1 = I
or A–1 (AB) (AB)–1 =A–1I (Pre multiplying both sides by A–1)
or (A–1A) B (AB)–1 =A–1 (Since A–1 I = A–1)
or IB (AB) –1 =A–1 or B (AB) –1 =A–1
or B–1 B (AB) –1 =B–1 A–1
or I (AB) –1 =B–1 A–1
Hence (AB) –1 =B–1 A–1
Example 1:
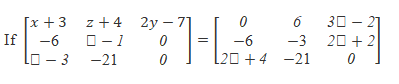
, then find the value of a, b, c, x, y, and z.
Solution:
It is given that, the two matrices are equal. Therefore, the corresponding elements present in matrices should be equal to each other. By comparing the corresponding elements in the matrices, we get:
x+3 = 0. ⇒ x = -3
z +4 = 6 ⇒ z = 6-4
⇒ z = 2
2y-7 = 3y-2 ⇒3y-2y =-7+2
⇒y = -5
a-1 = -3
⇒a = -3+1
⇒a=-2
2c+2 = 0
⇒2c = -2
⇒ c = -1
b-3 = 2b+4
⇒2b-b = -3-4
⇒ b = -7
Therefore, the values of the variables are:
a = -2
b = -7
c = -1
x = -3
y = -5
z = 2
Example 2:
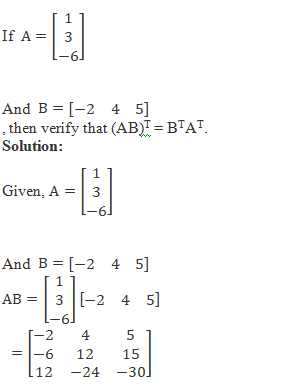
Now, we need to calculate the transpose of AB.
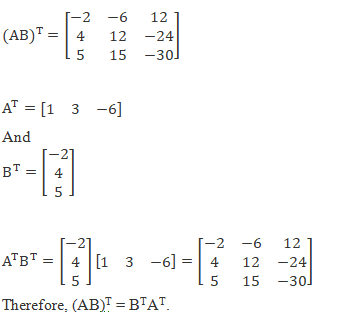
Hence verified.

 KRISHNA PUBLICATIONS
KRISHNA PUBLICATIONS
