1. Cartesian product and different types of relations
Lorem Ipsum is simply dummy text of the printing and typesetting industry. Lorem Ipsum has been the industry's standard dummy text ever since the 1500s, when an unknown printer took a galley of type and scrambled it to make a type specimen book. It has survived not only five centuries, but also the leap into electronic typesetting, remaining essentially unchanged. It was popularised in the 1960s with the release of Letraset sheets containing Lorem Ipsum passages, and more recently with desktop publishing software like Aldus PageMaker including versions of Lorem Ipsum.
1. Cartesian product and different types of relations
sudhanshu@kaysonseducation.co.in
Sagar Daksh Mathmatics Book > Unit I: Relations and Functions > 1. Relations and Functions > Types of relations: reflexive, symmetric, transitive and equivalence relations
Notes added through Teacher.
1. Cartesian product and different types of relations
- Books Name
- srverma@yahoo.com Chemistry Book
- Publication
- srverma@yahoo.com
- Course
- CBSE Class 12
- Subject
- Mathmatics
ddd
1. Cartesian product and different types of relations
- Books Name
- SonikaAnandAcademy Mathmatics Book
- Publication
- SonikaAnandAcademy
- Course
- CBSE Class 12
- Subject
- Mathmatics
Equivalence Relation
A function is an equivalence relation if a function satisfies the three conditions
1 the function must be reflexive
2 a function must be symmetric
3 function is transitive
1. Cartesian product and different types of relations
- Books Name
- ABCD CLASSES Mathmatics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 12
- Subject
- Mathmatics
Chapter-1
Relations and Functions
Cartesian Product , Relations and Types of Relations
Cartesian Product
Suppose there are two non-empty sets A and B.
Then the Cartesian product of A and B is the set of all ordered pairs of elements from A and B.
i.e., A × B = {(a , b) : a ∊ A, b ∊ B}
Example: Let A = {a1,a2,a3,a4} and B = {b1,b2}
Then, The Cartesian product of A and B will be;
A × B = {(a1,b1), (a2,b1),( a3,b1),( a4,b1).( a1,b2),( a2,b2),( a3,b2),( a4,b2 )}
Example: Let us say, A = {1,2} and B = { a,b,c}
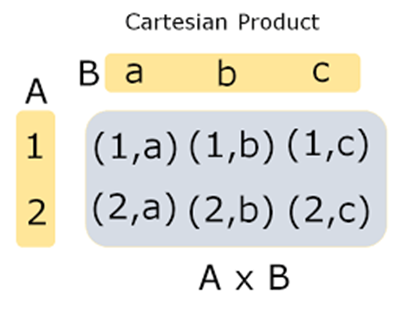
Therefore, A × B = {(1,a),(1,b),(1,c),(2,a),(2,b),(2,c)}.
This set has 8 ordered pairs. We can also represent it as in a tabular form.
Note: Two ordered pair X and Y are equal, if and only if the corresponding first elements and second elements are equal.
Example: Suppose, A = {cow, horse} B = {egg, juice}
then, A×B = {(cow, egg), (horse, juice), (cow, juice), (horse, egg)}
If either of the two sets is a null set, i.e., either A = Φ or B = Φ, then, A × B = Φ i.e., A × B will also be a null set
Number of Ordered Pairs
For two non-empty sets, A and B. If the number of elements of A is p
i.e., n(A) = p & that of B is q
i.e., n(B) = q,
then the number of ordered pairs in Cartesian product will be n(A × B) = n(A) × n(B) = pq.
Properties
- The Cartesian Product is non-commutative: A × B ≠ B × A.
- The cardinality of the Cartesian Product is defined as the number of elements in A × B and is equal to the product of cardinality of both sets:
|A × B| = |A| * |B|
- A × B = ∅, if either A = ∅ or B = ∅
- If (x,y) = (a,b) ,then x=a , y=b
- A×B=B×A, if only A=B
- The Cartesian product is associative:
(A×B)×C=A×(B×C). It means the Cartesian product of the three-set is the same, i.e., it doesn’t depend upon which bracket is multiplied first as the final result will be the same.
- Distributive property over a set intersection:
A×(B∩C)=(A×B)∩(A×C)
- Distributive property over set union:
A×(B∪C)=(A×B)∪(A×C)
- If A⊆B, then A×C⊆B×C for any set C.
- AxBxC = {(a,b,c) : aÎA, bÎ B ,cÎ C}
Here (a,b,c) is called ordered triplet.
Relation
Relation is association between two well-defined objects.
Relations can be represented in different forms such as arrow representation, algebraic form, set-builder form, graphically, roster form, and tabular form.
Definition
Let A and B be two non empty sets.
Then R : A ® B is said to be a relation if R Í AxB .
The element of A (first element) of AxB in the relation is called Domain or Pre-image of relation R.
The element of B (second element) of AxB in the relation is called Range or image of relation R.
The whole B set of AxB in the relation is called Codomain of relation R.
Range Í Codomain
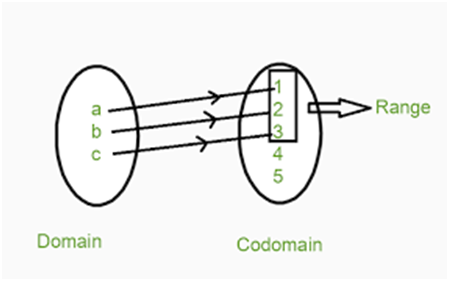
Example : Define a relation R from A to A = {1, 2, 3, 4, 5, 6} as R = {(x, y) : y = x + 1}. Determine the domain, codomain and range of R.
Answer: We can see that A = {1, 2, 3, 4, 5, 6} is the domain and codomain of R.
To determine the range, we determine the values of y for each value of x, that is, when x = 1, 2, 3, 4, 5, 6
-
- x = 1, y = 1 + 1 = 2;
- x = 2, y = 2 + 1 = 3;
- x = 3, y = 3 + 1 = 4;
- x = 4, y = 4 + 1 = 5;
- x = 5, y = 5 + 1 = 6;
- x = 6, y = 6 + 1 = 7.
Since 7 does not belong to A and the relation R is defined on A, hence, x = 6 has no image in A.
Therefore range of R = {2, 3, 4, 5, 6}
Answer: Domain = Codomain = {1, 2, 3, 4, 5, 6}, Range = {2, 3, 4, 5, 6}
Example :
Let A = {1, 2, 3, … , 14}. Define a relation R from A to A by R = {(x, y): 3x – y = 0, where x, y ∈ A}. Write down its domain, codomain and range.
ANSWER:
The relation R from A to A is given as
R = {(x, y): 3x – y = 0, where x, y ∈ A}
i.e., R = {(x, y): 3x = y, where x, y ∈ A}
∴R = {(1, 3), (2, 6), (3, 9), (4, 12)}
The domain of R is the set of all first elements of the ordered pairs in the relation.
∴Domain of R = {1, 2, 3, 4}
The whole set A is the codomainof the relation R.
∴Codomain of R = A = {1, 2, 3, …, 14}
The range of R is the set of all second elements of the ordered pairs in the relation.
∴Range of R = {3, 6, 9, 12}
Example:
The given figure shows a relationship between the sets P and Q. write this relation
(i) in set-builder form (ii) in roster form.
What is its domain and range?
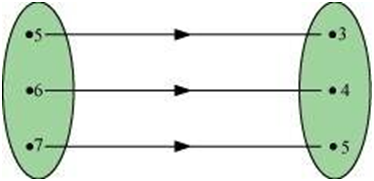
ANSWER:
According to the given figure, P = {5, 6, 7}, Q = {3, 4, 5}
(i) R = {(x, y): y = x – 2; x ∈ P} or R = {(x, y): y = x – 2 for x = 5, 6, 7}
(ii) R = {(5, 3), (6, 4), (7, 5)}
Domain of R = {5, 6, 7}
Range of R = {3, 4, 5}
Example:
Let R be the relation on Z defined by R = {(a, b): a, b ∈ Z, a – b is an integer}. Find the domain and range of R.
ANSWER:
R = {(a, b): a, b ∈ Z, a – b is an integer}
It is known that the difference between any two integers is always an integer.
∴Domain of R = Z
Range of R = Z
1. Cartesian product and different types of relations
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Chapter-1
Relations and Functions
Cartesian Product , Relations and Types of Relations
Cartesian Product
Suppose there are two non-empty sets A and B.
Then the Cartesian product of A and B is the set of all ordered pairs of elements from A and B.
i.e., A × B = {(a , b) : a ∊ A, b ∊ B}
Example: Let A = {a1,a2,a3,a4} and B = {b1,b2}
Then, The Cartesian product of A and B will be;
A × B = {(a1,b1), (a2,b1),( a3,b1),( a4,b1).( a1,b2),( a2,b2),( a3,b2),( a4,b2 )}
Example: Let us say, A = {1,2} and B = { a,b,c}

Therefore, A × B = {(1,a),(1,b),(1,c),(2,a),(2,b),(2,c)}.
This set has 8 ordered pairs. We can also represent it as in a tabular form.
Note: Two ordered pair X and Y are equal, if and only if the corresponding first elements and second elements are equal.
Example: Suppose, A = {cow, horse} B = {egg, juice}
then, A×B = {(cow, egg), (horse, juice), (cow, juice), (horse, egg)}
If either of the two sets is a null set, i.e., either A = Φ or B = Φ, then, A × B = Φ i.e., A × B will also be a null set
Number of Ordered Pairs
For two non-empty sets, A and B. If the number of elements of A is p
i.e., n(A) = p & that of B is q
i.e., n(B) = q,
then the number of ordered pairs in Cartesian product will be n(A × B) = n(A) × n(B) = pq.
Properties
- The Cartesian Product is non-commutative: A × B ≠ B × A.
- The cardinality of the Cartesian Product is defined as the number of elements in A × B and is equal to the product of cardinality of both sets:
|A × B| = |A| * |B|
- A × B = ∅, if either A = ∅ or B = ∅
- If (x,y) = (a,b) ,then x=a , y=b
- A×B=B×A, if only A=B
- The Cartesian product is associative:
(A×B)×C=A×(B×C). It means the Cartesian product of the three-set is the same, i.e., it doesn’t depend upon which bracket is multiplied first as the final result will be the same.
- Distributive property over a set intersection:
A×(B∩C)=(A×B)∩(A×C)
- Distributive property over set union:
A×(B∪C)=(A×B)∪(A×C)
- If A⊆B, then A×C⊆B×C for any set C.
- AxBxC = {(a,b,c) : aÎA, bÎ B ,cÎ C}
Here (a,b,c) is called ordered triplet.
Relation
Relation is association between two well-defined objects.
Relation in real life give us the link between any two objects or entities. In our daily life, we come across many patterns and links that characterize relations such as a relation of a father and a son, brother and sister, etc.
Relations can be represented in different forms such as arrow representation, algebraic form, set-builder form, graphically, roster form, and tabular form.
Definition
Let A and B be two non empty sets.
Then R : A ® B is said to be a relation if R Í AxB .
The element of A (first element) of AxB in the relation is called Domain or Pre-image of relation R.
The element of B (second element) of AxB in the relation is called Range or image of relation R.
The whole B set of AxB in the relation is called Codomain of relation R.
Range Í Co-domain

Example : Define a relation R from A to A = {1, 2, 3, 4, 5, 6} as R = {(x, y) : y = x + 1}. Determine the domain, codomain and range of R.
Answer: We can see that A = {1, 2, 3, 4, 5, 6} is the domain and codomain of R.
To determine the range, we determine the values of y for each value of x, that is, when x = 1, 2, 3, 4, 5, 6
-
- x = 1, y = 1 + 1 = 2;
- x = 2, y = 2 + 1 = 3;
- x = 3, y = 3 + 1 = 4;
- x = 4, y = 4 + 1 = 5;
- x = 5, y = 5 + 1 = 6;
- x = 6, y = 6 + 1 = 7.
Since 7 does not belong to A and the relation R is defined on A, hence, x = 6 has no image in A.
Therefore range of R = {2, 3, 4, 5, 6}
Answer: Domain = Codomain = {1, 2, 3, 4, 5, 6}, Range = {2, 3, 4, 5, 6}
Example :
Let A = {1, 2, 3, … , 14}. Define a relation R from A to A by R = {(x, y): 3x – y = 0, where x, y ∈ A}. Write down its domain, codomain and range.
ANSWER:
The relation R from A to A is given as
R = {(x, y): 3x – y = 0, where x, y ∈ A}
i.e., R = {(x, y): 3x = y, where x, y ∈ A}
∴R = {(1, 3), (2, 6), (3, 9), (4, 12)}
The domain of R is the set of all first elements of the ordered pairs in the relation.
∴Domain of R = {1, 2, 3, 4}
The whole set A is the codomainof the relation R.
∴Codomain of R = A = {1, 2, 3, …, 14}
The range of R is the set of all second elements of the ordered pairs in the relation.
∴Range of R = {3, 6, 9, 12}
Example :
The given figure shows a relationship between the sets P and Q. write this relation
(i) in set-builder form (ii) in roster form.
What is its domain and range?

ANSWER:
According to the given figure, P = {5, 6, 7}, Q = {3, 4, 5}
(i) R = {(x, y): y = x – 2; x ∈ P} or R = {(x, y): y = x – 2 for x = 5, 6, 7}
(ii) R = {(5, 3), (6, 4), (7, 5)}
Domain of R = {5, 6, 7}
Range of R = {3, 4, 5}
Example:
Let R be the relation on Z defined by R = {(a, b): a, b ∈ Z, a – b is an integer}. Find the domain and range of R.
ANSWER:
R = {(a, b): a, b ∈ Z, a – b is an integer}
It is known that the difference between any two integers is always an integer.
∴Domain of R = Z
Range of R = Z
1. Basic concepts , Domain and Range ,Principal Branch
It is a long established fact that a reader will be distracted by the readable content of a page when looking at its layout. The point of using Lorem Ipsum is that it has a more-or-less normal distribution of letters, as opposed to using 'Content here, content here', making it look like readable English. Many desktop publishing packages and web page editors now use Lorem Ipsum as their default model text, and a search for 'lorem ipsum' will uncover many web sites still in their infancy. Various versions have evolved over the years, sometimes by accident, sometimes on purpose (injected humour and the like).
1. Basic concepts , Domain and Range ,Principal Branch
sudhanshu@kaysonseducation.co
Create professional doodle videos in minutes. No tech or design skills needed.
© Bryxen, Inc. All rights reserved.
Third-party components are the property of their respective owners.
1. Basic concepts , Domain and Range ,Principal Branch
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Chapter-2
Inverse Trigonometric functions
Basic concepts , Domain and Range ,Principal Branch:
Let y = sinx => x = sin-1y
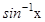 should not be confused with
should not be confused with 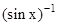 . In fact
. In fact 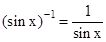
- i.e.,
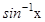 ¹
¹ 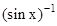
- And similarly for other trigonometric functions.
- The value of an inverse trigonometric functions which lies in its principal value branch is called the principal value of that inverse trigonometric functions.
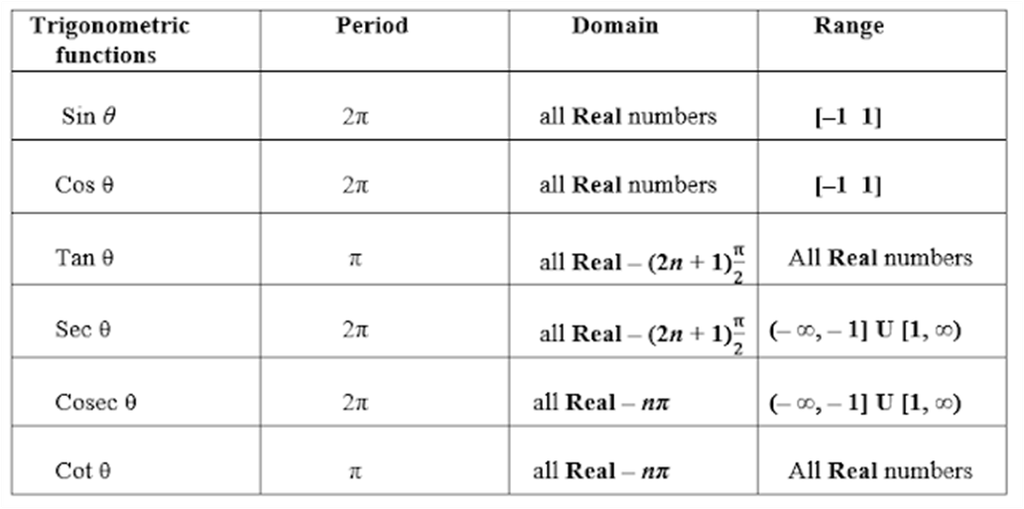
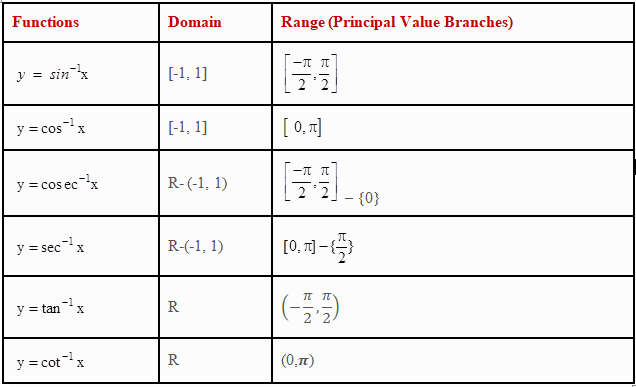
- The domains and ranges (principal value branches) of inverse trigonometric functions are given in the following table:
- The functions
sin−1x & tan−1x
are increasing functions in their domain.
- The functions
cos−1x & cot−1x
are decreasing functions in over domain.
For suitable values of domain, we have
• ![]()
• ![]()
2. Reflexive, symmetric, transitive and equivalence and equivalence classes
PHP (Hypertext Preprocessor)
PHP is an open-source, interpreted, and object-oriented scripting language that can be executed at the server-side. PHP is well suited for web development. Therefore, it is used to develop web applications (an application that executes on the server and generates the dynamic page.).
More About PHP
PHP was developed by Rasmus Lerdorf in 1995 and is later being developed as an open-source. PHP group now manages the implementation of PHP.
PHP has many syntaxes similar to C, Java, and Perl, and has many unique features and specific functions.
PHP page is a file with a .php extension can contain a combination of HTML Tags and PHP scripts.
PHP recursive acronym for PHP (Hypertext Preprocessor): HyperText means, text containing all sorts of web markups, PreProcessor means all of the HyperText is processed first and then the result is sent as pure HTML to the web browser. A client cannot see the PHP source code because it is preprocessed and interpreted.
PHP is Server-side scripting language: Server-side scripting means that the PHP code is processed on the web server rather than the client machine.
PHP supports many databases (MySQL and PHP combination is widely used).
PHP is an open-source scripting language.
PHP is free to download and use.
Popular Online Web Applications Developed in PHP / Frameworks of PHP.
|
CMS Made in PHP |
FrameWorks in PHP |
WordPress |
Laravel |
Joomla |
CodeIgniter |
Drupal |
Symfony |
SilverStripe |
CakePHP |
PHP Fusion |
Yii |
PHP Features
Execution of PHP
To run PHP code, you need the following three software on your local machine:
- Web Server (e.g., Apache)
- PHP (Interpreter)
- MySQL Databases (optional)
I will suggest you to install AMP (Apache, MySQL, PHP) software stack. It is available for all operating systems. There are many AMP options available in the market that are given below:
- WAMP for Windows
- LAMP for Linux
- MAMP for Mac
- XAMPP (Cross, Apache, MySQL, PHP, Perl) for Cross Platform: It includes some other components too such as FileZilla, OpenSSL, Webalizer, Mercury Mail, etc.
How PHP Works
There are 80% websites are developed using php, some of the best websites are:
|
|
|
|
Wikipedia |
|
|
Tumblr |
|
|
Yahoo |
|
|
Flickr |
|
|
Friendster |
|
|
Istockphoto |
|
|
sourceforge.net |
2. Reflexive, symmetric, transitive and equivalence and equivalence classes
- Books Name
- Max Foundation Mathmatics Book
- Publication
- Max Publication
- Course
- CBSE Class 12
- Subject
- Mathmatics
Chapter no. 1 : Electric charges and Field
Topic no. 1.1 Basics of electric charges
Lecture no. 1/3
Lecture Topic: Basics of Electric Charges
Electrostatics : Electro = Charge + Statics = Rest
Electrostatics – The branch of physics tht deals with study of electrostatic force, electric field and electric potential due to stationary charge.
Chapter 01. Electric charges and Field
1.1. Electric charges
1.2. Coulomb’s law in electrostatics
1.3. Electric field and electric dipole
1.4. Electric field lines and gauss’s theorem
Chapter 0 2. Electric Potential and Capacitance
2.1 Electric potential
2.2 Capacitance
2. Reflexive, symmetric, transitive and equivalence and equivalence classes
- Books Name
- SonikaAnandAcademy Mathmatics Book
- Publication
- SonikaAnandAcademy
- Course
- CBSE Class 12
- Subject
- Mathmatics
How we will distinguish between one one and many one function
It is also explained as what is the other name of one one function that is one one function is also named as injective function whereas many one function is also known as surjective function
A function as both one one and onto then it is also known as bijective function
2. Reflexive, symmetric, transitive and equivalence and equivalence classes
- Books Name
- ABCD CLASSES Mathmatics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 12
- Subject
- Mathmatics
Types of Relations
Given below is a list of different types of relations:
- Empty Relation
- Universal Relation
- Identity Relation
- Inverse Relation
- Reflexive Relation
- Symmetric Relation
- Transitive Relation
- Equivalence Relation
1) Empty Relation - A relation is an empty relation if it has no elements, that is, no element of set A is mapped or linked to any element of A. It is denoted by R = ∅.
For example, if set A = {1, 2, 3} then, one of the void relations can be R = {x, y} where, |x – y| = 8. For empty relation,
R = φ ⊂ A × A
2) Universal Relation - A relation R in a set A is a universal relation if each element of A is related to every element of A, i.e., R = A × A. It is called the full relation.
Consider set A = {a, b, c}. Now one of the universal relations will be R = {x, y} where, |x – y| ≥ 0. For universal relation,
R = A × A
3) Identity Relation - A relation R on A is said to be an identity relation if each element of A is related to itself, that is, R = {(a, a) : for all a ∈ A}
For example, in a set A = {a, b, c}, the identity relation will be I = {a, a}, {b, b}, {c, c}. For identity relation,
I = {(a, a), a ∈ A}
4) Inverse Relation - Define R to be a relation from set P to set Q i.e., R ∈ P × Q. The relation R-1 is said to be an Inverse relation if R-1 from set Q to P is denoted by R-1 = {(q, p): (p, q) ∈ R}.
For example if set A = {(a, b), (c, d)}, then inverse relation will be R-1 = {(b, a), (d, c)}. So, for an inverse relation,
R-1 = {(b, a): (a, b) ∈ R}
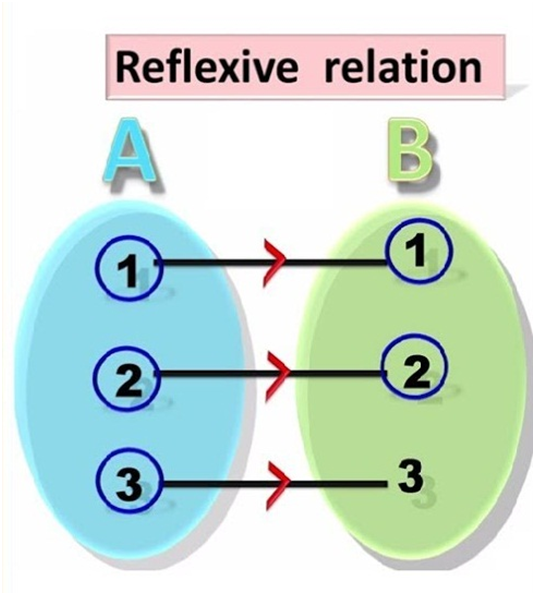
5) Reflexive Relation - A binary relation R defined on a set A is said to be reflexive if, for every element a ∈ A, we have aRa, that is, (a, a) ∈ R.
For example, consider a set A = {1, 2,}. Now an example of reflexive relation will be R = {(1, 1), (2, 2), (1, 2), (2, 1)}. The reflexive relation is given by-
(a, a) ∈ R

6) Symmetric Relation - A binary relation R defined on a set A is said to be symmetric if and only if, for elements a, b ∈ A, we have aRb, that is, (a, b) ∈ R, then we must have bRa, that is, (b, a) ∈ R.
An example of symmetric relation will be R = {(1, 2), (2, 1)} for a set A = {1, 2}. So, for a symmetric relation,
aRb ⇒ bRa, ∀ a, b ∈ A
Example: For the set P={a,b}, the relation R={(a,b),(b,a)} is called symmetric relation, where a,b∈P.
7) Transitive Relation - A relation R is transitive if and only if (a, b) ∈ R and (b, c) ∈ R ⇒ (a, c) ∈ R for a, b, c ∈ A
Example: For the set A ={a,b,c}, the relation R={(a,b),(b,c),(a,c)} is called transitive relation, where a,b,c∈ A.
8) Equivalence Relation - A relation R defined on a set A is said to be an equivalence relation if and only if it is reflexive, symmetric and transitive.
Conditions:
1. If the relation (R) is reflexive, then all the elements of set A are mapped with itself, such that for every x∈ A , then (x,x)∈R.
2. The relation (R) is symmetric on set A, if (x,y)∈R, then (y,x)∈R, such that a,b∈ A.
3. The relation R on set A, if (x,y)∈R and (y,z)∈R, then (x,z)∈R, for all a,b,c∈ A is called transitive relation.
Example: Let A = {1, 2, 3, 4} and R = {(1, 1), (1, 3), (2, 2), (2, 4), (3, 1), (3, 3), (4, 2), (4, 4)}.
Show that R is an Equivalence Relation.
Solution:
Reflexive: Relation R is reflexive as (1, 1), (2, 2), (3, 3) and (4, 4) ∈ R.
Symmetric: Relation R is symmetric because whenever (a, b) ∈ R, (b, a) also belongs to R.
Example: (2, 4) ∈ R ⟹ (4, 2) ∈ R.
Transitive: Relation R is transitive because whenever (a, b) and (b, c) belongs to R, (a, c) also belongs to R.
Example: (3, 1) ∈ R and (1, 3) ∈ R ⟹ (3, 3) ∈ R.
So, as R is reflexive, symmetric and transitive, hence, R is an Equivalence Relation.
Question 1:
Let us assume that F is a relation on the set R real numbers defined by x F y if and only if x-y is an integer. Prove that F is an equivalence relation on R.
Solution:
Reflexive: Let x belongs to R,then x – x = 0 which is an integer.
Therefore x F x.
So , F is reflexive.
Symmetric: Let x and y belongs to R and x F y.
- x – y is an integer.
- Thus, y – x = – ( x – y), y – x is also an integer.
- Therefore yFx.
So , F is Symmetric.
Transitive: Let x and y belongs to R, xFy and yFz.
- x-y and y-z are integers.
- ( x – y ) + ( y – z ) = x – z is also an integer.
- So that xFz.
So , F is Transitive.
Thus, R is an equivalence relation on R.
Question 2:
Show that the relation R is an equivalence relation in the set A = { 1, 2, 3, 4, 5 } given by the relation R = { (a, b):|a-b| is even }.
Solution:
R = { (a, b):|a-b| is even }. Where a, b belongs to A
Reflexive Property :
Let a is belongs to A.
|a – a| = | 0 |=0
- 0 is always even.
- Thus, |a-a| is even
- Therefore, (a, a) belongs to R
Hence R is Reflexive
Symmetric Property :
Let a, b belongs to A
|a – b| = |b – a|
Let a R b
We know that |a – b| = |-(b – a)|= |b – a|
- |a – b| is even,
- |b – a| is also even.
Therefore, if (a, b) ∈ R, then (b, a) belongs to R
Hence R is symmetric.
Transitive Property :
Let a, b, c belongs to A
Let a R b and b R c
- |b-c| is even and (b-c) is even
Since , If |a-b| is even, then (a-b) is even.
Sum of even number is also even
- a-b+ b-c is even
- a – c is also even
Then, a R c
So,
|a – b| and |b – c| is even , then |a-c| is even.
Therefore, if (a, b) ∈ R and (b, c) ∈ R, then (a, c) also belongs to R
Hence R is transitive.
Therefore R is an equivalence relation.
Equivalence Class
Let R be an equivalence relation on set A. For each a∈A, we denote the equivalence class of a as [a] defined as:
[a]={x ∈A ∣ x R a}
Example:
Define a relation ∼ on Z by
a∼b⇔a mod 4=b mod 4
Find the equivalence classes of ∼
Answer
Two integers will be related by ∼ if they have the same remainder after dividing
by 4. The possible remainders are 0, 1, 2, 3
[0]={...,−12,−8,−4,0,4,8,12,...}
[1]={...,−11,−7,−3,1,5,9,13,...}
[2]={...,−10,−6,−2,2,6,10,14,...}
[3]={...,−9,−5,−1,3,7,11,15,...}
Example:
Let S=P({1,2,3})={∅,{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}}.
For convenience, label
S0=∅,S1={1},S2={2},S3={3},S4={1,2},S5={1,3},S6={2,3},S7={1,2,3}.
Define this equivalence relation ∼ on S by
Si∼Sj⇔|Si|=|Sj|
Find the equivalence classes of ∼.
Answer
Two sets will be related by ∼ if they have the same number of elements.
[S0]={S0}
[S2]={S1,S2,S3}
[S4]={S4,S5,S6}
[S7]={S7}
Example:
Consider set S={a,b,c,d} with this partition: {{a,b},{c},{d}}.
Find the ordered pairs for the relation R, induced by the partition.
Proof
R={(a,a),(a,b),(b,a),(b,b),(c,c),(d,d)}
Question :
Let R be a relation from N to N defined by R = {(a, b): a, b ∈ N and a = b2}. Are the following true?
(i) (a, a) ∈ R, for all a ∈ N
(ii) (a, b) ∈ R, implies (b, a) ∈ R
(iii) (a, b) ∈ R, (b, c) ∈ R implies (a, c) ∈ R.
Justify your answer in each case.
ANSWER:
R = {(a, b): a, b ∈ N and a = b2}
(i) It can be seen that 2 ∈ N;however, 2 ≠ 22 = 4.
Therefore, the statement “(a, a) ∈ R, for all a ∈ N” is not true.
(ii) It can be seen that (9, 3) ∈ N because 9, 3 ∈ N and 9 = 32.
Now, 3 ≠ 92 = 81; therefore, (3, 9) ∉ N
Therefore, the statement “(a, b) ∈ R, implies (b, a) ∈ R” is not true.
(iii) It can be seen that (16, 4) ∈ R, (4, 2) ∈ R because 16, 4, 2 ∈ N and 16 = 42 and 4 = 22.
Now, 16 ≠ 22 = 4; therefore, (16, 2) ∉ N
Therefore, the statement “(a, b) ∈ R, (b, c) ∈ R implies (a, c) ∈ R” is not true.
Example 5: Check whether the relation R defined in the set {1, 2, 3, 4, 5, 6} as R = {(a, b): b = a + 1} is reflexive, symmetric or transitive.
Solution:
Given R = {(a, b): b = a + 1}
Now for this relation we have to check whether it is reflexive, transitive and symmetric Reflexivity:
Let a be an arbitrary element of R.
Then, a = a + 1 cannot be true for all a ∈ A.
⇒ (a, a) ∉ R
So, R is not reflexive on A.
Symmetry:
Let (a, b) ∈ R
⇒ b = a + 1
⇒ −a = −b + 1
⇒ a = b − 1
Thus, (b, a) ∉ R
So, R is not symmetric on A.
Transitivity:
Let (1, 2) and (2, 3) ∈ R
⇒ 2 = 1 + 1 and 3
2 + 1 is true.
But 3 ≠ 1+1
⇒ (1, 3) ∉ R
So, R is not transitive on A.
Example 6: Check whether the relation R on R defined as R = {(a, b): a ≤ b3} is reflexive, symmetric or transitive.
Solution:
Given R = {(a, b): a ≤ b3}
It is observed that (1/2, 1/2) in R as 1/2 > (1/2)3 = 1/8
∴ R is not reflexive.
Now,
(1, 2) ∈ R (as 1 < 23 = 8)
But,
(2, 1) ∉ R (as 2 > 13 = 1)
∴ R is not symmetric.
We have (3, 3/2), (3/2, 6/5) in “R as” 3 < (3/2)3 and 3/2 < (6/5)3
But (3, 6/5) ∉ R as 3 > (6/5)3
∴ R is not transitive.
Hence, R is neither reflexive, nor symmetric, nor transitive.
Example 7: Prove that every identity relation on a set is reflexive, but the converse is not necessarily true.
Solution:
Let A be a set.
Then, Identity relation IA=IA is reflexive, since (a, a) ∈ A ∀a
The converse of it need not be necessarily true.
Consider the set A = {1, 2, 3}
Here,
Relation R = {(1, 1), (2, 2) , (3, 3), (2, 1), (1, 3)} is reflexive on A.
However, R is not an identity relation.
Example 8: If A = {1, 2, 3, 4} define relations on A which have properties of being
(i) Reflexive, transitive but not symmetric
(ii) Symmetric but neither reflexive nor transitive.
(iii) Reflexive, symmetric and transitive.
Solution:
(i) The relation on A having properties of being reflexive, transitive, but not symmetric is
R = {(1, 1), (2, 2), (3, 3), (4, 4), (2, 1)}
Relation R satisfies reflexivity and transitivity.
⇒ (1, 1), (2, 2), (3, 3) ∈ R
And (1, 1), (2, 1) ∈ R ⇒ (1, 1) ∈ R
However, (2, 1) ∈ R, but (1, 2) ∉ R
(ii) The relation on A having properties of being reflexive, transitive, but not symmetric is
R = {(1, 1), (2, 2), (3, 3), (4, 4), (2, 1)}
Relation R satisfies reflexivity and transitivity.
⇒ (1, 1), (2, 2), (3, 3) ∈ R
And (1, 1), (2, 1) ∈ R ⇒ (1, 1) ∈ R
However, (2, 1) ∈ R, but (1, 2) ∉ R
(iii) The relation on A having properties of being symmetric, reflexive and transitive is
R = {(1, 1), (2, 2), (3, 3), (4, 4), (1, 2), (2, 1)}
The relation R is an equivalence relation on A.
Example 9:. Show that the relation R defined by R = {(a, b): a – b is divisible by 3; a, b ∈ Z} is an equivalence relation.
Solution:
Given R = {(a, b): a – b is divisible by 3; a, b ∈ Z} is a relation
To prove equivalence relation it is necessary that the given relation should be reflexive, symmetric and transitive.
Let us check these properties on R.
Reflexivity:
Let a be an arbitrary element of R.
Then, a – a = 0 = 0 × 3
⇒ a − a is divisible by 3
⇒ (a, a) ∈ R for all a ∈ Z
So, R is reflexive on Z.
Symmetry:
Let (a, b) ∈ R
⇒ a − b is divisible by 3
⇒ a − b = 3p for some p ∈ Z
⇒ b − a = 3 (−p)
Here, −p ∈ Z
⇒ b − a is divisible by 3
⇒ (b, a) ∈ R for all a, b ∈ Z
So, R is symmetric on Z.
Transitivity:
Let (a, b) and (b, c) ∈ R
⇒ a − b and b − c are divisible by 3
⇒ a – b = 3p for some p ∈ Z
And b − c = 3q for some q ∈ Z
Adding the above two equations, we get
a − b + b – c = 3p + 3q
⇒ a − c = 3 (p + q)
Here, p + q ∈ Z
⇒ a − c is divisible by 3
⇒ (a, c) ∈ R for all a, c ∈ Z
So, R is transitive on Z.
Therefore R is reflexive, symmetric and transitive.
Hence, R is an equivalence relation on Z.
Example 10: Show that the relation R on the set Z of integers, given by
R = {(a, b): 2 divides a – b}, is an equivalence relation.
Solution:
Given R = {(a, b): 2 divides a – b} is a relation defined on Z.
To prove equivalence relation it is necessary that the given relation should be reflexive, symmetric and transitive.
Let us check these properties on R.
Reflexivity:
Let a be an arbitrary element of the set Z.
Then, a ∈ R
⇒ a − a = 0 = 0 × 2
⇒ 2 divides a − a
⇒ (a, a) ∈ R for all a ∈ Z
So, R is reflexive on Z.
Symmetry:
Let (a, b) ∈ R
⇒ 2 divides a − b
⇒ (a-b)/2 = p for some p ∈ Z
⇒ (b-a)/2 = – p
Here, −p ∈ Z
⇒ 2 divides b − a
⇒ (b, a) ∈ R for all a, b ∈ Z
So, R is symmetric on Z
Transitivity:
Let (a, b) and (b, c) ∈ R
⇒ 2 divides a−b and 2 divides b−c
⇒ (a-b)/2 = p and (b-c)/2 = q for some p, q ∈ Z
Adding the above two equations, we get
(a – b)/2 + (b – c)/2 = p + q
⇒ (a – c)/2 = p +q
Here, p+ q ∈ Z
⇒ 2 divides a − c
⇒ (a, c) ∈ R for all a, c ∈ Z
So, R is transitive on Z.
Therefore R is reflexive, symmetric and transitive.
Hence, R is an equivalence relation on Z.
Example 11:. Prove that the relation R on Z defined by (a, b) ∈ R ⇔ a − b is divisible by 5 is an equivalence relation on Z.
Solution:
Given relation R on Z defined by (a, b) ∈ R ⇔ a − b is divisible by 5
To prove equivalence relation it is necessary that the given relation should be reflexive, symmetric and transitive.
Let us check these properties on R.
Reflexivity:
Let a be an arbitrary element of R. Then,
⇒ a − a = 0 = 0 × 5
⇒ a − a is divisible by 5
⇒ (a, a) ∈ R for all a ∈ Z
So, R is reflexive on Z.
Symmetry:
Let (a, b) ∈ R
⇒ a − b is divisible by 5
⇒ a − b = 5p for some p ∈ Z
⇒ b − a = 5 (−p)
Here, −p ∈ Z [Since p ∈ Z]
⇒ b − a is divisible by 5
⇒ (b, a) ∈ R for all a, b ∈ Z
So, R is symmetric on Z.
Transitivity:
Let (a, b) and (b, c) ∈ R
⇒ a − b is divisible by 5
⇒ a − b = 5p for some Z
Also, b − c is divisible by 5
⇒ b − c = 5q for some Z
Adding the above two equations, we get
a −b + b − c = 5p + 5q
⇒ a − c = 5 ( p + q )
⇒ a − c is divisible by 5
Here, p + q ∈ Z
⇒ (a, c) ∈ R for all a, c ∈ Z
So, R is transitive on Z.
Therefore R is reflexive, symmetric and transitive.
Hence, R is an equivalence relation on Z.
Example 12:. Let n be a fixed positive integer. Define a relation R on Z as follows:
(a, b) ∈ R ⇔ a − b is divisible by n.
Show that R is an equivalence relation on Z.
Solution:
Given (a, b) ∈ R ⇔ a − b is divisible by n is a relation R defined on Z.
To prove equivalence relation it is necessary that the given relation should be reflexive, symmetric and transitive.
Let us check these properties on R.
Reflexivity:
Let a ∈ N
Here, a − a = 0 = 0 × n
⇒ a − a is divisible by n
⇒ (a, a) ∈ R
⇒ (a, a) ∈ R for all a ∈ Z
So, R is reflexive on Z.
Symmetry:
Let (a, b) ∈ R
Here, a − b is divisible by n
⇒ a − b = n p for some p ∈ Z
⇒ b − a = n (−p)
⇒ b − a is divisible by n [ p ∈ Z⇒ − p ∈ Z]
⇒ (b, a) ∈ R
So, R is symmetric on Z.
Transitivity:
Let (a, b) and (b, c) ∈ R
Here, a − b is divisible by n and b − c is divisible by n.
⇒ a − b= n p for some p ∈ Z
And b−c = n q for some q ∈ Z
a – b + b − c = n p + n q
⇒ a − c = n (p + q)
⇒ (a, c) ∈ R for all a, c ∈ Z
So, R is transitive on Z.
Therefore R is reflexive, symmetric and transitive.
Hence, R is an equivalence relation on Z
2. Reflexive, symmetric, transitive and equivalence and equivalence classes
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Types of Relations
Given below is a list of different types of relations:
- Empty Relation
- Universal Relation
- Identity Relation
- Inverse Relation
- Reflexive Relation
- Symmetric Relation
- Transitive Relation
- Equivalence Relation
1) Empty Relation - A relation is an empty relation if it has no elements, that is, no element of set A is mapped or linked to any element of A. It is denoted by R = ∅.
For example, if set A = {1, 2, 3} then, one of the void relations can be R = {x, y} where, |x – y| = 8. For empty relation,
R = φ ⊂ A × A
2) Universal Relation - A relation R in a set A is a universal relation if each element of A is related to every element of A, i.e., R = A × A. It is called the full relation.
Consider set A = {a, b, c}. Now one of the universal relations will be R = {x, y} where, |x – y| ≥ 0. For universal relation,
R = A × A
3) Identity Relation - A relation R on A is said to be an identity relation if each element of A is related to itself, that is, R = {(a, a) : for all a ∈ A}
For example, in a set A = {a, b, c}, the identity relation will be I = {a, a}, {b, b}, {c, c}. For identity relation,
I = {(a, a), a ∈ A}
4) Inverse Relation - Define R to be a relation from set P to set Q i.e., R ∈ P × Q. The relation R-1 is said to be an Inverse relation if R-1 from set Q to P is denoted by R-1 = {(q, p): (p, q) ∈ R}.
For example if set A = {(a, b), (c, d)}, then inverse relation will be R-1 = {(b, a), (d, c)}. So, for an inverse relation,
R-1 = {(b, a): (a, b) ∈ R}
5) Reflexive Relation - A binary relation R defined on a set A is said to be reflexive if, for every element a ∈ A, we have aRa, that is, (a, a) ∈ R.
For example, consider a set A = {1, 2,}. Now an example of reflexive relation will be R = {(1, 1), (2, 2), (1, 2), (2, 1)}. The reflexive relation is given by-
(a, a) ∈ R


6) Symmetric Relation - A binary relation R defined on a set A is said to be symmetric if and only if, for elements a, b ∈ A, we have aRb, that is, (a, b) ∈ R, then we must have bRa, that is, (b, a) ∈ R.
An example of symmetric relation will be R = {(1, 2), (2, 1)} for a set A = {1, 2}. So, for a symmetric relation,
aRb ⇒ bRa, ∀ a, b ∈ A
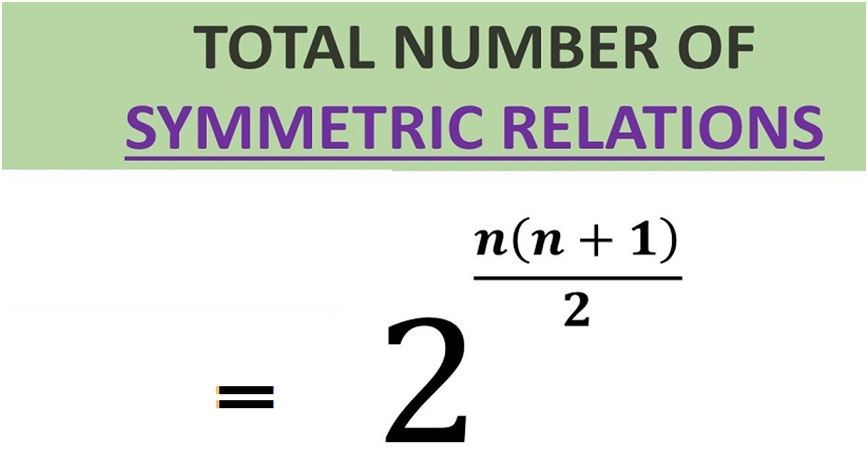
Example: For the set P={a,b}, the relation R={(a,b),(b,a)} is called symmetric relation, where a,b∈P.
7) Transitive Relation - A relation R is transitive if and only if (a, b) ∈ R and (b, c) ∈ R ⇒ (a, c) ∈ R for a, b, c ∈ A
Example: For the set A ={a,b,c}, the relation R={(a,b),(b,c),(a,c)} is called transitive relation, where a,b,c∈ A.
8) Equivalence Relation - A relation R defined on a set A is said to be an equivalence relation if and only if it is reflexive, symmetric and transitive.
Conditions:
1. If the relation (R) is reflexive, then all the elements of set A are mapped with itself, such that for every x∈ A , then (x,x)∈R.
2. The relation (R) is symmetric on set A, if (x,y)∈R, then (y,x)∈R, such that a,b∈ A.
3. The relation R on set A, if (x,y)∈R and (y,z)∈R, then (x,z)∈R, for all a,b,c∈ A is called transitive relation.
Example: Let A = {1, 2, 3, 4} and R = {(1, 1), (1, 3), (2, 2), (2, 4), (3, 1), (3, 3), (4, 2), (4, 4)}.
Show that R is an Equivalence Relation.
Solution:
Reflexive: Relation R is reflexive as (1, 1), (2, 2), (3, 3) and (4, 4) ∈ R.
Symmetric: Relation R is symmetric because whenever (a, b) ∈ R, (b, a) also belongs to R.
Example: (2, 4) ∈ R ⟹ (4, 2) ∈ R.
Transitive: Relation R is transitive because whenever (a, b) and (b, c) belongs to R, (a, c) also belongs to R.
Example: (3, 1) ∈ R and (1, 3) ∈ R ⟹ (3, 3) ∈ R.
So, as R is reflexive, symmetric and transitive, hence, R is an Equivalence Relation.
Question 1:
Let us assume that F is a relation on the set R real numbers defined by x F y if and only if x-y is an integer. Prove that F is an equivalence relation on R.
Solution:
Reflexive: Let x belongs to R,then x – x = 0 which is an integer.
Therefore x F x.
So , F is reflexive.
Symmetric: Let x and y belongs to R and x F y.
- x – y is an integer.
- Thus, y – x = – ( x – y), y – x is also an integer.
- Therefore yFx.
So , F is Symmetric.
Transitive: Let x and y belongs to R, xFy and yFz.
- x-y and y-z are integers.
- ( x – y ) + ( y – z ) = x – z is also an integer.
- So that xFz.
So , F is Transitive.
Thus, R is an equivalence relation on R.
Question 2:
Show that the relation R is an equivalence relation in the set A = { 1, 2, 3, 4, 5 } given by the relation R = { (a, b):|a-b| is even }.
Solution:
R = { (a, b):|a-b| is even }. Where a, b belongs to A
Reflexive Property :
Let a is belongs to A.
|a – a| = | 0 |=0
- 0 is always even.
- Thus, |a-a| is even
- Therefore, (a, a) belongs to R
Hence R is Reflexive
Symmetric Property :
Let a, b belongs to A
|a – b| = |b – a|
Let a R b
We know that |a – b| = |-(b – a)|= |b – a|
- |a – b| is even,
- |b – a| is also even.
Therefore, if (a, b) ∈ R, then (b, a) belongs to R
Hence R is symmetric.
Transitive Property :
Let a, b, c belongs to A
Let a R b and b R c
- |b-c| is even and (b-c) is even
Since , If |a-b| is even, then (a-b) is even.
Sum of even number is also even
- a-b+ b-c is even
- a – c is also even
Then, a R c
So,
|a – b| and |b – c| is even , then |a-c| is even.
Therefore, if (a, b) ∈ R and (b, c) ∈ R, then (a, c) also belongs to R
Hence R is transitive.
Therefore R is an equivalence relation.
Equivalence Class
Let R be an equivalence relation on set A. For each a∈A, we denote the equivalence class of a as [a] defined as:
[a]={x ∈A ∣ x R a}
Example:
Define a relation ∼ on Z by
a∼b⇔a mod 4=b mod 4
Find the equivalence classes of ∼
Answer
Two integers will be related by ∼ if they have the same remainder after dividing
by 4. The possible remainders are 0, 1, 2, 3
[0]={...,−12,−8,−4,0,4,8,12,...}
[1]={...,−11,−7,−3,1,5,9,13,...}
[2]={...,−10,−6,−2,2,6,10,14,...}
[3]={...,−9,−5,−1,3,7,11,15,...}
Example:
Let S=P({1,2,3})={∅,{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}}.
For convenience, label
S0=∅,S1={1},S2={2},S3={3},S4={1,2},S5={1,3},S6={2,3},S7={1,2,3}.
Define this equivalence relation ∼ on S by
Si∼Sj⇔|Si|=|Sj|
Find the equivalence classes of ∼.
Answer
Two sets will be related by ∼ if they have the same number of elements.
[S0]={S0}
[S2]={S1,S2,S3}
[S4]={S4,S5,S6}
[S7]={S7}
Example:
Consider set S={a,b,c,d} with this partition: {{a,b},{c},{d}}.
Find the ordered pairs for the relation R, induced by the partition.
Proof
R={(a,a),(a,b),(b,a),(b,b),(c,c),(d,d)}
Question :
Let R be a relation from N to N defined by R = {(a, b): a, b ∈ N and a = b2}. Are the following true?
(i) (a, a) ∈ R, for all a ∈ N
(ii) (a, b) ∈ R, implies (b, a) ∈ R
(iii) (a, b) ∈ R, (b, c) ∈ R implies (a, c) ∈ R.
Justify your answer in each case.
ANSWER:
R = {(a, b): a, b ∈ N and a = b2}
(i) It can be seen that 2 ∈ N;however, 2 ≠ 22 = 4.
Therefore, the statement “(a, a) ∈ R, for all a ∈ N” is not true.
(ii) It can be seen that (9, 3) ∈ N because 9, 3 ∈ N and 9 = 32.
Now, 3 ≠ 92 = 81; therefore, (3, 9) ∉ N
Therefore, the statement “(a, b) ∈ R, implies (b, a) ∈ R” is not true.
(iii) It can be seen that (16, 4) ∈ R, (4, 2) ∈ R because 16, 4, 2 ∈ N and 16 = 42 and 4 = 22.
Now, 16 ≠ 22 = 4; therefore, (16, 2) ∉ N
Therefore, the statement “(a, b) ∈ R, (b, c) ∈ R implies (a, c) ∈ R” is not true.
Example 5: Check whether the relation R defined in the set {1, 2, 3, 4, 5, 6} as R = {(a, b): b = a + 1} is reflexive, symmetric or transitive.
Solution:
Given R = {(a, b): b = a + 1}
Now for this relation we have to check whether it is reflexive, transitive and symmetric Reflexivity:
Let a be an arbitrary element of R.
Then, a = a + 1 cannot be true for all a ∈ A.
⇒ (a, a) ∉ R
So, R is not reflexive on A.
Symmetry:
Let (a, b) ∈ R
⇒ b = a + 1
⇒ −a = −b + 1
⇒ a = b − 1
Thus, (b, a) ∉ R
So, R is not symmetric on A.
Transitivity:
Let (1, 2) and (2, 3) ∈ R
⇒ 2 = 1 + 1 and 3
2 + 1 is true.
But 3 ≠ 1+1
⇒ (1, 3) ∉ R
So, R is not transitive on A.
Example 6: Check whether the relation R on R defined as R = {(a, b): a ≤ b3} is reflexive, symmetric or transitive.
Solution:
Given R = {(a, b): a ≤ b3}
It is observed that (1/2, 1/2) in R as 1/2 > (1/2)3 = 1/8
∴ R is not reflexive.
Now,
(1, 2) ∈ R (as 1 < 23 = 8)
But,
(2, 1) ∉ R (as 2 > 13 = 1)
∴ R is not symmetric.
We have (3, 3/2), (3/2, 6/5) in “R as” 3 < (3/2)3 and 3/2 < (6/5)3
But (3, 6/5) ∉ R as 3 > (6/5)3
∴ R is not transitive.
Hence, R is neither reflexive, nor symmetric, nor transitive.
Example 7: Prove that every identity relation on a set is reflexive, but the converse is not necessarily true.
Solution:
Let A be a set.
Then, Identity relation IA=IA is reflexive, since (a, a) ∈ A ∀a
The converse of it need not be necessarily true.
Consider the set A = {1, 2, 3}
Here,
Relation R = {(1, 1), (2, 2) , (3, 3), (2, 1), (1, 3)} is reflexive on A.
However, R is not an identity relation.
Example 8: If A = {1, 2, 3, 4} define relations on A which have properties of being
(i) Reflexive, transitive but not symmetric
(ii) Symmetric but neither reflexive nor transitive.
(iii) Reflexive, symmetric and transitive.
Solution:
(i) The relation on A having properties of being reflexive, transitive, but not symmetric is
R = {(1, 1), (2, 2), (3, 3), (4, 4), (2, 1)}
Relation R satisfies reflexivity and transitivity.
⇒ (1, 1), (2, 2), (3, 3) ∈ R
And (1, 1), (2, 1) ∈ R ⇒ (1, 1) ∈ R
However, (2, 1) ∈ R, but (1, 2) ∉ R
(ii) The relation on A having properties of being reflexive, transitive, but not symmetric is
R = {(1, 1), (2, 2), (3, 3), (4, 4), (2, 1)}
Relation R satisfies reflexivity and transitivity.
⇒ (1, 1), (2, 2), (3, 3) ∈ R
And (1, 1), (2, 1) ∈ R ⇒ (1, 1) ∈ R
However, (2, 1) ∈ R, but (1, 2) ∉ R
(iii) The relation on A having properties of being symmetric, reflexive and transitive is
R = {(1, 1), (2, 2), (3, 3), (4, 4), (1, 2), (2, 1)}
The relation R is an equivalence relation on A.
Example 9:. Show that the relation R defined by R = {(a, b): a – b is divisible by 3; a, b ∈ Z} is an equivalence relation.
Solution:
Given R = {(a, b): a – b is divisible by 3; a, b ∈ Z} is a relation
To prove equivalence relation it is necessary that the given relation should be reflexive, symmetric and transitive.
Let us check these properties on R.
Reflexivity:
Let a be an arbitrary element of R.
Then, a – a = 0 = 0 × 3
⇒ a − a is divisible by 3
⇒ (a, a) ∈ R for all a ∈ Z
So, R is reflexive on Z.
Symmetry:
Let (a, b) ∈ R
⇒ a − b is divisible by 3
⇒ a − b = 3p for some p ∈ Z
⇒ b − a = 3 (−p)
Here, −p ∈ Z
⇒ b − a is divisible by 3
⇒ (b, a) ∈ R for all a, b ∈ Z
So, R is symmetric on Z.
Transitivity:
Let (a, b) and (b, c) ∈ R
⇒ a − b and b − c are divisible by 3
⇒ a – b = 3p for some p ∈ Z
And b − c = 3q for some q ∈ Z
Adding the above two equations, we get
a − b + b – c = 3p + 3q
⇒ a − c = 3 (p + q)
Here, p + q ∈ Z
⇒ a − c is divisible by 3
⇒ (a, c) ∈ R for all a, c ∈ Z
So, R is transitive on Z.
Therefore R is reflexive, symmetric and transitive.
Hence, R is an equivalence relation on Z.
Example 10: Show that the relation R on the set Z of integers, given by
R = {(a, b): 2 divides a – b}, is an equivalence relation.
Solution:
Given R = {(a, b): 2 divides a – b} is a relation defined on Z.
To prove equivalence relation it is necessary that the given relation should be reflexive, symmetric and transitive.
Let us check these properties on R.
Reflexivity:
Let a be an arbitrary element of the set Z.
Then, a ∈ R
⇒ a − a = 0 = 0 × 2
⇒ 2 divides a − a
⇒ (a, a) ∈ R for all a ∈ Z
So, R is reflexive on Z.
Symmetry:
Let (a, b) ∈ R
⇒ 2 divides a − b
⇒ (a-b)/2 = p for some p ∈ Z
⇒ (b-a)/2 = – p
Here, −p ∈ Z
⇒ 2 divides b − a
⇒ (b, a) ∈ R for all a, b ∈ Z
So, R is symmetric on Z
Transitivity:
Let (a, b) and (b, c) ∈ R
⇒ 2 divides a−b and 2 divides b−c
⇒ (a-b)/2 = p and (b-c)/2 = q for some p, q ∈ Z
Adding the above two equations, we get
(a – b)/2 + (b – c)/2 = p + q
⇒ (a – c)/2 = p +q
Here, p+ q ∈ Z
⇒ 2 divides a − c
⇒ (a, c) ∈ R for all a, c ∈ Z
So, R is transitive on Z.
Therefore R is reflexive, symmetric and transitive.
Hence, R is an equivalence relation on Z.
Example 11:. Prove that the relation R on Z defined by (a, b) ∈ R ⇔ a − b is divisible by 5 is an equivalence relation on Z.
Solution:
Given relation R on Z defined by (a, b) ∈ R ⇔ a − b is divisible by 5
To prove equivalence relation it is necessary that the given relation should be reflexive, symmetric and transitive.
Let us check these properties on R.
Reflexivity:
Let a be an arbitrary element of R. Then,
⇒ a − a = 0 = 0 × 5
⇒ a − a is divisible by 5
⇒ (a, a) ∈ R for all a ∈ Z
So, R is reflexive on Z.
Symmetry:
Let (a, b) ∈ R
⇒ a − b is divisible by 5
⇒ a − b = 5p for some p ∈ Z
⇒ b − a = 5 (−p)
Here, −p ∈ Z [Since p ∈ Z]
⇒ b − a is divisible by 5
⇒ (b, a) ∈ R for all a, b ∈ Z
So, R is symmetric on Z.
Transitivity:
Let (a, b) and (b, c) ∈ R
⇒ a − b is divisible by 5
⇒ a − b = 5p for some Z
Also, b − c is divisible by 5
⇒ b − c = 5q for some Z
Adding the above two equations, we get
a −b + b − c = 5p + 5q
⇒ a − c = 5 ( p + q )
⇒ a − c is divisible by 5
Here, p + q ∈ Z
⇒ (a, c) ∈ R for all a, c ∈ Z
So, R is transitive on Z.
Therefore R is reflexive, symmetric and transitive.
Hence, R is an equivalence relation on Z.
Example 12:. Let n be a fixed positive integer. Define a relation R on Z as follows:
(a, b) ∈ R ⇔ a − b is divisible by n.
Show that R is an equivalence relation on Z.
Solution:
Given (a, b) ∈ R ⇔ a − b is divisible by n is a relation R defined on Z.
To prove equivalence relation it is necessary that the given relation should be reflexive, symmetric and transitive.
Let us check these properties on R.
Reflexivity:
Let a ∈ N
Here, a − a = 0 = 0 × n
⇒ a − a is divisible by n
⇒ (a, a) ∈ R
⇒ (a, a) ∈ R for all a ∈ Z
So, R is reflexive on Z.
Symmetry:
Let (a, b) ∈ R
Here, a − b is divisible by n
⇒ a − b = n p for some p ∈ Z
⇒ b − a = n (−p)
⇒ b − a is divisible by n [ p ∈ Z⇒ − p ∈ Z]
⇒ (b, a) ∈ R
So, R is symmetric on Z.
Transitivity:
Let (a, b) and (b, c) ∈ R
Here, a − b is divisible by n and b − c is divisible by n.
⇒ a − b= n p for some p ∈ Z
And b−c = n q for some q ∈ Z
a – b + b − c = n p + n q
⇒ a − c = n (p + q)
⇒ (a, c) ∈ R for all a, c ∈ Z
So, R is transitive on Z.
Therefore R is reflexive, symmetric and transitive.
Hence, R is an equivalence relation on Z.
3. Different types of functions their domain and range
- Books Name
- SonikaAnandAcademy Mathmatics Book
- Publication
- SonikaAnandAcademy
- Course
- CBSE Class 12
- Subject
- Mathmatics
This concept is started in class 12 that is what are the commutative and associative properties of the binary functions
a*b=b*a. Commutative property
a*(b*c)=(a*b)*c associative property
How to check whether a function is infimum function or superinfimum function
How will we obtain a binary composition table for any given function
3. Different types of functions their domain and range
- Books Name
- ABCD CLASSES Mathmatics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 12
- Subject
- Mathmatics
FUNCTIONS
It is a special type of relation.
Defn: A relation R:AàB is said to be a function if every element of a set A has only one image in set B.
Or
A relation R:AàB is said to be a function if Domain(R)=A and One many relation is not present.
Or
A special relationship where each input has a single output. It is often written as "f(x)" where x is the input value.
Example:
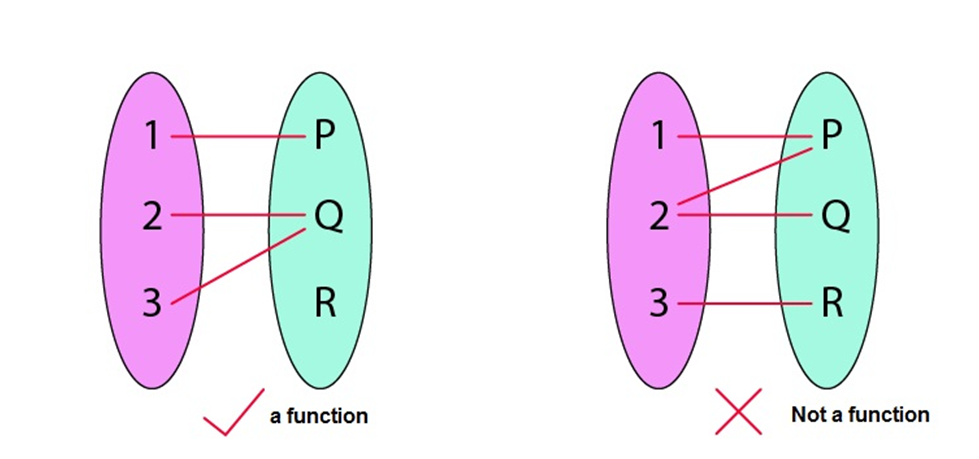
Different types of functions their domain and range
3. Different types of functions their domain and range
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
FUNCTIONS

It is a special type of relation.
Defn: A relation R:AàB is said to be a function if every element of a set A has only one image in set B.
Or
A relation R:AàB is said to be a function if Domain(R)=A and One many relation is not present.
Or
A special relationship where each input has a single output. It is often written as "f(x)" where x is the input value.

Example:

Different types of functions their domain and range


2. Graphs of inverse trigonometric functions
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
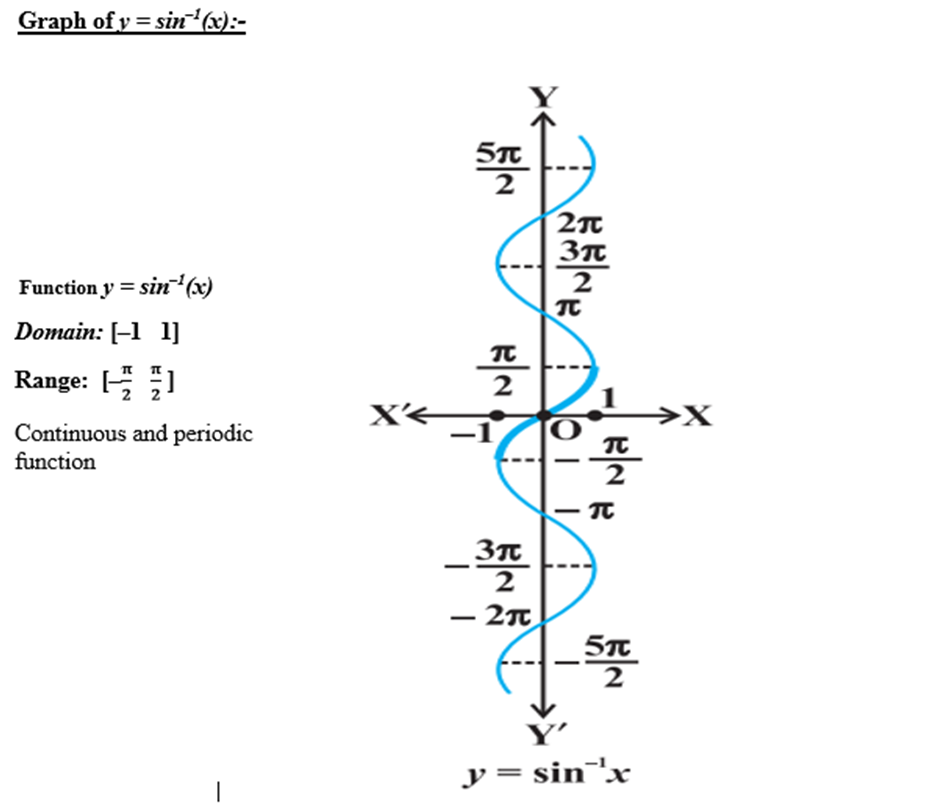
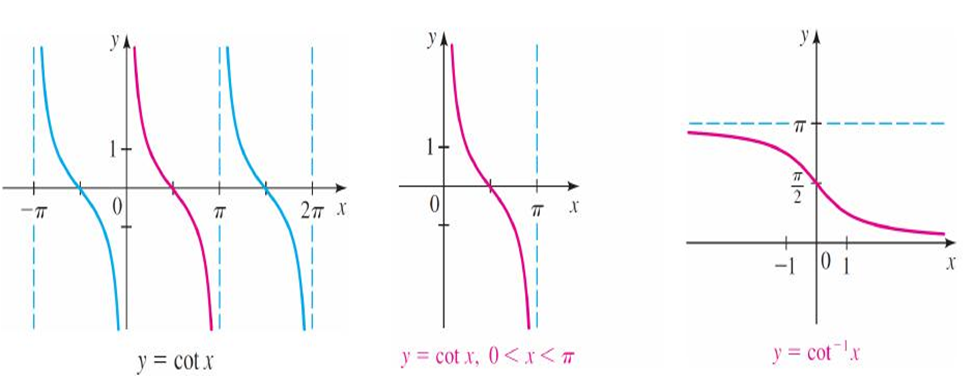
Graphs of inverse trigonometric functions
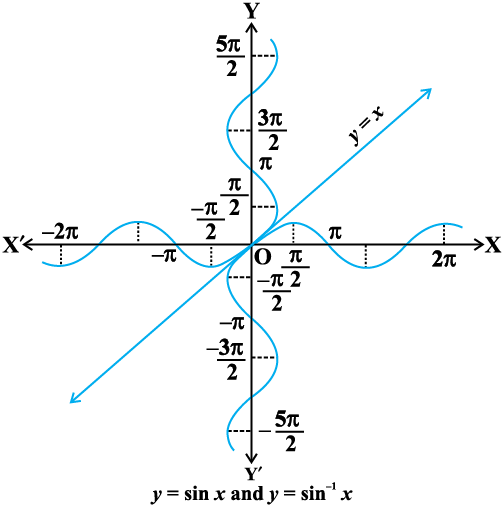
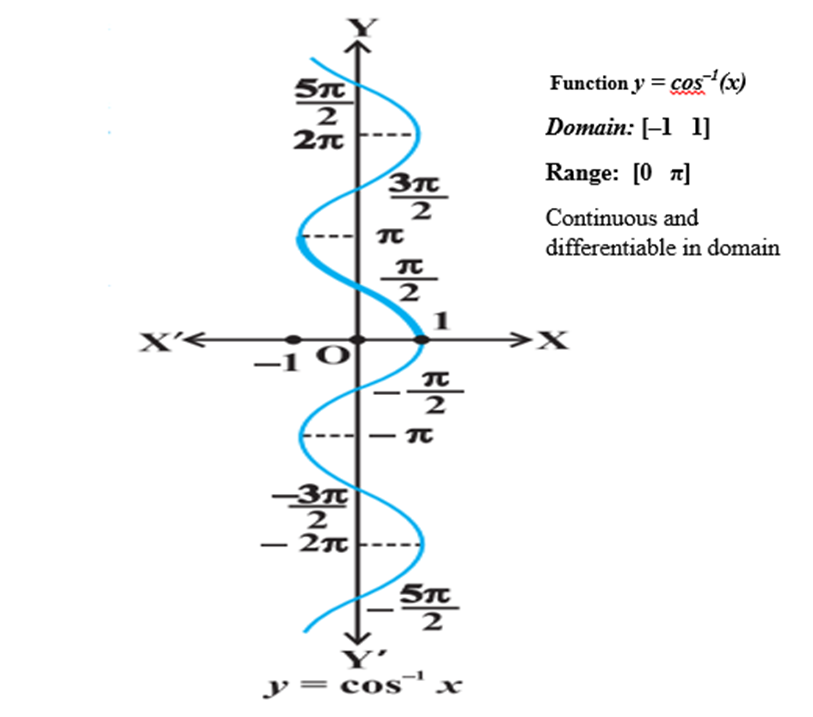
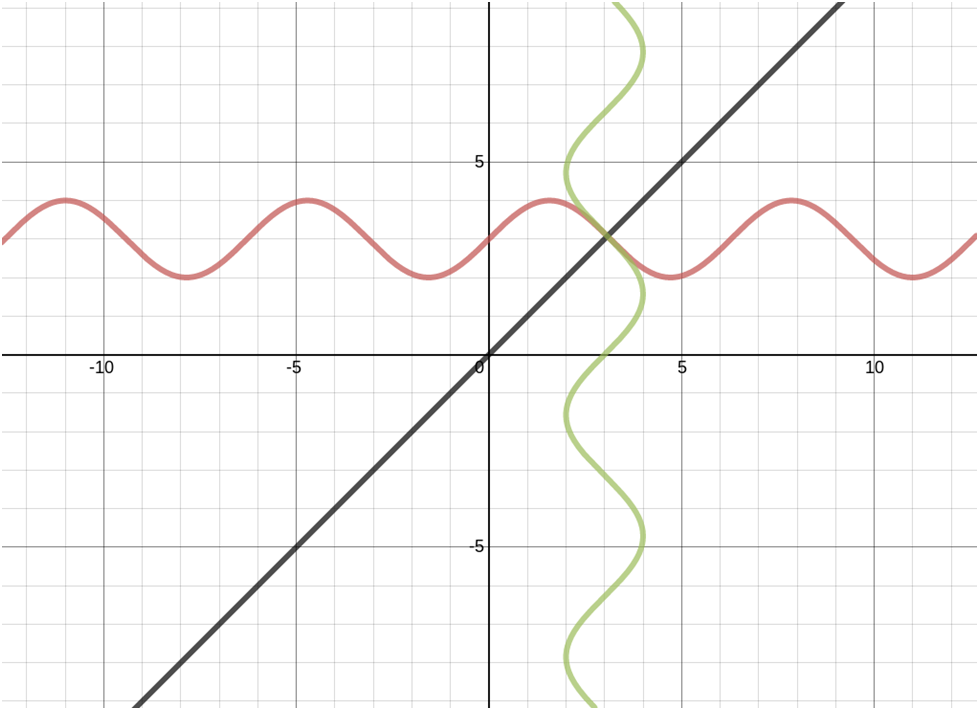
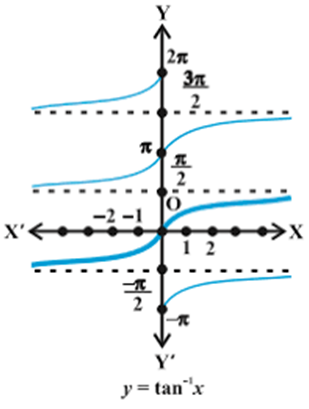
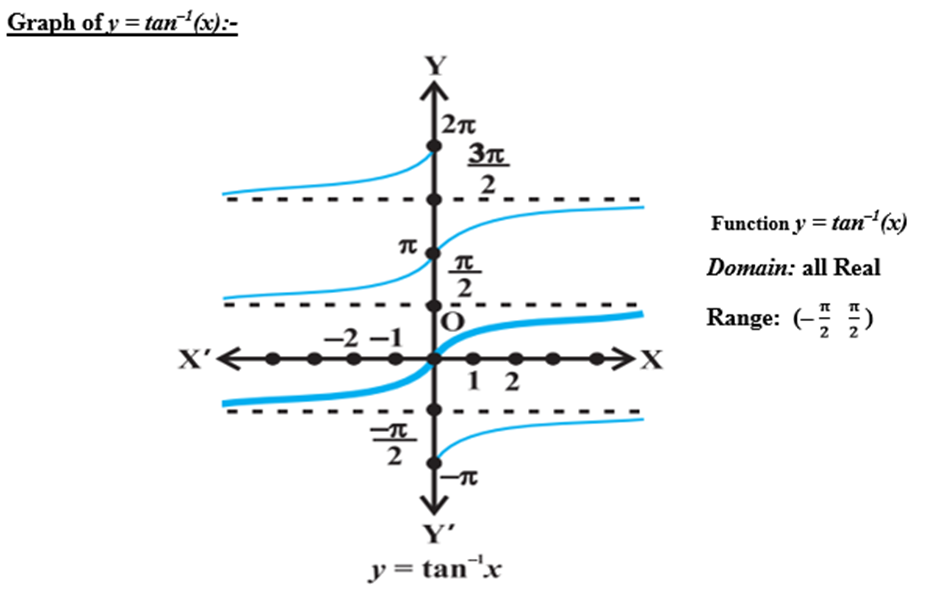
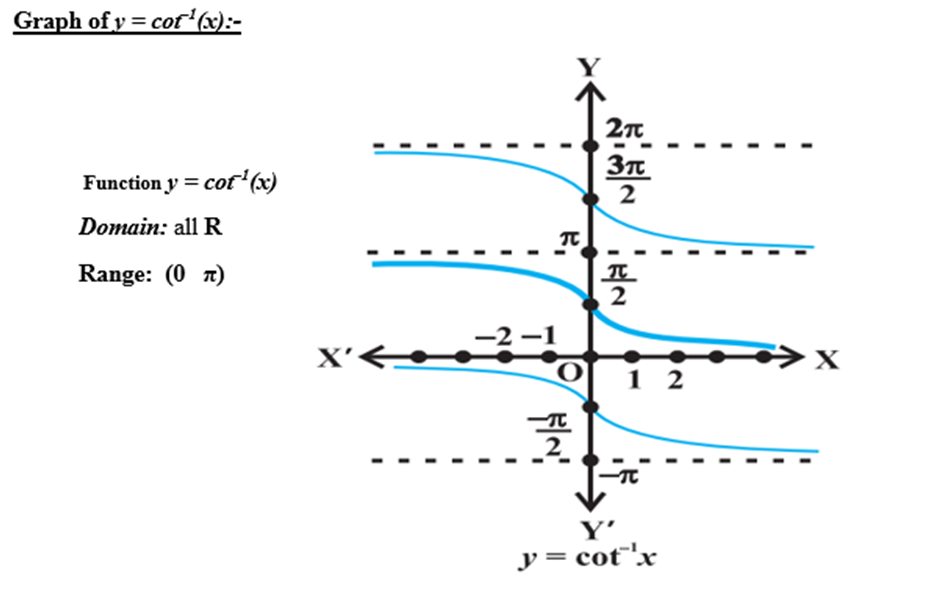
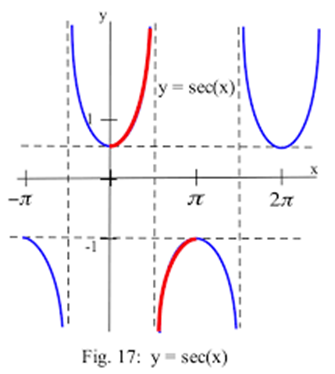
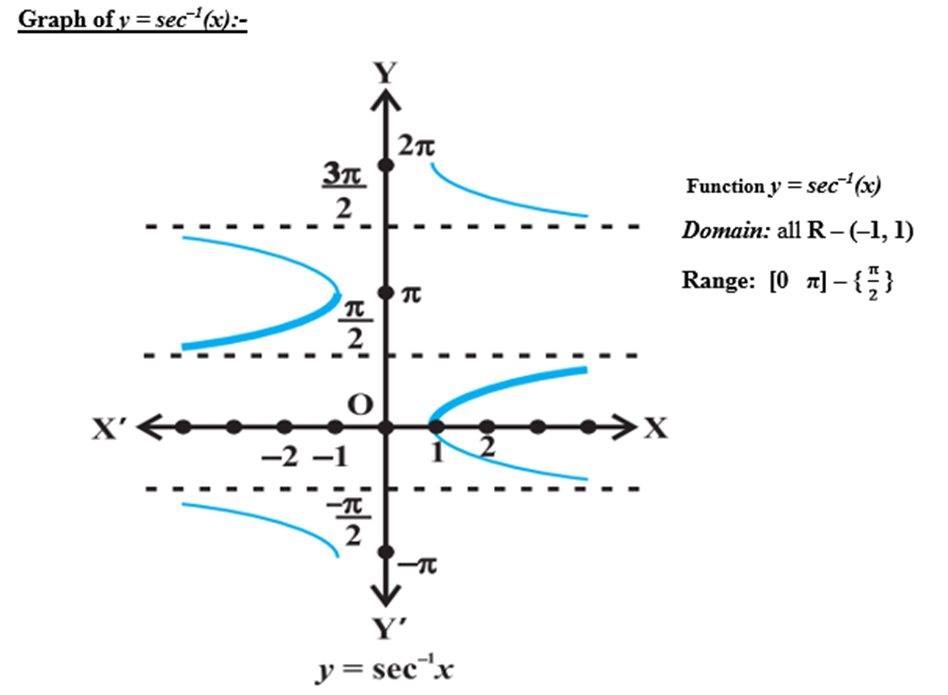
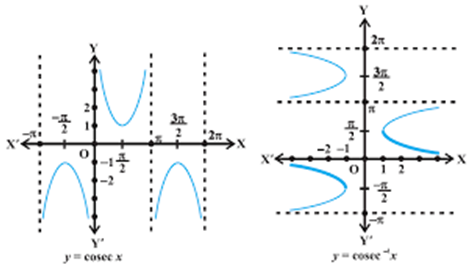
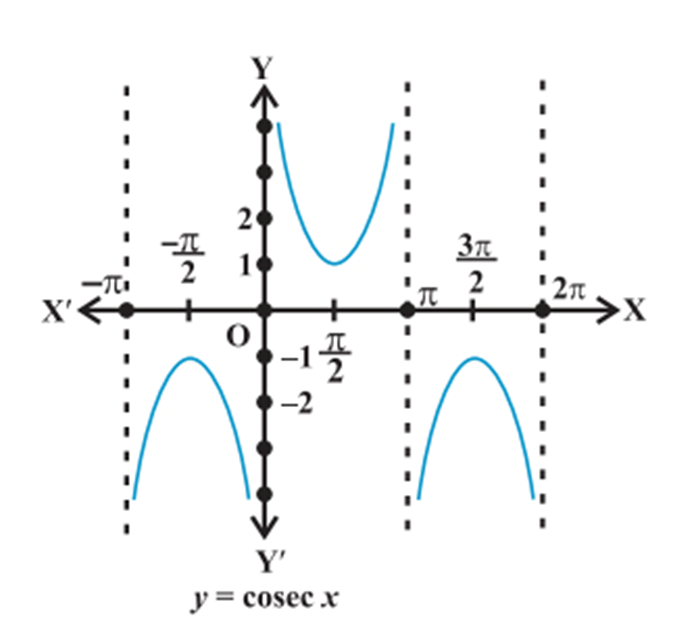
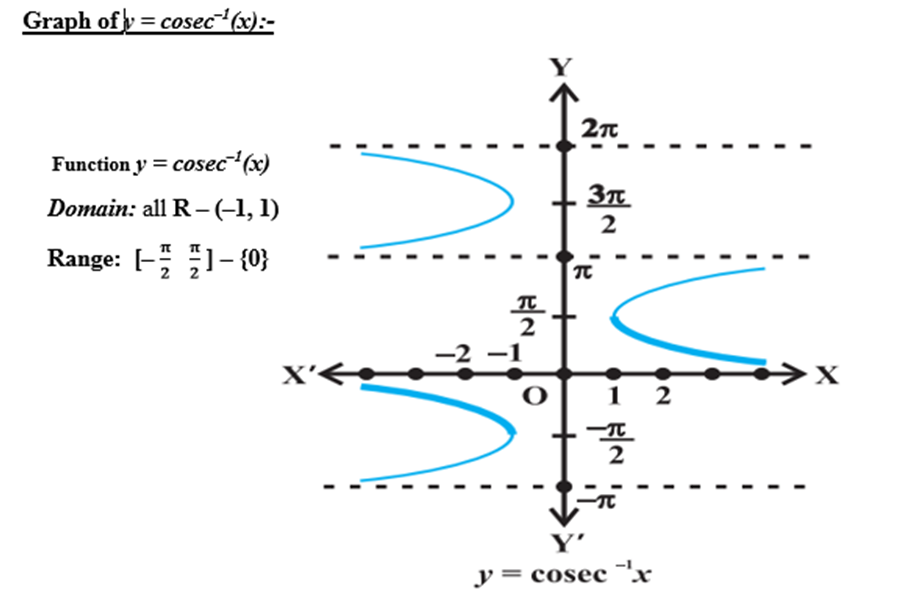
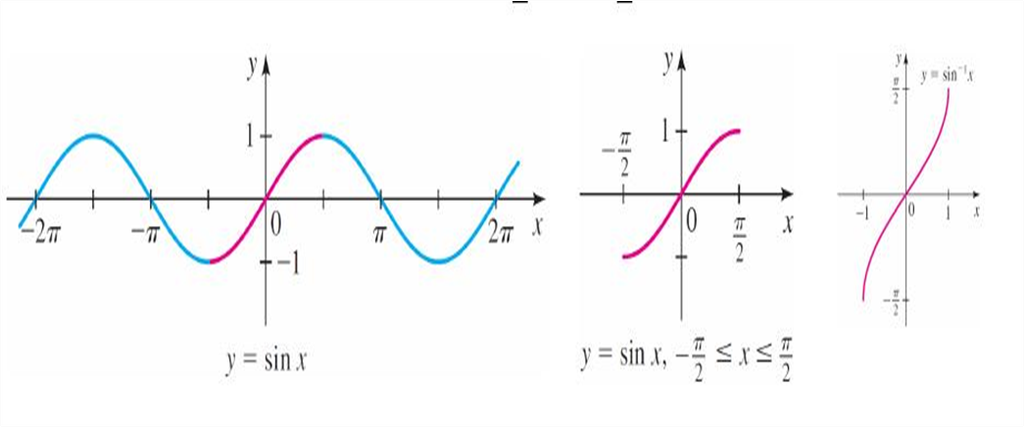

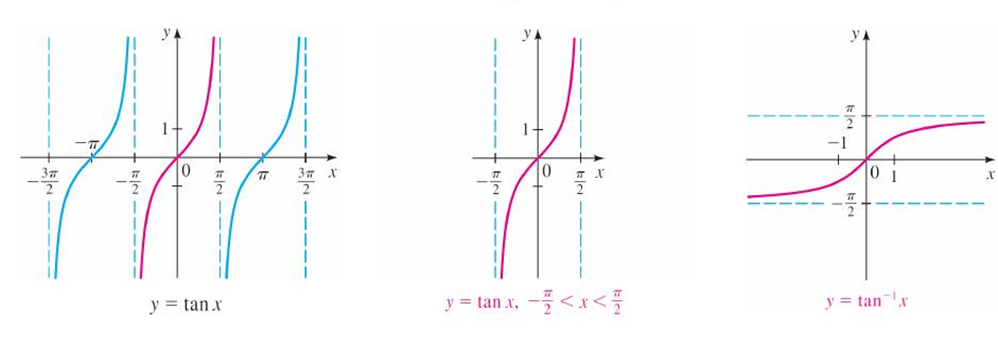
3. Properties of inverse trigonometric functions and important results
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Properties of inverse trigonometric functions and important results
Properties:
[1]
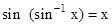
- cos(cos-1x)=x
- tan(tan-1x)=x
- cot(cot-1x)=x
- cosec(cosec-1x)=x
- sec(sec-1x)=x
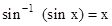
- Cos-1(cosx)=x
- tan-1(tanx)=x
- cot-1 (cotx)=x
- cosec-1 (cosecx)=x
- sec-1 (secx)=x
[2]
[3]
- sin–1 (–x) = – sin–1 x
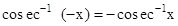
- tan–1 (–x) = – tan–1 x
[4]
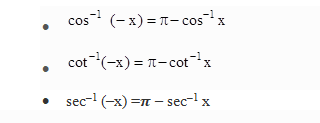
[5]
- tan–1 x + cot–1 x = π/2
- sin–1 x + cos–1 x = π/2
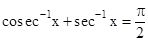
[6]
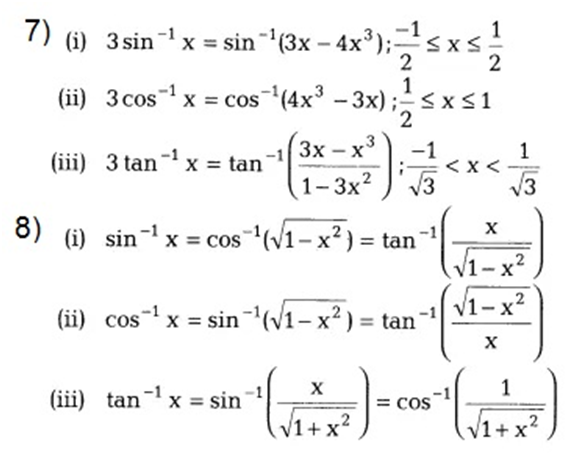
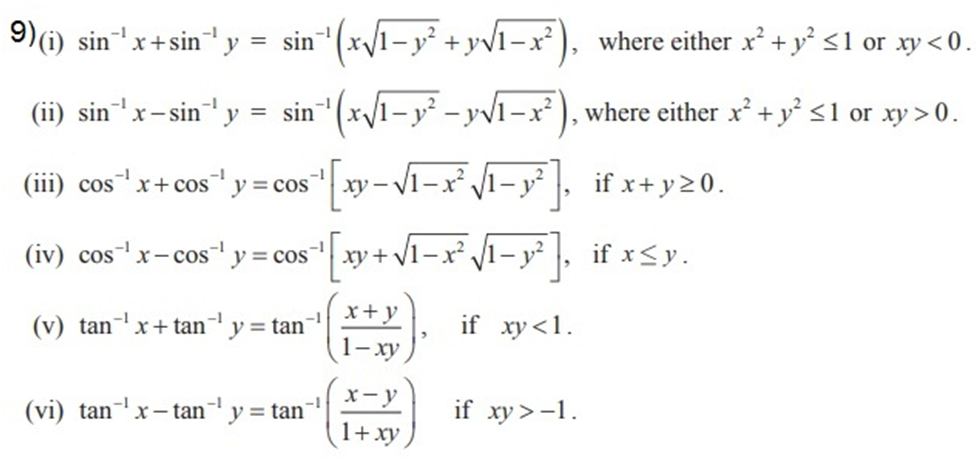
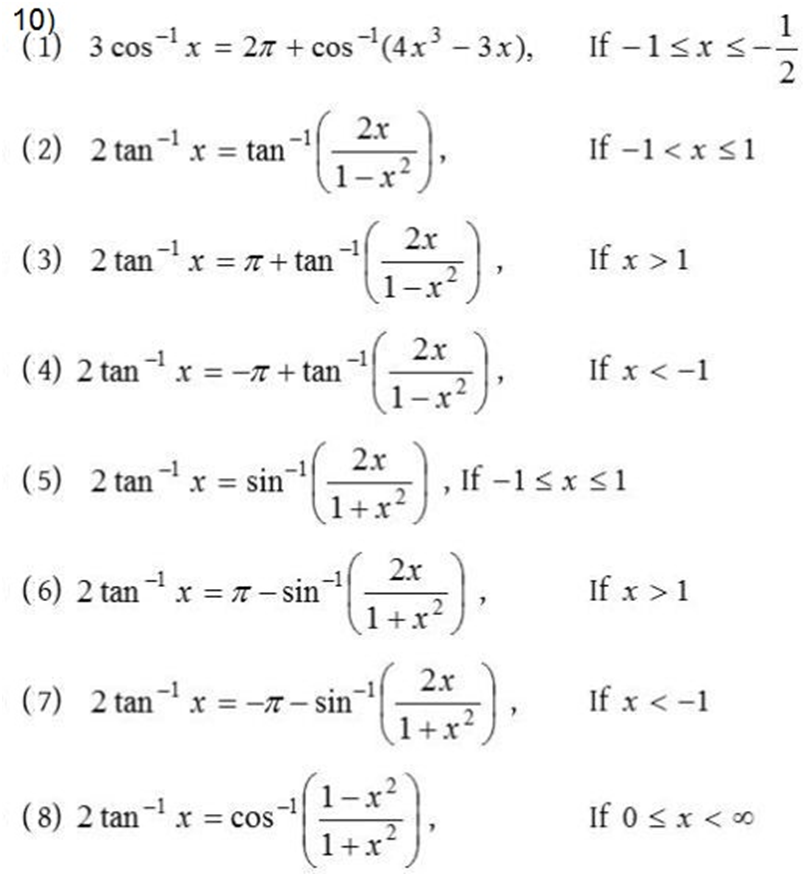
Examples:
1. Find the domain of definition of f(x) = cos -1 (x2 – 4)
Solution:
Given f(x) = cos -1 (x2 – 4)
We know that domain of cos-1 (x2 – 4) lies in the interval [-1, 1]
Therefore, we can write as
-1 ≤ x2 – 4 ≤ 1
4 – 1 ≤ x2 ≤ 1 + 4
3 ≤ x2 ≤ 5
±√ 3 ≤ x ≤ ±√5
– √5 ≤ x ≤ – √3 and √3 ≤ x ≤ √5
Therefore domain of cos-1 (x2 – 4) is [- √5, – √3] ∪ [√3, √5]
2. Find the domain of f(x) = cos-1 2x + sin-1 x.
Solution:
Given that f(x) = cos-1 2x + sin-1 x.
Now we have to find the domain of f(x),
We know that domain of cos-1 x lies in the interval [-1, 1]
Also know that domain of sin-1 x lies in the interval [-1, 1]
Therefore, the domain of cos-1 (2x) lies in the interval [-1, 1]
Hence we can write as,
-1 ≤ 2x ≤ 1
– ½ ≤ x ≤ ½
Hence, domain of cos-1(2x) + sin-1 x lies in the interval [- ½, ½]
3. Find the principal value of each of the following:
(i) sec-1 (-√2)
(ii) sec-1 (2)
(iii) sec-1 (2 sin (3π/4))
(iv) sec-1 (2 tan (3π/4))
Solution:
(i) Given sec-1 (-√2)
Now let y = sec-1 (-√2)
Sec y = -√2
We know that sec π/4 = √2
Therefore, -sec (π/4) = -√2
= sec (π – π/4)
= sec (3π/4)
Thus the range of principal value of sec-1 is [0, π] – {π/2}
And sec (3π/4) = – √2
Hence the principal value of sec-1 (-√2) is 3π/4
(ii) Given sec-1 (2)
Let y = sec-1 (2)
Sec y = 2
= Sec π/3
Therefore the range of principal value of sec-1 is [0, π] – {π/2} and sec π/3 = 2
Thus the principal value of sec-1 (2) is π/3
(iii) Given sec-1 (2 sin (3π/4))
But we know that sin (3π/4) = 1/√2
Therefore 2 sin (3π/4) = 2 × 1/√2
2 sin (3π/4) = √2
Therefore by substituting above values in sec-1 (2 sin (3π/4)), we get
Sec-1 (√2)
Let Sec-1 (√2) = y
Sec y = √2
Sec (π/4) = √2
Therefore range of principal value of sec-1 is [0, π] – {π/2} and sec (π/4) = √2
Thus the principal value of sec-1 (2 sin (3π/4)) is π/4.
(iv) Given sec-1 (2 tan (3π/4))
But we know that tan (3π/4) = -1
Therefore, 2 tan (3π/4) = 2 × -1
2 tan (3π/4) = -2
By substituting these values in sec-1 (2 tan (3π/4)), we get
Sec-1 (-2)
Now let y = Sec-1 (-2)
Sec y = – 2
– sec (π/3) = -2
= sec (π – π/3)
= sec (2π/3)
Therefore the range of principal value of sec-1 is [0, π] – {π/2} and sec (2π/3) = -2
Thus, the principal value of sec-1 (2 tan (3π/4)) is (2π/3).
4. Evaluate:
(i) Cot (sin-1 (3/4) + sec-1 (4/3))
(ii) Sin (tan-1 x + tan-1 1/x) for x < 0
Solution:
(i) Given Cot (sin-1 (3/4) + sec-1 (4/3))
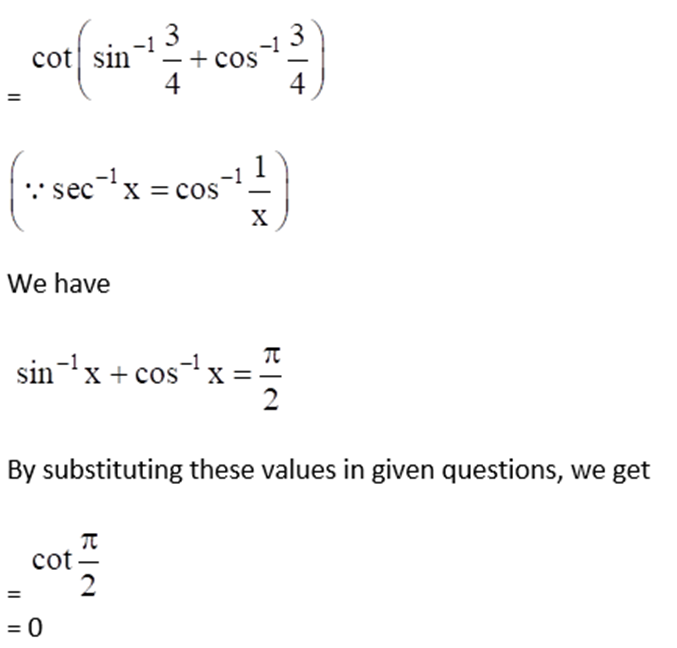
(ii) Given Sin (tan-1 x + tan-1 1/x) for x < 0
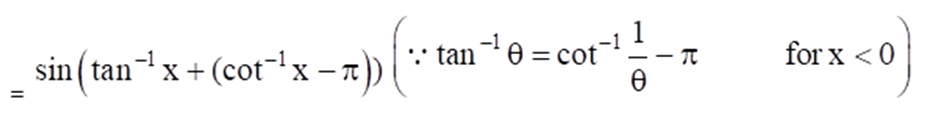
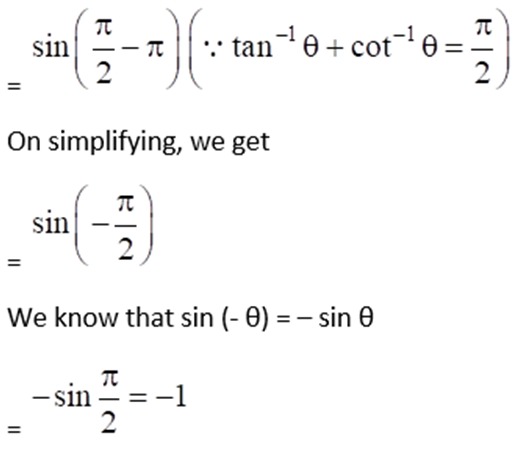
5. If cos-1 (x/2) + cos-1 (y/3) = α, then prove that 9x2 – 12xy cos α + 4y2 = 36 sin2 α
Solution:
Given cos-1 (x/2) + cos-1 (y/3) = α
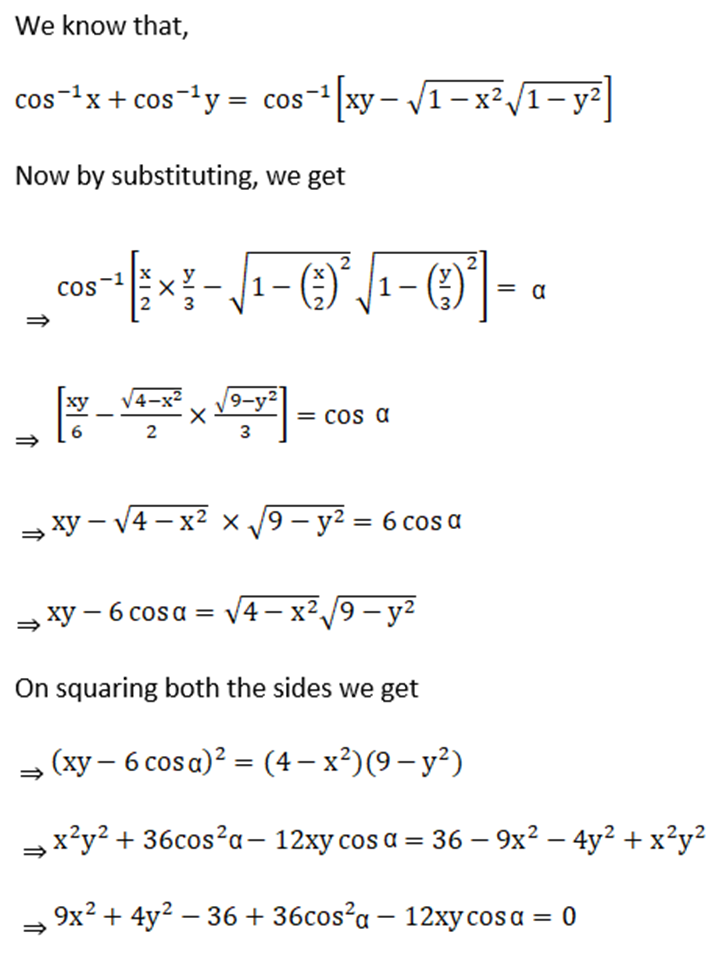
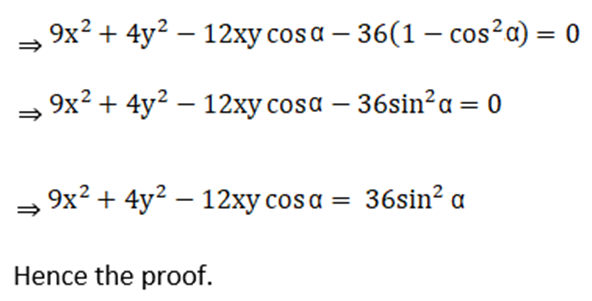
6. If sin-1 (2a/1 + a2) – cos-1(1 – b2/1 + b2) = tan-1(2x/1 – x2), then prove that x = (a – b)/ (1 + a b)
Solution:
Given sin-1 (2a/1 + a2) – cos-1(1 – b2/1 + b2) = tan-1(2x/1 – x2)

7. If sin-1 x + sin-1 y = π/3 and cos-1 x – cos-1 y = π/6, find the values of x and y.
Solution:
Given sin-1 x + sin-1 y = π/3 ……. Equation (i)
And cos-1 x – cos-1 y = π/6 ……… Equation (ii)
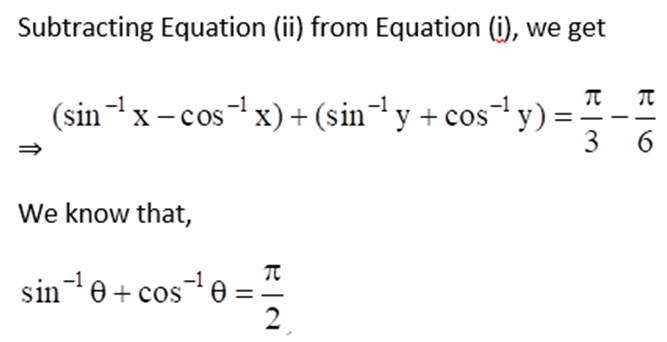
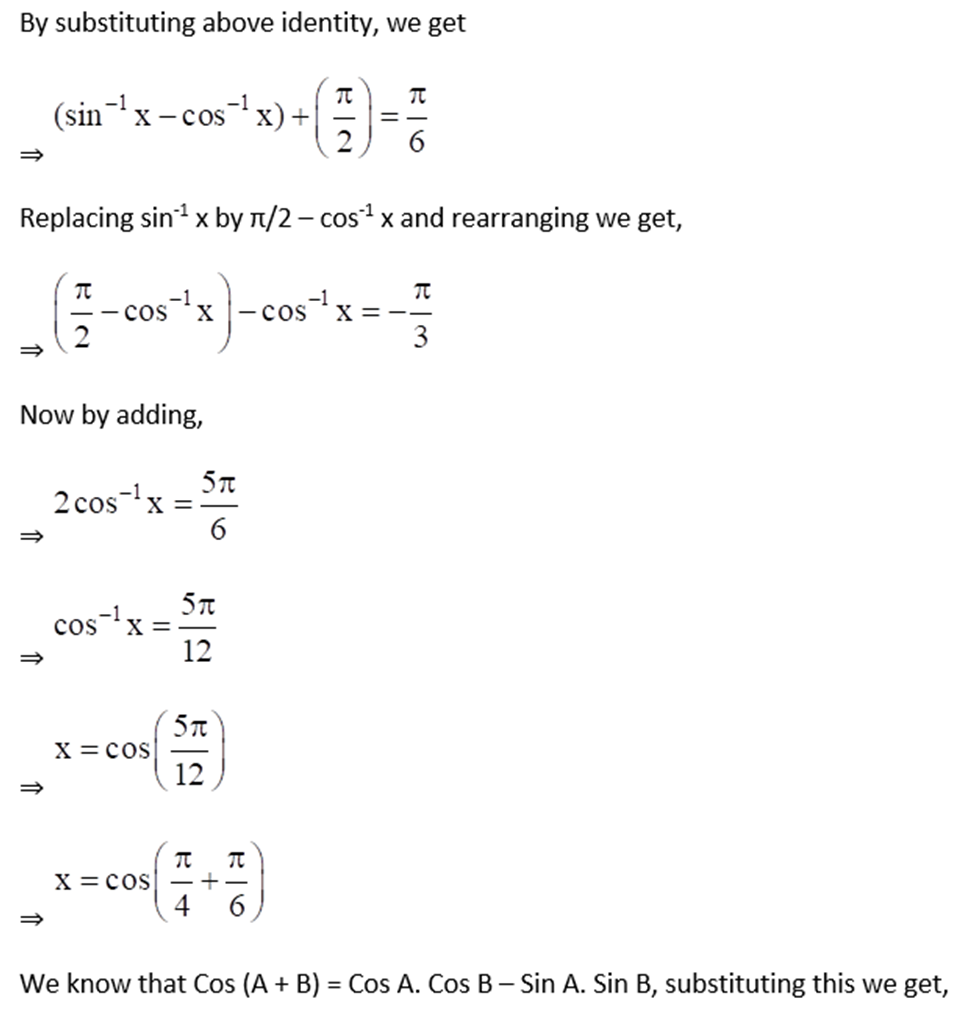
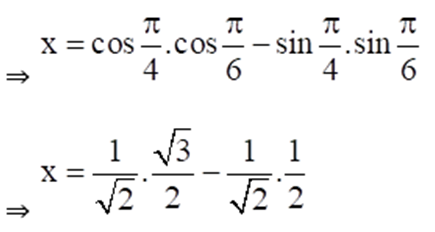
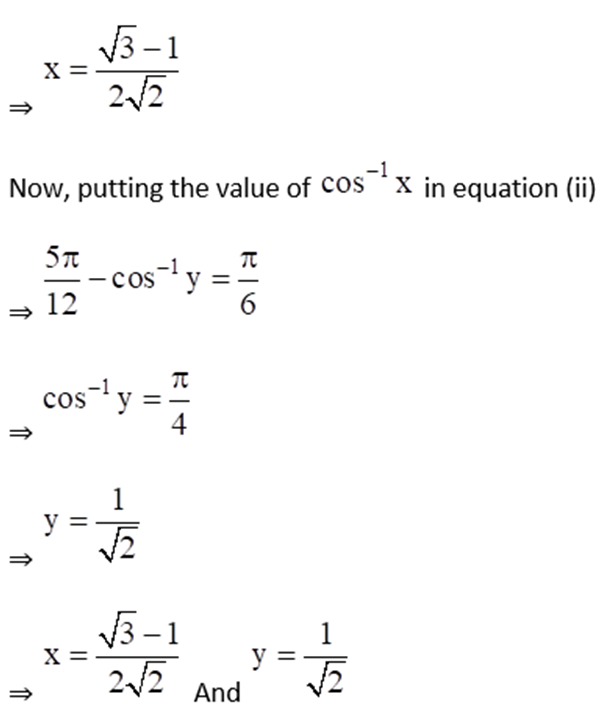

8. Which of the following is the principal value branch of cos-1 x?
(a) [-π/2, π/2] (b) (0, π) (c) [0. π] (d) [0, π] – {π/2}
Solution:
(c) [0. π]
As we know that the principal value branch cos-1 x is [0, π].
9. Which of the following is the principal value branch of cosec-1 x?
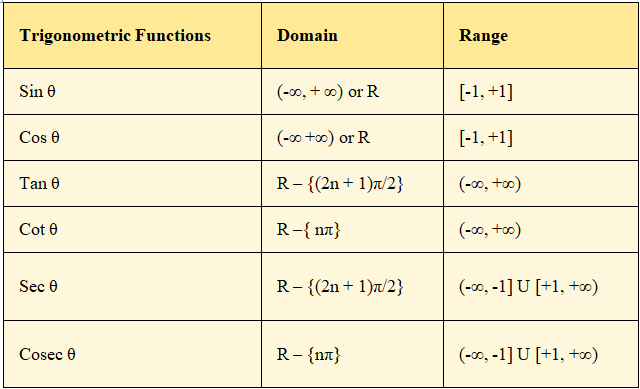
(a) (-π/2, π/2) (b) [0, π] – {π/2} (c) [-π/2, π/2] (d) [-π/2, π/2] – {0}
Solution:
(d) [-π/2, π/2] – {0}
As the principal branch of cosec-1 x is [-π/2, π/2] – {0}.
10. If 3 tan-1 x + cot-1 x = π, then x equals
(a) 0 (b) 1 (c) -1 (d) ½
Solution:
(b) 1
Given, 3 tan-1 x + cot-1 x = π
2 tan-1 x + tan-1 x + cot-1 x = π
2 tan-1 x + π/2 = π (As tan-1 + cot-1 = π/2)
2 tan-1 x = π/2
tan-1 x = π/4
x = 1
11. The value of sin-1 cos 33π/5 is
(a) 3π/5 (b) -7π/5 (c) π/10 (d) -π/10
Solution:
(d) -π/10
4. One-one(injective) functions, onto (surjective) functions, bijective functions.
- Books Name
- ABCD CLASSES Mathmatics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 12
- Subject
- Mathmatics
Types of Functions
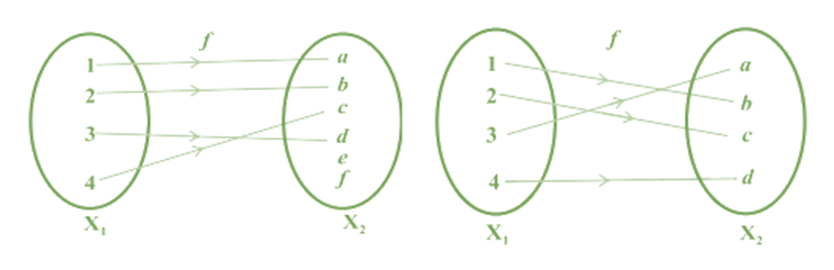
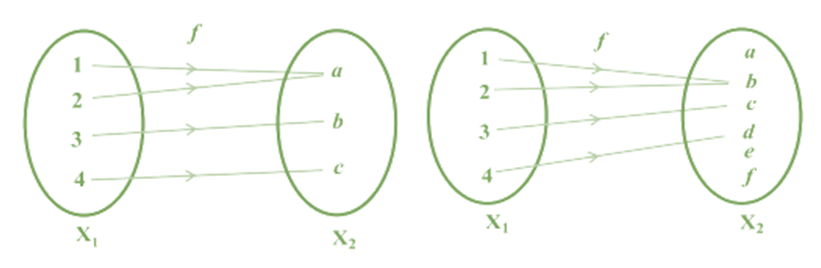
One to one Function: A function f : X → Y is defined to be one-one (or injective), if the images of distinct elements of X under f are distinct,
i.e., for every x1 , x2 ∈ X, f(x1 ) = f(x2 ) implies x1 = x2 . Otherwise, f is called many-one.
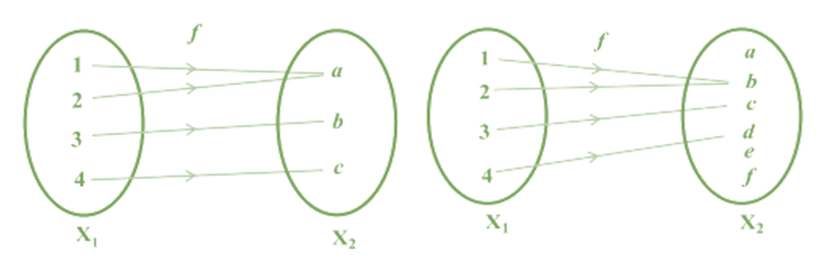
Examples
Examples of one-one / injective Function
- The identity function X → X is always one-one.
- If function f: R→ R, then f(x) = 2x is one-one.
- If function f: R→ R, then f(x) = 2x+1 is one-one.
- If function f: R→ R, then f(x) = x2 is not an injective function, because here
if x = -1, then f(-1) = 1 = f(1). Hence, the element of co-domain is not discrete here.
- If function f: R→ R, then f(x) = x/2 is one-one.
- If function f: R→ R, then f(x) = x3 is one-one.
- If function f: R→ R, then f(x) = 4x+5 is one-one.
Properties of One-One Function
- If f and g are both one to one, then f ∘ g follows one-one.
- If g ∘ f is one to one, then function f is one to one, but function g may not be.
- f: X → Y is one-one, if and only if, given any functions g, h : P → X whenever f ∘ g = f ∘ h, then g = h..
- If f: X → Y is one-one and P is a subset of X, then f-1 (f(A)) = P. Thus, P can be retrieved from its image f(P).
- If f: X → Y is one-one and P and Q are both subsets of X, then f(P ∩ Q) = f(P) ∩ f(Q).
- If both X and Y are limited with the same number of elements, then f: X → Y is one-one, if and only if f is surjective or onto function.
Example :
Show that f: R→ R defined as f(a) = 3x3 – 4 is one to one function?
Solution:
Let f ( x1 ) = f ( x2 ) for all a1 , a2 ∈ R
- 3x13 – 4 = 3x23 – 4
- x13 = x23
- x13 – x23 = 0
- (x1 – x2) (x1 + x1x2 + x22) = 0
- x1 = x2 and (x12 + x1x2 + x22) = 0
- (x12 + x1x2 + x22) = 0 is not considered because there are no real values of x1 and x2.
Therefore, the given function f is one-one.
- Onto Function: A function f: X → Y is said to be onto (or surjective), if every element of Y is the image of some element of X under f,(Codomain=Range)
i.e., for every y ∈ Y, there exists an element x in X such that f(x) = y.
4. One-one(injective) functions, onto (surjective) functions, bijective functions.
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Types of Functions
One to one Function:
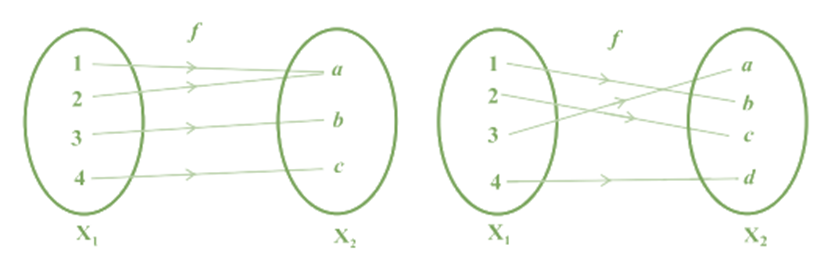
A function f : X → Y is defined to be one-one (or injective), if the images of distinct elements of
X under f are distinct,
i.e., for every x1 , x2 ∈ X, f(x1 ) = f(x2 ) implies x1 = x2 . Otherwise, f is called many-one.
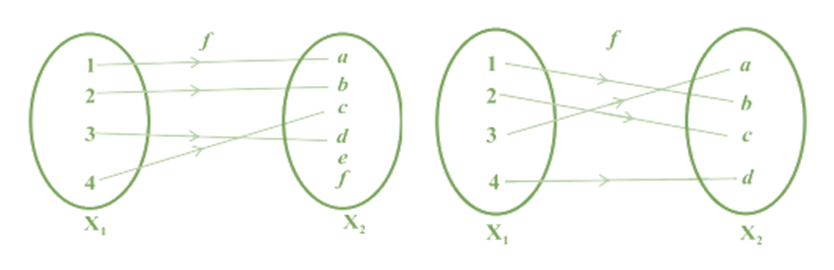
Examples
Examples of one-one / injective Function
- The identity function X → X is always one-one.
- If function f: R→ R, then f(x) = 2x is one-one.
- If function f: R→ R, then f(x) = 2x+1 is one-one.
- If function f: R→ R, then f(x) = x2 is not an injective function, because here
if x = -1, then f(-1) = 1 = f(1). Hence, the element of co-domain is not discrete here.
- If function f: R→ R, then f(x) = x/2 is one-one.
- If function f: R→ R, then f(x) = x3 is one-one.
- If function f: R→ R, then f(x) = 4x+5 is one-one.
Properties of One-One Function
- If f and g are both one to one, then f ∘ g follows one-one.
- If g ∘ f is one to one, then function f is one to one, but function g may not be.
- f: X → Y is one-one, if and only if, given any functions g, h : P → X whenever f ∘ g = f ∘ h, then g = h..
- If f: X → Y is one-one and P is a subset of X, then f-1 (f(A)) = P. Thus, P can be retrieved from its image f(P).
- If f: X → Y is one-one and P and Q are both subsets of X, then f(P ∩ Q) = f(P) ∩ f(Q).
- If both X and Y are limited with the same number of elements, then f: X → Y is one-one, if and only if f is surjective or onto function.
Example :
Show that f: R→ R defined as f(a) = 3x3 – 4 is one to one function?
Solution:
Let f ( x1 ) = f ( x2 ) for all a1 , a2 ∈ R
- 3x13 – 4 = 3x23 – 4
- x13 = x23
- x13 – x23 = 0
- (x1 – x2) (x1 + x1x2 + x22) = 0
- x1 = x2 and (x12 + x1x2 + x22) = 0
- (x12 + x1x2 + x22) = 0 is not considered because there are no real values of x1 and x2.
Therefore, the given function f is one-one.
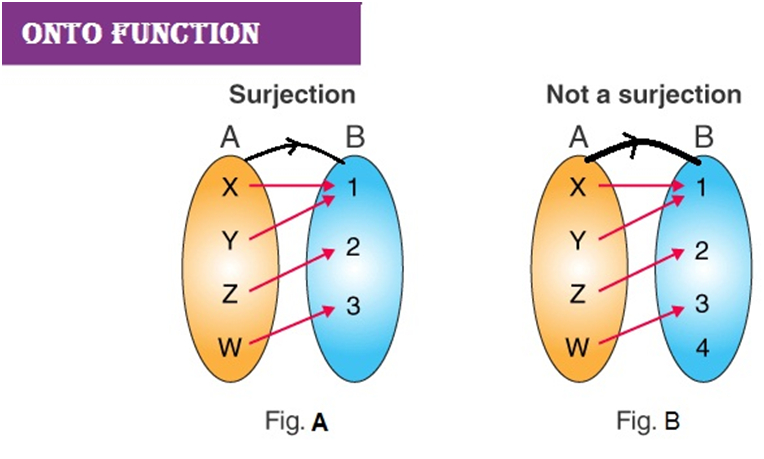
Onto Function:
A function f: X → Y is said to be onto (or surjective), if every element of Y is the image of some element of X under f,(Codomain=Range)
i.e., for every y ∈ Y, there exists an element x in X such that f(x) = y.
Properties of Onto Function:
- In the onto function, every element in the codomain will be assigned to at least one value in the domain.
- Every function that is an onto function has a right inverse.
- Every function which has a right inverse can be considered as an onto function.
- A function f: A →B is an onto, or surjective, function if the range of f equals the codomain of the function f.
- Let f: A →B be an arbitrary function then, every member of A has an image under f and all the images will be considered as members of T. The set R of these images can be considered as the range of the function f.
Example :
Find the number of onto functions from the set X = {1, 2, 3, 4} to the set y= {a, b, c} .
Given:
Set X = {1, 2, 3, 4}
Set Y = {a, b, c}
Here, n=4 and m=3
Now, substitute the values of m and n in the formula, we get
= 34 – 3C1(2)4 + 3C2(1)4
= 81 – 3 (16) + 3(1)
= 81 – 48 + 3
= 84-48
= 36
Thus, the number of onto functions from set X to set Y is 36.
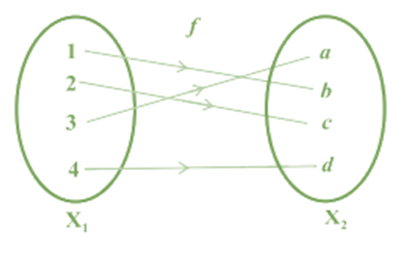
One-one and Onto Function:
A function f: X → Y is said to be one-one and onto (or bijective), if f is both one-one and onto.
One-one and Onto function
N.B.:
1) Let X and Y are two sets having m and n elements respectively.
Function f: Xà Y then total no. of functions= nm
2) total no. of one-one function = mPn if m>=n otherwise 0
3) total no. of onto function =![]() if 1≤n≤m otherwise 0.
if 1≤n≤m otherwise 0.
4) total no. of Bijective function = m!. if m=n otherwise 0.
Example 1:
Find the domain and range of a function f(x) = 3x2 – 5.
Solution:
Given function:
f(x) = 3x2 – 5
We know the domain of a function is the set of input values for f(x), in which the function is real and defined.
The given function has no undefined values of x.
Thus, for the given function, the domain is the set of all real numbers.
Domain = [-∞, ∞]
Also, the range of a function comprises the set of values of a dependent variable for which the given function is defined.
Let y = 3x2 – 5
3x2 = y + 5
x2 = (y + 5)/3
x = √[(y + 5)/3]
Square root function will be defined for non-negative values.
So, √[(y + 5)/3] ≥ 0
This is possible when y is greater than y ≥ -5.
Hence, the range of f(x) is [-5, ∞).
Example 2:
Find the domain and range of a function f(x) = (2x – 1)/(x + 4).
Solution:
Given function is:
f(x) = (2x – 1)/(x + 4)
We know that the domain of a function is the set of input values for f(x), in which the function is real and defined.
The given function is not defined when x + 4 = 0, i.e. x = -4
So, the domain of given function is the set of all real number except -4.
i.e. Domain = (-∞, -4) U (-4, ∞)
Also, the range of a function comprises the set of values of a dependent variable for which the given function is defined.
Let y = (2x – 1)/(x + 4)
xy + 4y = 2x – 1
2x – xy = 4y + 1
x(2 – y) = 4y + 1
x = (4y + 1)/(2 – y)
This is defined only when y is not equal to 2.
Hence, the range of the given function is (-∞, 2) U (2, ∞).
Example 3 :
The number of bijective functions from set A to itself when A contains 50 elements is
(A) 50
(B) 50!
(C) 502
(D) 250
Solution:
n(A) = m = 50
The number of bijective functions = m!
= 50!
Hence, option B is the answer.
Example 4: Given that the set A = {1, 2, 3}, set B = {4, 5} and let the function f = {(1, 4), (2, 5), (3, 5)}. Show that the function f is a surjective function from A to B.
Solution: Domain = set A = {1, 2, 3}
We can see that the element from set A, 1 has an image 4, and both 2 and 3 have the same image 5. Thus, the range of the function is {4, 5} which is equal to set B.
So F: A →B is an onto function.
Therefore, the given function f is a surjective function.
Example 5 : Prove that the function f: N → N, defined by f(x) = x2 + x + 1, is one-one but not onto
Solution:
Given f: N → N, defined by f(x) = x2 + x + 1
Now we have to prove that given function is one-one
Injectivity:
Let x and y be any two elements in the domain (N), such that f(x) = f(y).
⇒ x2 + x + 1 = y2 + y + 1
⇒ (x2 – y2) + (x – y) = 0 `
⇒ (x + y) (x- y ) + (x – y ) = 0
⇒ (x – y) (x + y + 1) = 0
⇒ x – y = 0 [x + y + 1 cannot be zero because x and y are natural numbers
⇒ x = y
So, f is one-one.
Surjectivity:
When x = 1
x2 + x + 1 = 1 + 1 + 1 = 3
⇒ x2 + x +1 ≥ 3, for every x in N.
⇒ f(x) will not assume the values 1 and 2.
So, f is not onto.
Example 6 :
Let A = {−1, 0, 1} and f = {(x, x2) : x ∈ A}. Show that f : A → A is neither one-one nor onto.
Solution:
Given A = {−1, 0, 1} and f = {(x, x2): x ∈ A}
Also given that, f(x) = x2
Now we have to prove that given function neither one-one or nor onto.
Injectivity:
Let x = 1
Therefore f(1) = 12=1 and
f(-1)=(-1)2=1
⇒ 1 and -1 have the same images.
So, f is not one-one.
Surjectivity:
Co-domain of f = {-1, 0, 1}
f(1) = 12 = 1,
f(-1) = (-1)2 = 1 and
f(0) = 0
⇒ Range of f = {0, 1}
So, both are not same.
Hence, f is not onto
Example 7 :
Let A = [-1, 1]. Then, discuss whether the following function from A to itself is one-one, onto or bijective:
(i) f (x) = x/2
(ii) g (x) = |x|
(iii) h (x) = x2
Solution:
(i) Given f: A → A, given by f (x) = x/2
Now we have to show that the given function is one-one and on-to
Injection test:
Let x and y be any two elements in the domain (A), such that f(x) = f(y).
f(x) = f(y)
x/2 = y/2
x = y
So, f is one-one.
Surjection test:
Let y be any element in the co-domain (A), such that f(x) = y for some element x in A (domain)
f(x) = y
x/2 = y
x = 2y, which may not be in A.
For example, if y = 1, then
x = 2, which is not in A.
So, f is not onto.
So, f is not bijective.
(ii) Given g: A → A, given by g (x) = |x|
Now we have to show that the given function is one-one and on-to
Injection test:
Let x and y be any two elements in the domain (A), such that f(x) = f(y).
g(x) = g(y)
|x| = |y|
x = ± y
So, f is not one-one.
Surjection test:
For y = -1, there is no value of x in A.
So, g is not onto.
So, g is not bijective.
(iii) Given h: A → A, given by h (x) = x2
Now we have to show that the given function is one-one and on-to
Injection test:
Let x and y be any two elements in the domain (A), such that h(x) = h(y).
h(x) = h(y)
x2 = y2
x = ±y
So, f is not one-one.
Surjection test:
For y = – 1, there is no value of x in A.
So, h is not onto.
So, h is not bijective.
Example 8 :
Are the following set of ordered pair of a function? If so, examine whether the mapping is injective or surjective:
(i) {(x, y): x is a person, y is the mother of x}
(ii) {(a, b): a is a person, b is an ancestor of a}
Solution:
Let f = {(x, y): x is a person, y is the mother of x}
As, for each element x in domain set, there is a unique related element y in co-domain set.
So, f is the function.
Injection test:
As, y can be mother of two or more persons
So, f is not injective.
Surjection test:
For every mother y defined by (x, y), there exists a person x for whom y is mother.
So, f is surjective.
Therefore, f is surjective function.
(ii) Let g = {(a, b): a is a person, b is an ancestor of a}
Since, the ordered map (a, b) does not map ‘a’ – a person to a living person.
So, g is not a function.
Example 9:
. Let A = {1, 2, 3}. Write all one-one from A to itself.
Solution:
Given A = {1, 2, 3}
Number of elements in A = 3
Number of one-one functions = number of ways of arranging 3 elements = 3! = 6
(i) {(1, 1), (2, 2), (3, 3)}
(ii) {(1, 1), (2, 3), (3, 2)}
(iii) {(1, 2 ), (2, 2), (3, 3 )}
(iv) {(1, 2), (2, 1), (3, 3)}
(v) {(1, 3), (2, 2), (3, 1)}
(vi) {(1, 3), (2, 1), (3,2 )}
Example 10 :
If f: R → R be the function defined by f(x) = 4x3 + 7, show that f is a bijection.
Solution:
Given f: R → R is a function defined by f(x) = 4x3 + 7
Injectivity:
Let x and y be any two elements in the domain (R), such that f(x) = f(y)
⇒ 4x3 + 7 = 4y3 + 7
⇒ 4x3 = 4y3
⇒ x3 = y3
⇒ x = y
So, f is one-one.
Surjectivity:
Let y be any element in the co-domain (R), such that f(x) = y for some element x in R (domain)
f(x) = y
⇒ 4x3 + 7 = y
⇒ 4x3 = y − 7
⇒ x3 = (y – 7)/4
⇒ x = ∛(y-7)/4 in R
So, for every element in the co-domain, there exists some pre-image in the domain. f is onto.
Since, f is both one-to-one and onto, it is a bijection.
5. Composition of Functions
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Composition of Functions
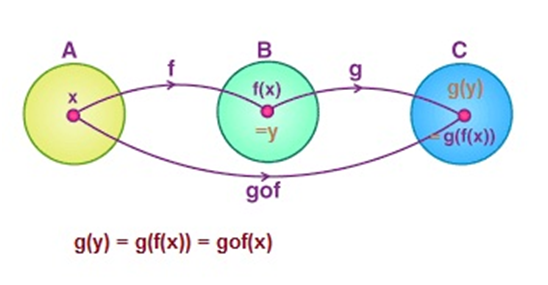
Let f: A → B and g: B → C be two functions. Then the composition of f and g, denoted by gof, is defined as the function gof: A → C given by;
gof (x) = g(f (x)), ∀ x ∈ A
Example 1. Find gof and fog when f: R → R and g : R → R is defined by
(i) f(x) = 2x + 3 and g(x) = x2 + 5.
(ii) f(x) = 2x + x2 and g(x) = x3
(iii) f (x) = x2 + 8 and g(x) = 3x3 + 1
(iv) f (x) = x and g(x) = |x|
(v) f(x) = x2 + 2x − 3 and g(x) = 3x − 4
(vi) f(x) = 8x3 and g(x) = x1/3
Solution:
(i) Given, f: R → R and g: R → R
So, gof: R → R and fog: R → R
Also given that f(x) = 2x + 3 and g(x) = x2 + 5
Now, (gof) (x) = g (f (x))
= g (2x +3)
= (2x + 3)2 + 5
= 4x2+ 9 + 12x +5
=4x2+ 12x + 14
Now, (fog) (x) = f (g (x))
= f (x2 + 5)
= 2 (x2 + 5) +3
= 2 x2+ 10 + 3
= 2x2 + 13
(ii) Given, f: R → R and g: R → R
so, gof: R → R and fog: R → R
f(x) = 2x + x2 and g(x) = x3
(gof) (x)= g (f (x))
= g (2x+x2)
= (2x+x2)3
Now, (fog) (x) = f (g (x))
= f (x3)
= 2 (x3) + (x3)2
= 2x3 + x6
(iii) Given, f: R → R and g: R → R
So, gof: R → R and fog: R → R
f(x) = x2 + 8 and g(x) = 3x3 + 1
(gof) (x) = g (f (x))
= g (x2 + 8)
= 3 (x2+8)3 + 1
Now, (fog) (x) = f (g (x))
= f (3x3 + 1)
= (3x3+1)2 + 8
= 9x6 + 6x3 + 1 + 8
= 9x6 + 6x3 + 9
(iv) Given, f: R → R and g: R → R
So, gof: R → R and fog: R → R
f(x) = x and g(x) = |x|
(gof) (x) = g (f (x))
= g (x)
= |x|
Now (fog) (x) = f (g (x))
= f (|x|)
= |x|
(v) Given, f: R → R and g: R → R
So, gof: R → R and fog: R → R
f(x) = x2 + 2x − 3 and g(x) = 3x − 4
(gof) (x) = g (f(x))
= g (x2 + 2x − 3)
= 3 (x2 + 2x − 3) − 4
= 3x2 + 6x − 9 − 4
= 3x2 + 6x − 13
Now, (fog) (x) = f (g (x))
= f (3x − 4)
= (3x − 4)2 + 2 (3x − 4) −3
= 9x2 + 16 − 24x + 6x – 8 − 3
= 9x2 − 18x + 5
(vi) Given, f: R → R and g: R → R
So, gof: R → R and fog: R → R
f(x) = 8x3 and g(x) = x1/3
(gof) (x) = g (f (x))
= g (8x3)
= (8x3)1/3
= [(2x)3]1/3
= 2x
Now, (fog) (x) = f (g (x))
= f (x1/3)
= 8 (x1/3)3
= 8x
Example 2. Let f = {(3, 1), (9, 3), (12, 4)} and g = {(1, 3), (3, 3) (4, 9) (5, 9)}. Show that gof and fog are both defined. Also, find fog and gof.
Solution:
Given f = {(3, 1), (9, 3), (12, 4)} and g = {(1, 3), (3, 3) (4, 9) (5, 9)}
f : {3, 9, 12} → {1, 3, 4} and g : {1, 3, 4, 5} → {3, 9}
Co-domain of f is a subset of the domain of g.
So, gof exists and gof: {3, 9, 12} → {3, 9}
(gof) (3) = g (f (3)) = g (1) = 3
(gof) (9) = g (f (9)) = g (3) = 3
(gof) (12) = g (f (12)) = g (4) = 9
⇒ gof = {(3, 3), (9, 3), (12, 9)}
Co-domain of g is a subset of the domain of f.
So, fog exists and fog: {1, 3, 4, 5} → {3, 9, 12}
(fog) (1) = f (g (1)) = f (3) = 1
(fog) (3) = f (g (3)) = f (3) = 1
(fog) (4) = f (g (4)) = f (9) = 3
(fog) (5) = f (g (5)) = f (9) = 3
⇒ fog = {(1, 1), (3, 1), (4, 3), (5, 3)}
Example 3. Let f = {(1, −1), (4, −2), (9, −3), (16, 4)} and g = {(−1, −2), (−2, −4), (−3, −6), (4, 8)}. Show that gof is defined while fog is not defined. Also, find gof.
Solution:
Given f = {(1, −1), (4, −2), (9, −3), (16, 4)} and g = {(−1, −2), (−2, −4), (−3, −6), (4, 8)}
f: {1, 4, 9, 16} → {-1, -2, -3, 4} and g: {-1, -2, -3, 4} → {-2, -4, -6, 8}
Co-domain of f = domain of g
So, gof exists and gof: {1, 4, 9, 16} → {-2, -4, -6, 8}
(gof) (1) = g (f (1)) = g (−1) = −2
(gof) (4) = g (f (4)) = g (−2) = −4
(gof) (9) = g (f (9)) = g (−3) = −6
(gof) (16) = g (f (16)) = g (4) = 8
So, gof = {(1, −2), (4, −4), (9, −6), (16, 8)}
But the co-domain of g is not same as the domain of f.
So, fog does not exist.
Example 4:. If f(x) = |x|, prove that fof = f.
Solution:
Given f(x) = |x|,
Now we have to prove that fof = f.
Consider (fof) (x) = f (f (x))
= f (|x|)
= ||x||
= |x|
= f (x)
So,
(fof) (x) = f (x), ∀x ∈ R
Hence, fof = f.
6. Invertible and inverse of functions
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Invertible Functions
A function f : X → Y is defined to be invertible if there exists a function g : Y → X such that gof = IX and fog = IY. The function g is called the inverse of f and is denoted by f–1.
An important note is that, if f is invertible, then f must be one-one and onto and conversely if f is one-one and onto, then f must be invertible.
Example 1:. Find f −1 if it exists: f: A → B, where
(i) A = {0, −1, −3, 2}; B = {−9, −3, 0, 6} and f(x) = 3 x.
(ii) A = {1, 3, 5, 7, 9}; B = {0, 1, 9, 25, 49, 81} and f(x) = x2
Solution:
(i) Given A = {0, −1, −3, 2}; B = {−9, −3, 0, 6} and f(x) = 3 x.
So, f = {(0, 0), (-1, -3), (-3, -9), (2, 6)}
Here, different elements of the domain have different images in the co-domain.
Clearly, this is one-one.
Range of f = Range of f = B
so, f is a bijection and,
Thus, f -1 exists.
Hence, f -1= {(0, 0), (-3, -1), (-9, -3), (6, 2)}
(ii) Given A = {1, 3, 5, 7, 9}; B = {0, 1, 9, 25, 49, 81} and f(x) = x2
So, f = {(1, 1), (3, 9), (5, 25), (7, 49), (9, 81)}
Here, different elements of the domain have different images in the co-domain.
Clearly, f is one-one.
But this is not onto because the element 0 in the co-domain (B) has no pre-image in the domain (A)
⇒ f is not a bijection.
So, f -1does not exist.
Example 2:. Consider f: {1, 2, 3} → {a, b, c} and g: {a, b, c} → {apple, ball, cat} defined as f (1) = a, f (2) = b, f (3) = c, g (a) = apple, g (b) = ball and g (c) = cat. Show that f, g and gof are invertible. Find f−1, g−1 and gof−1and show that (gof)−1 = f −1o g−1
Solution:
Given f = {(1, a), (2, b), (c , 3)} and g = {(a , apple) , (b , ball) , (c , cat)} Clearly , f and g are bijections.
So, f and g are invertible.
Now,
f -1 = {(a ,1) , (b , 2) , (3,c)} and g-1 = {(apple, a), (ball , b), (cat , c)}
So, f-1 o g-1= {apple, 1), (ball, 2), (cat, 3)}……… (1)
f: {1,2,3,} → {a, b, c} and g: {a, b, c} → {apple, ball, cat}
So, gof: {1, 2, 3} → {apple, ball, cat}
⇒ (gof) (1) = g (f (1)) = g (a) = apple
(gof) (2) = g (f (2))
= g (b)
= ball,
And (gof) (3) = g (f (3))
= g (c)
= cat
∴ gof = {(1, apple), (2, ball), (3, cat)}
Clearly, gof is a bijection.
So, gof is invertible.
(gof)-1 = {(apple, 1), (ball, 2), (cat, 3)}……. (2)
Form (1) and (2), we get
(gof)-1 = f-1 o g -1
Example 3:. Let A = {1, 2, 3, 4}; B = {3, 5, 7, 9}; C = {7, 23, 47, 79} and f: A → B, g: B → C be defined as f(x) = 2x + 1 and g(x) = x2 − 2. Express (gof)−1 and f−1 og−1 as the sets of ordered pairs and verify that (gof)−1 = f−1 og−1.
Solution:
Given that f (x) = 2x + 1
⇒ f= {(1, 2(1) + 1), (2, 2(2) + 1), (3, 2(3) + 1), (4, 2(4) + 1)}
= {(1, 3), (2, 5), (3, 7), (4, 9)}
Also given that g(x) = x2−2
⇒ g = {(3, 32−2), (5, 52−2), (7, 72−2), (9, 92−2)}
= {(3, 7), (5, 23), (7, 47), (9, 79)}
Clearly f and g are bijections and, hence, f−1: B→ A and g−1: C→ B exist.
So, f−1= {(3, 1), (5, 2), (7, 3), (9, 4)}
And g−1= {(7, 3), (23, 5), (47, 7), (79, 9)}
Now, (f−1 o g−1): C→ A
f−1 o g−1 = {(7, 1), (23, 2), (47, 3), (79, 4)}……….(1)
Also, f: A→B and g: B → C,
⇒ gof: A → C, (gof) −1 : C→ A
So, f−1 o g−1and (gof)−1 have same domains.
(gof) (x) = g (f (x))
=g (2x + 1)
=(2x +1 )2− 2
⇒ (gof) (x) = 4x2 + 4x + 1 − 2
⇒ (gof) (x) = 4x2+ 4x −1
Then, (gof) (1) = g (f (1))
= 4 + 4 − 1
=7,
(gof) (2) = g (f (2))
= 4(2)2 + 4(2) – 1 = 23,
(gof) (3) = g (f (3))
= 4(3)2 + 4(3) – 1 = 47 and
(gof) (4) = g (f (4))
= 4(4)2 + 4(4) − 1 = 79
So, gof = {(1, 7), (2, 23), (3, 47), (4, 79)}
⇒ (gof)– 1 = {(7, 1), (23, 2), (47, 3), (79, 4)}…… (2)
From (1) and (2), we get:
(gof)−1 = f−1 o g−1
Example 4:. Show that the function f: Q → Q, defined by f(x) = 3x + 5, is invertible. Also, find f−1
Solution:
Given function f: Q → Q, defined by f(x) = 3x + 5
Now we have to show that the given function is invertible.
Injection of f:
Let x and y be two elements of the domain (Q),
Such that f(x) = f(y)
⇒ 3x + 5 = 3y + 5
⇒ 3x = 3y
⇒ x = y
so, f is one-one.
Surjection of f:
Let y be in the co-domain (Q),
Such that f(x) = y
⇒ 3x +5 = y
⇒ 3x = y – 5
⇒ x = (y -5)/3 belongs to Q domain
⇒ f is onto.
So, f is a bijection and, hence, it is invertible.
Now we have to find f-1:
Let f-1(x) = y…… (1)
⇒ x = f(y)
⇒ x = 3y + 5
⇒ x −5 = 3y
⇒ y = (x – 5)/3
Now substituting this value in (1) we get
So, f-1(x) = (x – 5)/3
Example 5: Consider f: R → R given by f(x) = 4x + 3. Show that f is invertible. Find the inverse of f.
Solution:
Given f: R → R given by f(x) = 4x + 3
Now we have to show that the given function is invertible.
Consider injection of f:
Let x and y be two elements of domain (R),
Such that f(x) = f(y)
⇒ 4x + 3 = 4y + 3
⇒ 4x = 4y
⇒ x = y
So, f is one-one.
Now surjection of f:
Let y be in the co-domain (R),
Such that f(x) = y.
⇒ 4x + 3 = y
⇒ 4x = y -3
⇒ x = (y-3)/4 in R (domain)
⇒ f is onto.
So, f is a bijection and, hence, it is invertible.
Now we have to find f -1
Let f-1(x) = y……. (1)
⇒ x = f (y)
⇒ x = 4y + 3
⇒ x − 3 = 4y
⇒ y = (x -3)/4
Now substituting this value in (1) we get
So, f-1(x) = (x-3)/4
Example 6: Consider f: R → R+ → [4, ∞) given by f(x) = x2 + 4. Show that f is invertible with inverse f−1 of f given by f−1(x) = √ (x-4) where R+ is the set of all non-negative real numbers.
Solution:
Given f: R → R+ → [4, ∞) given by f(x) = x2 + 4.
Now we have to show that f is invertible,
Consider injection of f:
Let x and y be two elements of the domain (Q),
Such that f(x) = f(y)
⇒ x2 + 4 = y2 + 4
⇒ x2 = y2
⇒ x = y (as co-domain as R+)
So, f is one-one
Now surjection of f:
Let y be in the co-domain (Q),
Such that f(x) = y
⇒ x2 + 4 = y
⇒ x2 = y – 4
⇒ x = √ (y-4) in R
⇒ f is onto.
So, f is a bijection and, hence, it is invertible.
Now we have to find f-1:
Let f−1 (x) = y…… (1)
⇒ x = f (y)
⇒ x = y2 + 4
⇒ x − 4 = y2
⇒ y = √ (x-4)
So, f-1(x) = √ (x-4)
Now substituting this value in (1) we get,
So, f-1(x) = √ (x-4)
Example 7:. If f(x) = (4x + 3)/ (6x – 4), x ≠ (2/3) show that fof(x) = x, for all x ≠ (2/3). What is the inverse of f?
Solution:
It is given that f(x) = (4x + 3)/ (6x – 4), x ≠ 2/3
Now we have to show fof(x) = x
(fof)(x) = f (f(x))
= f ((4x+ 3)/ (6x – 4))
= (4((4x + 3)/ (6x -4)) + 3)/ (6 ((4x +3)/ (6x – 4)) – 4)
= (16x + 12 + 18x – 12)/ (24x + 18 – 24x + 16)
= (34x)/ (34)
= x
Therefore, fof(x) = x for all x ≠ 2/3
=> fof = 1
Hence, the given function f is invertible and the inverse of f is f itself.
Example 8:. Consider f: R+ → [−5, ∞) given by f(x) = 9x2 + 6x − 5. Show that f is invertible with
f-1(x) = (√(x +6)-1)/3
Solution:
Given f: R+ → [−5, ∞) given by f(x) = 9x2 + 6x – 5
We have to show that f is invertible.
Injectivity of f:
Let x and y be two elements of domain (R+),
Such that f(x) = f(y)
⇒ 9x2 + 6x – 5 = 9y2 + 6y − 5
⇒ 9x2 + 6x = 9y2 + 6y
⇒ x = y (As, x, y ∈ R+)
So, f is one-one.
Surjectivity of f:
Let y is in the co domain (Q)
Such that f(x) = y
⇒ 9x2 + 6x – 5 = y
⇒ 9x2 + 6x = y + 5
⇒ 9x2 + 6x +1 = y + 6 (By adding 1 on both sides)
⇒ (3x + 1)2 = y + 6
⇒ 3x + 1 = √(y + 6)
⇒ 3x = √ (y + 6) – 1
⇒ x = (√ (y + 6)-1)/3 in R+ (domain)
f is onto.
So, f is a bijection and hence, it is invertible.
Now we have to find f-1
Let f−1(x) = y….. (1)
⇒ x = f (y)
⇒ x = 9y2 + 6y − 5
⇒ x + 5 = 9y2 + 6y
⇒ x + 6 = 9y2+ 6y + 1 (adding 1 on both sides)
⇒ x + 6 = (3y + 1)2
⇒ 3y + 1 = √ (x + 6)
⇒ 3y =√(x +6) -1
⇒ y = (√ (x+6)-1)/3
Now substituting this value in (1) we get,
So, f-1(x) = (√ (x+6)-1)/3
Example 9:. If f: R → R be defined by f(x) = x3 −3, then prove that f−1 exists and find a formula for f−1. Hence, find f−1 (24) and f−1 (5).
Solution:
Given f: R → R be defined by f(x) = x3 −3
Now we have to prove that f−1 exists
Injectivity of f:
Let x and y be two elements in domain (R),
Such that, x3 − 3 = y3 − 3
⇒ x3 = y3
⇒ x = y
So, f is one-one.
Surjectivity of f:
Let y be in the co-domain (R)
Such that f(x) = y
⇒ x3 – 3 = y
⇒ x3 = y + 3
⇒ x = ∛(y+3) in R
⇒ f is onto.
So, f is a bijection and, hence, it is invertible.
Finding f -1:
Let f-1(x) = y…….. (1)
⇒ x= f(y)
⇒ x = y3 − 3
⇒ x + 3 = y3
⇒ y = ∛(x + 3) = f-1(x) [from (1)]
So, f-1(x) = ∛(x + 3)
Now, f-1(24) = ∛ (24 + 3)
= ∛27
= ∛33
= 3
And f-1(5) =∛ (5 + 3)
= ∛8
= ∛23
= 2
Binary Operations
A binary operation ∗ on a set A is a function ∗ : A × A → A.
We denote * (a, b) by a * b.
Example Problems
Example 1: Show that subtraction and division are not binary operations on R.
Solution: N × N → N, given by (a, b) → a – b, is not binary operation, as the image of (2, 5) under ‘–’ is 2 – 5 = – 3 ∉ N.
Similarly, ÷: N × N → N, given by (a, b) → a ÷ b is not a binary operation, as the image of (2, 5) under ÷ is 2 ÷ 5 = 2/5 ∉ N.
Example 2: Let f : {2, 3, 4, 5} → {3, 4, 5, 9} and g : {3, 4, 5, 9} → {7, 11, 15} be functions defined as f(2) = 3, f(3) = 4, f(4) = f(5) = 5 and g (3) = g (4) = 7 and g (5) = g (9) = 11. Find gof.
Solution: From the given, we have:
gof(2) = g (f(2)) = g (3) = 7
gof (3) = g (f(3)) = g (4) = 7
gof(4) = g (f(4)) = g (5) = 11
gof(5) = g (5) = 11
Example 3: Show that the relation R in the set Z of integers given by R = {(a, b) : 2 divides a – b} is an equivalence relation.
Solution: R is reflexive, as 2 divides (a – a) for all a ∈ Z.
Further, if (a, b) ∈ R, then 2 divides a – b.
Therefore, 2 divides b – a.
Hence, (b, a) ∈ R, which shows that R is symmetric.
Similarly, if (a, b) ∈ R and (b, c) ∈ R, then (a – b) and (b – c) are divisible by 2.
Now, a – c = (a – b) + (b – c) is even. (from the above statements)
From this,
(a – c) is divisible by 2.
This shows that R is transitive.
Thus, R is an equivalence relation in Z.

 Chintu
Chintu
