LINES AND ANGLES

Chapter -5

Lines And Angles

Basic Terms and Definitions

Recall that a part (or portion) of a line with two end points is called a line-segment and a part of a line with one end point is called a ray. Note that the line segment AB is denoted by AB, and its length is denoted by AB. The ray AB is denoted by AB , and a line is denoted by AB . However, we will not use these symbols, and will denote the line segment AB, ray AB, length AB and line AB by the same symbol, AB. The meaning will be clear from the context. Sometimes small letters l , m, n, etc. will be used to denote lines.
If three or more points lie on the same line, they are called collinear points; otherwise they are called non-collinear points.
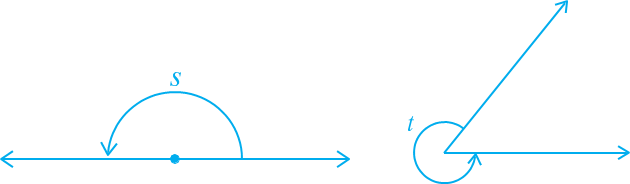
Recall that an angle is formed when two rays originate from the same end point. The rays making an angle are called the arms of the angle and the end point is called the ver. tax of the angle. You have studied different types of angles, such as acute angle, right angle, obtuse angle, straight angle and reflex angle in earlier classes.

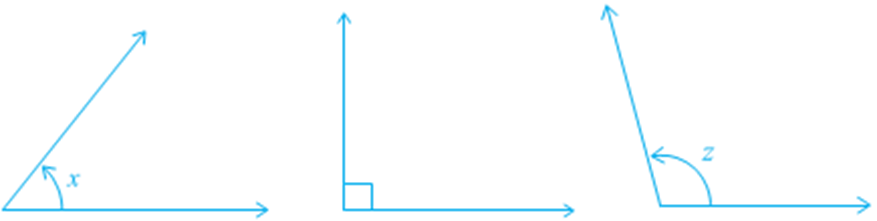
Types of Angles

An acute angle measures between 0° and 90°, whereas a right angle is exactly equal to 90°. An angle greater than 90° but less than 180° is called an obtuse angle. Also, recall that a straight angle is equal to 180°. An angle which is greater than 180° but less than 360° is called a reflex angle. Further, two angles whose sum is 90° are called complementary angles, and two angles whose sum is 180° are called supplementary angles.
You have also studied about adjacent angles in the earlier classes. Two angles are adjacent, if they have a common vertex, a common arm and their non-common arms are on different sides of the common arm. In Fig., ∠ ABD and ∠ DBC are adjacent Angles. Ray BD is their common arm and point B is their common vertex. Ray BA and ray BC are non common arms. Moreover, when two angles are adjacent, then their sum is always equal to the angle formed by the two non- common arms. So, we can write.

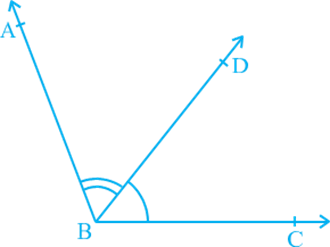
Adjacent angles

∠ ABC = ∠ ABD + ∠ DBC.
Note that ∠ ABC and ∠ ABD are not adjacent angles. Why? Because their non- common arms BD and BC lie on the same side of the common arm BA.
If the non-common arms BA and BC in, form a line then it will look like Fig. 6.3. In this case, ∠ ABD and ∠ DBC are called linear pair of angles.

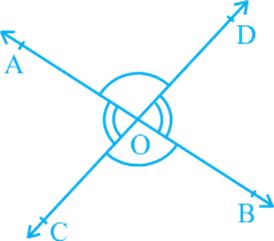
You may also recall the vertically opposite angles formed when two lines, say AB and CD, intersect each other, say at the point O. There are two pairs of vertically opposite angles.
One pair is ∠AOD and ∠BOC. Can you find the other pair?

Intersecting Lines and Non-intersecting Lines
Draw two different lines PQ and RS on a paper. You will see that you can draw them in two different ways as shown in Fig.

 

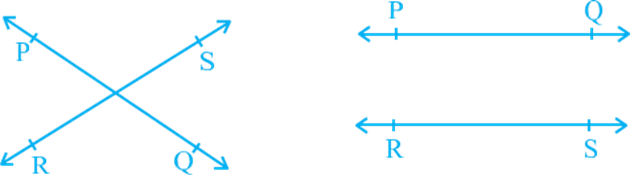
Recall the notion of a line that it extends indefinitely in both directions. Lines PQ and RS in Fig. 6.5 (i) are intersecting lines and in Fig. 6.5 (ii) are parallel lines. Note that the lengths of the common perpendiculars at different points on these parallel lines are the same. This equal length is called the distance between two parallel lines.

Pairs of Angles

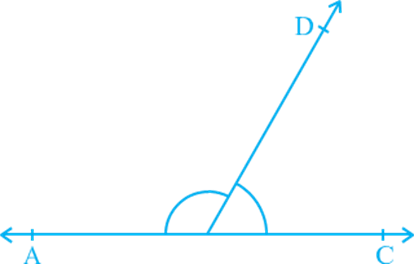
In Section 6.2, you have learnt the definitions of some of the pairs of angles such as complementary angles, supplementary angles, adjacent angles, linear pair of angles, etc. Can you think of some relations between these angles? Now, let us find out the relation between the angles formed when a ray stands on a line. Draw a figure in which a ray stands on a line as shown in. Name the line as AB and the ray as OC. What are the angles formed at the point O? They are ∠ AOC, ∠ BOC and ∠ AOB.

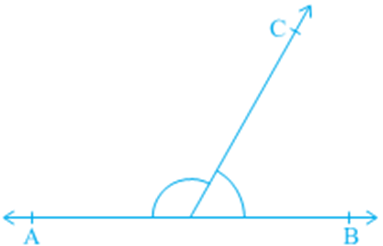
Can we write ∠ AOC + ∠ BOC = ∠ AOB?                                                        (1)
Yes! (Why? Refer to adjacent angles in Section 6.2)
What is the measure of ∠ AOB? It is 180°.   (Why?)                                         (2)
 From (1) and (2), can you say that ∠ AOC + ∠ BOC = 180°?    Yes! (Why?)
From the above discussion, we can state the following Axiom:

Axiom 6.1: If a ray stands on a line, then the sum of two adjacent angles so formed is 180°.
Recall that when the sum of two adjacent angles is 180°, then they are called a Linear pair of angles.
In Axiom 6.1, it is given that ‘a ray stands on a line’. From this ‘given’, we have concluded that ‘the sum of two adjacent angles so formed is 180°’. Can we write Axiom 6.1 the other way? That is, take the ‘conclusion’ of Axiom 6.1 as ‘given’ and the ‘given’ as the ‘conclusion’. So it becomes:
(A) If the sum of two adjacent angles is 180°, then a ray stands on a line (that is, the non-common arms form a line).

Axiom

Let us now examine the case when two lines intersect each other.
Recall, from earlier classes, that when two lines intersect, the vertically opposite angles are equal. Let us prove this result now. See Appendix 1 for the ingredients of a proof, and keep those in mind while studying the proof given below.
Theorem 6.1: If two lines intersect each other, then the vertically opposite angles  are equal.
Proof: In the statement above, it is given that ‘two lines intersect each other’. So, let AB and CD be two lines intersecting at O as shown in. They lead to two pairs of vertically opposite angles, namely,

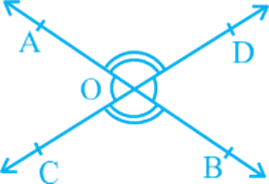
 (i) ∠ AOC and ∠ BOD (ii) ∠ AOD and ∠ BOC.
We need to prove that ∠ AOC = ∠ BOD  and ∠ AOD = ∠ BOC.
Now, ray OA stands on line CD.
Therefore, ∠ AOC + ∠ AOD = 180°   (Linear pair axiom)                        (1)
Can we write ∠ AOD + ∠ BOD = 180°? Yes! (Why?)                               (2)
From (1) and (2), we can write
∠ AOC + ∠ AOD = ∠ AOD + ∠ BOD
This implies that ∠ AOC = ∠ BOD     (Refer Section 5.2, Axiom 3)
Similarly, it can be proved that ∠AOD = ∠BOC   
Now, let us do some examples based on Linear Pair Axiom and Theorem 6.1.

Parallel Lines and a Transversal

Recall that a line which intersects two or more lines at   distinct  points  is  called  a   transversal (see Fig.  6.18). Line l intersects lines m and n at points P and  Q respectively. Therefore, line l is a transversal for lines m and n. Observe that four angles are formed at each of the points P and Q.
Let us name these angles as ∠ 1, ∠ 2, . . ., ∠8 as shown in Fig. 6.18..

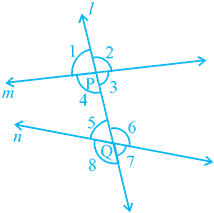
∠ 1, ∠ 2, ∠ 7 and ∠ 8 are called exterior angles, while ∠ 3, ∠ 4, ∠ 5 and ∠ 6 are called interior angles.
Recall that in the earlier classes, you have named some pairs of angles formed when a transversal intersects two lines. These are as follows:
(a) Corresponding angles:
(i) ∠ 1 and ∠ 5      (ii) ∠ 2 and ∠ 6
(b)  Alternate interior angles:
(i) ∠ 4 and ∠ 6      (ii) ∠ 3 and ∠ 5
(c)  Alternate exterior angles:
(i) ∠ 1 and ∠ 7      (ii) ∠ 2 and ∠ 8
(d)  Interior angles on the same side of the transversal:
(i) ∠ 4 and ∠ 5      (ii) ∠ 3 and ∠ 6
Interior angles on the same side of the transversal are also referred to as consecutive    interior angles or allied angles or co-interior angles. Further, many a times, we simply use the words alternate angles for alternate interior angles.

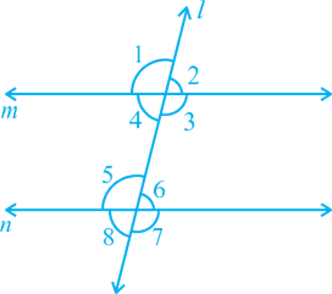
Now, let us find out the relation between the angles in these pairs when line m is parallel to line n. You know that the ruled lines of your notebook are parallel to each other. So, with ruler and pencil, draw two parallel lines along any two of these lines and a transversal to intersect them as shown in Fig. 6.19.
Now, measure any pair of corresponding angles and find out the relation between them. You may find that : ∠1 = ∠5, ∠2 = ∠6, ∠4 = ∠8 and ∠3 = ∠7. From this, you may conclude the following axiom.
Axiom 6.3: If a transversal intersects two parallel lines, then each pair of corresponding angles is equal.
Axiom 6.3 is also referred to as the corresponding angles axiom . Now, let us discuss the converse of this axiom which is as follows:
If a transversal intersects two lines such that a pair of corresponding angles is equal, then the two lines are parallel.
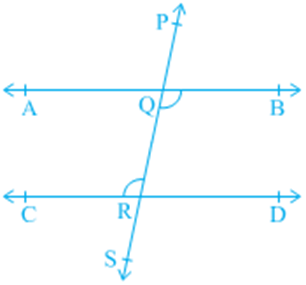
Does this statement hold true? It can be verified as follows: Draw a line AD and mark points B and C on it. At B and C, construct ∠ ABQ and ∠ BCS equal to each other as shown in Fig. 6.20 (i).

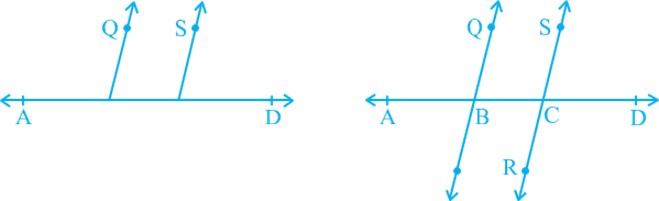
Produce QB and SC on the other side of AD to form two lines PQ and RS [see Fig. 6.20 (ii)]. You may observe that the two lines do not intersect each other. You may also draw common perpendiculars to the two lines PQ and RS at different points and measure their lengths. You will find it the same everywhere. So, you may conclude that the lines are parallel. Therefore, the converse of corresponding angles axiom is also true. So, we have the following axiom:
Axiom 6.4: If a transversal intersects two lines such that a pair of corresponding angles is equal, then the two lines are parallel to each other.
Can we use corresponding angles axiom to find out the relation between the alternate interior angles when a transversal intersects two parallel lines? In Fig. 6.21, transversal PS intersects parallel lines AB and CD at points Q and R respectively.

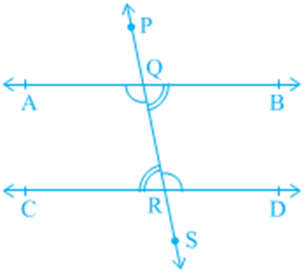
Is ∠ BQR = ∠ QRC and ∠ AQR = ∠ QRD? You know that ∠ PQA = ∠ QRC            (1)
                     (Corresponding angles axiom)
Is       ∠ PQA = ∠ BQR? Yes! (Why?)             (2)
So, from (1) and (2), you may conclude that
               ∠ BQR = ∠ QRC.
Similarly,    ∠ AQR = ∠ QRD.
This result can be stated as a theorem given below:
Theorem: If a transversal intersects two parallel lines, then each pair of alternate interior angles is equal.
Now, using the converse of the corresponding angles axiom, can we show the two lines parallel if a pair of alternate interior angles is equal? In Fig. 6.22, the transversal PS  intersects lines AB and CD at points Q and R respectively such that

∠ BQR = ∠ QRC.
Is AB || CD?
∠ BQR = ∠ PQA   (Why?)       (1)
But,   ∠ BQR = ∠ QRC  (Given)       (2)
So, from (1) and (2), you may conclude that
∠ PQA = ∠ QRC
But they are corresponding angles.

So, AB || CD  (Converse of corresponding angles axiom)
This result can be stated as a theorem given below:
Theorem 6.3: If a transversal intersects two lines such that a pair of alternate interior angles is equal, then the two lines are parallel.
In a similar way, you can obtain the following two theorems related to interior angles on the same side of the transversal.
Theorem 6.4: If a transversal intersects two parallel lines, then each pair of interior angles on the same side of the transversal is supplementary.
Theorem 6.5: If a transversal intersects two lines such that a pair of interior angles  on the same side of the transversal is supplementary, then the two lines are parallel.
You may recall that you have verified all the above axioms and theorems in earlier classes through activities. You may repeat those activities here also.

Lines Parallel to the Same Line

If two lines are parallel to the same line, will they be parallel to each other? Let us check it. See Fig. 6.23 in which line m || line l and line n || line l.
Let us draw a line t transversal for the lines, l, m and n. It is given that line m || line l and line n || line l.
Therefore, ∠ 1 = ∠ 2 and ∠ 1 = ∠ 3
                (Corresponding angles axiom)
So,    ∠ 2 = ∠ 3 (Why?)
But ∠ 2 and ∠ 3 are corresponding angles and they are equal.
Therefore, you can say that

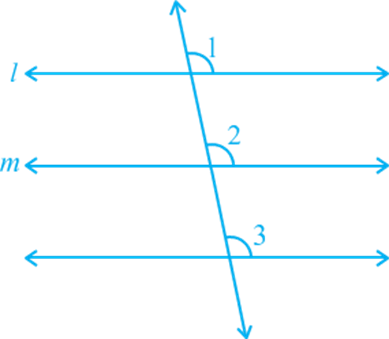
Line m || Line n
(Converse of corresponding angles axiom)
This result can be stated in the form of the following theorem:
Theorem 6.6: Lines which are parallel to the same line are parallel to each other.
Note: The property above can be extended to more than two lines also. Now, let us solve some examples related to parallel lines.

Angle Sum Property of a Triangle

In the earlier classes, you have studied through activities that the sum of all the angles of a triangle is 180°. We can prove this statement using the axioms and theorems related to parallel lines.
Theorem 6.7: The sum of the angles of a triangle is 180º.
Proof: Let us see what is given in the statement above, that is, the hypothesis and what we need to prove. We are given a triangle PQR and ∠ 1, ∠ 2 and ∠ 3 are the angles of Δ PQR (see Fig.)

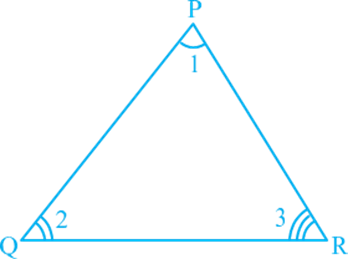
We need to prove that ∠ 1 + ∠ 2 + ∠ 3 = 180°. Let us  draw a line XPY parallel to QR through the opposite vertex P, as shown in Fig. 6.35, so that we can use the properties related to parallel lines.
Now, XPY is a line.
Therefore,   ∠ 4 + ∠ 1 + ∠ 5 = 180°   (1)
But XPY || QR and PQ, PR are transversal.
So,    ∠ 4 = ∠ 2     and    ∠ 5 = ∠ 3
            (Pairs of alternate angles)

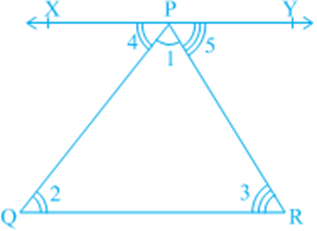
Substituting ∠ 4 and ∠ 5 in (1), we get
                                       ∠ 2 + ∠ 1 + ∠ 3 = 180°
            That is,      ∠ 1 + ∠ 2 + ∠ 3 = 180° 
Recall that you have studied about the formation of an exterior angle of a triangle in the earlier classes (see Fig. 6.36). Side QR is produced to point S, ∠ PRS is called an exterior angle of ΔPQR.
 Is     ∠ 3 + ∠ 4 = 180°? (Why?)        (1)
Also, see that
∠ 1 + ∠ 2 + ∠ 3 = 180° (Why?)         (2)
From (1) and (2), you can see that
∠ 4 = ∠ 1 + ∠ 2.
This result can be stated in the form of a theorem as given below:

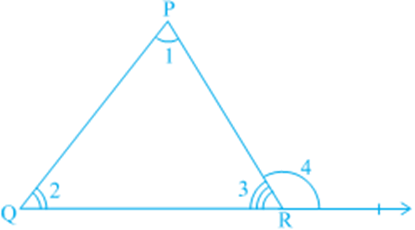
Theorem: If a side of a triangle is produced, then the exterior angle so formed is equal to the sum of the two interior opposite angles.
It is obvious from the above theorem that an exterior angle of a triangle is greater than either of its interior apposite angles.
Now, let us take some examples based on the above theorems.