NUMBER SYSTEMS

Chapter -1

Number Systems

Introduction

In your earlier classes, you have learnt about the number line and how to represent various types of numbers on it.

Just imagine you start from zero and go on walking along this number line in the positive direction. As far as your eyes can see, there are numbers, numbers and numbers! 

Now suppose you start walking along the number line, and collecting some of the numbers. Get a bag ready to store them! 
You might begin with picking up only natural numbers like 1, 2, 3, and so on. You   know that this list goes on forever. (Why is this true?) So, now your bag contains infinitely many natural numbers! Recall that we denote this collection by the symbol N.  

Now turn and walk all the way back, pick up zero and put it into the bag. You now have the collection of whole numbers which is denoted by the symbol W.

Now, stretching in front of you are many, many negative integers. Put all the negative integers into your bag. What is your new collection? Recall that it is the collection of all integers, and it is denoted by the symbol Z.

Are there some numbers still left on the line? Of course! There are numbers like                                                              

 

Collection of rational numbers. The collection of rational numbers is denoted by Q.
‘Rational’ comes from the word ‘ratio’, and Q comes from the word ‘quotient’.
You may recall the definition of rational numbers:
A number ‘r’ is called a rational number, if it can be written in the form P/q, where p and q are integers and q ≠ 0. (Why do we insist that q ≠ 0?)
Notice that all the numbers now in the bag can be written in the form   , where p and q are integers and q ≠ 0. For example, – 25 can be written as (-25)/1; here p = – 25 and q = 1. Therefore, the rational numbers do not have a unique representation in the form p/q, where p and q are integers and q ≠ 0. For example, 1/2=2/4=10/20=25/50=47/94, and so on. These are equivalent rational numbers (or fractions). However,
When we say that p/q is a rational number, or when we represent p/q on the number line, we assume that q ≠ 0 and that p and q have no common factors other than 1 (that is, p and q are co-prime). So, on the number line, among the infinitely many fractions equivalent to 1/2, we will choose 1/2 to represent all of them.
Now, let us solve some examples about the different types of numbers, which you have studied in earlier classes. 

Irrational Numbers

We saw, in the previous section, that there may be numbers on the number line that are not rationals. In this section, we are going to investigate these numbers. So far, all The numbers you have come across, are of the form p/q, where p and q are integers and q ≠ 0. So, you may ask: are there numbers which are not of this form? There are indeed such numbers. Let us formally define these numbers.
A number’s’ is called irrational, if it cannot be written in the form p/q, where p and q are integers and q ≠ 0. we call the collection of real numbers,
Which is denoted by R.? Therefore, a real number is either rational or irrational. So, we can say that every real number is represented by a unique point on the number line. Also, every point on the number line represents a unique real number. This is why we call the number line, the real number line.

Let us see how we can locate some of the irrational numbers on the number line.
We have just seen that OB = √2. Using a compass with centre O and radius OB, draw an arc intersecting the number line at the point P. Then P corresponds to √2 on the number line.
The decimal expansion of a rational number is terminating or non- terminating recurring. Moreover, a number whose decimal expansion is terminating or non-terminating recurring is rational.
The decimal expansion of an irrational number is non-terminating non-recurring. Moreover, a number whose decimal expansion is non-terminating non-recurring is irrational.

Representing Real Numbers on the Number Line

Suppose we want to locate 2.665 on the number line. We know that this lies between     2and 3.So, let us look closely at the portion of the number line between 2 and 3. Suppose we divide this into 10 equal parts and mark each point of division as (i). Then the first mark to the right of 2 will represent 2.1, the second 2.2, and so on. You might be finding some difficulty in observing these points of division between 2 and 3
(i). To have a clear view of the same, you may take a magnifying glass and look at the portion between 2 and 3. It will look like what you see

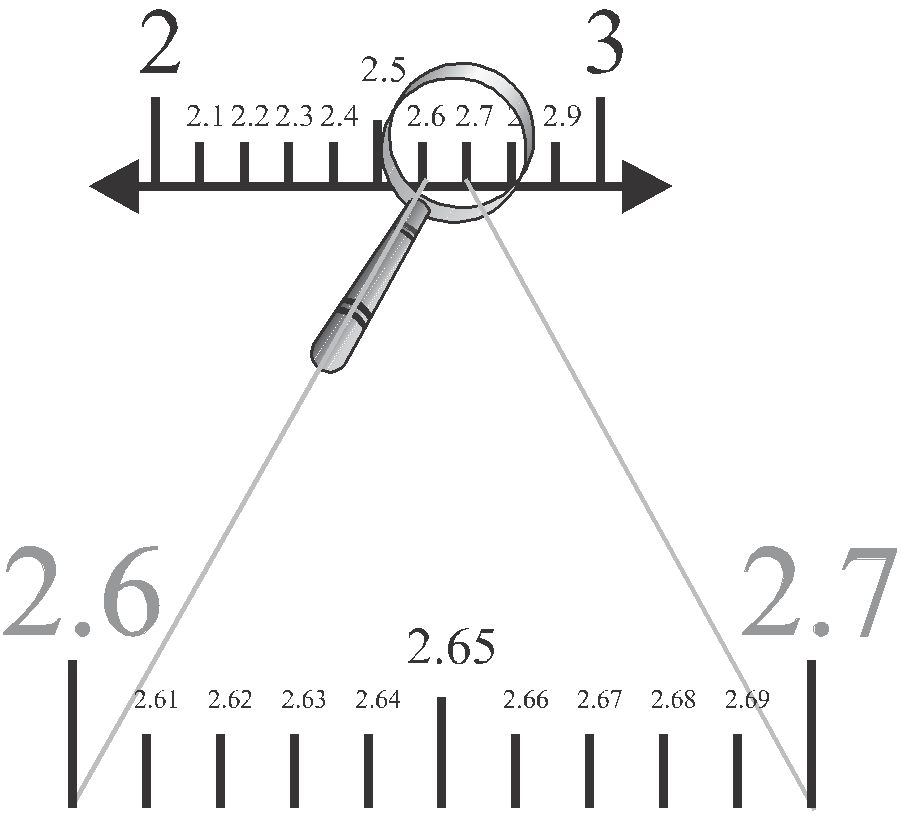
(ii). Now, 2.665 lie between 2.6 and 2.7. So, let us focus on the portion between 2.6 and 2.7. We imagine dividing this again into ten equal parts. The first mark will represent 2.61, the next 2.62, and so on. To see this clearly, we magnify this as shown (ii).

Operations on Real Numbers

You have learnt, in earlier classes that rational numbers satisfy the commutative, associative and distributive laws for addition and multiplication. Moreover, if we add, subtract, multiply or divide (except by zero) two rational numbers, we still get a rational number (that is, rational numbers are ‘closed’ with respect to addition, subtraction, multiplication and division). It turns out that irrational numbers also satisfy the commutative, associative and distributive laws for addition and multiplication. However, the sum, difference, quotients and products of irrational numbers are not always

 

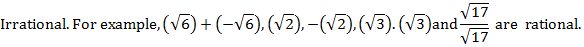
Let us look at what happens when we add and multiply a rational number with an irrational number. For example,  is irrational. What about 2 +  and  since  has a non-recurring decimal expansion, the same is true for 2 +  and . Therefore, both 2 +  and  are also irrational numbers.