LINEAR EQUATIONS IN TWO VARIABLES

Chapter -7

Linear Equations In Two Variables

 Introduction

In earlier classes, you have studied linear equations in one variable. Can you write down a linear equation in one variable? You may say that x + 1 = 0, x + √2 = 0 and √2 y+√3=0 are examples of linear equations in one variable. You also know that such equations have a unique (i.e., one and only one) solution. You may also remember how to represent the solution on a number line. In this chapter, the knowledge of linear equations in one variable shall be recalled and extended to that of two variables. You will be considering questions like: Does a linear equation in two variables have a solution? If yes, is it unique? What does the solution look like on the Cartesian plane? You shall also use the concepts you studied in Chapter 3 to answer these questions.

Linear Equations

Let us first recall what you have studied so far. Consider the following equation:
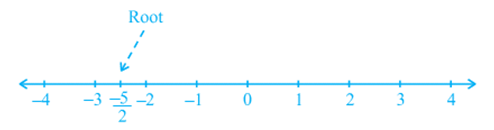
                                             2x + 5 = 0

Its solution, i.e., the root of the equation, is – 5/2. This can be represented on the number line as shown below:  

While solving an equation, you must always keep the following points in mind: The solution of a linear equation is not affected when:
(i) The same number is added to (or subtracted from) both the sides of the equation.
(ii)You multiply or divide both the sides of the equation by the same non-zero number.
Let us now consider the following situation:
In a One-day International Cricket match between India and Sri Lanka played in Nagpur, two Indian batsmen together scored 176 runs. Express this information in the form of an equation.
Here, you can see that the score of neither of them is known, i.e., there are two unknown quantities. Let us use x and y to denote them. So, the number of runs scored by one of the batsmen is x, and the number of runs scored by the other is y.
We know that
                                                            x + y = 176,

Which is the required equation?
This is an example of a linear equation in two variables. It is customary to denote the variables in such equations by x and y, but other letters may also be used. Some examples of linear equations in two variables are:

2s + 3t = 5, p + 4q = 7, πu + 5v = 9 and 3=√2 x-7y.
Note that you can put these equations in the form 1.2s + 3t – 5 = 0,

P + 4q – 7 = 0, πu + 5v – 9 = 0 and             -3=0,     respectively.

So, any equation which can be put in the form ax + by + c = 0, where a, b and c are real numbers, a and b are not

both zero, is called a linear equation in two variables.

This means that you can think of many such equations.

Solution of a Linear Equation

You have seen that every linear equation in one variable has a unique solution. What can you say about the solution of a linear equation involving two variables? As there are two variables in the equation, a solution means a pair of values, one for x and one for y which satisfy the given equation. Let us consider the equation 2 x + 3y = 12. Here, x = 3 and y = 2 is a solution because when you substitute x = 3 and y = 2 in the equation above, you find that

  2x + 3y = (2 × 3) + (3 × 2) = 12       

This solution is written as an ordered pair (3, 2), first writing the value for x and then the value for y. Similarly, (0, 4) is also a solution for the equation above.
On the other hand, (1, 4) is not a solution of 2x + 3y = 12, because on putting x = 1 and y = 4 we get 2x + 3y = 14, which is not 12. Note that (0, 4) is a solution but not (4, 0).
You have seen at least two solutions for 2x + 3y = 12, i.e., (3, 2) and (0, 4). Can you find any other solution? Do you agree that (6, 0) is another solution? Verify the same. In fact, we can get many many solutions in the following way. Pick a value of your choice for x (say x = 2) in 2x + 3y = 12. Then the equation reduces to 4 + 3 y = 12,
Which is a linear equation in one variable. On solving this, you get y=8/3.so (2,8/3) is another solution of 2x + 3y = 12. This gives y=22/3.So,(-5,22/3) is another solution of 2x + 3y = 12. So there is no end to different solutions of a linear equation in two variables. That is, a linear equation in two variables has infinitely many solutions.

Graph of a Linear Equation in Two Variables  

So far, you have obtained the solutions of a linear equation in two variables algebraically. Now, let us look at their geometric representation. You know that each such equation has infinitely many solutions. How can we show them in the coordinate plane? You may have got some indication in which we write the solution as pairs of values. The solutions of the linear equation in Example 3, namely,

                                                     x + 2y = 6
Can be expressed in the form of a table as follows by writing the values of y below the corresponding values of x:

In the previous chapter, you studied how to plot the points on a graph paper. Let us plot the points (0, 3), (2, 2), (4, 1) and (6, 0) on a graph paper. Now join any two of these points and obtain a line. Let us call this as line AB (see Fig). 
 

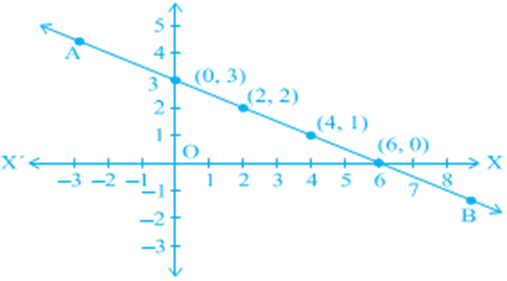
 Do you see that the other two points also lie on the line AB? Now, pick another point on this line, say (8, –1). Is this a solution? In fact, 8 + 2(–1) = 6. So, (8, –1) is a solution. Pick any other point on this line AB and verify whether its coordinates satisfy the equation or not. Now, take any point not lying on the line AB, say (2, 0). Do its coordinates satisfy the equation? Check, and see that they do not.

Let us list our observations:

Every point whose coordinates satisfy Equation (1) lies on the line AB.
Every point (a, b) on the line AB gives a solution x = a, y = b of Equation (1).
Any point, which does not lie on the line AB, is not a solution of Equation (1).

So, you can conclude that every point on the line satisfies the equation of the line and every solution of the equation is a point on the line. In fact, a linear equation in two variables is represented geometrically by a line whose points make up the collection of solutions of the equation. This is called the graph of the linear equation. So, to obtain the graph of a linear equation in two variables, it is enough to plot two points corresponding to two solutions and join them by a line. However, it is advisable to plot more than two such points so that you can immediately check the correctness of the graph.