SURFACE AREAS AND VOLUMES

Chapter -11

SURFACE AREAS AND VOLUMES

Surface Area of a Cuboid and a Cube

Have you looked at a bundle of many sheets of paper? How does it look? Does it look like what you see in Fig.

That makes up a cuboid. How much of brown paper would you need, if you want to cover this cuboid? Let us see:
First we would need a rectangular piece to cover the bottom of the bundle. That would be as shown in Fig (a)
 

Then we would need two long rectangular pieces to cover the two side ends. Now, it would look like Fig (b).

Now to cover the front and back ends, we would need two more rectangular pieces of a different size. With them, we would now have a figure as shown in Fig (c).

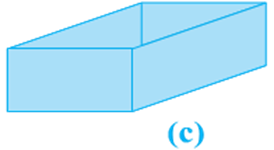
This figure, when opened out, would look like Fig (d).

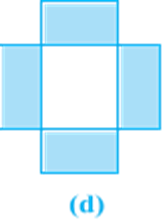
Finally, to cover the top of the bundle, we would require another rectangular piece exactly like the one at the bottom, which if we attach on the right side, it would look like Fig (e).

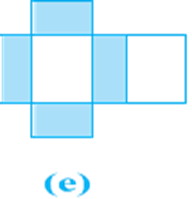
So we have used six rectangular pieces to cover the complete outer surface of the cuboid.

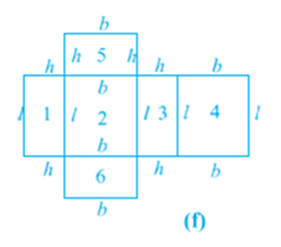
This shows us that the outer surface of a cuboid is made up of six rectangles (in fact, rectangular regions, called the faces of the cuboid), who’s areas can be found by multiplying length by breadth for each of them separately and then adding the six areas together.
Now, if we take the length of the cuboid as l, breadth as b and the height as h, then the figure with these dimensions would be like the shape you see in Fig (f).
So, the sum of the areas of the six rectangles is:

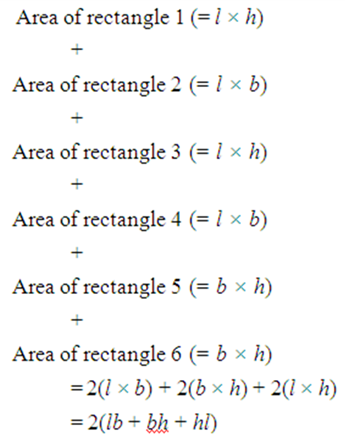
This gives us:

Where l, b and h are respectively the three edges of the cuboid.
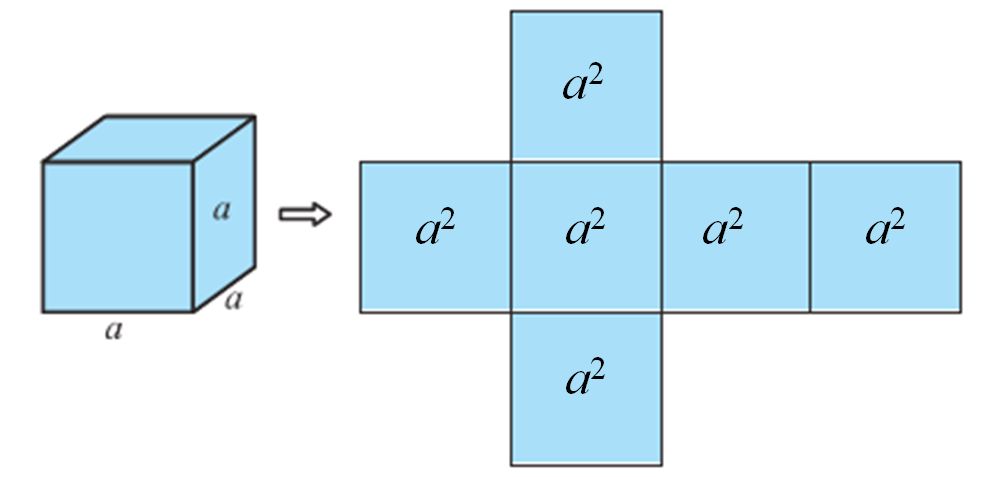
Recall that a cuboid, whose length, breadth and height are all equal, is called a cube. If   each edge of the cube is a, then the surface area of this cube would be

 

Where a is the edge of the cube.

Suppose, out of the six faces of a cuboid, we only find the area of the four faces, leaving the bottom and top faces. In such a case, the area of these four faces is called the  lateral surface area of the cuboid. So, lateral surface area of a cuboid of length l, breadth b and height h is equal to 2lh + 2bh or 2(l + b)h. Similarly, lateral surface area of a cube of side a is equal to 4a².
Keeping in view of the above, the surface area of a cuboid (or a cube) is sometimes also referred to as the total surface area.

Surface Area of a Right Circular Cylinder

If we take a number of circular sheets of paper and stack them up as we stacked up rectangular sheets earlier, what would we get (see Fig.)

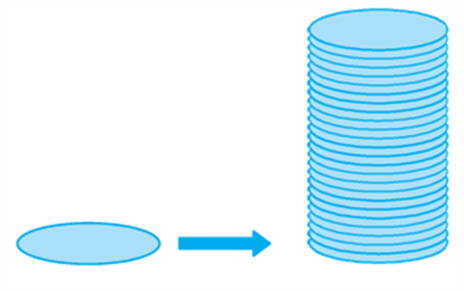
Here, if the stack is kept vertically up, we get what is called a right circular cylinder, since it has been kept at right angles to the base, and the base is circular. Let us see what kind of cylinder is not a right circular cylinder.
In Fig (a), you see a cylinder, which is certainly circular, but it is not at right angles to the base. So, we can not say this a right circular cylinder.

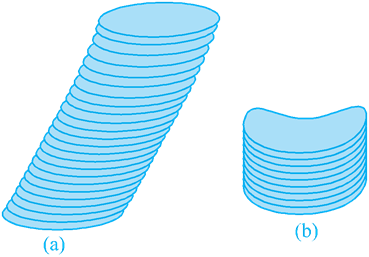
Of course, if we have a cylinder with a non circular base, as you see in Fig (b). then we also cannot call it a right circular cylinder.
So curved surface area of the cylinder = area of the rectangular sheet = length × breadth
 = perimeter of the base of the cylinder x h    

Where r is the radius of the base of the cylinder and h is the height of the cylinder.

Where h is the height of the cylinder and r its radius.

Surface Area of a Right Circular Cone

So, far have been generating solids by stacking up congruent figures. Incidentally, such figures are called prisms. Now let us look at another kind of solid which is not a prism. (These kinds of solids are called pyramids). Let us see how we can generate them.

Activity: Cut out a right-angled triangle ABC right angled at B. Paste a long thick string along one of the perpendicular sides say AB of the triangle [see Fig (a)]. Hold the string with your hands on either sides of the triangle and rotate the triangle about the string a number of times. What happens? Do you recognize the shape that the triangle is forming as it rotates around the string [see Fig (b)] Does it remind you of the time you had eaten an ice-cream heaped into a container of that shape [see Fig (c) and (d)]?

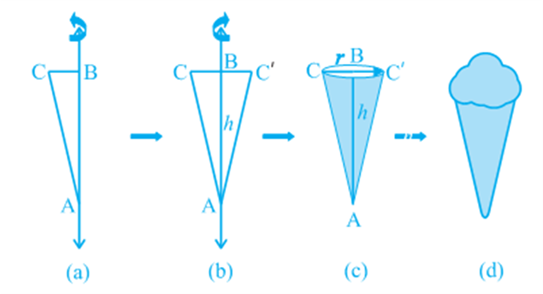
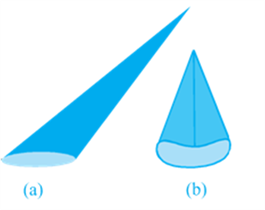
This is called a right circular cone. In Fig (c) of the right circular cone, the point A is called the vertex, AB is called the height, BC is called the radius and AC is called the slant height of the cone. Here B will be the centre of circular base of the cone. The height, radius and slant height of the cone are usually denoted by h, r and l respectively. Once again, let us see what kind of cone we can not call a right circular cone. Here, you are (see Fig)! What you see in these figures are not right circular cones; because in (a), the line joining its vertex to the centre of its base is not at right angle to the base, and in (b) the base is not circular.

As in the case of cylinder, since we will be studying only about right circular cones, remember that by ‘cone’ in this chapter, we shall mean a ‘right circular cone.’

Where r is its base radius and l its slant height.

Surface Area of a Sphere

What is a sphere? Is it the same as a circle? Can you draw a circle on a paper? Yes, you can, because a circle is a plane closed figure whose every point lies at a constant distance (called radius) from a fixed point, which is called the centre of the circle. Now if you paste a string along a diameter of a circular disc and rotate it as you had rotated the triangle in the previous section, you see a new solid (see Fig). What does it resemble? A ball? Yes. It is called a sphere.

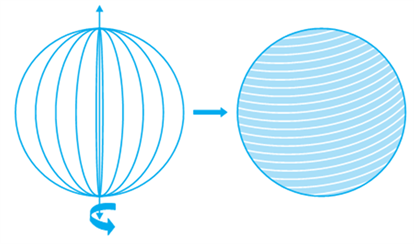
Can you guess what happens to the centre of the circle, when it forms a sphere on rotation? Of course, it becomes the centre of the sphere. So, a sphere is a three dimensional figure (solid figure), which is made up of all points in the space,
which lie at a constant distance called the radius, from a fixed point called the centre of the sphere.
The string, which had completely covered the surface area of the sphere, has been used to completely fill the regions of four circles, all of the same radius as of the sphere.
So, what does that mean? This suggests that the surface area of a sphere of radius 
r = 4 times the area of a circle of radius r = 4 = × (πr²)

Where r is the radius of the sphere,

Where r is the radius of the sphere of which the hemisphere is a part.
Now taking the two faces of a hemisphere, its surface  

Volume of a Cuboid

You have already learnt about volumes of certain figures (objects) in earlier classes. Recall that solid objects occupy space. The measure of this occupied space is called the Volume of the object.
Note: If an object is solid, then the space occupied by such an object is measured, and is termed the Volume of the object. On the other hand, if the object is hollow, then interior is empty, and can be filled with air, or some liquid that will take the shape of its container. In this case, the volume of the substance that can fill the interior is called the capacity of the container. In short, the volume of an object is the measure of the space it occupies, and the capacity of an object is the volume of substance its interior can accommodate. Hence, the unit of measurement of either of the two is cubic unit.
So, if we were to talk of the volume of a cuboid, we would be considering the measure of the space occupied by the cuboid.
Further, the area or the volume is measured as the magnitude of a region. So, correctly speaking, we should be finding the area of a circular region, or volume of a cuboidal region, or volume of a spherical region, etc. But for the sake of simplicity, we say, find the area of a circle, volume of a cuboid or a sphere even though these mean only their boundaries.

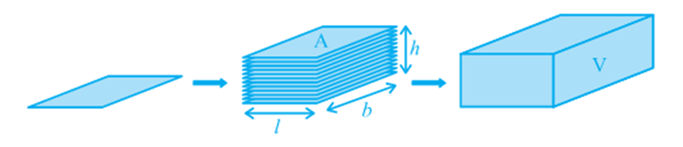
Observe Fig. Suppose we say that the area of each rectangle is A, the height up to which the rectangles are stacked is h and the volume of the cuboid is V. Can you tell what would be the relationship between V, A and h?
The  area  of  the  plane  region  occupied  by  each  rectangle  ×  height
                                = Measure of the space occupied by the cuboid

So, we get A × h = V

or l × b × h, where l, b and h are respectively the length, breadth and height of the cuboid.

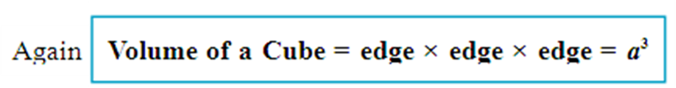
Where a is the edge of the cube (see Fig).
So, if a cube has edge of 12 cm,
then volume of the cube = 12 × 12 × 12 cm³
                                        = 1728 cm³.

Recall that you have learnt these formulae in earlier classes. Now let us take some examples to illustrate the use of these formulae:

Volume of a Cylinder Volume of a Right Circular Cone

Just as a cuboid is built up with rectangles of the same size, we have seen that a right circular cylinder can be built up using circles of the same size. So, using the same argument as for a cuboid, we can see that the volume of a cylinder can be obtained as:
base area × height  = area of circular base × height = πr²h

Where r is the base radius and h is the height of the cylinder.
In Fig, can you see that there is a right circular cylinder and a right circular cone of the same base radius and the same height?

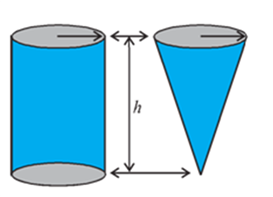
Activity: Try to make a hollow cylinder and a hollow cone like this with the same base radius and the same height (see Fig). Then, we can try out an experiment that will help us, to see practically what the volume of a right circular cone would be!

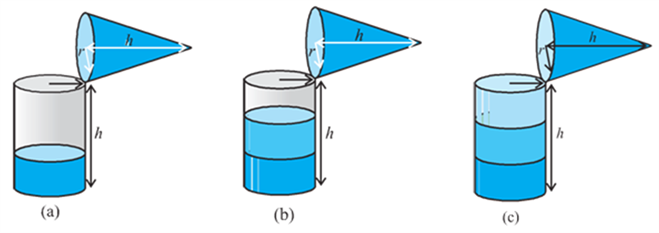
So, let us start like this.
Fill the cone up to the brim with sand once, and empty it into the cylinder. We find that it fills up only a part of the cylinder [see Fig (a)].
When we fill up the cone again to the brim, and empty it into the cylinder, we see that the cylinder is still not full [see Fig (b)].
When the cone is filled up for the third time, and emptied into the cylinder, it can be seen that the cylinder is also full to the brim [see Fig (c)].
With this, we can safely come to the conclusion that three times the volume of a cone, makes up the volume of a cylinder, which has the same base radius and the same height as the cone, which means that the volume of the cone is one-third the volume of the cylinder.

Where r is the base radius and h is the height of the cone. 

Volume of a sphere

Now, let us see how to go about measuring the volume of a sphere. First, take two or three spheres of different radii, and a container big enough to be able to put each of the spheres into it, one at a time. Also, take a large trough in which you can place the container. Then, fill the container up to the brim with water [see Fig (a)].
Now, carefully place one of the spheres in the container. Some of the water from the container will over flow into the trough in which it is kept [see Fig (b)]. Carefully pour out the water from the trough into a measuring cylinder (i.e., a graduated cylindrical jar) and measure the water over flowed [see Fig (c)]. Suppose the radius of the immersed sphere is r (you can find the radius by measuring the diameter of the sphere).

Then evaluate   Do you find this value almost equal to the measure of the volume over flowed?

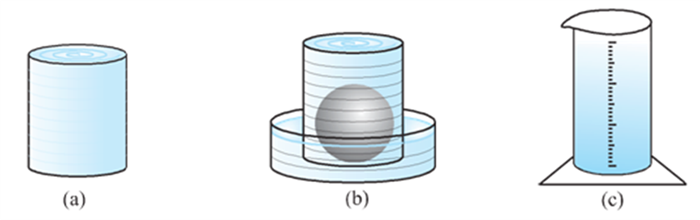
Once again repeat the procedure done just now, with a different size of sphere.
Find the radius R of this sphere and then calculate the value of  Once again this
value is nearly equal to the measure of the volume of the water displaced (over flowed)
by the sphere. What does this tell us? We know that the volume of the sphere is the same as the measure of the volume of the water displaced by it. By doing this experiment repeatedly with spheres of varying radii, we are getting the same result,
namely, the volume of a sphere is equal to 43π  times the cube of its radius. This gives us the idea that

Where r is the radius of he sphere.
Later, in higher classes it can be proved also. But at this stage, we will just take it as true.
 Since a hemisphere is half of a sphere, can you guess what the volume of a hemisphere will be? Yes. It is  

 

Where r is the radius of the hemisphere.
 Let us take some examples to illustrate the use of these formulae.