TRIANGLES

Chapter-6

Triangles

Congruence of Triangles

You must have observed that two copies of your photographs of the same size are identical. Similarly, two bangles of the same size, two ATM cards issued by the same bank are identical. You may recall that on placing a one rupee coin on another minted in the same year, they cover each other completely.
Do you remember what such figures are called? Indeed they are called congruent figures (‘congruent’ means equal in all respects or figures whose shapes and sizes are both the same).
Now, draw two circles of the same radius and place one on the other. What do you observe? They cover each other completely and we call them as congruent circles.
Repeat this activity by placing one square on the other with sides of the same measure or by placing two equilateral triangles of equal sides on each other. You will observe that the squares are congruent to each other and so are the equilateral triangles.

You may wonder why we are studying congruence. You all must have seen the ice tray in your refrigerator. Observe that the moulds for making ice are all congruent. The cast used for moulding in the tray also has congruent depressions (may be all are rectangular or all circular or all triangular). So, whenever identical objects have to be produced, the concept of congruence is used in making the cast.
Sometimes, you may find it difficult to replace the refill in your pen by a new one and this is so when the new refill is not of the same size as the one you want to remove. Obviously, if the two refills are identical or congruent, the new refill fits.
So, you can find numerous examples where congruence of objects is applied in daily life situations.
Can you think of some more examples of congruent figures?

Now, which of the following figures are not congruent to the square in

The large squares (ii) and (iii) are obviously not congruent to the one in
(i), but the square (iv) is congruent to the one given.
Let us now discuss the congruence of two triangles.
You already know that two triangles are congruent if the sides and angles of one triangle are equal to the corresponding sides and angles of the other triangle.
Now, which of the triangles given below are congruent to triangle ABC

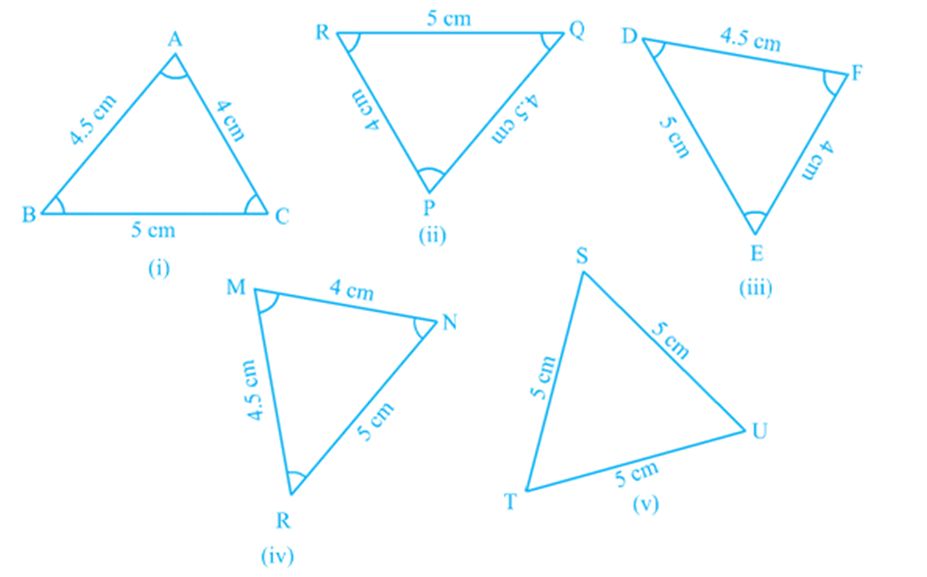
Cut out each of these triangles from Fig. (ii) to (v) and turn them around and try to cover Δ ABC. Observe that triangles in Fig. 7.4 (ii), (iii) and (iv) are congruent to Δ ABC while Δ TSU of Fig 7.4 (v) is not congruent to Δ ABC.
If Δ PQR is congruent to Δ ABC, we write Δ PQR ≅ Δ ABC.
Notice that when Δ PQR ≅ Δ ABC, then sides of Δ PQR fall on corresponding equal sides of Δ ABC and so is the case for the angles.
That is, PQ covers AB, QR covers BC and RP covers CA; ∠ P  covers ∠ A,
∠ Q covers ∠ B and ∠ R covers ∠ C. Also, there is a one-one correspondence
Between the vertices. That is, P corresponds to A, Q to B, R to C and so on which is written as
                P ↔ A, Q ↔ B, R ↔ C
Note that under this correspondence, Δ PQR ≅ Δ ABC; but it will not be correct to write ΔQRP ≅ Δ ABC.
 Similarly, for
                      FD ↔ AB, DE ↔ BC  and EF ↔ CA
                      and  F ↔ A, D ↔ B  and E ↔ C
So, Δ FDE ≅ Δ ABC but writing Δ DEF ≅ Δ ABC is not correct.
Give the correspondence between the triangle in Fig. 7.4 (iv) and Δ ABC.
So, it is necessary to write the correspondence of vertices correctly for writing of congruence of triangles in symbolic form.
Note that in congruent triangles corresponding parts are equal and we write in  short  ‘CPCT’ for corresponding parts of congruent triangles .

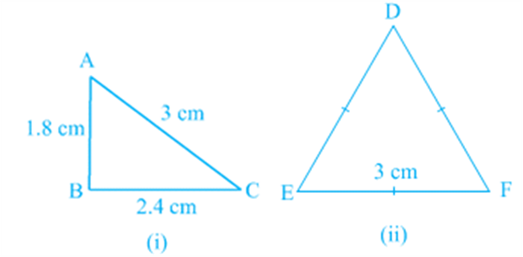
Now, draw two triangles with one side 4 cm and one angle 50°. Are they congruent?

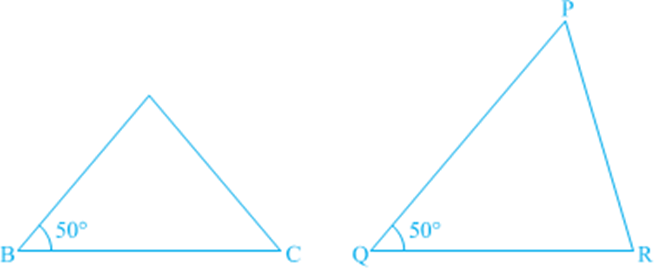
See that these two triangles are not congruent.
Repeat this activity with some more pairs of triangles.
So, equality of one pair of sides or one pair of sides and one pair of angles is not sufficient to give us congruent triangles.
What would happen if the other pair of arms (sides) of the equal angles are also equal?
BC = QR, ∠ B = ∠ Q and also, AB = PQ. Now, what can you say
about congruence of Δ ABC and Δ PQR?
Recall from your earlier classes that, in this case, the two triangles are congruent.
Verify this for Δ ABC and Δ PQR
Repeat this activity with other pairs of triangles. Do you observe that the equality of two sides and the included angle is enough for the congruence of triangles? Yes, it is enough.

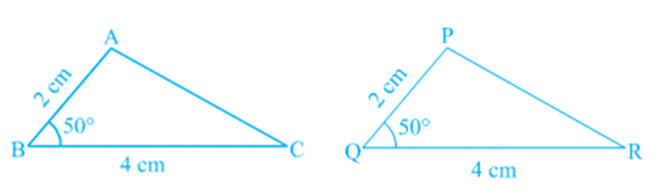
This is the first criterion for congruence of triangles.
Axiom 7.1 (SAS congruence rule) : Two triangles are congruent if two sides and the included angle of one triangle are equal to the two sides and the included angle of the  other triangle.
This result cannot be proved with the help of previously known results and so it is accepted true as an axiom (see Appendix 1).
Let us now take some examples.

Theorem

Theorem 7.1  (ASA congruence rule) : Two triangles are congruent if two angles and  the included side of one triangle are equal to two angles and the included side of other  triangle.
So, two triangles are congruent if any two pairs of angles and one pair of corresponding sides are equal. We may call it as the AAS Congruence Rule.

Some Properties of a Triangle
In the above section you have studied two criteria for congruence of triangles. Let us now apply these results to study some properties related to a triangle whose two sides are equal.
Perform the activity given below:
Construct a triangle in which two sides are equal, say each equal to 3.5 cm and the third side equal to 5 cm. You have done such constructions in earlier classes

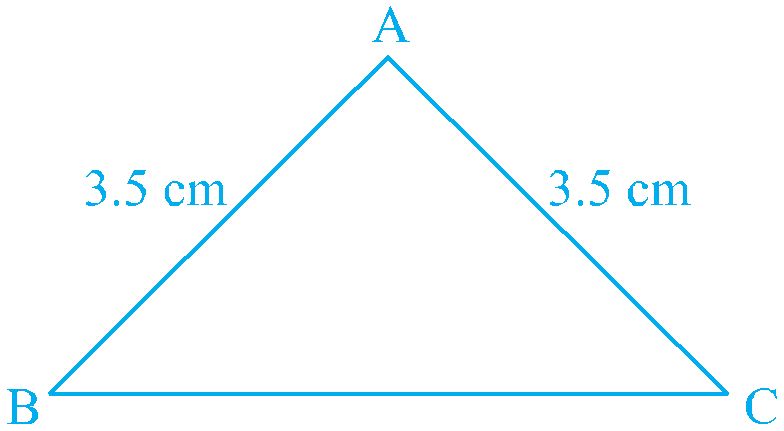
Do you remember what is such a triangle called?
A triangle in which two sides are equal is called an isosceles triangle . So, Δ ABC
an isosceles triangle with AB = AC.
Now, measure ∠ B and ∠ C. What do you observe?
Repeat this activity with other isosceles triangles with different sides.
You may observe that in each such triangle, the angles opposite to the equal sides are equal.
This is a very important result and is indeed true for any isosceles triangle. It can be proved as shown below.
Theorem 7.2: Angles opposite to equal sides of an isosceles triangle are equal.
This result can be proved in many ways. One of the proofs is given here.
Theorem 7.3: The sides opposite to equal angles of a triangle are equal.
This is the converse of Theorem 7.2.
You can prove this theorem by ASA congruence rule.
Let us take some examples to apply these results.

Some More Criteria for Congruence of Triangles

You have seen earlier in this chapter that equality of three angles of one triangle to three angles of the other is not sufficient for the congruence of the two triangles. You may wonder whether equality of three sides of one triangle to three sides of another triangle is enough for congruence of the two triangles. You have already verified in earlier classes that this is indeed true.
To be sure, construct two triangles with sides 4 cm, 3.5 cm and 4.5 cm. Cut them out and place them on each other. What do you observe? They cover each other completely, if the equal sides are placed on each other. So, the triangles are congruent.

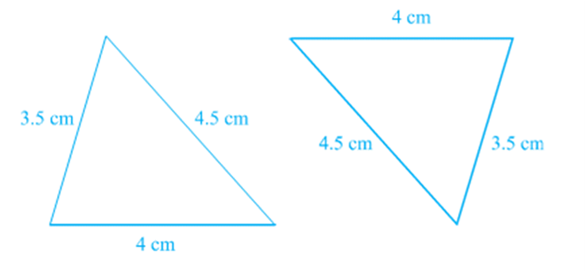
Repeat this activity with some more triangles. We arrive at another rule for congruence.
Theorem 7.4 (SSS congruence rule) : If three sides of one triangle are equal to the  three sides of another triangle, then the two triangles are congruent.
This theorem can be proved using a suitable construction.
You have already seen that in the SAS congruence rule, the pair of equal angles has to be the included angle between the pairs of corresponding pair of equal sides and if this is not so, the two triangles may not be congruent.
Perform this activity:
Construct two right angled triangles with hypotenuse equal to 5 cm and one side equal to  4 cm each

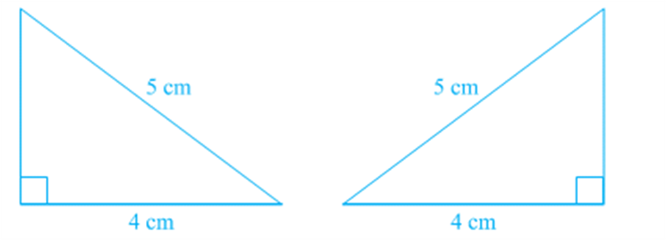
Cut them out and place one triangle over the other with equal side placed on each other. Turn the triangles, if necessary. What do you observe?
The two triangles cover each other completely and so they are congruent. Repeat this activity with other pairs of right triangles. What do you observe?
You will find that two right triangles are congruent if one pair of sides and the hypotenuse are equal. You have verified this in earlier classes.
Note that, the right angle is not the included angle in this case.
So, you arrive at the following congruence rule:
Theorem 7.5 (RHS congruence rule): If in two right triangles the hypotenuse and  one  side of one triangle are equal to the hypotenuse and one side of the other  triangle, then the two triangles are congruent.
Note that RHS stands for Right angle - Hypotenuse - Side.
Let us now take some examples.

Inequalities in a Triangle

So far, you have been mainly studying the equality of sides and angles of a triangle or triangles. Sometimes, we do come across unequal objects, we need to compare them. For example, line-segment AB is greater in length as compared to line segment CD (i) and ∠ A is greater than ∠ B

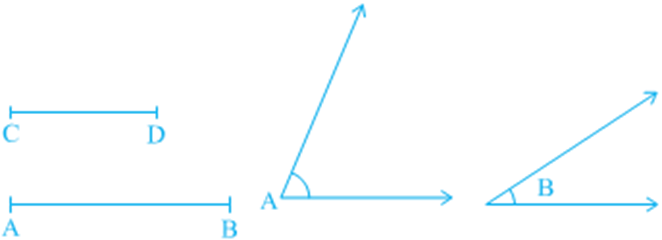
 Let us now examine whether there is any relation between unequal sides and unequal angles of a triangle. For this, let us perform the following activity:
Activity: Fix two pins on a drawing board say at B and C and tie a thread to mark a side BC of a triangle.
Fix one end of another thread at C and tie a pencil at  the other (free) end . Mark a point A with the pencil and draw Δ ABC. Now, shift the pencil and mark another point A′ on CA beyond A (new position of it)

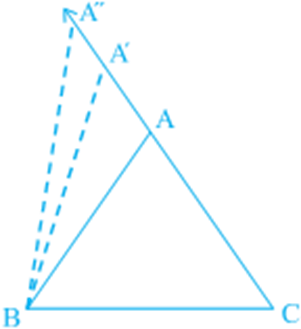
So, A′C > AC (Comparing the lengths) Join A′ to B and complete the triangle A′BC.
What can you say about ∠ A′BC and ∠ ABC? Compare them. What do you observe?
Clearly, ∠ A′BC > ∠ ABC
Continue to mark more points on CA (extended) and draw the triangles with the side BC and the points marked.
You will observe that as the length of the side AC is increased (by taking different positions of A), the angle opposite to it, that is, ∠ B also increases.
Let us now perform another activity:
Activity: Construct a scalene triangle (that is a triangle in which all sides are of different lengths). Measure the lengths of the sides.
Now, measure the angles.  What do you observe?

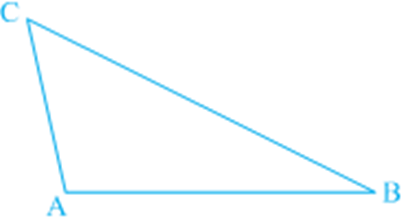
 In Δ ABC of BC is the longest side and AC is the shortest side.
Also, ∠ A is the largest and ∠ B is the smallest.
Repeat this activity with some other triangles.
We arrive at a very important result of inequalities in a triangle. It is stated in the form of a theorem as shown below: