CIRCLES

Chapter -10

Circles

Circles and Its Related Terms: A Review

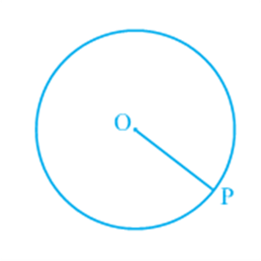
Take a compass and fix a pencil in it. Put its pointed leg on a point on a sheet of a paper. Open the other leg to some distance. Keeping the pointed leg on the same point, rotate the other leg through one revolution. What is the closed figure traced by the pencil on paper? As you know, it is a circle (see Fig). How did you get a circle? You kept one point fixed (A in Fig) and drew all the points that were at a fixed distance from A. This gives us the following definition:

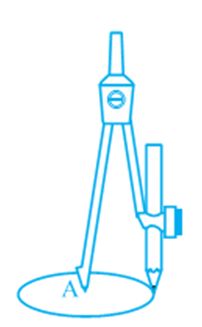
The collection of all the points in a plane, which are at a fixed distance from a fixed point in the plane, is called a circle.
The fixed point is called the centre of the circle and the fixed distance is called the radius of the circle. In Fig, O is the centre and the length OP is the radius of the circle.
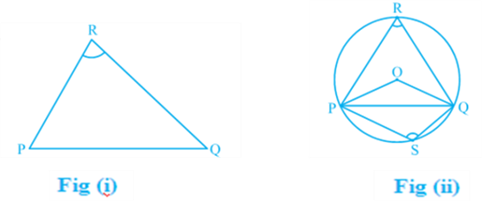
Angle Subtended by a Chord at a Point Take a line segment PQ and a point R not on the line containing PQ. Join PR and QR (see Fig (i)). Then ∠ PRQ is called the angle subtended by the line segment PQ at the point R. What are angles POQ, PRQ and PSQ called in Fig (ii)? ∠ POQ is the angle subtended by the chord PQ at the centre O, ∠ PRQ and ∠ PSQ are respectively the angles subtended by PQ at points R and S on the major and minor arcs PQ.

Let us examine the relationship between the size of the chord and the angle subtended by it at the centre. You may see by drawing different chords of a circle and angles subtended by them at the centre that the longer is the chord, the bigger will be the angle subtended by it at the centre. What will happen if you take two equal chords of a circle? Will the angles subtended at the centre be the same or not?
Draw two or more equal chords of a circle and measure the angles subtended by them at the centre (see Fig). You will find that the angles subtended by them at the centre are equal. Let us give a proof of this fact.

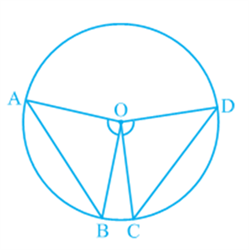
Theorem: Equal chords of a circle subtend equal angles at the centre.
Proof: You are given two equal chords AB and CD of a circle with centre O (see Fig). You want to prove that ∠ AOB = ∠ COD. In triangles AOB and COD,

In triangles AOB and COD,
                   OA = O C     (Radii of a circle)
                   OB = OD       (Radii of a circle)
                    AB = C D                      (Given)
Therefore,   Δ AOB ≅ Δ COD       (SSS rule)
This gives    ∠ AOB = ∠ COD
 (Corresponding parts of congruent triangles).

Which is denoted by R.? Therefore, a real number is either rational or irrational. So, we can say that every real number is represented by a unique point on the number line. Also, every point on the number line represents a unique real number. This is why we call the number line, the real number line.

A circle divides the plane on which it lies into three parts. They are: (i) inside the circle, which is also called the interior of the circle; (ii) the circle and (iii) outside the circle, which is also called the exterior of the circle (see Fig). The circle and its interior make up the circular region. 

Perpendicular from the Centre to a Chord

Activity: Draw a circle on a tracing paper. Let O be its centre. Draw a chord AB. Fold the paper along a line through O so that a portion of the chord falls on the other. Let the crease cut AB at the point M. Then, ∠ OMA = ∠ OMB = 90° or OM is perpendicular to AB. Does the point B coincide with A (see Fig)?

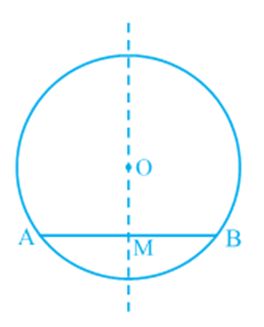
Give a proof yourself by joining OA and OB and proving the right triangles OMA and OMB to be congruent. This example is a particular instance of the following result:
Theorem: The perpendicular from the centre of a circle to a chord bisects the chord.
What is the converse of this theorem? To write this, first let us be clear what is assumed in Theorem and what is proved. Given that the perpendicular from the centre of a circle to a chord is drawn and to prove that it bisects the chord. Thus in the converse, what the hypothesis is ‘if a line from the centre bisects a chord of a circle’ and what is to be proved is ‘the line is perpendicular to the chord’. So the converse is:
Theorem: The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord.
Is this true? Try it for few cases and see. You will see that it is true for these cases. See if it is true, in general, by doing the following exercise. We will write the stages and you give the reasons.
Let AB be a chord of a circle with centre O and O is joined to the mid-point M of AB. You have to prove   that   OM ⊥ AB.   Join OA and OB (see Fig). In triangles OAM and OBM,

OA = O B                         (Why?)
AM = BM                        (Why?)   
OM = OM                     (Common)

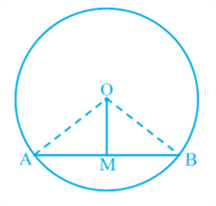
Therefore, ΔOAM ≅ ΔOBM                    (How?)
This gives ∠OMA = ∠OMB = 90            (Why?)

Circle through Three Points
You have learnt in Chapter 6, that two points are sufficient to determine a line. That is, there is one and only one line passing through two points. A natural question arises. How many points are sufficient to determine a circle?
Take a point P. How many circles can be drawn through this point? You see that there may be as many circles as you like passing through this point [see Fig (i)]. Now take two points P and Q. You again see that there may be an infinite number of circles passing through P and Q [see Fig (ii)]. What will happen when you take three points A, B and C? Can you draw a circle passing through three collinear points?

Theorem: There is one and only one circle passing through three given non-collinear points.

Angle Subtended by an Arc of a Circle

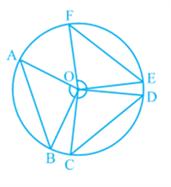
You have seen that the end points of a chord other than diameter of a circle cuts it  into two arcs – one major and other minor. If you take two equal chords, what can you say about the size of arcs? Is one arc made by first chord equal to the corresponding arc made by another chord? In fact, they are more than just equal in length. They are congruent in the sense that if one arc is put on the other, without bending or twisting, one superimposes the other completely.
You can verify this fact by cutting the arc, corresponding to the chord CD from the circle along CD and put it on the corresponding arc made by equal chord AB. You will find that the arc CD superimpose the arc AB completely (see Fig). This shows that equal chords make congruent arcs and conversely congruent arcs make equal chords of a circle. You can state it as follows:

If two chords of a circle are equal, then their corresponding arcs are congruent and conversely, if two arcs are congruent, then their corresponding chords are equal.
Also the angle subtended by an arc at the centre is defined to be angle subtended by the corresponding chord at the centre in the sense that the minor arc subtends the angle and the major arc subtends the reflex angle.  Therefore, in Fig, the angle subtended by the minor arc PQ at O is ∠POQ and the angle subtended by the major arc PQ at O is reflex angle POQ.
In view of the property above and Theorem, the following result is true:

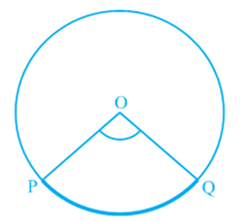
Congruent arcs (or equal arcs) of a circle subtend equal angles at the centre.
Therefore, the angle subtended by a chord of a circle at its centre is equal to the angle subtended by the corresponding (minor) arc at the centre. The following theorem gives the relationship between the angles subtended by an arc at the centre and at a point on the circle.

Cyclic Quadrilaterals

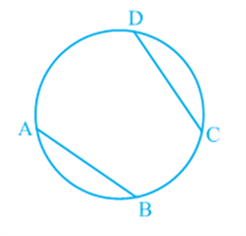
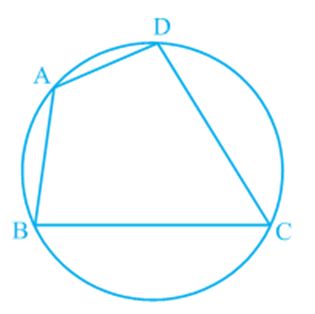
A quadrilateral ABCD is called cyclic if all the four vertices of it lie on a circle (see Fig). You will find a peculiar property in such quadrilaterals. Draw several cyclic quadrilaterals of different sides and name each of these as ABCD. (This can be done by drawing several circles of different radii and taking four points on each of them.) Measure the opposite angles and write your observations in the following table.

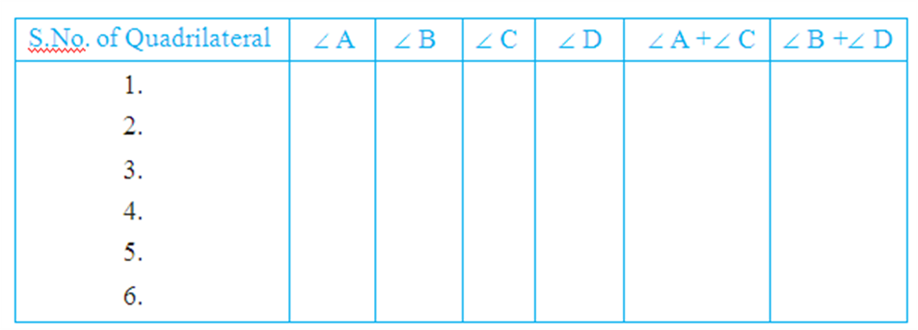
What do you infer from the table?
Theorem: The  sum  of  either  pair  of  opposite  angles  of  a  cyclic quadrilateral is 180º.
Theorem: If the sum of a pair of opposite angles of a quadrilateral is 180º, the quadrilateral is cyclic.