Introduction to Euclid’s Geometry

Chapter -4

Introduction To Euclid’s Geometry

Introduction

The word ‘geometry’ comes form the Greek words ‘geo’, meaning the ‘earth’, and ‘metrein’, meaning ‘to measure’. Geometry appears to have originated from the need for measuring land. This branch of mathematics was studied in various forms in every ancient civilisation, be it in Egypt, Babylonia, China, India, Greece, the Incas, etc. The people of these civilisations faced several practical problems which required the development of geometry in various ways.

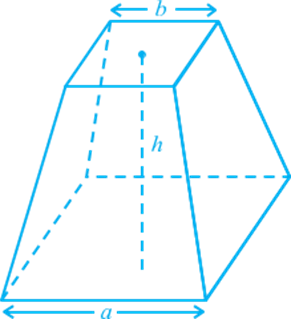
For example, whenever the river Nile overflowed, it wiped out the boundaries between the adjoining fields of different land owners. After such flooding, these boundaries had to be redrawn.  For this purpose, the Egyptians developed a number of geometric techniques and rules for calculating simple areas and also for doing simple constructions. The knowledge of geometry was also used by them for computing volumes of granaries, and for constructing canals and pyramids. They also knew the correct formula to find the volume of a truncated pyramid (see Fig.).You know that a pyramid is a solid figure, the base of which is a triangle, or square, or some Other polygon, and its side faces are triangles converging to a point at the top.

Euclid’s Definitions, Axioms and Postulates
The Greek mathematicians of Euclid’s time thought of geometry as an abstract model of the world in which they lived. The notions of point, line, plane (or surface) and so on were derived from what was seen around them. From studies of the space and solids in the space around them, an abstract geometrical notion of a solid object was developed. A solid has shape, size, position, and can be moved from one place to another. Its boundaries are called surfaces. They separate one part of the space from another, and are said to have no thickness. The boundaries of the surfaces are curves or straight lines. These lines end in points.
Consider the three steps from solids to points (solids-surfaces-lines-points). In each step we lose one extension, also called a dimension. So, a solid has three dimensions, a surface has two, a line has one and a point has none. Euclid summarised these statements as definitions. He began his exposition by listing 23 definitions in Book 1 of the ‘Elements’. A few of them are given below:

• •  
• A point is that which has no part.
• A line is breathless length.
•  The ends of a line are points.
• A straight line is a line which lies evenly with the points on itself.
• A surface is that which has length and breadth only.
• The edges of a surface are lines.
• A plane surface is a surface which lies evenly with the straight lines on itself.

Starting with his definitions, Euclid assumed certain properties, which were not to be proved. These assumptions are actually ‘obvious universal truths’. He divided them into two types: axioms and postulates. He used the term ‘postulate’ for the assumptions that were specific to geometry. Common notions (often called axioms), on the other hand, were assumptions used throughout mathematics and not specifically linked to geometry. For details about axioms and postulates, refer to Appendix 1. Some of Euclid’s axioms, not in his order, are given below:(1) Things which are equal to the same thing are equal to one another.
(2) If equals are added to equals, the wholes are equal.
(3) If equals are subtracted from equals, the remainders are equal.
(4)  Things which coincide with one another are equal to one another.
(5) The whole is greater than the part.
(6) Things which are double of the same things are equal to one another.
(7) Things which are halves of the same things are equal to one another.      

Now let us discuss Euclid’s five postulates. They are :
Postulate 1: A straight line may be drawn from any one point to any other point.
Note that this postulate tells us that at least one straight line passes through two distinct points, but it does not say that there cannot be more than one such line. However, in his work, Euclid has frequently assumed, without mentioning, that there is a unique line joining two distinct points. We state this result in the form of an axiom as follows:

Postulate 2: A terminated line can be produced indefinitely.Note that what we call a line segment now-a-days is what Euclid called a terminated line. So, according to the present day terms, the second postulate says that a line segment can be extended on either side to form a line.
Postulate 3: A circle can be drawn with any centre and any radius.
Postulate 4: All right angles are equal to one another.
Postulate 5: If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.

Equivalent Versions of Euclid’s Fifth Postulate
Euclid’s fifth postulate is very significant in the history of mathematics. Recall it again from Section 5.2. We see that by implication, no intersection of lines will take place when the sum of the measures of the interior angles on the same side of the falling line is exactly 180°. There are several equivalent versions of this postulate. One of them is ‘Playfair’s Axiom’ (given by a Scottish mathematician John Playfair in 1729), as stated below: ‘For every line l and for every point P not lying on l, there exists a unique line m  passing through P and parallel to l’.
From, you can see that of all the lines passing through the point P, only line m is parallel to line l.    

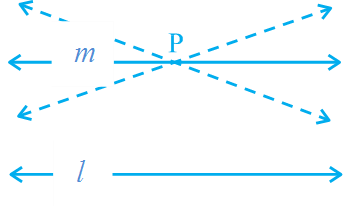
 This result can also be stated in the following form:
Two distinct intersecting lines cannot be parallel to the same line.