QUADRILATERALS

Chapter -8

Quadrilaterals

A quadrilateral has four sides, four angles and four vertices [see Fig. (i)].

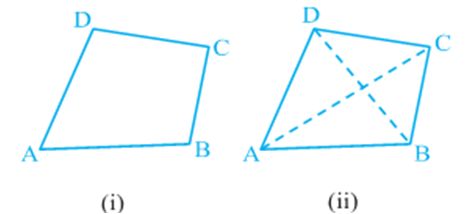
In quadrilateral ABCD, AB, BC, CD and DA are the four sides; A, B, C and D are the four vertices and ∠ A, ∠ B, ∠ C and ∠ D are the four angles formed at the vertices.
Now join the opposite vertices A to C and B to D [see Fig (ii)]. AC and BD are the two diagonals of the quadrilateral ABCD.
In this chapter, we will study more about different types of quadrilaterals, their properties and especially those of parallelograms.You may wonder why should we study about quadrilaterals (or parallelograms) Look around you and you will find so many objects which are of the shape of a quadrilateral - the floor, walls, ceiling, windows of your classroom, the blackboard, each face of the duster, each page of your book, the top of your study table etc. Some of these are given below (see Fig).

Although most of the objects we see around are of the shape of special quadrilateral called rectangle, we shall study more about quadrilaterals and especially parallelograms because a rectangle is also a parallelogram and all properties of a parallelogram are true for a rectangular as well.

Angle Sum Property of a Quadrilateral

Let us now recall the angle sum property of a quadrilateral.
The sum of the angles of a quadrilateral is 360º. This can be verified by drawing a diagonal and dividing the quadrilateral into two triangles.
 Let ABCD be a quadrilateral and AC be a diagonal (see Fig).
What is the sum of angles in Δ ADC?

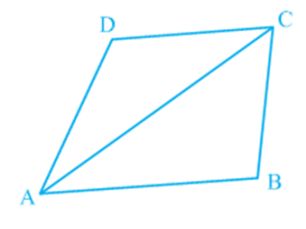
You know that
 

Similarly, in

Δ ABC,

    

Adding (1) and (2), we get

   

   

       

 i.e., the sum of the angles of a quadrilateral is 360^o.
Look at the different quadrilaterals drawn below

 

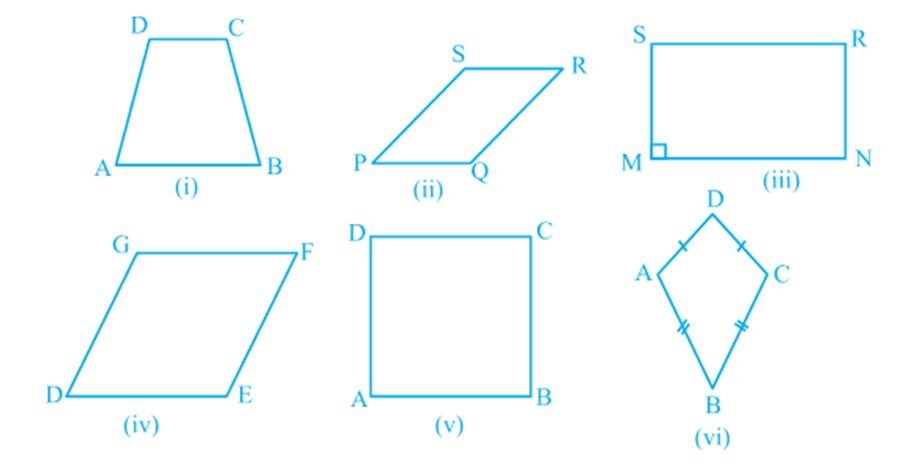
Observe that:
One pair of opposite sides of quadrilateral ABCD is Fig. (i) namely, AB and CD parallel. You know that it is called a trapezium.
Both pairs of opposite sides of quadrilaterals given in Fig. (ii), (iii), (iv) and (v) are parallel. Recall that such quadrilaterals are called parallelograms.
So, quadrilateral PQRS of Fig. (ii) is a parallelogram.

 

 

 

Properties of a Parallelogram

Let us perform an activity.
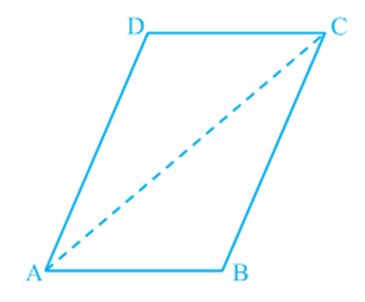
Cut out a parallelogram from a sheet of paper and cut it along a diagonal (see Fig). You obtain two triangles. What can you say about these triangles?
Place one triangle over the other. Turn one around, if necessary. What do you observe?
Observe that the two triangles are congruent to each other.
Repeat this activity with some more parallelograms. Each time you will observe that each diagonal divides the parallelogram into two congruent triangles.

Another Condition for a Quadrilateral to be a Parallelogram
You have studied many properties of a parallelogram in this chapter and you have also verified that if in a quadrilateral any one of those properties is satisfied, then it becomes a parallelogram.
We now study yet another condition which is the least required condition for a quadrilateral to be a parallelogram.
It is stated in the form of a theorem as given below:

The Mid –point Theorem
You have studied many properties of a triangle as well as a quadrilateral. Now let us study yet another result which is related to the mid-point of sides of a triangle. Perform the following activity.

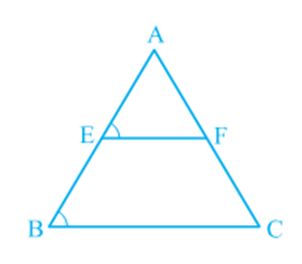
Draw a triangle and mark the mid-points E and F of two sides of the triangle. Join the points E and F (see Fig).
Measure EF and BC. Measure ∠AEF and ∠ABC.
What do you observe? You will find that:

 

 So,   EF || BC
Repeat this activity with some more triangles.
So, you arrive at the following theorem: