Gases and Liquids

STATES OF MATTER

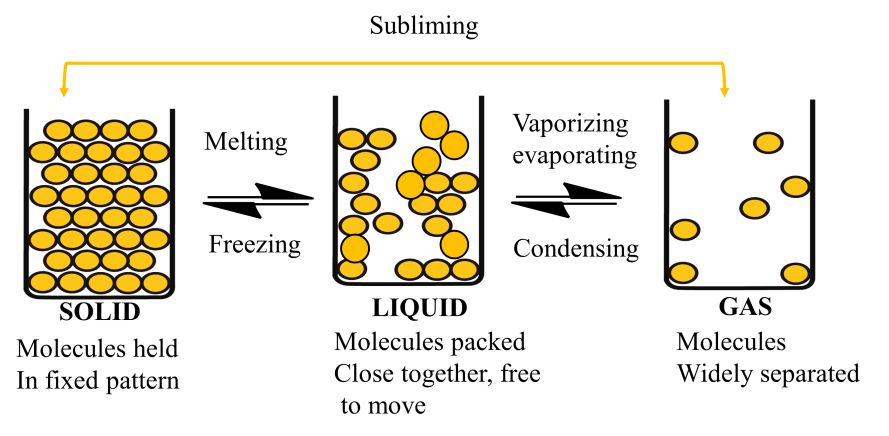
There are five known phases, or states, of matter: solids, liquids, gases, and plasma and Bose-Einstein condensates.

Here we will study only three. Solid, Liquid and Gas

GASEOUS STATE

Only eleven elements exist as gases under normal conditions

GASEOUS STATE

The gaseous state is characterized by the following physical properties.

• Gases are highly compressible.

• Gases exert pressure equally in all directions.

• Gases have much lower density than the solids and liquids.

• The volume and the shape of gases are not fixed. These assume volume and shape of the container.

• Gases mix evenly and completely in all proportions without any mechanical aid (Diffusion)

Gas Laws

1. Boyle’s Law: At constant temperature

   

   

      

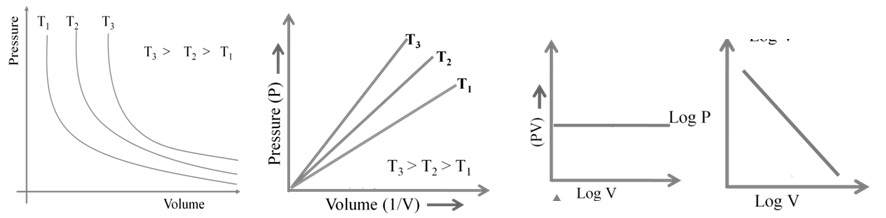
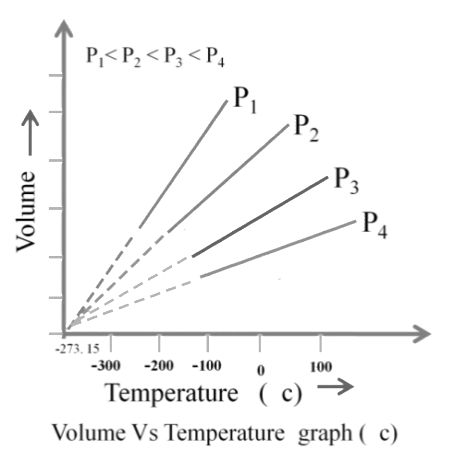
2. Charles Law:  At constant pressure

 

Here K is a constant that depends on the pressure of gas, the amount of gas and also unit of volume if V₁ and T₁ are the initial values of volume and temperature of a gas then, 

 

Also, if the temperature is now changed to T₂ such that the volume change to V₂

We can write,

  

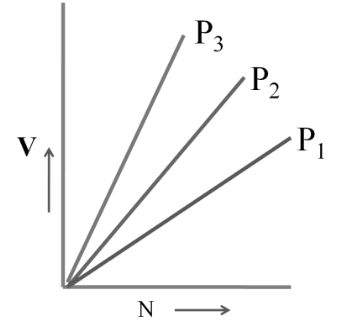
3. Avogadro's Law:  At constant pressure and temperature

V   µ  n (no. of moles)  

4. Ideal gas equation

Ideal gas equation

                                         

 

                    

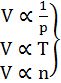
 R = gas constant

   w = mass of gas  ρ = density

  M = Mol weight of gas  R = gas constant

 

    

5.  Modified gas equation 

    

 

 

 

 Gas Constant ‘R’

 

= 0.0821 lit atm/ K. mole

= 8.314x 10⁷ erg/k. mole

= 8.314 J/k. mole

= 1.987 cal/k. mole

Units and conversion

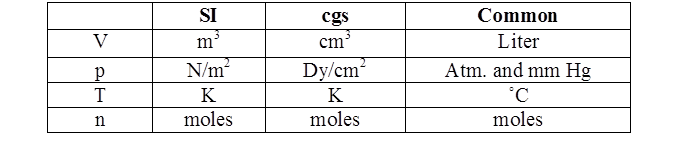
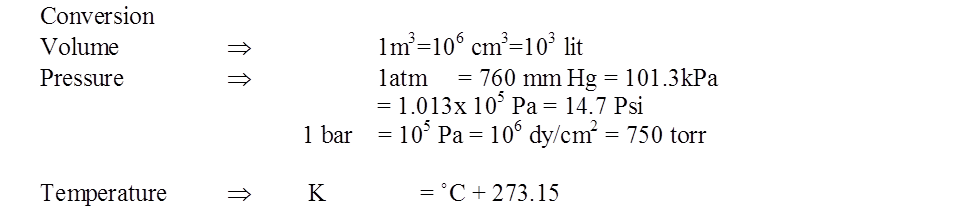
DALTON’S LAW

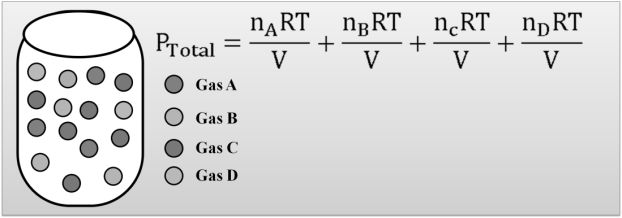
Dalton's law (also called Dalton's law of partial pressures) states that in a mixture of non-reacting ideal gases, the total pressure exerted is equal to the sum of the partial pressures of the individual gases.

KINETIC THEORY OF GASES

• Assumptions or postulates of the kinetic molecular theory of gases are given below.
  • Gases consist of large number of identical particles (atoms or molecules) that are so small and so far apart on the average that the actual volume of the molecules is negligible in comparison to the empty space between them
  • There is no force of attraction or repulsion  between the particles of a gas
  • Particles of a gas are always in constant and random motion.
  • Collisions of gas molecules are perfectly elastic.
  • At any particular time, different particles in the gas have different speeds and hence different kinetic energies

We can derive from kinetic theory they of gases

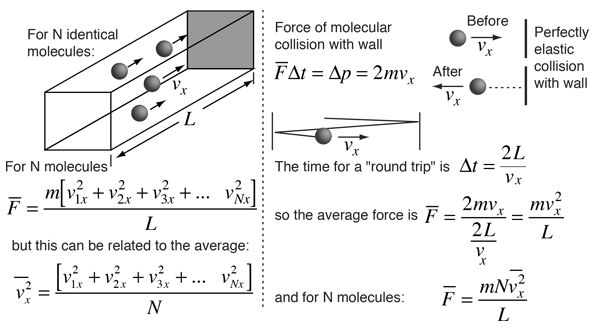
A gas molecule has velocity v and can be broken into thro components v_x, v_y and v_z.

Travelling in x-axis momentum = mv_x change in momentum after collision = - 2mv_x. If gone back of comes back after time ‘t’ 

                  

No. of collies is one second     

Change in momentum per second     

Change in momentum on all three axis   

   

     

               

For one mole of gas n = N and  m x N = M (Mol. Wt.)

  

     

Kinetic Energy    for one mole gas n = N and PV = RT

   

  

  

So kinetic energy, depends only on temperature

For one molecules    

k = Boltzman constant

  

 

m = mass of gas particle

 n = no. of gas particle

V_rms = root mean square velocity

PV =        m. n. V²_rms 

K.E. =    RT     for one mole of gas

K.E. =    kT      for one molecule where

    k = Boltzman constant =

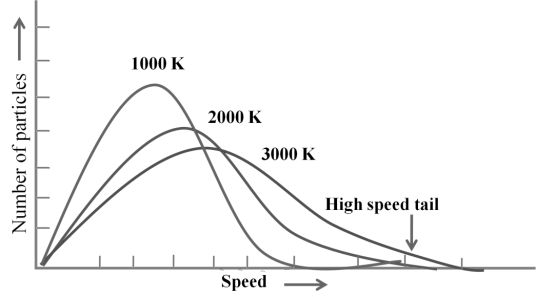
MAXWELL’S DISTRIBUTION OF SPEED AT DIFFERENT TEMPERATURE

MAXWELL’S DISTRIBUTION OF SPEED FOR DIFFERENT GASES

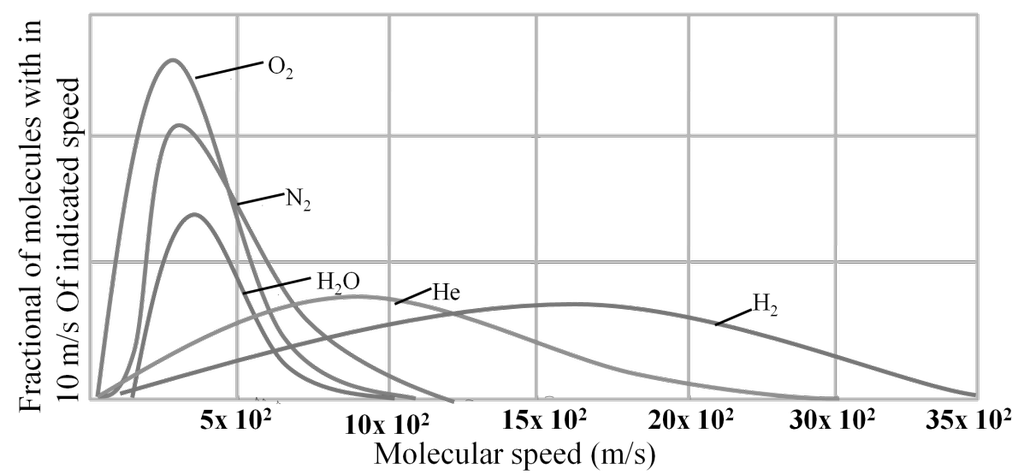
DIFFERENT VELOCITIES FOR GASES

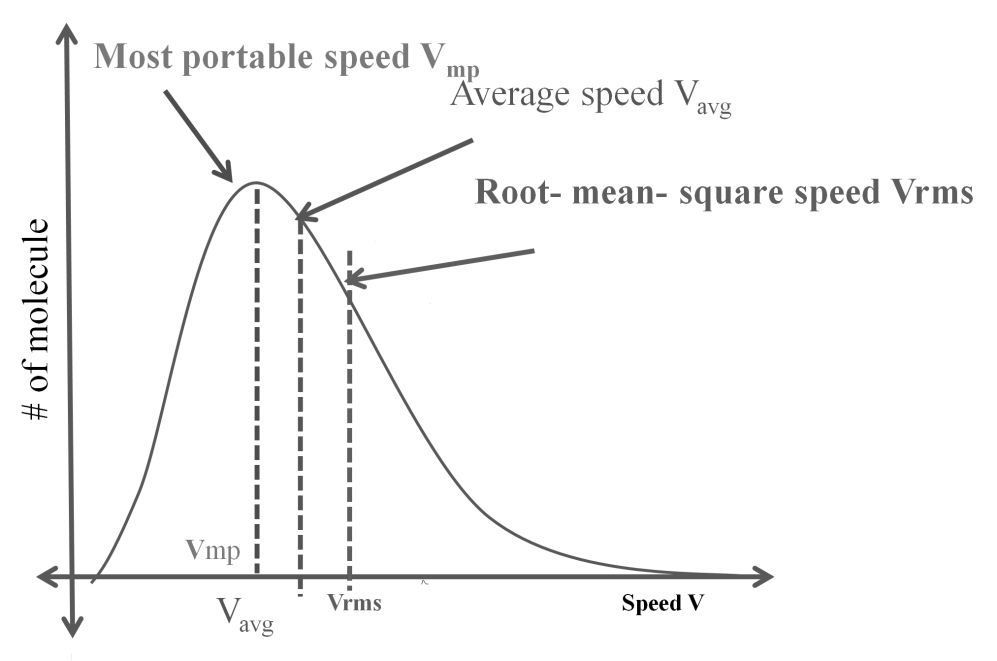
1. The first typical velocity is the easiest to calculate and termed as the most probable velocity V_MP. The velocity at the top of the curve is the most probable velocity as the largest number of molecules have this velocity.
2. Average velocity of gas is simply the mean of all gas speeds possessed by all gas particles.    
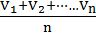
3. Root mean square velocity is the square root of the mean of velocity squares V_RMS =

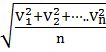
   DIFFERENT VELOCITIES FOR GASES

    

    

    

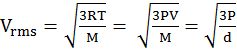
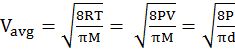
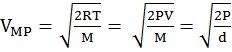
   IMPORTANT SHORTCUT

   V_rms: V_avg: V_MP = 1.224 :1.128:1 and = 1: 0.92 :0.816

DIFFUSION OF GASES

DIFFUSION VS. EFFUSION

Diffusion- The tendency of the molecules of a given substance to move from regions of higher concentration to regions of lower concentration.

Examples: A sent spreading throughout a room or people entering a theme park.

Effusion: The process by which gas particles under pressure pass through a tiny hole.

Example: Air slowly leaking out of a tire or helium leaking out of a balloon.

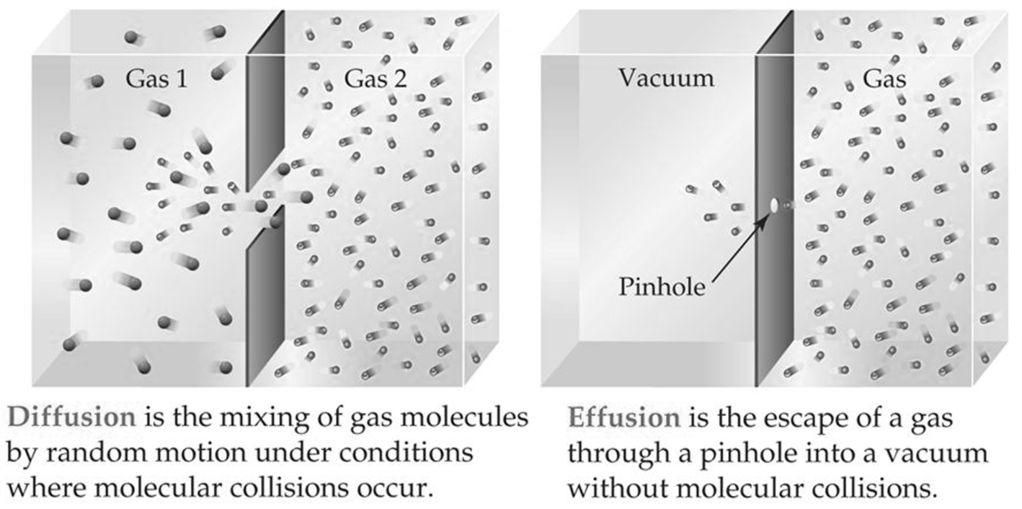
Graham’s law of diffusion  when pressure is same.

Graham’s law of diffusionr   when pressure is also different

REAL GAS

The Ideal gas equation shows big deviation at high pressures and low temperatures from ideal gas equation.

If you compress an Ideal gas to very high pressure when will it become a liquid? ????

Vanderwaal’s equation for real gas.

1. Volume correction.  Actual volume available for gas to freely move is

       V_R = V_j – n b      

      b = Volume correction constant taking into size and gas molecule.

2. Pressure correction:

      P_Real = P_Ideal – attractive forces between molecules.

     P_Real = P_ideal – 

     A = Pressure correction

. a, b are Vander Waals constant; n is the number of moles of gas

 V.W. Constants

‘b’  size of molecule

Thumb rule   b = 4 x Volume and one atom/molecule.

‘a’     Inter molecule forces between atom/molecule gas

Ex: put in increasing order ‘a’ and ‘b’ for H₂, He, NH₃, O₂

b = H₂ < He < NH₃ < O₂

a = He < H₂ < O₂ < NH₃

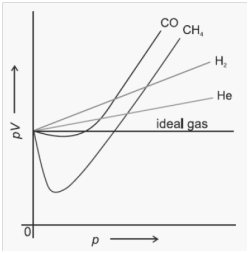
Compressibility factor   Z

Z = 1         Þ Ideal gas. No. attraction/Repulsion

Z < 1         ÞReal gas. Attractive forces dominate

Z > 1         ÞReal gas. Repulsive forces dominate

 

UNIT OF ‘a’ AND ‘b’

 

Real gas behaves like ideal gas at low pressure and high temperature.

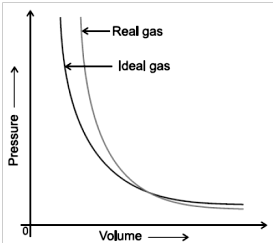
Boyle’s temp =  temperature at which Real gas behave like ideal gas.

Liquefaction of Gas

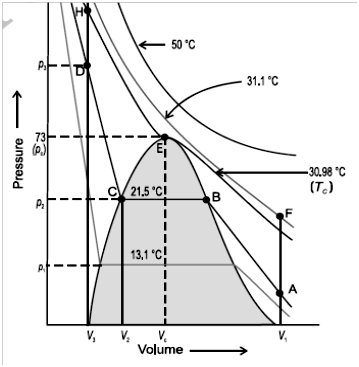
Critical temperature (T_C) is the temperature above which a gas cannot be liquefied however high pressure may be.

Critical pressure (P_C) is minimum pressure required to liquefy gas at the critical temperature.

Critical volume (V_C) is the volume occupied by one mole of gas at critical temperature and critical pressure.

 

For gas CO₂

 

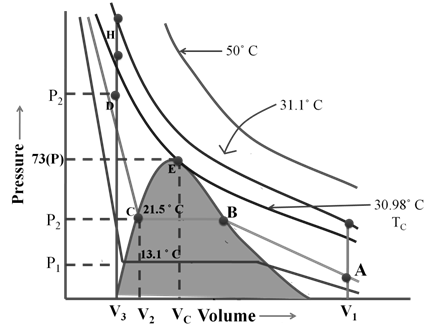
Real gases can only be liquefied by increasing pressure, if the temperature is below critical temperature

Here Vc and Pc volume and pressure at critical temperature when it touches the curve.

SURFACE TENSION

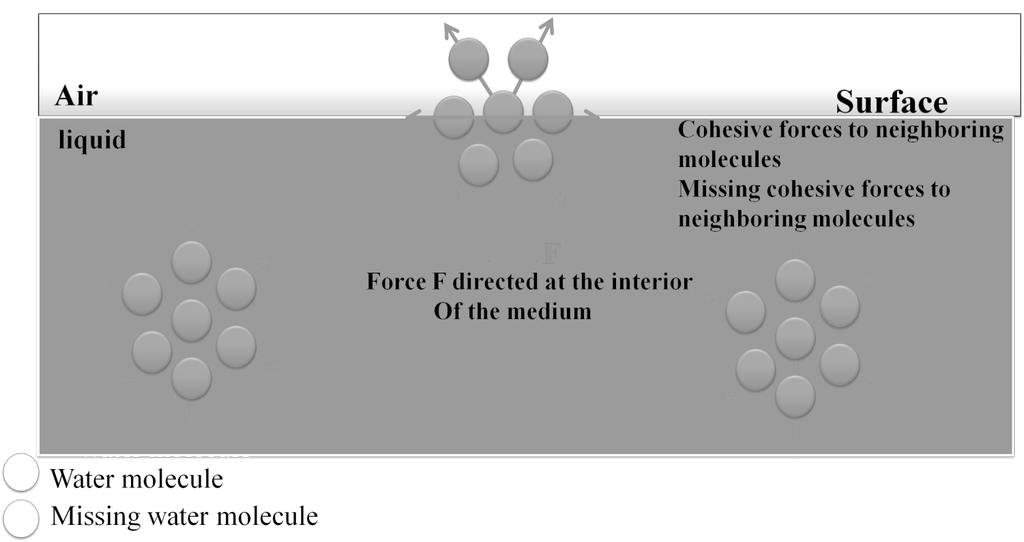
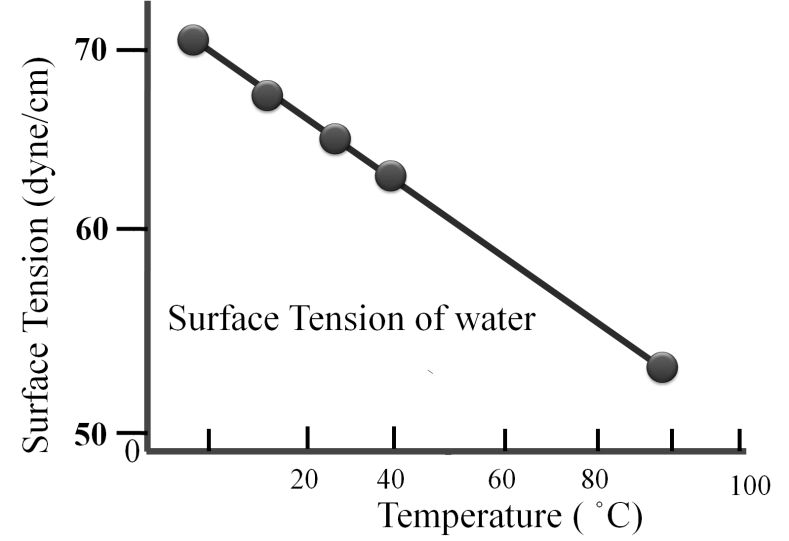
Surface tension is defined as the force acting per unit length perpendicular to the line drawn on the surface of liquid. It is denoted by Greek letter γ (Gamma). It has dimensions of kg s^-2 and in SI unit it is expressed as N m^-1. Surface tension reduces with increase in temperature.

​SURFACE TENSION VS. TEMPERATURE PLOT

​VISCOSITY

It is one of the characteristic properties of liquids. Viscosity is a measure of resistance to flow which arises due to the internal friction between layers of fluid as they slip past one another while liquid flows.

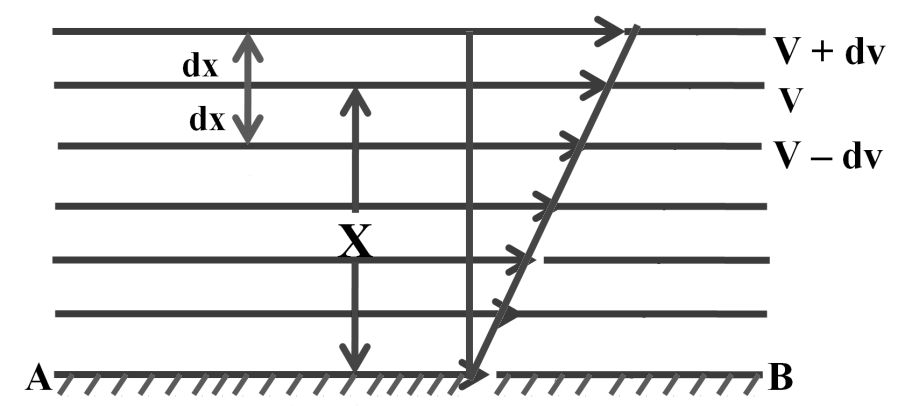
​F   A                   (A is the area of contact)

F                   (where, is velocity gradient)

 

‘n’ is proportionality constant and is called coefficient of viscosity.

Viscosity coefficient is the force when velocity gradient is unity and the area of contact is unit area.

SI unit of viscosity coefficient is Newton second per square meter (N s m^-2) = Pascal second (Pa s = 1kg m^-1s^-1). In cgs system the unit of coefficient of viscosity is poise

1 poise = 1 g cm^-1s^-1 = 10^-1kg m^-1s^-1

IMPORTANT FORMULA

1.  Ideal gas  PV = nRT =   
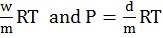
2. Graham’s law of diffusion  
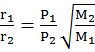
3. Separation by diffusion f=n1'n2'n1n2=AfterBefore    f1=M2M1=one stage separation f1=f here x=no. of shape   Kinetic Theory  PV = 1/3 mnv²_rms
4. Kinetic Energy/mole = 3/2 RT
5. Kinetic Energy/molecule = 3/2 kT     k(Boltzmann constant) =R/N_A
6. 
7. 
8.  
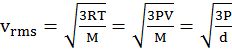
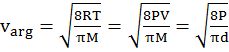
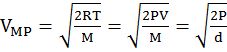
9. v_rms: v_avg: v_MP = 1.224 :1.128:1 = 1: 0.92 :0.816
10. Vanderwaal’s Gas  
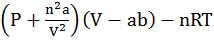
11. Boyles temp T_b =  
12. Critical constants   
13. Inversion temperature
14. C_p – C_V = R and C_P/C_V = g
15. Compression factor Z =    Z = 1 for ideal gas (Z < 1 lower P      Z > 1 higher P)
16. C_p – C_v = R    and   C_p/C_v = g

​