SI System, Significant Figures,
- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
Every field of science involves taking measurements, understanding them, and communicating them to others. In other words, we all have to speak the same basic language. Whether you are a chemist, a physicist, a biologist, an engineer, or even a medical doctor, you need a consistent way of communicating size, mass, shape, temperature, time, amount, energy, power, and speed.
The International System of Units (abbreviated SI, from the French Système international d’unités) is the metric system used in science, industry, and medicine. Depending on your age and geographic location, you might be very familiar with the “imperial” system, which includes units such as gallons, feet, miles, and pounds. The imperial system is used for “everyday” measurements in a few places, such as the United States. But in most of the world (including Europe) and in all scientific circles, the SI system is in common use.
The SI is made up of 7 base units that define the 22 derived units with special names and symbols.
History of the SI System

The SI units of measurement have an interesting history. Over time they have been refined for clarity and simplicity.
- The meter (m), or metre, was originally defined as 1/10,000,000 of the distance from the Earth’s equator to the North Pole measured on the circumference through Paris. In modern terms, it is defined as the distance traveled by light in a vacuum over a time interval of 1/299,792,458 of a second.
- The kilogram (kg) was originally defined as the mass of a liter (i.e., of one thousandth of a cubic meter). It is currently defined as the mass of a platinum-iridium kilogram sample maintained by the Bureau International des Poids et Mesures in Sevres, France.
- The second (s) was originally based on a “standard day” of 24 hours, with each hour divided in 60 minutes and each minute divided in 60 seconds. However, we now know that a complete rotation of the Earth actually takes 23 hours, 56 minutes, and 4.1 seconds. Therefore, a second is now defined as the duration of 9,192,631,770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the cesium-133 atom.
- The ampere (A) is a measure of the amount of electric charge passing a point in an electric circuit per unit time. 6.241×1018 electrons, or one coulomb, per second constitutes one ampere.
- The kelvin (K) is the unit of the thermodynamic temperature scale. This scale starts at 0 K. The incremental size of the kelvin is the same as that of the degree on the Celsius (also called centigrade) scale. The kelvin is the fraction 1/273.16 of the thermodynamic temperature of the triple point of water (exactly 0.01 °C, or 32.018 °F).
- The mole (mol) is a number that relates molecular or atomic mass to a constant number of particles. It is defined as the amount of a substance that contains as many elementary entities as there are atoms in 0.012 kg of carbon-12.
- The candela (cd) was so named to refer to “candlepower” back in the days when candles were the most common source of illumination (because so many people used candles, their properties were standardized). Now, with the prevalence of incandescent and fluorescent light sources, the candela is defined as the luminous intensity in a given direction of a source that emits monochromatic radiation of frequency 540⋅1012
Derived units – are defined in terms of the seven base quantities via a system of quantity equations. The SI derived units for these derived quantities are obtained from these equations and the seven SI base units
For ease of understanding and convenience, 22 SI derived units have been given special names and symbols,
Ex: volume = L x L x L = m3 or cm3
Density=massvolume=kgm3 or gmm3
Force: unit N (Newton) = kg.m/sec2
Conversion of one unit to another example
m3 = m x m x m = (100cm) x (100) cm x (100) cm = 106 cm3
Density kgm3=1000gm106cm3=10-3 gmcm3
Measurement of data: when conducting experiments we have to measure & report data. There are certain norms for reporting this data.
All very big and small values are expressed in exponents
PRECISION AND ACCURACY
- Precision indicates how closely repeated measurements match each other.
- Accuracy indicates how closely a measurement matches the correct or expected value.
- A result is valid only if it is both accurate and precise.
EXAMPLE
- If the true value for a result is 8.00 kg and a student “A” takes two measurements and reports the results as 7.95 kg and 7.93 kg. These values are precise as they are close to each other but are not accurate.
- Another student “B” repeats the experiment and obtains 7.94 kg and 8.05 kg as the results for two measurements. These observations are neither precise nor accurate.
- When a third student “C” repeats these measurements and reports 8.01 kg and 7.99 kg. These values are both precise and accurate.
SIGNIFICANT FIGURES
Significant figures are meaningful digits which are known with certainty. The uncertainty is indicated by writing the certain digits and the last uncertain digit. Thus, if we write a result as 11.2 ml, we say the 11 is certain and 2 is uncertain and the uncertainty would be ±1 in the last digit.
Unless otherwise stated, an uncertainty of ± 1 in the last digit is always understood.
RULES FOR DETERMINING THE NUMBER OF SIGNIFICANT FIGURES
- All non-zero digits are significant
- Zeros preceding the first non-zero digit are not significant
- Zeros between two non-zero digits are significant.
- Zeros at the end or right of the number are significant provided they are on the right side of the decimal point. But, if otherwise, the zeros are not significant
- Counting numbers of objects, for example, 2 balls or 20 eggs, have infinite significant figures as these are exact numbers
EXAMPLE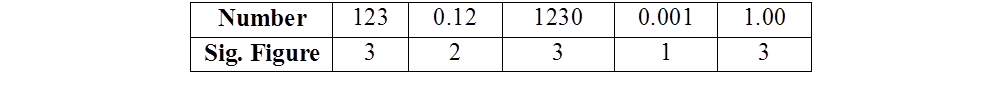
ADDITION AND SUBTRACTION OF SIGNIFICANT FIGURES
During addition and subtraction, the result cannot have more digits to the right of the decimal point than either of the original numbers.
MULTIPLICATION AND DIVISION OF SIGNIFICANT FIGURES
In multiplication and division with significant figures, the answer cannot have more significant figures than either of the original numbers.
Example Example
2.12 1.2
+ 6.1 x 1.3
0.012 1.56
8.232 Ans. 1.6
Ans.= 8.2
ROUNDING OFF THE SIGNIFICANT FIGURES
1. If the rightmost digit to be removed is more than 5, the preceding number is increased by one. For example, in figure 2.486 if we have to remove 6, we have to round it to 2.49
2. If the rightmost digit to be removed is less than 5, the preceding number is not changed.
For example, in figure 6.664 if 4 is to be removed, then the result is rounded of to 6.66.
3. If the rightmost digit to be removed is 5, then the preceding number is not changed, if it is an even number but it is increased by one if it is an odd number. For example, if 2.35 is to be rounded by removing 5, we have to increase 3 to 4 giving 2.4 as the result. However, if 2.25 is to be rounded off it is rounded off to 2.2
Ex.: A student performs a titration with different burettes and finds titre values of 25.2 mL, 25.25 mL, and 25.0 ml. The number of significant figures in the average titre value is
(IIT adv. 2010, integer type)
Sol. During addition and subtraction, the result cannot have more digits to the right of the decimal point than either of the original numbers Answer: 3
Ex.: If the value of Avogadro number is 6.023 × 1023 mol–1 and the value of Boltzmann constant is 1.380 × 10–23 J K–1, then the number of significant digits in the calculated value of the universal gas constant is (IIT adv. 2014, integer type)
Sol. K = R/NA R=KNA
R= 6.023 × 1023 × 1.380 × 10–23 J.mol–1.k–1= 8.31174 J.mol–1.k–1. There are 4 significant figures in each term. (4) Hence, these be 4 significant figure in R Answer. 4
Atomic Theory
- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
INTRODUCTION
The word .atom has been derived from the Greek word atomio which means .un-cutable or non-divisible.
DALTON’S ATOMIC THEORY
The matter is composed of small indivisible particles called atoms (from Greek word atomio, meaning indivisible). In 1808 Dalton proposed the following theory
- Matter consists of atoms, which cannot be divided further.
2. All the atoms of a given element have identical mass. Atoms of different elements differ in mass.
3. Atoms combine in a fixed ratio to form Compounds.
4 The atoms cannot be created or destroyed.
SUCCESS OF DALTON’S ATOMIC THEORY
- Atoms are the smallest part of matter
- Atoms cannot be created of destroyed
- Atoms of same element are similar in mass
- Atoms combine with each other in simple ratios.
FAILURES OF DALTON’S ATOMIC THEORY
It could explain lows of chemical combination, as on today we know that all four points are not correct.
CATHODE RAYS
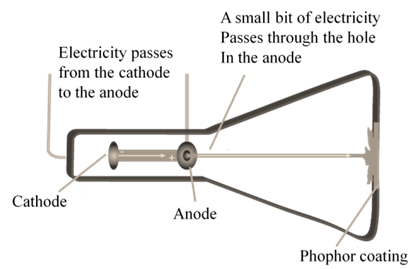
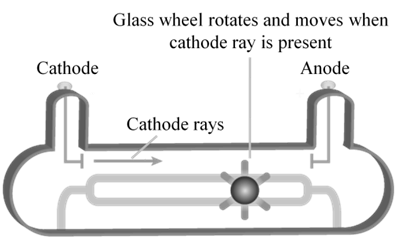
CATHODE RAYS ARE NEGATIVELY CHARGED
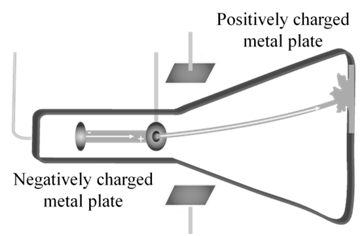
CATHODE RAYS TRAVEL IN STRAIGHT LINE.
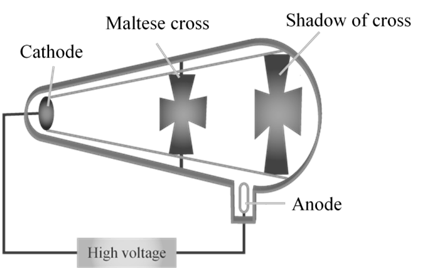
CATHODE RAYS ARE PARTICLES
CHARGE /MASS (E/M) RATIO
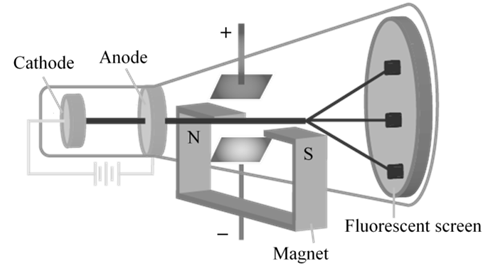
In 1897 JJ. Thomson determined the e/m value of cathode rays.
Thomson proved that e/m ratio is same, whatever material is of plates or gas filled in the tube
![]()
Ex.: Which of the following is never true for cathode rays?
- They possess kinetic energy
- They are electromagnetic waves
- They produce heat
- They produce mechanical pressure Answer (c)
MILLIKAN’S OIL DROP EXPERIMENT
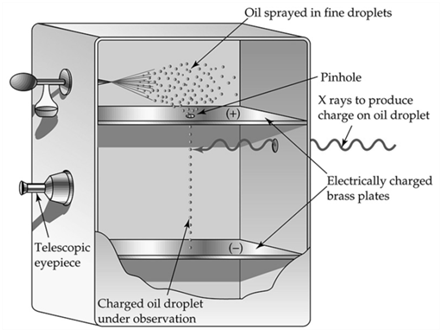
MASS OF ELECTRON
From Millikan's oil drop experiment e = 1.6022 x 10-19 coulombs
![]()
![]()
![]()
ANODE RAYS
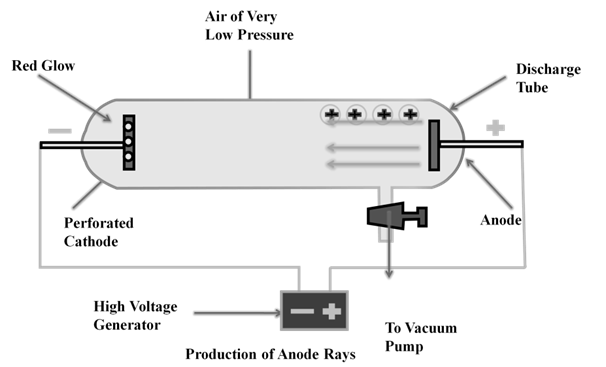

The smallest and lightest positive ion was obtained from hydrogen and was called proton. This characterized in 1919.
Later the presence of electrically neutral particle was found in the atom. These particles were discovered by Chadwick (1932) by bombarding a thin sheet of beryllium by α-particles, then electrically neutral particles having a mass slightly greater than that of the protons was emitted. He named these particles as neutrons.
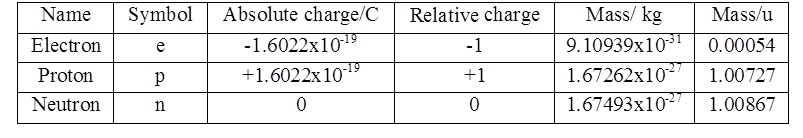
Thomson Model of Atom
Plum pudding model OR
Water melon model
FUN FACTS JJ THOMSON (NOBEL PRIZE IN 1906)

Stoichiometry and Volumetric
- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
.STOICHIOMETRY AND VOLUMETRIC
The word stoichiometry is derived from two Greek words - stoicheion (meaning element) and metron (meaning measure).
Stoichiometry, thus, deals with the calculation of masses (sometimes volumes also) of the reactants and the products involved in a chemical reaction.
How many moles of methane are required to produce 22g CO2 (g) after combustion?
Solution
According to the chemical equation.
CH4 (g) +2O2 (g) → CO2 (g) + 2H2O (g)
44g CO2 (g) is obtained from 16 g CH4 (g).
1 mol CO2 (g) is obtained from 1 mol of CH4 (g)]
![]()
= 0.5 mol CO2 (g)
Hence, 0.5 mol CO2 (g) would be obtained from 0.5 mol CH4 (g) or 0.5 mol of CH4 (g) would be required to produce 22 g CO2 (g)
Ex.:- At 300 K and I atmospheric pressure, 10mL of a hydrocarbon required 55mL of O2 for complete combustion and 40 mL, of CO2 is formed The formula of the hydrocarbon is (2019 Main, 10 April)
(a) C4H7Cl (b) C4H6
(c) C4H10 (d) C4H8
Solution: In eudiometry,
![]()
![]()
![]()
![]()
Given, (i) VCO2 = 10x = 40mL Þ x = 4
![]()
![]()
![]()
![]()
![]()
![]()
So, the hydrocarbon (Cx Hy) is C4H6 Answer (b)
LIMITING REAGENT
Many a time, the reactions are carried out when the reactants are not present in the amounts as required by a balanced chemical reaction. In such situations, one reactant is in excess over the other. The reactant which is present in the lesser amount gets consumed after sometime and after that no further reaction takes place whatever be the amount of the other reactant present. Hence, the reactant which gets consumed, limits the amount of product formed and is, therefore, called the limiting reagent.
IMPORTANT: Product formed is calculated by limiting reagent
Limiting reagent
2A + 3B → 4C
If we have 3 mole of A of 4 mole of B, find out mole of C farmed
2A + 3B → 4C
3 4
3/2x 3 = 4.5 > 4 so B is limiting reagent
3 mole of B form 4 mole C
4 mole of B will form
![]() Answer: 5.33 moles
Answer: 5.33 moles
Ex.:- If 0.50 mole of BaCl2 is mixed with 0.20 mole of Na3PO4, the maximum number of moles of Ba3 (PO4)2 that can be formed is (1981, 1M)
(a) 0.70 (b) 0.50
(b) 0.20 (d) 0.10
Solution: The balanced chemical reaction is
![]()
In this reaction, 3 moles of BaCl2 combines with 2 moles of Na3PO4. Hence, 0.5 mole of BaCl2 require
![]()
Since, available Na3PO4 (0.2 mole) is less than required mole (0.33), it is the limiting reactant and would determine the amount of product Ba3(PO4)2
∵ 2 moles of Na3PO4 gives 1 mole Ba3 (PO4)2
![]()
Answer (d)
Mole Concept
- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
MOLE CONCEPT
- One mole is the amount of a substance that contains as many particles or entities as there are atoms in exactly 12 g (or 0.012 kg) of the C12
- 12gm of C12 contains 6.022 x1023 atoms
- The number 6.022 x1023 is called Avogadro’s constant or Avogadro’s number.
- The mass of one mole of a substance in grams is called its molar mass.
- The molar mass in grams is numerically equal to the atomic/molecular/formula mass in u.(u is the unified mass)
CONVERSION OF MASS & VOLUME TO MOLES
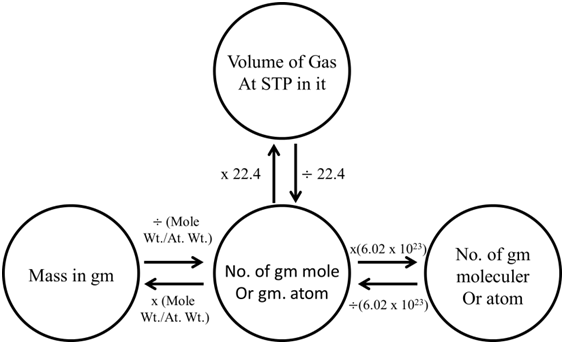
 Ex. Which has maximum number of atom? (2003, 1M)
Ex. Which has maximum number of atom? (2003, 1M)
(a) 24 g of C (12) (b) 56 g of Fe (56)
(c) 27 g of Al (27) (d) 108 g of Ag (108)
Solution: Number of atoms = Number of moles
Numbers of atoms in 24g C= 2412 ×NA=2NA
Number of atoms in 56 g of Fe= 5656NA=NA
Number of atoms in 27 g of Al= 2727NA=NA
Number of atoms in 108 of Ag= 108108NA=NA
Hence, 24g of carbon has the maximum number of atoms. Answer (a)
Ex. The ratio mass of oxygen and nitrogen particular gaseous mixture is 1: 4. The ratio of number of their molecule is (2014 Main)
Solution: no2nN2= (mO2)(MO2)(mN2)(MN2)
Where, mO2 = given mass O2, mN2
= given mass O2, mN2 = given mass of N2, MO2
= given mass of N2, MO2 = molecular mass of O2, MN2
= molecular mass of O2, MN2 = molecular mass of N2, nO2
= molecular mass of N2, nO2 = Number of moles of O2, nN2
= Number of moles of O2, nN2 = number of moles of N2
= number of moles of N2
=mO2mN22832=14×2832=732 Answer (b)
Answer (b)
Ex.:- How many moles of electron weighs 1 kg? (2002, 3M)
a 6.023×1023 b19.108×1031
b19.108×1031
c 6.0239.108×1054 d19.108×6.023×108
d19.108×6.023×108
Solution: Mass of electron = 9.108 x 10-31 kg
9.108 x 10-31 kg = 1.0 electron
∴ 1 kg = 19.108 ×10-31 electrons= 10319.108× 16.023 ×1023
∴ 19.108×6.023 ×108 mole of electrons Answer (d)
Answer (d)
MOLARITY MOLALITY, MOLE FRACTION AND NORMALITY
- Molarity is the number of moles of solute in per liter of solution. Unit is moles per liter.
Molarity= Gram Mole of solutelitre of solutiuon 
- Molality is the number of solute present in 1kg of solvent.
Molarity= Moles of solutewt. of solvent in kg
- Normality= Gram Equivalent of soluteLitre of solution

- Mole fraction of solute= Moles of solute Moles of solute+moles of solvent

Ex.: 3g of activated charcoal was added to 50mL of acetic acid solution (0.06N) in a flask. After an hour it was filtered and the strength of the filtrate was found to be 0.042N. The amount of acetic acid adsorbed (per gram of charcoal) is. (2015 JEE MAINS)
(a) 18 mg (b) 36 mg
(c) 42 mg (d) 54 mg
Solution. Given, initial strength of acetic acid = 0.06N
Final strength = 0.042 N; Volume = 50mL
\ Initial millimoles of CH3COOH = 0.06 x 50 =3
Final millimoles of CH3COOH = 0.042 x 50 = 2.1
\ Millimoles of CH3COOH adsorbed = 3 – 2.1 = 0.9 mmol.
= 0.9 x 60mg = 54 mg Answer (d)
Ex.: Dissolving 120 g of urea (mol. wt. 60) in 1000 g of water gave a solution of density 1.15 g/mL. The molarity of the solution is (2011)
(a) 1.78 M (b) 2.00M
(c) 2.05 M (d) 2.22 M
Solution: Molarity= Moles of solute Volume of Solution(L)
Moles of urea= 12060=2
Weight of solution = weight of solvent + weight of solute
= 1000 +120 = 1120 g
⇒ Volume= 1120g1.15g/mL×11000L/L=0.973L
⇒ Molarity= 2.0000.973=2.05M Answer (c)
Answer (c)
Ex.: The molarity of a solution obtained by mixing 750 mL of 0.5 M HCl 250 mL of 2 M HCl will be (2013 Main)
(a) 0.875 M (b) 1.00 M
(c) 1.75 M (d) 0.0975 M
Solution: From the formula, Mf= M1V1+M2V2V1+V2
Given, V1 = 750 mL, M1 = 0.5 M
V2 = 250mL, M2 = 2 M
= 750 × 0.5+250 × 2750+250= 8751000=0.875M Answer (a)
Answer (a)
Day - 3
PERCENTAGE COMPOSITION
Mass % of an element=mass of that element in the compound ×100molar mass of the compound
Let’s take example of carbon-dioxide (CO2)
Mass % of C=1244 x 100=27.2%
Mass % of O= 3244x 100=72.73%
Ex.:- The most abundant element by mass in the body of a healthy human adult are oxygen (61.4%) carbon (22.9%), hydrogen (10.0%) and nitrogen (2.6%) The weight which a 75 kg person would gain if all Hatoms are replaced by 2 Hatoms are replaced by 2H atoms is 2017 JEE Main)
(a) 15Kg (b) 37.5 kg
(b) 7.5 Kg (d) 10kg
Solution: Given, abundance of element by mass
Oxygen = 61.4% carbon= 22.9%, hydrogen = 10% and nitrogen = 2.6%
Total weight of person = 75 kg
Mass due to 1H= 75 ×10100=7.5kg 
1H atoms are replaced by 2H atoms
Mass due to 2H=7.5 ×2kg
\ Mass gain by person = 7.5 kg Answer (c)
Ex.:- Given that the abundances of isotopes 54Fe, 56Fe and 57Fe are 5% 90% and 5% respectively the atomic mass of Fe is (2009)
(a) 55. 85 (b) 55.95
(c) 55.75 (d) 56.05
Solution: From the given relative abundance the average weight of Fe can be calculated as
A= 54 × 5 × 56 × 90 ×57 ×5100=55.95 Answer (b)
Answer (b)
If we know percent composition we can find empirical formula
An empirical formula represents the simplest whole number ratio of various atoms present in a compound
- Molecular formula shows the exact number of different types of atoms present in a molecule of a compound.
- If the mass per cent of various elements present in a compound is known, its empirical formula can be determined.
- Molecular formula = n x (Empirical formula), where n is a simple number and may have values 1, 2, 3….
Following steps should be followed to determine empirical formula of the compound
- Step 1: Conversion of mass per cent of various elements into grams.
- Step 2: Convert mass obtained in step1 into number of moles
- Step 3: Divide the mole value obtained in step 2 by the smallest mole value (out of the mole value of various elements calculated)
- Step 4: In case the ratios are not whole numbers, then they may be converted into whole number by multiplying by the suitable coefficient.
- Step 5: Write empirical formula by mentioning the numbers after writing the symbols of respective elements
Example: - In an organic compound contains 37% carbon 50% oxygen and 13% hydrogen what is the empirical formula of compound. If it’s V. D is to find the molecular formula.
Empirical formula CH4O.
Mol. Wt. = VD x 2 = 32
Emp. formula wt = 32
n = M.W/E.W =1
So molecular formula = CH4O
Rutherford and Electromagnetic
- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
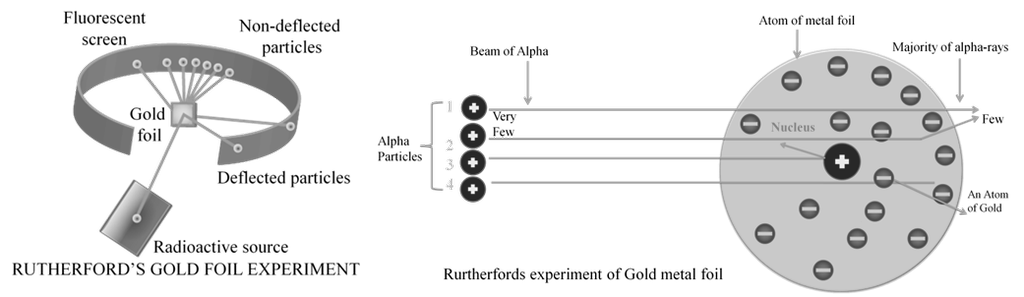
RUTHERFORD MODEL
Observations from a - particles scattering experiment by Rutherford:
a. Most of the a - particles (nearly 99 %) passed through gold foil undeflected
b. A small fraction of a- particles got deflected through small angles
c. Very few a - particles did not pass through foil but suffered large deflection nearly 180O
Inferences Rutherford drew from - particles scattering experiment:
a. Since most of the a -particles passed through foil undeflected, it means most of the space in atom is empty
b. Since some of the a -particles are deflected to certain angles; it means that there is positively mass present in atom
c. Since only some of the a -particles suffered large deflections; the positively charged mass must be occupying very small space
d. Strong deflections or even bouncing back of a -particles from metal foil were due to direct collision with positively charged mass in atom
As per Rutherford the size of nucleus is 104-105 times smaller than atom. Mardsen & Rutherford calculated density of nucleus.
Volume of atom / Volume of nucleus = 1015
Volume of earth approximately 1.08x1021 cubic meters
If earth was an atom then volume of nucleus = 1.08x1021/1015 = 1.08x106
That is ball of radius = 44m
Rutherford and Marsden gave an equation to find radius of nucleus of any atom.
R = RO A1/3
Ro = 1.33x 10-13 cm
A = no. of nucleons (Neutrons + protons)
Example calculate the density of nucleus of oxygen atom.
![]()
![]()
=1.685 x 1014 gm. /cm3 = 1.685 x 1017 kg/m3
Mass of moon = 7.34767309 × 1022 kilograms
If moon is all made of nucleus it will become a ball of radius 32m. Slightly bigger than basketball court!!!!!!!
Drawback of Rutherford model
- According to Rutherford’s model of atom, electrons which are negatively charged particles revolve around the nucleus in fixed orbits. Thus, the electrons undergo acceleration. According to electromagnetic theory of Maxwell, a charged particle undergoing acceleration should emit electromagnetic radiation. Thus, an electron in an orbit should emit radiation. Thus, the orbit should shrink. But this does not happen.
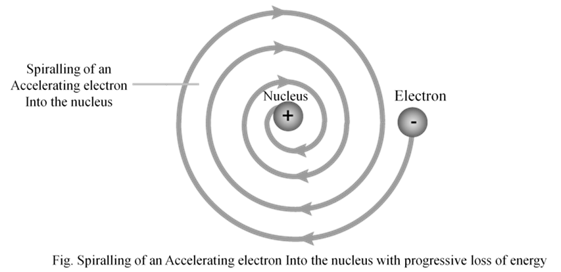
2. The model does not give any information about how electrons are distributed around nucleus and what are energies of these electrons
Atomic number (Z): It is equal to the number of protons in an atom. It is also equal to the number of electrons in a neutral atom.
Mass number (A): It is equal to the sum of protons and neutrons.
Isotopes: These are the atoms of the same element having the same atomic number but different mass number. Ex 6C12 and 6C14
Isobars: Isobars are the atoms of different elements having the same mass number but different atomic number. 18Ar40 and 20Ca40
Isoelectronic species: These are those species which have the same number of electrons. Ex. N2 and CO
Isotones: Two nuclides are called isotones if they have same neutron number N, but different proton numbers Z. For example, Boron- 12 and Carbon-13 nuclei, but both contain 7 neutrons
ELECTROMAGNETIC WAVES
The radiations which are associated with electrical and magnetic fields are called electromagnetic radiations. When an electrically charged particle moves under acceleration, alternating electrical and magnetic fields are produced and transmitted. These fields are transmitted in the form of waves. These waves are called electromagnetic waves or electromagnetic radiations.
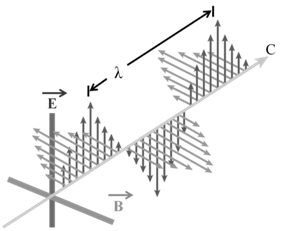
PROPERTIES OF ELECTROMAGNETIC RADIATIONS:
a. Oscillating electric and magnetic field are produced by oscillating charged particles. These fields are perpendicular to each other and both are perpendicular to the direction of propagation of the wave.
b. They do not need a medium to travel. That means they can even travel in vacuum.
WAVE NATURE OF ELECTROMAGNETIC RADIATION
Characteristics of electromagnetic radiations:
a. Wavelength: It may be defined as the distance between two neighbouring crests or troughs of wave as shown. It is denoted by l.
b. Frequency (n): It may be defined as the number of waves which pass through a particular point in one second.
c. Velocity (v): It is defined as the distance travelled by a wave in one second. In vacuum all types of electromagnetic radiations travel with the same velocity. Its value is 3 X108 m sec-1. It is denoted by v
d. Wave number: Wave number (ν![]() ) is defined as the number of wavelengths per unit length.
) is defined as the number of wavelengths per unit length.
Relationship between velocity, frequency and wavelength Velocity = frequency x wavelength
Velocity = frequency x wavelength

THE SPECTRUM OF ELECTROMAGNETIC RADIATION
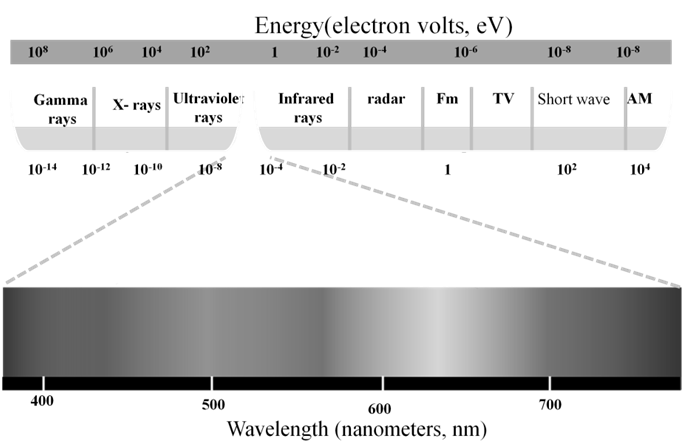
Ex.-The Vividh Bharati station of All India Radio, Delhi, broadcasts on a frequency of 1,368 kHz (kilo hertz).
Calculate the wavelength of the electromagnetic radiation emitted by transmitter. Which part of the electromagnetic spectrum does it belong to?
![]()
![]()
![]() = 219.3m
= 219.3m
This is a characteristic radio wave wavelength.
Ex.: Calculate (a) wave number and (b) frequency of yellow radiation having wavelength 5800 Å.
Solution
- Calculation of wavenumber
λ = 5800Ǻ = 5800 x 10-8 cm
= 5800 x 10-10 m
![]()
= 1.724 x 106 m-1
= 1.724 x 104 cm-1
(b) Calculation of the frequency (n)
![]()
TYPES OF SPECTRUM (CAN BE CLASSIFIED IN TWO DIFFERENT WAYS
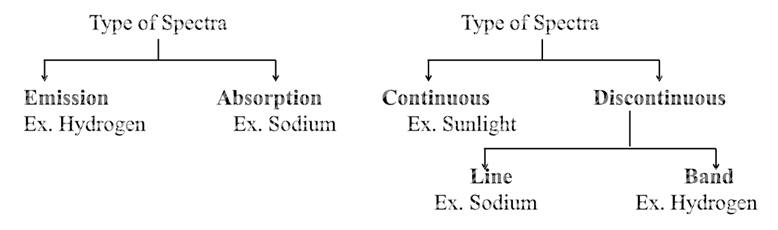
FIRST CLASSIFICATION SPECTRUM IS OF TWO TYPES: CONTINUOUS AND LINE SPECTRUM
a. The spectrum which consists of all the wavelengths is called continuous spectrum.
b. A spectrum in which only specific wavelengths are present is known as a line spectrum. It has bright lines with dark spaces between them.
Electromagnetic spectrum is a continuous spectrum. It consists of a range of electromagnetic radiations arranged in the order of increasing wavelengths or decreasing frequencies. It extends from radio waves to gamma rays.
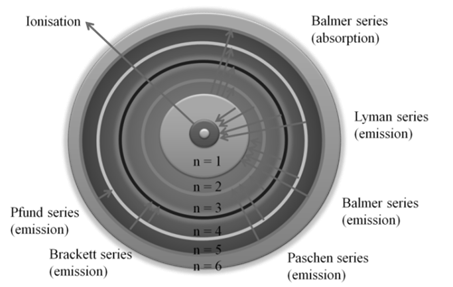
SPECTRUM IS ALSO CLASSIFIED AS EMISSION AND ABSORPTION SPECTRUM.
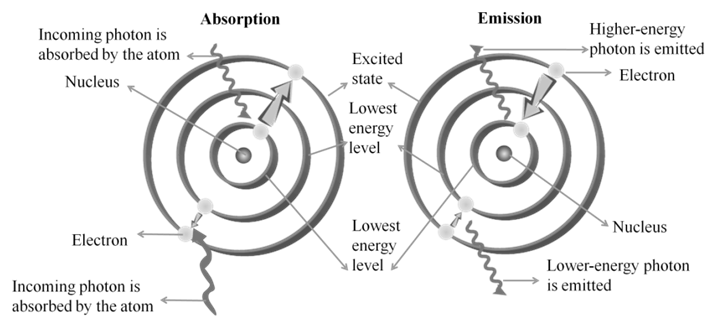
- Emission spectrum: A substance absorbs energy and moves to a higher energy state. The atoms, molecules or ions that have absorbed radiation are said to be excited. Since the higher energy state is unstable they return to the more stable energy state by emitting the absorbed radiation in various regions of electromagnetic spectrum. The spectrum of radiation emitted by a substance that has absorbed energy is called an emission spectrum.
- Absorption spectrum is the spectrum obtained when radiation is passed through a sample of material. The sample absorbs radiation of certain wavelengths. The wavelengths which are absorbed are missing and come as dark lines

Bohr's Model
- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
BOHR’S MODEL FOR HYDROGEN ATOM
a. An electron in the hydrogen atom can move around the nucleus in a circular path of fixed radius and energy. These paths are called orbits or energy levels. These orbits are arranged concentrically around the nucleus.
b. As long as an electron remains in a particular orbit, it does not lose or gain energy and its energy remains constant.
c. When transition occurs between two stationary states that differ in energy, the frequency of the radiation absorbed or emitted can be calculated. n = DE/h = (E2-E1)/h
n= Frequency of radiation
h = Planck's constant
E1 Energy of lower energy state
E2 Energy of higher energy state
d. An electron can move only in those orbits for which its angular momentum is an integral multiple of h/2p Þ mevr = n ![]() where n = 1, 2 ,3 ….
where n = 1, 2 ,3 ….
Bohr’s theory for hydrogen atom:
a. Stationary states for electron are numbered in terms of Principal Quantum numbered as n=1, 2, 3…
b. For hydrogen atom: The radii of the stationary states is expressed as rn = n2a0 where a0= 52.9 pm
c. Energy of stationary state En = -RH![]() where n 1, 2,3,.... and RH is 2.18x10-18 ( rhydberg’s constant)
where n 1, 2,3,.... and RH is 2.18x10-18 ( rhydberg’s constant)
CALCULATION OF WAVELENGTH FOR HYDROGEN SPECTRUM
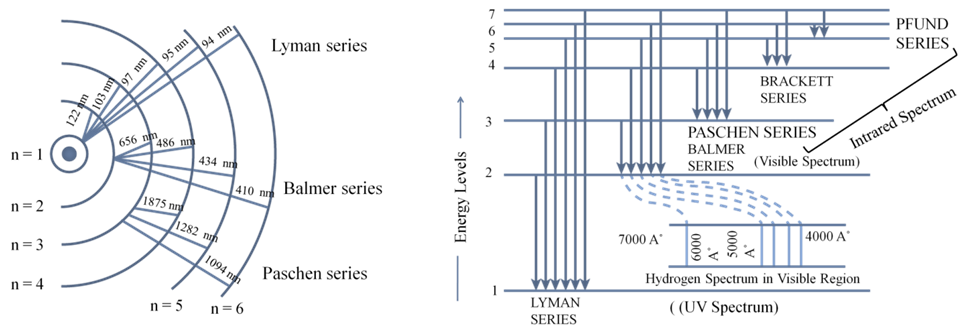
BOHR MODEL OF THE HYDROGEN ATOM
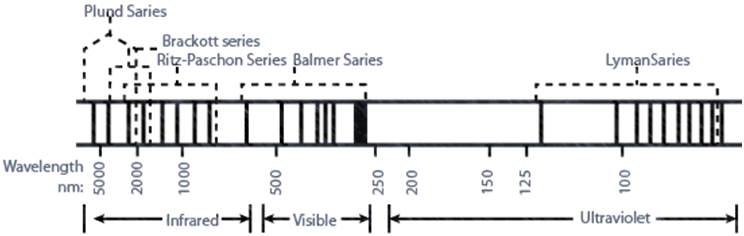

![]()
For equilibrium Þ centripetal force = centrifugal force
![]()
q1 = Ze q2 = e
![]()
On solving equation (1) & (3)
![]()
![]()
From equation (3)
Þ rn = r1 x n2 Different orbit Some Atom (DOSA)
![]() Same Orbit Different Atom (SODA)
Same Orbit Different Atom (SODA)
From equation (4)
Þ Vn = V1 / n DOSA
Þ VZ = VH x Z SODA
Total Energy = K.E. + P.E.
![]()
Putting value form equation (3) & (4) ![]()
![]()
From equation (5)
![]() D.O.S.A
D.O.S.A
![]() S.O.D.A
S.O.D.A
For Hydrogen Atom Z =1
As per Bohr model
∆E = hv
![]()
![]()
![]()
RH=109677 cm-1 and is called Rydberg’s constant
SUCCESS AND FAILURES OF BOHR’S MODEL OF ATOM
Success of Bohr’s model
1. The frequencies of spectrum in hydrogen lines were successfully explained.
2. The value of Rydberg’s constant calculated matched the experimental value.
3. It could explain the spectrum of hydrogen like species like He+, Li+2 etc
LIMITATIONS OF BOHR’S MODEL OF ATOM
-
- Bohr’s model failed to account for the finer details of the hydrogen spectrum. For instance splitting of a line in the spectrum into two closely spaced lines.
- Bohr’s model was also unable to explain spectrum of atoms containing more than one electron.
- Bohr’s model was unable to explain Zeeman Effect i.e. splitting of spectral line in presence of magnetic effect.
- Bohr’s model also failed to explain Stark effect i.e. splitting of spectral line in presence of electric field.
- Bohr’s model could not explain the ability of atoms to form molecules by chemical bonds
Bohr's Model and Planck's Quantum Theory
- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
Black body: An ideal body, which emits and absorbs all frequencies, is called a black body. The radiation emitted by such a body is called black body radiation.
Planck’s Quantum Theory
Planck said that atoms and molecules could emit (or absorb) energy only in discrete quantities and not in a continuous manner, a belief popular at that time.
Planck gave the name quantum to the smallest quantity of energy that can be emitted or absorbed in the form of electromagnetic radiation.
E µ n Þ E = hn Þ ![]()
The proportionality constant, ’h’ is known as Planck’s constant and has the value 6.626 10-34 Js.
Photoelectric Effect
- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
PHOTOELECTRIC EFFECT
Experimental results observed for the experiment of Photoelectric effect observed by Hertz:
a. When beam of light falls on a metal surface electrons are ejected immediately i.e. there is not time lag between light striking metal surface and ejection of electrons
b. Number of electrons ejected is proportional to intensity or brightness of light
c. Threshold frequency ( no ): For each metal there is a characteristic minimum frequency below which photoelectric effect is not observed. This is called threshold frequency.
d. If frequency of light is less than the threshold frequency there is no ejection of electrons no matter how long it falls on surface or how high is its intensity.
Photoelectric work function (Wo): The minimum energy required to eject electrons is called photoelectric work function. Wo= h no
Energy of the ejected electrons: ½ mev2 = h(n-no)
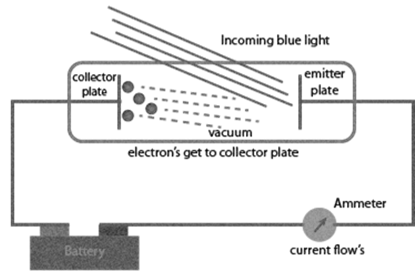
The kinetic energies of these electrons increase with the increase of frequency of the light used. All the above results could not be explained on the basis of laws of classical physics.
Photoelectric work function (Wo): The minimum energy required to eject electrons is called photoelectric work function. Wo= h no
Energy of the ejected electrons: ½ mev2 = h(n-no)
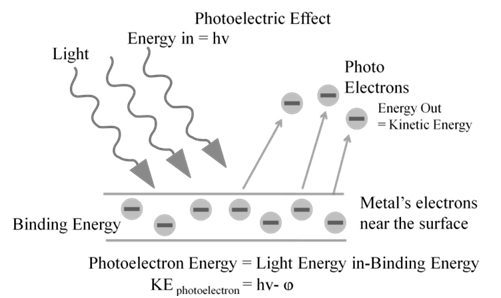
DUAL BEHAVIOUR OF ELECTROMAGNETIC RADIATION
It is concluded from active experiment that electromagnetic radiation have due nature. Wave nature as confirmed by experiments and particle nature is confirmed by photo electric effect.
de Broglie proposed that matter exhibits dual behaviour i.e. matter shows both particle and wave nature.
1. de Broglie’s relation: l = ![]() =
=![]()
Where: l - Wavelength; p – Momentum; v – Velocity; h – Planck’s constant
2. According to de Broglie, every object in motion has a wave character. Wavelengths of macroscopic objects cannot be detected but for microscopic particles it can be detected. This is because for microscopic objects, the mass is less. Since mass and wavelength are inversely proportional to each other, the wavelength will be more. But for macroscopic objects, the mass is large. Therefore, wavelength will be too short to be detected. Dual
Heisenberg’s uncertainty principle
It states that it is impossible to determine simultaneously, the exact position and exact momentum (or velocity) of an electron
![]()
Assuming mass is constant and does not change with velocity
![]()
Schrodinger wave equation
![]()
The probability of finding an electron at a point within an atom is proportional to the square of the orbital wave function i.e., ψ2 at that point. ψ2 is known as probability density and is always positive. From the value of ψ2 at different points within an atom, it is possible to predict the region around the nucleus where electron will most probably be found
IMPORTANT FEATURES OF THE QUANTUM MECHANICAL MODEL OF ATOM
Quantum mechanical model of atom is the picture of the structure of the atom, which emerges from the application of the Schrödinger equation to atoms. The following are the important features of the quantum me chemical model of atom:
1. The energy of electrons in atoms is quantized (i.e., can only have certain specific values), for example when electrons are bound to the nucleus in atoms.
2. The existence of quantized electronic energy levels is a direct result of the wave like properties of electrons and is allowed solutions of Schrödinger wave equation.
3. Both the exact position and exact velocity of an electron in an atom cannot be determined simultaneously (Heisenberg uncertainty principle). The path of an electron in an atom therefore, can never be determined or known accurately. That is why, as you shall see later on, one talks of only probability of finding the electron at different points in an atom.
4. An atomic orbital is the wave function ψ for an electron in an atom. Whenever an electron is described by a wave function, we say that the electron occupies that orbital. Since many such wave functions are possible for an electron, there are many atomic orbitals in an atom. These one electron orbital wave functions. or orbitals form the basis of the electronic structure of atoms. In each orbital, the electron has a definite energy. An orbital cannot contain more than two electrons. In a multi-electron atom, the electrons are filled in various orbitals in the order of increasing energy. For each electron of a multi-electron atom, there shall, therefore, be an orbital wave function characteristic of the orbital it occupies. All the information about the electron in an atom is stored in its orbital wave function ψ and quantum mechanics makes it possible to extract this information out of ψ.
Orbitals and Quantum Numbers
- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
ORBITALS AND QUANTUM NUMBERS

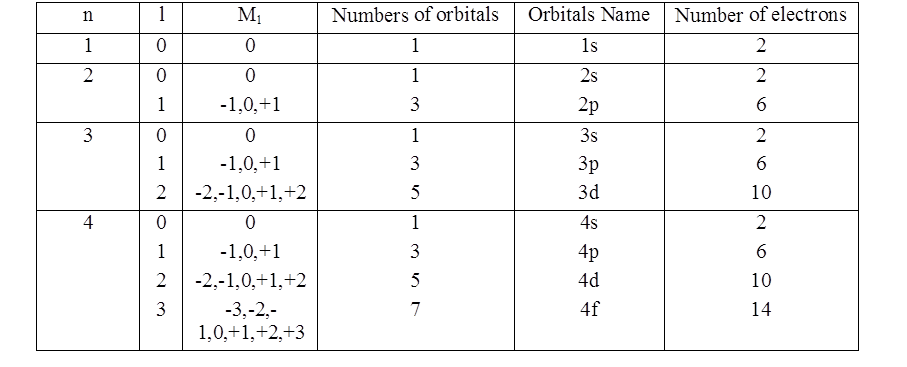
ORBIT VS. ORBITAL

PHYSICAL SIGNIFICANCE OF THE QUANTUM NUMBERS
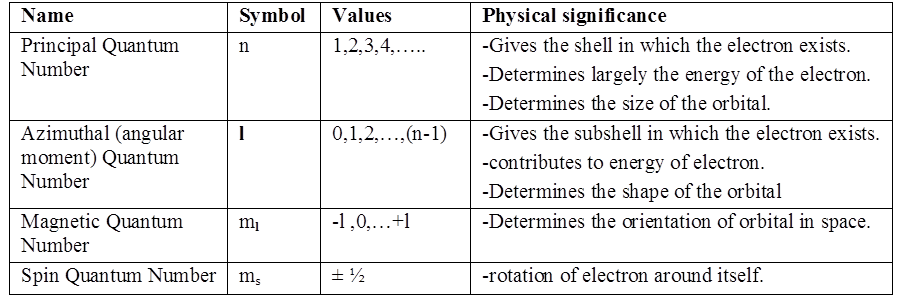
1s and 2s orbitals

2s and 2p Orbitals
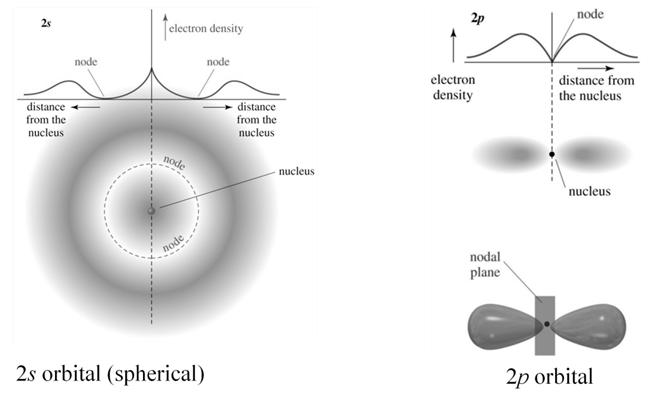
d orbital
ELECTRONIC CONFIGURATION OF ATOMS
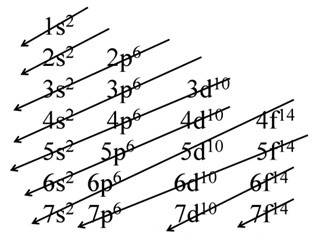
Aufbau principle Electrons are placed in the lowest energetically available subshell. Thus orbitals are filled in the order of increasing energy, using two general rules to help predict electronic configurations:-
- Electrons are assigned to orbitals in order of increasing value of (n+ℓ). Orbitals with lower value of (n+l) are filled first as they have lower energy.
- For subshells with the same value of (n+ℓ), electrons are assigned first to the sub shell with lower n.
- The order in which the orbitals are filled is as follows:
- 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 4f, 5d, 6p, 7s...
- It is based on (n+ l) rule. It states that the orbital with lower value of (n +l) has lower energy.
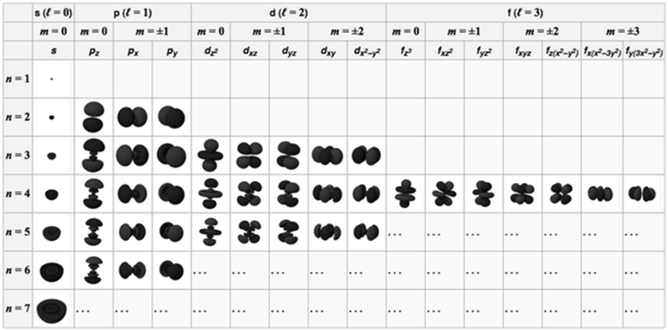
AUFBAU DIAGRAM
PAULI'S EXCLUSION PRINCIPLE
It is impossible for any two electrons of an atom to have the same values of the all four quantum numbers. If even three quantum numbers are same for any two electrons of the atom then fourth quantum number will definitely be different.
In other words an orbital can have maximum of two electrons
Hund’s Rule of Maximum Multiplicity
This rule deals filling of electrons in the orbitals belonging to the same subshells of equal energy called degenerate orbitals.
- It states that pairing of electrons in the orbitals belonging to the same sub shell (p, d or f) does not take place until each orbital of that sub shell gets one electron that is singly occupied.
- Some of the orbitals acquire extra stability due to their symmetry.
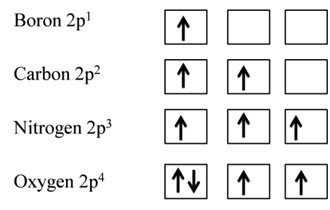
EXCEPTION: HALF-FILLED AND FILLED D ORBITALS
- When a subshell is half-filled or completely filled, it lowers the overall energy of the atom.
- In other words, this is favoured.
- This usually doesn't affect electron configurations, except in the d and f subshells.
- Example: Copper (29 electrons)
- Normal electron configuration:
1s22s22p63s23p64s23d9
- Added stability if 3 d is full (electron gets promoted to 3 d from 4s)
- 1s22s22p63s23p64s13d10
The region where this probability density function reduces to zero is called nodal surfaces or simply nodes.
Boundary surface diagram: In this representation, a boundary surface or contour surface is drawn in space for an orbital on which the value of probability density ψ 2(r) is constant. However, for a given orbital, only that boundary surface diagram of constant probability density is taken to be good representation of the shape of the orbital which encloses a region or volume in which the probability of finding the electron is very high, say, 90%.
Radial nodes: Radial nodes occur when the probability density wave function for the electron is zero on a spherical surface of a particular radius. Number of radial nodes = n – l – 1
Angular nodes: Angular nodes occur when the probability density wave function for the electron is zero along the directions specified by a particular angle. Number of angular nodes = l
Total number of nodes = n – 1
Degenerate orbitals: Orbitals having the same energy are called degenerate orbitals
IMPORTANT FORMULAE
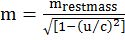
- Frequency of electromagnetic wave
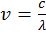
- Energy of photon E = hn =
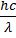
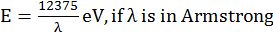
- Bohr’s postulate mvr =
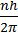 (Angular momentum of ‘e’ in an orbit)
(Angular momentum of ‘e’ in an orbit) 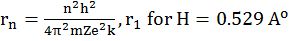
- rn = r1 x n2 same atom different orbit
- rZ = rH / Z same orbit different atom
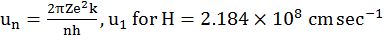
- un = u1 / n same atom different orbit
- uZ = uH x Z same orbit different atom
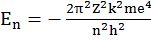 E1 for H= -21.72X10-12 erg = -13.6 eV
E1 for H= -21.72X10-12 erg = -13.6 eV- En = E1/n2 same atom different orbit
- EZ = EH x Z2 same orbit different atom
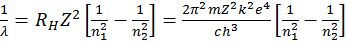
 Ao
Ao- Ön=a (Z – b), where n is frequency of X-rays given out by metal of at. No. Z
- Average atomic weight =
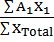
- KE of photoelectric electron (½ mv2) = hn - hno (hno = work function) & no threshold frequency
- deBroglie equation l =
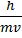
- Uncertainty
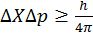
- (Schrodinger wave equation)
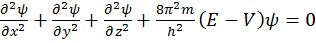
- Angular momentum of ‘e’ in an orbital=
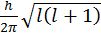
- Magnetic moment of an atom=.
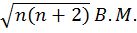 where n is no. of unpaired electrons
where n is no. of unpaired electrons - Nodes
- Radial (spherical) nodes=(n – l – 1)
- Angular (non spherical) nodes=l
- Total nodes= (n - 1)
- No of spectral lines =
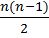
Laws of Chemical Combinations
- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
LAWS OF CHEMICAL COMBINATIONS
There are 5 basic laws of chemical combinations that govern every reaction: Law of conservation of mass, law of definite proportions, law of multiple proportions, Gay Lussac’s law of gaseous volumes, and lastly, Avogadro law
- Law of Conservation of Mass: Antoine Lavoisier established the Law of Conservation of Mass. It states that matter can neither be created nor destroyed. In other words, we can say that during any physical or chemical change, the total mass of reactants is equal to the total mass of products
- Law of definite proportions: Joseph Proust showed that a given compound always contains exactly the same proportion of elements by weight.
- Law of multiple proportions: Dalton proposed the law of multiple proportions. According to this law if two elements can combine to form more than one compound, the mass of one element that combines with the fixed mass of the other element is in the ratio of small whole numbers.
- Gay Lussac’s Law of gaseous volumes: When gases combine or are produced in a chemical reaction they do so in a simple ratio by volume, provided all the gases are at same temperature and Pressure.
- Avogadro law: At the same temperature and pressure, equal volumes of gases contain equal number of molecules.
Introduction to Periodic Properties
- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
INTRODUCTION
In 1800, only 31 elements were known. By 1865, the number of identified elements had more than doubled to 63. At present 114 elements are known.
With such a large number of elements it is very difficult to study individually. the chemistry of all these elements is also difficult to handle individually.
LAW OF TRIADS
Johann Döbereiner classified elements in group of three elements called triads.
In Döbereiner triad the atomic weight of the middle element is very close to the arithmetic mean of the other two elements
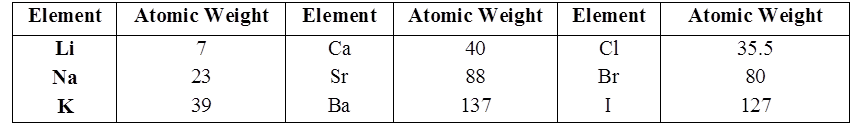
LAW OF OCTAVES
Since Döbereiner Law of triads worked only for few elements, it was dismissed.
Chancourtois arranged elements in order of increasing atomic weights and made a cylindrical table of elements.
John Newland arranged the elements in the increasing order of atomic weight and noted that the properties of the every eighth element are similar to the first one. This relationship is called as “Law of octaves”
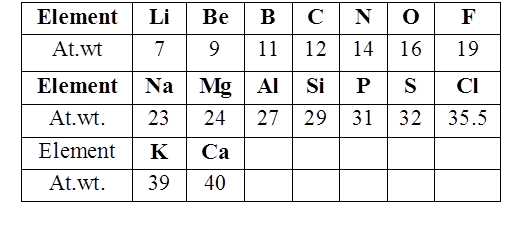
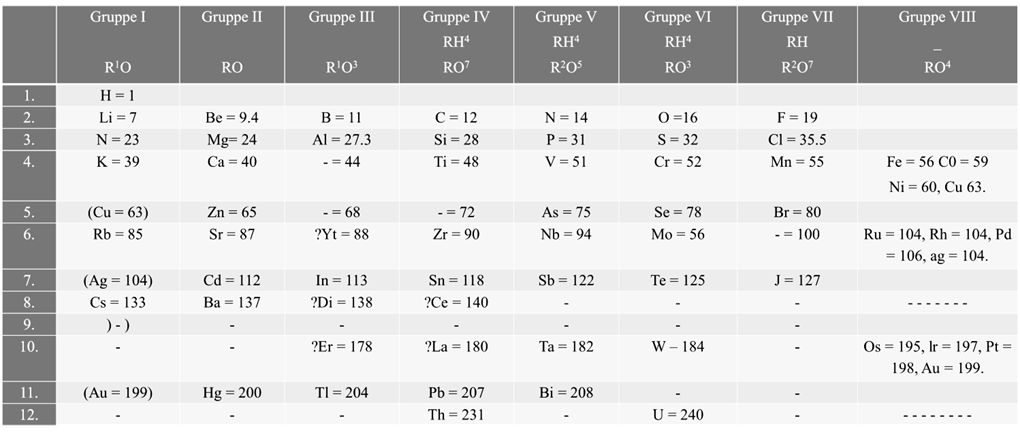
MENDELEEV’S PERIODIC TABLE
According to Mendeleev’s periodic law the physical and chemical properties of elements are periodic functions of their atomic weights.
Merits of Mendeleev’s periodic table:
- Mendeleev’s periodic table was very helpful in remembering and studying the properties of large number of elements
- Mendeleev’s periodic table helped in correcting the atomic masses of some of the elements like gold, beryllium and platinum based on their positions in the periodic table
- Mendeleev could predict the properties of some undiscovered elements like scandium, gallium and germanium. By this intuition, he had left gaps for the undiscovered elements while arranging elements in his periodic table
SUCCESS OF MENDELEEV’S WORK
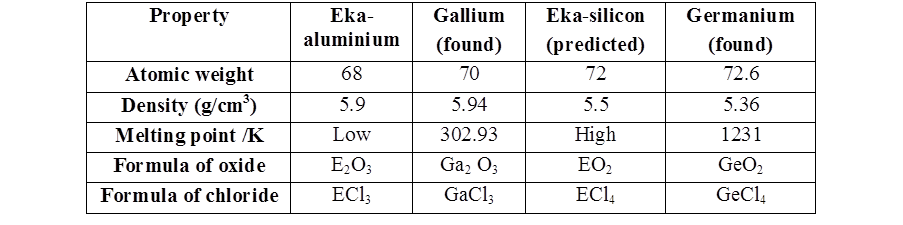
Limitation of Mendeleev’s table
- Position of hydrogen is not correctly defined in periodic table. It is placed in group I though it resembles both group 1 and 17.
- In certain pairs of elements increasing order of atomic masses was not obeyed. For example argon (Ar, atomic mass 39.9) is placed before potassium (K, atomic mass 39.1)
- Isotopes were not given separate places in the periodic table although Mendeleev's classification is based on the atomic masses.
- Some similar elements are separated and dissimilar elements are grouped together. For example copper and mercury resembled in their properties but had been placed in different groups. On the other hand lithium and copper were placed together although their properties are quite different.
- Mendeleev did not explain the cause of periodicity among the elements.
- Lanthanoids and actinoids were not given a separate position in the table.
Modern Periodic Table
Henry Moseley showed that the atomic number is a more fundamental property of an element than its atomic mass.
Mendeleev’s Periodic Law was, therefore, accordingly modified.
Modern Periodic Law:
The physical and chemical properties of the elements are periodic functions of their atomic numbers
Nomenclature of elements of Atomic mass > 100
Electronic Configurations for Periods and groups
Electronic configuration of Zirconium (A. No. 40): 1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d2
Iodine I53 = 1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d10 5p5
We can classify the elements into four blocks viz.,
s-block, p-block, d-block and f-block depending on the type of atomic orbitals that are being filled with electrons.
Hydrogen and Helium are exception to this rule
The s-Block Elements
The elements of Group 1 (alkali metals) and Group 2 (alkaline earth metals) which have ns1 and ns2 outermost electronic configuration belong to the s-Block Elements.
The p-Block Elements
The outermost electronic configuration varies from ns2np1 to ns2np6 in each period. The p-Block Elements comprise those belonging to Group 13 to 18 and these together with the s-Block Elements are called the Representative Elements or Main Group Elements.
The d-Block Elements (Transition Elements)
These elements have the general outer electronic configuration (n-1)d1-10ns0-2 . These are the elements of Group 3 to 12 in the centre of the Periodic Table. These are characterised by the filling of inner d orbitals by electrons and are therefore referred to as d-Block Elements. They are all metals.
The f-Block Elements (Inner-Transition Elements)
They have outer electronic configuration (n-2)f1-14 (n-1)d0-1ns2
The two rows of elements at the bottom of the Periodic Table, called the Lanthanoids, Ce(Z = 58) to Lu(Z = 71) and Actinoids, Th(Z = 90) to Lr (Z = 103) .
METALS, NON METALS AND METALLOIDS
Metals comprise more than 78% of all known elements and appear on the left side of the Periodic Table. Metals are usually solids at room temperature [mercury is an exception; gallium and caesium also have very low melting points (303K and 302K, respectively)]. Metals usually have high melting and boiling points. They are good conductors of heat and electricity. They are malleable (can be flattened into thin sheets by hammering) and ductile (can be drawn into wires). In contrast, non-metals are located at the top right hand side of the Periodic Table. In fact, in a horizontal row, the property of elements change from metallic on the left to non-metallic on the right. Non-metals are usually solids or gases at room temperature with low melting and boiling points (boron and carbon are exceptions). They are poor conductors of heat and electricity.
Most non-metallic solids are brittle and are neither malleable nor ductile. The elements become more metallic as we go down a group; the non-metallic character increases as one goes from left to right across the Periodic Table. The change from metallic to non-metallic character is not abrupt as shown by the thick zigzag line in periodic table.
The elements (e.g., silicon, germanium, arsenic, antimony and tellurium) bordering this line and running diagonally across the Periodic Table show properties that are characteristic of both metals and non-metals. These elements are called Semi-metals or Metalloids
Sheilding Effect and Radii
- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
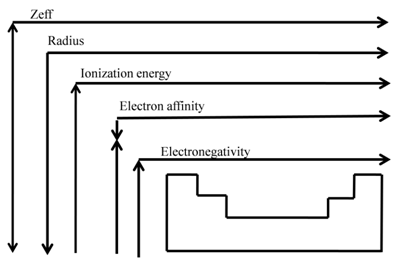
SHIELDING EFFECT
Shielding effect or screening effect: Due to the presence of electrons in the inner shells, the electron in the outer shell will not experience the full positive charge on the nucleus.
So due to the screening effect, the net positive charge experienced by the electron from the nucleus is lowered and is known as effective nuclear charge.
- Effective nuclear charge, Zeff, experienced by an electron is less than actual nuclear charge , Z
- Electrons in the outermost shell are repelled (shielded) by electrons in the inner shells. This repulsion counteracts the attraction caused by the positive nuclear charge
Coulomb’s law:

SHIELDING EFFECT
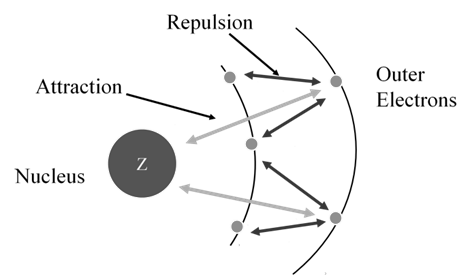
Effective nuclear charge, Zeff, experienced by an electron is less than the actual nuclear charge, Z. „Electrons in the outermost shell are repelled (shielded) by electrons in the inner shells. This repulsion counteracts the attraction caused by the positive nuclear charge
Zeff = Z – S (S = screening constant)
Shielding effect
- Electrons in inner orbitals have greater shielding effect than electrons in same shell.
- Shielding effect s > p > d > f
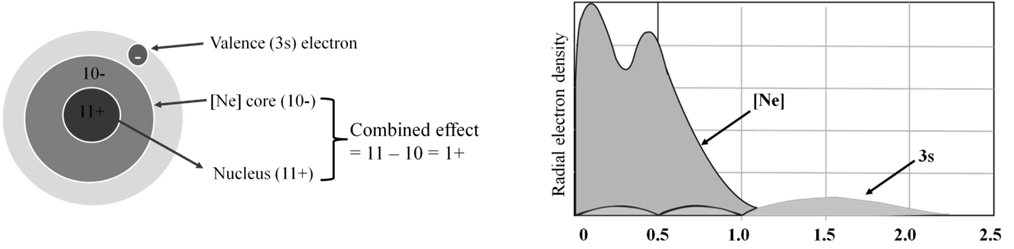
ATOMIC RADII
Periodicity
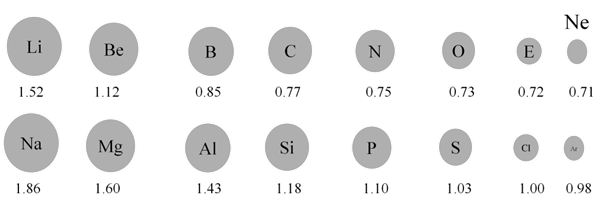
- As we move from left to right along the period, the effective nuclear charge "felt" by the outermost electron increases while the distance from the nucleus doesn't change that much (electrons are filling the same shell)
- Outermost electrons are attracted stronger by the nucleus, and the atomic radius decreases

IONIC RADII
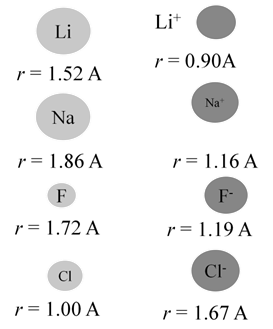
When atom loses an electron, its radius always decreases
- Cations (positive ions) are always smaller than their respective neutral atoms.
When atom gains an electron, its radius always increases
- Anions (negative ions) are always larger than their respective neutral atoms
ISOELECTRONIC SPECIES
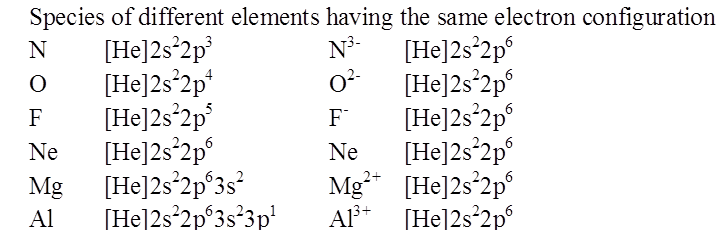
RADII OF ISOELECTRONIC IONS

Ionization Energy
- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
IONIZATION ENERGY
• If sufficient energy is provided, the attraction between the outer electron and the nucleus can be overcome and the electron will be removed from the atom
FIRST IONIZATION ENERGY (IE1)
• The minimum amount of energy required to remove the most loosely bound electron from an isolated gaseous atom to form a 1+ ion
Na (g) + 496 KJ/ Mol → Na+ (g) + e-
• Second ionization energy (IE2)
The minimum amount of energy required to remove the 2nd electron from a gaseous 1+ ion
IE1: Ca(g) + 590 kJ/mol ® Ca+(g) + e-
IE2: Ca+(g) + 1145 kJ/mol ® Ca2+(g) + e-
The 2nd electron "feels" higher nuclear charge (stronger attractive force) since the electron-electron repulsion has been decreased: For all atoms IE2 > IE1
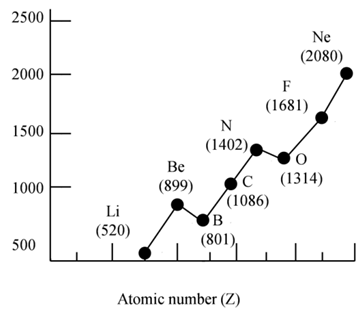
Ionization Energy: Trends
• IE1 increases from left to right along a period since the effective nuclear charge (Zeff) "felt" by the outermost electrons increases
- There are some exceptions to this general trend caused by additional stability of filled and half- filled subshells (orbitals with the same )
- IE1 decreases as we go down a group since the outermost electrons are farther from the nucleus
IONIZATION ENERGY: PERIODICITY
IMPORTANT CONCLUSIONS
- Atoms of noble gases have completely filled outer shell, the smallest radii among the elements in the same period, and the highest ionization energies
- Atoms of metals, especially those to the left in the periodic chart, ionize easily forming cations and attaining the electron configuration of noble gases
- Atoms of non-metals, especially those to the right in the periodic chart, are very unlikely to loose electrons easily - their ionization energies are high
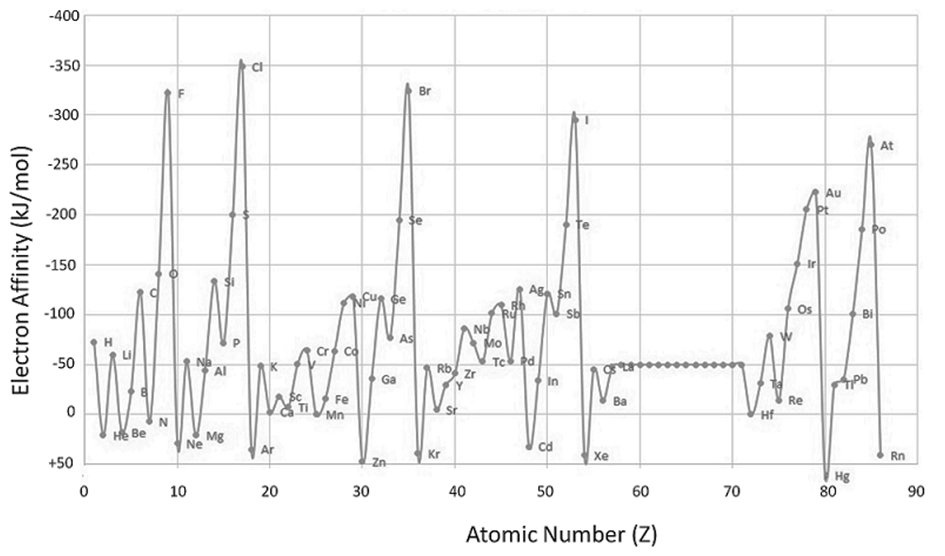
ELECTRON AFFINITY
- For most non-metals, it is much easier to achieve the stable electron configuration of a noble gas by gaining rather than losing electrons
- Therefore, non-metals tend to form anions
- Electron affinity is a measure of an atom's ability to form negative ions
- The amount of energy released when an electron is added to an isolated gaseous atom to form an ion with a -1 charge.
Cl(g) + e- ® Cl-(g) + 349 kJ/mol
Sign conventions for electron affinity
• If electron affinity < 0 (energy is released)
• If electron affinity > 0 (energy is absorbed)
Compare cation- and anion-forming processes:
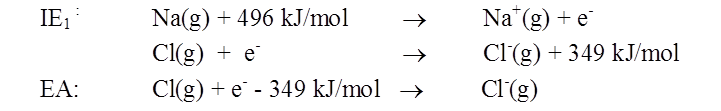
ELECTRON AFFINITY: TRENDS
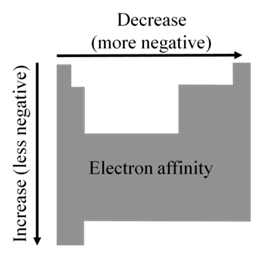
EA becomes more negative on going from left to right along a period
• There are some exceptions to this general trend caused by
additional stability of filled and half- filled subshells
(orbitals with the same l )
• EA becomes less negative as we go down a group because
the attraction of the outermost electrons to the nucleus weakens
ELECTRON AFFINITY: PERIODICITY
• Important conclusions
- Noble gases have completely filled outer shell and therefore zero electron affinity
- Non-metals, especially halogens, gain electrons easily forming anions and attaining the electron configuration of noble gases
- Metals are usually quite unlikely to gain electrons and form anions
Electron Gain Enthalpies (kJ mol-1) of group17 elements
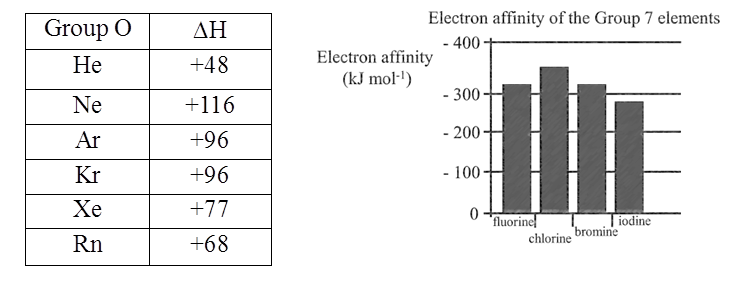
ELECTRONEGATIVITY
• Measures the tendency of an atom to attract electrons when chemically combined with another element
• If element "likes" electrons - high electronegativity (electronegative element)
• If element "dislikes" electrons - low electronegativity (electropositive element)
Sounds like the electron affinity but different
• Electron affinity measures the degree of attraction of an electron by a single atom forming an anion
• Electronegativity measures the attraction of electrons to the atom in chemical compounds
- The scale for electronegativity was suggested by Linus Pauling
- It is a semi-qualitative scale based on data collected from studying many compounds

ANOMALOUS PROPERTIES OF SECOND PERIOD ELEMENTS
The first element of each of the groups 1 (lithium) and 2 (beryllium) and groups 13-17 (boron to fluorine) differs in many respects from the other members of their respective group. Behaviour of lithium and beryllium is more similar with the second element of the following group i.e., magnesium and aluminium, respectively. This sort of similarity is commonly referred to as diagonal relationship in the periodic properties. What are the reasons for the different chemical behaviour of the first member of a group of elements in the s- and p-blocks compared to that of the subsequent members in the same group? The anomalous behaviour is attributed to their small size, large charge/ radius ratio, high Electronegativity and absence of d orbital
Lewis structure
- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
INTRODUCTION
The attractive force which holds together the constituent particles (atoms, ions or molecules) in chemical species is known as chemical bond.
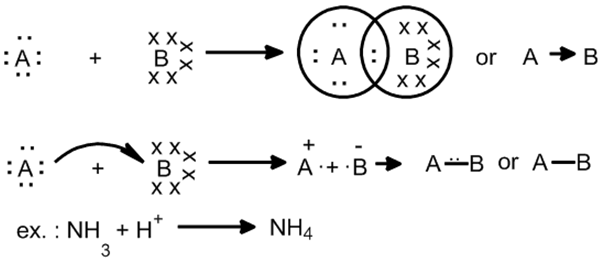
- Kössel-Lewis Approach to Chemical Bonding
They assumed that atom have positive kernel surrounded by electrons occupying the corners of a cube. If they have all the eight electrons in their outer shell they will be stable (octet rule). Otherwise they achieve stability (octet) through chemical bonding.
LEWIS STRUCTURE
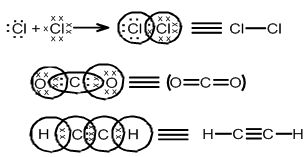
Why chemical bonds are formed.
If the resultant molecule has lower Gibb's energy then the reacting species, then chemical bonds are formed.
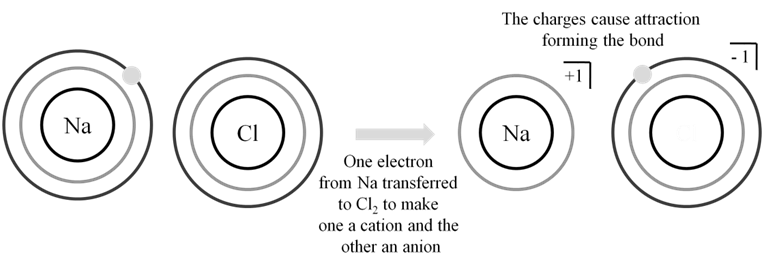
IONIC BOND
Ionic bonds are strong electrostatic forces between cation & anion which are formed when an atom looses an electron or gains an electron.
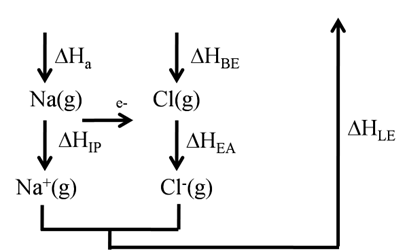
BORN HABER CYCLE FOR SODIUM CHLORIDE
![]()
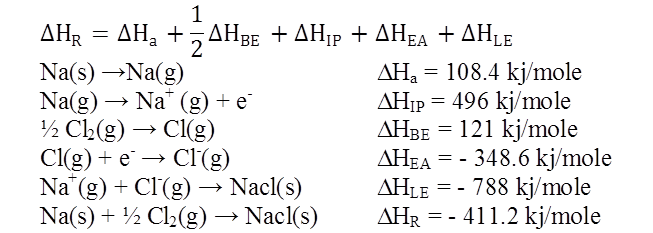
Ex.1: Draw Born Haber cycle for formation of Magnesium chloride
![]()
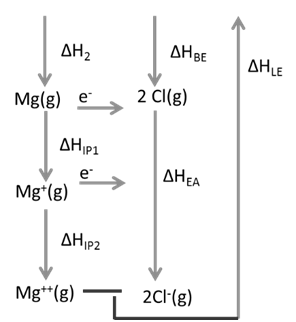
![]()
PROPERTIES OF IONIC COMPOUNDS
- They are crystalline in nature
- They have high Melting and Boiling point
- Hard and Brittle
- Soluble in polar solvents
- Conduct electricity in molten state and aqueous state but not in solid state.
- Do not show Isomerism.
VARIABLE ELECTROVALENCY
Fe (26) → 3s2 3p6 3d6 4s2
Fe+2 (24) → 3s2 3p6 3d6 (less stable)
Fe+3 (23) → 3s2 3p6 3d5 (more stable)
Solubility of ionic compounds in water. There are two things happen on dissolving ionic compounds in water.
1. Breaking of ionic lattice
2. Mixing of ions in water
For the first process, lattice energy to be provided to the solution and for second process hydration energy will be released by the system
If ΔHhyd >ΔHL.E. Compound is soluble in water
(a) Lattice Energy
1. If depends on size of cation and anion.
Smaller the size greater is the Lattice Energy.
Ex. → LiCl > NaCl > KCl
→ NaCl > NaBr > NaI
2. If depends on Charge of cation and anion.
Bigger the charge, lesser is it Lattice energy.
Ex. MgCl2 > NaCl
3. In case anions are extremely large, then the rule one charges smaller the cation lesser is Lattice Energy.
Ex. MgSO4 < CaSO4 < SrSO3 < BaSO4
(b) Hydrogen energy
Smaller the cation, greater is the hydration enthalpy.
Ex. Compare Solubility BaSO4 and CaSO4
L.E. Þ BaSO4 > CaSO4
Hyd. Energy Þ CaSO4 > BaSO4
So CaSO4 is more soluble.
Ex. Compare solubility of NaCl and BaCl2
L.E. Þ BaCl2 > NaCl
Hyd. Energy Þ NaCl > BaCl2
So NaCl is more soluble.
COVALENT BOND
Combining of unpaired electrons of atoms to achieve a stable configuration and formation of molecules is called covalent bond.
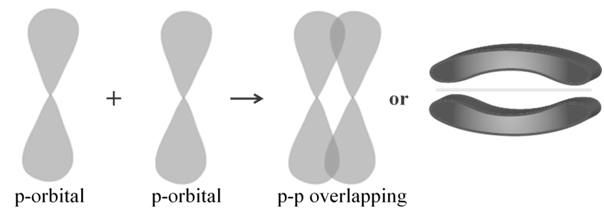
SIGMA (s) BOND: THIS TYPE OF COVALENT BOND is formed by the end to end (head-on) overlap of bonding orbitals along the inter-nuclear axis. This is called as head on overlap or axial overlap
s - s overlapping: In this case, there is overlap of two half killed s-orbitals along the inter-nuclear axis as shown below:

s-p overlapping: This type of overlap occurs between half filled s-orbitals of one atom and half filled p-orbitals of another atom:
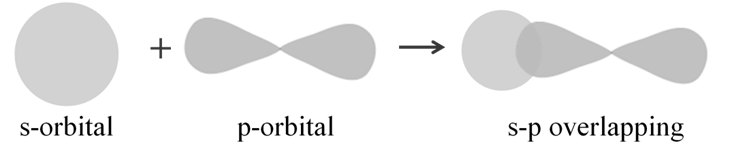
p-p overlapping: This type of overlap takes place between half filled p-orbitals of the two approaching atoms:

Pi (π) BOND: IN THE FORMATION OF π BOND
The atomic orbitals overlap in such a way that their axes remain parallel to each other and perpendicular to the inter-nuclear axis.
Characteristic of Convent compounds
- Physical state ® gases, liquids of law b.p. & soft solids
- Melting Point/Boiling point ® with exception of network solids, they have low M.P. and B.P.
- Electrical conductance ® generally bad conductors
- Solubility ® soluble in non-polar solvents
- Isomerism ® yes Physical state ® gases, liquids of law b.p. & soft solids
- Melting Point/Boiling point ® with exception of network solids, they have low MP/B.
- Electrical conduce ® generally bed conductors
- Solubility ® soluble in non-polar solvents
- Isomerises ® yes
COMPARISON BETWEEN IONIC AND COVALENT BONDS

COMPARISON BETWEEN IONIC AND COVALENT COMPOUNDS

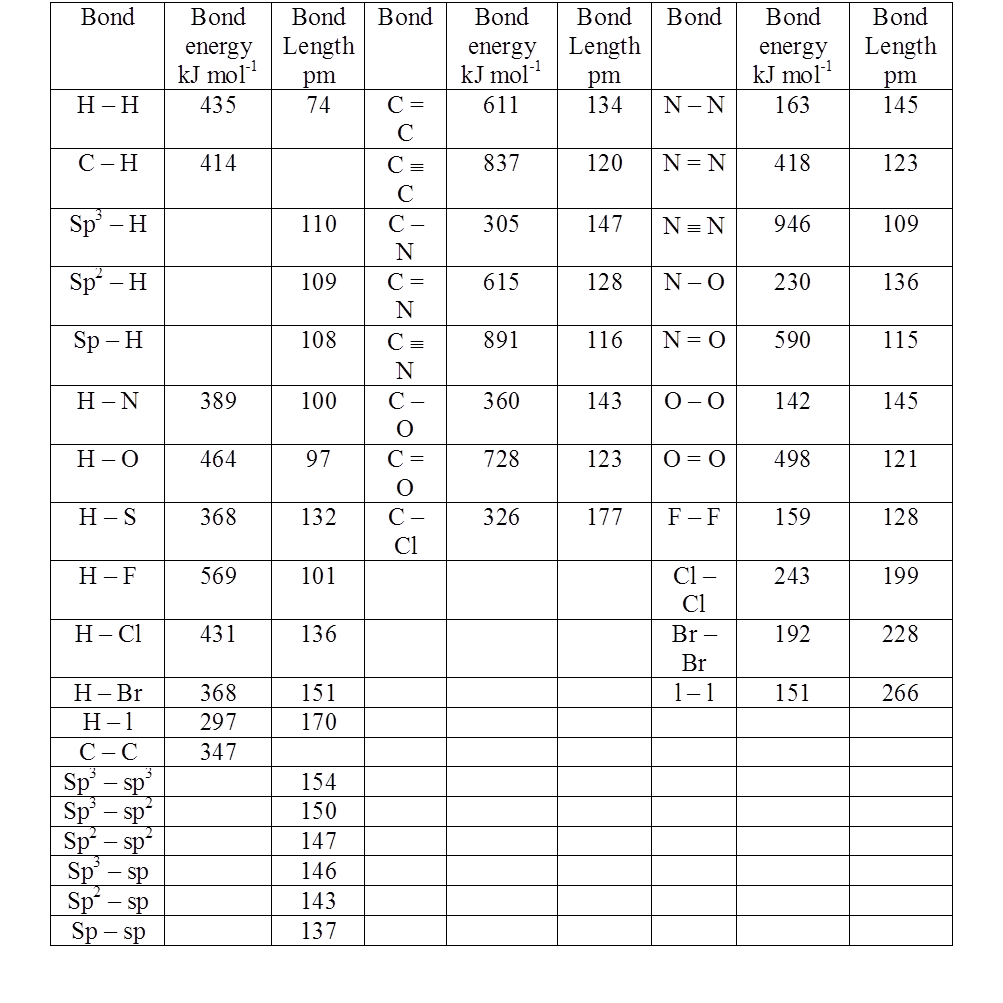
Some representative Bond Energies and Bond Lengths
Coordinate Bond
- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
COORDINATE BOND
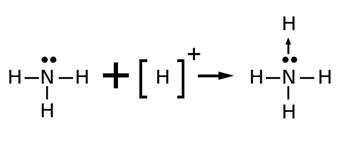
Dative bond or semi-polar bond.
METALLIC BOND
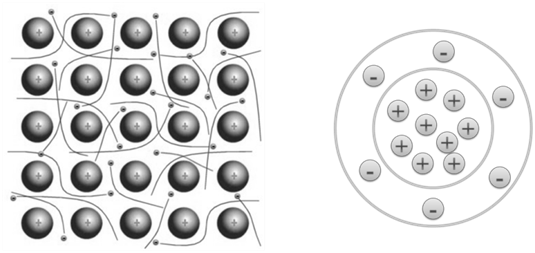
The bonding which holds metals atoms firmly together on account of force & attraction between metal cation and mobile sea electrons is called metallic bonding.
PROPERTIES OF METALS & NON METALS

LANDON FORCES AND DISPERSION FORCES
London forces between two Helium atoms

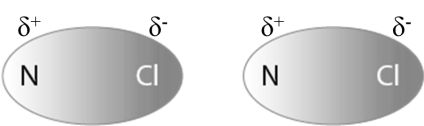
DIPOLE - DIPOLE FORCES
Dipole-dipole forces act between the molecules possessing permanent dipole. Ends of the dipoles possess partial charges, and these charges are shown by Greek letter delta (δ). Partial charges are always less than the unit electronic charge. The polar molecules interact with neighboring molecules.
Dipole-dipole interaction energy between stationary polar molecules (as in solids) is proportional to ![]() , Where r is the distance between polar molecules.
, Where r is the distance between polar molecules.
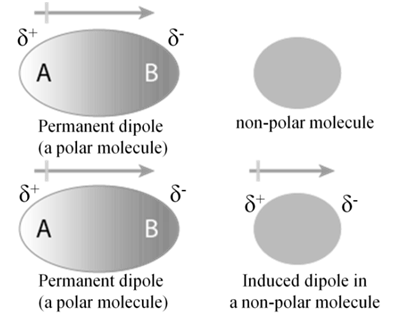
DIPOLE INDUCED DIPOLE FORCES
This type of attractive forces operate between the polar molecules having permanent dipole and the molecules lacking permanent dipole.
Permanent dipole of the polar molecule induces dipole on the electrically neutral molecule by deforming its electronic cloud
Hydrogen Bond
- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
HYDROGEN BOND
This is special case of dipole-dipole interaction.. This is found in the molecules in which highly polar N-H, O-H or H-F bonds are present. Although hydrogen bonding is regarded as being limited to N, O and F; but species such as Chlorine may also participate in hydrogen bonding. Energy of hydrogen bond varies between 10 to 100 kJ mol.
Hydrogen bond can be classified in three types
1. Inter molecular H bond. Same molecule
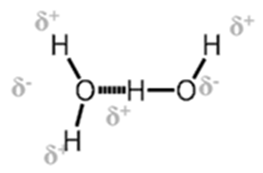
- Inter molecular H bond. Different molecule
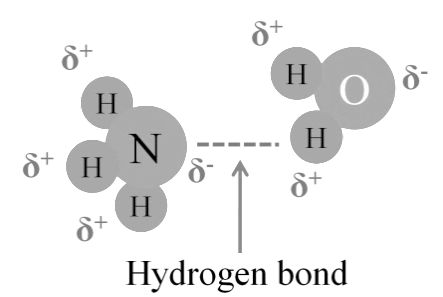
Hydrogen Bonding between Ammonia and Water
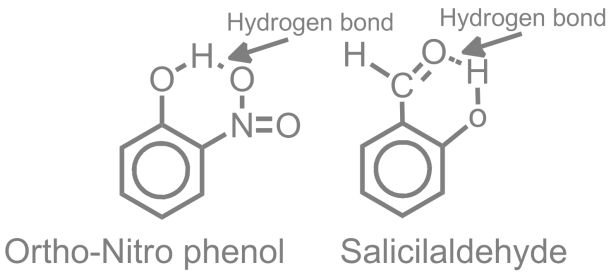
- Intra Molecular Hyrogen Bond
HYDROGEN BOND STRENGTH
Hydrogen bonds can vary in strength from weak (1–2 kJ mol−1) to strong (161.5 kJ mol−1 in the ion Typical enthalpies in vapour include:
F − H···: F (161.5 kJ/mol or 38.6 kcal/mol), illustrated uniquely by HF2−,
O − H···: N (29 kJ/mol or 6.9 kcal/mol), illustrated water-ammonia
O − H···: O (21 kJ/mol or 5.0 kcal/mol), illustrated water-water, and alcohol-alcohol
N − H···: N (13 kJ/mol or 3.1 kcal/mol), illustrated by ammonia-ammonia
N − H···: O (8 kJ/mol or 1.9 kcal/mol), illustrated water-amide
Bond Length
It is defined as the angle between the orbitals containing bonding electron pairs around the central atom in a molecule/complex ion. Bond angle is always determined experimentally
A. Ionic Compound:- bond length is sum of cationic radius and anionic radius.
B. Covalent compound:
The bond length is measured by spectroscopic, x-ray diffraction and electron diffraction. Covalent radius is then calculated from this.
Lewis structure:- unable to give bond angle
VESPR they:- much better in predicate bond angle
M. O. T:- Give bond angle much better
Bond Energy or Enthalpy
It is defined as the amount of energy required to break one mole of bonds of a particular type between two atoms in a gaseous state.
For a diatomic molecular Bond energy simply energy required to break the bond.
![]()
![]()
For Hetero-nuclear molecular it is average energy or mean energy.
Ex. H2O(g) → H(g) + OH(g) ∆H = 502
OH(g) → H(g) + O(g) ∆H = 427
![]()
Bond length or bond distance is the average distance between nuclei of two bonded atoms in a molecule. It is a transferable property of a bond between atoms of fixed types, relatively independent of the rest of the molecule
.![]()
1. Sigma bond (s )> Pie (p) bond
2. Triple bond > double bond > single bond
3. s – s overlap > s – p overlap > p – p overlap
OCTET RULE
Kössel and Lewis in 1916 developed an important theory of chemical combination between atoms known as electronic theory of chemical bonding. According to this, atoms can combine either by transfer of valence electrons from one atom to another (gaining or losing) or by sharing of valence electrons in order to have an eight electrons in their valence shells.
Exceptions to the Octet Rule:
- Hydrogen molecule: Hydrogen has one electron in its first energy shell (n = 1). It needs only one more electron to fill this shell, because the first shell cannot have more than two electrons. This configuration (1s2) is similar to that of noble gas helium and is stable. In this case, therefore, octet is not needed to achieve a stable configuration
Incomplete octet of the central atom: The octet rule cannot explain the formation of certain molecules of lithium, beryllium, boron, aluminium, etc. (LiCl, BeH2, BeCl2, BH3, BF3) in which the central atom has less than eight electrons in the valence shell as shown below:
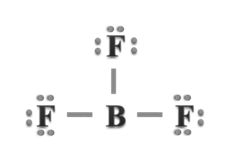
Expanded octet of the central atom: There are many stable molecules which have more than eight electrons in their valence shells. For example, PF5, has ten; SF6 has twelve and IF7 ha fourteen electrons around the central atoms, P, S, and I respectively
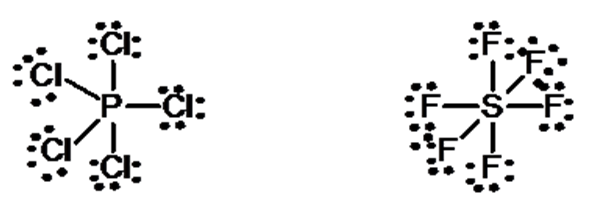
Odd electron molecules: There are certain molecules which have odd number of electrons, like nitric oxide, NO and Nitrogen dioxide, NO2. In these cases, octet rule is not satisfied for all the atoms.

It may be noted that the octet rule is based upon the chemical inertness of noble gases. However, it has been found that some noble gases (especially xenon and krypton) also combine with oxygen and fluorine to form a large number of compounds such a XeF2, KrF2, XeOF2, XeOF4, XeF6, etc.
This theory does not account for the shape of the molecules. It cannot explain the relative stability of the molecule in terms of the energy.
LEWIS STRUCTURE
Lewis structure and bonding theory cannot explain the shape of molecule.
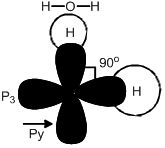
Shape of H2O.
H → 1s2
O → 1s2 2s2 px2 py1 pz1
Angle H ─ O ─ H
Is 90o as per this mode but shell L = 104.5o
Hybridisation
- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
HYBRIDISATION AND SHAPE
Salient features of hybridisation: The main features of hybridisation are as under:
1. The number of hybrid orbitals is equal to the number of the atomic orbitals that get hybridised.
2. The hybridised orbitals are always equivalent in energy and shape
3. The hybrid orbitals are more effective in forming stable bonds than the pure atomic orbitals.
4. These hybrid orbitals are directed in space in some preferred direction to have minimum repulsion between electron pairs and thus a stable arrangement.
Therefore, the type of hybridisation indicates the geometry of the molecules
Important conditions for hybridisation
(i) The orbitals present in the valence shell of the atom are hybridised.
(ii) The orbitals undergoing hybridisation should have almost equal energy.
(iii) Promotion of electron is not essential condition prior to hybridisation.
(iv) It is not necessary that only half filled orbitals participate in hybridisation. In some cases, even filled orbitals of valence shell take part in hybridisation
(i) sp HYBRIDISATION:
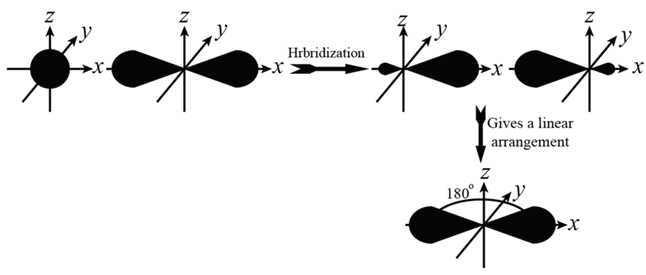
(II) sp2 hybridisation:
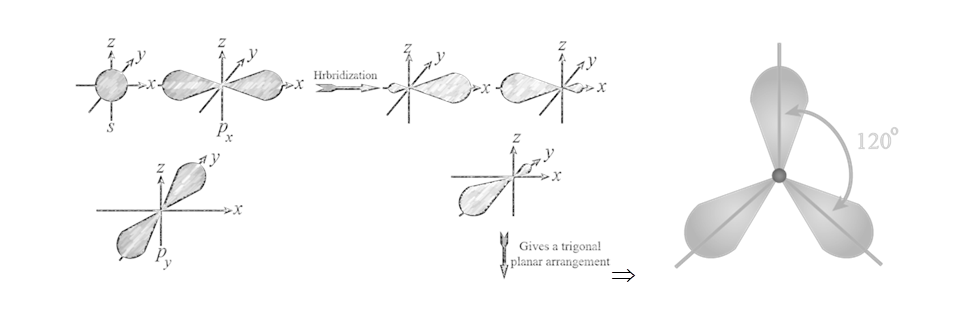
(iii) sp3 HYBRIDISATION
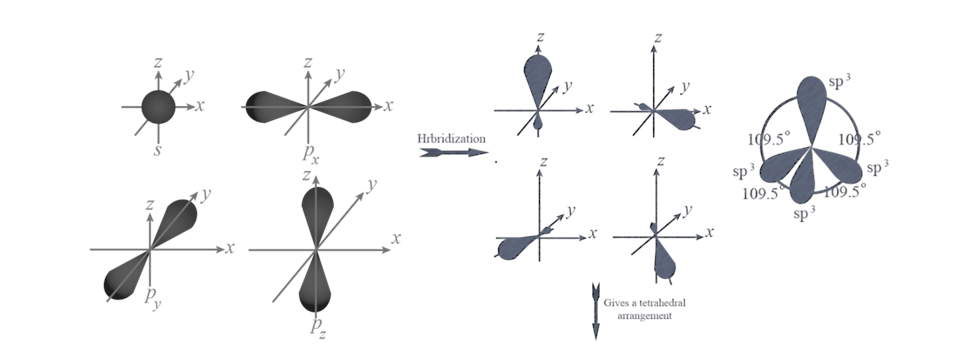
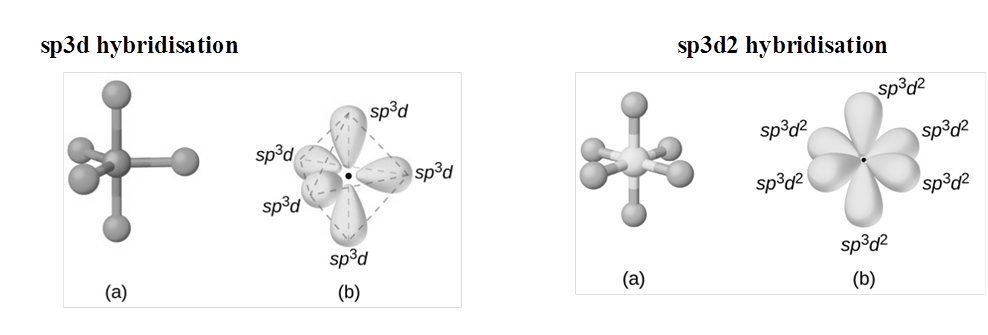
RULES TO FIND HYBRIZATION AND SHAPE (HOMONUCLEAR MOLECULAR)
- Draw the Lewis structure count σ and π bonds.
- Write the electronic configuration of central atom.
- Match no. of unpaired electrons with total bonds. If it does match, then to step 5
- If it does not match drawn the E. C. of atom in exited states to match total number of bonds.
- All orbital in valence shell having unpaired e- & lone pairs undergo hybridization (π)- electrons do not hybridize.
- Shape is not hybridization. For shape only bond pairs are counted not lone pairs.
- The actual bond angle may be different then hybridization angle because of following.
(a) Repulsion lp – lp > lp – bp > bp – bp
(b) Difference in E. N. of atoms in the bond.
Resonance
- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
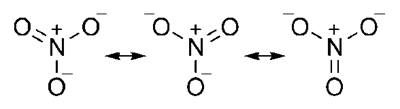
RESONANCE
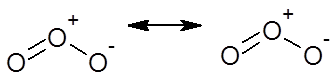
(1) Whenever a molecule can be represented by two or more structure that are different only in arrangement of electrons – i.e. they have some arrangement of atoms (both structural and stereo) there is Resonance
(2) When these structures are of about same stability (i.e. have same energy content), then resonance is important.
(3) The actual molecular is a hybrid of all there structures and cannot be satisfactorily explained by any are of them. Each structure contributes to the hybrid.
(4) The actual structure cannot be drawn as per Lewis structure and the lewis structures is not actual molecule.
(5) The resonance hybrid is more stable than any of the contributing structures.
(6) The contributing structures do not exist at all.
(7) The contributing structures are called canonical forms.
Ozone molecule
Carbon monoxide molecule
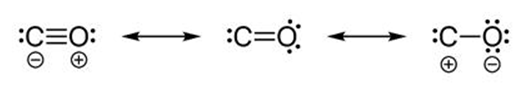
Nitrate ion
POLARITY IN COVALENT BONDS
When covalent bond is formed between two similar atoms, for example in H2, O2, or F2, the shared pair of electrons is equally attracted by the two nuclei. The electron pair is situated exactly between the two identical nuclei. The bond so formed is called nonpolar covalent bond.
In case of a hetero-nuclear molecule like HCl, the shared electron pair between the two atoms gets displaced more towards chlorine as E.N. of fluorine is far greater than that of hydrogen. The resultant covalent bond is a polar covalent bond
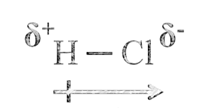
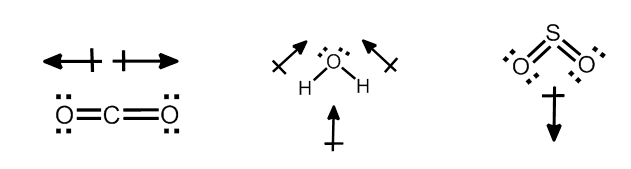
Dipole Moment has a Magnitude and a Direction
Dipoles:
Molecular orbital theory
- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
Limitation of VSEPR theory
- It cannot explain why oxygen molecule is paramagnetic
- It cannot explain formation of H2+ molecule. And may more
MOLECULAR ORBITAL THEORY (MOT)
· Basic idea of MOT is that atomic orbitals of individual atoms combine to form molecular orbitals. Electrons in molecule are present in the molecular orbitals which are associated with several nuclei.
· The molecular orbital formed by the addition of atomic orbitals is called the bonding molecular orbital ( s ).
· The molecular orbital formed by the subtraction of atomic orbital is called antibonding molecular orbital (s *).
· The sigma (s ) molecular orbitals are symmetrical around the bond-axis while pi (p ) molecular orbitals are not symmetrical.
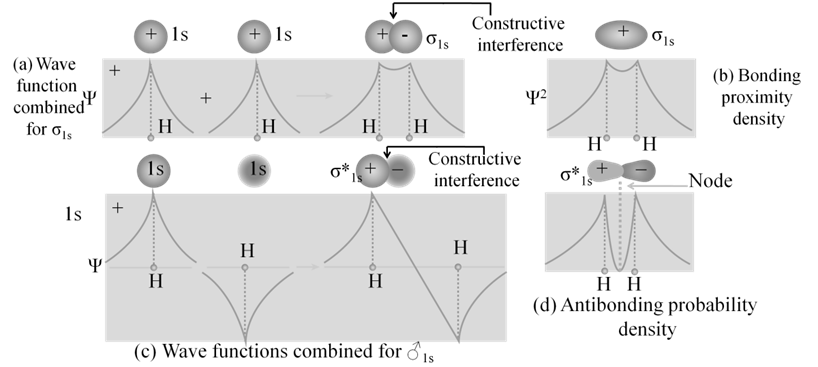
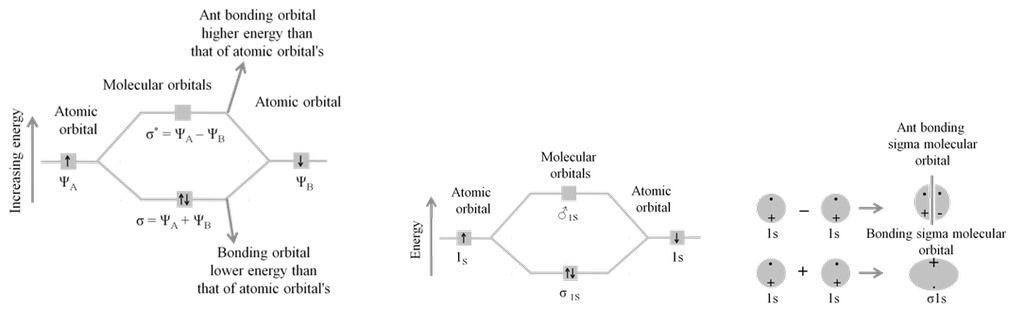
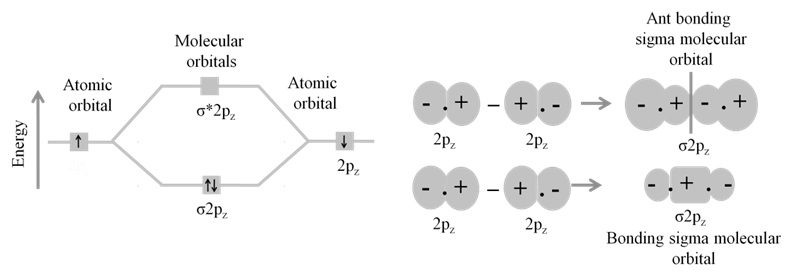
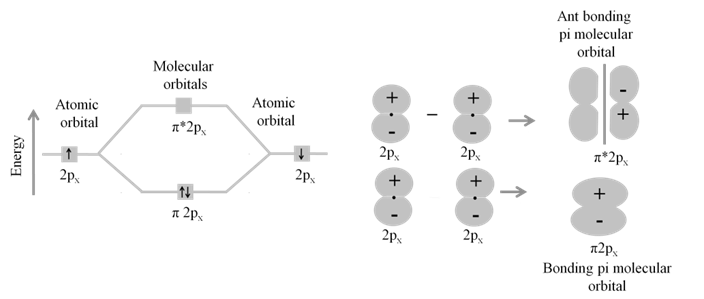
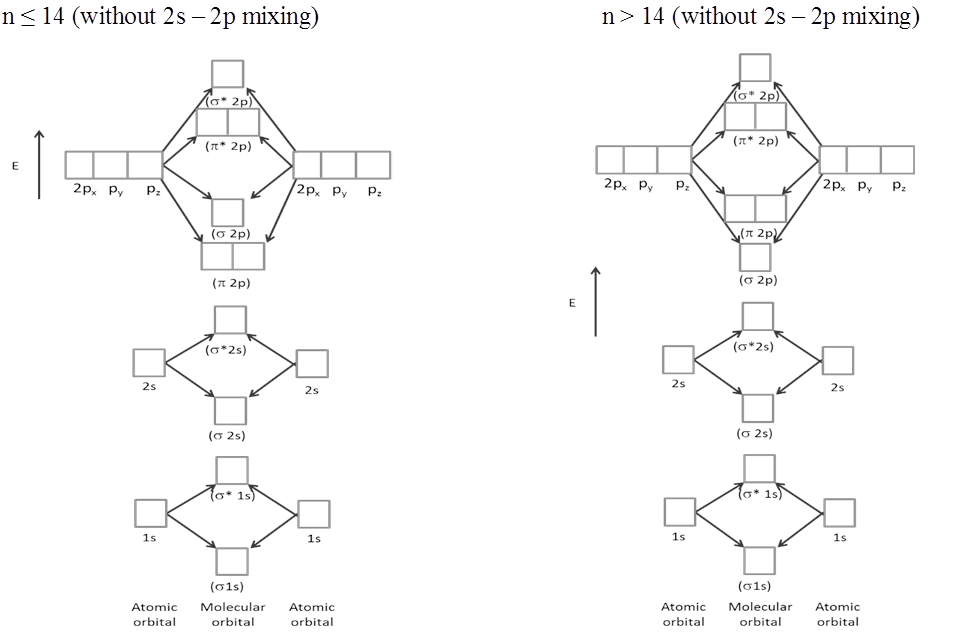
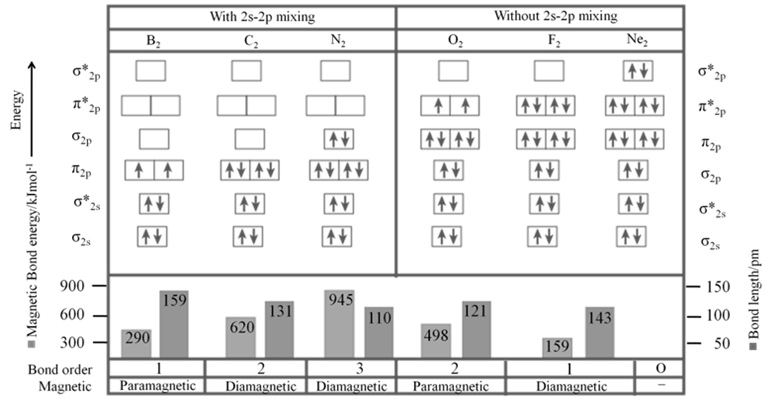
- Sequence of energy levels of molecular orbitals changes for diatomic molecules like Li2, Be2, B2, C2, N2 is (For n £ 14) ; s1s < s*1s < s2s < s*2s < p2py = p2pZ < s2px < p*2py = p*2pZ < s*2px
- Sequence of energy levels of molecular orbitals changes for diatomic molecules like O2, F2, Ne2 ( for n >14) is s1s < s*1s < s2s < s*2s < s2px < p2py = p2pZ < p*2py = p*2pZ < s*2px
- Bond order (b.o.) is defined as one half the differences between the number of electrons present in the bonding and the antibonding orbitals.
- Bond Order =
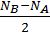
NB = Bonding electrons NA = anti-bonding electrons
States of Matter
- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
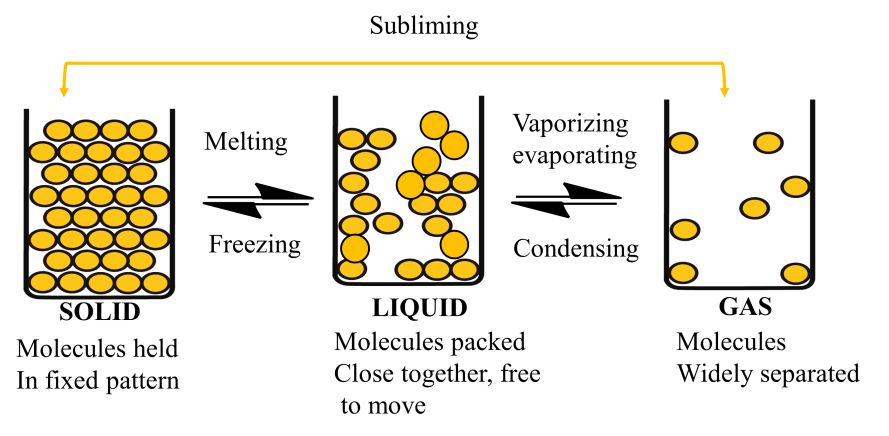
STATES OF MATTER
There are five known phases, or states, of matter: solids, liquids, gases, and plasma and Bose-Einstein condensates.
Here we will study only three. Solid, Liquid and Gas


GASEOUS STATE
Only eleven elements exist as gases under normal conditions
GASEOUS STATE
The gaseous state is characterized by the following physical properties.
• Gases are highly compressible.
• Gases exert pressure equally in all directions.
• Gases have much lower density than the solids and liquids.
• The volume and the shape of gases are not fixed. These assume volume and shape of the container.
• Gases mix evenly and completely in all proportions without any mechanical aid (Diffusion)
Gas Laws
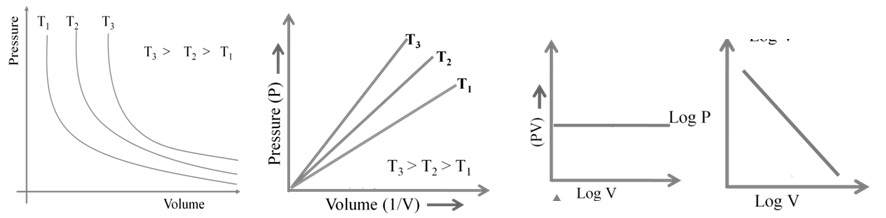
1. Boyle’s Law: At constant temperature
![]()
![]()
![]()
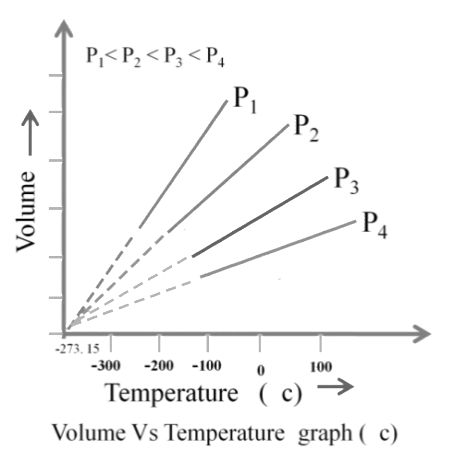
2. Charles Law: At constant pressure
![]()
Here K is a constant that depends on the pressure of gas, the amount of gas and also unit of volume if V1 and T1 are the initial values of volume and temperature of a gas then,
![]()
Also, if the temperature is now changed to T2 such that the volume change to V2
We can write,
![]()
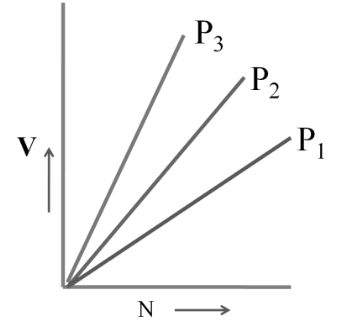
3. Avogadro's Law: At constant pressure and temperature
V µ n (no. of moles)
4. Ideal gas equation
Ideal gas equation
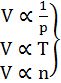
![]()
![]()
R = gas constant
w = mass of gas ρ = density
M = Mol weight of gas R = gas constant
![]()
![]()
5. Modified gas equation
![]()
![]()
![]()
![]()
Gas Constant ‘R’
![]()
= 0.0821 lit atm/ K. mole
= 8.314x 107 erg/k. mole
= 8.314 J/k. mole
= 1.987 cal/k. mole
Units and conversion
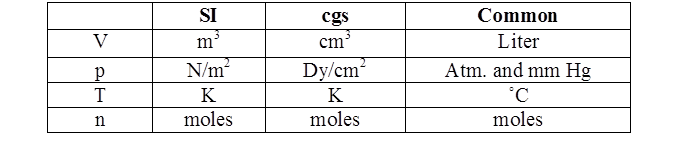
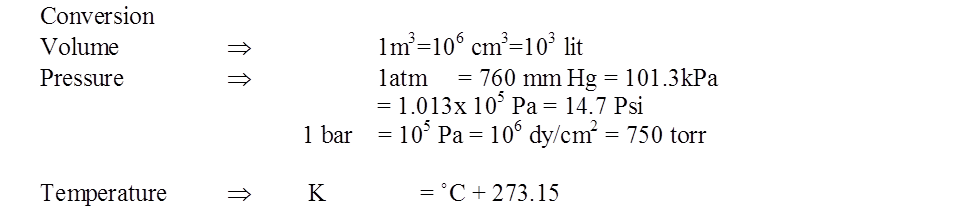
Dalton's law
- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
DALTON’S LAW
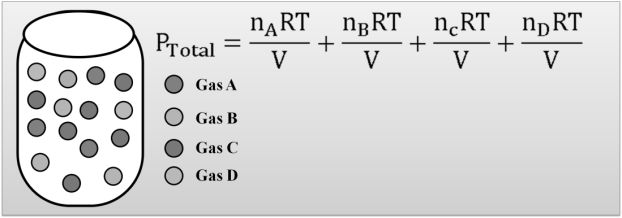
Dalton's law (also called Dalton's law of partial pressures) states that in a mixture of non-reacting ideal gases, the total pressure exerted is equal to the sum of the partial pressures of the individual gases.
KINETIC THEORY OF GASES
- Assumptions or postulates of the kinetic molecular theory of gases are given below.
- Gases consist of large number of identical particles (atoms or molecules) that are so small and so far apart on the average that the actual volume of the molecules is negligible in comparison to the empty space between them
- There is no force of attraction or repulsion between the particles of a gas
- Particles of a gas are always in constant and random motion.
- Collisions of gas molecules are perfectly elastic.
- At any particular time, different particles in the gas have different speeds and hence different kinetic energies
We can derive from kinetic theory they of gases
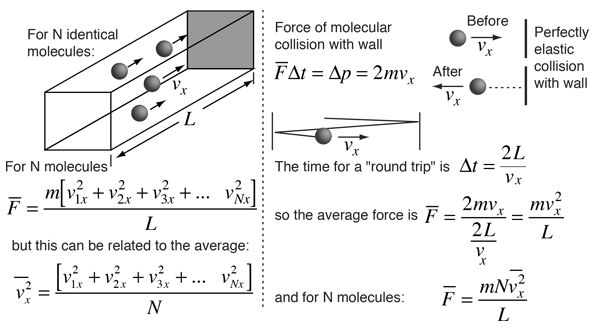
A gas molecule has velocity v and can be broken into thro components vx, vy and vz.
Travelling in x-axis momentum = mvx change in momentum after collision = - 2mvx. If gone back of comes back after time ‘t’
![]()
No. of collies is one second![]()
Change in momentum per second ![]()
Change in momentum on all three axis ![]()
![]()
![]()
![]()
For one mole of gas n = N and m x N = M (Mol. Wt.)
![]()
![]()
Kinetic Energy ![]() for one mole gas n = N and PV = RT
for one mole gas n = N and PV = RT
![]()
![]()
![]()
So kinetic energy, depends only on temperature
For one molecules ![]()
k = Boltzman constant
![]()
![]()
m = mass of gas particle
n = no. of gas particle
Vrms = root mean square velocity
PV = ![]() m. n. V2rms
m. n. V2rms
K.E. = ![]() RT for one mole of gas
RT for one mole of gas
K.E. = ![]() kT for one molecule where
kT for one molecule where
k = Boltzman constant =![]()
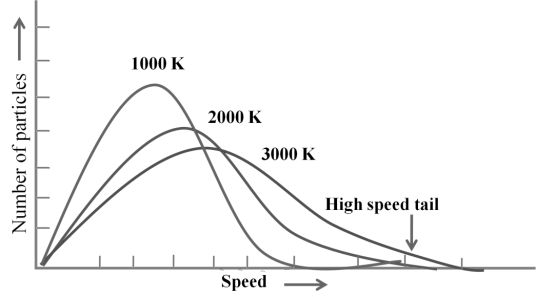
MAXWELL’S DISTRIBUTION OF SPEED AT DIFFERENT TEMPERATURE
MAXWELL’S DISTRIBUTION OF SPEED FOR DIFFERENT GASES
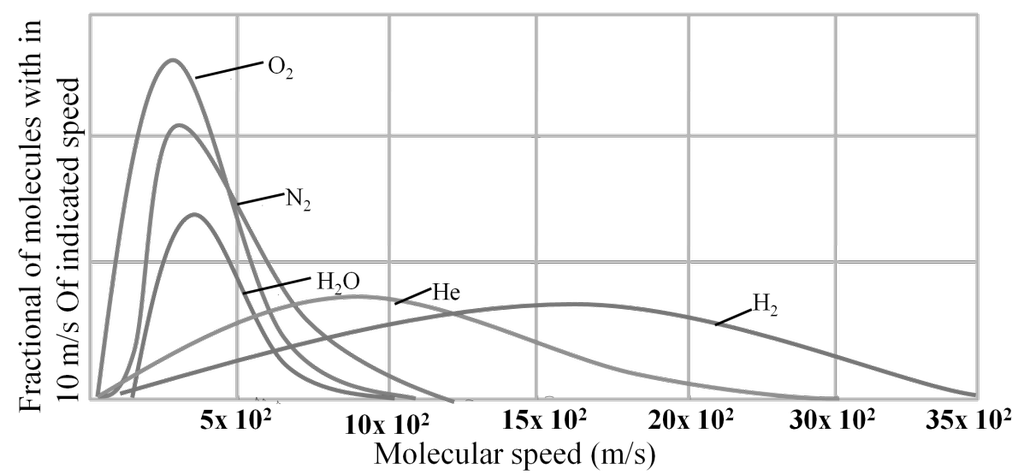
DIFFERENT VELOCITIES FOR GASES
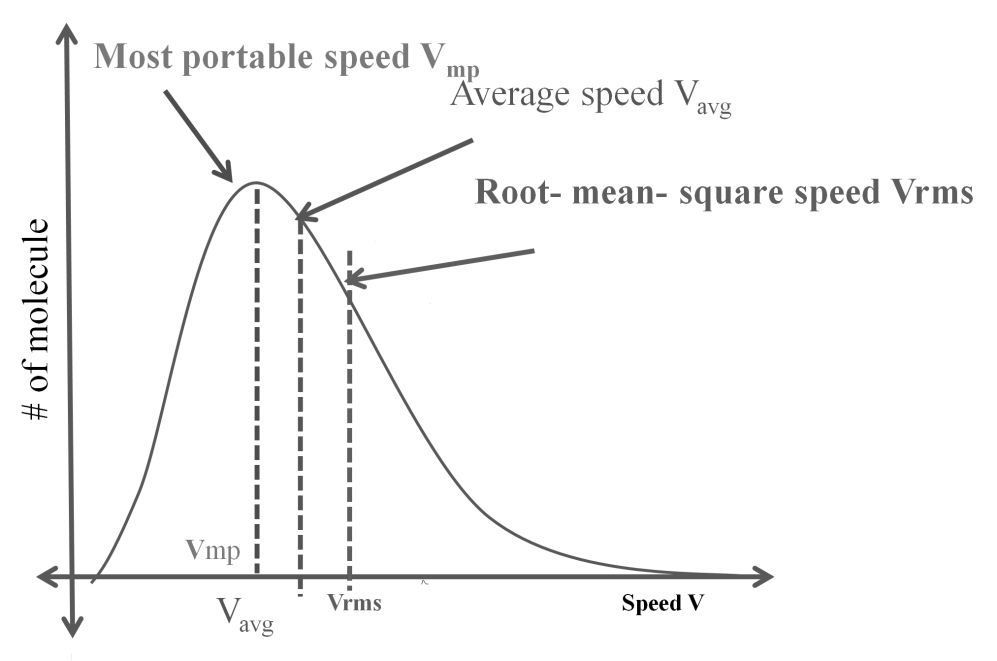
- The first typical velocity is the easiest to calculate and termed as the most probable velocity VMP. The velocity at the top of the curve is the most probable velocity as the largest number of molecules have this velocity.
- Average velocity of gas is simply the mean of all gas speeds possessed by all gas particles.
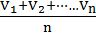
- Root mean square velocity is the square root of the mean of velocity squares VRMS =
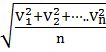
DIFFERENT VELOCITIES FOR GASES
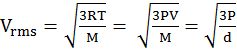
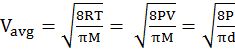
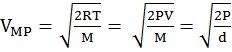
IMPORTANT SHORTCUT
Vrms: Vavg: VMP = 1.224 :1.128:1 and = 1: 0.92 :0.816
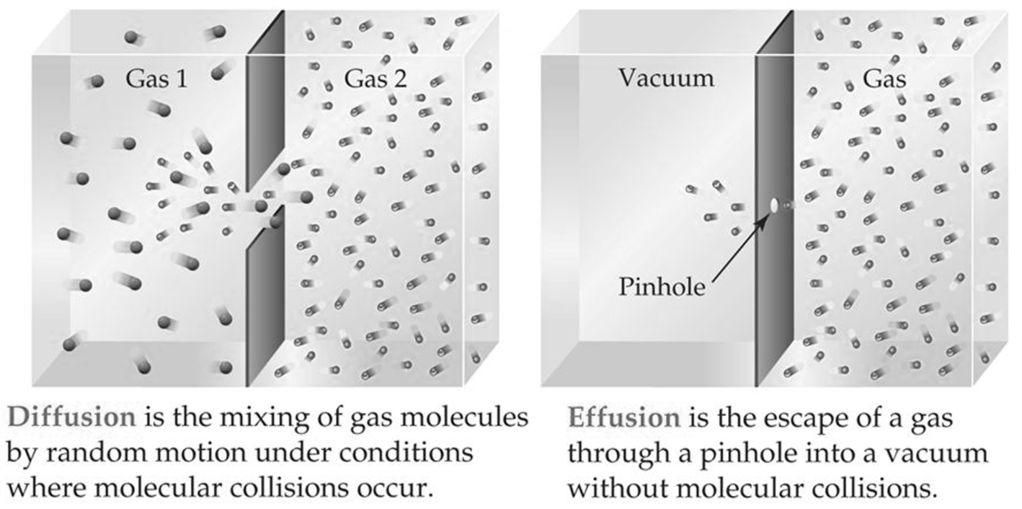
DIFFUSION OF GASES

DIFFUSION VS. EFFUSION
Diffusion- The tendency of the molecules of a given substance to move from regions of higher concentration to regions of lower concentration.
Examples: A sent spreading throughout a room or people entering a theme park.
Effusion: The process by which gas particles under pressure pass through a tiny hole.
Example: Air slowly leaking out of a tire or helium leaking out of a balloon.
Graham’s law of diffusion![]() when pressure is same.
when pressure is same.
Graham’s law of diffusionr![]() when pressure is also different
when pressure is also different
Real gas, Vanderwaal's Equation
- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
REAL GAS
The Ideal gas equation shows big deviation at high pressures and low temperatures from ideal gas equation.
If you compress an Ideal gas to very high pressure when will it become a liquid? ????
Vanderwaal’s equation for real gas.
1. Volume correction. Actual volume available for gas to freely move is
VR = Vj – n b
b = Volume correction constant taking into size and gas molecule.
2. Pressure correction:
PReal = PIdeal – attractive forces between molecules.

PReal = Pideal – ![]()
A = Pressure correction
![]()
![]()
![]() . a, b are Vander Waals constant; n is the number of moles of gas
. a, b are Vander Waals constant; n is the number of moles of gas
V.W. Constants
‘b’ ![]() size of molecule
size of molecule
Thumb rule b = 4 x Volume and one atom/molecule.
‘a’ ![]() Inter molecule forces between atom/molecule gas
Inter molecule forces between atom/molecule gas
Ex: put in increasing order ‘a’ and ‘b’ for H2, He, NH3, O2
b = H2 < He < NH3 < O2
a = He < H2 < O2 < NH3
Compressibility factor Z
![]()
Z = 1 Þ Ideal gas. No. attraction/Repulsion
Z < 1 ÞReal gas. Attractive forces dominate
Z > 1 ÞReal gas. Repulsive forces dominate
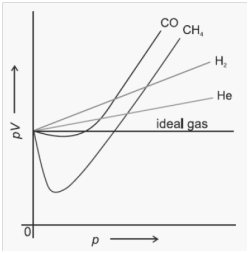
UNIT OF ‘a’ AND ‘b’
![]()
![]()
Real gas behaves like ideal gas at low pressure and high temperature.
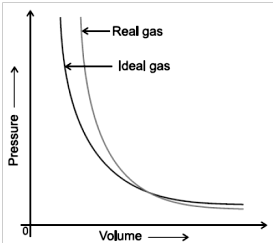
Boyle’s temp =![]() temperature at which Real gas behave like ideal gas.
temperature at which Real gas behave like ideal gas.
Liquefaction of Gas
Critical temperature (TC) is the temperature above which a gas cannot be liquefied however high pressure may be.
Critical pressure (PC) is minimum pressure required to liquefy gas at the critical temperature.
Critical volume (VC) is the volume occupied by one mole of gas at critical temperature and critical pressure.
![]()
For gas CO2
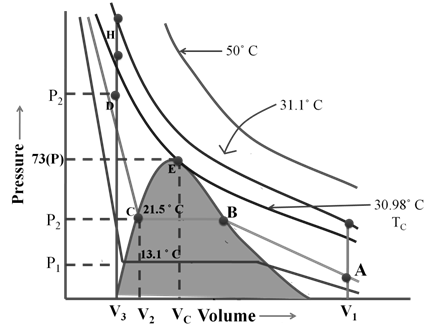
Real gases can only be liquefied by increasing pressure, if the temperature is below critical temperature
Here Vc and Pc volume and pressure at critical temperature when it touches the curve.
Surface tension, Viscosity
- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
SURFACE TENSION
Surface tension is defined as the force acting per unit length perpendicular to the line drawn on the surface of liquid. It is denoted by Greek letter γ (Gamma). It has dimensions of kg s-2 and in SI unit it is expressed as N m-1. Surface tension reduces with increase in temperature.
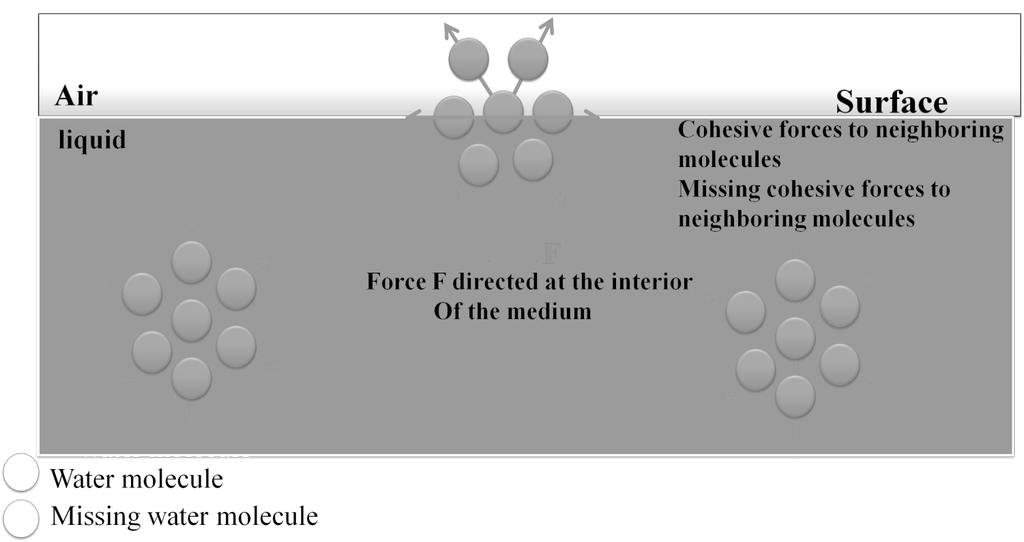
SURFACE TENSION VS. TEMPERATURE PLOT
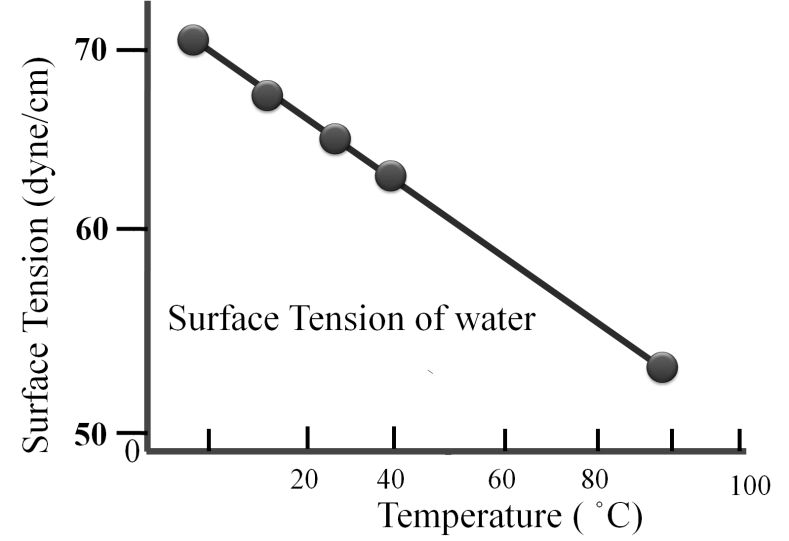
VISCOSITY
It is one of the characteristic properties of liquids. Viscosity is a measure of resistance to flow which arises due to the internal friction between layers of fluid as they slip past one another while liquid flows.
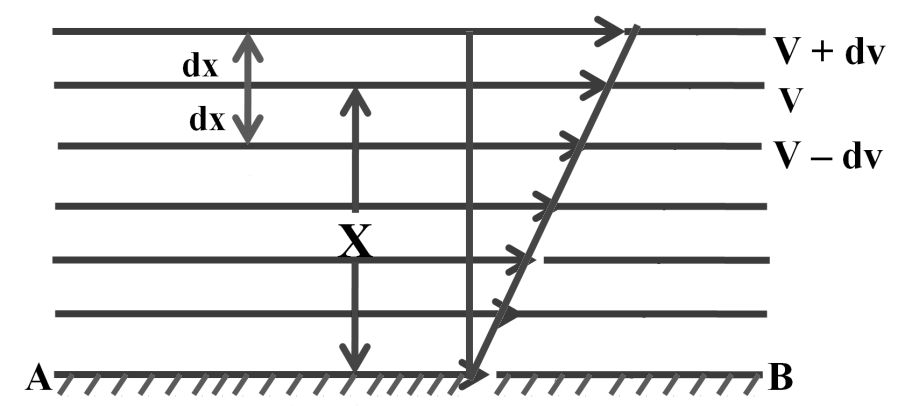
F ![]() A (A is the area of contact)
A (A is the area of contact)
F ![]() (where,
(where,![]() is velocity gradient)
is velocity gradient)
![]()
‘n’ is proportionality constant and is called coefficient of viscosity.
Viscosity coefficient is the force when velocity gradient is unity and the area of contact is unit area.
SI unit of viscosity coefficient is Newton second per square meter (N s m-2) = Pascal second (Pa s = 1kg m-1s-1). In cgs system the unit of coefficient of viscosity is poise
1 poise = 1 g cm-1s-1 = 10-1kg m-1s-1
IMPORTANT FORMULA
- Ideal gas PV = nRT =
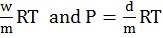
- Graham’s law of diffusion
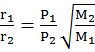
- Separation by diffusion f=n1'n2'n1n2=AfterBefore f1=M2M1=one stage separation f1=f here x=no. of shape
 Kinetic Theory PV = 1/3 mnv2rms
Kinetic Theory PV = 1/3 mnv2rms - Kinetic Energy/mole = 3/2 RT
- Kinetic Energy/molecule = 3/2 kT k(Boltzmann constant) =R/NA
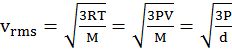
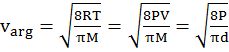
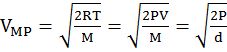
- vrms: vavg: vMP = 1.224 :1.128:1 = 1: 0.92 :0.816
- Vanderwaal’s Gas
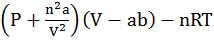
- Boyles temp Tb =
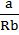
- Critical constants
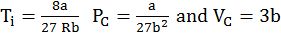
- Inversion temperature
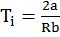
- Cp – CV = R and CP/CV = g
- Compression factor Z =
 Z = 1 for ideal gas (Z < 1 lower P Z > 1 higher P)
Z = 1 for ideal gas (Z < 1 lower P Z > 1 higher P) - Cp – Cv = R and Cp/Cv = g
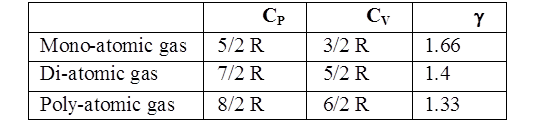
Solutions, Henry's law
- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
SOLUTIONS
When two or more than two substances are mixed with each other but do not react with each other it is called a solution.
Solutions are of two types
Homogeneous Solutions are mixtures of two or more than two components whose composition and properties are uniform throughout the mixture. Heterogeneous mixture don’t have uniform composition and properties
BINARY SOLUTIONS
Binary solution is a solution which contains only two components which are called solute and solvent
Solvent: The component whose mole fraction is greater than other
Solute: The component whose mole fraction is smaller than solvent
TYPES OF BINARY SOLUTIONS

CONCENTRATION OF BINARY SOLUTIONS
If we take a binary solution consisting of A & B.
- Mass percentage :
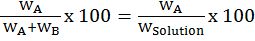
- Volume percentage :
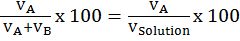
- Mass/volume percentage =
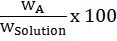
- Parts per million (ppm) =

Solution
- Mole fraction: moles of A in one mole of solution
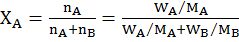
- Molality: mole of A in one kg of B

- Molarity: moles of A in one litre of solution (A + B)
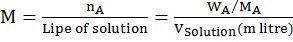
- Normality: gm eqn. of A per lite of solution
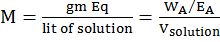
SOLUTION OF GASES IN LIQUIDS
HENRY’S LAW
The mole fraction of volatile solute is proportional to the vapor pressure of the solute.
P = KHX
KH= Henry‘s Law constant, X = mole fractions.
Increasing the partial pressure of a gas over a liquid increases the amount of gas dissolved in the liquid
KH depends on temperature
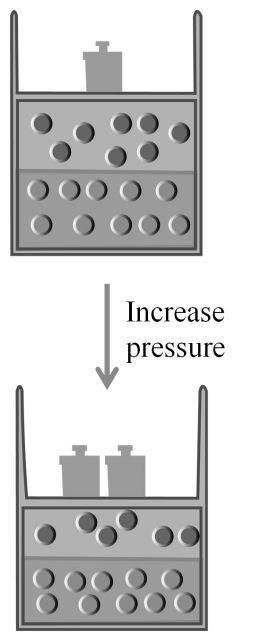
Henry’s law finds several applications in industry
To increase the solubility of CO2 in soft drinks and soda water, the bottle is sealed under high pressure
Bends: Scuba divers while breathing air at high pressure underwater increases the solubility of atmospheric gases in blood. When the divers come towards surface, the pressure gradually decreases. This releases the dissolved gases and leads to the formation of bubbles of nitrogen in the blood. This blocks capillaries and creates a medical condition known as bends, which are painful and dangerous to life
Anoxia: at high altitudes due to low pressure the solubility of oxygen in blood decreases.
Effect of temperature, pressure and different gases
Temperature: Increase in temperature leads to less solubility of gases in liquid.
This can be explained by kinetic theory as well as thermodynamics
Types of Gases: Heavier gases have more solubility. At same temperature and pressure as compared to lighter gases. (Value of ‘a’)
Pressure: Increase in pressure leads to greater solubility of gases in liquids.
SOLUTIONS LIQUID IN LIQUID
In this Section, we shall discuss the solutions of liquids and solids in a liquid. Such solutions may contain one or more volatile components. Ex: water-alcohol
- Solubility: Solubility of a substance is defined as the maximum amount of substance that can be dissolved in a specified amount of solvent to a given temperature
- Saturated solution : A solution in which no more solute can be dissolved at the same temperature and pressure is called a saturated solution
- Effect of temperature: mass %, mole fraction and molality do not change with temperature whereas Molarity changes with temperature because volume of solution (liquid) changes with temperature.
- Effect of dilution;-Moles, milli-moles, equivalent, milli-equivalent of solute does not change on dilution, but Molarity , molality and mole fraction change with dilution
- Like dissolves like: Polar solutes dissolve in polar solvents and non-polar solutes dissolves in non-polar solvents. In general, a solute dissolves in a solvent if the intermolecular attractions are similar in both.
A liquid may or may not be solute in another liquid Depending upon the relative solubility of a liquid in another the following three cases are possible:

Miscible liquid form three types of solution, which can be ideal or non ideal solutions.
When solute and solvent both are Volatile
Volatile: When the vapour pressure of substance is low. Ex. Ethyl alcohol, hexane etc.
Non Volatile: When the vapour pressure of substance is high. All solids are non-volatile. Some liquids like Glycerol etc. are non-volatile.
Vapour pressure
- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
VAPOUR PRESSURE
Vapor pressure is the pressure of the vapor over a liquid (and some solids) at equilibrium.
1) Imagine a closed box of several liters in size. It has rigid walls and is totally empty of all substances.
2) Now, I inject some liquid into the box, but the box is not full of liquid. What will happen to the liquid?
3) That's right. Some, maybe all, of the liquid will evaporate into gas, filling the empty space. Now if all the liquid evaporates, we just have a box of gas. That's not what we want. So let's suppose that only some of the liquid evaporated and that there are both the liquid state and the gas state present in the box.
The gas that is above the liquid is called its vapor and it creates a pressure called vapor pressure.
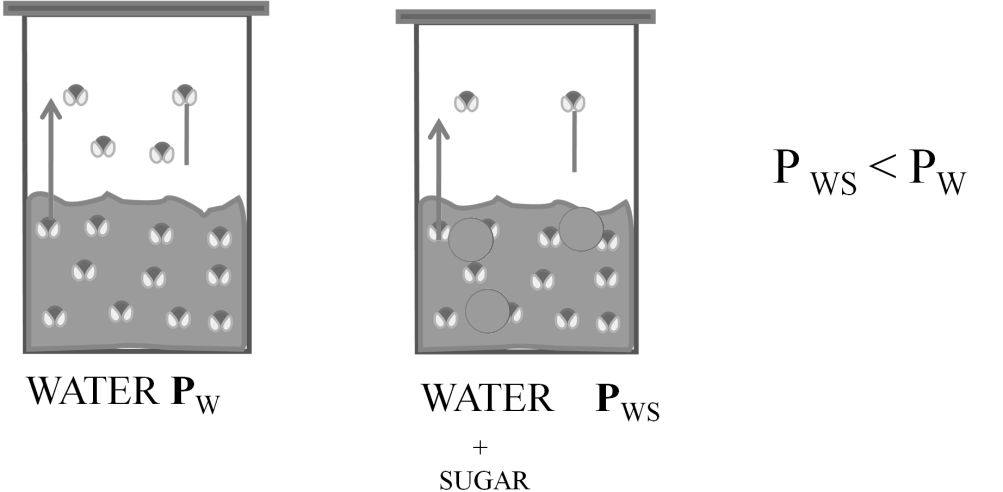
RAOULT’S LAW
When two liquids (A&B) are mixed.
Partial pressure of A = PPA = XA P°A
Partial pressure of B = PPB = XB P°B
P°A = vapour of pressure of pure A
P°B = vapour Pressure Of pure B
Total pressure P = PPA + PPB ® Dalton’s law
P = P°A XA + P°B XB ® Raoult’s law

Ideal and non-ideal solutions

Non ideal solutions
For a non-ideal solution
(1) DHmix ¹ 0 (It may be less or more)
(2) DVmix ¹ 0 (It may be less or more)
(3) Does not follow Raoult’s law.

Non ideal solutions
Non ideal solutions

Azeotropes are binary solutions (liquid mixtures) having the same composition in liquid and vapour phase and it is not possible to separate the components of an azeotrope by fractional distillation.
Types of azeotropes:
(a) Minimum boiling azeotrope: The non- ideal solutions showing large positive deviation form minimum boiling azeotrope at a specific composition. Example; 95% ethanol and 5% water (by volume) Ethanol = 351.3K, Water = 373 K, Azeotrope = 351.1K
(b) Maximum boiling azeotrope. The non- ideal solutions showing large negative deviation form maximum boiling azeotrope at a specific composition. Example : 68% Nitric acid and 32% water (by mass) Nitric acid = 359K , Water = 373 K, Azeotrope = 393.5K
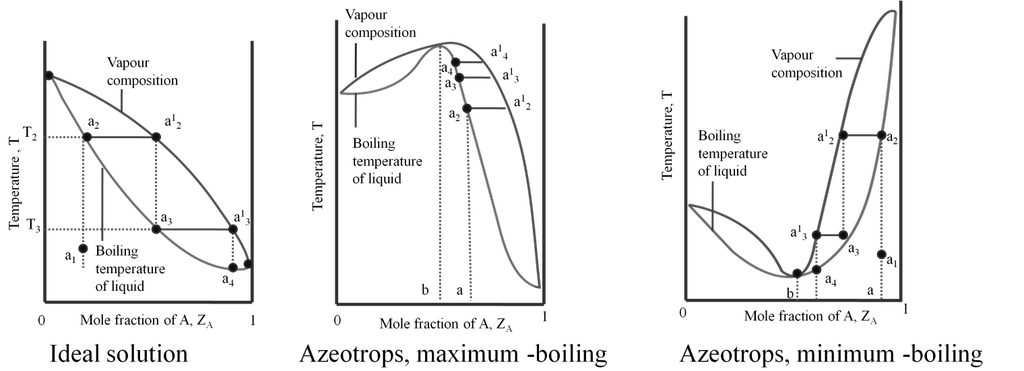
Solid in liquid solutions
- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
SOLID IN LIQUID SOLUTIONS
Solubility of solid (or Non-volatile liquids) in Liquid
Colligative Properties: The properties of solutions which depends on the no. of solute particles but irrespective of nature of solute particles.
There are four Colligative properties:
a. Relative lowering of vapour pressure
b. Elevation of boiling point
c. Depression of freezing point
d. Osmotic pressure
a. Relative lowering of vapour pressure
P = poA XA + PoB XB → Raoult’s law
Dilute solution is where nA < < nB
Or XA < < < XB
Non volable solute is where ![]()
![]()
![]()
![]()
![]()
b. Elevation of boiling point
Boiling point is the temperature at which the vapour pressure of liquid equals the atmospheric pressure.
Elevation in boiling point (∆Tb) is the difference in boiling point of pure liquid and boiling of solution of this liquid with a non-volatile solute.
![]()
Solutions
As can be clean seen from graph
![]()
![]()
![]()
![]()
![]()
![]()
Kb = Boiling point elevation constant of modal elevation constant (Ebullioscopic) constant
c. Depression of freezing point:
Freezing point: Temperature at which the vapour pressure of the substance in its liquid phase is equal to its vapour pressure in its solid phase
The lowering of vapour pressure of solution causes a lowering of freezing point compared to that of pure solvent. The difference in freezing point of the pure solvent and solution is called depression in freezing point
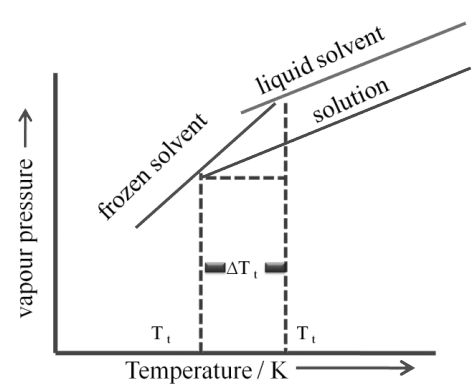
Depression in freezing point
Similar to elevation in boiling point
∆Tf α ∆P
α XA P˚ solvent
α molality
![]()
Kf = depression in freezing point constant or molal depression constant or cryoscopic constant.
Osmotic pressure
- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
d. Osmotic pressure
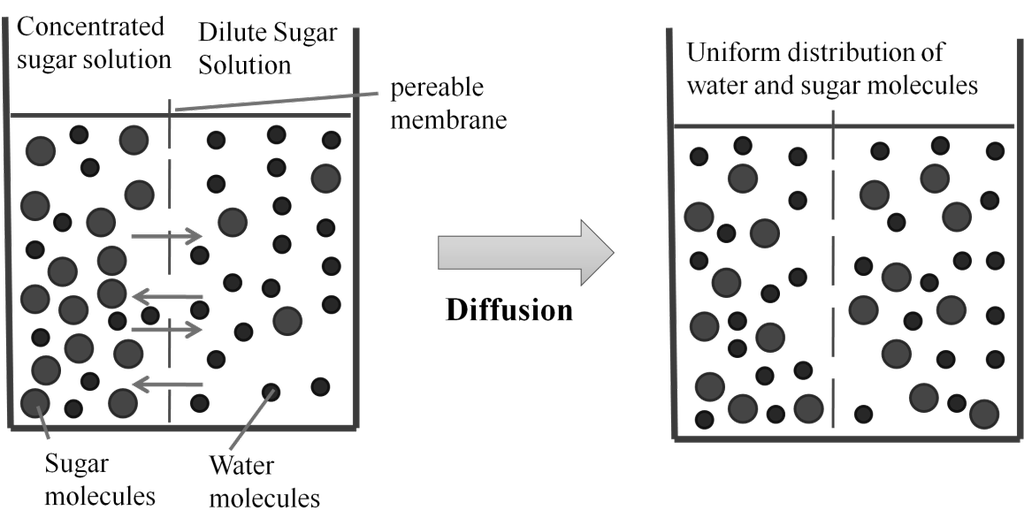
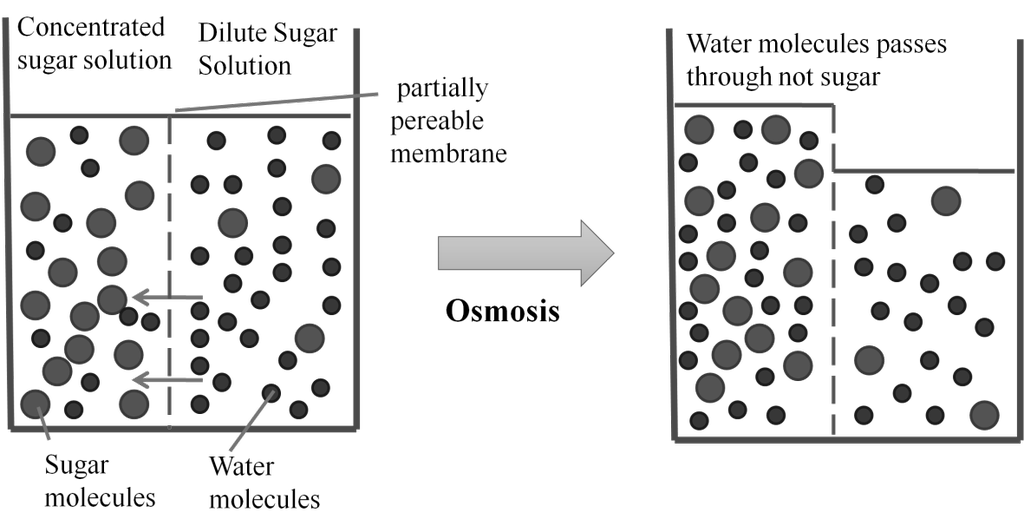
Osmosis: The process of flow of solvent molecules from pure solvent to the solution through semi permeable membrane.
Osmotic pressure (p) : Minimum pressure that must be applied to the solution to prevent the flow of solvent into the solution through a semipermeable membrane
p(Osmotic pressure) = nVRTi=wmVRTi
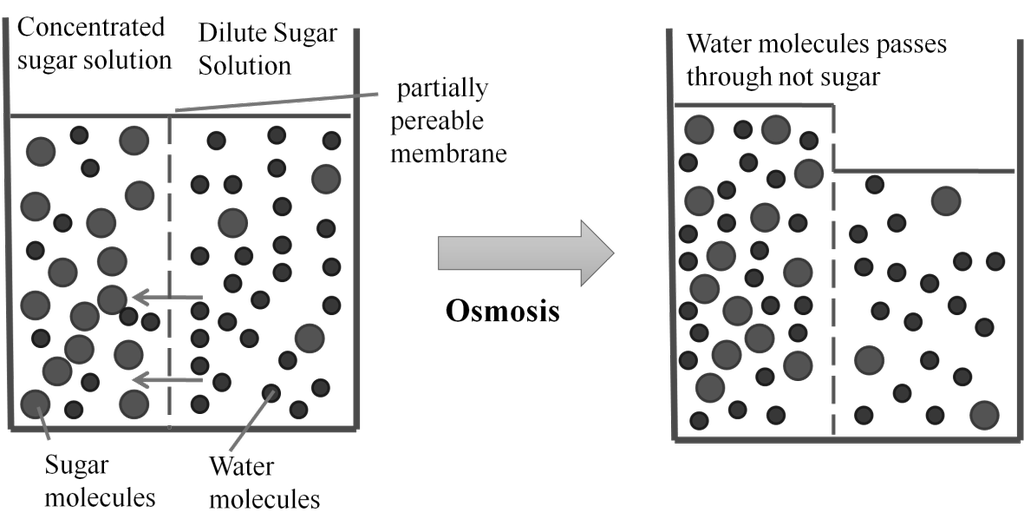
Isotonic solution: Two solutions having same osmotic pressure at a given temperature are called isotonic solution p1 = p2
Hypertonic solutions: If a solution has more osmotic pressure than other solution it is called hypertonic solution.
Hypotonic solution: If a solution has less osmotic pressure than other solution it is called hypotonic solution
Reverse osmosis: When a pressure larger than osmotic pressure is applied to the solution side, the pure solvent flows out of solution to solvent side through semi permeable membrane this process is called reverse osmosis Use: Reverse osmosis is used to desalination of sea water (into drinking water)
Application of Colligative property: By measuring a colligative property of a solution molar mass of the non-volatile solute can be calculated Conditions for getting accurate value of molar mass:
- Solute must be non-volatile
- Solution must be dilute
- Solute particles must not undergo any association or dissociation in the solution
Abnormal molar mass and Van’t Hoff factor (i): When the non-volatile solute particles undergo association (Eg: acetic acid in benzene) or dissociation (Eg: electrolytes like KCl, NaCl in water), the abnormal molar mass is observed.
NaCl No+ + Cl-
1 mole 0 0 total moles = 0
1- α α α total moles= 1+α
α = degree of dissociation
Actual moles are (1 + α) not (1)
![]()
![]()
![]()
1. For solutions undergoing dissociation
i >1 { Exp coll .prop > normal cell. Property}
{exp. Mol. wt < normal mol.wt }
2. For solution undergoing association
i < 1 { exp. Coll. Property < normal. Coll. property}
{ exp. Mol. Wt > normal .mol .wt}
![]()
![]()
Association of solute
CH3COOH Anociation in benzene to form dimer
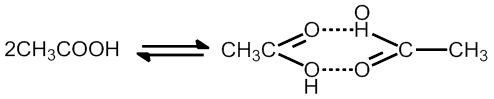
Note CH3COOh dissociate in water
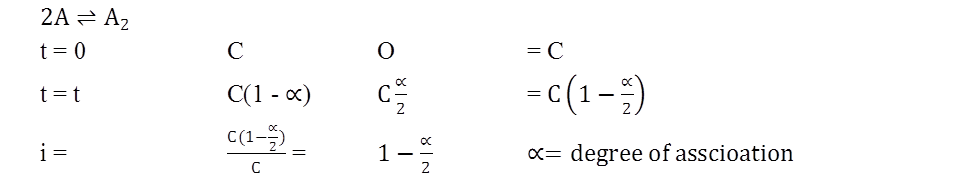
General formula (both for anociation an well an dissociation)
![]()
y = no. of particle from parhole.
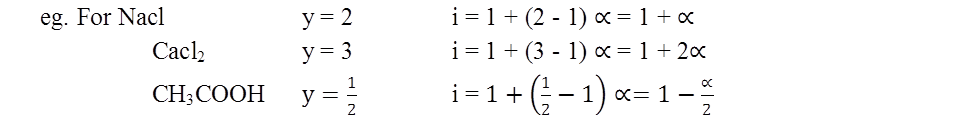
Important Formulae:
- p(osmotic pressure) =
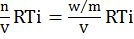
- Isotonic solution p1 = p2
- Vapour pressure variation with temperature 2.303 log10
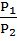 =
= 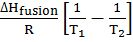
- Raoult’s Law For liquid-liquid systems: P=PPA+PPB+…
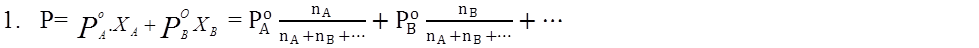
Relative lowering of vapour pressure:
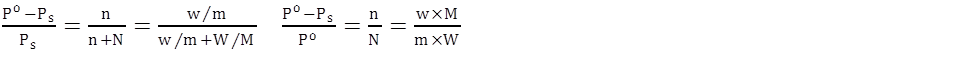 [for dilute solutions]
[for dilute solutions]
- Elevation in boiling point. ∆Tb=Kb×molality xi=1000 KbwmWi
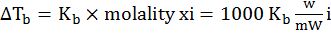
- Depression in freezing point: ∆Tf=Kf×molality xi=1000 KfwmWi

 and
and 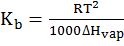
- For solutes undergoing dissolution AxByà xAy++ yBx- i>1. Experimental colligative property > normal colligative property and Experimental molecular weight < normal molecular weight
- For solutes undergoing association A +A +..nà An i<1 Experimental colligative property < normal colligative property and Experimental molecular weight > normal molecular weight
- Vant Hoff Coefficient i = 1 + (y-1)a a=degree of dissociation or association and y = no of particles from one particle

![]()
Axis of symmetry
- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
PROPERTIES OF SOLIDS
1. Solids have definite mass.
2. Solids have definite Volume
3. Solids have definite shape
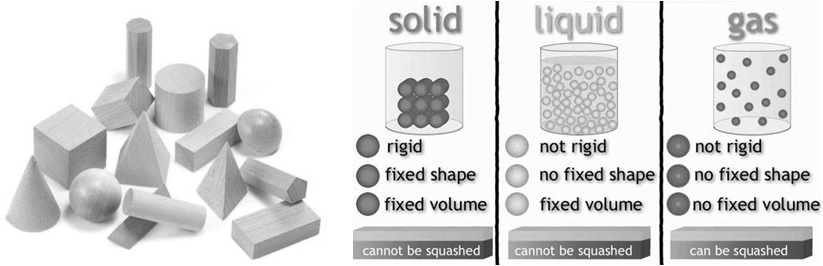
PROPERTIES OF SOLIDS
- Intermolecular distances are short.
- Intermolecular forces are strong.
- Their constituent particles (atoms, molecules or ions) have fixed positions and can only oscillate about their mean positions.
- In general they are incompressible and rigid
Solids are classified as crystalline and amorphous

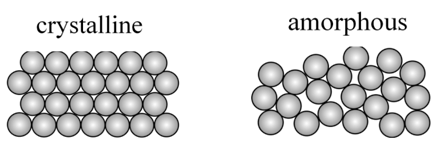
AXIS OF SYMMETRY
- An imaginary axis through which if we rotate the solid then same figure is seen more than once before completing 360o
- For a cube we have
- Two fold symmetry
- Three fold symmetry
- four fold symmetry
Axis of symmetry
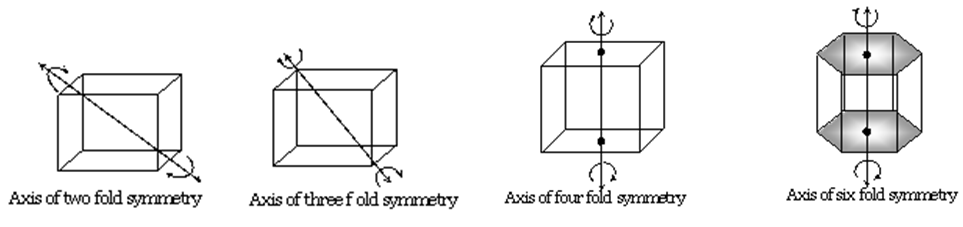
PLANE OF SYMMETRY
An imaginary plane through if we cut the solid the two parts will be mirror image of each other
Centre of symmetry
- An imaginary point through if we pass an imaginary line it will touch the opposite plane, edge or vertices at equal distance
PROPERTIES OF SOLIDS
- Cleavage plains: Cleavage is the tendency of a mineral to break along smooth planes parallel to zones of weak bonding. Crystals have cleavage plains where as amorphous solids do not have these plains
- Crystals are called true solids whereas amorphous solids are called pseudo solids or super cooled liquid.
Polymorphic forms or polymorphs: The different crystalline forms of a same substance are known as polymorphic forms or polymorphs. For example: graphite and diamond are polymorph’s of carbon
Crystals classification based on the nature of intermolecular forces
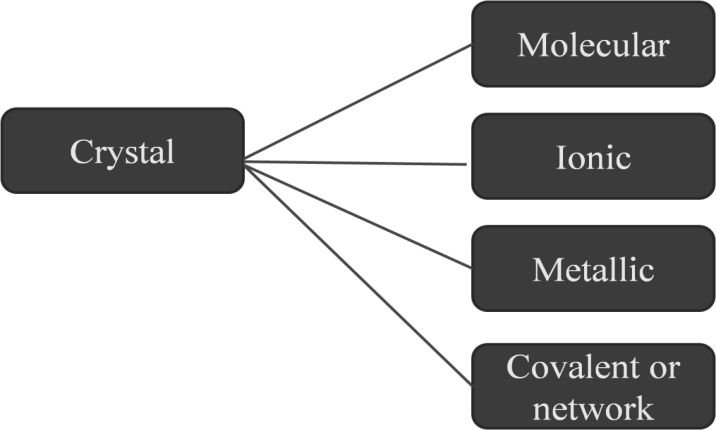
Molecular crystals
They have constituent particles as molecules and are divided into three parts
- Non polar: here the intermolecular forces are weak Vanderwaal's forces (Dispersion or London forces) . They are soft, do not conduct electricity and have very low melting point. Ex: Argon, CCl4
- Polar: here the intermolecular forces are Dipole-dipole interactions. They are soft, do not conduct electricity and have low melting point. Ex: HCl, SO2
- Hydrogen bonding: here the intermolecular forces are Hydrogen bonds. They are hard, do not conduct electricity and have low melting point. Ex: Ice(H2O)
- Ionic crystals: The constituent particles are ions. These have strong columbic intermolecular forces. They are hard but brittle. They do not conduct electricity in solid state but are good conductors on molten and aqueous state. They have very high melting point. Ex: Rock salt (NaCl), MgCl2
- Metallic solid: The constituent particles are positive ions floating in sea delocalized electrons. These have strong metallic intermolecular forces. They are hard but ductile and malleable. They are good conductor of electricity. They have high melting point. Ex: Iron, Copper etc
- Covalent or network solids: The constituent particles are atoms. These have strong covalent bonding. They are hard .They do not conduct electricity. They have very high melting point. Ex: Silica, Diamond etc. Graphite is an exception because it is soft and conducts electricity.

Crystal lattices
- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
CRYSTAL LATTICES
- Lattice: Regular 3-D arrangements of equivalent LATTICE POINTS in space.
- UNIT CELLS
- Smallest repeating internal unit that has the symmetry characteristic of the solid.
- Actual unit cell
- Unit cell as drawn
- Whole crystal
CRYSTAL LATTICE GEOMETRY
- Based on shape of unit cell ignoring actual atomic locations
- Unit cell = 3-dimensional unit that repeats in space
- Unit cell geometry completely specified by a, b, c (distance in x, y & z axis)& a, b, g (angles between a,b & c (lattice parameters or lattice constants)
- Seven possible combinations of a, b, c & a, b, g, resulting in seven basic crystal systems
14 Bravais Lattices: seven basic lattices and fourteen overall
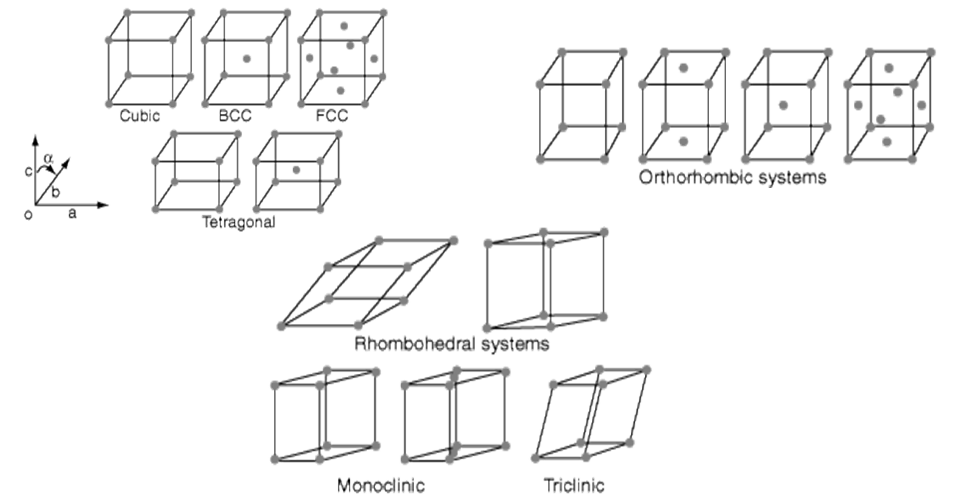
14 Bravais Lattices from seven basic lattices
Cubic Unit Cells
There are 7 basic crystal systems, but we are only concerned with CUBIC.
DIFFERENT CUBIC UNIT CELLS
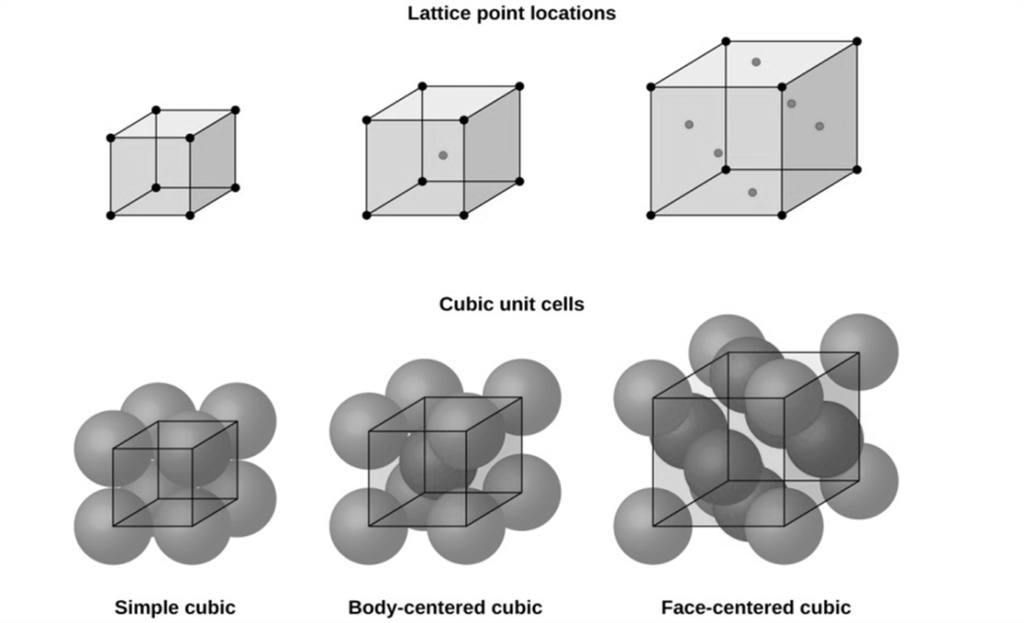
ATOM SHARING AT CUBE FACES AND CORNERS
Atom shared in corner
à 1/8 inside each unit cell
Atom shared in face
à ½ inside each unit cell
Atoms shared on edges
à ¼ inside each unit cell
Atoms inside the unit cell
à 1 inside each unit cell
NUMBER OF ATOMS PER UNIT CELL
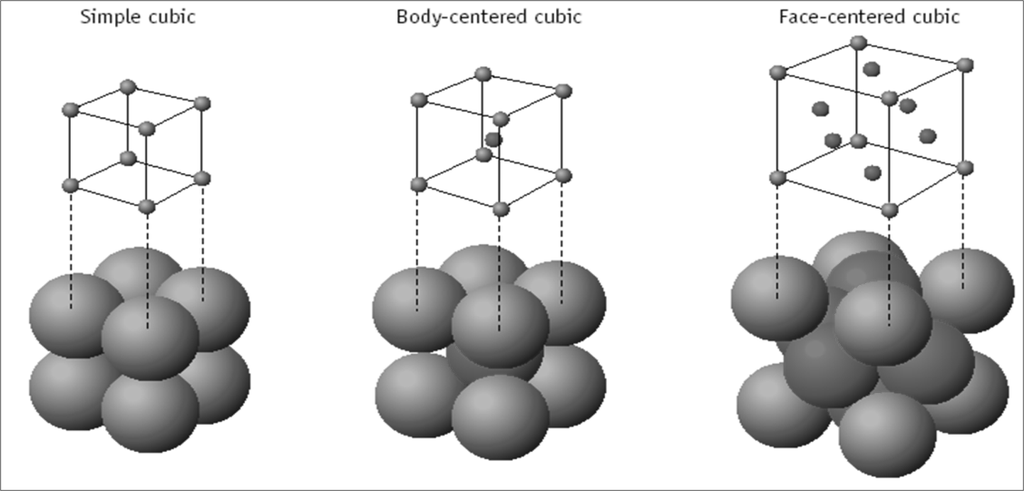
PACKING FRACTION
![]()
![]()
![]()
a = edge length of unit cell
R = radius of atoms( assuming they are hard spheres)
Z= no of atoms in one unit cell
PACKING FRACTION: SC

PACKING RACTION: BCC
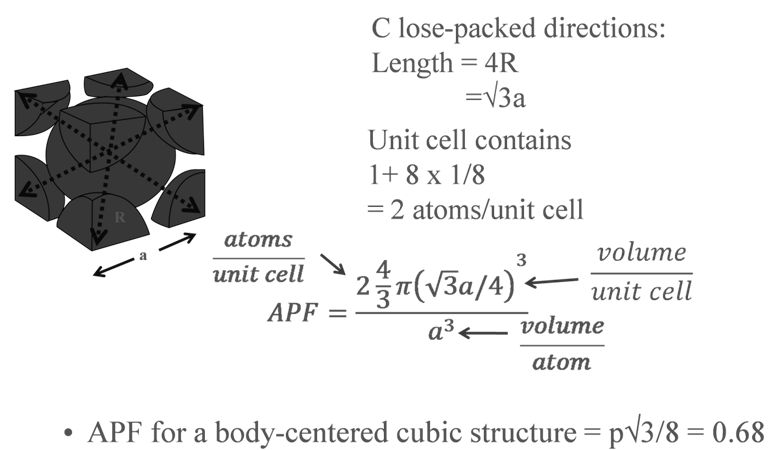
PACKING FRACTION: FCC

Voids:- gaps between atoms in a crystal are called voids.
- There are two types of voids
- Tetrahedral voids and octahedral voids
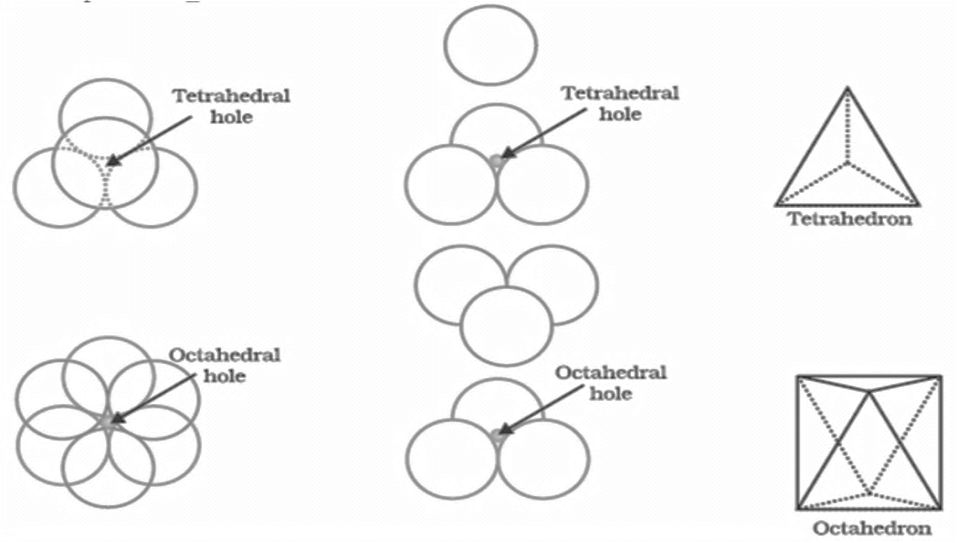
HOW TO LOCATE VOIDS
- No. of tetrahedral voids = 2 x effective atoms/unit cell
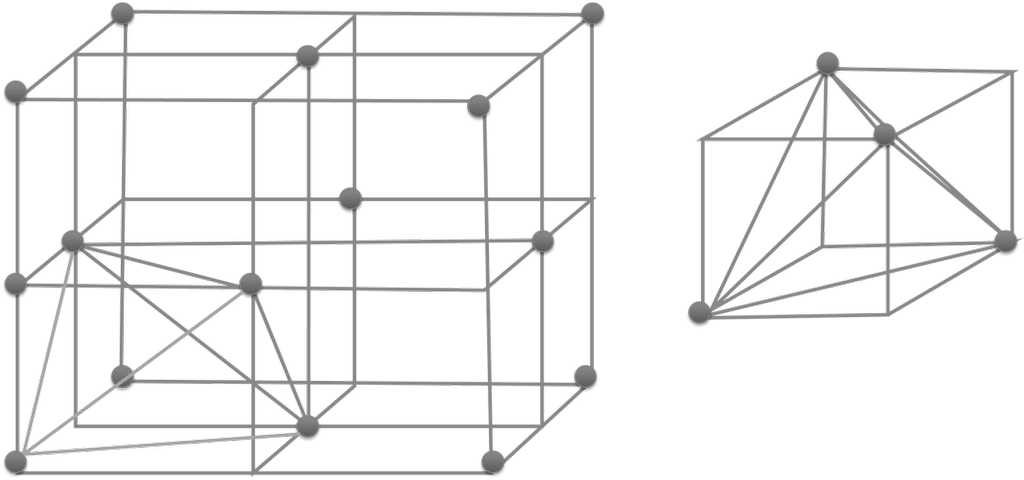
- No. of octahedral voids = 1 x effective atoms/unit cell
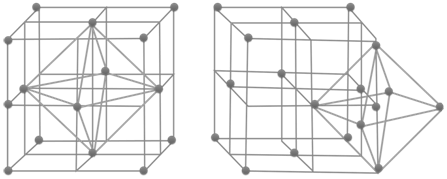
COMPARISON OF CRYSTAL STRUCTURES
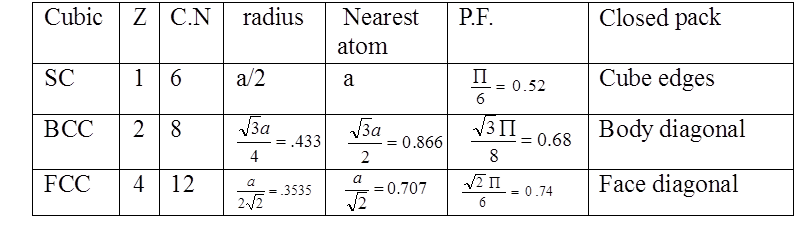
Theoretical density
- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
THEORETICAL DENSITY, r
![]()
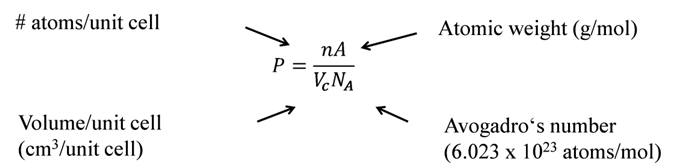
CLOSE PACKED CRYSTALS
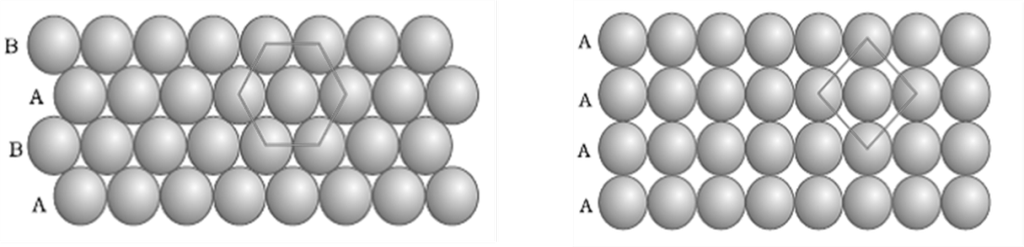
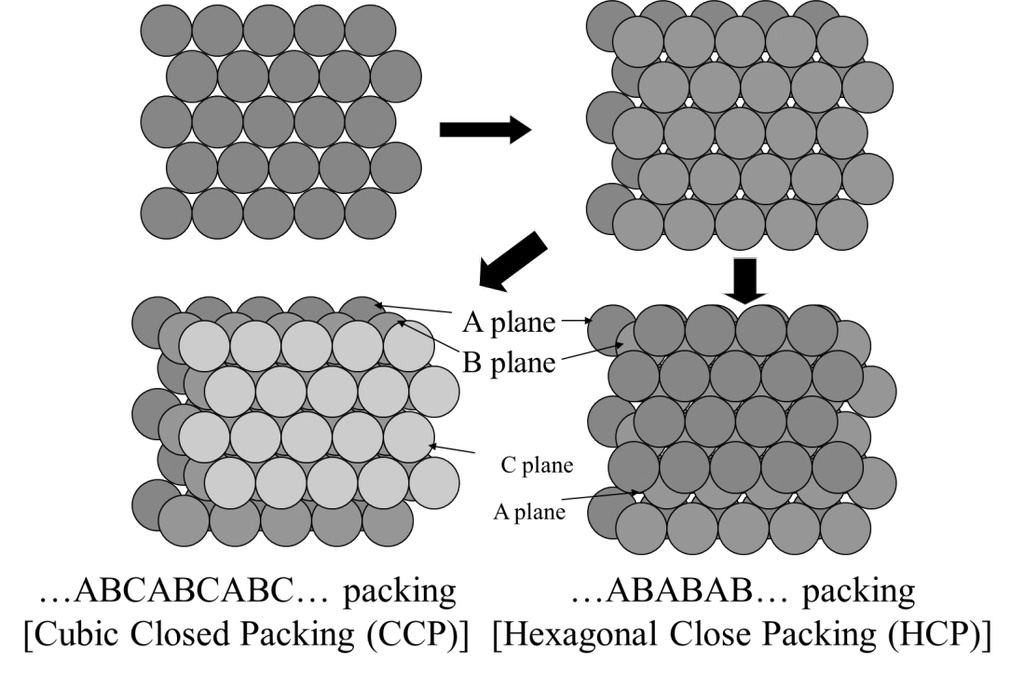
IONIC CRYSTALS
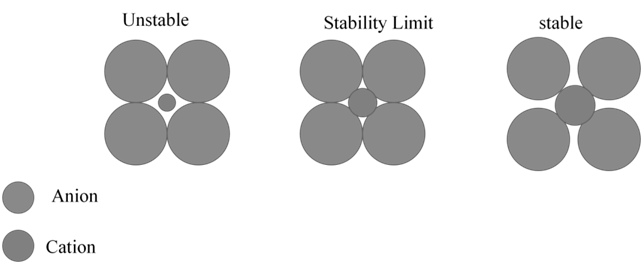
COORDINATION NO 3
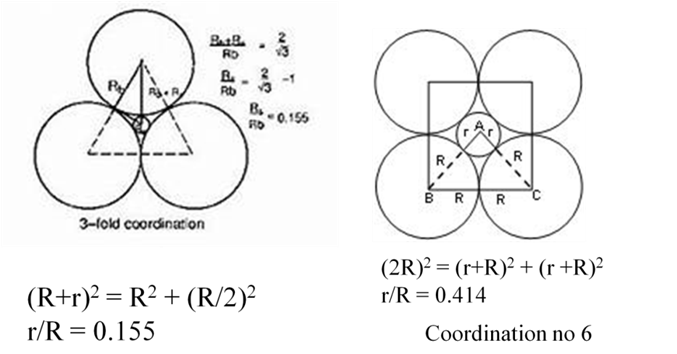
IONIC CRYSTALS

SIMPLE IONIC COMPOUNDS
Two Views of CsCl Unit Cell
Either arrangement leads to formula of 1 Cs+ and 1 Cl- per unit cell
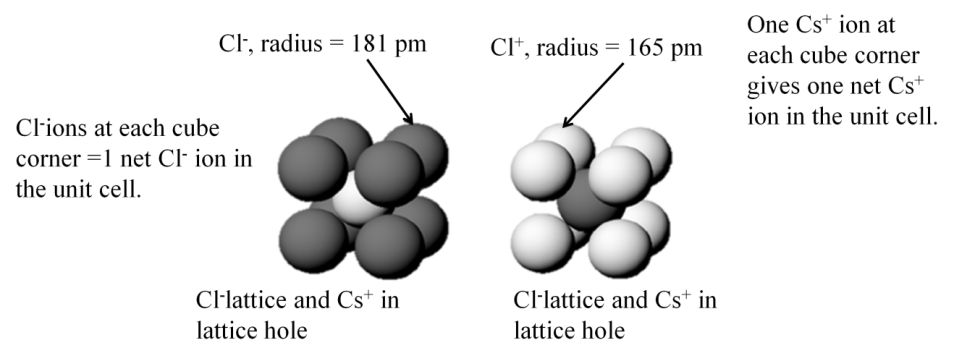
NaCl CONSTRUCTION
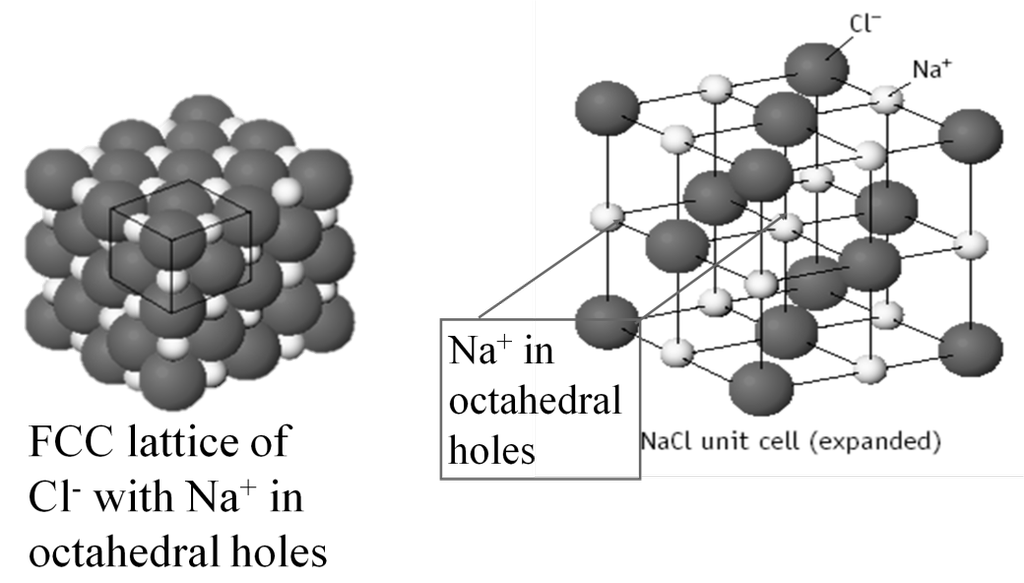
THE SODIUM CHLORIDE LATTICE
Many common salts have FCC arrangements of anions with cations in OCTAHEDRAL HOLES — e.g., salts such as NaCl
• FCC lattice of anions ----> 4 A-/unit cell
• C+ in octahedral holes ---> 1 C+ at center
+ [12 edges • 1/4 C+ per edge]
= 4 C+ per unit cell
Formula Na4Cl4 = NaCl
NETWORK SOLIDS
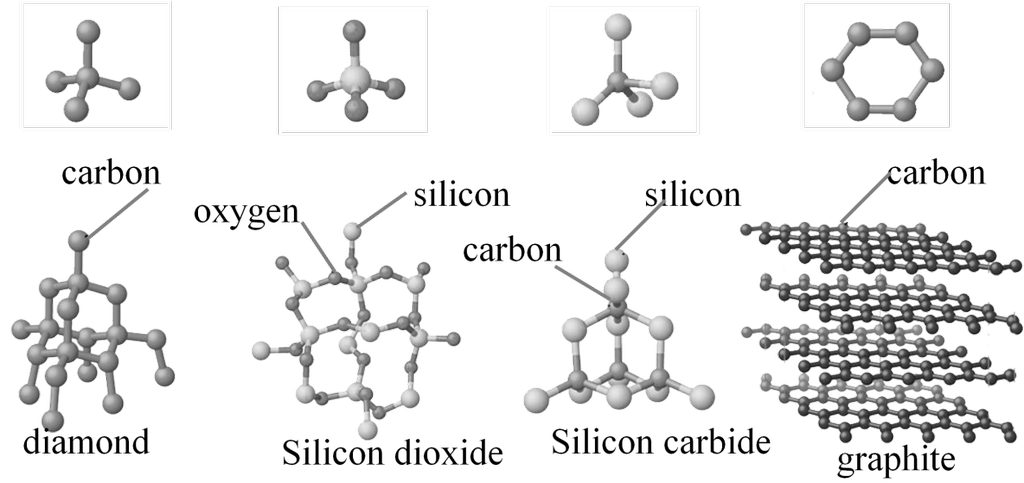
BRAGG’S LAW
• Incoming X-rays diffract from crystal planes Braggs law Þ nl = 2dsin(q)
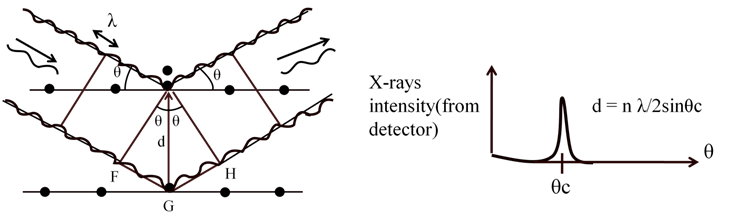
FUN FACTS ABOUT BRAG’ LAW
Sir William Lawrence Bragg was an Australian-born British physicist who discovered (1912) Bragg's law of X-ray diffraction. He was joint winner (with his father, William Henry Bragg) of the Nobel Prize in Physics in 1915 Bragg was knighted in 1941.
As of 2018, he is the youngest ever Nobel laureate in physics, having received the award at the age of 25 years.[4
Bragg was the director of the Cavendish Laboratory, Cambridge, when the discovery of the structure of DNA was reported by James D. Watson and Francis Crick in February 1953.
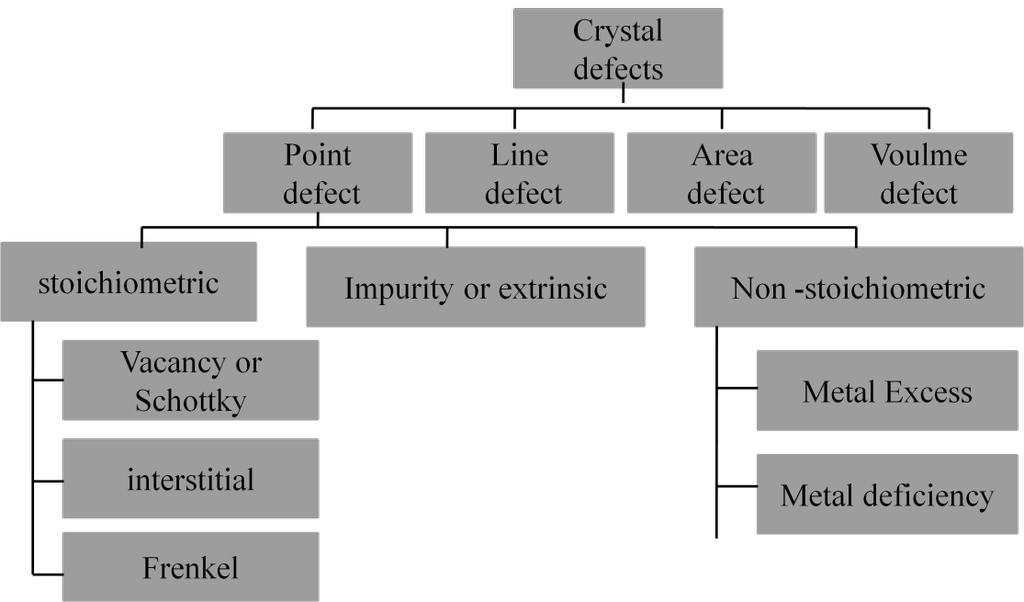
Stoichiometric defects are point defects that do not disturb or change the Stoichiometry (Stoichiometric composition or formula) of the crystalline substance. They are also called intrinsic or thermodynamic defects.
-
- Vacancy defects or Schottky Defect
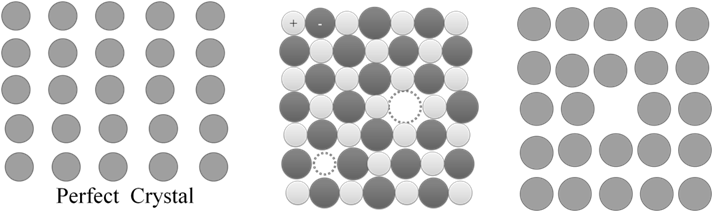
Vacancy defects or Schottky Defect
-
-
-
- Some of the lattice sites of the crystal are vacant.
- This defect decreases the density of the crystal.
- This defect can be developed by heating the substance. Due to irradiation or sputtering effect. Due to presence of residual tensile stress within the solid.
- Vacancy defect for ionic crystals is called Schottky defect. Here equal no of cations and anions are missing so the stoichiometry of salt does not change
-
-
Interstitial defects
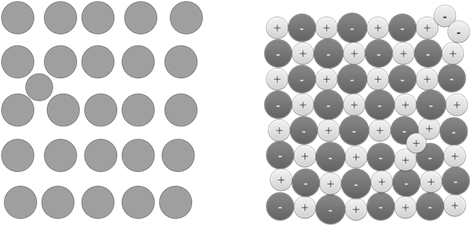
Interstitial defects: -
-
-
-
- Some constituent particles occupy the interstitial sites of the crystal.
- This defect increases the density of the crystal
- In case of ionic solids equal no of cations and anions are added
-
-
Frenkel Defect: -
(i) The ion (smaller ion, usually cation) is dislocated (moved) from its normal lattice site to an interstitial site. So it is also called dislocation defect It creates vacancy defect at its normal lattice site and interstitial defect at its new location Condition:
(ii) The difference between the size of the ions (cation and anion) should be larger. Examples: ZnS ,AgCl, AgBr, and AgI due to small size of Zn2+ and Ag+ ions
(iii) It does not change the density of the crystal
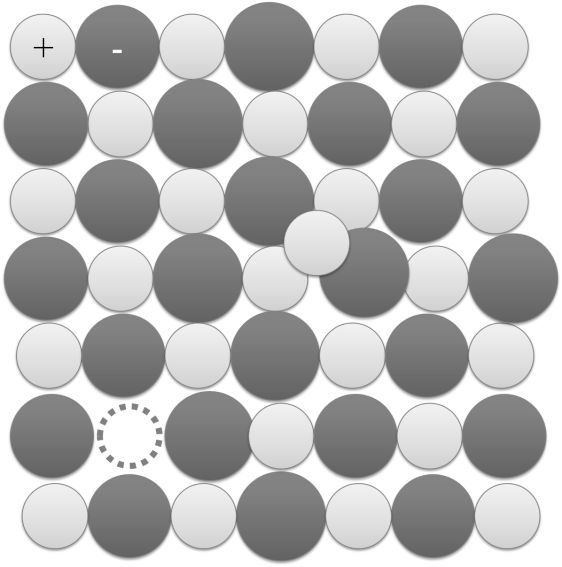
Non Stoichiometric defects are point defects that disturb the Stoichiometry of the crystalline substance
Metal deficiency defect Due to cation vacancies. Eg. In FeO crystal, some Fe2+ cations are missing and extra negative charge is balanced by acquiring extra positive charge by adjacent Fe2+ ion to become Fe3+ ion
METAL EXCESS OR F-CENTRE
(i) Due to anionic vacancies or F- Centres: The anionic vacancies occupied by unpaired electrons. F-centres impart colour to the crystals (Eg. NaCl to Yellow, KCl to violet) due to excitation of these electrons by absorbing energy from the visible light falling on the crystals
(ii) Due to presence of extra cations interstitial sites, Eg. ZnO
IMPURITY DEFECTS
Impurity defects – Ex- Solid solution of NaCl containing SrCl2 impurity. Solid solution of AgCl and CdCl2
Doping: The process of adding an appropriate amount of suitable impurity to increase the conductivity of semiconductors
Solids can also be classified into three types based on their electrical conductivities:
- a. Conductors-The solids with conductivities ranging between 104 to 107 ohm–1m–1 are called conductors.
- b. Insulators - These are the solids with very low conductivities ranging between 10–20 to 10–10 ohm–1m–1.
- c. Semi- conductors. These are the solids with conductivities in the intermediate range from 10–6-104 ohm–1
ELECTRICAL CONDUCTION
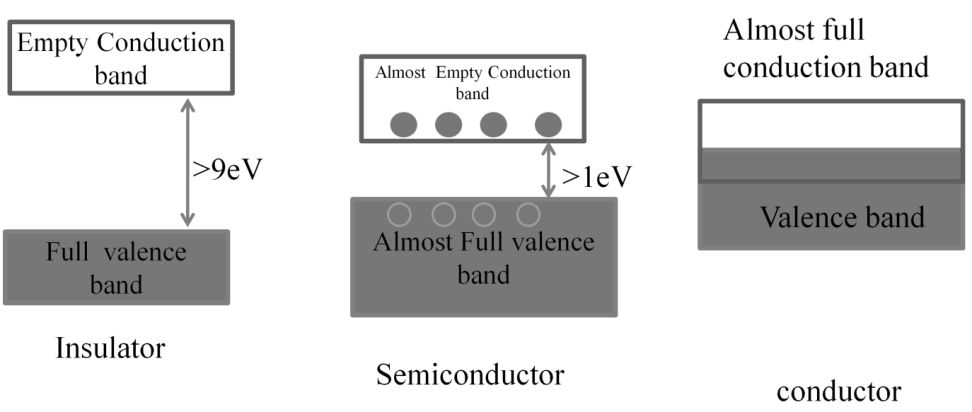
TYPES OF SEMICONDUCTORS:
- a. Intrinsic: These are those semiconductors in which the forbidden gap is small. Only some electrons may jump to conduction band and show some conductivity. They have very low electrical conductivity. Example: Silicon, germanium
- b. Extrinsic: When an appropriate impurity is added (doping) to an intrinsic semiconductor. Their electrical conductivity is high.
Types of extrinsic semi conductors:

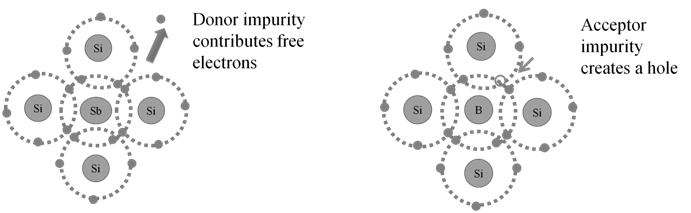
MAGNETIC PROPERTIES

- Piezoelectricity:- When polar crystal is subjected to mechanical stress, electricity is produced. E.g. BaTiO3, Rochelle salt
- Pyroelectricity:- When polar crystal is subjected to heat stress, electricity is produced. E.g. PbZrO3
IMPORTANT FORMULAE
- Elements of symmetry in simple cubic crystals
- Plane of symmetry = 3 + 6 =9
- Axis of symmetry = 3 + 4 + 6 =13
- Center of symmetry = 1
- Total elements of symmetry = 9 + 13 + 1= 23
- Density of lattice matter=
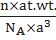 n is number of atoms per unit cell and ‘a’ is the unit cell edge length
n is number of atoms per unit cell and ‘a’ is the unit cell edge length - Braggs law: 2dsinq = nl
- Atoms per unit cell(n) = Nc + NF/2 + NE/4+ NV/8
- No. of tetrahedral voids = 2 x n
- No of octahedral voids = n
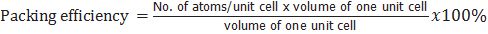

 Kaysons Publication
Kaysons Publication
