Mole Concept

Every field of science involves taking measurements, understanding them, and communicating them to others. In other words, we all have to speak the same basic language. Whether you are a chemist, a physicist, a biologist, an engineer, or even a medical doctor, you need a consistent way of communicating size, mass, shape, temperature, time, amount, energy, power, and speed.

The International System of Units (abbreviated SI, from the French Système international d’unités) is the metric system used in science, industry, and medicine. Depending on your age and geographic location, you might be very familiar with the “imperial” system, which includes units such as gallons, feet, miles, and pounds. The imperial system is used for “everyday” measurements in a few places, such as the United States. But in most of the world (including Europe) and in all scientific circles, the SI system is in common use.

The SI is made up of 7 base units that define the 22 derived units with special names and symbols.

History of the SI System

The SI units of measurement have an interesting history. Over time they have been refined for clarity and simplicity.

1. The meter (m), or metre, was originally defined as 1/10,000,000 of the distance from the Earth’s equator to the North Pole measured on the circumference through Paris. In modern terms, it is defined as the distance traveled by light in a vacuum over a time interval of 1/299,792,458 of a second.
2. The kilogram (kg) was originally defined as the mass of a liter (i.e., of one thousandth of a cubic meter). It is currently defined as the mass of a platinum-iridium kilogram sample maintained by the Bureau International des Poids et Mesures in Sevres, France.
3. The second (s) was originally based on a “standard day” of 24 hours, with each hour divided in 60 minutes and each minute divided in 60 seconds. However, we now know that a complete rotation of the Earth actually takes 23 hours, 56 minutes, and 4.1 seconds. Therefore, a second is now defined as the duration of 9,192,631,770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the cesium-133 atom.
4. The ampere (A) is a measure of the amount of electric charge passing a point in an electric circuit per unit time. 6.241×10¹⁸ electrons, or one coulomb, per second constitutes one ampere.
5. The kelvin (K) is the unit of the thermodynamic temperature scale. This scale starts at 0 K. The incremental size of the kelvin is the same as that of the degree on the Celsius (also called centigrade) scale. The kelvin is the fraction 1/273.16 of the thermodynamic temperature of the triple point of water (exactly 0.01 °C, or 32.018 °F).
6. The mole (mol) is a number that relates molecular or atomic mass to a constant number of particles. It is defined as the amount of a substance that contains as many elementary entities as there are atoms in 0.012 kg of carbon-12.
7. The candela (cd) was so named to refer to “candlepower” back in the days when candles were the most common source of illumination (because so many people used candles, their properties were standardized). Now, with the prevalence of incandescent and fluorescent light sources, the candela is defined as the luminous intensity in a given direction of a source that emits monochromatic radiation of frequency 540⋅1012

Derived units – are defined in terms of the seven base quantities via a system of quantity equations. The SI derived units for these derived quantities are obtained from these equations and the seven SI base units

For ease of understanding and convenience, 22 SI derived units have been given special names and symbols,

Ex: volume = L x L x L = m³ or cm³ 

Density=massvolume=kgm3 or gmm3  

Force: unit N (Newton) = kg.m/sec²

Conversion of one unit to another example

                       m³ = m x m x m = (100cm) x (100) cm x (100) cm = 10⁶ cm³

 Density kgm3=1000gm106cm3=10-3 gmcm3

Measurement of data: when conducting experiments we have to measure & report data. There are certain norms for reporting this data.   

All very big and small values are expressed in exponents

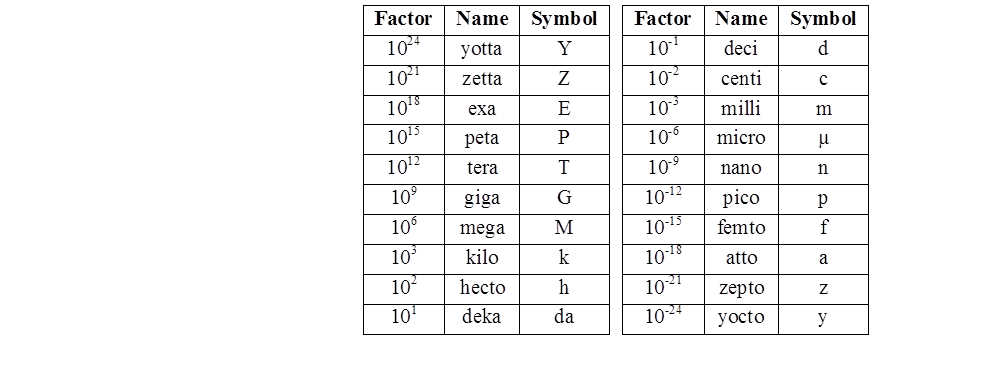
PRECISION AND ACCURACY

•  Precision indicates how closely repeated measurements match each other.
•  Accuracy indicates how closely a measurement matches the correct or expected value.
•  A result is valid only if it is both accurate and precise.

EXAMPLE

• If the true value for a result is 8.00 kg and a student  “A” takes two measurements and reports the results as 7.95 kg and 7.93 kg. These values are precise as they are close to each other but are not accurate.
• Another student “B” repeats the experiment and obtains 7.94 kg and 8.05 kg as the results for two measurements. These observations are neither precise nor accurate.
• When a third student “C” repeats these measurements and reports 8.01 kg and 7.99 kg. These values are both precise and accurate.

SIGNIFICANT FIGURES

Significant figures are meaningful digits which are known with certainty. The uncertainty is indicated by writing the certain digits and the last uncertain digit. Thus, if we write a result as 11.2 ml, we say the 11 is certain and 2 is uncertain and the uncertainty would be ±1 in the last digit.

Unless otherwise stated, an uncertainty of ± 1 in the last digit is always understood.

RULES FOR DETERMINING THE NUMBER OF SIGNIFICANT FIGURES

1. All non-zero digits are significant
2. Zeros preceding the first non-zero digit are not significant
3.  Zeros between two non-zero digits are significant.
4.  Zeros at the end or right of the number are significant provided they are on the right side of the decimal point. But, if otherwise, the zeros are not significant
5. Counting numbers of objects, for example, 2 balls or 20 eggs, have infinite significant figures as these are exact numbers

EXAMPLE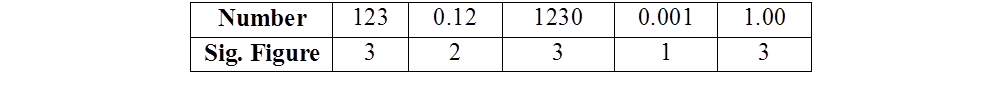

ADDITION AND SUBTRACTION OF SIGNIFICANT FIGURES

During addition and subtraction, the result cannot have more digits to the right of the decimal point than either of the original numbers.

MULTIPLICATION AND DIVISION OF SIGNIFICANT FIGURES

In multiplication and division with significant figures, the answer cannot have more significant figures than either of the original numbers.

                                Example               Example

                                  2.12                         1.2

                             +  6.1                    x     1.3

                                 0.012                       1.56

                                 8.232             Ans.   1.6

                      Ans.= 8.2                             

ROUNDING OFF THE SIGNIFICANT FIGURES

1. If the rightmost digit to be removed is more than 5, the preceding number is increased by one. For example, in figure 2.486 if we have to remove 6, we have to round it to 2.49

2. If the rightmost digit to be removed is less than 5, the preceding number is not changed.

For example, in figure 6.664 if 4 is to be removed, then the result is rounded of to 6.66.

3. If the rightmost digit to be removed is 5, then the preceding number is not changed, if it is an even number but it is increased by one if it is an odd number. For example, if 2.35 is to be rounded by removing 5, we have to increase 3 to 4 giving 2.4 as the result. However, if 2.25 is to be rounded off it is rounded off to 2.2

Ex.:  A student performs a titration with different burettes and finds titre values of 25.2 mL, 25.25 mL, and 25.0 ml. The number of significant figures in the average titre value is

(IIT adv. 2010, integer type)

Sol. During addition and subtraction, the result cannot have more digits to the right of the decimal point than either of the original numbers                                                                            Answer:  3

Ex.:  If the value of Avogadro number is 6.023 × 10²³ mol^–1 and the value of Boltzmann constant is 1.380 × 10^–23 J K^–1, then the number of significant digits in the calculated value of the universal gas constant is                                                                                                          (IIT adv. 2014, integer type)

Sol. K = R/N_A  R=KN_A

R= 6.023 × 10²³ × 1.380 × 10^–23 J.mol^–1.k^–1= 8.31174 J.mol^–1.k^–1. There are 4 significant figures in each term. (4) Hence, these be 4 significant figure in R                                                  Answer. 4

.STOICHIOMETRY AND VOLUMETRIC

The word stoichiometry is derived from two Greek words - stoicheion (meaning element) and metron (meaning measure).

Stoichiometry, thus, deals with the calculation of masses (sometimes volumes also) of the reactants and the products involved in a chemical reaction.

How many moles of methane are required to produce 22g CO₂ (g) after combustion?

Solution

According to the chemical equation.

CH₄ (g) +2O₂ (g) → CO₂ (g) + 2H₂O (g)

44g CO₂ (g) is obtained from 16 g CH₄ (g).

1 mol CO₂ (g) is obtained from 1 mol of CH₄ (g)]

 

= 0.5 mol CO₂ (g)

Hence, 0.5 mol CO₂ (g) would be obtained from 0.5 mol CH₄ (g) or 0.5 mol of CH₄ (g) would be required to produce 22 g CO₂ (g)

Ex.:- At 300 K and I atmospheric pressure, 10mL of a hydrocarbon required 55mL of O₂ for complete combustion and 40 mL, of CO₂ is formed The formula of the hydrocarbon is        (2019 Main, 10 April)

(a) C₄H₇Cl                                             (b) C₄H₆

(c) C₄H₁₀                                               (d) C₄H₈

Solution: In eudiometry,

  

 

 

 

Given, (i) VCO₂ = 10x = 40mL Þ x = 4

 

 

          

 

 

So, the hydrocarbon (C_x H_y) is C₄H₆         Answer (b)

LIMITING REAGENT

Many a time, the reactions are carried out when the reactants are not present in the amounts as required by a balanced chemical reaction. In such situations, one reactant is in excess over the other. The reactant which is present in the lesser amount gets consumed after sometime and after that no further reaction takes place whatever be the amount of the other reactant present. Hence, the reactant which gets consumed, limits the amount of product formed and is, therefore, called the limiting reagent.

IMPORTANT: Product formed is calculated by limiting reagent

Limiting reagent

2A + 3B → 4C

If we have 3 mole of A of 4 mole of B, find out mole of C farmed

2A + 3B → 4C

   3      4

3/2x  3 = 4.5 > 4 so B is limiting reagent

3 mole of B form 4 mole C

4 mole of B will form

       Answer_: 5.33 moles

Ex.:- If 0.50 mole of BaCl₂ is mixed with 0.20 mole of Na₃PO₄, the maximum number of moles of Ba₃ (PO₄)₂ that can be formed is                                                                                      (1981, 1M)

(a) 0.70                                                 (b) 0.50

(b) 0.20                                                 (d) 0.10

Solution: The balanced chemical reaction is

In this reaction, 3 moles of BaCl₂ combines with 2 moles of Na₃PO₄. Hence, 0.5 mole of BaCl₂ require

 

Since, available Na₃PO₄ (0.2 mole) is less than required mole (0.33), it is the limiting reactant and would determine the amount of product Ba₃(PO₄)₂

∵ 2 moles of Na₃PO₄ gives 1 mole Ba₃ (PO₄)₂

       

 Answer (d)

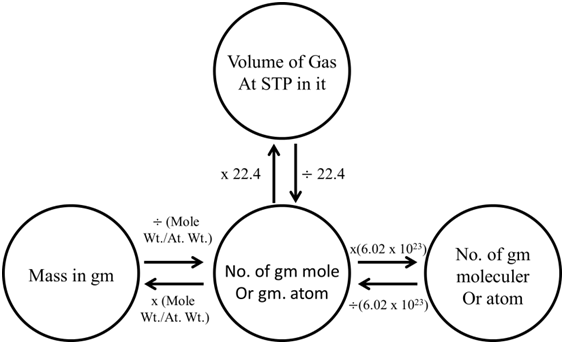
MOLE CONCEPT

• One mole is the amount of a substance that contains as many particles or entities as there are atoms in exactly 12 g (or 0.012 kg) of the C¹²
• 12gm of C¹² contains 6.022 x10²³ atoms
• The number 6.022 x10²³ is called Avogadro’s constant or Avogadro’s number.
• The mass of one mole of a substance in grams is called its molar mass.
• The molar mass in grams is numerically equal to the atomic/molecular/formula mass in u.(u is the unified mass)

CONVERSION OF MASS & VOLUME TO MOLES

Ex. Which has maximum number of atom?                                                              (2003, 1M)

(a) 24 g of C (12)                                             (b) 56 g of Fe (56)

(c) 27 g of Al (27)                                            (d) 108 g of Ag (108)

Solution: Number of atoms = Number of moles

Numbers of atoms in 24g C= 2412 ×NA=2NA

Number of atoms in 56 g of Fe= 5656NA=NA  

Number of atoms in 27 g of Al= 2727NA=NA  

Number of atoms in 108 of Ag= 108108NA=NA  

Hence, 24g of carbon has the maximum number of atoms.                                      Answer (a)

Ex. The ratio mass of oxygen and nitrogen particular gaseous mixture is 1: 4. The ratio of number of their molecule is                                                                                              (2014 Main)

 

Solution: no2nN2= (mO2)(MO2)(mN2)(MN2)  

Where, mO2  = given mass O₂, mN2  = given mass of N₂, MO2  = molecular mass of O₂, MN2  = molecular mass of N₂, nO2  = Number of moles of O₂, nN2  = number of moles of N₂

=mO2mN22832=14×2832=732                                                                                      Answer (b)

Ex.:- How many moles of electron weighs 1 kg?                                               (2002, 3M)

a 6.023×1023                                       b19.108×1031

c 6.0239.108×1054                             d19.108×6.023×108

Solution: Mass of electron = 9.108 x 10^-31 kg

9.108 x 10^-31 kg = 1.0 electron

∴   1 kg = 19.108 ×10-31  electrons= 10319.108× 16.023 ×1023  

∴  19.108×6.023 ×108 mole of electrons                                                                Answer (d)

 

MOLARITY MOLALITY, MOLE FRACTION AND NORMALITY

• Molarity is the number of moles of solute in per liter of solution. Unit is moles per liter.

Molarity= Gram Mole of solutelitre of solutiuon  

• Molality is the number of solute present in 1kg of solvent.

Molarity= Moles of solutewt. of solvent in kg  

• Normality= Gram Equivalent of soluteLitre of solution            
• Mole fraction of solute= Moles of solute Moles of solute+moles of solvent  

Ex.:  3g of activated charcoal was added to 50mL of acetic acid solution (0.06N) in a flask. After an hour it was filtered and the strength of the filtrate was found to be 0.042N. The amount of acetic acid adsorbed (per gram of charcoal) is.                                                      (2015 JEE MAINS)

(a) 18 mg                                            (b) 36 mg

(c) 42 mg                                            (d) 54 mg

Solution. Given, initial strength of acetic acid = 0.06N

Final strength = 0.042 N;        Volume = 50mL

\ Initial millimoles of CH₃COOH = 0.06 x 50 =3

Final millimoles of CH₃COOH = 0.042 x 50 = 2.1

\ Millimoles of CH₃COOH adsorbed = 3 – 2.1 = 0.9 mmol.

                                                              = 0.9 x 60mg = 54 mg                                  Answer (d)

Ex.: Dissolving 120 g of urea (mol. wt. 60) in 1000 g of water gave a solution of density 1.15 g/mL. The molarity of the solution is                                                                                        (2011)

(a) 1.78 M                                         (b) 2.00M

(c) 2.05 M                                         (d) 2.22 M

Solution: Molarity= Moles of solute Volume of Solution(L)  

Moles of urea= 12060=2  

Weight of solution = weight of solvent + weight of solute

                              = 1000 +120 = 1120 g

⇒       Volume= 1120g1.15g/mL×11000L/L=0.973L  

⇒    Molarity= 2.0000.973=2.05M                                                                                 Answer (c)

Ex.: The molarity of a solution obtained by mixing 750 mL of 0.5 M HCl 250 mL of 2 M HCl will be                                                                                                                                      (2013 Main)

(a) 0.875 M                                            (b) 1.00 M

(c) 1.75 M                                              (d) 0.0975 M

Solution: From the formula, Mf= M1V1+M2V2V1+V2  

Given, V₁ = 750 mL,  M₁ = 0.5 M

             V₂ = 250mL, M₂ = 2 M

                                                    = 750 × 0.5+250 × 2750+250= 8751000=0.875M                      Answer (a)

 

 

 

Day - 3

 

 

PERCENTAGE COMPOSITION

Mass % of an element=mass of that element in the compound ×100molar mass of the compound  

Let’s take example of carbon-dioxide (CO₂)

Mass % of C=1244 x 100=27.2%         

Mass % of O= 3244x 100=72.73%  

Ex.:- The most abundant element by mass in the body of a healthy human adult are oxygen (61.4%) carbon (22.9%), hydrogen (10.0%) and nitrogen (2.6%) The weight which a 75 kg person would gain if all Hatoms are replaced by 2 Hatoms are replaced by 2H atoms is       2017 JEE Main)

(a) 15Kg                                                  (b) 37.5 kg

(b) 7.5 Kg                                                (d) 10kg

Solution: Given, abundance of element by mass

Oxygen = 61.4% carbon= 22.9%, hydrogen = 10% and nitrogen = 2.6%

Total weight of person = 75 kg

Mass due to 1H= 75 ×10100=7.5kg    

1H atoms are replaced by 2H atoms  

Mass due to 2H=7.5 ×2kg  

\    Mass gain by person = 7.5 kg                                                                             Answer (c)

Ex.:- Given that the abundances of isotopes ₅₄Fe, ₅₆Fe and ₅₇Fe are 5% 90% and 5% respectively the atomic mass of Fe is                                                                                                            (2009)  

(a) 55. 85                                                          (b) 55.95

(c) 55.75                                                           (d) 56.05

Solution: From the given relative abundance the average weight of Fe can be calculated as

A= 54 × 5 × 56 × 90 ×57 ×5100=55.95                                                            Answer (b)

If we know percent composition we can find empirical formula

 

An empirical formula represents the simplest whole number ratio of various atoms present in a compound

•  Molecular formula shows the exact number of different types of atoms present in a molecule of a compound.
•  If the mass per cent of various elements present in a compound is known, its empirical formula can be determined.
•  Molecular formula = n x (Empirical formula), where n is a simple number and may have values 1, 2, 3….

Following steps should be followed to determine empirical formula of the compound

5.  Step 1: Conversion of mass per cent of various elements into grams.
5.  Step 2: Convert mass obtained in step1 into number of moles
5.  Step 3: Divide the mole value obtained in step 2 by the smallest mole value (out of the mole value of various elements calculated)
5.  Step 4: In case the ratios are not whole numbers, then they may be converted into whole number by multiplying by the suitable coefficient.
5.  Step 5: Write empirical formula by mentioning the numbers after writing the symbols of respective elements

Example: - In an organic compound contains 37% carbon 50% oxygen and 13% hydrogen what is the empirical formula of compound. If it’s V. D is to find the molecular formula.

Empirical formula CH₄O.

Mol. Wt. = VD x 2 = 32

Emp. formula wt = 32

n = M.W/E.W =1

So molecular formula = CH₄O

LAWS OF CHEMICAL COMBINATIONS

There are 5 basic laws of chemical combinations that govern every reaction: Law of conservation of mass, law of definite proportions, law of multiple proportions, Gay Lussac’s law of gaseous volumes, and lastly, Avogadro law

• Law of Conservation of Mass: Antoine Lavoisier established the Law of Conservation of Mass. It states that matter can neither be created nor destroyed. In other words, we can say that during any physical or chemical change, the total mass of reactants is equal to the total mass of products
• Law of definite proportions: Joseph Proust showed that a given compound always contains exactly the same proportion of elements by weight.
• Law of multiple proportions: Dalton proposed the law of multiple proportions. According to this law if two elements can combine to form more than one compound, the mass of one element that combines with the fixed mass of the other element is in the ratio of small whole numbers.
• Gay Lussac’s Law of gaseous volumes: When gases combine or are produced in a chemical reaction they do so in a simple ratio by volume, provided all the gases are at same temperature and Pressure.
• Avogadro law: At the same temperature and pressure, equal volumes of gases contain equal number of molecules.