Axis of symmetry
- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
PROPERTIES OF SOLIDS
1. Solids have definite mass.
2. Solids have definite Volume
3. Solids have definite shape
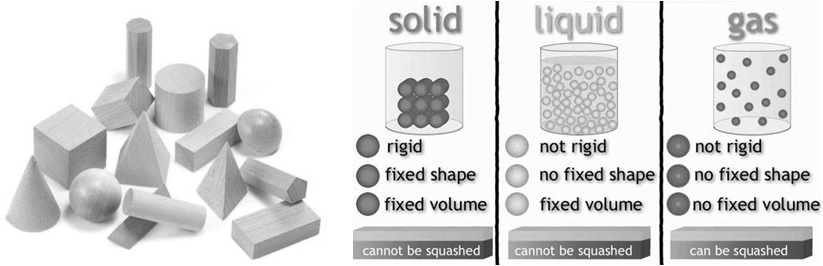
PROPERTIES OF SOLIDS
- Intermolecular distances are short.
- Intermolecular forces are strong.
- Their constituent particles (atoms, molecules or ions) have fixed positions and can only oscillate about their mean positions.
- In general they are incompressible and rigid
Solids are classified as crystalline and amorphous

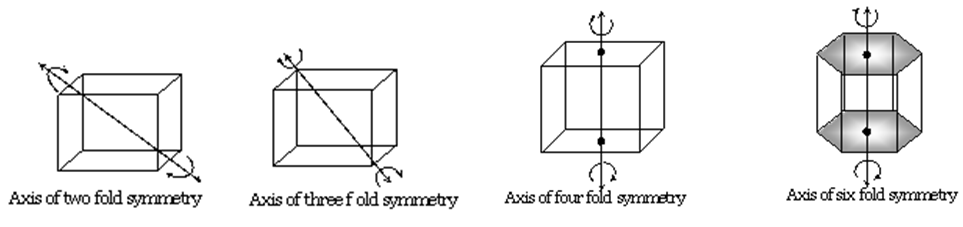
AXIS OF SYMMETRY
- An imaginary axis through which if we rotate the solid then same figure is seen more than once before completing 360o
- For a cube we have
- Two fold symmetry
- Three fold symmetry
- four fold symmetry
Axis of symmetry
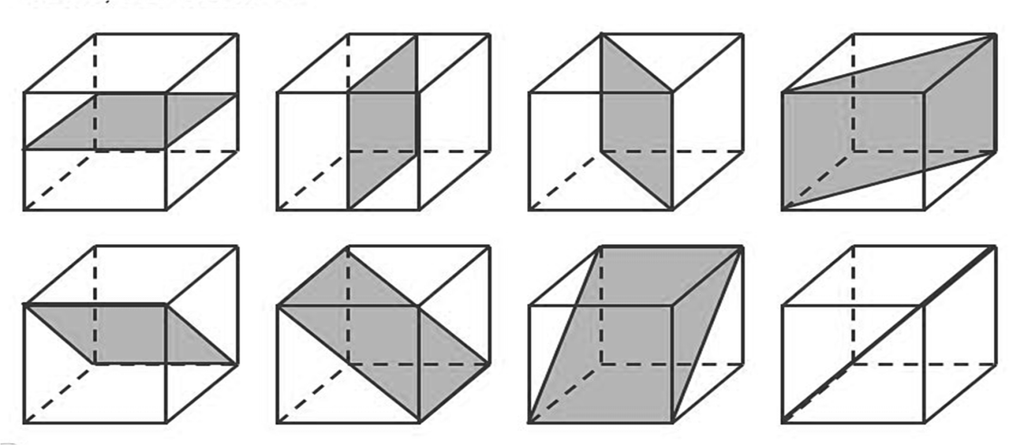
PLANE OF SYMMETRY
An imaginary plane through if we cut the solid the two parts will be mirror image of each other
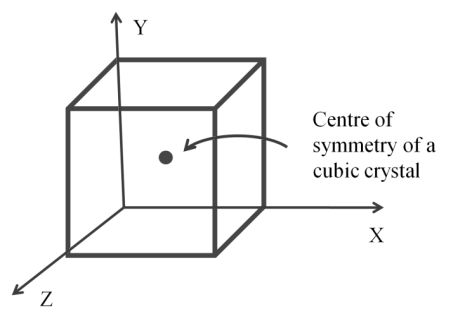
Centre of symmetry
- An imaginary point through if we pass an imaginary line it will touch the opposite plane, edge or vertices at equal distance
PROPERTIES OF SOLIDS
- Cleavage plains: Cleavage is the tendency of a mineral to break along smooth planes parallel to zones of weak bonding. Crystals have cleavage plains where as amorphous solids do not have these plains
- Crystals are called true solids whereas amorphous solids are called pseudo solids or super cooled liquid.
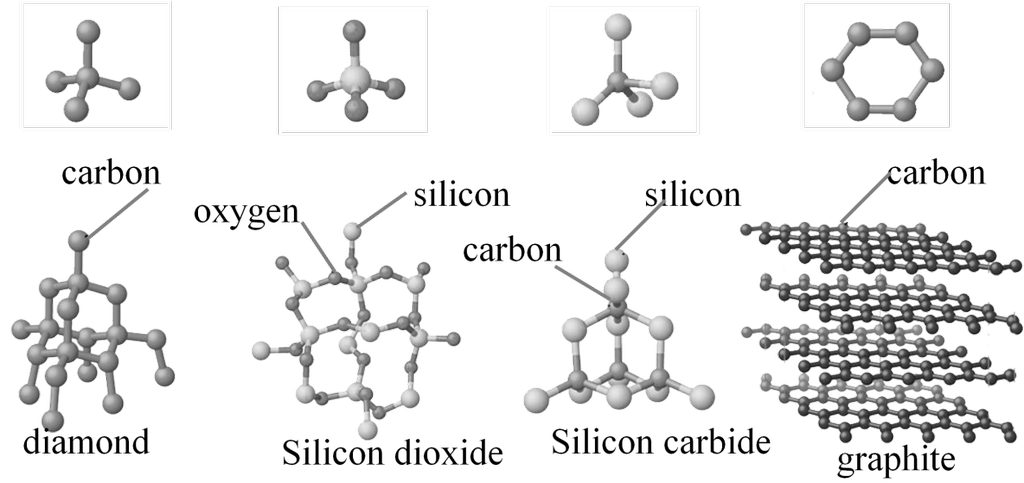
Polymorphic forms or polymorphs: The different crystalline forms of a same substance are known as polymorphic forms or polymorphs. For example: graphite and diamond are polymorph’s of carbon
Crystals classification based on the nature of intermolecular forces
Molecular crystals
They have constituent particles as molecules and are divided into three parts
- Non polar: here the intermolecular forces are weak Vanderwaal's forces (Dispersion or London forces) . They are soft, do not conduct electricity and have very low melting point. Ex: Argon, CCl4
- Polar: here the intermolecular forces are Dipole-dipole interactions. They are soft, do not conduct electricity and have low melting point. Ex: HCl, SO2
- Hydrogen bonding: here the intermolecular forces are Hydrogen bonds. They are hard, do not conduct electricity and have low melting point. Ex: Ice(H2O)
- Ionic crystals: The constituent particles are ions. These have strong columbic intermolecular forces. They are hard but brittle. They do not conduct electricity in solid state but are good conductors on molten and aqueous state. They have very high melting point. Ex: Rock salt (NaCl), MgCl2
- Metallic solid: The constituent particles are positive ions floating in sea delocalized electrons. These have strong metallic intermolecular forces. They are hard but ductile and malleable. They are good conductor of electricity. They have high melting point. Ex: Iron, Copper etc
- Covalent or network solids: The constituent particles are atoms. These have strong covalent bonding. They are hard .They do not conduct electricity. They have very high melting point. Ex: Silica, Diamond etc. Graphite is an exception because it is soft and conducts electricity.

Crystal lattices
- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
CRYSTAL LATTICES
- Lattice: Regular 3-D arrangements of equivalent LATTICE POINTS in space.
- UNIT CELLS
- Smallest repeating internal unit that has the symmetry characteristic of the solid.
- Actual unit cell
- Unit cell as drawn
- Whole crystal
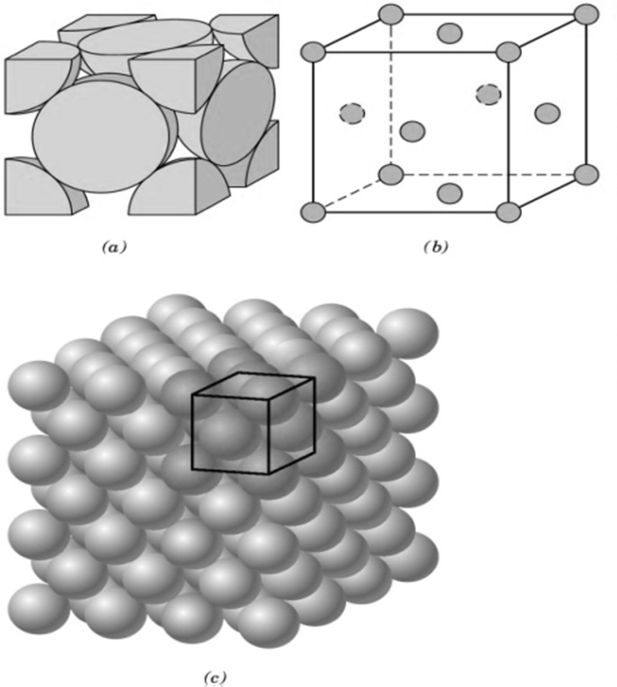
CRYSTAL LATTICE GEOMETRY
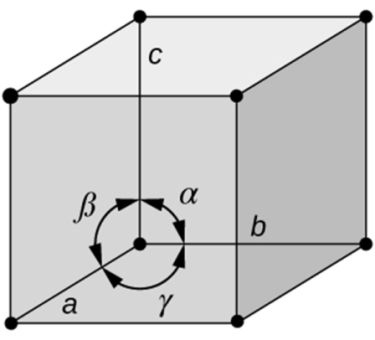
- Based on shape of unit cell ignoring actual atomic locations
- Unit cell = 3-dimensional unit that repeats in space
- Unit cell geometry completely specified by a, b, c (distance in x, y & z axis)& a, b, g (angles between a,b & c (lattice parameters or lattice constants)
- Seven possible combinations of a, b, c & a, b, g, resulting in seven basic crystal systems
14 Bravais Lattices: seven basic lattices and fourteen overall
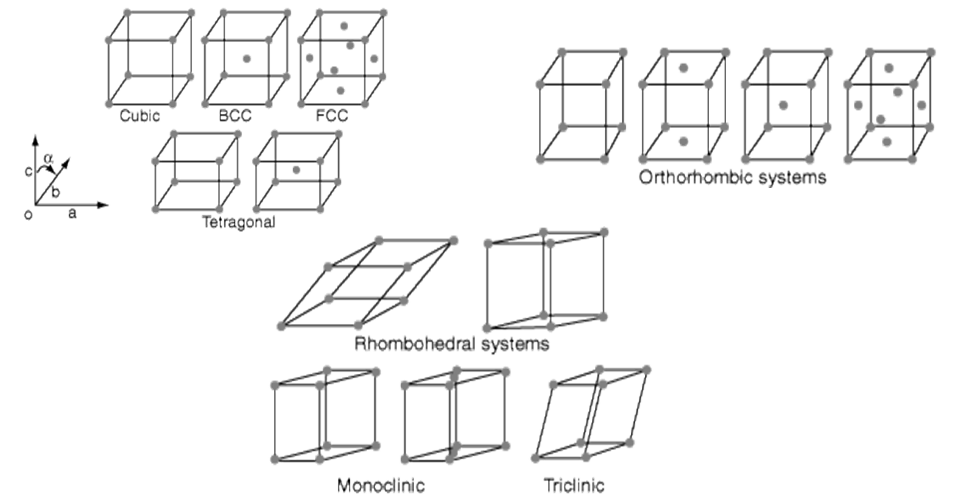
14 Bravais Lattices from seven basic lattices
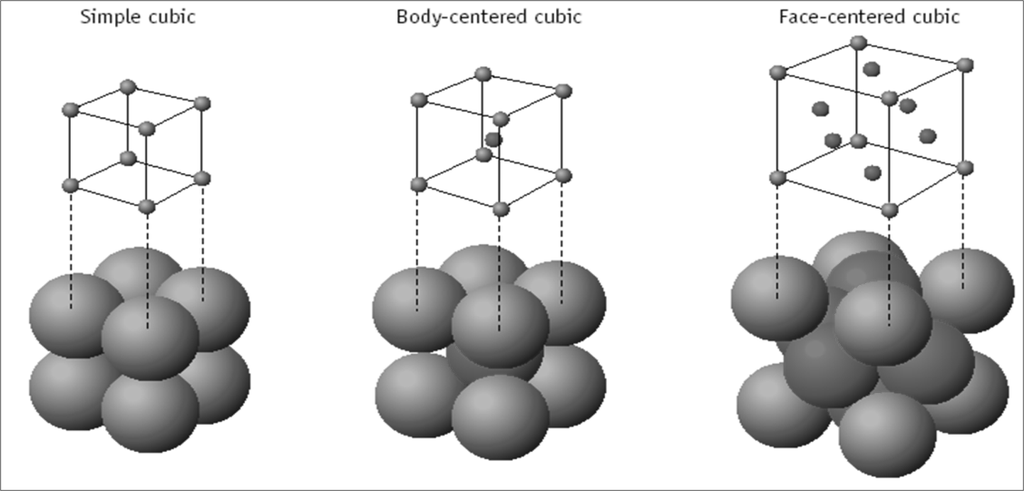
Cubic Unit Cells
There are 7 basic crystal systems, but we are only concerned with CUBIC.
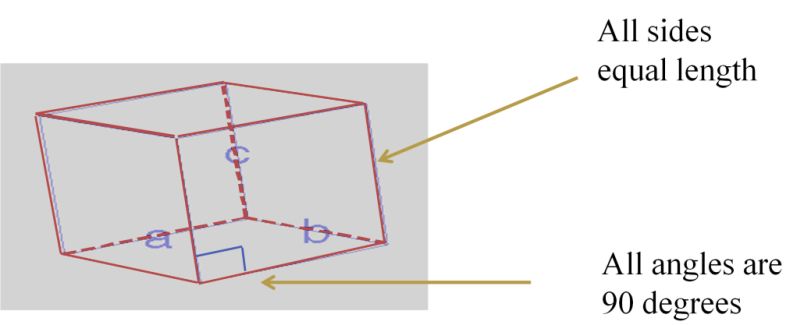
DIFFERENT CUBIC UNIT CELLS
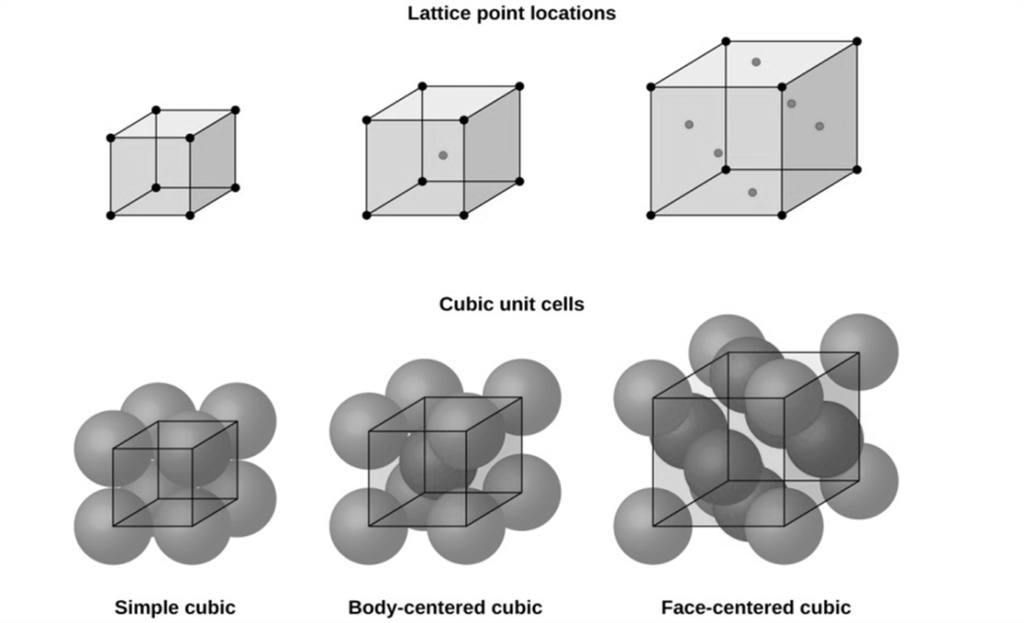
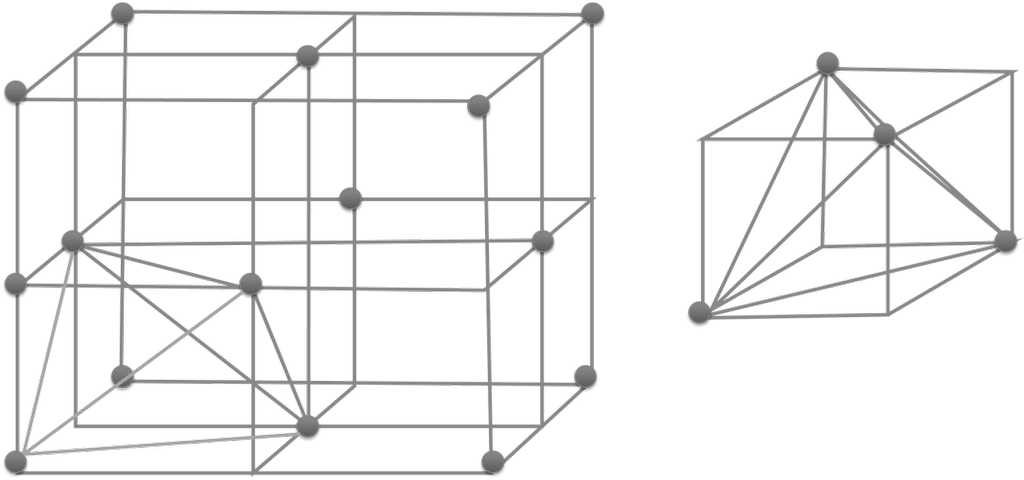
ATOM SHARING AT CUBE FACES AND CORNERS
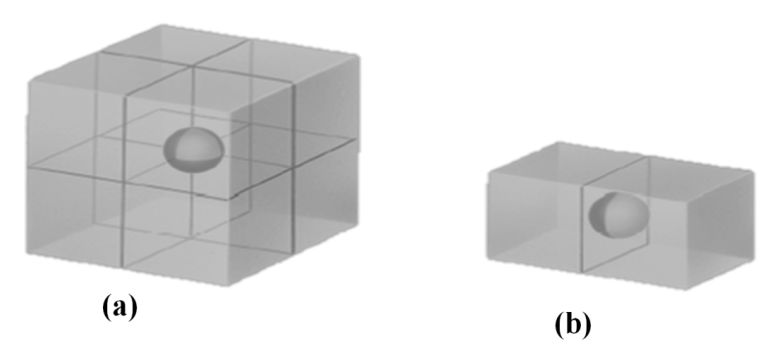
Atom shared in corner
à 1/8 inside each unit cell
Atom shared in face
à ½ inside each unit cell
Atoms shared on edges
à ¼ inside each unit cell
Atoms inside the unit cell
à 1 inside each unit cell
NUMBER OF ATOMS PER UNIT CELL
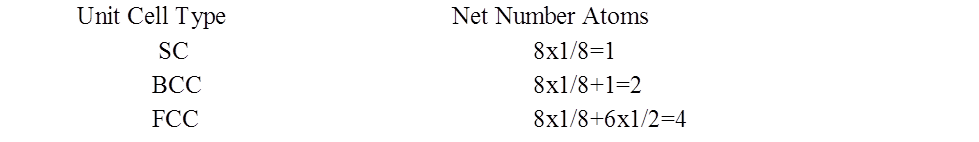
PACKING FRACTION
![]()
![]()
![]()
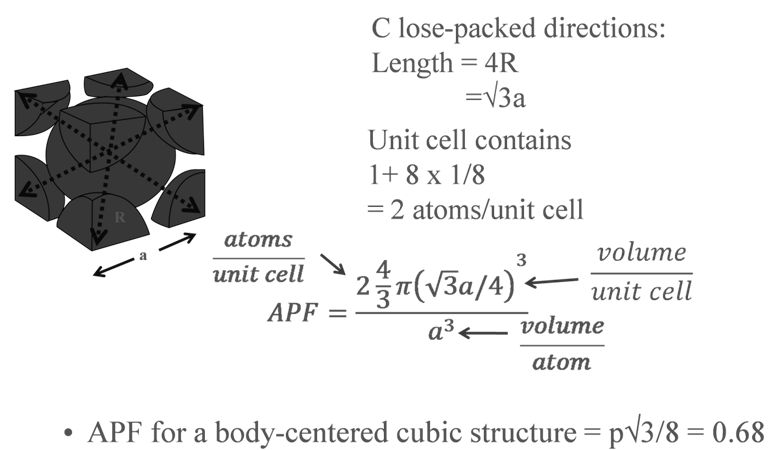
a = edge length of unit cell
R = radius of atoms( assuming they are hard spheres)
Z= no of atoms in one unit cell
PACKING FRACTION: SC

PACKING RACTION: BCC
PACKING FRACTION: FCC

Voids:- gaps between atoms in a crystal are called voids.
- There are two types of voids
- Tetrahedral voids and octahedral voids
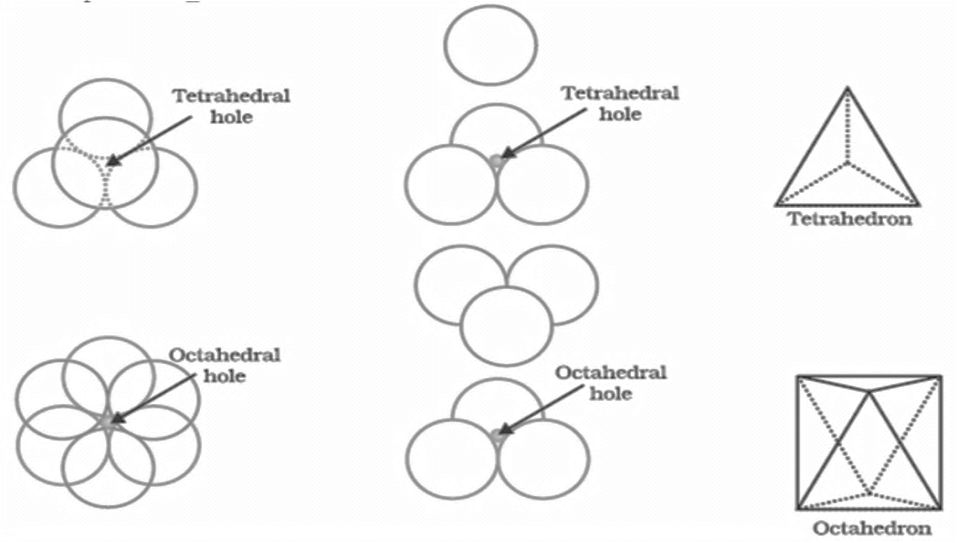
HOW TO LOCATE VOIDS
- No. of tetrahedral voids = 2 x effective atoms/unit cell
- No. of octahedral voids = 1 x effective atoms/unit cell
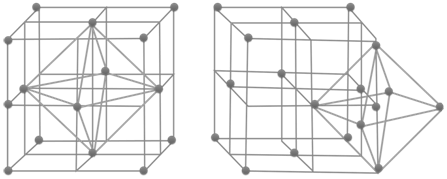
COMPARISON OF CRYSTAL STRUCTURES
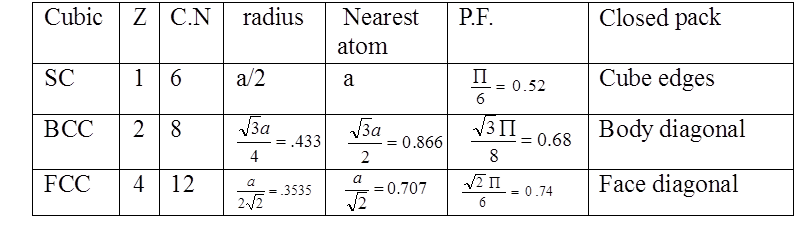
Theoretical density
- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
THEORETICAL DENSITY, r
![]()
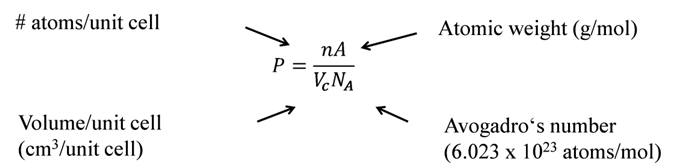
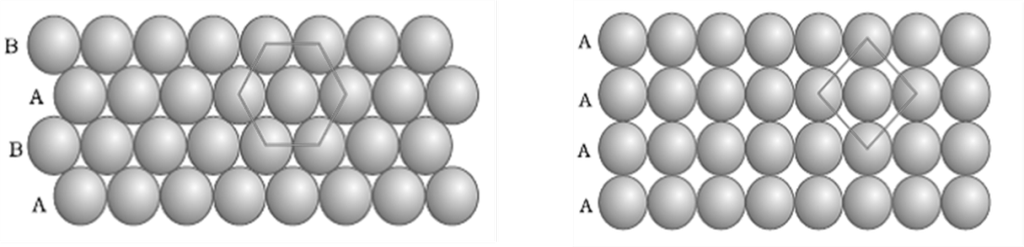
CLOSE PACKED CRYSTALS
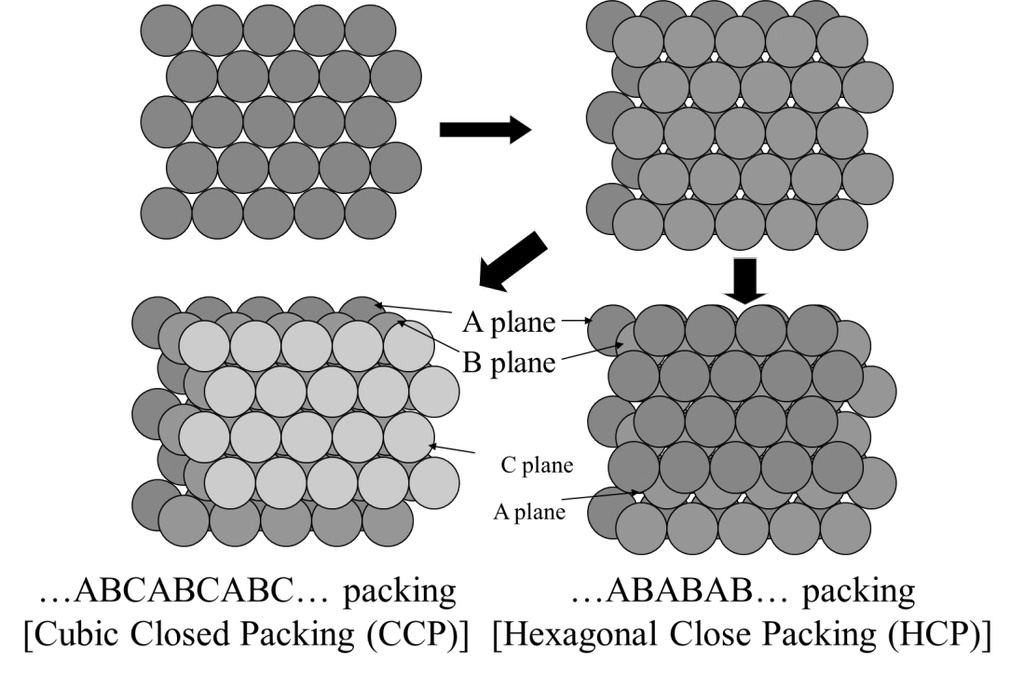
IONIC CRYSTALS
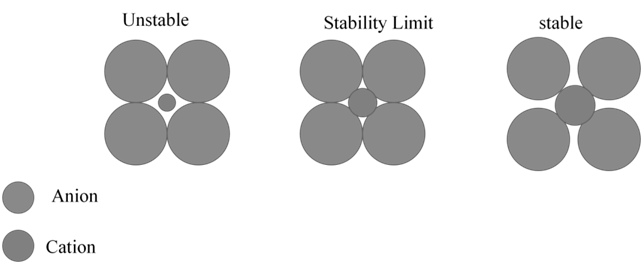
COORDINATION NO 3
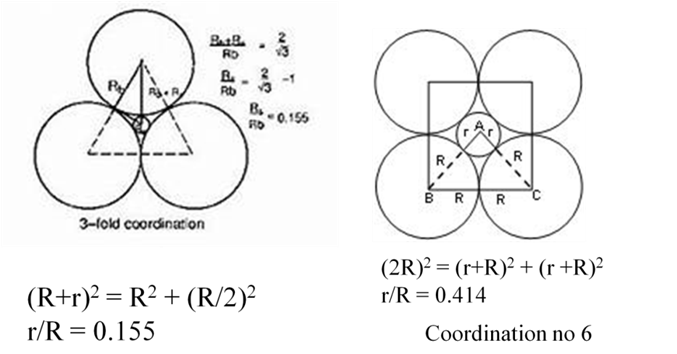
IONIC CRYSTALS

SIMPLE IONIC COMPOUNDS
Two Views of CsCl Unit Cell
Either arrangement leads to formula of 1 Cs+ and 1 Cl- per unit cell
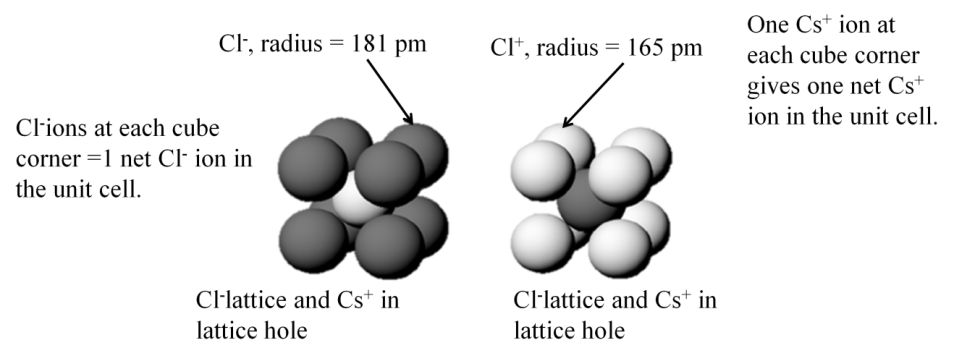
NaCl CONSTRUCTION
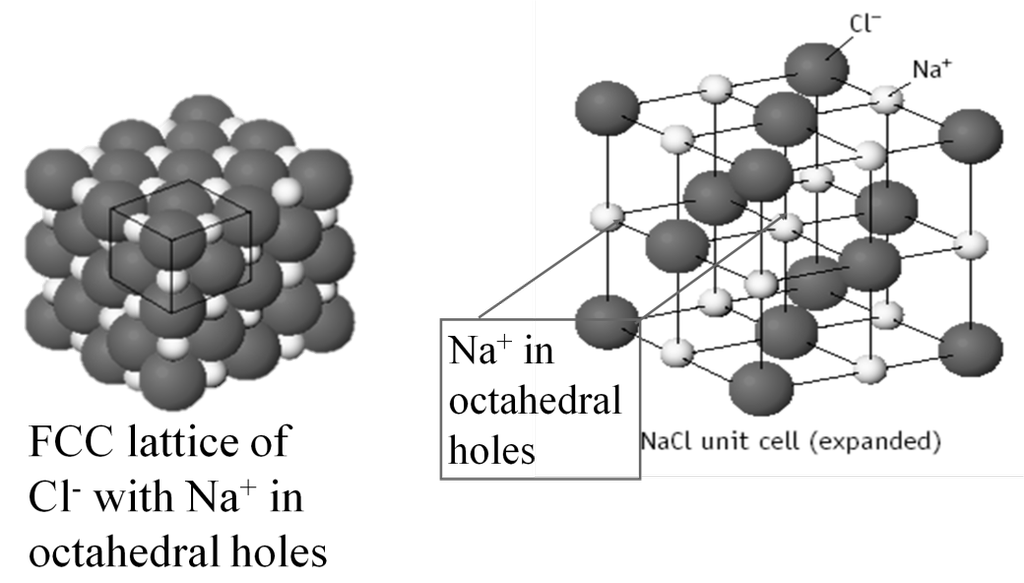
THE SODIUM CHLORIDE LATTICE
Many common salts have FCC arrangements of anions with cations in OCTAHEDRAL HOLES — e.g., salts such as NaCl
• FCC lattice of anions ----> 4 A-/unit cell
• C+ in octahedral holes ---> 1 C+ at center
+ [12 edges • 1/4 C+ per edge]
= 4 C+ per unit cell
Formula Na4Cl4 = NaCl
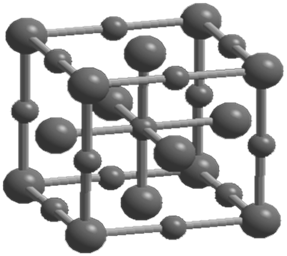
NETWORK SOLIDS
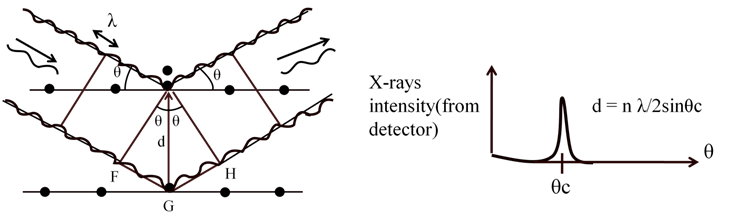
BRAGG’S LAW
• Incoming X-rays diffract from crystal planes Braggs law Þ nl = 2dsin(q)
FUN FACTS ABOUT BRAG’ LAW
Sir William Lawrence Bragg was an Australian-born British physicist who discovered (1912) Bragg's law of X-ray diffraction. He was joint winner (with his father, William Henry Bragg) of the Nobel Prize in Physics in 1915 Bragg was knighted in 1941.
As of 2018, he is the youngest ever Nobel laureate in physics, having received the award at the age of 25 years.[4
Bragg was the director of the Cavendish Laboratory, Cambridge, when the discovery of the structure of DNA was reported by James D. Watson and Francis Crick in February 1953.
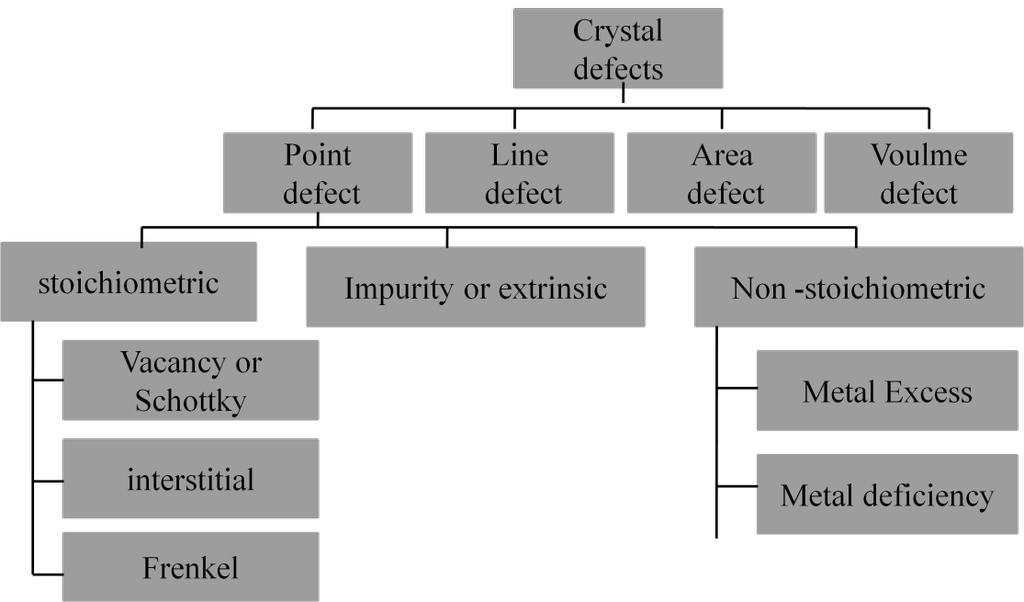
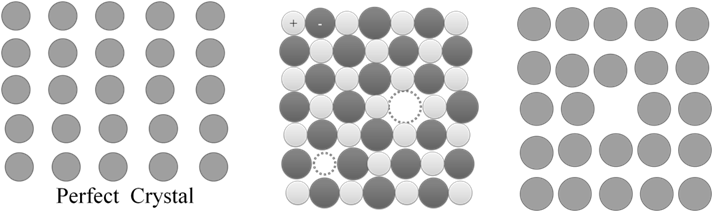
Stoichiometric defects are point defects that do not disturb or change the Stoichiometry (Stoichiometric composition or formula) of the crystalline substance. They are also called intrinsic or thermodynamic defects.
-
- Vacancy defects or Schottky Defect
Vacancy defects or Schottky Defect
-
-
-
- Some of the lattice sites of the crystal are vacant.
- This defect decreases the density of the crystal.
- This defect can be developed by heating the substance. Due to irradiation or sputtering effect. Due to presence of residual tensile stress within the solid.
- Vacancy defect for ionic crystals is called Schottky defect. Here equal no of cations and anions are missing so the stoichiometry of salt does not change
-
-
Interstitial defects
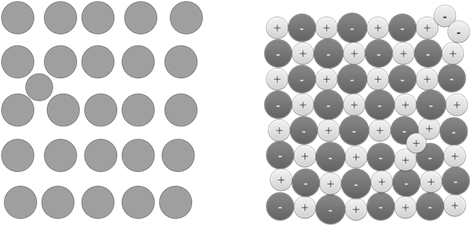
Interstitial defects: -
-
-
-
- Some constituent particles occupy the interstitial sites of the crystal.
- This defect increases the density of the crystal
- In case of ionic solids equal no of cations and anions are added
-
-
Frenkel Defect: -
(i) The ion (smaller ion, usually cation) is dislocated (moved) from its normal lattice site to an interstitial site. So it is also called dislocation defect It creates vacancy defect at its normal lattice site and interstitial defect at its new location Condition:
(ii) The difference between the size of the ions (cation and anion) should be larger. Examples: ZnS ,AgCl, AgBr, and AgI due to small size of Zn2+ and Ag+ ions
(iii) It does not change the density of the crystal
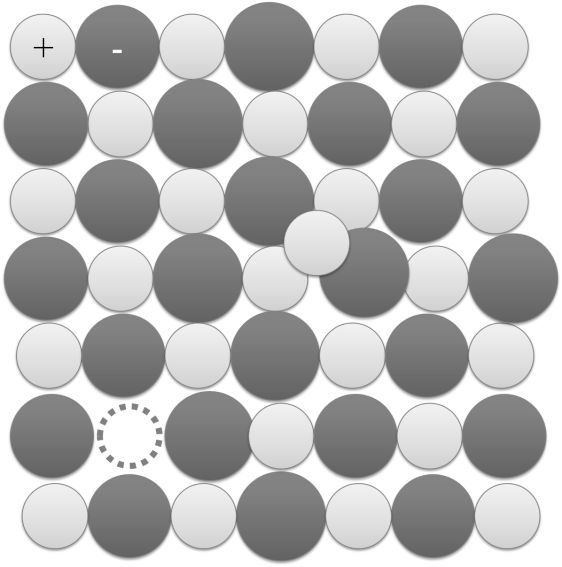
Non Stoichiometric defects are point defects that disturb the Stoichiometry of the crystalline substance
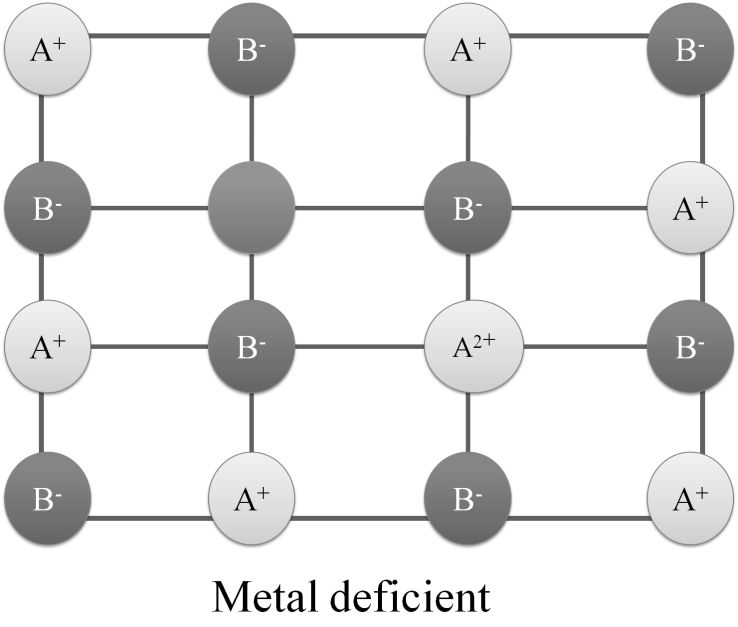
Metal deficiency defect Due to cation vacancies. Eg. In FeO crystal, some Fe2+ cations are missing and extra negative charge is balanced by acquiring extra positive charge by adjacent Fe2+ ion to become Fe3+ ion
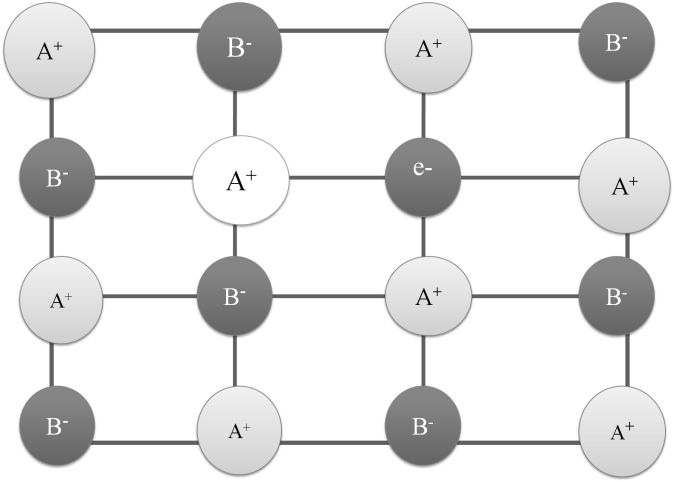
METAL EXCESS OR F-CENTRE
(i) Due to anionic vacancies or F- Centres: The anionic vacancies occupied by unpaired electrons. F-centres impart colour to the crystals (Eg. NaCl to Yellow, KCl to violet) due to excitation of these electrons by absorbing energy from the visible light falling on the crystals
(ii) Due to presence of extra cations interstitial sites, Eg. ZnO
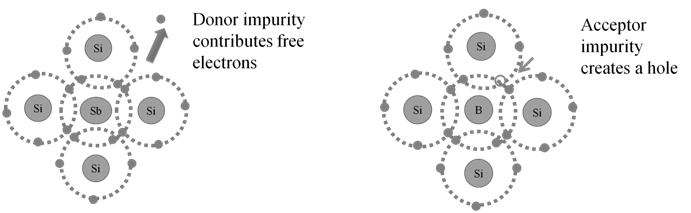
IMPURITY DEFECTS
Impurity defects – Ex- Solid solution of NaCl containing SrCl2 impurity. Solid solution of AgCl and CdCl2
Doping: The process of adding an appropriate amount of suitable impurity to increase the conductivity of semiconductors
Solids can also be classified into three types based on their electrical conductivities:
- a. Conductors-The solids with conductivities ranging between 104 to 107 ohm–1m–1 are called conductors.
- b. Insulators - These are the solids with very low conductivities ranging between 10–20 to 10–10 ohm–1m–1.
- c. Semi- conductors. These are the solids with conductivities in the intermediate range from 10–6-104 ohm–1
ELECTRICAL CONDUCTION
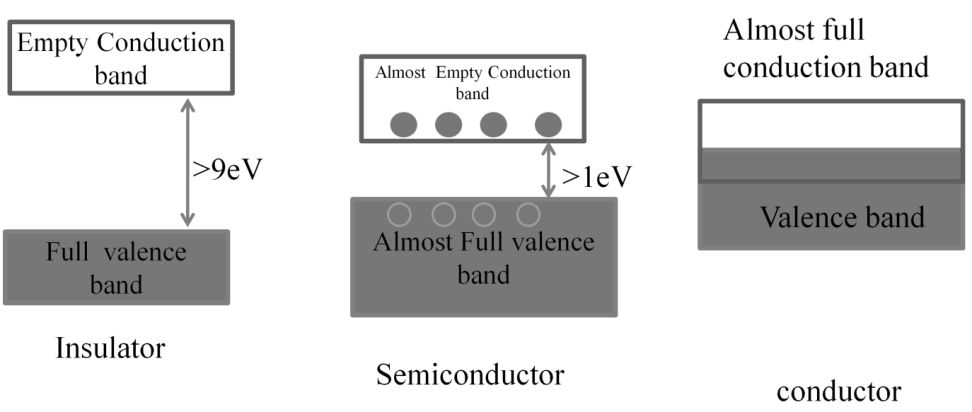
TYPES OF SEMICONDUCTORS:
- a. Intrinsic: These are those semiconductors in which the forbidden gap is small. Only some electrons may jump to conduction band and show some conductivity. They have very low electrical conductivity. Example: Silicon, germanium
- b. Extrinsic: When an appropriate impurity is added (doping) to an intrinsic semiconductor. Their electrical conductivity is high.
Types of extrinsic semi conductors:

MAGNETIC PROPERTIES

- Piezoelectricity:- When polar crystal is subjected to mechanical stress, electricity is produced. E.g. BaTiO3, Rochelle salt
- Pyroelectricity:- When polar crystal is subjected to heat stress, electricity is produced. E.g. PbZrO3
IMPORTANT FORMULAE
- Elements of symmetry in simple cubic crystals
- Plane of symmetry = 3 + 6 =9
- Axis of symmetry = 3 + 4 + 6 =13
- Center of symmetry = 1
- Total elements of symmetry = 9 + 13 + 1= 23
- Density of lattice matter=
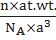 n is number of atoms per unit cell and ‘a’ is the unit cell edge length
n is number of atoms per unit cell and ‘a’ is the unit cell edge length - Braggs law: 2dsinq = nl
- Atoms per unit cell(n) = Nc + NF/2 + NE/4+ NV/8
- No. of tetrahedral voids = 2 x n
- No of octahedral voids = n
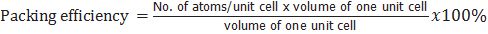

 Kaysons Publication
Kaysons Publication
