1. Polygons and its types
- Books Name
- class 8 th Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 8
- Subject
- Mathmatics
Understanding Quadrilaterals
Polygons and its types
Nature of polygon,
Line and Line segments: A line segment is the shortest distance between two points. The line segment joining points A and B denoted by AB¯¯¯¯¯.

A line can be obtained from a line segment like AB←→ is extended on both sides indefinitely.
Polygon is made up of line segments. Triangle is the smallest polygon made up of three line segments, a quadrilateral is a polygon made up of four line segments, a pentagon is made up of five line segments and so on.
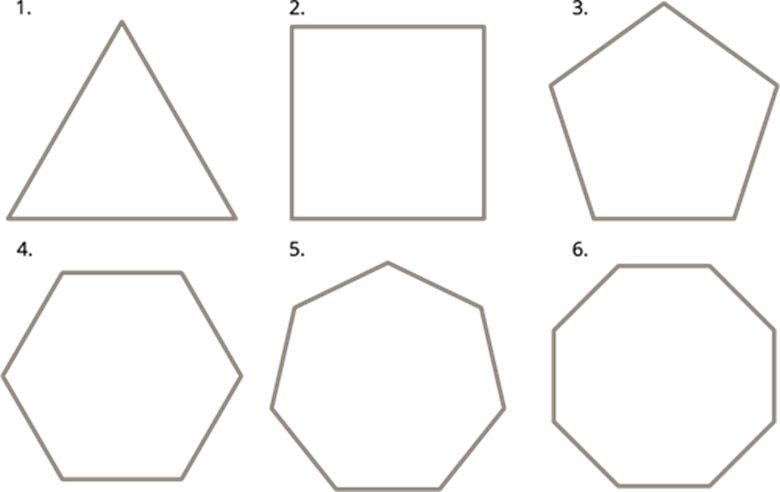
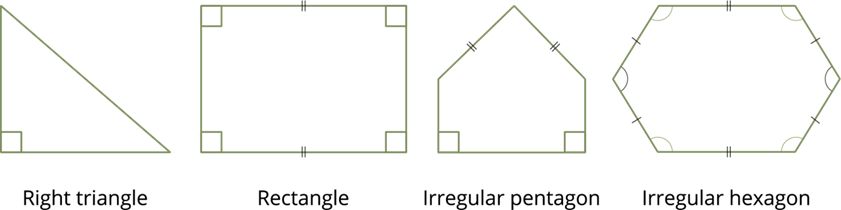
all six figures are polygons.
Classification of polygon
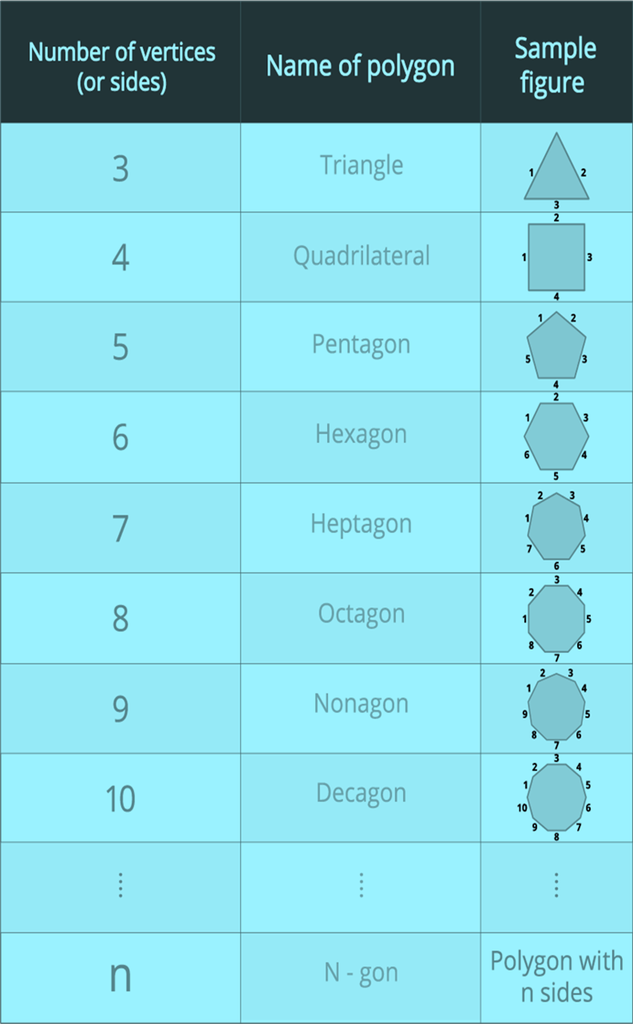
Polygons are classified according to the number of sides (or vertices) as follows:
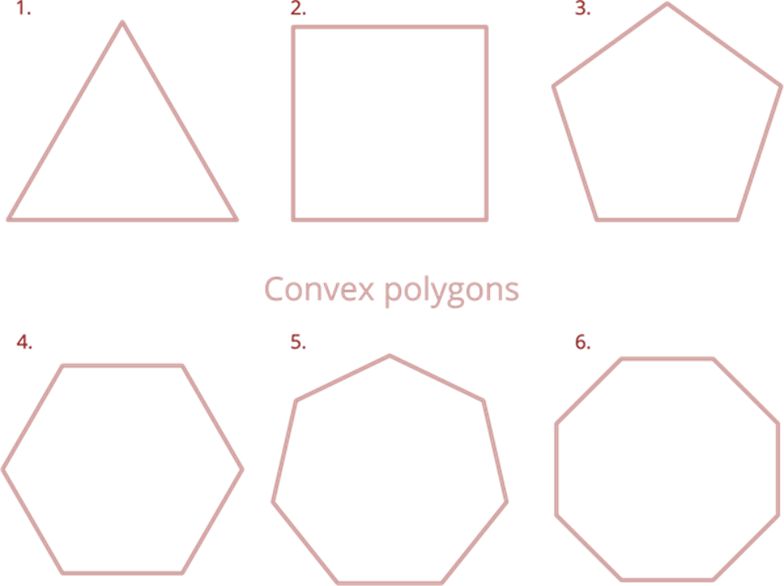
Concave and convex polygon: If each of the interior angles of a polygon is less than 180°, then it is called a convex polygon. If at least one angle of a polygon is more than 180°, then it is called a concave polygon.

each of the interior angles is less than 180°. So they are called convex polygons.
Regular and irregular polygon: A regular polygon is a polygon whose all sides and all angles are equal. Thus, a regular polygon is both equiangular and equilateral.
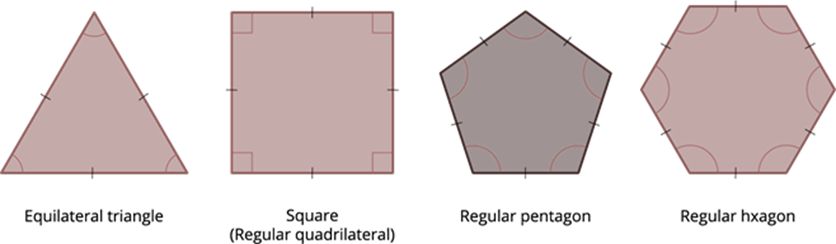
In the above polygons, each of the sides and angles is equal. So they are regular polygons.
If at least one side measures are different and at least one angle measures are different when compared to others. So they are irregular polygons.
Diagonals of a polygon
Adjacent vertices: The end-points of the same side of a polygon are called the adjacent vertices.
Adjacent sides: Sides of a polygon that have a common vertex are called adjacent sides. If the sides of a polygon don't have any common vertex is called non-adjacent sides.
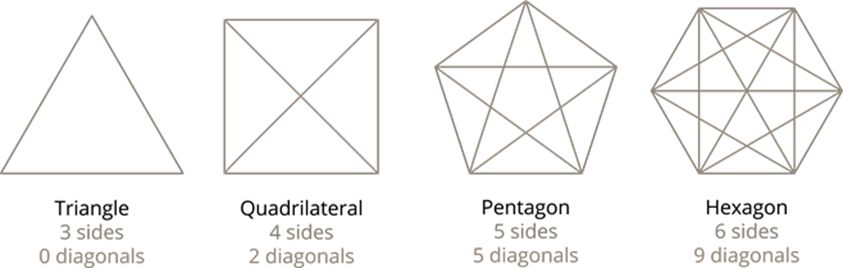
Diagonals: The line segments obtained by joining vertices which are not adjacent are called the diagonals of a polygon.
The number of diagonals of a convex polygon: If there are n-sides in a convex polygon and n>3, then it has ![]() diagonals. A triangle has no diagonals.
diagonals. A triangle has no diagonals.
2. Properties of polygon
- Books Name
- class 8 th Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 8
- Subject
- Mathmatics
Properties of polygon
Interior angle sum property of a quadrilateral
The sum of the measure of three angles of a triangle is 180°.
Proof:
Consider a triangle ABC with interior angles measures ∠1, ∠2 and ∠3.
Draw a line DE parallel to BC.
Now the angle formed by the parallel line DE with the triangle ABC is ∠4 and ∠5.
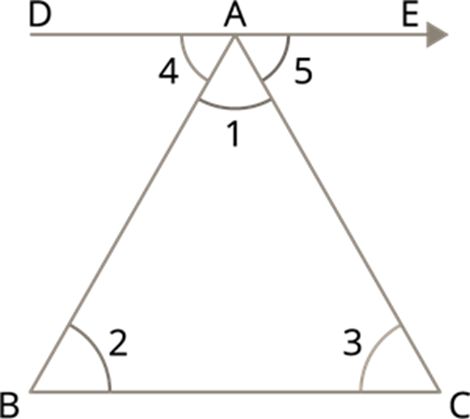
Since DE is parallel to BC, using the alternate interior angle property ∠2 must equal to ∠4. Similarly, ∠3 must be equal to ∠5.
That is ∠2=∠4 and ∠3=∠5. As DE is a straight line, ∠5 and ∠CAD are linear pairs (Pair of adjacent supplementary angles).
∠5+∠CAD=180° .
That is, ∠5+∠1+∠4=180°.
Equivalently, ∠1+∠2+∠3=180°.
It states that the total measures of the three angles of a triangle is 180°.
Interior angle sum property of polygons
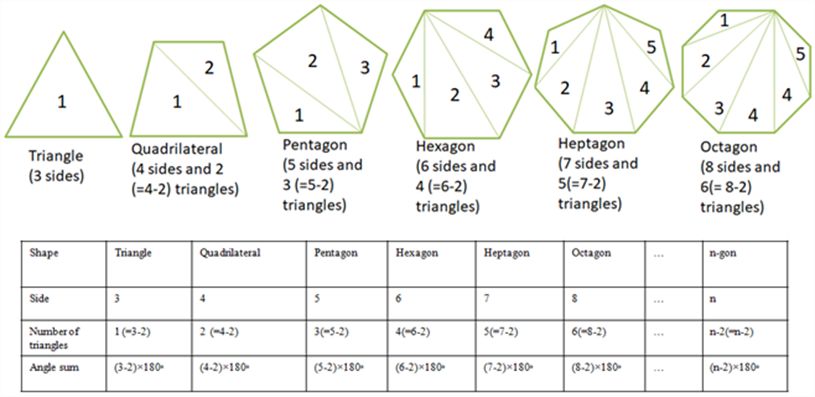
Exterior angle property of the polygons
If the side of a polygon is extended, the angle formed outside the polygon is the exterior angle.
The sum of all the exterior angles of a polygon is 360°.
Geometrical approach:
When all of the angles of a convex polygon converge or pushed together, they form one angle called one complete turn (Perigon angle), which measures 360 degrees.
If the sides of the convex polygon are increased or decreased, the sum of all of the exterior angles is still 360 degrees. More sides can be added to the polygon and they will still form 360°.
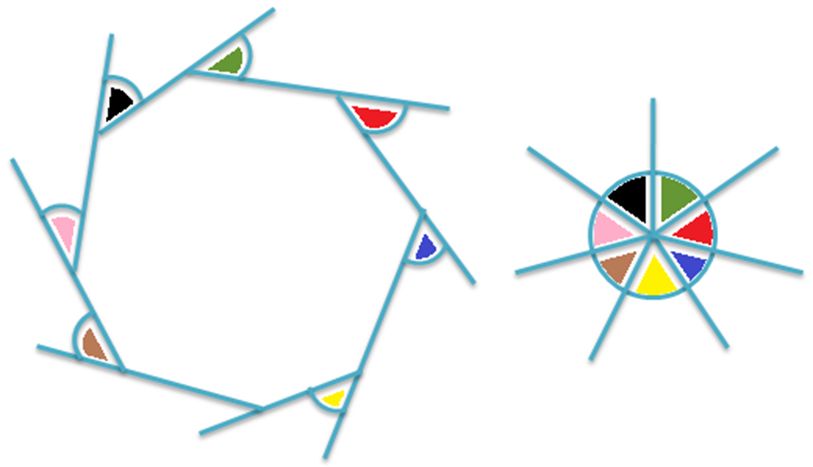
Therefore, the number of sides does not change the sum of the exterior angles of a convex polygon
Algebraic approach:
For any polygon, exterior angle + interior adjacent angle =180°
So, if the polygon has n sides, then:
Sum of all exterior angles + Sum of all interior angles =n×180°
So, the sum of all exterior angles =n×180° − Sum of all interior angles
Sum of all exterior angles =n×180°−(n−2)×180°
= n×180° −n×180° +2×180°
= 180°n −180°n +360°
=360°
Therefore, we conclude that the sum of all the exterior angles of the polygon having n sides = 360°.
- The sum of measures of all the exterior angles of a polygon is 360°.
- Each exterior angle of a regular polygon is 360°n, where n is the number of sides.
- The number of sides of a regular polygon n=360°eachexteriorangle.
- The sum of all the exterior angles formed by producing the sides of a convex polygon in the same order is equal to four right angles (4×90°=360°).
3. Properties of Parallelogram
- Books Name
- class 8 th Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 8
- Subject
- Mathmatics
Parallelogram and its elements, Properties of parallelogram
Parallelogram and its elements
A parallelogram is a quadrilateral whose opposite sides are parallel and equal.
Elements of parallelogram: Parallelogram is made up of four sides and four angles. There are some terms we usually use to denote parallelogram.
They are:
- Opposite sides
- Opposite angles
- Adjacent sides and
- Adjacent angles.
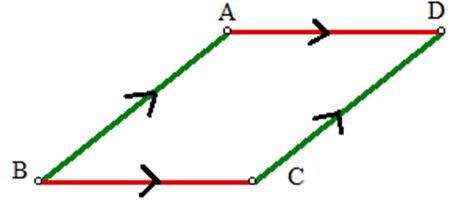
Let's see the elements of the parallelogram ABCD.
- The side AB is opposite to the side CD and the side AD is opposite to the side BC. The angle A is opposite to the angle C and the angle B is opposite to the angle D.
- The side AB is adjacent to the side BC because one of the sides starts where the other ends. In here, the side AB ends at the vertex B and the side BC starts from there.
- The angles A and B are adjacent angles as they are at the ends of the same side AB.
Properties of parallelogram
In a parallelogram, the following properties are true:
- the opposite sides are equal in length.
- the opposite angles are equal in measure.
- the adjacent angles are supplementary.
- the diagonals bisect each other.
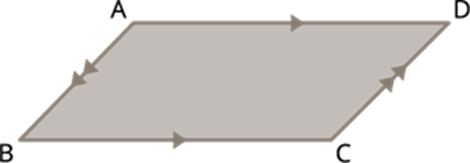
4. Special types of parallelogram
- Books Name
- class 8 th Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 8
- Subject
- Mathmatics
Special types of parallelogram
- Concept of trapezium
A quadrilateral with one pair of parallel side is called trapezium.
A trapezium is isosceles trapezium, if its non-parallel sides are equal.
In a trapezium, the following properties are true:
- The sum of all the four angles of the trapezium is equal to 360°.
- A trapezium has 4 unequal sides.
- A trapezium has two parallel sides and two non-parallel sides.
- The diagonals of trapezium bisect each other.
- The length of the mid-segment is equal to 12 the sum of the parallel bases, in a trapezium.
- Sum of adjacent angles on non-parallel sides of trapezium is 180°.
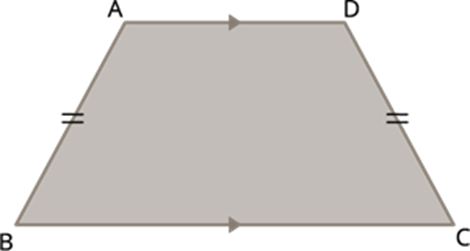
a quadrilateral ABCD is an isosceles trapezium, if AD||BC and AB=CD.
A quadrilateral is a parallelogram if its both pairs of opposite sides are parallel.
- Concept of kite
A quadrilateral with two pairs of equal adjacent sides and unequal opposite sides is called a kite.
define a kite ABCD is a quadrilateral having two pairs of equal adjacent sides and unequal opposite sides.
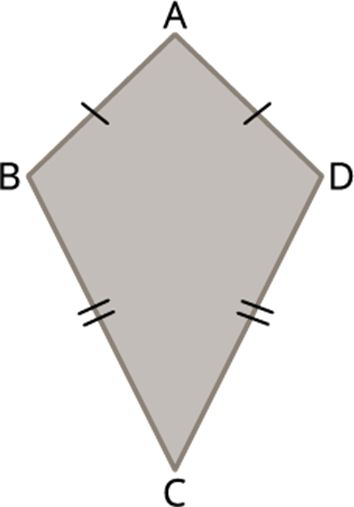
Thus, if ABCD is a kite, then AB=AD and BC=CD.
In a kite, the following properties are true:
- The sum of all the four angles of the kite is equal to 360°.
- A kite has two pairs of equal adjacent sides.
- A kite has unequal opposite sides.
- The diagonals of kite perpendicular bisect of each other.
- One of the diagonals bisects the other diagonal.
- In the figure, ∠B=∠D but \(∠A ≠ ∠C\).
- Concept of rhombus
A parallelogram with all sides are equal is called a rhombus.
Rhombus is a special case of kite. Note that the sides of a rhombus are all of the same length; this is not the case with the kite.
A rhombus has all the properties of a parallelogram and also that of a kite.
In a rhombus, the following properties are true:
- The sum of all the four angles of the rhombus is equal to 360°.
- The opposite sides are equal in length.
- The opposite angles are equal in measure.
- The adjacent angles are supplementary.
- The diagonals are perpendicular bisector of each other.
define a rhombus ABCD as a quadrilateral is a parallelogram with all the sides are in equal measures.
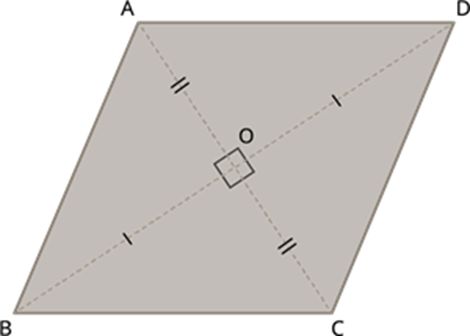
Thus, if ABCD is a rhombus then AB=BC=CD=AD, AB||CD and BC||AD.
- Concept of rectangle
A parallelogram whose each angle is a right angle is called a rectangle.
A rectangle has all the properties of a parallelogram with interior.
In a rectangle, the following properties are true:
- The opposite sides are parallel and equal in length.
- The interior angles of the rectangle is 90°.
- The diagonals are equal in measure and bisect each other.
- The adjacent angles are supplementary.
define a rectangle ABCD as a quadrilateral is a parallelogram whose each interior angle is 90°

Thus, if ABCD is a rectangle then AB=BC=CD=AD and AB||CD and BC||AD.
Important!
- Concept of square
A rectangle is called a square whose adjacent sides are equal.
Rhombus is a special case of kite. Note that the sides of a rhombus are all of the same length; this is not the case with the kite.
A rectangle has all the properties of a parallelogram.
In a square, the following properties are true:
- The opposite sides are parallel.
- All the four sides are in equal measure.
- The interior angles of the square is 90°.
- The diagonals are equal in measure and perpendicular bisector of each other.
- The adjacent angles are supplementary.
define a square ABCD as a quadrilateral is a rectangle whose sides are in the same measure.

Thus, if ABCD is a rectangle then AB=BC=CD=AD and AB||CD and BC||AD.

 ReginaTagebücher
ReginaTagebücher
