Chapter 6: Squares and Square Roots

Square and Square Roots

Square Numbers

Introduction to square and square numbers

The first picture has 1 row and 1 column.

 The second picture has 2 rows and 2 columns.

 The third picture has 3 rows and 3 columns.

 The fourth picture has 4 rows and 4 columns.

 1×1=12=1

 2×2=22=4

 3×3=32=9

 4×4=42=16

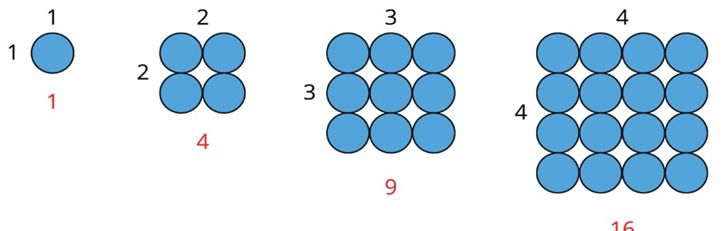
 Here, we multiply the number by itself, and we obtained a square of that number.

 The numbers 1, 4, 9 and 16 are called square numbers.

If a natural number (m) is expressed as a power of 2, then the number (m) is called a square number. That is m=n2. A square number is also called a perfect number.

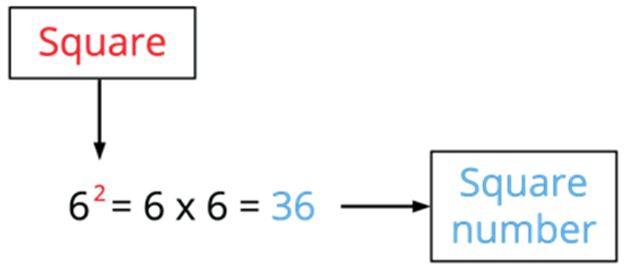
The properties of square numbers

1. The square numbers end in 0, 1, 4, 5, 6 or 9 only.
2. If a number ends with 1 or 9, its square ends with 1.
3. If a number ends with 2 or 8, its square ends with 4.
4. If a number ends with 3 or 7, its square ends with 9.
5. If a number ends with 4 or 6, its square ends with 6.
6. If a number ends with 5 or 0, its square also ends with 5 or 0, respectively.
7. Square of an odd number is always odd, and the square of an even number is always even.
8. Numbers that end with 2, 3, 7 and 8 are not perfect squares.

Zero in the unit's place gets doubled itself if it is squared.

The below table shows the squares of the first 20 numbers:

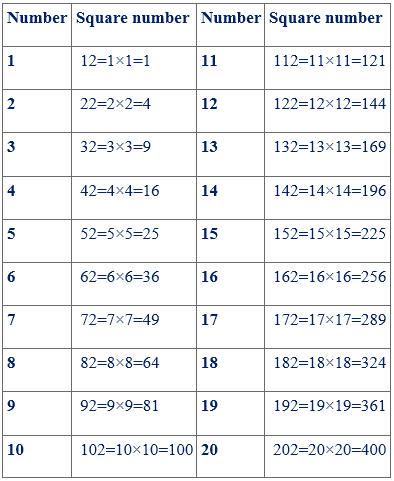
Steps to find out the perfect square

To check whether the given natural number is a perfect square or not, we can follow the below steps:

Step 1. Write the given natural number as a product of prime factors.

Step 2. Now, group the factors in pairs so that both factors in each pair are equal.

Step 3. Now, see whether some factors are leftover or not. If no factor is leftover in grouping, then the given number is a perfect square. Otherwise, it is not a perfect square.

Step 4. Take one factor from each group and multiply them to obtain the number whose square is the given number.

All numbers are not perfect squares. If any number is not a perfect square, we need to multiply or divide the given number by one of the factor(s) to make it a perfect square.

A perfect number cannot be a perfect square number. Perfect numbers such as 6, 28, 496, 8128,... are not square numbers.

Interesting patterns in square numbers

In general, we can say that there are 2n non-perfect square numbers between the squares of the numbers n and (n+1).

The sum of the first n consecutive odd natural numbers is n2.

The square of any odd number can be written as the sum of two consecutive natural numbers.

In general, we can say that (a−1)×(a+1)=a2−1.

Pythagorean triplets

Triplet means a set of three numbers.

A triplet (a,b,c) of three natural numbers is called a Pythagorean triplets if it satisfies a2+b2=c2.

Let us consider any natural a>1.

The triplet (2a,a2−1,a2+1) will form a Pythagorean triplet.

The general formula to find a Pythagorean triplet is (2a)2+(a2−1)2=(a2+1)2, for any natural number a>1.

Example: Find a Pythagorean triplet one of whose least number is 10.

General form of Pythagorean triplet is (2a,a2−1,a2+1).

Least number (2a)=10

a=102

a=5

a2−1=52−1=24

a2+1=52+1=26

The triplet is (10,24,26).

Steps to find the square of decimal numbers

Step 1: Calculate the square of the given decimal number without the decimal.

Step 2: Put the decimal point in the obtained number such that it is twice that of the original number.

Note:

(i) If the original number contains single decimal, then the square of that number will have double decimal.

 Number of decimals in the given number ×2=1×2=2

(ii) If the original number contains double decimal, then the square of that number will have four decimal.

Number of decimals in the given number ×2=2×2=4

Example: Find the square of 2.4.

Step 1: Calculate the square of the given number without decimal.

(242)=24×24=576.

Step 2: Now, put the decimal point in the obtained number such that it is twice that of the original number.

That is, the given number has a single decimal, and the answer would be the double decimal.

2.42=5.76

Therefore the square of a given decimal number is 2.4 = 5.76.

Square of a number using diagonal method

Steps to find the square of a number using the diagonal method:

Step 1: Count the number of digits in the given number.

Step 2: Form a square block with the number of rows and columns equal to the number of digits in the block.

 Step 3: On the top and right sides of the blocks, write the given number.

 Step 4: Divide each square block by diagonals.

 Step 5: Multiply the digits at the top of the column by the digits on the row's right side. Write the product's tens digit above the diagonal and the product's units digit below the corresponding square block's diagonal.

 Step 6: Add the digits diagonally starting from the bottom right.

 Step 7: Finally, write the number starting from the top-left side and ending at the bottom right side. We obtained the square of the given number.

Example: Find the square of 367 using the diagonal method.

Solution:

Step 1: Given number is 367. There are 3 digits in the given number.

Step 2: Now, create a 3×3 square block.

Step 3: Write 367 on the top side and right side of the square block.

Step 4: Divide each square block by diagonals.

Step 5: Place the product value, say, 3×7=21, 2 in the upper part and 1 in the lower part of the square. Similarly, fill all the square blocks.

Step 6: Now, add the digits on the diagonal starting from the bottom right (9).

Step 7: The arrow indicated numbers from left to right is 134689.

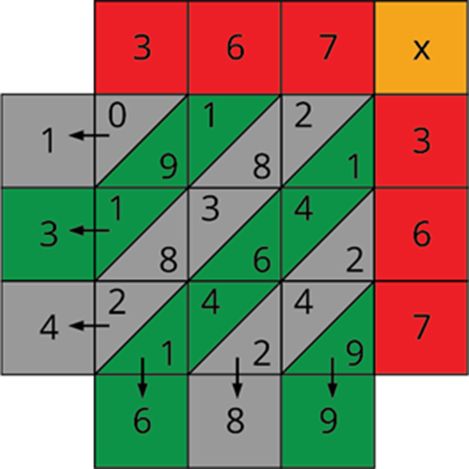
Therefore, the square of the number 367 is 134689.

Square Root

Square root

square root is the inverse operation of squaring.

That is, the square root is the inverse operation of a square.

The square root of a number is represented by the symbol of √.

The square root of a number n can be written as n−−√ (or) n12.

The square of 2 is 4. That is 22=4.

The square root (inverse) of 4 is 2. That is 4–√=2.

Positive root and Negative root

If we square the negative number, we get the positive number as a product.

(−1)2=(−1)×(−1)=1, because  (−)×(−)=+

Example:(−5)2=(−5)×(−5)=25=(5)2

25−−√=−5;     25−−√=5

25−−√=±5

squares and square roots of the first 20 numbers.

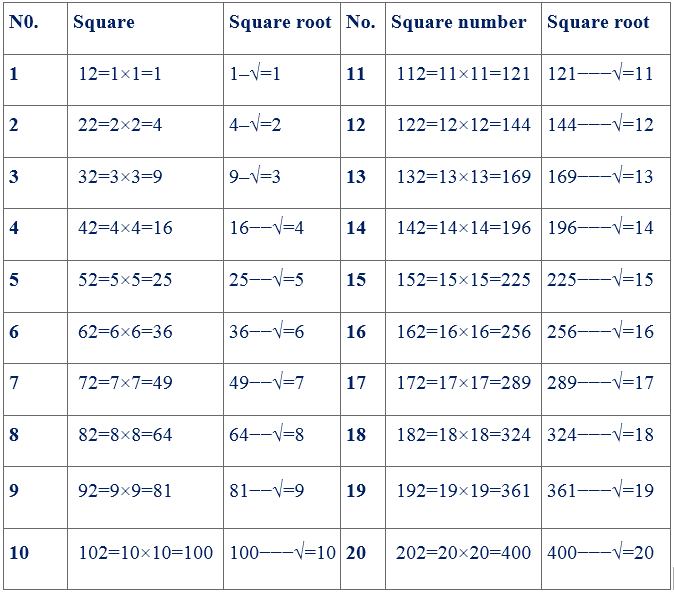
Square root by repeated subtraction of successive odd numbers,

square number can be written as the sum of consecutive odd numbers starting from 1.

We can obtain the square root of a number by repeatedly subtracting the  successive odd numbers (starting from 1) from the given square number till we reach zero.

 At one particular step, we get zero. The step where we get zero is the square root of a given number.

If we did not get zero, the given number is not a perfect square.

Example:

Obtain the square root of 49 by repeated subtraction method.

Solution:

The given number is 49.

We need to find the square root of 49 by the repeated subtraction method.

Subtract the given number by the odd numbers starting from 1 till we get 0.

Step 1: 49−1=48

Step 2: 48−3=45

Step 3: 45−5=40

Step 4: 40−7=33

Step 5: 33−9=24

Step 6: 24−11=13

Step 7:  13−13=0

Here we get zero on the 7th step. That is 49−−√=7.

Therefore, the square root of 49 is 7.

Square root through prime factorisation

Steps to find the square root of a number:

Step 1: Write the given natural number as a product of prime factors.

Step 2: Group the factors in pairs so that both factors in each pair are equal.

Step 3: Now, see whether some factors are leftover or not. If no factor is leftover in grouping, then the given number is a perfect square. Otherwise, it is not a perfect square.

 Step 4: Take one factor from each group and multiply them to obtain the number whose square is the given number.

Example:

Find  √324

Step 1: Write 324 as a product of prime factors. 

324=2×2×3×3×3×3

Step 2: Group the prime factors.

324=(2×2)×(3×3)×(3×3) 

Step 3: Here, no factor is leftover in grouping. 

So, the given number is a perfect square.

Step 4: Now, take one factor commonly from each group.

324−−−√ = 2×3×3

324−−−√ = 18

Therefore, the square root of 324−−−√ is 18.

Finding the square root of a number by long division method

Steps to find the square root using the long division method:

Step 1: Starting with the digit in the unit's position, group the digits in pairs. Each pair and the
remaining digit (if any) is called a period. Starting from the right of the given number, place a bar over each pair of digits. If the number of digits is odd, the extreme left digit may not have a bar sign above it. For example, 2 34¯¯¯¯.

Step 2: Recognise the largest number whose square is equal to or slightly less than the first period. This number should be used as both a divisor and a quotient.

Step 3: Subtract the product of the divisor and the quotient from the first period and bring down the next period to the right of the remainder. This becomes the new dividend.

Step 4: The new divisor is created by multiplying the quotient by two and adding a suitable digit to it, which is also the quotient's next digit. The product of the new divisor and this digit is equal to or less than the new dividend.

Step 5: Repeat steps 2, 3 and 4 till all the periods have been taken up. The final obtained quotient is the square root of the given number.

Example:

Find the square root of 65536.

Solution:

Step 1: Group the digits in pairs and place a bar over each pair of digits. The given number digits is  odd, so the extreme left digit does not have a bar sign above it. That is, 6  55¯¯  36¯¯.

Step 2: The extreme left number here is 6. The largest number whose square is equal to or slightly less than 6 is 2. This number should be used as both a divisor and a quotient.

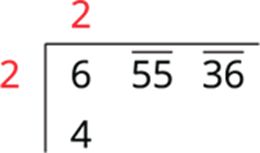
Step 3: Subtract the product of the divisor and the quotient from the first period and bring down the next period to the right of the remainder. That is 255. This becomes the new dividend.

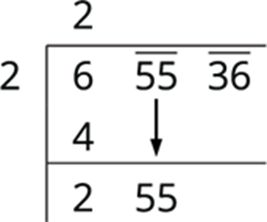
Step 4: Find the new divisor, multiply the earlier quotient (2) by 2 (always) and write it, leaving a blank space next to it.

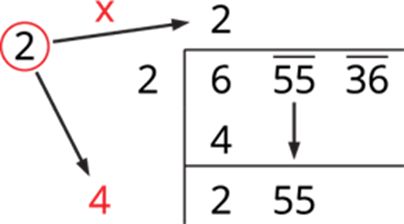
Step 5: The new divisor is 5, followed by a digit. We should choose this digit next to 4 such that the new quotient multiplied by the new divisor will be less than or equal to 255.

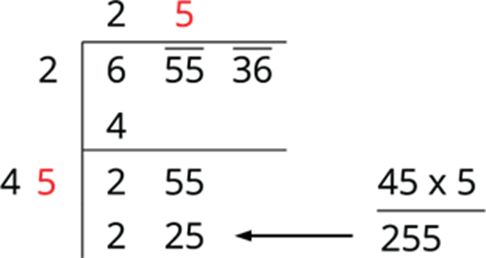
Now, subtract 225 from 255 and bring down the next period to the right of the remainder. That is 3036. This becomes the new dividend.

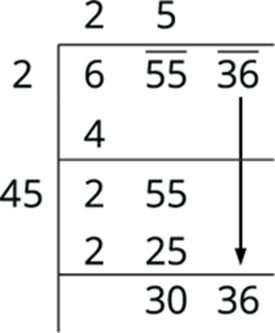
To find the new divisor, multiply the earlier quotient (25) by 2 (always) and write it, leaving a blank space next.

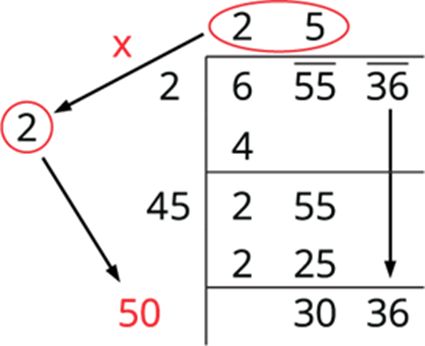
 The new divisor is 50, followed by a digit. The required digit here has to be 6. We put 6 in the blank space and write 3036 below 3036 and subtract to get the remainder 0.

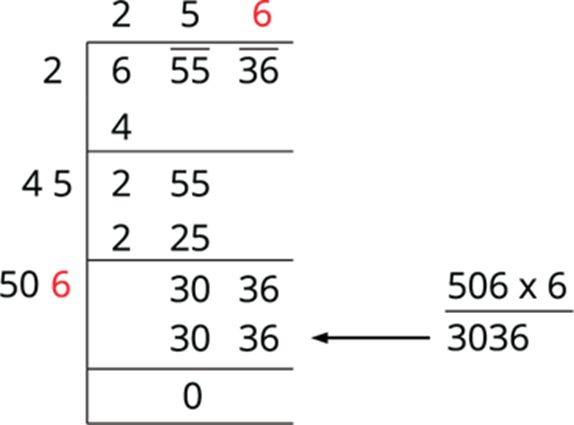
Therefore, √65536  = 256.

Number of digits in the square root of a perfect square number

To find the number of digits in the square root without calculation:

Case I: If n is the number of digits of a number and n is odd:

Number of digits in the square root of the number = n+12

Case II: If n is the number of digits of a number and n is even:

Number of digits in the square root of the number = n2

Example:

1. Find the number of digits in the square root of 196.

Solution:

Number of digits, (n)=3

Since n is odd:

Number of digits in the square root of the number = n+12

= 3+12

= 42

= 2

Therefore, the number of digits in the square root of 196 is 2.

Square root of decimal numbers,

Step 1: Calculate the square root of the given decimal number without the decimal.

Step 2: Put the decimal point in the obtained number such that it is half that of the original number.

 (i) If the original number contains a double decimal, then the square of that number will be a single decimal.

 Number of decimals in the original number2=22=1

 ii) If the original number contains four decimal, then the square of that number will have two decimal.

 Number of decimals in the original number2=42=2

Let's see an example to understand this concept clear.

Example:

Calculate the square root of 1.44.

Solution:

The given number is 1.44.

First, calculate the square root of the given decimal number without the decimal.

We have to write 144 as a product of prime factors.

144=2×2×2×2×3×3

Now, group the prime factors.

144=(2×2)×(2×2)×(3×3)

Here, no factor is leftover in grouping.

Therefore, the given number is a perfect square.

Square root of product and quotient of numbers

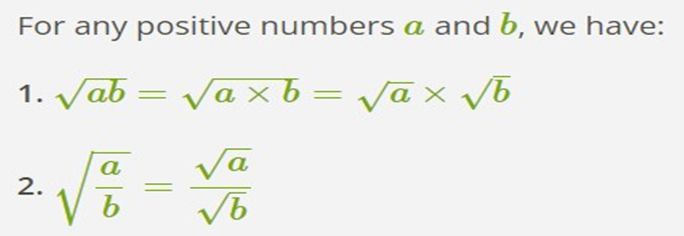
Multiplying identical square root numbers

 Approximating the square roots