1. Trapezium

Mensuration

Trapezium

Recalling trapezium

A trapezium is a quadrilateral with one pair of opposite side parallel.

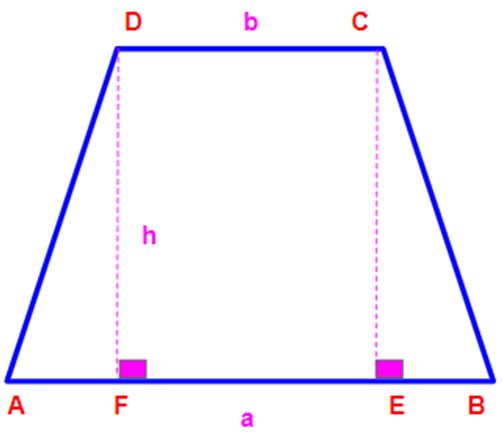
For the trapezium ABCD, the following will be true:

• AB||DC,where AB and DC are parallel sides
• CE⊥AB, where CE is perpendicular to AB
• DF⊥AB, where DF is perpendicular to AB
• CE=DF=h, where h is the height of the trapezium

Area, perimeter of trapezium

Area of trapezium: To obtain the area of a trapezium, multiply the sum of the bases by the height and then divide by 2.

The area of a trapezium is computed with the following formula:

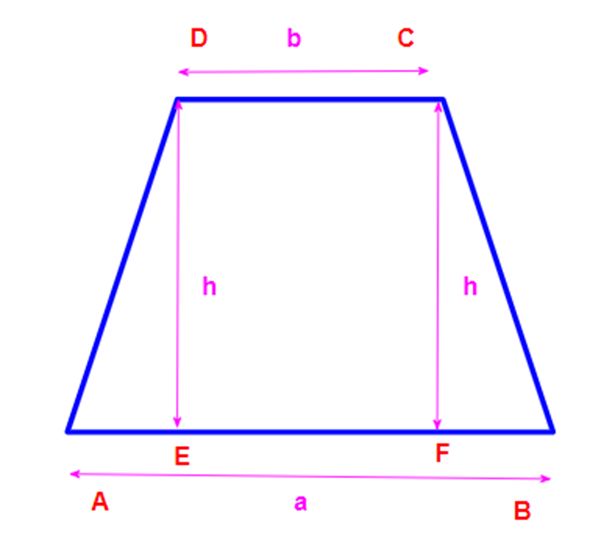
Area of trapezium = 12×(a+b)×(h) square units.

(where a and b is bases (parallel sides) and h is leg or height (between the non-parallel sides)).

Area of the trapezium ABCD:

Proof: Area of a trapezium ABCD.

Area of trapezium ABCD = 12(AB+DC)×(h) squareunits.

= area of triangle (DEA) + area of rectangle (DEFC) + area of triangle (CFB)

= 12×AE×DE + DE×EF + 12×FB×CF

= 12×AE×h + h×EF + 12×FB×h

= 12×(AE+2EF+FB)×h

= 12×(AE+EF+CD+FB)×h

= 12×(AE+EF+FB+CD)×h

= 12×(AB+CD)×(h)

= 12×(a+b)×(h)

= 12×(sum of parallel side) ×(height) square units.

Therefore, Area of trapezium ABCD= 12×(a+b)×(h) or

Perimeter of trapezium: The Perimeter is the sum of all side lengths.

The perimeter of a trapezium is computed with the following formula:

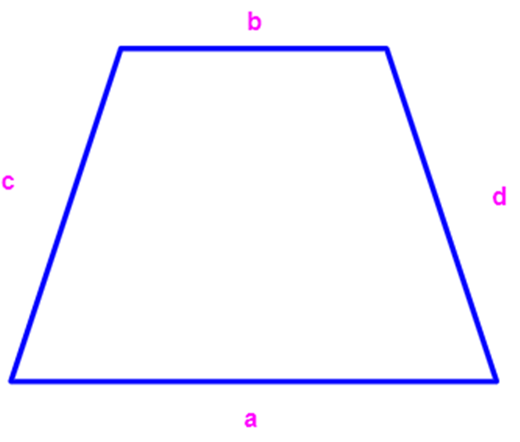
Perimeter of trapezium = a+b+c+d (where a, b are denoted as bases (parallel sides) and c, d are denoted as legs (non-parallel sides)).