1. Direct proportions
- Books Name
- class 8 th Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 8
- Subject
- Mathmatics
Direct and Inverse Proportions
Direct proportions
We consider the task of finish the work in the company by workers:
(i) When more number of workers are involved, the time taken to finish the same work will be less.
(ii) When the number of workers is more, the work done will also be more.
In the first case, the number of workers is compared with the time taken, and in the second case, the number of workers is compared with the amount of work.
The quantities taken for comparison decides the type of variation.
When one quantity varies, that brings a change in other quantity in two ways, that is,
- Both the quantities increase or decrease.
- Increase in one quantity causes a decrease in the other quantity or vice-versa.
If such quantities vary in a constant ratio, they are said to be in proportion.
Two different variations give rise to two types of proportion which is mentioned below.
- Direct proportion
- Inverse proportion
Introduction to proportions
Introduction to direct proportion
As one amount increases, another amount increases at the same rate or as one amount decreases, and another amount decreases at the same rate is known as direct proportional.
The symbol for "directly proportional" is α.
Example:
You are paid ₹30 an hour. How much you earn is direct proportional to how many hours you work.
Work more hours, get more pay; in direct proportion.
This could be written:
Earnings α Hours worked
If you work for 1 hour, you get paid ₹10.
If you work for 4 hours, you get paid ₹40.
If you work for 7 hours, you get paid ₹70.
Direct proportions
If the cost of a watch is ₹700, then the price of 1 watch will be ₹700. The price of the watch increases as the number of watches increases. Proceeding the same way we can find the cost of any number of such watches.
Consider the above situation, when two quantities, namely the number of watches and their prices are related to each other. When the number of watches increases, the price also increases in such a way that their ratio remains constant.
Let us denote the number of the watch as X and the price of the watch as Y rupees. Now observe the following table
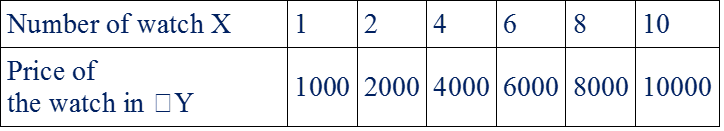
From the table, we can observe that when the values of X increase the corresponding values of ₹Y also increases in such way that the ratio of XY in each case has the same value which is a constant (say k).
Unitary method
- This is one of the methods to find out the values.
- First, the value of one unit will be found. It will be useful to find the value of the required number of units.
Example:
Consider that 4 apples cost ₹100. Then what will be the cost of 10 apples?
To find this first, we have to determine the cost of one apple (price per unit).
Then we can use this single quantity value to find our required quantity.
Therefore the cost of 4 apples =₹100.
Then the cost of 1 apple =₹1004 =₹25.
That is the cost of 10 apples =₹25⋅10 =₹ 250.
2. Inverse proportions
- Books Name
- class 8 th Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 8
- Subject
- Mathmatics
Inverse proportions
Introduction to inverse proportion
Inverse proportion: As one amount increases, another amount decreases at the same rate or as one amount decreases, another amount increases at the same rate is known as inverse proportion.
The symbol for "Inverse proportion" is 1/α
Speed∝1/Time
Therefore speed and time are in inverse proportion.
Inverse proportion
Now, in this condition, are the number of pits, and the number of workers is in direct proportion?
If your answer is NO, that is correct. Because when the number of workers is increasing, the days are decreasing accordingly at the same rate.
Now we say that these quantities are in inverse proportion.
Find out the values of Y2, Y3 and Y4?
Step 1
Let's consider that X1 and Y1 are in 1 series, X2 and X3 are in 2 series and so on.
If X1, X2 and Y1 values are given using these values, we can find out Y2.
Step 2
Similarly to find Y3 value first, you have to make sure that you know the values of X2, X3 and Y2.
If you don't know that you have to find out that unknown value using previous series values.
After that using the 3 variables X2, X3 and Y2, we can find out the value of Y3.
Step 3
Now we know the value of Y3 then using X3, X4 and Y3 values we can calculate the value of Y4.

 ReginaTagebücher
ReginaTagebücher
