- Books Name
- class 8 th Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 8
- Subject
- Mathmatics
Visualising Solid Shapes
Introduction to 3D shapes
3D shapes are three-dimensional solid objects. The three dimensions are length, breadth, and height.
While 2D shapes are flat, the objects of 3D shapes have the depth to them.
Introduction to vertex, edge, face, Face, Edges and vertices of 3D shapes
A corners or vertex (plural: vertices) is a point where two or more line segments meet.
An edge is a line segment that connects one vertex (corner point) to another at the boundary.
A face is any of the solid objects individually flat.
Example:
A cube has 8 corners, 12 edges, 6 faces.
A cube has 6 faces, 12 straight edges, and 8 corners or vertices.
A cone has 2 faces, 1 curved edge, and 1 corner or vertex.
A cylinder has 3 faces, 2 edges, and 0 corner or vertices

A pyramid has 5 faces, 5 vertices or corners and 8 edges.
Nets for making a 3D shapes
A net may be a two-dimensional plan or shape which will be folded to form a three dimensional solid.
Example:
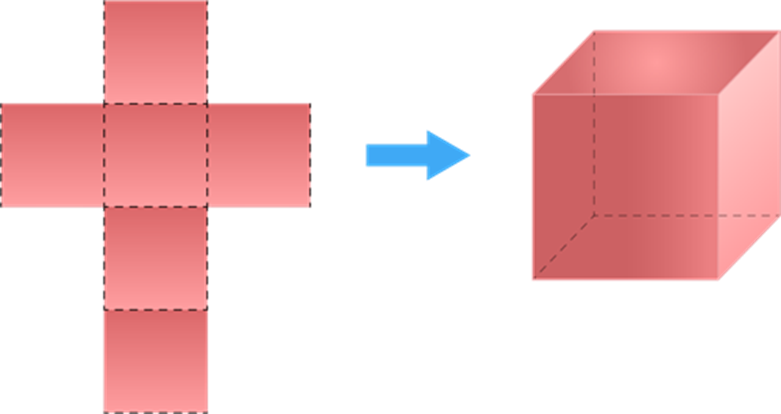
Here come the nets for the 3D shape cube.
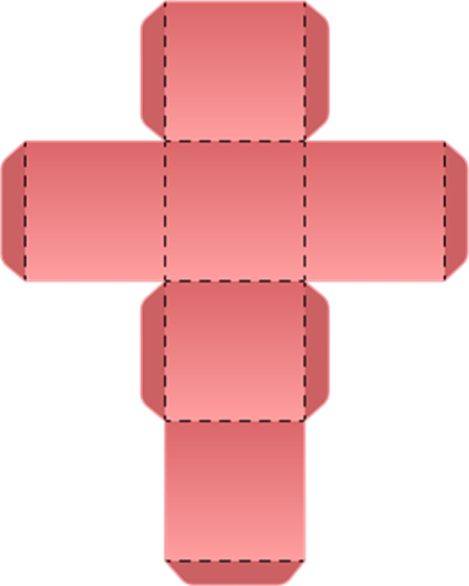
Steps involved to make a 3D shape:
- Cutting out the net below.

- Fold along the dotted lines and use the tabs to glue the solid together.
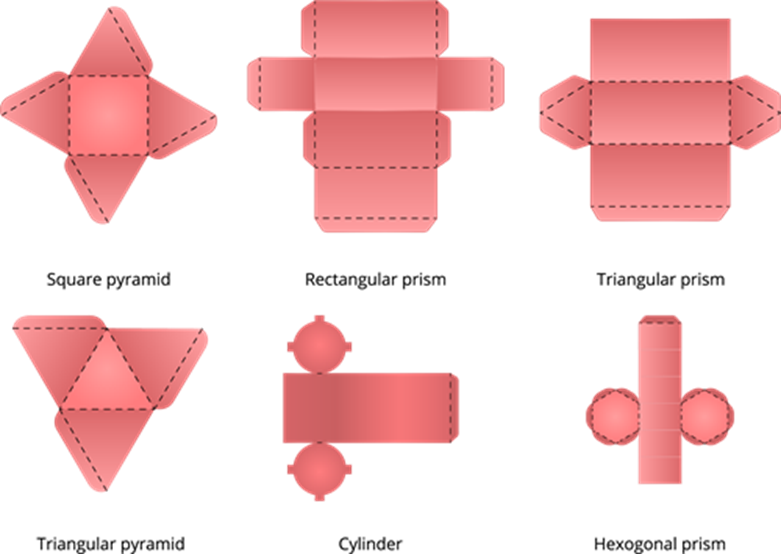
Some of the nets like a square pyramid, rectangular prism, triangular prism, triangular pyramid, cylinder, and hexagonal prism are shown below.
Euler's formula
A polyhedron is a three-dimensional shape with flat polygonal faces, straight edges and sharp vertices. In other words, the 3D solids with flat surfaces are called polyhedrons.

There are two types of polyhedrons.
1. Convex polyhedron
2. Concave polyhedron
A polyhedron whose surface(faces, edges and vertices) does not intersect is referred to as a convex polyhedron.

A polyhedron the surface of which intersects is called a concave polyhedron.

Some special types:
A non-polyhedron is a three-dimensional, curved-faced shape.
A polyhedron is said to be regular if its faces consist of regular polygons and meet on each vertex with the same number of faces.
There are five regular polyhedrons in it:
- A regular polyhedron which is made up of six square is called a cube. It consists of 6 square faces, 12 edges and 8 vertex corners.
- A triangular pyramid, also known as a tetrahedron. It consists of 4 equilateral triangular faces, 6 straight edges, and 4 vertex corners.
- A regular polygon which is made up of eight equilateral triangles is called octahedron. It consists of 8 equilateral triangular faces, 12 edges, and 6 vertex corners.
- A regular polygon which is made up of twelve flat faces of pentagons is called a dodecahedron. It consists of 12 pentagon faces, 30 edges, and 20 vertex corners.
- A regular polygon which is made up of twenty equilateral triangles is called an icosahedron. It consists of 20 equilateral triangular faces, 30 edges, and 12 vertex corners.
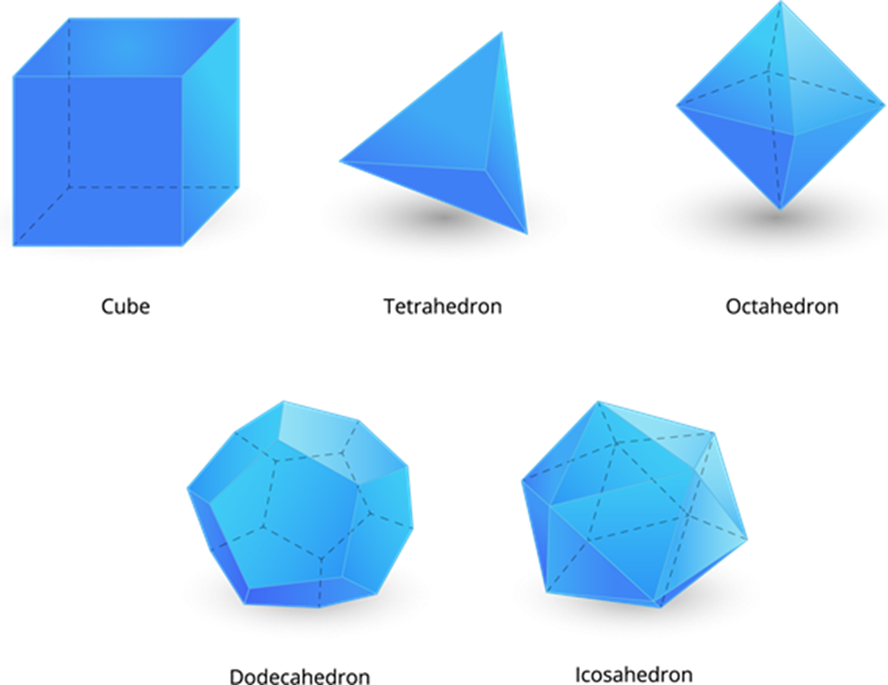
These five convex regular polyhedrons are called platonic solids.
Euler Formula: For any convex polyhedrons, F+V−E=2.
Where 'F' is the number of faces, 'V' the number of vertices and 'E' is the number of edges.
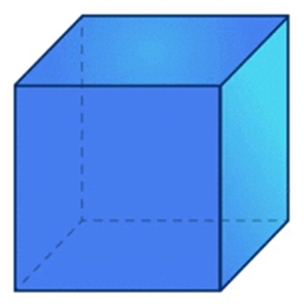
We know that the cube has 6 faces, 8 corners, and 12 edges.
Now, we substitute all the values in the Euler's formula.
F+V−E=26+8−12=214−12=22=2
Important!
1. Sometimes adding an edge between two non-adjacent vertices will not affect Euler formula.
Example: Imagine taking the cube and adding an edge (It means corner to corner of one face) between two non-adjacent vertices.
So we get an additional edge and also an additional face.
In this case, the number of vertices V=8, the number of faces F=6+1 =7, and the number of edges E=12+1 =12.
Euler Formula: F+V−E=2.
Substitute the known values.
7 + 8 − 13 = 2.
15 − 13 = 2
2 = 2
Thus, the Euler formula does not satisfy if the shapes stuck together.
Cross section of 3D shapes
A cross-section may be a shape we get when cutting 3D figures by a plane.
Example:
Cross-section of a cone.
There are two different types of the cross-section.
- Horizontal or parallel cross-section
- Vertical or perpendicular cross-section
Horizontal cross-section: A plane cuts the solid shape in the horizontal direction(parallel to the base).
Vertical cross-section: A plane cuts the solid shape in the vertical direction(perpendicular to the base).
Example: The horizontal cross-section of the cylinder is a circle and the vertical cross-section of the cylinder is a rectangle.
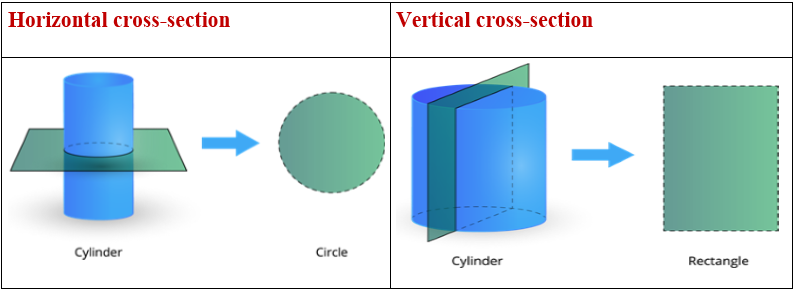
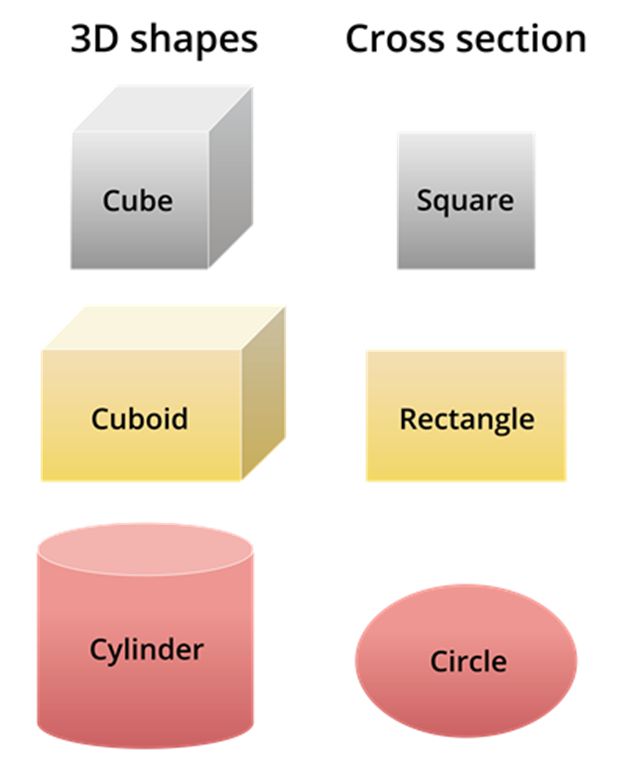
Some of the 3D shapes with its horizontal cross-section are given below.
Side view, top view and front view of 3D shapes,
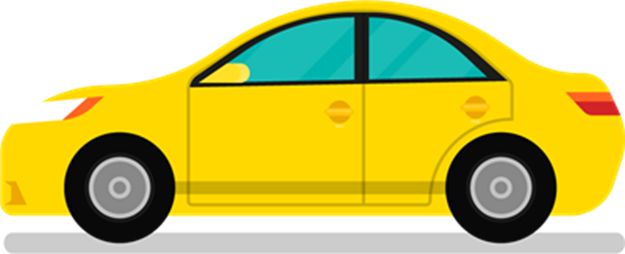
Side View: It is what something seems like when viewed from the side(left or right).
Example: The side view of the car. When you stand the left side or right side of the car, you can see this view.
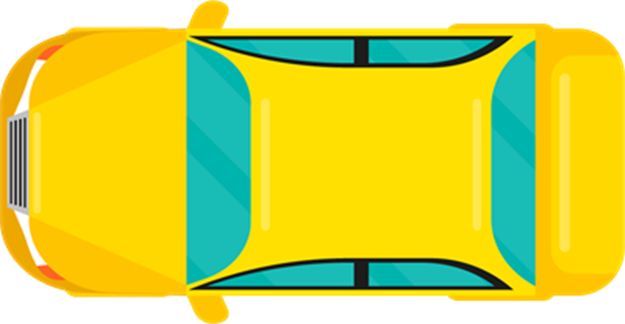
Top view: It is what something seems when viewed from directly above. It's also referred to as a plane view.
Example: The top view of the car. When you stand at the top of your home, you can see this view.
Front view: It is what something seems like when viewed from the front.
Example: The front view of the car. When you stand in front of the car, you can see this view.

Mapping space around us
Have you seen the GPS maps application in the mobile phone?
Here comes the sample GPS map from Anna Centenarylibrary to Marina beach.
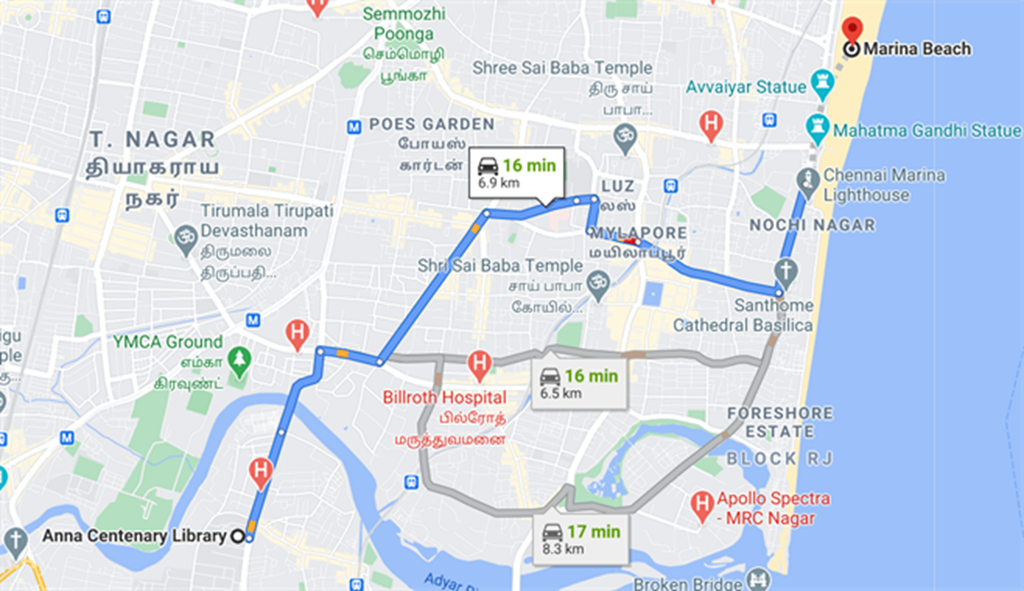
Using the above Google map, we will be able to reach Marina beach from Anna Centenary Library. It shows the route to reach the destination that we want
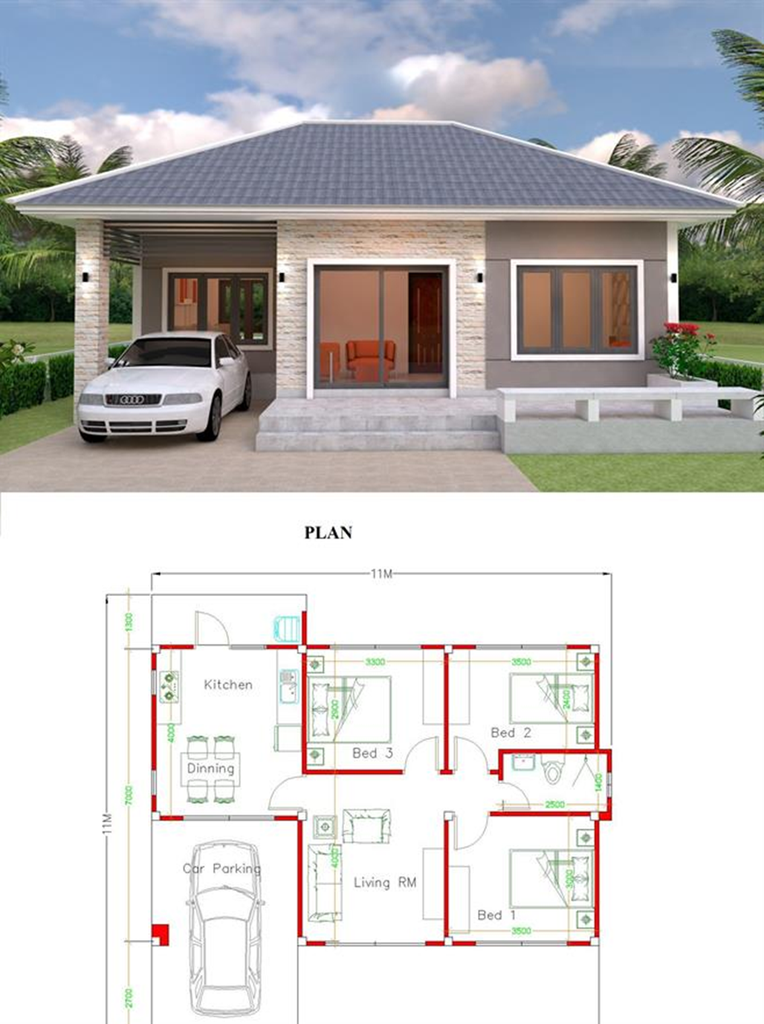
The architecture plan gives us the map of the constructed home. It gives us the way to reach room.

 ReginaTagebücher
ReginaTagebücher
