- Books Name
- class 8 th Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 8
- Subject
- Mathmatics
Factorisation
Introduction to Factorization
Type I-Factorisation by common factor
1. Consider the expression 3x3−15x2+12x.
In all the term, 3x is taken commonly outside.
(3x×x2)+(3x ×−5x)+(3x×4)
=3x(x2−5x+4)
2. Consider the expression 10xy+5x 3y.
Here the term 5xy is common in the expression.
10xy+5x 3y
=(5xy×2+5xy×x2)=5xy(2+x2)
Type II-Factorisation by common binomial factor
Consider (n2+1)(m−n)+(m2+1)(m−n).
Take binomial factor from each term commonly outside.
(n2+1)(m−n) +(m2+1)(m−n)
=(m−n)(n2+1+m2+1)
=(m−n)(n 2+m2+2)
Type III-Factorisation by grouping
Consider the expression 3m2 +mn+3mn+n2.
Let us take the common factor for the first two terms separately and take the common factor second two terms separately.
3m2+mn+3mn+n2
=m(3m+n)+n(3m+n)
=(3m+n)(m+n)
Type IV-Factorisation using identities
Use the following identities to factorise the expressions.
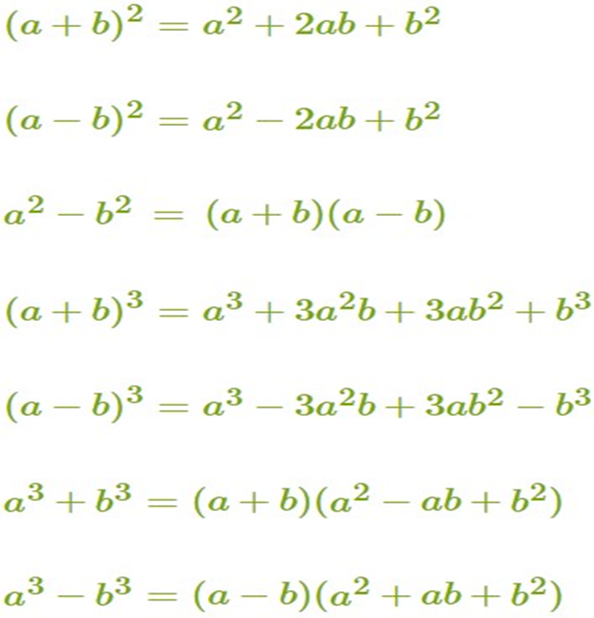
Type V- Factorisation of expression in Quadratic form
Procedure to factorise the expression
Step 1: Determine the coefficient a,b and c.
Step 2: Calculate the product of a and c. Product =ac and sum =b. Thus the middle coefficient is the sum and extreme product is the product value.
Step 3: Express the middle term as sum of two terms such that the sum satisfies the middle term and the product satisfies the extreme product.
Step 4: Now group the expression into two factors by taking the common expression outside.

 ReginaTagebücher
ReginaTagebücher
