1 IMPORTANCE OF CHEMISTRY
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
CHAPTER-1 SOME BASIC CONCEPT OF CHEMISTRY
DEFFINATION OF CHEMISTRY: Chemistry is the science of molecules and their transformations. It is the science not so much of the one hundred elements but of the infinite variety of molecules that may be built from them.
IMPORTANCE OF CHEMISTRY:
Chemistry has a direct impact on our life and has wide range of applications in different fields. These are given below:
(A) In Agriculture and Food:
(i) It has provided chemical fertilizers such as urea, calcium phosphate, sodium nitrate, ammonium phosphate etc.
(ii) It has helped to protect the crops from insects and harmful bacteria, by the use of certain effective insecticides, fungicides and pesticides.
(iii) The use of preservatives has helped to preserve food products like jam, butter, squashes etc. for longer periods.
(B) In Health and Sanitation:
(i) It has provided mankind with a large number of life-saving drugs. Today, dysentery and pneumonia are curable due to discovery of sulpha drugs and penicillin life-saving drugs. Cisplatin and Taxol have been found to be very effective for cancer therapy and AZT (Azido thymidine) is used for AIDS victims.
(ii) Disinfectants such as phenol are used to kill the micro-organisms present in drains, toilet, floors etc.
(iii) A low concentration of chlorine i.e., 0.2 to 0.4 parts per million (ppm) is used for sterilization of water to make it fit for drinking purposes.
(C) Saving the Environment:
The rapid industrialisation all over the world has resulted in lot of pollution.
Poisonous gases and chemicals are being constantly released in the atmosphere. They are polluting environment at an alarming rate. Scientists are working day and night to develop substitutes which may cause lower pollution. For example, CNG (Compressed Natural Gas), a substitute of petrol, is very effective in checking pollution caused by automobiles.
(D) Application in Industry:
Chemistry has played an important role in developing many industrially ^ manufactured fertilizers, alkalis, acids, salts, dyes, polymers, drugs, soaps,
detergents, metal alloys and other inorganic and organic chemicals including new materials contribute in a big way to the national economy.
1 IMPORTANCE OF CHEMISTRY
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 11
- Subject
- Chemistry
Chapter 1:
SOME BASIC CONCEPTS OF CHEMISTRY
DEVELOPMENT OF CHEMISTRY
Very early chemists were typically intended principally for the accomplishment of a selected goal or product. Creating fragrances and soaps didn't need abundant theory, simply a decent formula and careful attention to detail. There was no customary method of naming materials (and no table that everybody may agree on). However, science developed over the centuries.
Major progress was created in putt chemistry on a solid foundation once Boyle (1637-1691) began his analysis in chemistry. He developed the fundamental concepts for the behaviour of gases; gases may thenceforth be represented mathematically. Boyle conjointly helped pioneer the concept that tiny particles may mix to create molecules. a few years later, John Dalton used these concepts to develop the atomic theory.
The field of science started to grow quickly during the 1700s. Joseph Priestley (1733-1804) separated and described a few gases: oxygen, carbon monoxide, and nitrous oxide. It was subsequently found that nitrous oxide ("chuckling gas") filled in as a sedative. This gas was utilized for that reason without precedent for 1844 during a tooth extraction. Different gases found during that opportunity were chlorine, by C.W. Scheele (1742-1786) and nitrogen, by Antoine Lavoisier (1743-1794). Lavoisier has been viewed as by numerous researchers to be the "father of science".
Scientific experts kept on finding new mixtures during the 1800s. The science likewise started to foster a more hypothetical establishment. John Dalton (1766-1844) set forth his nuclear hypothesis in 1807. This thought permitted researchers to contemplate science in a substantially more orderly manner. Amadeo Avogadro (1776-1856) laid the foundation for a more quantitative way to deal with science by computing the quantity of particles in a given measure of a gas. A great deal of exertion was advanced in concentrating on compound responses. These endeavors prompted new materials being created. Following the innovation of the battery by Alessandro Volta (1745-1827), the field of electrochemistry (both hypothesis and application) created through significant commitments by Humphry Davy (1778-1829) and Michael Faraday (1791-1867). Different region of the discipline additionally advanced quickly.
It would take an enormous book to cover improvements in science during the 20th hundred years and up to the present time. One significant area of development was in the space of the science of living cycles. Research in photosynthesis in plants, the revelation and portrayal of compounds as biochemical impetuses, explanation of the designs of biomolecules like insulin and DNA — these endeavors brought about a blast of data in the field of organic chemistry.
The viable parts of science were not overlooked. Crafted by Volta, Davy, and Faraday at last prompted the improvement of batteries that gave a wellspring of power to control various gadgets.
Charles Goodyear (1800-1860) found the course of vulcanization, permitting rubber to be created for the tires of the relative multitude of vehicles that we have today. Louis Pasteur (1822-1895) spearheaded the utilization of intensity cleansing to dispose of undesirable microorganisms in wine and milk. Alfred Nobel (1833-1896) created explosive. After his passing, the fortune he produced using this item was utilized to finance the Nobel Prizes in science and the humanities. J.W. Hyatt (1837-1920) fostered the primary plastic. Leo Baekeland (1863-1944) fostered the primary engineered gum, which is broadly utilized for economical and solid dinnerware.
IMPORTANCE OF CHEMISTRY
Chemistry is one the most important subject. This subject plays an important role in science and is also related to other branches of science. Being chemistry an important subject it is used in every aspect of a person’s life from the food consumed to the products used. The improvement of chemical science has altered the premise of current medication. With ever-increasing research in chemistry, wonder drugs like penicillin and streptomycin have been developed. Not only in medicine but chemistry is also applied in many different areas of science and technology. It is applied in agriculture, supply of food, contribution to better hygiene and sanitation, saving the environment, increase in comfort, pleasure and luxuries, transport and communication, and atomic energy.
2. NATURE OF MATTER
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
NATURE OF MATTER
MATTER
Anything which has mass and occupies space is called matter.
For example, book, pencil, water, air are composed of matter as we know that they have
mass and they occupy space.
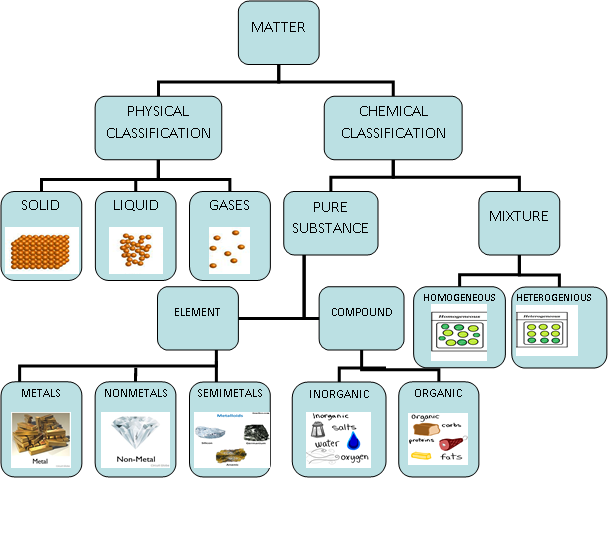
(A) Classification of Matter
There are two ways of classifying the matter:
(i) Physical classification
(ii) Chemical classification
(i) Physical Classification:
Matter can exist in three physical states:
1. Solids
2. Liquids
3. Gases
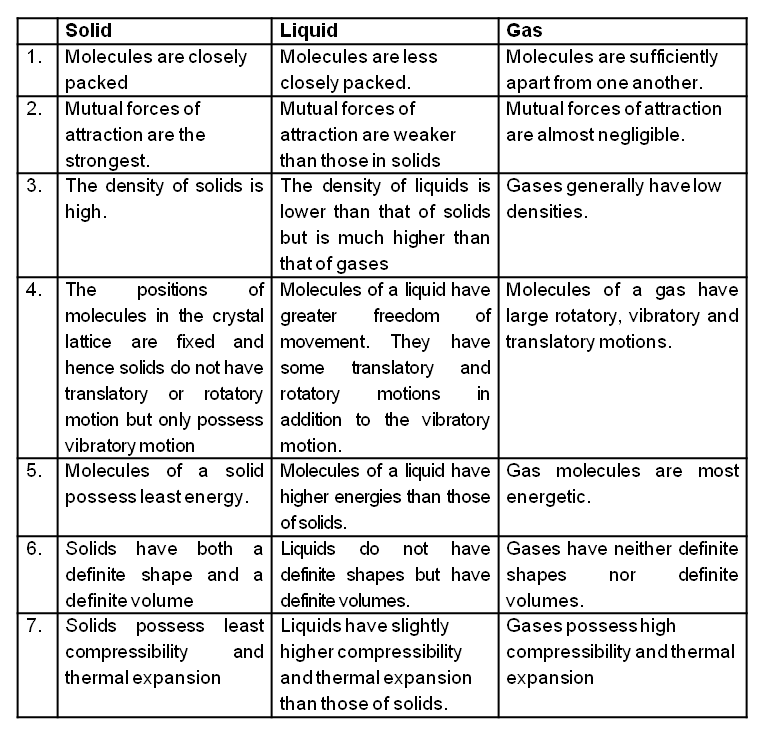
1. Solids: The particles are held very close to each other in an orderly fashion and there is not much freedom of movement.
Characteristics of solids: Solids have definite volume and definite shape.
2. Liquids: In liquids, the particles are close to each other but can move around. Characteristics of liquids: Liquids have definite volume but not definite shape.
3. Gases: In gases, the particles are far apart as compared to those present in solid or liquid states. Their movement is easy and fast.
Characteristics of Gases: Gases have neither definite volume nor definite shape. They completely occupy the container in which they are placed.
(ii) Chemical classification :
Based upon the composition, matter can be divided into two main types:
1. Pure Substances
2. Mixtures.
1. Pure substances: A pure substance may be defined as a single substance (or matter) which cannot be separated by simple physical methods.
Pure substances can be further classified as (a)Elements (b)Compounds
(a)Elements: An element consists of only one type of particles. These particles may be atoms or molecules.
For example, sodium, copper, silver, hydrogen, oxygen etc. are some examples of elements. They all contain atoms of one type. However, atoms of different elements are different in nature. Some elements such as sodium . or copper contain single atoms held together as their constituent particles whereas in some others two or more atoms combine to give molecules of the element. Thus, hydrogen, nitrogen and oxygen gases consist of molecules in which two atoms combine to give the respective molecules of the element.
(b)Compounds: It may be defined as a pure substance containing two or more elements combined together in a fixed proportion by weight and can be decomposed into these elements by suitable chemical methods. Moreover, the properties of a compound are altogether different from the constituting elements.
The compounds have been classified into two types. These are:
(i) Inorganic Compounds: These are compounds which are obtained from non-living sources such as rocks and minerals. A few
examples are: Common salt, marble, gypsum, washing soda etc.
(ii) Organic Compounds are the compounds which are present in plants and animals. All the organic compounds have been found to contain carbon as their essential constituent. For example, carbohydrates, proteins, oils, fats etc.
2. Mixtures: The combination of two or more elements or compounds which are not chemically combined together and may also be present in any proportion, is called mixture. A few examples of mixtures are: milk, sea water, petrol, lime water, paint glass, cement, wood etc.
Types of mixtures: Mixtures are of two types:
(i) Homogeneous mixtures: A mixture is said to be homogeneous if it has a uniform composition throughout and there are no visible boundaries of separation between the constituents.
For example: A mixture of sugar solution in water has the same sugar water composition throughout and all portions have the same sweetness.
(ii) Heterogeneous mixtures: A mixture is said to be heterogeneous if it does not have uniform composition throughout and has visible boundaries of separation between the various constituents. The different constituents of a heterogeneous mixture can be seen even with naked eye.
For example: When iron filings and sulphur powder are mixed together, the mixture formed is heterogeneous. It has greyish-yellow appearance and the two constituents, iron and sulphur, can be easily identified with naked eye.
• Differences between Compounds and Mixtures
Compounds
1. In a compound, two or more elements are combined chemically.
2. In a compound, the elements are present in the fixed ratio by mass. This ratio cannot change.
3. Compounds are always homogeneous i.e., they have the same composition throughout.
4 In a compound, constituents cannot be separated by physical methods
5. In a compound, the constituents lose their identities i.e., i compound does not show the characteristics of the constituting elements.
Mixtures
1. In a mixture, or more elements or compounds are simply mixed and not combined chemically.
2. In a mixture the constituents are not present in fixed ratio. It can vary
3. Mixtures may be either homogeneous or heterogeneous in nature.
4. Constituents of mixtures can be separated by physical methods.
5, In a mixture, the constituents do not lose their identities i.e., a mixture shows the characteristics of all the constituents
We have discussed the physical and chemical classification of matter. A flow sheet representation of the same is given below.
2. NATURE OF MATTER
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 11
- Subject
- Chemistry
STATES OF MATTER
On the basis of physical properties, matter may be classified into the following three states :
- Solid State
- Liquid State
- Gaseous State
Comparison of the characteristics of a solid, a liquid and a gas
Gases
The molecules of a gas are free to move in all directions. The space in between them is very large. The gaseous molecules possess motion of all three types, namely translational, rotational and vibrational. The molecular forces of attraction between gases are very much weak. Hence a gas has neither a definite shape nor a definite volume.
- Gases are highly compressible
- Gases expand without limits
- Gases exert pressure on the walls of the container uniformly in all directions.
- Gases diffuse rapidly through each other to form a homogeneous mixture.
3. PROPERTIES OF MATTER AND THEIR MEASUREMENT
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
PROPERTIES OF MATTER AND THEIR MEASUREMENTS
Physical Properties: Those properties which can be measured or observed without changing the identity or the composition of the substance.
Some examples of physical properties are colour, odour, melting point, boiling point etc. Chemical Properties: It requires a chemical change to occur. The examples of chemical properties are characteristic reactions of different substances. These include acidity, basicity, combustibility etc.
• Units of Measurement
Fundamental Units: The quantities mass, length and time are called fundamental quantities and their units are known as fundamental units.
There are seven basic units of measurement for the quantities: length, mass, time, temperature, amount of substance, electric current and luminous intensity.
Si-System: This system of measurement is the most common system employed throughout the world.
It has given units of all the seven basic quantities listed above.
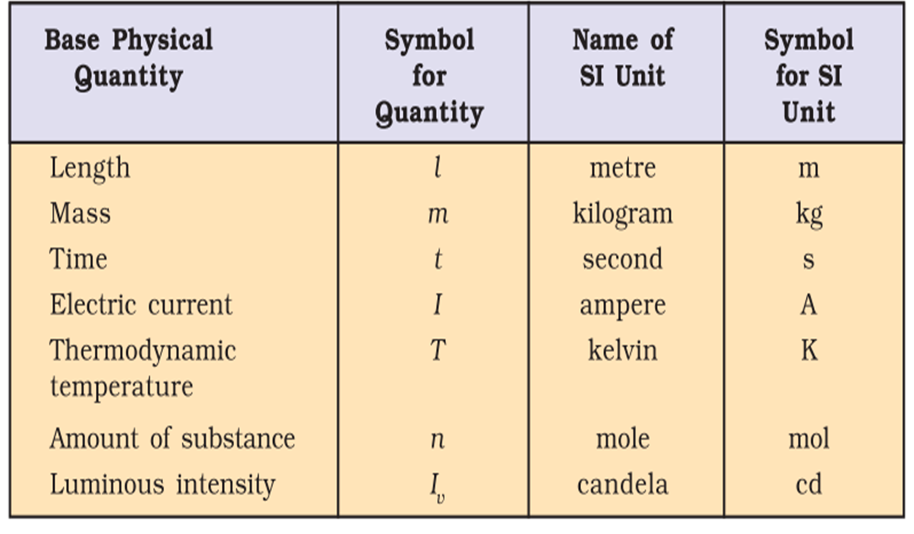
• Definitions of Basic SI Units
1. Metre: It is the length of the path travelled by light in vacuum during a time interval of 1/299792458 of a second.
2. Kilogram: It is the unit of mass. It is equal to the mass of the international prototype
of the kilogram. ,
3. Second: It is the duration of 9192631, 770 periods of radiation which correspond to the transition between the two hyper fine levels of the ground state of caesium- 133 atom.
4. Kelvin: It is the unit of thermodynamic temperature and is equal to 1/273.16 of the thermodynamic temperature of the triple point of water.
5. Ampere: The ampere is that constant current which if maintained in two straight parallel conductors of infinite length, of negligible circular cross section and placed, 1 metre apart in vacuum, would produce between these conductors a force equal to 2 x 10-7 N per metre of length.
6. Candela: It may be defined as the luminous intensity in a given direction, from a source which emits monochromatic radiation of frequency 540 x 1012 Hz and that has a radiant intensity in that direction of 1/ 683 watt per steradian.
7. Mole: It is the amount of substance which contains as many elementary entities as there are atoms in 0.012 kilogram of carbon -12. Its symbol is ‘mol’.
• Mass and Weight
Mass: Mass of a substance is the amount of matter present in it.
The mass of a substance is constant.
The mass of a substance can be determined accurately in the laboratory by using an analytical
balance. SI unit of mass is kilogram.
Weight: It is the force exerted by gravity on an object. Weight of substance may vary from one place to another due to change in gravity.
Volume: Volume means the space occupied by matter. It has the units of (length)3. In SI units, volume is expressed in metre3 (m3). However, a popular unit of measuring volume, particularly in liquids is litre (L) but it is not in SI units or an S.I. unit.
Mathematically,
1L = 1000 mL = 1000 cm3 = 1dm3.
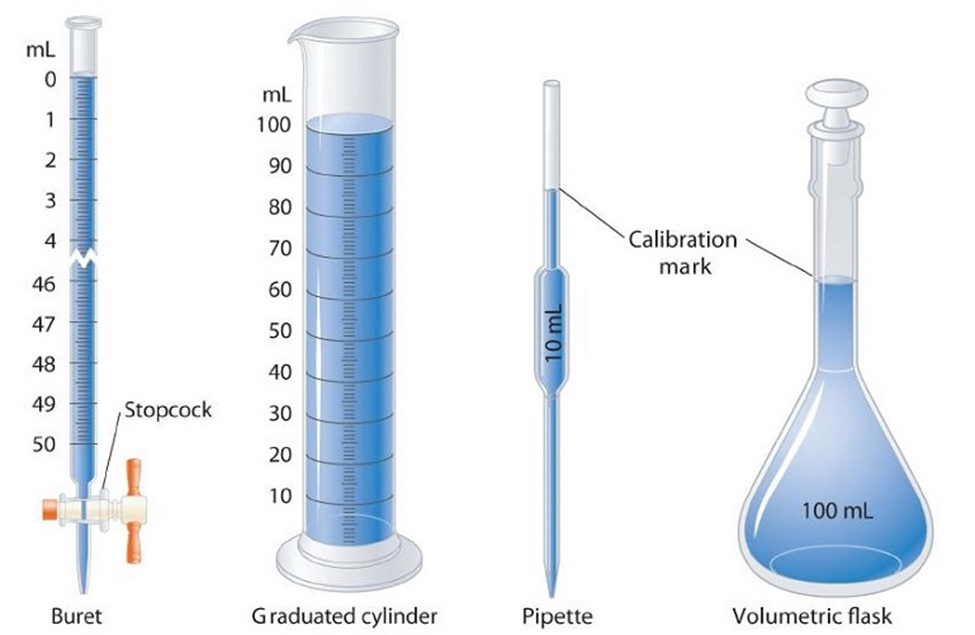
Volume of liquids can be measured by different devices like burette, pipette, cylinder, measuring flask etc. All of them have been calibrated.
Temperature: There are three scales in which temperature can be measured. These are known as Celsius scale (°C), Fahrenheit scale (°F) and Kelvin scale (K).
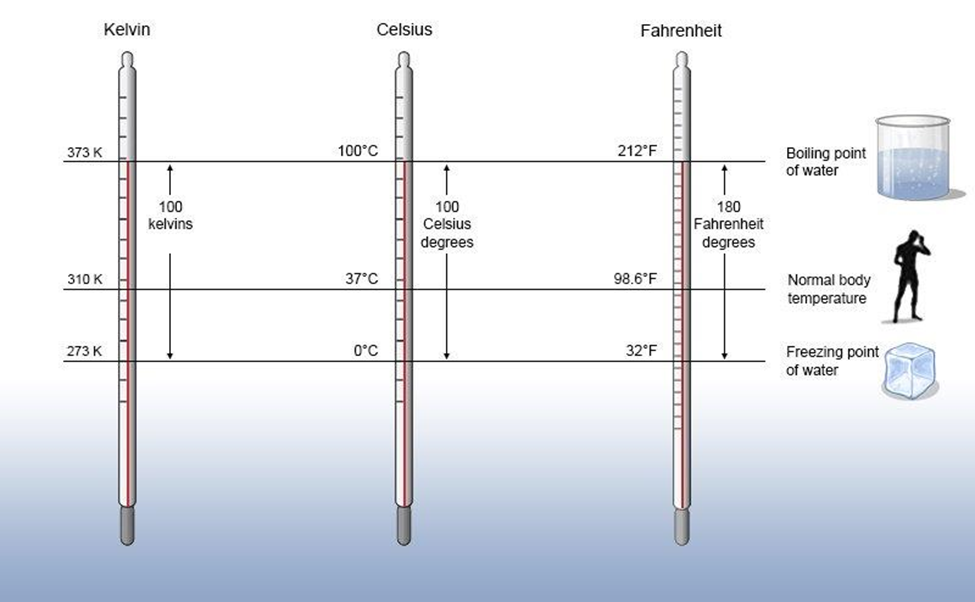
-> Thermometers with Celsius scale are calibrated from 0°C to 100°C.
-> Thermometers with Fahrenheit scale are calibrated from 32°F to 212°F.
-> Kelvin ‘scale of temperature is S.I. scale and is very common these days. Temperature on this scale is shown by the sign K.
The temperature on two scales are related to each other by the relationship

Density: Density of a substance is its amount of mass per unit volume. So, SI unit of density can be obtained as follows:
Matter is defined as something which has mass and occupies a certain volume. Mass of a body may or may not be uniformly distributed throughout the volume of the body. In order to understand the distribution of mass in a body we define a quantity called density.
Density is defined as the mass per unit volume of the substance.
The symbol for density is ρ and the formula to calculate density from mass and volume is
ρ=M/V
This formula implies that greater the mass of a body, greater is its density while greater the volume occupied by a body, smaller is the density of that body.
The S.I. unit of density is kg/m3. Its dimensional formula is [M1 L-3 T0].
4. UNCERTAINTY IN MEASUREMENT
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
UNCERTAINTY IN MEASUREMENT
All scientific measurements involve certain degree of error or uncertainty. The errors which arise depend upon two factors.
(i) Skill and accuracy of the worker
(ii) Limitations of measuring instruments.
• Scientific Notation
It is an exponential notation in which any number can be represented in the form N x 10n where n is an exponent having positive or negative values and N can vary between 1 to 10. Thus, 232.508 can be written as 2.32508 x 102in scientific notation.
Now let us see how calculations are carried out with numbers expressed in scientific notation.
(i) Calculation involving multiplication and division
(a) (5.7×106) × (4.2×105) = (5.7×4.2) (106+5) = 23.94 × 1011
(b) (5.7×106) ÷ (4.2×103)
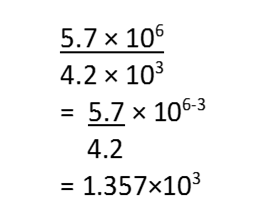
(ii) Calculation involving addition and subtraction: For these two operations, the first numbers are written in such a way that they have the same exponent. After that, the coefficients are added or subtracted as the case may be. For example,
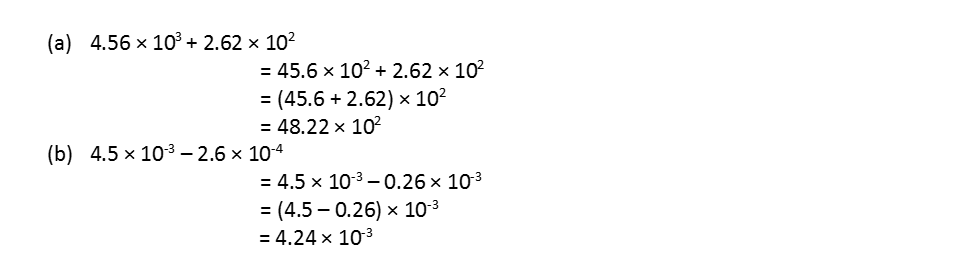
Significant Figures
Significant figures are meaningful digits which are known with certainty. There are certain rules for determining the number of significant figures. These are stated below:
1. All non-zero digits are significant. For example, in 285 cm, there are three significant figures and in 0.25 mL, there are two significant figures.
2. Zeros preceding to first non-zero digit are not significant. Such zeros indicates the position of decimal point.
For example, 0.03 has one significant figure and 0.0052 has two significant figures.
3. Zeros between two non-zero digits are significant. Thus, 2.005 has four significant figures.
4. Zeros at the end or right of a number are significant provided they are on the right side of the decimal point. For example, 0.200 g has three significant figures.
5. Counting numbers of objects. For example, 2 balls or 20 eggs have infinite significant figures as these are exact numbers and can be represented by writing infinite number of zeros after placing a decimal.
i.e., 2 = 2.000000
or 20 = 20.000000
• Addition and Subtraction of Significant Figures
In addition or subtraction of the numbers having different precisions, the final result should be reported to the same number of decimal places as in the term having the least number of decimal places.
For example, let us carry out the addition of three numbers 3.52, 2.3 and 6.24, having different precisions or different number of decimal places.
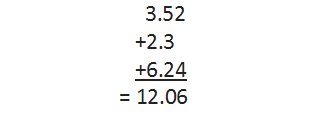
The final result has two decimal places but the answer has to be reported only up to one decimal place, i.e., the answer would be 12.0.
Subtraction of numbers can be done in the same way as the addition.

The final result has four decimal places. But it has to be reported only up to two decimal places, i.e., the answer would be 11.36.
• Multiplication and Division of Significant Figures
In the multiplication or division, the final result should be reported up to the same number of significant figures as present in the least precise number.
Multiplication of Numbers: 2.2120 x 0.011 = 0.024332
According to the rule the final result = 0.024
Division of Numbers: 4.2211÷3.76 = 1.12263
The correct answer = 1.12
• Dimensional Analysis
Often while calculating, there is a need to convert units from one system to other. The method used to accomplish this is called factor label method or unit factor method or dimensional analysis.
5. LAWS OF CHEMICAL COMBINATIONS
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
LAWS OF CHEMICAL COMBINATION
The combination of elements to form compounds is governed by the following five basic laws.
(i) Law of Conservation of Mass
(ii) Law of Definite Proportions
(iii) Law of Multiple Proportions
(iv) Law of Gaseous Volume (Gay Lussac’s Law)
(v) Avogadro’s Law
(i) Law of Conservation of Mass
The law was established by a French chemist, A. Lavoisier. The law states:
In all physical and chemical changes, the total mass of the reactants is equal to that of the products.
In other words, matter can neither be created nor destroyed.
The following experiments illustrate the truth of this law.
(a) When matter undergoes a physical change.
![]()
It is found that there is no change in weight though a physical change has taken place.
(b) When matter undergoes a chemical change.
For example, decomposition of mercuric oxide.
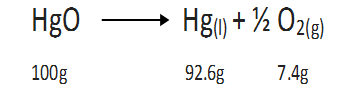
During the above decomposition reaction, matter is neither gained nor lost.
(ii) Law of Definite Proportions
According to this law:
A pure chemical compound always consists of the same elements combined together in a fixed proportion by weight.
For example, Carbon dioxide may be formed in a number of ways i.e.,
(a) By burning coke in air

(b)By the decomposition of ;limestone(CaCO3) on heating

(c)By the action of dil HCL on washing soda (Na2CO3)
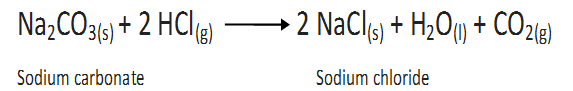
In all the three samples of CO2 carbon and oxygen are in the ratio 3:8 by weight
(iii) Law of Multiple Proportions
If two elements combine to form two or more compounds, the weight of one of the elements which combines with a fixed weight of the other in these compounds, bears simple whole number ratio by weight.
For example,

Hear, the masses of oxygen (16g and 32g ) which combine with a fixed mass of hydrogen (2g) bear a simple ratio 16:32 or 1:2 .
(iv) Gay Lussac’s Law of Gaseous Volumes
The law states that, under similar conditions of temperature and pressure, whenever gases combine, they do so in volumes which bear simple whole number ratio with each other and also with the gaseous products. The law may be illustrated by the following examples.
(a) Combination between hydrogen and chlorine:
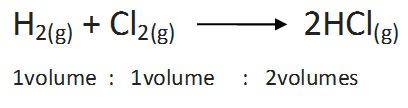
(b)Combination between nitrogen and hydrogen: The two gases lead to the formation of ammonia gas under suitable conditions. The chemical equation is
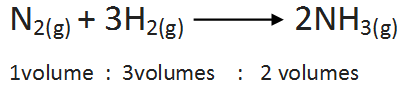
(v) Avogadro’s Law: Avogadro proposed that, equal volumes of gases at the same temperature and pressure should contain equal number of molecules.
For example,
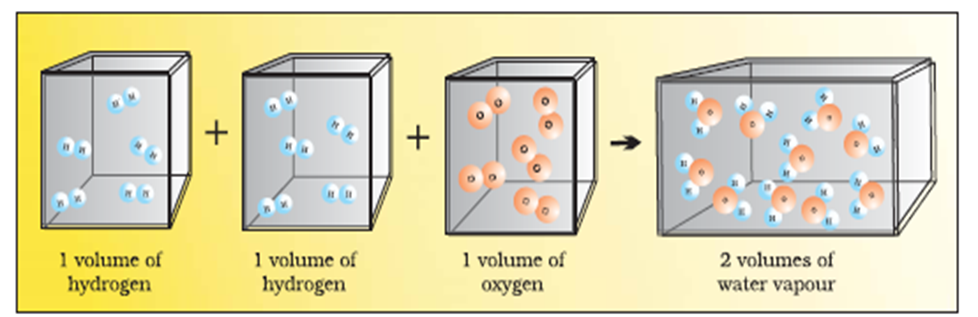
If we consider the reaction of hydrogen and oxygen to produce water, we see that two volumes of hydrogen combine with one volume of oxygen to give two volumes of water without leaving any unreacted oxygen.
Two volumes of hydrogen react with one volume of oxygen to give two volumes of water vapour.
6. DALTON’S ATOMIC THEORY
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
DALTON’S ATOMIC THEORY
In 1808, Dalton published ‘A New System of Chemical Philosophy’ in which he proposed the following:
1. Matter consists of indivisible atoms.
2. All the atoms of a given element have identical properties including identical mass. Atoms of different elements differ in mass.
3. Compounds are formed when atoms of different elements combine in a fixed ratio.
4. Chemical reactions involve reorganisation of atoms. These are neither created nor destroyed in a chemical reaction.
6. DALTON’S ATOMIC THEORY
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 11
- Subject
- Chemistry
DALTON LAW OF PARTIAL PRESSURE
At a given temperature, the total pressure exerted by two or more non-reacting gases occupying a definite volume is equal to the sum of the partial pressures of the component gases. Mathematically,
P = pA + pB + pC + …..
when P is the total pressure and pA, pB, pC, ….. are the partial pressures of the component gases A, B, C, ….. respectively. The pressure that a component gas of the gaseous mixture would exert if it were only present in the volume under consideration at a given temperature, is the partial pressure of the component.
Derivation of Dalton’s Law
Let n1 and n2 be the no. of moles of two non-reacting gases ‘A’ and ‘B’ filled in a vessel of volume ‘V’ at temperature T.
Total pressure in the vessel ‘P’ may be calculated as
PV = (n1 + n2)RT …….(i)
Individual or partial pressure may be calculated as,
pAV = n1RT …….(ii)
pBV = n2RT …….(iii)
Adding (ii) and (iii), we get
(pA + pB)V = (n1 + n2)RT …….(iv)
Comparing equations (i) and (iv), we get
P = pA + pB (Dalton’ expression)
Dividing equation (ii) by (i), we get
![]() = xA
= xA
pA = xA ´ P
where xA = mole fraction of ‘A’. Similarly, dividing (iii) by (i), we get
pB = xB ´ P
i.e., Partial pressure of a component = Mole fraction ´ total pressure
Relationship between total pressure and individual pressures (before mixing) of the constituent gases at constant temperature
At constant temperature, let V1 volume of a gas A at a pressure p1 be mixed with V2 volume of gas B at a pressure p2. Both these gases do not react chemically.
Total volume = V1 + V2
Let the total pressure be P and partial pressures of A and B be pA and pB respectively. Applying Boyle’s law,
PA(V1 + V2) = p1V1 …….(i)
and pB(V1 + V2) = p2V2 …….(ii)
Adding (i) and (ii)
pA + pB = 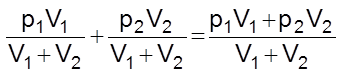
or P = 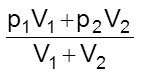
Dalton’s Law fails in those gases which react chemically so not applicable to the following mixtures.
(i) NH3+HCl
(ii) NO +O2
(iii) H2+F2
(iv) H2+Cl2
(v) SO2+ Cl2
Applications
(i) In the determination of pressure of dry gas : When a gas is called over water, then it is moist , water also vaporizes simultaneously and exerts its own partial pressure. Partial pressure of water is called its aqueous tension. It depends upon temperature.
If P and P¢ are the pressure of the dry gas and the moist gas respectively at t°C and p is the aqueous tension at that temperature, then by Dalton’s Law of Partial Pressures
P = P¢ - p
(ii) In the calculation of partial pressures : In a mixture of non-reacting gases A, B, C etc., if each gas is considered to be an ideal gas, then applying PV = nRT
PA = nA ![]() , pB = nB
, pB = nB ![]() pC = nC
pC = nC ![]()
And so on.
By Dalton’s law of partial pressures,
Total pressure, P = pA + pB + pC + … = ![]() (nA + nB + nC + …)
(nA + nB + nC + …)
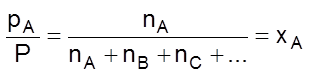 (mole fraction of A)
(mole fraction of A)
or pA = xA ´ P
Similarly, pB = xB ´ P and so on. Thus
Partial pressure of A = Mole fraction of A ´ Total pressure
Amagat Law of Partial volume
Total volume of a mixture of gases which do not react at constant temperature and pressure is equal to sum of individual volumes (partial volumes) of constituent gases.
V = åVi = V1 + V2 + V3 + ….. + Vn
7. ATOMIC AND MOLECULAR MASSES
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
ATOMIC AND MOLECULAR MASSES
• Atomic MassThe atomic mass of an element is the number of times an atom of that element is heavier than an atom of carbon taken as 12. It may be noted that the atomic masses as obtained above are the relative atomic masses and not the actual masses of the atoms.
One atomic mass unit (amu) is equal to l/12th of the mass of an atom of carbon-12 isotope. It is also known as unified mass.
• Average Atomic Mass
Most of the elements exist as isotopes which are different atoms of the same element with different mass numbers and the same atomic number. Therefore, the atomic mass of an element must be its average atomic mass and it may be defined as the average relative mass of an atom of an element as compared to the mass of carbon atoms (C-12) taken as 12w.
• Molecular Mass
Molecular mass is the sum of atomic masses of the elements present in a molecule. It is obtained by multiplying the atomic mass of each element by number of its atoms and adding them together.
For example,
Molecular mass of methane (CH4)
= 12.011 u + 4 (1.008 u)
= 16.043 u
• Formula Mass
Ionic compounds such as NaCl, KNO3, Na2C03 etc. do not consist of molecules i.e., single entities but exist “as ions closely packed together in a three dimensional space as shown in -Fig. 1.5.
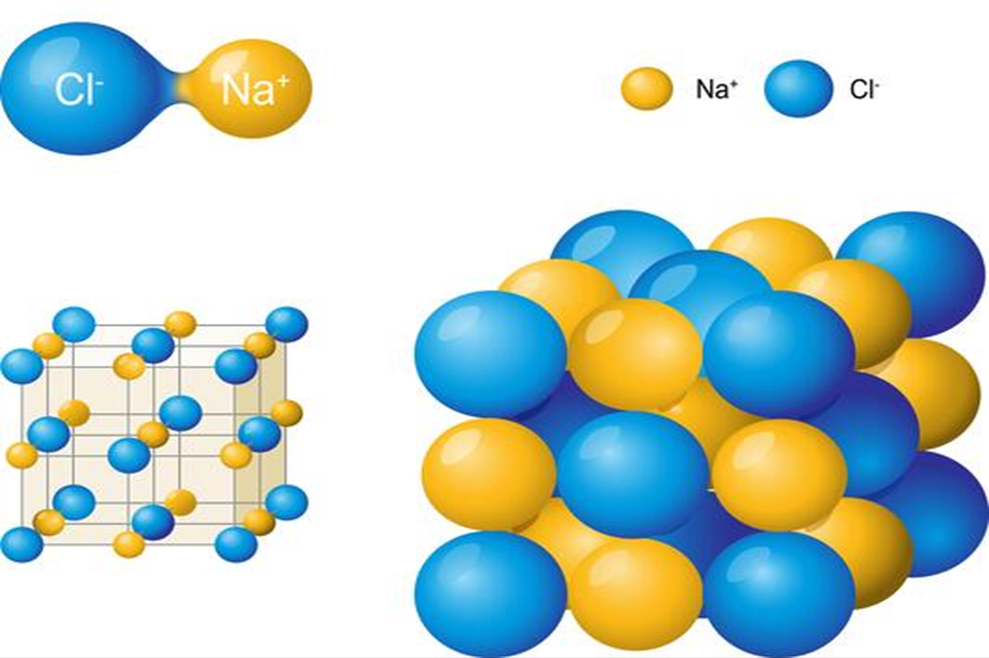
Packing of Na+ and Cl- ions in Sodium chloride molecule
In such cases, the formula is used to calculate the formula mass instead of molecular mass. Thus, formula mass of NaCl = Atomic mass of sodium + atomic mass of chlorine
= 23.0 u + 35.5 u = 58.5 u.
8. MOLE CONCEPT AND MOLAR MASSES
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
MOLE CONCEPT AND MOLAR MASSES
It is found that one gram atom of any element contains the same number of atoms and one gram molecule of any substance contains the same number of molecules. This number has been experimentally determined and found to be equal to 6.022137 x 1023 The value is generally called Avogadro’s number or Avogadro’s constant.
It is usually represented by NA:
Avogadro’s Number, NA = 6.022 × 1023
9. PERCENTAGE COMPOSITION
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
PERCENTAGE COMPOSITION
One can check the purity of a given sample by analysing this data. Let us understand by taking the example of water (H20). Since water contains hydrogen and oxygen, the percentage composition of both these elements can be calculated as follows:
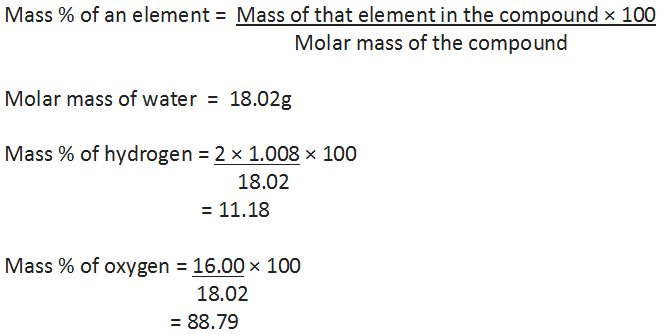
• Empirical Formula
The formula of the compound which gives the simplest whole number ratio of the atoms of yarious elements present in one molecule of the compound.
For example, the formula of hydrogen peroxide is H202. In order to express its empirical formula, we have to take out a common factor 2. The simplest whole number ratio of the atoms is 1:1 and the empirical formula is HO. Similarly, the formula of glucose is C6H1206. In order to get the simplest whole number of the atoms,
Common factor = 6
The ratio is = 1 : 2 : 1 The empirical formula of glucose = CH20
• Molecular Formula
The formula of a compound which gives the actual ratio of the atoms of various elements present in one molecule of the compound.
For example, molecular formula of hydrogen peroxide = H202and Glucose = C6H1206
Molecular formula = n x Empirical formula
Where n is the common factor and also called multiplying factor. The value of n may be 1, 2, 3, 4, 5, 6 etc.
In case n is 1, Molecular formula of a compound = Empirical formula of the compound.
10. STOICHIOMETRY AND STOICHIOMETRIC CALCULATIONS
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
STOICHIOMETRY AND STOICHIOMETRIC CALCULATIONS
The word ‘stoichiometry’ is derived from two Greek words—Stoicheion (meaning element) and matron (meaning measure). Stoichiometry, thus deals with the calculation of masses (sometimes volume also) of the reactants and the products involved in a chemical reaction. Let us consider the combustion of methane. A balanced equation for this reaction is as given below:
![]()
Hear, methane and dioxygen are called reactants and carbon dioxide and water are called products.

From these relationship the given data can be interconverted as follows
• Limiting Reactant/Reagent
Sometimes, in alchemical equation, the reactants present are not the amount as required according to the balanced equation. The amount of products formed then depends upon the reactant which has reacted completely. This reactant which reacts completely in the reaction is called the limiting reactant or limiting reagent. The reactant which is not consumed completely in the reaction is called excess reactant.
• Reactions in Solutions
When the reactions are carried out in solutions, the amount of substance present in its given volume can be expressed in any of the following ways:
1. Mass percent or weight percent (w/w%)
2. Mole fraction
3. Molarity
4. Molality
1. Mass percent: It is obtained by using the following relation:

2. Mole fraction: It is the ratio of number of moles of a particular component to the total number of moles of the solution. For a solution containing n2 moles of the solute dissolved in n1 moles of the solvent,


The sum of the mole fraction of the components is equal to 1
![]()
3. Molarity: It is defined as the number of moles of solute in 1 litre of the solution.
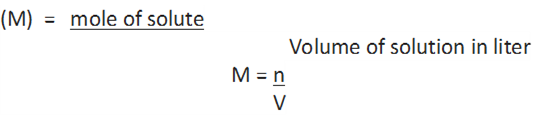
4. Molality: It is defined as the number of moles of solute present in 1 kg of solvent. It is denoted by m.

• All substances contain matter which can exist in three states — solid, liquid or gas.
• Matter can also be classified into elements, compounds and mixtures.
• Element: An element contains particles of only one type which may be atoms or molecules.
• Compounds are formed when atoms of two or more elements combine in a fixed ratio to each other.
• Mixtures: Many of the substances present around us are mixtures.
• Scientific notation: The measurement of quantities in chemistry are spread over a wide range of 10-31to 1023. Hence, a convenient system of expressing the number in scientific notation is used.
• Scientific figures: The uncertainty is taken care of by specifying the number of significant figures in which the observations are reported.
• Dimensional analysis: It helps to express the measured quantities in different systems of units.
• Laws of Chemical Combinations are:
(i) Law of Conservation of Mass
(ii) Law of Definite Proportions
(iii) Law of Multiple Proportions
(iv) Gay Lussac’s Law of Gaseous Volumes
(v) Avogadro’s Law.
• Atomic mass: The atomic mass of an element is expressed relative to 12C isotope of carbon which has an exact value of 12u.
• Average atomic mass: Obtained by taking into account the natural abundance of different isotopes of that element.
• Molecular mass: The molecular mass of a molecule is obtained by taking sum of atomic masses of different atoms present in a molecule.
• Avogadro number: The number of atoms, molecules or any other particles present in a given system are expressed in terms of Avogadro constant.
= 6.022 x 1023
• Balanced chemical equation: A balanced equation has the same number of atoms of each element on both sides of the equation.
• Stoichiometry: The quantitative study of the reactants required or the products formed is called stoichiometry. Using stoichiometric calculations, the amounts of one or more reactants required to produce a particular amount of product can be determined and vice-versa.
1. DISCOVERY OF SUB -ATOMIC PARTICLES
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
Chapter 2: STRUCTURE OF ATOM
DISCOVERY OF SUB -ATOMIC PARTICLES
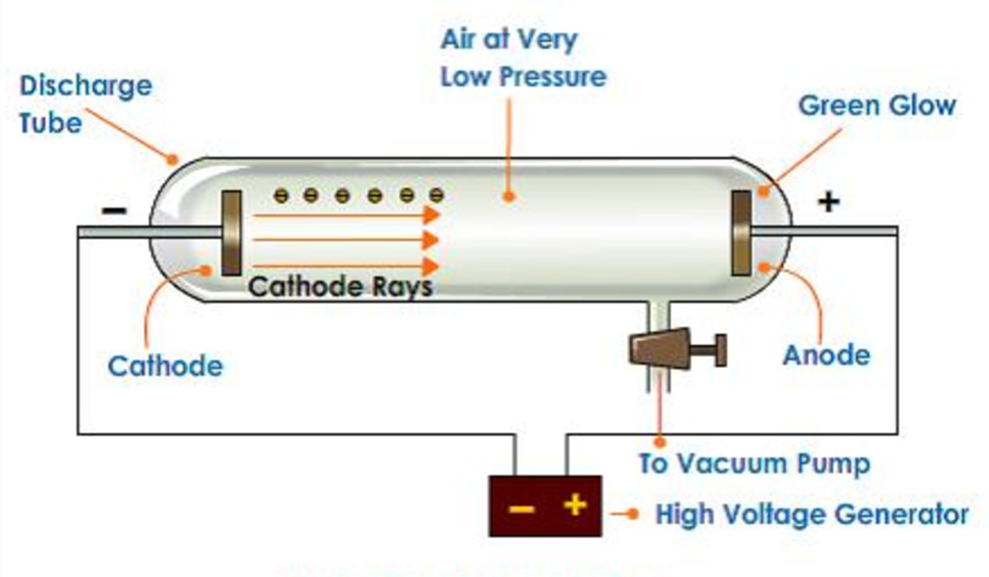
In 1879, William Crooks studied the conduction of electricity through gases at low pressure. He performed the experiment in a discharge tube which is a cylindrical hard glass tube about 60 cm in length. It is sealed at both the ends and fitted with two metal electrodes as shown in Fig. 2.1.
![]()
The electrical discharge through the gases could be observed only at very low pressures and at very high voltages.
The pressure of different gases could be adjusted by evacuation. When sufficiently high voltage is applied across the electrodes, current starts flowing through a stream of particles moving in the tube from the negative electrode (cathode) to the positive electrode (anode). These were called cathode rays or cathode ray particles.
• Properties of Cathode Rays
(i) Cathode rays travel in straight line.
(ii) Cathode rays start from cathode and move towards the anode.
(iii) These rays themselves are not visible but their behaviour can be observed with the help of certain kind of materials (fluorescent or phosphorescent) which glow when hit by them.
(iv) Cathode rays consist of negatively charged particles. When electric field is applied on the cathode rays with the help of a pair of metal plates, these are found to be deflected towards the positive plate indicating the presence of negative charge.
(v) The characteristics of cathode rays do not depend upon the material of electrodes and the nature of gas present in the cathode ray’tube.
• Determination of Charge/Mass (elm) Ratio for Electrons
J. J. Thomson for the first time experimentally determined charge/mass ratio called elm ratio for the electrons. For this, he subjected the beam of electrons released in the discharge tube as cathode rays to influence the electric and magnetic fields. These were acting perpendicular to one another as well as to the path followed by electrons.
According to Thomson, the amount of deviation of the particles from their path in presence of electrical and magnetic field depends upon following factors:
(i) Greater the magnitude of the charge on the particle, greater is the interaction with the electric or magnetic field and thus greater is the deflection.
(ii)The mass of the particle — lighter the particle, greater the deflection.
(iii) The deflection of electrons from their original path increases with the increase in the voltage across the electrodes or strength of the magnetic field.
By carrying out accurate measurements on the amount of deflections observed by the electrons on the electric field strength or magnetic field strength, Thomson was able to determine the value of
e/me = 1.758820 x 1011 C kg-1 where me = Mass of the electron in kg
e = magnitude of charge on the electron in coulomb (C).
• Charge on the Electron
R.A. Millikan devised a method known as oil drop experiment to determine the charge on the electrons.

• Discovery of Proton—Anode Rays
In 1886, Goldstein modified the discharge tube by using a perforated cathode. On reducing the pressure, he observed a new type of luminous rays passing through the holes or perforations of the cathode and moving in a direction opposite to the cathode rays. These rays were named as positive rays or anode rays or as canal rays. Anode rays are not emitted from the anode but from a space between anode and cathode.
• Properties of Anode Rays
(i) The value of positive charge (e) on the particles constituting anode rays depends upon the nature of the gas in the discharge tube.
(ii) The charge to mass ratio of the particles is found to depend on the gas from which these originate.
(iii) Some of the positively charged particles carry a multiple of the fundamental unit of electrical charge.
(iv) The behaviour of these particles in the magnetic or electric field is opposite to that observed for electron or cathode rays.
• Proton
The smallest and lightest positive ion was obtained from hydrogen and was called proton. Mass of proton = 1.676 x 10-27 kg
Charge on a proton = (+) 1.602 x 10-19 C
• Neutron
It is a neutral particle. It was discovered by Chadwick (1932).
By the bombardment of thin sheets of beryllium with fast moving a-particles he observed that highly penetrating rays consist of neutral particles which were named neutrons.
1. Classification of elements
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
CHAPTER - 3
CLASSIFICATION OF ELEMENTS AND PERIODICITY IN PROPERTIES
WHY DO WE NEED TO CLASSIFY ELEMENTS ?
The elements are the basic units of all types of matter. In 1800, only 31 elements were known. By 1865, the number of identified elements had more than doubled to 63. At present 114 elements are known. Of them, the recently discovered elements are man-made. Efforts to synthesise new elements are continuing. With such a large number of elements it is very difficult to study individually the chemistry of all these elements and their innumerable compounds individually. To ease out this problem, scientists searched for a systematic way to organise their knowledge by classifying the elements. Not only that it would rationalize known chemical facts about elements, but even predict new ones for undertaking further study.
1.KÖSSEL-LEWIS APPROACH TO CHEMICAL BONDING
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
CHAPTER – 4
CHEMICAL BONDING AND MOLECULAR STRUCTURE
KÖSSEL-LEWIS APPROACH TO CHEMICAL BONDING
• Chemical Bond
The force that holds different atoms in a molecule is called chemical bond.
• Octet Rule
Atoms of different elements take part in chemical combination in order to complete their octet or to attain the noble gas configuration.
• Valence Electrons
It is the outermost shell electron which takes part in chemical combination.
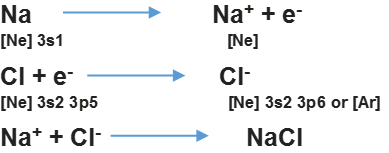
• Facts Stated by Kossel in Relation to Chemical Bonding
— In the periodic table, the highly electronegative halogens and the highly electro-positive alkali metals are separated by noble gases.
— Formation of an anion and cation by the halogens and alkali metals are formed by gain of electron and loss of electron respectively.
— Both the negative and positive ions acquire the noble gas configuration.
— The negative and positive ions are stabilized by electrostatic attraction Example,
• Modes of Chemical Combination
— By the transfer of electrons: The chemical bond which formed by the complete transfer of one or more electrons from one atom to another is termed as electrovalent bond or ionic bond.
— By sharing of electrons: The bond which is formed by the equal sharing of electrons between one or two atoms is called covalent bond. In these bonds electrons are contributed by both.
— Co-ordinate bond: When the electrons are contributed by one atom and shared by both, the bond is formed and it is known as dative bond or co-ordinate bond.
1. INTERMOLECULAR FORCES
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
CHAPTER – 5 STATES OF MATTER
INTERMOLECULAR FORCES
Intermolecular forces are the forces of attraction and repulsion between interacting particles
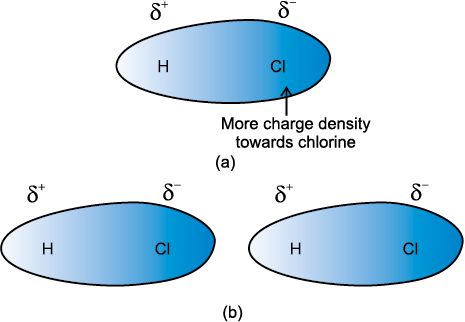
have permanent dipole moments. This interaction is stronger than the London forces but is weaker than ion-ion interaction because only partial charges are involved.
The attractive forces decrease with the increase of distance between dipoles. The interaction energy is proportional to 1/r6 where r is the distance between polar molecules.
Ion-Dipole Interaction: This is the force of attraction which exists between the ions (cations or anions) and polar molecules. The ion is attracted towards the oppositely charged end of dipolar molecules.
The strength of attraction depends upon the charge and size of the ion and the dipole moment and the size of the polar molecule.
For example: Solubility of common salt (NaCl) in water.
• Ion-induced Dipolar Interactions
In this type of interaction permanent dipole of the polar molecule induces dipole on the electrically neutral molecule by deforming its electronic cloud. Interaction energy is proportional to 1/r6 where r is the distance between two molecules
• London Forces or Dispersion Forces
As we know that in non-polar molecules, there is no dipole moment because their electronic . charge cloud is symmetrically distributed. But, it is believed that at any instant of time, the electron cloud of the molecule may be distorted so that an instantaneous dipole or momentary dipole is produced in which one part of the molecule is slightly more negative than the other part. This momentary dipole induces dipoles in the neighbouring molecules. Thus, the force of attraction exists between them and are exactly same as between permanent dipoles. This force of attraction is known as London forces or Dispersion forces. These forces are always attractive and the interaction energy is inversely proportional to the sixth power of the
distance between two interacting particles, (i.e. 1/r6 where r is the distance between two particles). This can be shown by fig. given below.
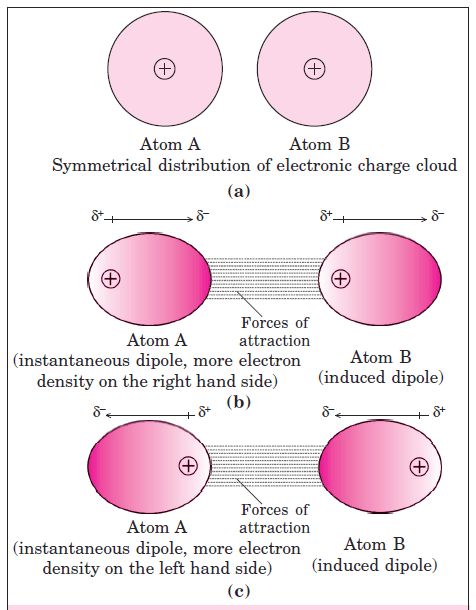
Hydrogen bonding: When hydrogen atom is attached to highly electronegative element by covalent bond, electrons are shifted towards the more electronegative atom. Thus a partial positive charge develops on the hydrogen atom. Now, the positively charged hydrogen atom of one molecule may attract the negatively charged atom of some other molecule and the two molecules can be linked together through a weak force of attraction.
![]()
1. THERMODYNAMIC TERMS
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
CHAPER – 6 THERMODINAMICS
IMPORTANT TERMS AND DEFINITIONS
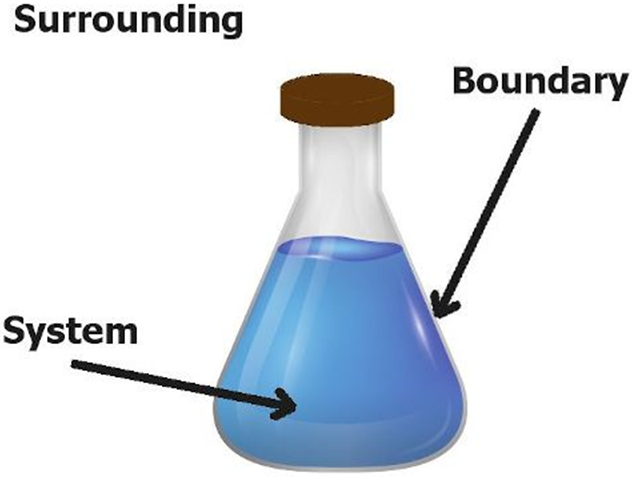
System: Refers to the portion of universe which is under observation.
Surroundings: Everything else in the universe except system is called surroundings. The Universe = The System + The Surroundings.
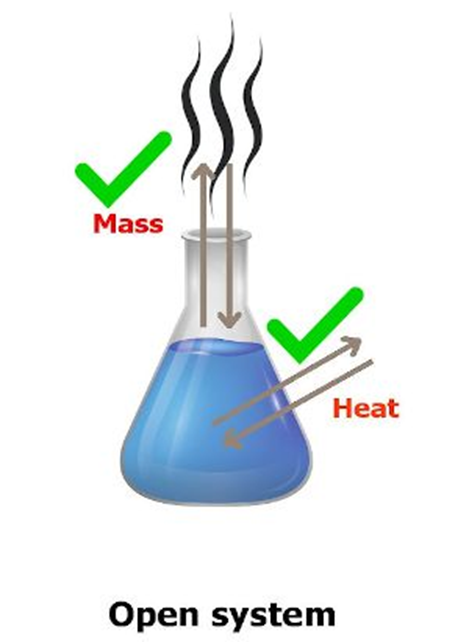
Open System: In a system, when there is exchange of energy and matter taking place with
the surroundings, then it is called an open system.
For Example: Presence of reactants in an open beaker is an example of an open system. Closed System: A system is said to be a closed system when there is no exchange of matter ‘ but exchange of energy is possible.
For example: The presence of reactants in a closed vessel made of conducting material.
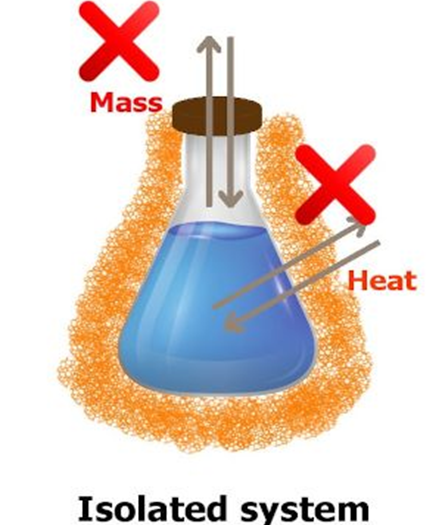
Isolated System: In a system, when no exchange of energy or matter takes place with the surroundings, is called isolated system.
For example: The presence of reactants in a thermoflask, or substance in an insulated closed vessel is an example of isolated system.
Homogeneous System: A system is said to be homogeneous when all the constituents present is in the same phase and is uniform throughout the system.
For example: A- mixture of two miscible liquids.
Heterogeneous system: A mixture is said to be heterogeneous when it consists of two or more phases and the composition is not uniform.
For example: A mixture of insoluble solid in water. ’
The state of the system: The state of a thermodynamic system means its macroscopic or bulk properties which can be described by state variables:
Pressure (P), volume (V), temperature (T) and amount (n) etc.
They are also known as state functions.
Isothermal process: When the operation is carried out at constant temperature, the process is said to be isothermal. For isothermal process, dT = 0 Where dT is the change in temperature.
Adiabatic process: It is a process in which no transfer of heat between system and surroundings, takes place.
Isobaric process: When the process is carried out at constant pressure, it is said to be isobaric. i.e. dP = 0
Isochoric process: A process when carried out at constant volume, it is known as isochoric in nature.
Cyclic process: If a system undergoes a series of changes and finally returns to its initial state, it is said to be cyclic process.
Reversible Process: When in a process, a change is brought in such a way that the process could, at any moment, be reversed by an infinitesimal change. The change r is called reversible.
•Internal Energy
It is the sum of all the forms of energies that a system can possess.
In thermodynamics, it is denoted by AM which may change, when
— Heat passes into or out of the system
— Work is done on or by the system
— Matter enters or leaves the system.
Change in Internal Energy by Doing Work
Let us bring the change in the internal energy by doing work.
Let the initial state of the system is state A and Temp. TA Internal energy = uA
On doing’some mechanical work the new state is called state B and the temp. TB. It is found to be
TB > TA
uB is the internal energy after change.
∴ Δu = uB – uA
Change in Internal Energy by Transfer of Heat
Internal energy of a system can be changed by the transfer of heat from the surroundings to the system without doing work.
Δu = q
Where q is the heat absorbed by the system. It can be measured in terms of temperature difference.
q is +ve when heat is transferred from the surroundings to the system. q is -ve when heat is transferred from system to surroundings.
When change of state is done both by doing work and transfer of heat.
Δu = q + w
First law of thermodynamics (Law of Conservation of Energy). It states that, energy can neither be created nor be destroyed. The energy of an isolated system is constant.
Δu = q + w.
1. EQUILIBRIUM IN PHYSICAL PROCESSES
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
CHAPTER – 7 EQUILIBRIUM
• Chemical Equilibrium
In a chemical reaction chemical equilibrium is defined as the state at which there is no further change in concentration of reactants and products.
For example,
Consider a hypothetical reaction,
A + B ↔ C + D
At equilibrium the rate of forward reaction is equal to the rate of backward reaction. Equilibrium
mixture: The mixture of reactants and products in the equilibrium state is called an equilibrium mixtures.
Based on the extent to which the reactions proceed to reach the state of equilibrium, these may be classified in three groups:
(i) The reactions which proceed almost to completion and the concentrations of the reactants left are negligible.
(ii) The reactions in which most of the reactants remains unchanged, i.e. only small amounts of products are formed.
(iii) The reactions in which the concentrations of both the reactants and products are comparable when the system is in equilibrium.
EQUILIBRIUM IN PHYSICAL PROCESSES
(i) Solid-Liquid Equilibrium: The equilibrium is represented as H2O(S) ↔ H2O(l)
Rate of melting of ice = Rate of freezing of water.
The system here is in dynamic equilibriums and following can be inferred.
(a) Both the opposing processes occur simultaneously
(b) Both the processes occur at the same rate so that the amount of ice and water – remains constant.
(ii) Liquid-Vapour Equilibrium
The equilibrium can be represented as
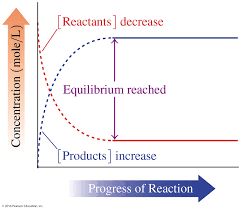
Rate of evaporation = Rate of condensation
When there is an equilibrium between liquid and vapours, it is called liquid-vapour equilibrium.
(iii) Solid-Vapour Equilibrium
This type of equilibrium is attained where solids sublime to vapour phase. For example, when solid iodine is placed in a closed vessel, violet vapours start appearing in the vessel whose intensity increases with time and ultimately, it becomes constant.
The equilibrium may be represented as I2 (s) ↔ I2 (vapour)
Rate of sublimation of solid I2 to from vapour = rate of condensation of I2 vapour to give solid I2.
• Equilibrium involving Dissolution of Solid in Liquid
Solution: When a limited amount of salt or sugar or any solute dissolves in a given amount of water solution is formed.
At a given temperature state is reached when no more solute can be dissolved then the solution is called saturated solution.
The equilibrium between a solid and its solution is indicated by the saturated solution and may be represented as
Rate of dissolution = rate of precipitation
Sugar (s) ↔ Sugaer (in solution)
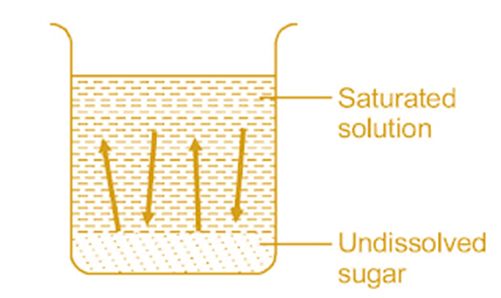
Here dissolution and precipitation takes place with the same speed.
On adding a small amount of radioactive sugar to the saturated solution it will be found that the sugar present in the solution as well as in the solid state is radioactive.
• Equilibrium between a Gas and its Solution in Liquid
This type of equilibrium can be seen by the following example:
Let us consider a sealed soda water bottle in which C02 gas is dissolved under high pressure. A state of equilibrium is attained between CO2 present in the solution and vapours of the gas
CO2(g) ↔ CO2 (present in solution)
Henry’s law: The solubility of a gas in a liquid at a certain temperature is governed by Henry’s law. It states that the mass of a gas that dissolves in a given mass of a solvent at any temperature is proportional to the pressure of the gas above the surface of the solvent.
Mathematically,
m ∝ p
m = KH p
where, KH = Henry’s constant
• Characteristics of Equilibria Involving Physical Processes
(i) The equilibrium can be attained only in closed systems at a given temperature.
(ii) At the equilibrium the measurable properties of the system remain constant.
(iii) The equilibrium is dynamic since both the forward and backward processes occur at same rate.
(iv) At equilibrium, the concentrations of substances become constant at constant temperature.
(v) The value of equilibrium constant represents the extent to which the process proceeds before equilibrium is achieved.
2. ATOMIC MODELS
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
ATOMIC MODELS
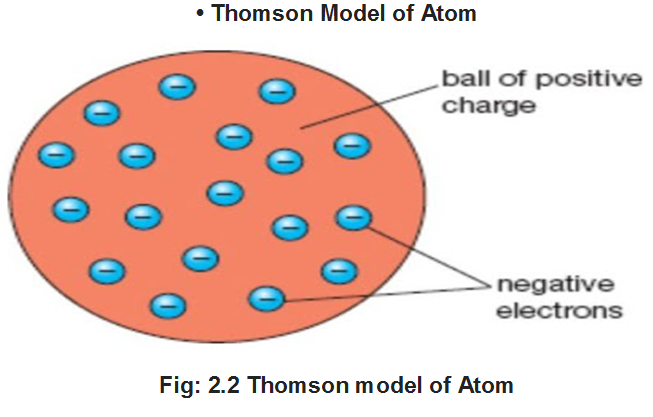
(i) J. J. Thomson proposed that an atom may be regarded as a sphere of approximate radius 1CT8 cm carrying positive charge due to protons and in which negatively charged electrons are embedded.
(ii) In this model, the atom is visualized as a pudding or cake of positive charge with electrons embedded into it.
(iii) The mass of atom is considered to be evenly spread over the atom according to this model.
Drawback of Thomson Model of Atom This model was able to explain the overall neutrality of the atom, it could not satisfactorily, explain the results of scattering experiments carried out by Rutherford in 1911.
• Rutherford’s a-particle Scattering Experiment
Rutherford in 1911, performed some scattering experiments in which he bombarded thin foils of metals like gold, silver, platinum or copper with a beam of fast moving a-particles. The thin gold foil had a circular fluorescent zinc sulphide screen around it. Whenever a-particles struck the screen, a tiny flash of light was produced at that point.
From these experiments, he made the following observations:
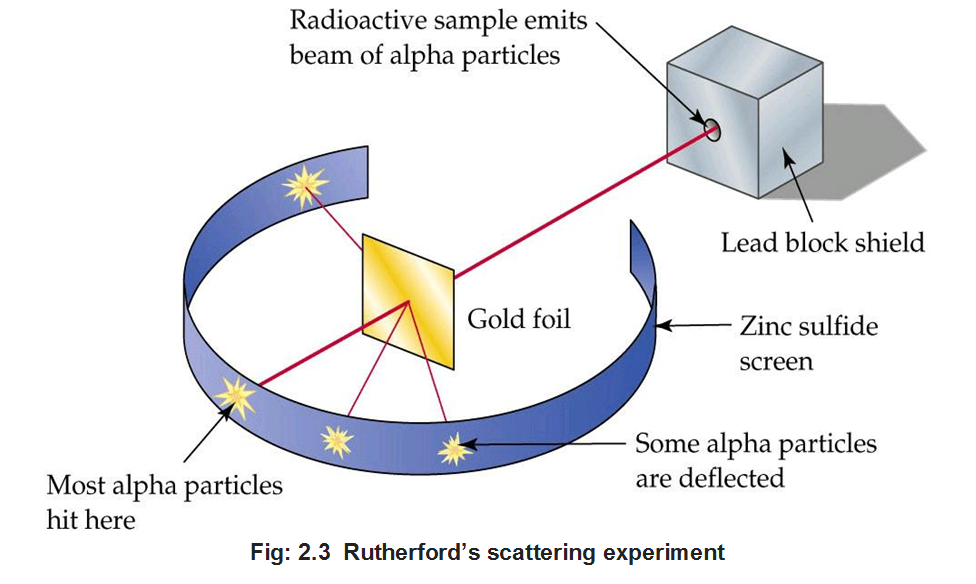
(i) Most of the a-particles passed through the foil without undergoing any deflection,
(ii) A few a-particles underwent deflection through small angles.
(iii) Very few mere deflected back i.e., through an angle of nearly 180°.
From these observations, Rutherford drew the following conclusions:
(i) Since most of the a-particles passed through the foil without undergoing any deflection, there must be sufficient empty space within the atom.
(ii) A small fraction of a-particles was deflected by small angles. The positive charge has to be concentrated in a very small volume that repelled and deflected a few positively charged a-particles. This very small portion of the atom was called nucleus.
(iii) The volume of nucleus is very small as compared to total volume of atom.
• Rutherford’s Nuclear Model of an Atom
(i) The positive charge and most of the mass of the atom was densely concentrated in an extremely small region. This very small portion of the atom was called nucleus by Rutherford.
(ii) The nucleus is surrounded by electrons that move around the nucleus with a very high speed in circular paths called orbits.
(iii) Electrons and nucleus are held together by electrostatic forces of attraction.
• Atomic Number
The number of protons present in the nucleus is equal to the atomic number (z). For example, the number of protons in the hydrogen nucleus is 1, in sodium atom it is 11, therefore, their atomic numbers are 1 and 11. In order to keep the electrical neutrality, the number of electrons in an atom is equal to the number of protons (atomic number, z). For example, number of electrons in hydrogen atom and sodium atom are 1 and 11 respectively.
Atomic Number (z) = Number of protons in the nucleus of an atom.
= Number of electrons in a neutral atom.
• Mass Number
Number of protons and neutrons present in the nucleus are collectively known as nucleons. The total number of nucleons is termed as mass number (A) of the atom.
Mass Number (A) = Number of protons (p) + Number of neutrons (n).
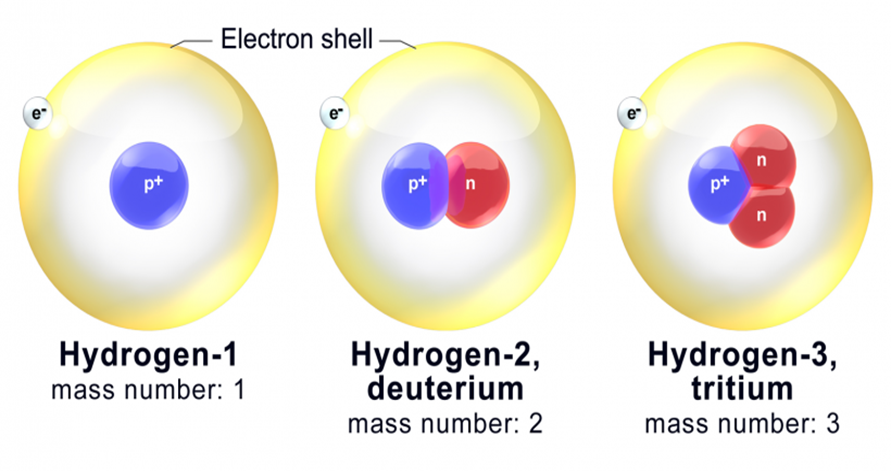
• Isotopes
Atoms with identical atomic number but different atomic mass number are known as Isotopes.
Isotopes of Hydrogen:

These three isotopes are shown in the figure below:
Isotope of Chlorine:
There are two isotope of chlorine with mass numbers 35 and 37.

The two isotope differ in their number of neutron having 18 and 20 neutrons respectively.
Isotope of some common elements

Characteristics of Isotopes
(i) Since the isotopes of an element have the same atomic number, but different mass number, the nuclei of isotopes contain the same number of protons, but different number of neutrons.
(ii) Since, the isotopes differ in their atomic masses, all the properties of the isotopes depending upon the mass are different.
(iii) Since, the chemical properties are mainly determined by the number of protons in the nucleus, and the number of electrons in the atom, the different isotopes of an element exhibit similar chemical properties For example, all the isotopes of carbon on burning give carbon dioxide.
• Isobars
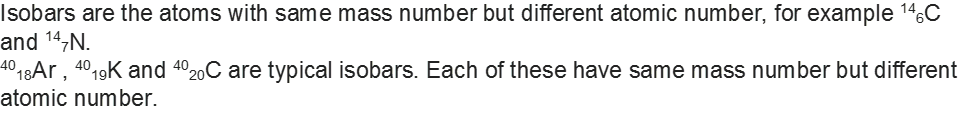
• Drawbacks of Rutherford Model
(i) When a body is moving in an orbit, it achieves acceleration. Thus, an electron moving around nucleus in an orbit is under acceleration.
According to Maxwell’s electromagnetic theory, charged particles when accelerated must emit electromagnetic radiations. Therefore, an electron in an orbit will emit radiations, the energy carried by radiation comes from electronic motion. Its path will become closer to nucleus and ultimately should spiral into nucleus within . 10-8 s. But actually this does not happen.
Thus, Rutherford’s model cannot explain the stability of atom if the motion of electrons is described on the basis of classical mechanics and electromagnetic theory.
(ii) Rutherford’s model does not give any idea about distribution of electrons around the nucleus and about their energies.
3. DEVELOPMENTS LEADING TO THE BOHR’S MODEL OF ATOM
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
DEVELOPMENTS LEADING TO THE BOHR’S MODEL OF ATOM
Two developments played a major role in the formulation of Bohr’s model of atom. These were:
(i) Dual character of the electromagnetic radiation which means that radiations possess both wave like and particle like properties.
(ii) Experimental results regarding atomic spectra which can be explained only by assuming quantized electronic energy levels in atoms.
• Nature of Electromagnetic Radiation (Electromagnetic Wave Theory)
This theory was put forward by James Clark Maxwell in 1864. The main points of this theory are as follows:
(i) The energy is emitted from any source (like the heated rod or the filament of a bulb through which electric current is passed) continuously in the form of radiations and is called the radiant energy.
(ii) The radiations consist of electric and magnetic fields oscillating perpendicular to each other and both perpendicular to the direction of propagation of the radiation.
(iii) The radiations possess wave character and travel with the velocity of light 3 x 108 m/sec.
(iv) These waves do not require any material medium for propagation. For example, rays from the sun reach us through space which is a non-material medium.
• Characteristics of a Wave
Wavelength: It is defined as the distance between any two consecutive crests or troughs. It is represented by X and its S.I. unit is metre.
![]()
Frequency: Frequency of a wave is defined as the number of waves passing through a point in one second. It is represented by v (nu) and is expressed in Hertz (Hz).
1 Hz = 1 cycle/sec.
Velocity: Velocity of a wave is defined as the linear distance travelled by the wave in one second.
It is represented by c and is expressed in cm/sec or m/sec.
Amplitude: Amplitude of a wave is the height of the crest or the depth of the through. It is represented by V and is expressed in the units of length.
Wave Number: It is defined as the number of waves present in 1 metre length. Evidently it will be equal to the reciprocal of the wavelength. It is represented by bar v (read as nu bar).
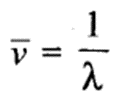
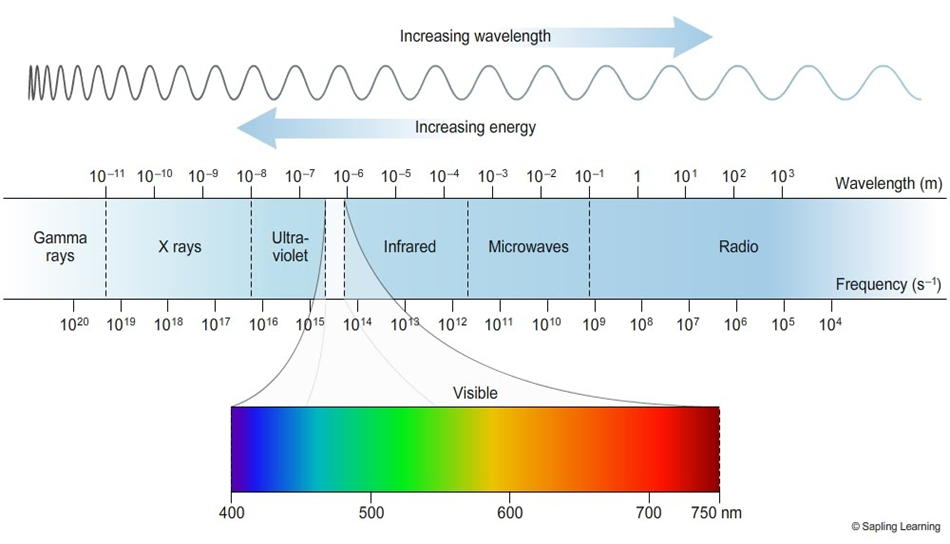
Electromagnetic Spectrum: When electromagnetic radiations are arranged in order of their increasing wavelengths or decreasing frequencies, the complete spectrum obtained is called electromagnetic spectrum.
![]()
• Limitations of Electromagnetic Wave Theory
Electromagnetic wave theory was successful in explaining properties of light such as interference, diffraction etc; but it could not explain the following:
(i) The phenomenon of black body radiation.
(ii) The photoelectric effect.
(iii) The variation of heat capacity of solids as a function of temperature.
(iv) The line spectra of atoms with reference to hydrogen.
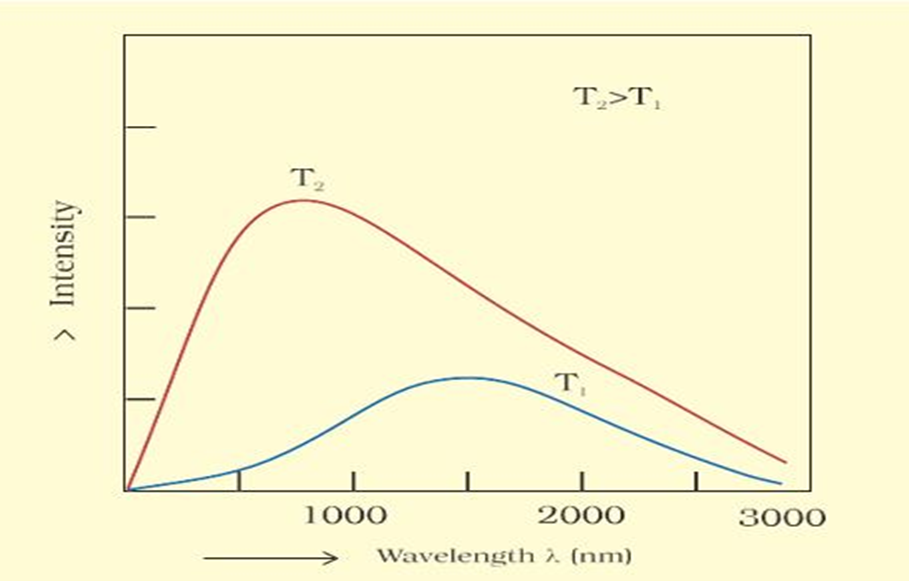
• Black Body Radiation
The ideal body, which emits and absorbs all frequencies is called a black body and the radiation emitted by such a body is called black body radiation. The. exact frequency distribution of the emitted radiation from a black body depends only on its temperature.
![]()
At a given temperature, intensity of radiation emitted increases with decrease of wavelength, reaches a maximum value at a given wavelength and then starts decreasing with further decrease of wavelength as shown in Fig 2.6.
• Planck’s Quantum Theory
To explain the phenomenon of ‘Black body radiation’ and photoelectric effect, Max Planck in 1900, put forward a theory known as Planck’s Quantum Theory.
This theory was further extended by Einstein in 1905. The main points of this theory was as follows: ,
(i) The radiant energy emitted or absorbed in the form of small packets of energy. Each such packets of energy is called a quantum.
(ii) The energy of each quantum is directly proportional to the frequency of the radiation
E ∝ ν
E = hν
where h is a proportionality constant, called Planck’s constant. Its value is equal to
6.626 x 10-34 J sec.
• Photoelectric Effect
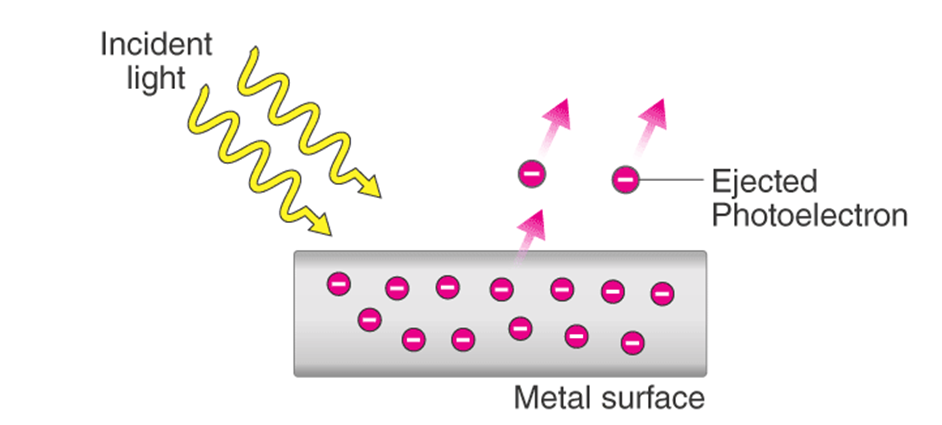
Hertz, in 1887, discovered that when a beam of light of certain frequency strikes the surface of some metals, electrons are emitted or ejected from the metal surface. The phenomenon is called photoelectric effect.
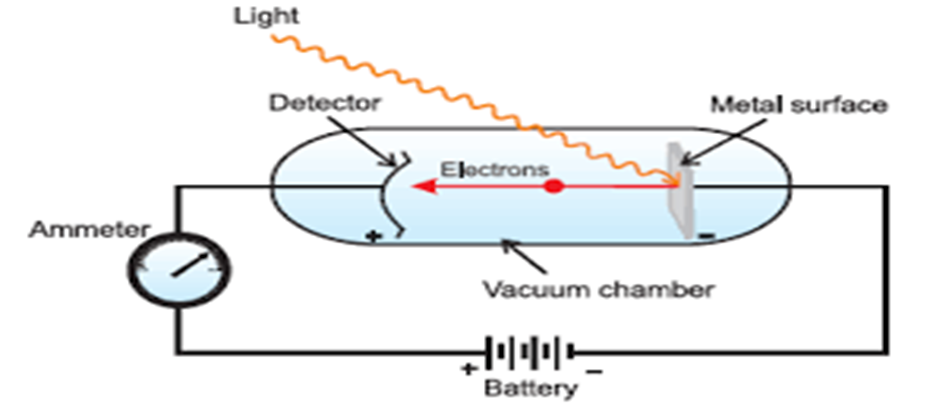
Observations in Photoelectric Effect
(i) Only photons of light of certain minimum frequency called threshold frequency (v0) can cause the photoelectric effect. The value of v0 is different for different metals.
(ii) The kinetic energy of the electrons which are emitted is directly proportional to the frequency of the striking photons and is quite independent of their intensity.
(iii) The number of electrons that are ejected per second from the metal surface depends upon the intensity of the striking photons or radiations and not upon their frequency.
Explanation of Photoelectric Effect
Einstein in (1905) was able to give an explanation of the different points of the photoelectric effect using Planck’s quantum theory as under:
(i) Photoelectrons are ejected only when the incident light has a certain minimum frequency (threshold frequency v0)
(ii) If the frequency of the incident light (v) is more than the threshold frequency (v0), the excess energy (hv – hv0) is imparted to the electron as kinetic energy.
K.E. of the ejected electron
energy of the emitted electron.
(iii) On increasing the intensity of light, more electrons are ejected but the energies of the electrons are not altered.
• Dual Behaviour of Electromagnetic Radiation
From the study of behaviour of light, scientists came to the conclusion that light and other electromagnetic radiations have dual nature. These are wave nature as well as particle nature. Whenever radiation interacts with matter, it displays particle like properties in contrast to the wavelike properties (interference and diffraction) which it exhibits when it propagates. Some microscopic particles, like electrons, also exhibit this wave-particle duality.
• Spectrum
When a ray of white light is passed through a prism the wave with shorter wavelength bends more than the one with a longer wavelength. Since ordinary white light consists of waves with all the wavelengths in the visible range, array of white light is spread out into a series of coloured bands called spectrum. The light of red colour which has longest wavelength is deviated the least while the violet light, which has shortest wavelength is deviated the most.
Continuous Spectrum
When a ray of white light is analysed by passing through a prism it is observed that it splits up into seven different wide bands of colours from violet to red (like rainbow). These colours are so continuous that each of them merges into the next. Hence, the spectrum is called continuous spectrum.
Emission Spectra
Emission Spectra is noticed when the radiations emitted from a source are passed through a prism and then received on the photographic plate. Radiations can be emitted in a number of ways such as:
(i) from sun or glowing electric bulb.
(ii) by passing electric discharge through a gas at low pressure.
(iii) by heating a substance to high temperature.
Line Spectra When the vapours of some volatile substance are allowed to fall on the flame of a Bunsen burner and then analysed with the help of a spectroscope. Some specific coloured lines appear on the photographic plate which are different for different substances. For example, sodium or its salts emit yellow light while potassium or its salts give out violet light.
Absorption Spectra
When white light is passed through the vapours of a substance and the transmitted light is then allowed to strike a prism, dark lines appear in the otherwise continuous spectrum. The dark lines indicate that the radiations corresponding to them were absorbed by the substance from the white light. This spectrum is called absorption spectrum.
Dark lines appear exactly at the same positions where the lines in the emission spectra appear.
• Line Spectrum of Hydrogen
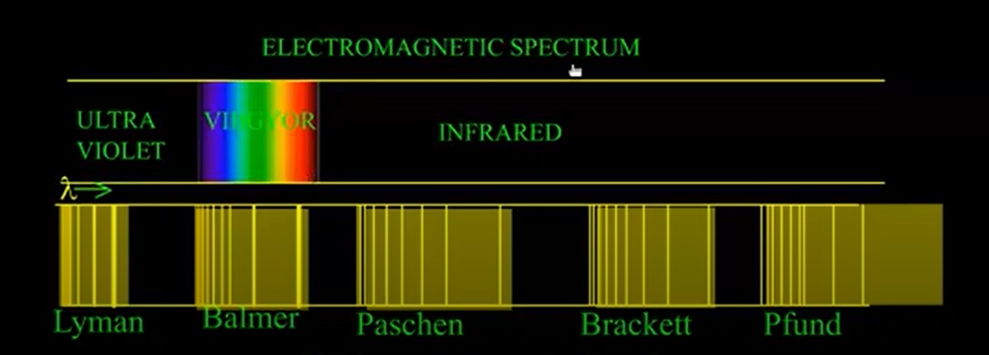
When electric discharge is passed through hydrogen gas enclosed in discharge tube under low pressure and the emitted light is analysed by a spectroscope, the spectrum consists of a large number of lines which are grouped into different series. The complete spectrum is known as hydrogen spectrum.
On the basis of experimental observations, Johannes Rydberg noted that all series of lines in the hydrogen spectrum could be described by the following expression:

![]()
Rydberg in 1890, and has given a simple theoretical equation for the calculation of wavelengths and wave numbers of the spectral lines in different series of hydrogen spectrum. The equation is known as Rydberg formula (or equation).
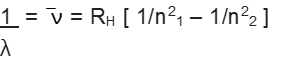
This relation is valid for hydrogen atom only. For other species,
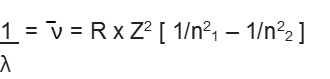
where Z is the atomic number of the species.
Here RH = constant, called Rydberg constant for hydrogen and n1 , n2 are integers (n2 > n1)
For any particular series, the value of n1 is constant while that of n2 changes. For example,
For Lyman series, n1= 1, n2= 2, 3, 4, 5………..
For Balmer series, n1 = 2, n2 = 3, 4, 5, 6………..
For Paschen series, n1= 3, n2 = 4, 5, 6, 7………..
For Brackett series,n1 = 4, n2 = 5, 6, 7, 8………..
For Pjund series, n1 =5, n2 = 6, 7, 8, 9………..
Thus, by substituting the values of n1 and n2 in the above equation, wavelengths and wave number of different spectral lines can be calculated. When n1 = 2, the expression given above is called Balmer’s formula.
4. BOHR’S MODEL FOR HYDROGEN ATOM
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
BOHR’S MODEL OF ATOM
Niels Bohr in 1913, proposed a new model of atom on the basis of Planck’s Quantum Theory. The main points of this model are as follows:
(i) In an atom, the electrons revolve around the nucleus in certain definite circular paths called orbits.
(ii) Each orbit is associated with definite energy and therefore these are known as energy
levels or energy shells. These are numbered as 1, 2, 3, 4……….. or K, L, M, N………..
(iii) Only those energy orbits are permitted for the electron in which angular momentum of the electron is a whole number multiple of h/2π
Angular momentum of electron (mvr) = nh/2π (n = 1, 2, 3, 4 etc).
m = mass of the electron.
v = tangential velocity of the revolving electron.
r = radius of the orbit.
h = Planck’s constant.
n is an integer.
(iv) As long as electron is present in a particular orbit, it neither absorbs nor loses energy and its energy, therefore, remains constant.
(v) When energy is supplied to an electron, it absorbs energy only in fixed amounts as quanta and jumps to higher energy state away from the nucleus known as excited state. The excited state is unstable, the electron may jump back to the lower energy state and in doing so, it emits the same amount of energy. (∆E = E2 – E1).
• Achievements of Bohr’s Theory
1. Bohr’s theory has explained the stability of an atom.
2. Bohr’s theory has helped in calculating the energy of electron in hydrogen atom and one electron species. The mathematical expression for the energy in the nth orbit is,
The main achievements of Bohr’s theory of the atom are:
1. It can explain the stability of atom.
2. It successfully explain the line spectrum of hydrogen.
3. It explain the line spectra of single electron ions like He+ and Li2+
• Limitations of Bohr’s Model
(i) The theory could not explain the atomic spectra of the atoms containing more than one electron or multi electron atoms.
(ii) Bohr7s theory failed to explain the fine structure of the spectral lines.
(iii) Bohr’s theory could not offer any satisfactory explanation of Zeeman effect and Stark effect.
(iv)Bohr’s theory failed to explain the ability of atoms to form molecule formed by chemical bonds.
(v) It was not in accordance with the Heisenberg’s uncertainty principle.
5. TOWARDS QUANTUM MECHANICAL MODEL OF THE ATOM
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
TOWARDS QUANTUM MECHANICAL MODEL OF THE ATOM
• Dual Behaviour of Matter (de Broglie Equation)
de Broglie in 1924, proposed that matter, like radiation, should also exhibit dual behaviour i.e., both particle like and wave like properties. This means that like photons, electrons also have momentum as well as wavelength.
From this analogy, de Broglie gave the following relation between wavelength (λ) and momentum (p) of a material particle.
λ = h/mv
= h/p
Where, m = mass of the particle
v = velocity of particle
p = momentum of the particle
this relationship has been verified by an experiment.
• Heisenberg’s Uncertainty Principle
It states that, “It is impossible to determine simultaneously, the exact position and exact momentum (or velocity) of an electron”.
Mathematically it can be given as,
Δx × ΔPx ≥ h/4π
Or
Δx × Δ(mvx) ≥ h/4π
Or
Δx × Δvx ≥ h/4πm
Where Δx is the uncertainty in position and ΔPx (or ΔVx) is the uncertainty in momentum (velocity) of the particle and h is ‘Plank’s constant.
• Significance of Uncertainty Principle
(i) It rules out existence of definite paths or trajectories of electrons and other similar particles.
(ii) The effect of Heisenberg’s uncertainty principle is significant only for microscopic objects and is negligible for macroscopic objects.
• Reasons for the Failure of Bohr Model
(i) The wave character of the electron is not considered in Bohr Model.
(ii) According to Bohr Model an orbit is a clearly defined path and this path can completely be defined only if both the position and the velocity of the electron are known exactly at the same time. This is not possible according to the Heisenberg’s uncertainty principle.
6. QUANTUM MECHANICAL MODEL OF ATOM
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
QUANTUM MECHANICAL MODEL OF ATOM
Quantum mechanics: Quantum mechanics is a theoretical science that deals with the study of the motions of the microscopic objects that have both observable wave like and particle like properties.
Important Features of Quantum Mechanical Model of Atom
(i) The energy of electrons in atom is quantized i.e., can only have certain values.
(ii) The existence of quantized electronic energy level is a direct result of the wave like properties of electrons.
(iii) Both the exact position and exact velocity of an electron in an atom cannot be determined simultaneously.
(iv) An atomic orbital has wave function φ. There are many orbitals in an atom. Electron occupy an atomic orbital which has definite energy. An orbital cannot have more than two electrons. The orbitals are filled in increasing order of energy. All the information about the electron in an atom is stored in orbital wave function φ.
(v) The probability of finding electron at a point within an atom is proportional to square of orbital wave function i.e., |φ2|at that point. It is known as probability density and is always positive.
From the value of φ2 at different points within atom, it is possible to predict the region around the nucleus where electron most probably will be found.
• Quantum Numbers
Atomic orbitals can be specified by giving their corresponding energies and angular momentums which are quantized (i.e., they have specific values). The quantized values can be expressed in terms of quantum number. These are used to get complete information about electron i.e., its location, energy, spin etc.
Principal Quantum Number (n)
It is the most important quantum number since it tells the principal energy level or shell to which the electron belongs. It is denoted by the letter V and can have any integral value except zero, i.e., n = 1, 2, 3, 4……….. etc.
The various principal energy shells are also designated by the letters, K, L, M, N, O, P ….. etc. Starting from the nucleus.
The principal quantum number gives us the following information:
(i) It gives the average distance of the electron from the nucleus.
(ii) It completely determines the energy of the electron in hydrogen atom and hydrogen like particles.
(iii) The maximum number of electrons present in any principal shell is given by 2n2 where n is the number of the principal shell.
Azimuthal or Subsidiary or Orbital Angular Quantum Number (l)
It is found that the spectra of the elements contain not only the main lines but there are many fine lines also present. This number helps to explain the fine lines of the spectrum.
The azimuthal quantum number gives the following information:
(i) The number of subshells present in the main shell.
(ii) The angular momentum of the electron present in any subshell.
(iii) The relative energies of various subshells.
(iv) The shapes of the various subshells present within the same principal shell.
This quantum number is denoted by the letter T. For a given value of n, it can have any value ranging from 0 to n – 1. For example,
For the 1st shell (k), n = 1, l can have only one value i.e., l = 0 For n = 2, the possible value of l can be 0 and 1.
Subshells corresponding to different values of l are represented by the following symbols:
value of l 0 1 2 3 4 5 ……………..
Notation for subshell s p d f g h ………………..
Magnetic Orbital Quantum Number (m or m1)
The magnetic orbital quantum number determines the number of preferred orientations of the electrons present in a subshell. Since each orientation corresponds to an orbital, therefore, the magnetic orbital quantum number determines the number of orbitals present in any subshell.
The magnetic quantum number is denoted by letter m or ml and for a given value of l, it can have all the values ranging from – l to + l including zero.
Thus, for energy value of l, m has 2l + 1 values.
For example,
For l = 0 (s-subshell), ml can have only one value i.e., m1 = 0.
This means that s-subshell has only one orientation in space. In other words, s-subshell has only one orbital called s-orbital.
Spin Quantum Number (S or ms)
This quantum number helps to explain the magnetic properties of the substances. A spinning electron behaves like a micro magnet with a definite magnetic moment. If an orbital contains two electrons, the two magnetic moments oppose and cancel each other.
• Shapes of s-orbitals
s-orbital is present in the s-subshell. For this subshell, l = 0 and ml = 0. Thus, s-orbital with only one orientation has a spherical shape with uniform electron density along all the three axes.
The probability of Is electron is found to be maximum near the nucleus and decreases with the increase in the distance from the nucleus. In 2s electron, the probability is also maximum near the nucleus and decreases to zero probability. The spherical empty shell for 2s electron is called nodal surface or simply node.
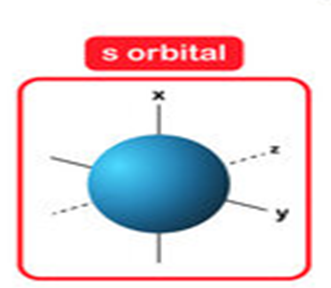
![]()
• Shapes of p-orbitals
p-orbitals are present in the p-subshell for which l = 1 and m1 can have three possible orientations – 1, 0, + 1.
Thus, there are three orbitals in the p-subshell which are designated as px, py and pz orbitals depending upon the axis along which they are directed. The general shape of a p-orbital is dumb-bell consisting of two portions known as lobes. Moreover, there is a plane passing through the nucleus along which finding of the electron density is almost nil. This is known as nodal plane as shown in the fig.
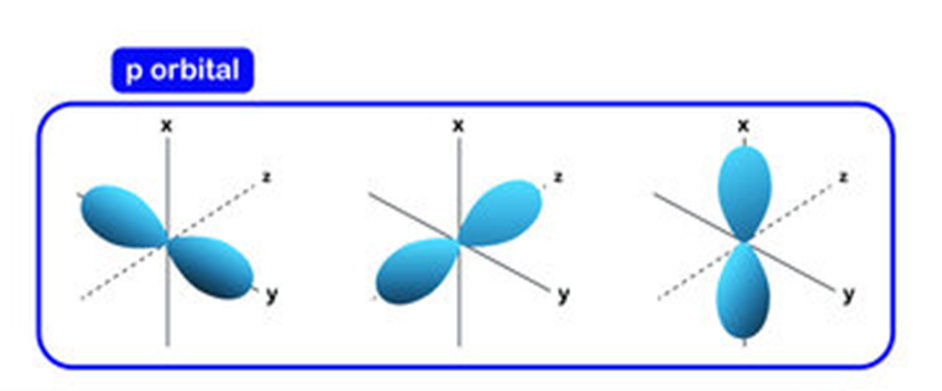
From the dumb-bell pictures, it is quite obvious that unlike s-orbital, a p-orbital is directional in nature and hence it influences the shapes of the molecules in the formation of which it participates.
• Shapes of d-orbitals
d-orbitals are present in d-subshell for which l = 2 and m[ = -2, -1, 0, +1 and +2. This means that there are five orientations leading to five different orbitals.
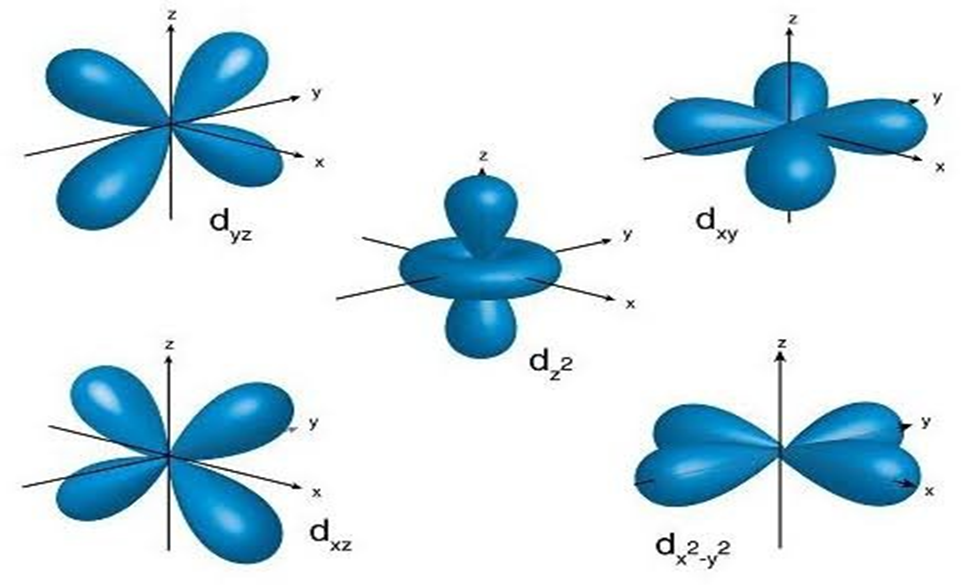
These five orientation are designated as dzy , dyz , dzx , dx2-y2 , dz2 . However they have the same energy are in degeneracy state and are known as degenerated orbitals. The first three orbitals have clover leaf shape and lie in different planes which are xy,yz,and zx planes respectively. The dx2-y2 orbital is also clover leaf shaped but its lobes are directed along the X and Y axis.
• Aufbau Principle
The principle states: In the ground state of the atoms, the orbitals are filled in order of their increasing energies.
In other words, electrons first occupy the lowest energy orbital available to them and enter into higher energy orbitals only after the lower energy orbitals are filled.
The order in which the energies of the orbitals increase and hence the order in which the orbitals are filled is as follows:
Is, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, id, 5p, 6s, if, 3d, 6p, 7s, 5f 6d, 7p
The order may be remembered by using the method given in fig. 2.11.
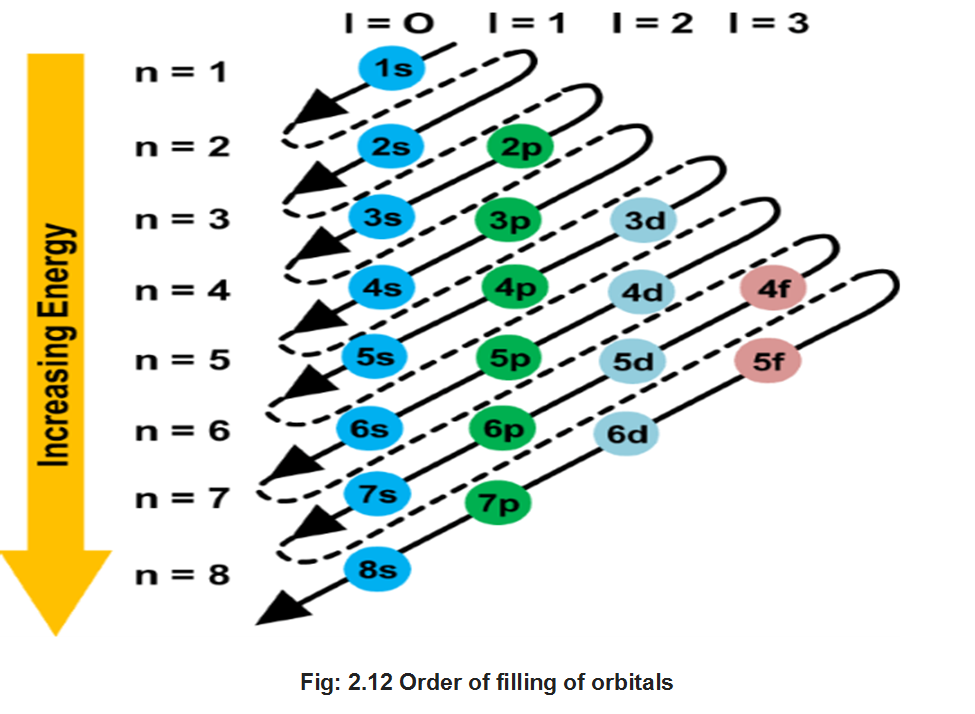
• Pauli Exclusion Principle
According to this principle, no two electrons in an atom can have the same set of four quantum numbers.
Pauli exclusion principle can also be stated as: Only two electrons may exist in the same orbital and these electrons must have opposite spins.
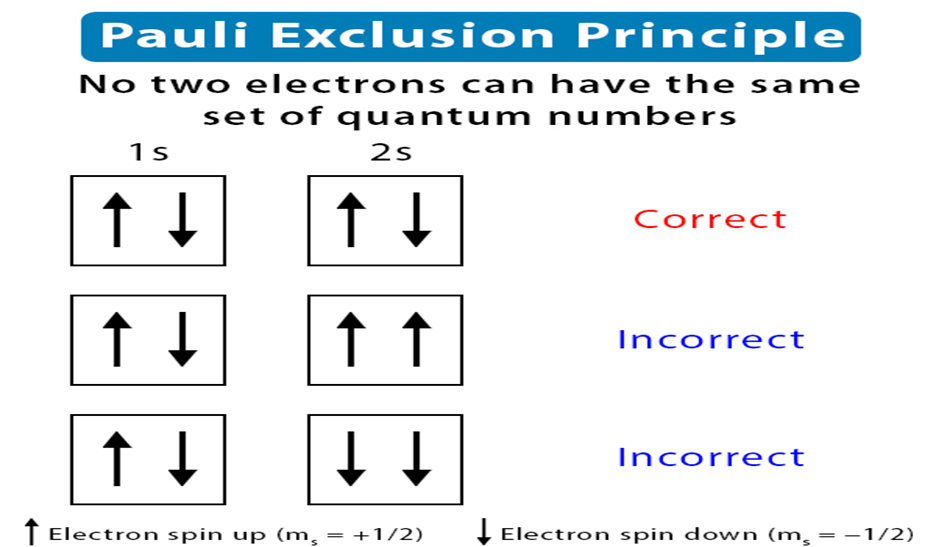
• Hund’s Rule of Maximum Multiplicity
It states that: pairing of electrons in the orbitals belonging to the same subshell (p, d or f) does not take place until each orbital belonging to that subshell has got one electron each i.e., it is singly occupied.
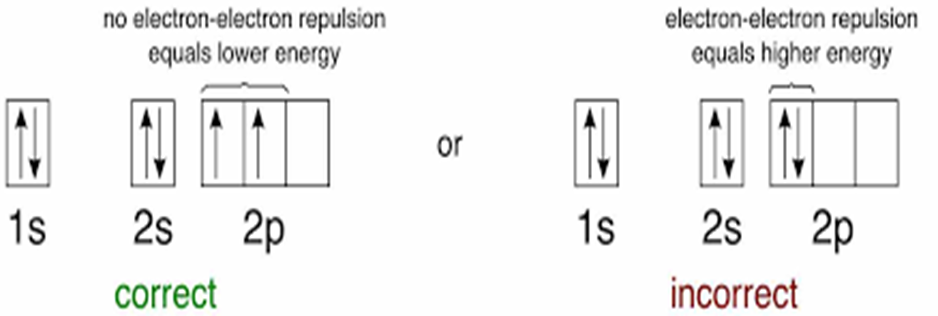
• Electronic Configuration of Atoms
The distribution of electrons into orbitals of an atom is called its electronic configuration. The electronic configuration of different atoms can be represented in two ways.
For example:

For example: the electronic configuration of hydrogen is

• Causes of Stability of Completely Filled and Half Filled Subshells
The completely filled and half filled subshells are stable due to the following reasons:
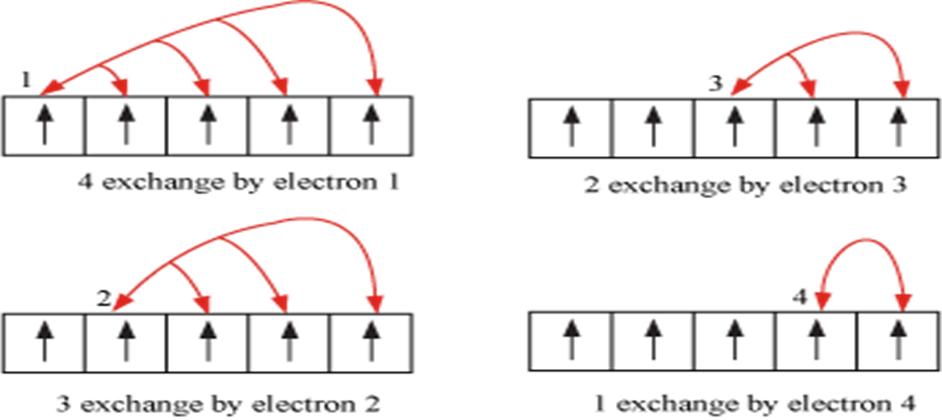
1. Symmetrical distribution of electrons: The completely filled or half filled subshells have symmetrical distribution of electrons in them and are therefore more stable.
2. The stabilizing effect arises whenever two or more electrons with same spin are present in the degenerate orbitals of a subshell. These electrons tend to exchange their positions
and the energy released due to their exchange is called exchange energy. The number of exchanges that can takes place is maximum when the subshell is either half filled or completely filled.
-As a result the exchange energy is maximum and so is the stability.
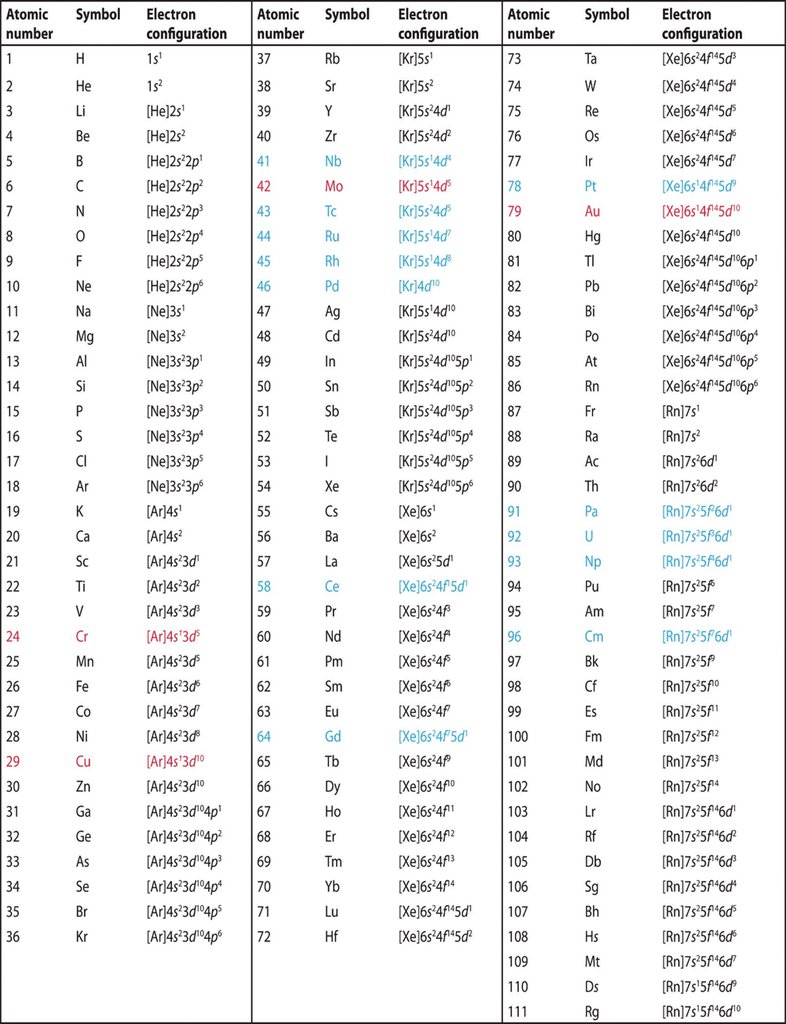
2. Genesis of periodic classification
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
GENESIS OF PERIODIC CLASSIFICATION DOBEREINER’S TRIADS
In 1829, Dobereiner arranged certain elements with similar properties in groups of three in such a way that the atomic mass of the middle element was nearly the same as the average atomic masses of the first and the third elements. A few triads proposed by him are listed.

Limitations of Dobereiner’s Trids
The triads given by Dobereiner were helpful in grouping some elements with similar characteristics together, but he could not arrange all the elements known at that time into triads.
• Newlands’ Law of Octaves
John Newlands proposed the law of octaves by stating that when elements are arranged in order of increasing atomic masses, every eighth element has properties similar to the first. Newlands called it law of octaves because similar relationship exists in the musical notes also.
This can be illustrated as

Limitations of Newlands’ Law of Octaves
(i) This classification was successful only up to the element calcium. After that, every eighth element did not possess the same properties as the element lying above it in the same group.
(ii) When noble gas elements were discovered at a later stage, their inclusion in the table disturbed the entire arrangement.
• Mendeleev’s Periodic Table
Mendeleev’s Periodic Law: The physical and chemical properties of the elements are a periodic
function of their atomic masses.
Mendeleev arranged the elements known at that time in order of increasing atomic masses
and this arrangement was called periodic table.
Elements with similar characteristics were present in vertical rows called groups. The horizontal
rows were known as periods.
Description of Mendeleev’s Periodic Table
(i) In the periodic table, the elements are arranged in vertical rows called groups and horizontal rows known as periods.
(ii) There are nine groups indicated by Roman Numerals as I, II, III, IV, V, VI, VII, VIII and zero. Group VIII consists of nine elements which are arranged in three triads. The zero group contains elements belonging to inert gases or noble gases and elements present have zero valency.
(iii) There are seven periods (numbered from 1 to 7) or, horizontal rows in the Mendeleev’s periodic table.
Importance of Mendeleev’s Periodic Table
(i) This made the study of the elements quite systematic in the sense that if the properties of one element in a particular group are known, those of others can be pridicted.
(ii) This helped to a great extent in the discovery of these elements at a later stage.
(iii) Mendeleev corrected the atomic masses of certain elements with the help of their expected positions and properties.
Defects in Mendeleev’s Periodic Table
(i) Hydrogen has been placed in group IA along with alkali metals. But it also resembles halogens of group VII A in many properties. Thus, its position is the Mendeleev’s periodic table is controversial.
(ii) Although the elements in the Mendeleev’s periodic table have been arranged in order of their atomic masses, but in some cases the element with higher atomic mass precedes the element with lower atomic mass.
(iii) We know that the isotopes of an element have different atomic masses but same atomic number. Since, periodic table has been framed on the basis of increasing atomic masses of the elements, different positions must have been allotted to all the isotopes of a particular element.
(iv) According to Mendeleev, the elements placed in the same group must resemble in their properties. But there is no similarity among the elements in the two sub-groups of a particular group.
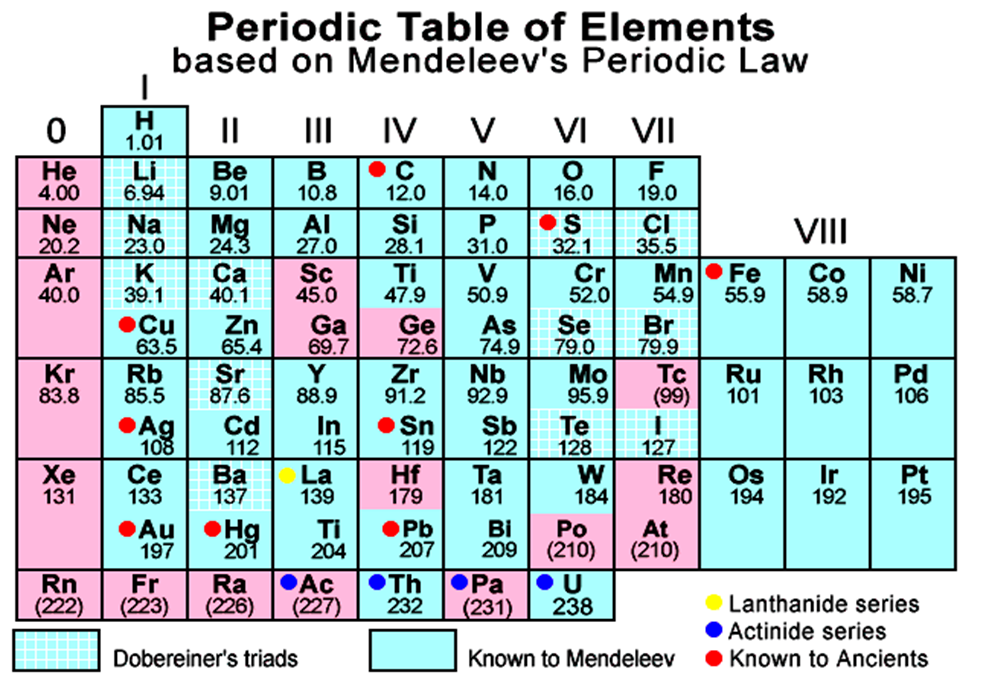
(v) In some cases, elements with similar properties have been placed in different groups.
(vi) Lanthanoids and actinoids were placed in two separate rows at the bottom of the periodic table without assigning a proper reason.
(vii) No proper explanation has been offered for the fact that why the elements placed in group show resemblance in their properties.
3. Modern periodic law
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
MODERN PERIODIC LAW
Physical and chemical properties of the elements are the periodic function of their atomic numbers.
• Present Form of the Periodic Table (Long form of Periodic Table)
The long form of periodic table, also called Modem Periodic Table, is based on Modern periodic law. In this table, the elements have been arranged in order of increasing atomic numbers.
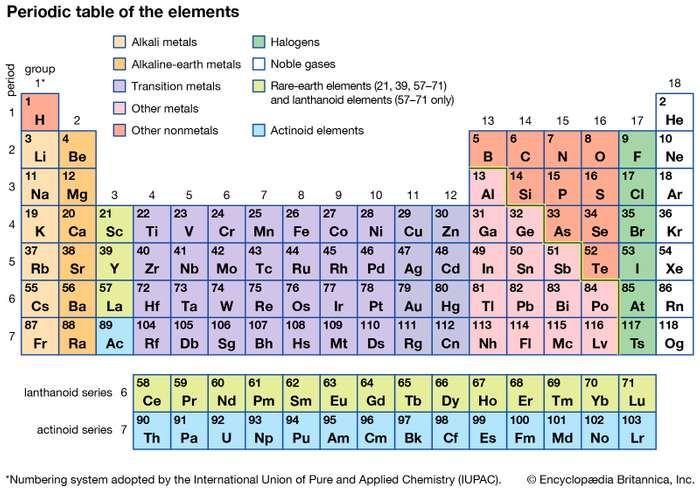
4. Nomenclature of elements
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
NOMENCLATURE OF ELEMENTS WITH ATOMIC NO. MORE THAN 100
There are around 118 elements in the modern periodic table.Out of 118 elements that have been discovered by scientists, 24 are synthetically developed by mankind and the rest are naturally occurring elements. Few of the elements from the 24 man-made elements were discovered much before and few others were discovered recently by a team that was headed by Glen Seaborg at the Lawrence Berkeley Laboratory in Berkeley, California.
The names and the symbols that are given to these elements are still not used universally. Some of them even had two names and symbols. For example, the element with the atomic number 104 was discovered by America as well as the Soviet Union. The American Scientist gave it the name Rutherfordium (Rf) whereas the name Kurchatovium (Ku) was established by scientists of the Soviet Union. In a similar manner, another element with the atomic number 107 is named Neilsbohrium (Ns) as well as Bohrium (Bh).
Thus a committee named commission on nomenclature of inorganic chemistry (CNIC) was issued by the IUPAC so that a particular IUPAC naming process should be assigned for the elements whose atomic number is greater than or equal to 100. In the year 1997, after an elaborate discussion with all the scientists around the world, IUPAC decided on the official names for elements with atomic numbers 104 to 110 and proposed a method for naming the elements.
In this article, you will get to know about the nomenclature of the elements above 100 and their IUPAC names as well. Generally, the discoverer of the element is given the honour to name the element discovered. The name of the chemical element comes from the physical or chemical properties, its origin, or mythical characters. The recommended name of an element is then consented to by the IUPAC (International Union of Pure and Applied Chemistry).
How The Elements With The Atomic Number (Z) Above 100 Assigned Names?
Most of the chemical elements have been assigned their symbols and names but still are not used universally. While studying the nomenclature of elements with an atomic number greater than 100, it was found that some elements are given two symbols or names.
For instance, an element with atomic number=104 was claimed by both Soviet and American scientists. The Americans assigned the element with the name Rutherfordium (Rf) whereas the Soviets named it Kurchatovium (Ku). Similarly, the element with Z=107 is assigned with the name Bohrium (Bh)
In 1978, IUPAC made a CNIC (Commission on Nomenclature of Inorganic Chemistry) to eradicate the element naming and symbol issues. The IUPAC gives a clear rule of the systematic nomenclature of elements with an atomic number above 100.
The Commission claimed that the elements must be named methodically by following the given below rules:
The names of the elements should be short. Additionally, the element name should be related to its atomic number.
Whether an element of atomic number 100 or above or it is a metal or non-metal, its name should end in ‘ium’.
In the systematic nomenclature of elements with atomic number 100, the element symbols should consist of three letters.
The symbol should be derived from the atomic numbers of the element and be visually connected to the names.
The elements with the atomic numbers (Z) from 101 to 103 have trivial names. Additionally, they have consistent two-letter symbols accepted by IUPAC. The chemical element with an atomic number above 100 is also referred to as super heavy elements.
The Commission mentions the use of three-letter structures for the chemical elements with Z=100 or above it. Because any scientifically derived set of two-letter symbols will tend to duplicate some of the elements of an atomic number less than 104.
Nomenclature Of Elements With Atomic Number (Z) Greater Than 100
The name of the element is directly derived from its atomic number by using the following numerical roots:
0 = nil (n)
1 = un (u)
2 = bi (b)
3 = tri (t)
4 = quad (q)
5 = pent (p)
6 = hex (h)
7 = sept (s)
8 = oct (o)
9 = enn (e)
The numerical roots are put together according to the digits, which make up the atomic number and end with “ium” to spell out the name.
The element symbol consists of the initial letters of the numerical roots, which make up the name.
In the name of the element, each root is pronounced separately such that the root ‘un’ should get pronounced with a long ‘u’.
For example, let us find the name of an element with atomic number 120:
Code for 1 is un
Code for 2 is bi
Code for 0 is nil
Hence the name of the element with atomic number 120 is un + bi + nil + ium (ending code), that is; unbinilium.
However, it is necessary to note that if the last digit code like bi ends with the letter ‘i’ then just add ‘um’. So, the ending, in that case, will be ‘um’ instead of ‘ium’.
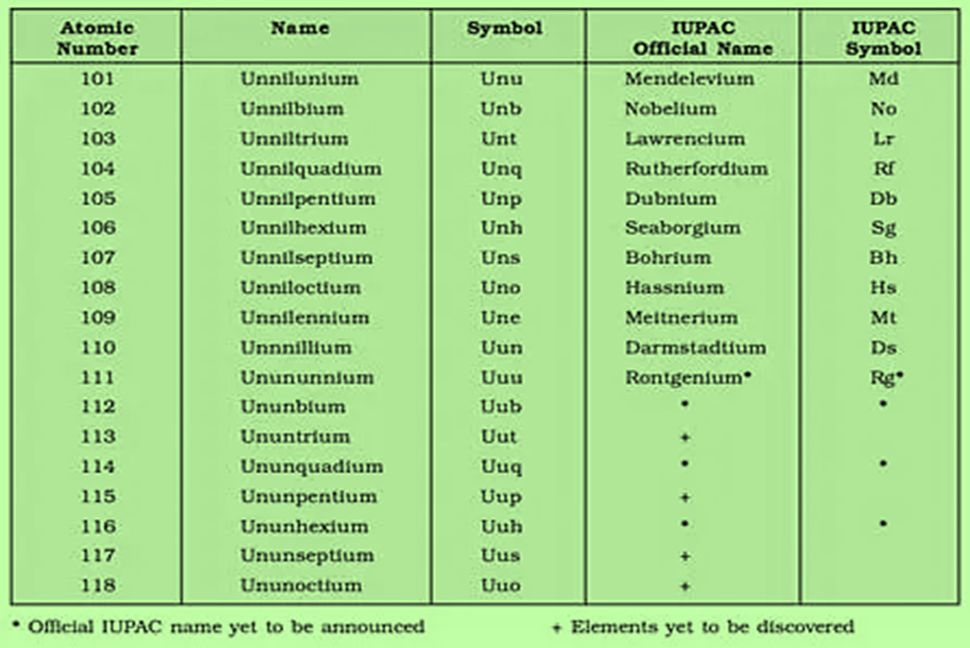
5. Electronic configurations
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
ELECTRONIC CONFIGURATIONS AND THE PERIODIC TABLE
The electronic configuration of an element is related to its position on the periodic table.
the number of circles in the electronic configuration of an element is represented in the periodic table as the period number that element is situated in
the number of electrons in the outermost shell of an element is represented in the periodic table as the group number that element is situated in
the number of electrons in all shells of an element is represented in the periodic table as the element's atomic number

The electronic configuration of sodium shows that sodium, Na:
- is in period 3
- is in group 1
- has an atomic number of (2 + 8 + 1) = 11
Electronic configurations and properties of elements
The electronic configurations of atoms help explain the properties of elements and the structure of the periodic table. When atoms collide and react, it is the outer electrons that meet and interact. So, elements in the same group have similar chemical properties because they have the same number of electrons in their outer shell.
The electronic configurations of the elements in group 1:
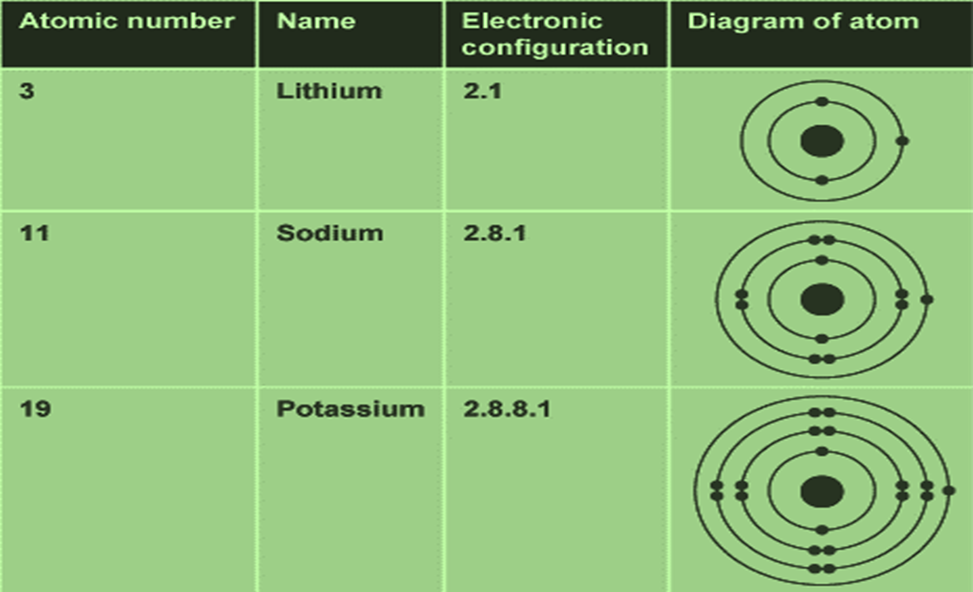
The atoms of all group 1 elements have similar chemical properties and reactions because they all have one electron in their outer shell. Similarly, the atoms of all group 7 elements have similar chemical properties and reactions to each other because all of them have seven electrons in their outer shell.
Groups
The long form of periodic table also consists of the vertical rows called groups. There are in all 18 groups in the periodic table. Unlike Mendeleev periodic table, each group is an independent group.
Characteristics of groups:
(i) All the elements present in a group have same general electronic configuration of the atoms.
(ii) The elements in a group are separated by definite gaps of atomic numbers (2, 8, 8,18, 18,32).
(iii) The atomic sizes of the elements in group increase down the group due to increase the number of shells.
(iv) The physical properties of the elements such as m.p., b.p. density, solubility etc., follow a systematic pattern.
(v) The elements in each group have generally similar chemical properties.
6. Electronic configurations and types of elements
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
ELECTRONIC CONFIGURATIONS AND TYPES OF ELEMENTS: s-, p-, d-, f- BLOCKS
Periods
Horizontal rows in a periodic table are known as periods.
There are in all seven periods in the long form of periodic table.
Characteristics of periods:
(i) In all the elements present in a period, the electrons are filled in the same valence shell.
(ii) The atomic sizes generally decrease from left to right.
s-Block Elements
General electronic configuration: ns1-2 Characteristics of s-block elements:
(i) All the elements are soft metals.
(ii) They have low melting and boiling points.
(iii) They are highly reactive.
(iv) Most of them impart colours to the flame.
(v) They generally form ionic compounds.
(vi) They are good conductors of heat and electricity. p-Block Elements
General electronic configuration: ns2np1-6
Characteristics of p-block elements:
(i) The compounds of these elements are mostly covalent in nature.
(ii) They show variable oxidation states.
(iii) In moving from left to right in a period, the non-metallic character of the elements increases.
(iv) The reactivity of elements in a group generally decreases downwards.
(v) At the end of each period is a noble gas element with a closed valence shell ns2 np6 configuration.
(vi) Metallic character increases as we go down the group.
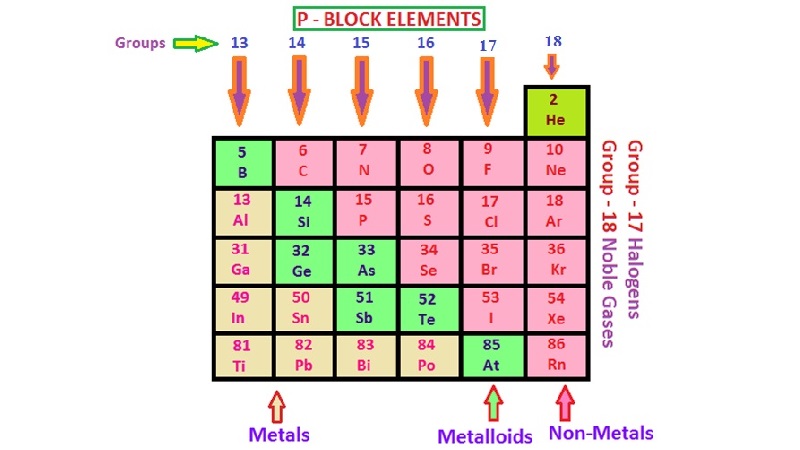
d-Block Elements:
General electronic configuration: (n -1) d1-10 ns0-2
The d-block elements are known as transition elements because they have incompletely filled d-orbitals in their ground state or in any of the oxidation states.
Characteristics of d-block elements:
(i) They are all metals with high melting and boiling points.
(ii) The compounds of the elements are generally paramagnetic in nature.
(iii) They mostly form coloured ions, exhibit variable valence (oxidation states).
(iv) They are of tenly used as catalysts.

f-Block Elements
General electronic configuration: (n – 2) f1-14 (n -1) d0-1 ns2
They are known as inner transition elements because in the transition elements of d-block, the electrons are filled in (n – 1) d sub-shell while in the inner transition elements of f-block the filling of electrons takes place in (n – 2) f subshell, which happens to be one inner subshell.
Characteristics of f-Block elements:
(i) The two rows of elements at the bottom of the Periodic Table, called the Lanthanoids Ce (Z = 58) – Lu (Z = 71) and Actinoids Th (Z = 90) – Lr (Z = 103).
(ii) These two series of elements are called Inner Transition Elements (f-Block Elements).
(iii) They are all metals. Within each series, the properties of the elements are quite similar.
(iv) Most of the elements pf the actinoid series are radio-active in nature.

• Metals
(i) Metals comprise more than 78% of all known elements and appear on the left side of the Periodic Table.
(ii) Metals are solids at room temperature.
(iii) Metal usually have high melting and boiling points.
(iv) They are good conductors of heat and electricity.
(u) They are malleable and ductile.
• Non-metals
(i) Non-metals are located at the top right hand side of the Periodic Table.
(ii) Non-metals are usually solids or gases at low temperature with low melting and boiling points.
(iii) They are poor conductors of heat and electricity.
(iv) The non-metallic character increases as one goes from left to right across the Periodic
Table.
(v) Most non-metallic solids are brittle and are neither malleable nor ductile.
• Metalloids
The elements (e.g., silicon, germanium, arsenic, antimony and tellurium) show the characteristic, of both metals and non-metals. These elements are also called semimetal.
• Noble Gases
– These are the elements present in group 18.
– Eash period ends with noble gas element.
– All the members are of gaseous nature and because of the presence of all the occupied filled orbitals, they have very little tendency to take part in chemical combination.
– These are also called inert gases.
• Representative Elements
The elements of group 1 (alkali metals), group 2 (alkaline earth metals) and group 13 to 17 constitute the representative elements. They are elements of s-block and p-block.
• Transition Elements
The transition elements include, all the d-block elements and they are present in the centre of the periodic table between s and p-block elements.
• Inner Transition Elements
Lanthanoids (the fourteen elements after Lanthanum) and actinides (the fourteen elements after actinium) are called inner transition elements. They are also called f-block elements.
The elements after uranium are also called transuranic elements.
7. Periodic trends of elements
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
PERIODIC TRENDS IN PROPERTIES OF ELEMENTS
Trends in Physical Properties
Atomic Radii: It is defined as the distance from the centre of the nucleus to the outermost shell containing the electrons. Depending upon whether an element is a non-metal or a metal, three different types of atomic radii are used. These are:
(a) Covalent radius (b) Ionic Radius (c) van der Waals radius (d) Metallic radius.
(a) Covalent Radius: It is equal to half of the distance between the centres of the nuclei of two atoms held together by a purely covalent single bond.
(b) Ionic Radius: It may be defined as the effictive distance from the nucleus of an ion upto which it has an influence in the ionic bond.
(c) van der Waals Radius: Atoms of Noble gases are held together by weak van der Waals forces of attraction. The van der Waals radius is half of the distance between the centre of nuclei of atoms of noble gases.
(d) Metallic Radius: It is defined as half of the intemuclear distance between the two adjacent metal ions in the metallic lattice.
• Variation of Atomic Radius in the Periodic Table
Variation in a Period: Along a period, the atomic radii of the elements generally decreases from left to right.
Variation in a group: The atomic radii of the elements in every group of the periodic table increases as we move downwards.

• Ionic Radius
The ionic radii can be estimated by measuring the distances between cations and anions in ionic crystals.
In general, the ionic radii of elements exhibit the same trend as the atomic radii.
Cation: The removal of an electron from an atom results in the formation of a cation. The radius of cation is always smaller than that of the atom.
Anion: Gain of an electron leads to an anion. The radius of the anion is always larger than that ‘ of the atom.
Isoelectronic Species: Some atoms and ions which contain the same number of electrons, we call them isoelectronic species. For example, O2-, F–, Na+ and Mg2+ have the same number of electrons (10). Their radii would be different because of their different nuclear charges.
• Ionization Enthalpy
It is the energy required to remove an electron from an isolated gaseous atom in its ground state.
M (g) + I.E ——->M+ (g) + e–
The unit of ionization enthalpy is kJ mol-1 and the unit of ionization potential is electron volt per atom.
Successive Ionization Enthalpies
If a gaseous atom is to lose more than one electron, they can be removed one after the other i.e., in succession and not simultaneously. This is known as successive ionization enthalpy (or potential).
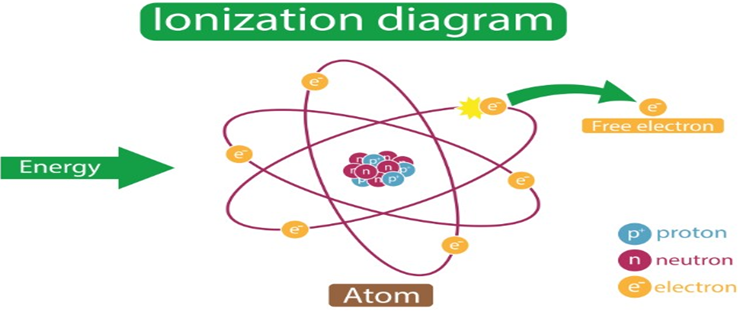
• Variation of Ionization Enthalpies in the Periodic Table:
Variation of Ionization Enthalpy Along a Period
Along a period ionization enthalpies are expected to increase in moving across from left to the right, because the nuclear charge increases and the atomic size decreases.
Variation of Ionization Ethalpy in a Group
The ionization enthalpies of the elements decrease on moving from top to the bottom in any group.
The decrease in ionization enthalpies down any group is because of the following factors.
(i) There is an increase in the number of the main energy shells (n) in moving from one element to the other.
(ii) There is also an increase in the magnitude of the screening effect due to the gradual increase in the number of inner electrons.
M(g) IE1 M+ + e-
M+(g) IE2 M2+ + e-
M2+(g) IE3 M3+ + e-
• Electron Gain Enthalpy
Electron Gain Enthalpy is the energy released when an electron is added to an isolated gaseous atom so as to convert it into a negative ion. The process is represented as:
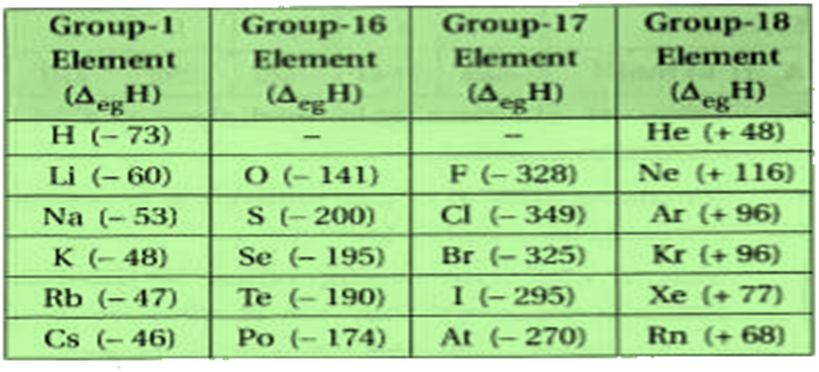
For majority of the elements the electron gain enthalpy is negative. For example, the electron gain enthalpy for halogens is highly negative because they can acquire the nearest noble gas configuration by accepting an extra electron.
In contrast, noble gases have large positive electron gain enthalpies because the extra electron has to be placed in the next higher principal quantum energy level thereby producing highly unstable electronic configuration.
Successive Electron Gain Enthalpies
We have studied that electrons from a gaseous atoms are lost in succession (i.e., one after the other). Similarly, these are also accepted one after the other, i.e., in succession. After the addition of one electron, the atom becomes negatively charged and the second electron is to be added to a negatively charged ion. But the addition of second electron is opposed by electrostatic repulsion and hence the energy has to be supplied for the addition of second electron. Thus the second electron gain enthalpy of an element is positive.
For example, when an electron is added to oxygen atom to form O– ion, energy is released. But when another electron is added to 0- ion to form O2- ion, energy is absorbed to overcome the strong electrostatic repulsion between the negatively charged 0– ion and the second electron being added. Thus, first electron gain enthalpy:
X(g) + e- X- (g)
Factors on which Electron Gain Enthalpy Depends
(i) Atomic size: As the size of an atom increases, the distance between its nucleus and the incoming electron also increases and electron gain enthalpy becomes less negative,
(ii)Nuclear charge: With the increase in nuclear charge, force of attraction between the nucleus and the incoming electron increases and thus electron gain enthalpy becomes more negative.
(iii) Symmetry of the Electronic Configuration: The atoms with symmetrical configuration (having fully filled or half filled orbitals in the same sub-shell) do not have any urge to take up extra electrons because their configuration will become unstable.
In that case the energy will be needed and electron gain enthalpy (Δ eg H) will be positive. For example, noble gas elements have positive electron gain enthalpies.
Variation of Electron Gain Enthalpy Across a Period
Electron gain ethalpy becomes more negative with increase in the atomic number across a period.
Variation of Electron Gain Enthalpy in a Group
Electron gain enthalpy becomes less negative as we go down a group.
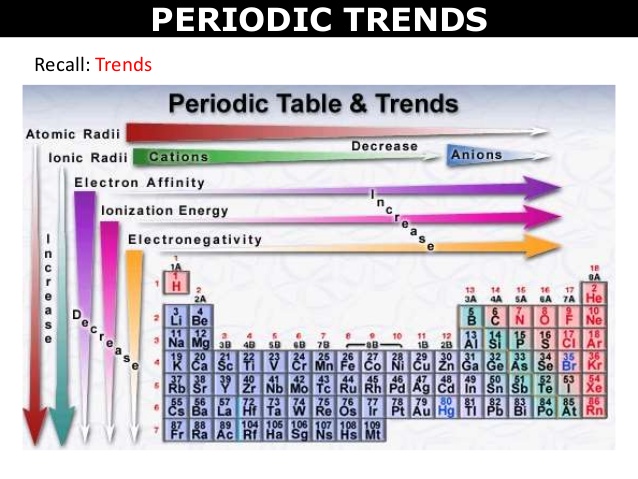
• Electronegativity
A qualitative measure of the ability of an atom in a chemical compound to attract shared electrons to itself is called electronegativity. Unlike ionization enthalpy and electron gain enthalpy, it is not a measurable quantity.
However, a number of numerical scales of electronegativity of elements viz, Pauling scale, Milliken- Jaffe scale, Allred Kochow scale have been developed. The electronegativity of any given element is not constant; it varies depending on the element to which it is bound.
Across a Period
Electronegativity generally increases across a period from left to right.
In a Group
It decreases down a group.
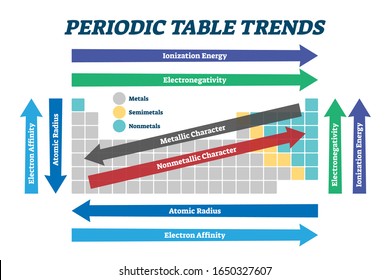
• Periodic Trends in Chemical Properties along a Period
(i) Metallic character: Decrease across a period maximum on the extreme left (alkali metals).
(ii) Non-metallic character: Increasess along a period. (From left to right).
(iii) Basic nature of oxides: Decreases from left to right in a period.
(iv) Acidic nature of oxides: Increases from left to right in a period.
• Variation from Top to Bottom on Moving Down a Group
(i) Metallic character. Generally increases because increase in atomic size and hence decrease in the ionizatiort energy of the elements in a group from top to bottom.
(ii) Non-metallic character. Generally decreases down a group. As electronegativity of elements decreases from top to bottom in a group.
(iii) Basic nature of oxides. Since metallic character or electropositivity of elements increases in going from top to bottom in a group basic nature of oxidise naturally increases.
(iv) Acidic character of oxides. Generally decreases as non-metallic character of elements decreases in going from top to bottom in a group.
(v) Reactivity of metals. Generally increases down a group. Since tendency to lose electron increases.
(vi) Reactivity of non-metals. Generally decreases down the group, Higher the electro-negativity of non-metals, greater is their reactivity. Since electronegativity of non-metals in a group decreases from top to bottom, their reactivity also decreases.
• Anomalous Properties of Second Period Elements
The first element of each of the group 1 (lithium) and 2 (beryllium) and group 13-17 (boron to fluorine) differs in many respect from the other members of their respective groups. For example, lithium unlike other alkali metals, and beryllium unlike other alkaline earth metals
form compounds which have significant covalent character; the other members of these groups, pre-dominatly form ionic compounds.
It has been observed that some elements of the second period show similarities with the elements of the third period placed diagonally to each other, though belonging to different groups.
For example,

This similarity in properties of elements placed diagonally to each other is called diagonal relationship.
• Mendeleev’s Periodic Law. Physical and chemical properties of elements are periodic function of their atomic masses.
• Modem Periodic Law. Physical and chemical properties of the elements are periodic function of their atomic numbers.
• Groups. There are 18 groups. These are vertical rows.
• Periods. There are 7 periods. These are horizontal rows.
• Representative Elements. The S and P block of elements are known as representative
elements.
• Transition Elements. They are also called d-block elements. They have general electronic
configuration (n – 1) d1-10 ns0-2.
• Inner Transition Elements. Lanthanoids (the fourteen elements after Lanthanum) and actinides (the fourteen elements after actinium) are called inner transition elements. General electronic configuration is (n – 2) f1-14(n – 1) d0-1 ns2.
They are also called f-block elements.
• Metals. Present on the left side of the periodic table. Comprise more than 78% of the known elements.
• Non-metals. Mostly located on the right hand side of the periodic table.
• Metalloids. Elements which line as the border line between metals and non-metals (e.g., Si, Ge, As) are called metalloids or semimetals.
• Atomic Radii and Ionic Radii, increase down the group decrease along the period.
• Ionization Enthalpy. Increases along the period and decreases down the group.
• Noble Gas Elements. Elements with symmetrical configuration are chemically inert in nature.
• Electric Nuclear Charge. Z = Nuclear charge – Screening constant.
• Electronegativity. Increases along a period decreases down the group,
• Chemical Reactivity. Chemical reactivity is highest at the two extremess of a period and lowest
in the centre.
• Oxides of Elements. Oxides formed of the Elements on the left are basic and of elements
on the right are acidic in nature.
Oxides of elements in the centre are amphoteric or neutral.
2. IONIC OR ELECTROVALENT BOND
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
IONIC OR ELECTROVALENT BOND
Ionic or Electrovalent bond is formed by the complete transfer of electrons from one atom to another. Generally, it is formed between metals and non-metals. We can say that it is the electrostatic force of attraction which holds the oppositely charged ions together.
The compounds which is formed by ionic or electrovalent bond is known as electrovalent compounds. For Example, ,
(i) NaCl is an electrovalent compound. Formation of NaCl is given below:
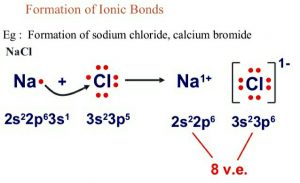
Na+ ion has the configuration of Ne while Cl– ion represents the configuration of Ar.
(ii) Formation of magnesium oxide from magnesium and oxygen.
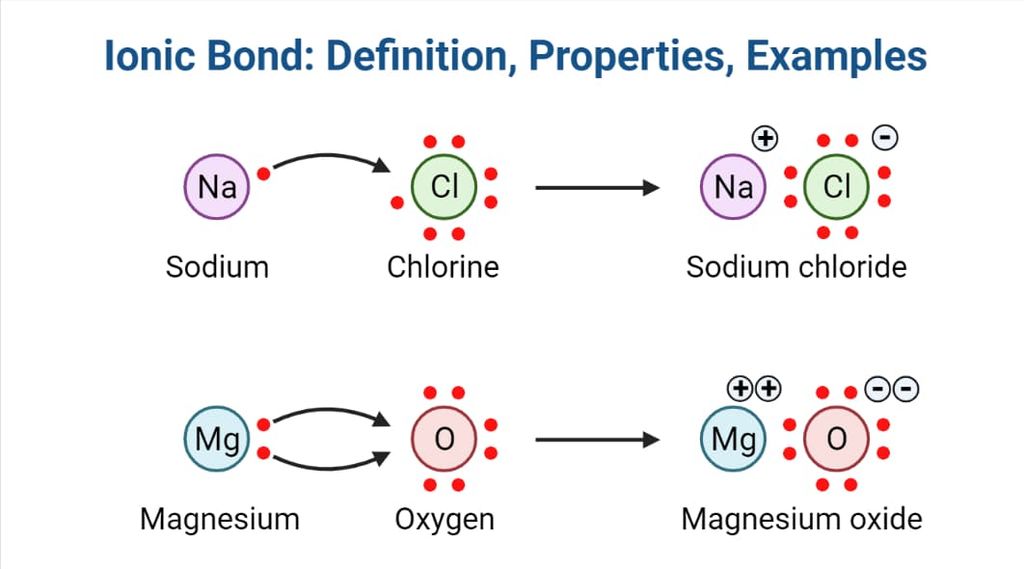
Electrovalency: Electrovalency is the number of electrons lost or gained during the formation of an ionic bond or electrovalent bond.
• Factors Affecting the Formation of Ionic Bond
(i) Ionization enthalpy: As we know that ionization enthalpy of any element is the amount of energy required to remove an electron from outermost shell of an isolated gaseous atom to convert it into cation.
Hence, lesser the ionization enthalpy, easier will be the formation of a cation and have greater chance to form an ionic bond. Due to this reason alkali metals have more tendency to form an ionic bond.
For example, in formation of Na+ ion I.E = 496 kJ/mole
While in case of magnesium, it is 743 kJ/mole. That’s why the formation of positive ion for sodium is easier than that of magnesium.
Therefore, we can conclude that lower the ionization enthalpy, greater the chances of ionic bond formation.
(ii) Electron gain enthalpy (Electron affinities): It is defined as the energy released when an isolated gaseous atom takes up an electron to form anion. Greater the negative electron gain enthalpy, easier will be the formation of anion. Consequently, the probability of formation of ionic bond increases.
For example. Halogens possess high electron affinity. So, the formation of anion is very common in halogens.
(iii) Lattice energy or enthalpy: It is defined as the amount of energy required to separate 1 mole of ionic compound into separate oppositely charged ions.
Lattice energy of an ionic compound depends upon following factors:
(i) Size of the ions: Smaller the size, greater will be the lattice energy.
(ii) Charge on the ions: Greater the magnitude of charge, greater the interionic attraction and hence higher the lattice energy.
• General Characteristics of ionic Compounds
(i) Physical’State: They generally exist as crystalline solids, known as crystal lattice. Ionic compounds do not exist as single molecules like other gaseous molecules e.g., H2 , N2 , 02 , Cl2 etc.
(ii) Melting and boiling points: Since ionic compounds contain high interionic force between them, they generally have high melting and boiling points.
(iii) Solubility: They are soluble in polar solvents such as water but do not dissolve in organic solvents like benzene, CCl4etc.
(iv) Electrical conductivity: In solid state they are poor conductors of electricity but in molten state or when dissolved in water, they conduct electricity.
(v) Ionic reactions: Ionic compounds produce ions in the solution which gives very fast reaction with oppositely charged ions.
For example,
![]()
• Covalent Bond—Lewis-Langmuir Concept
When the bond is formed between two or more atoms by mutual contribution and sharing of electrons, it is known as covalent bond.
If the combining atoms are same the covalent molecule is known as homoatomic. If they are different, they are known as heteroatomic molecule.
For Example,
• Lewis Representation of Simple Molecules (the Lewis Structures)
The Lewis dot Structure can be written through the following steps:
(i) Calculate the total number of valence electrons of the combining atoms.
(ii) Each anion means addition of one electron and each cation means removal of one electron. This gives the total number of electrons to be distributed.
(iii) By knowing the chemical symbols of the combining atoms.
(iv)After placing shared pairs of electrons for single bond, the remaining electrons may account for either multiple bonds or as lone pairs. It is to be noted that octet of each atom should be completed.
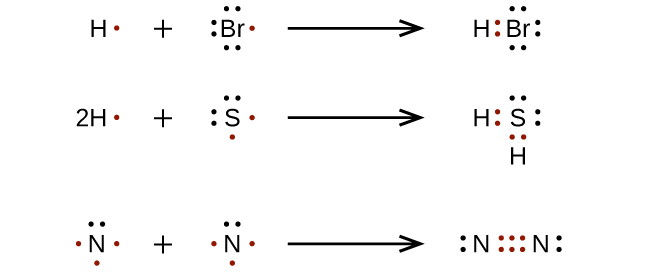
• Formal Charge
In polyatomic ions, the net charge is the charge on the ion as a whole and not by particular atom. However, charges can be assigned to individual atoms or ions. These are called formal charges.
It can be expressed as
It does not indicate the real charge. Let us consider the Ozone molecule (O3). The Lewis structure of O3 may be drawn as
The atoms have been numbered as 1,2 and 3. The formal charge on
The central O atom marked 1
= 6 - 2 - ½ (6) = +1
The end O atom marked 2
= 6 - 4 - ½ (4) = 0
The end O atom marked 3
= 6 - 6 - ½ (2) = -1
Hence, we represent O3 along with the formal charges as follows
• Limitations of the Octet Rule
(i) The incomplete octet of the central atoms: In some covalent compounds central atom has less than eight electrons, i.e., it has an incomplete octet. For example,
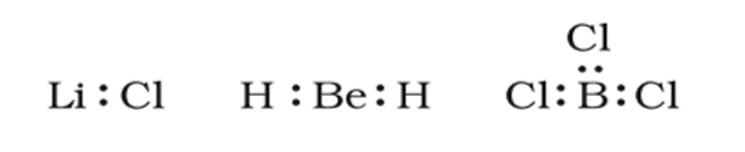
Li, Be and B have 1, 2, and 3 valence electrons only.
(ii) Odd-electron molecules: There are certain molecules which have odd number of electrons the octet rule is not applied for all the atoms.
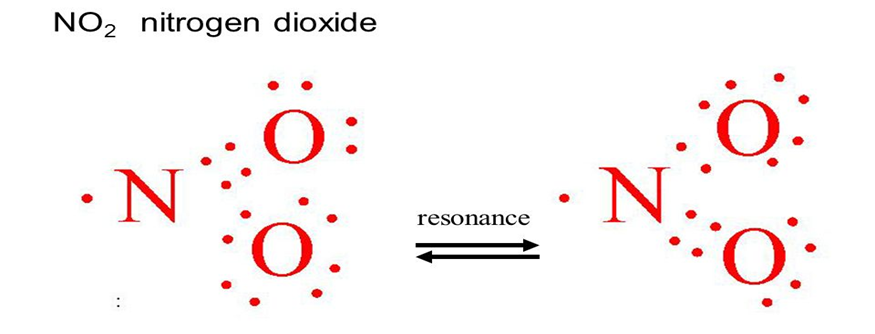
(iii) The expanded Octet: In many compounds there are more than eight valence electrons around the central atom. It is termed as expanded octet. For Example,
• Other Drawbacks of Octet Theory
(i) Some noble gases, also combine with oxygen and fluorine to form a number of compounds like XeF2 , XeOF2 etc.
(ii) This theory does not account for the shape of the molecule.
(iii) It does not give any idea about the energy of The molecule and relative stability.
3. BOND PARAMETERS
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
BOND PARAMETERS
• Bond Length
It is defined as the equilibrium distance between the centres of the nuclei of the two bonded atoms. It is expressed in terms of A. Experimentally, it can be defined by X-ray diffraction or electron diffraction method.
• Bond Angle
It is defined as -the angle between the lines representing the orbitals containing the bonding – electrons.
It helps us in determining the shape. It can be expressed in degree. Bond angle can be experimentally determined by spectroscopic methods.
• Bond Enthalpy
It is defined as the amount of energy required to break one mole of bonds of a particular type to separate them into gaseous atoms.
Bond Enthalpy is also known as bond dissociation enthalpy or simple bond enthalpy. Unit of bond enthalpy = kJ mol-1
Greater the bond enthalpy, stronger is the bond. For e.g., the H—H bond enthalpy in hydrogen is 435.8 kJ mol-1.
The magnitude of bond enthalpy is also related to bond multiplicity. Greater the bond multiplicity, more will be the bond enthalpy. For e.g., bond enthalpy of C —C bond is 347 kJ mol-1 while that of C = C bond is 610 kJ mol-1.
In polyatomic molecules, the term mean or average bond enthalpy is used.
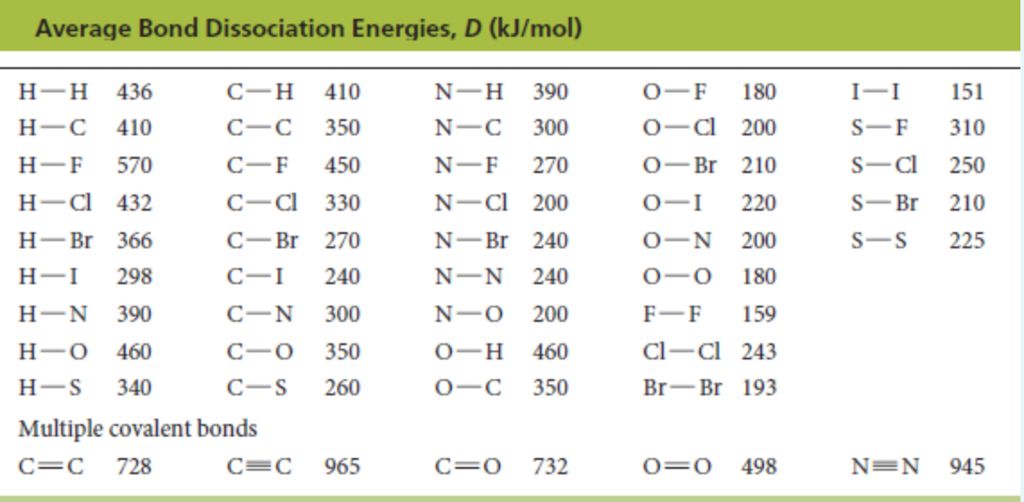
• Bond Order
According to Lewis, in a covalent bond, the bond order is given by the number of bonds between two atoms in a molecule. For example,
Bond order of H2 (H —H) =1
Bond order of 02 (O = O) =2
Bond order of N2 (N = N) =3
Isoelectronic molecules and ions have identical bond orders. For example, F2 and O22- have bond order = 1. N2, CO and NO+ have bond order = 3. With the increase in bond order, bond enthalpy increases and bond length decreases. For example,
• Resonance Structures
There are many molecules whose behaviour cannot be explained by a single-Lew is structure, Tor example, Lewis structure of Ozone represented as follows:
Thus, according to the concept of resonance, whenever a single Lewis structure cannot explain all the properties of the molecule, the molecule is then supposed to have many structures with similar energy.
Positions of nuclei, bonding and nonbonding pairs of electrons are taken as the canonical structure of the hybrid which describes the molecule accurately. For 03, the two structures shown above are canonical structures and the III structure represents the structure of 03 more accurately. This is also called resonance hybrid.
Some resonating structures of some more molecules and ions are shown as follows:
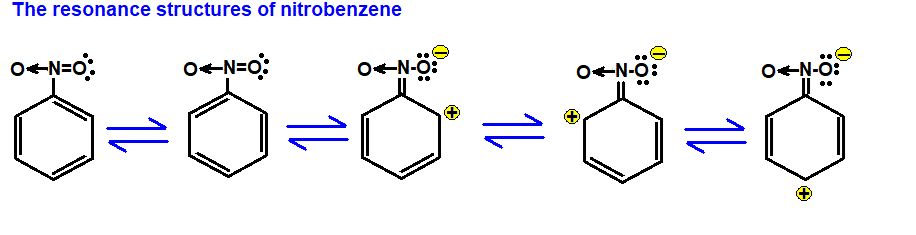
• Polarity of Bonds
Polar and Non-Polar Covalent bonds
Non-Polar Covalent bonds: When the atoms joined by covalent bond are the same like; H2, 02, Cl2, the shared pair of electrons is equally attracted by two atoms and thus the shared electron pair is equidistant to both of them.
Alternatively, we can say that it lies exactly in the centre of the bonding atoms. As a result, no poles are developed and the bond is called as non-polar covalent bond. The corresponding molecules are known as non-polar molecules.
For Example,
![]()
![]()
Polar bond: When covalent bonds formed between different atoms of different electronegativity, shared electron pair between two atoms gets displaced towards highly electronegative atoms.
For Example, in HCl molecule, since electronegativity of chlorine is high as compared to hydrogen thus, electron pair is displaced more towards chlorine atom, thus chlorine will acquire a partial negative charge (δ–) and hydrogen atom have a partial positive charge (δ+) with the magnitude of charge same as on chlorination. Such covalent bond is called polar covalent bond.
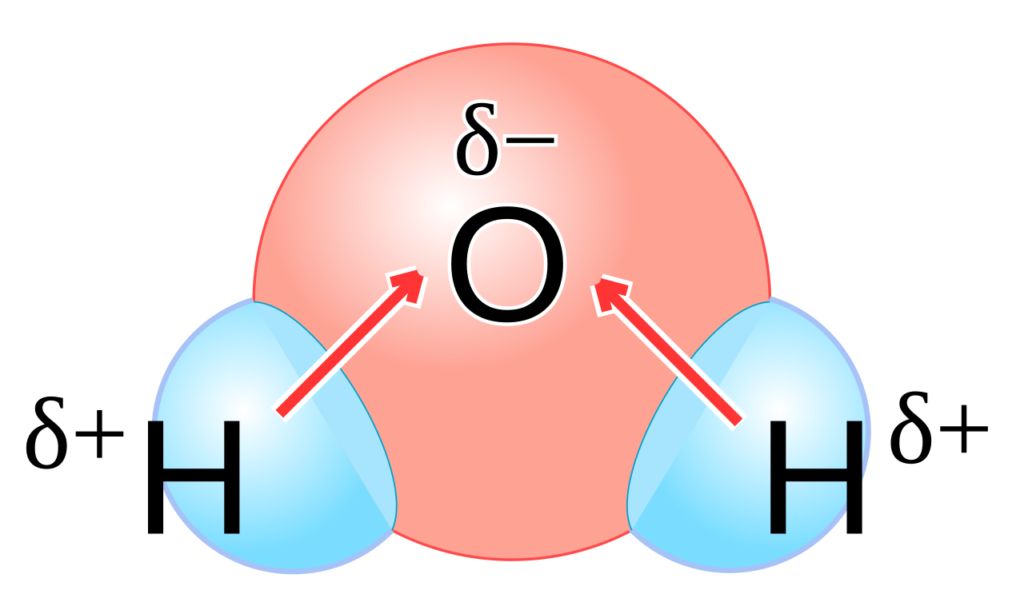
• Dipole Moment
Due to polarity, polar molecules are also known as dipole molecules and they possess dipole moment. Dipole moment is defined as the product of magnitude of the positive or negative charge and the distance between the charges.
Dipole Moment (μ) = Charge (Q) x (d) (Distance of Separation)
It is expressed in Debye units (D)
1D= 3.33564 x 10-30 cm
Dipole moment is a vector quantity. It is depicted by a small arrow with tail on positive center and head pointing towards the negative centre. For example, H – F
With the help of dipole moment the degree of polarity of bonds can be expressed.
• Applications of Dipole Moment
(i) For determining the polarity of the molecules.
(ii) In finding the shapes of the molecules.
For example, the molecules with zero dipole moment will be linear or symmetrical. Those molecules which have unsymmetrical shapes will be either bent or angular.
(e.g., NH3with μ = 1.47 D).
(iii) In calculating the percentage ionic character of polar bonds.
4. THE VALENCE SHELL ELECTRON PAIR REPULSION (VSEPR) THEORY
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
THE VALENCE SHELL ELECTRON PAIR REPULSION (VSEPR) THEORY
Sidgwick and Powell in 1940, proposed a simple theory based on repulsive character of electron pairs in the valence shell of the atoms. It was further developed by Nyholm and Gillespie (1957).
Main Postulates are the following:
(i) The exact shape of molecule depends upon the number of electron pairs (bonded or non bonded) around the central atoms.
(ii) The electron pairs have a tendency to repel each other since they exist around the central atom and the electron clouds are negatively charged.
(iii) Electron pairs try to take such position which can minimize the rupulsion between them.
(iv) The valence shell is taken as a sphere with the electron pairs placed at maximum distance.
(v) A multiple bond is treated as if it is a single electron pair and the electron pairs which constitute the bond as single pairs.
5. VALENCE BOND THEORY
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
VALENCE BOND THEORY
Valence bond theory was introduced by Heitler and London (1927) and developed by Pauling and others. It is based on the concept of atomic orbitals and the electronic configuration of the atoms.
Let us consider the formation of hydrogen molecule based on valence-bond theory.
Let two hydrogen atoms A and B having their nuclei NA and NB and electrons present in them are eA and eB .
As these two atoms come closer new attractive and repulsive forces begin to operate.
(i) The nucleus of one atom is attracted towards its own electron and the electron of the other and vice versa.
(ii) Repulsive forces arise between the electrons of two atoms and nuclei of two atoms. Attractive forces tend to bring the two atoms closer whereas repulsive forces tend to push them apart.
• Orbital Overlap Concept
According to orbital overlap concept, covalent bond formed between atoms results in the overlap of orbitals belonging to the atoms having opposite spins of electrons. Formation of hydrogen molecule as a result of overlap of the two atomic orbitals of hydrogen atoms is shown in the figures that follows:
Stability of a Molecular orbital depends upon the extent of the overlap of the atomic orbitals.
• Types of Orbital Overlap
Depending upon the type of overlapping, the covalent bonds are of two types, known as sigma (σ ) and pi (π) bonds.
(i) Sigma (σ bond): Sigma bond is formed by the end to end (head-on) overlap of bonding orbitals along the internuclear axis.
The axial overlap involving these orbitals is of three types:
• s-s overlapping: In this case, there is overlap of two half-filled s-orbitals along the internuclear axis as shown below:
• s-p overlapping: This type of overlapping occurs between half-filled s-orbitals of one atom and half filled p-orbitals of another atoms.
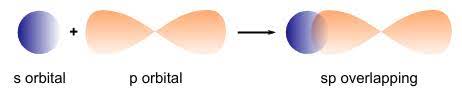
• p-p overlapping: This type of overlapping takes place between half filled p-orbitals of the two approaching atoms.

(ii) pi (π bond): π bond is formed by the atomic orbitals when they overlap in such a way that their axes remain parallel to each other and perpendicular to the internuclear axis.The orbital formed is due to lateral overlapping or side wise overlapping.
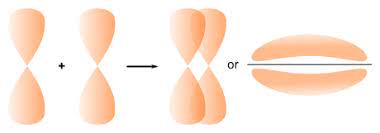
• Strength of Sigma and pf Bonds
Sigma bond (σ bond) is formed by the axial overlapping of the atomic orbitals while the π-bond is formed by side wise overlapping. Since axial overlapping is greater as compared to side wise. Thus, the sigma bond is said to be stronger bond in comparison to a π-bond.
Distinction between sigma and n bonds
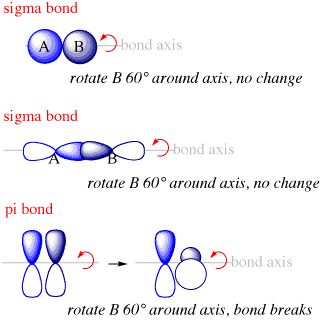
6. HYBRIDISATION
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
HYBRIDISATION
Hybridisation is the process of intermixing of the orbitals of slightly different energies so as to redistribute their energies resulting in the formation of new set of orbitals of equivalent energies and shape.
Salient Features of Hybridisation:
(i) Orbitals with almost equal energy take part in the hybridisation.
(ii) Number of hybrid orbitals produced is equal to the number of atomic orbitals mixed,
(iii) Geometry of a covalent molecule can be indicated by the type of hybridisation.
(iv) The hybrid orbitals are more effective in forming stable bonds than the pure atomic orbitals.
Conditions necessary for hybridisation:
(i) Orbitals of valence shell take part in the hybridisation.
(ii) Orbitals involved in hybridisation should have almost equal energy.
(iii) Promotion of electron is not necessary condition prior to hybridisation.
(iv) In some cases filled orbitals of valence shell also take part in hybridisation.
Types of Hybridisation:
(i) sp hybridisation: When one s and one p-orbital hybridise to form two equivalent orbitals, the orbital is known as sp hybrid orbital, and the type of hybridisation is called sp hybridisation.
Each of the hybrid orbitals formed has 50% s-characer and 50%, p-character. This type of hybridisation is also known as diagonal hybridisation.

(ii) sp2 hybridisation: In this type, one s and two p-orbitals hybridise to form three equivalent sp2 hybridised orbitals.
All the three hybrid orbitals remain in the same plane making an angle of 120°. Example. A few compounds in which sp2 hybridisation takes place are BF3, BH3, BCl3 carbon compounds containing double bond etc.

(iii) sp3 hybridisation: In this type, one s and three p-orbitals in the valence shell of an atom get hybridised to form four equivalent hybrid orbitals. There is 25% s-character and 75% p-character in each sp3 hybrid orbital. The four sp3 orbitals are directed towards four corners of the tetrahedron.

The angle between sp3 hybrid orbitals is 109.5°.
A compound in which sp3 hybridisation occurs is, (CH4). The structures of NH2 and H20 molecules can also be explained with the help of sp3 hybridisation.
7. MOLECULAR ORBITAL THEORY
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
MOLECULAR ORBITAL THEORY
• Formation of Molecular Orbitals: Linear Combination of Atomic Orbitals (LCAO)
The formation of molecular orbitals can be explained by the linear combination of atomic orbitals. Combination takes place either by addition or by subtraction of wave function as shown below.
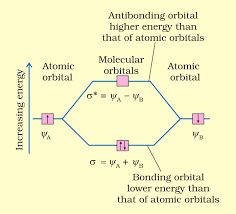
The molecular orbital formed by addition of atomic orbitals is called bonding molecular orbital while molecular orbital formed by subtraction of atomic orbitals is called antibonding molecular orbital.
Conditions for the combination of atomic orbitals:
(1) The combining atomic orbitals must have almost equal energy.
(2) The combining atomic orbitals must have same symmetry about the molecular axis.
(3) The combining atomic orbitals must overlap to the maximum extent.
• Types of Molecular Orbitals
Sigma (σ) Molecular Orbitals: They are symmetrical around the bond-axis.
pi (π) Molecular Orbitals: They are not symmetrical, because of the presence of positive lobes above and negative lobes below the molecular plane.
• Electronic configuration and Molecular Behaviour
The distribution of electrons among various molecular orbitals is called electronic configuration of the molecule.
• Stability of Molecules
If Nb = No. of electrons occupying bonding orbitals.
Na = No. of electrons occupying antibonding orbitals.
Then,
- If Nb > Na molecule will be stable.
- Nb < Na molecule will be unstable.
• Bond Order
Bond order is defined as half of the difference between the number of electrons present in bonding and antibonding molecular orbitals.
Bond order (B.O.) = 1/2 [Nb-Na]
The bond order may be a whole number, a fraction or even zero.
It may also be positive or negative.
Nature of the bond: Integral bond order value for single double and triple bond will be 1, 2 and 3 respectively.
Bond-Length: Bond order is inversely proportional to bond-length. Thus, greater the bond order, smaller will be the bond-length.
Magnetic Nature: If all the molecular orbitals have paired electrons, the substance is diamagnetic. If one or more molecular orbitals have unpaired electrons, it is paramagnetic e.g., 02 molecule.
8. BONDING IN SOME HOMONUCLEAR DIATOMIC MOLECULES
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
BONDING IN SOME HOMONUCLEAR DIATOMIC MOLECULES
(1) Hydrogen molecule (H2): It is formed by the combination of two hydrogen atoms. Each hydrogen atom has one electron in Is orbital, so, the electronic configuration of hydrogen molecule is
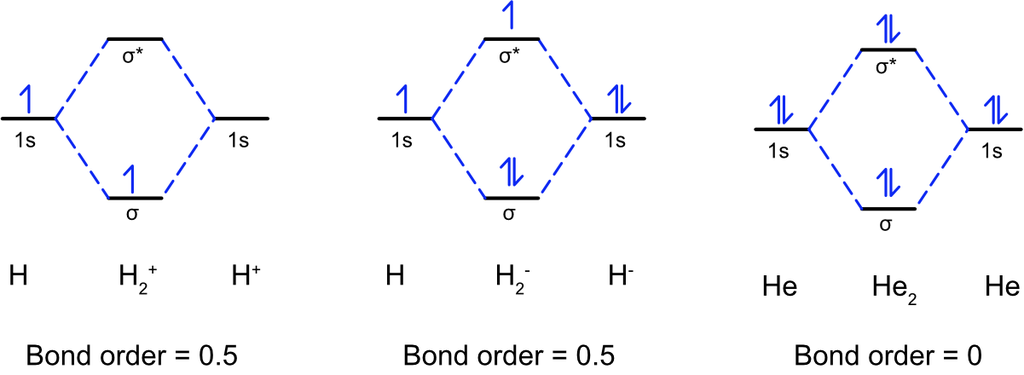
This indicates that two hydrogen atoms are bonded by a single covalent bond. Bond dissociation energy of hydrogen has been found = 438 kJ/mole. Bond-Length = 74 pm
No unpaired electron is present therefore,, it is diamagnetic.
(2) Helium molecule (He2): Each helium atom contains 2 electrons, thus in He2 molecule there would be 4 electrons.
The electrons will be accommodated in σ1s and σ*1s molecular orbitals:
Bond order (b.o.) = ½ (Nb–Na )
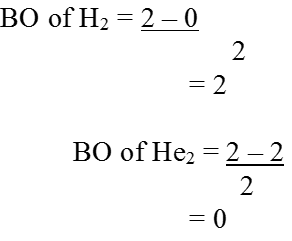
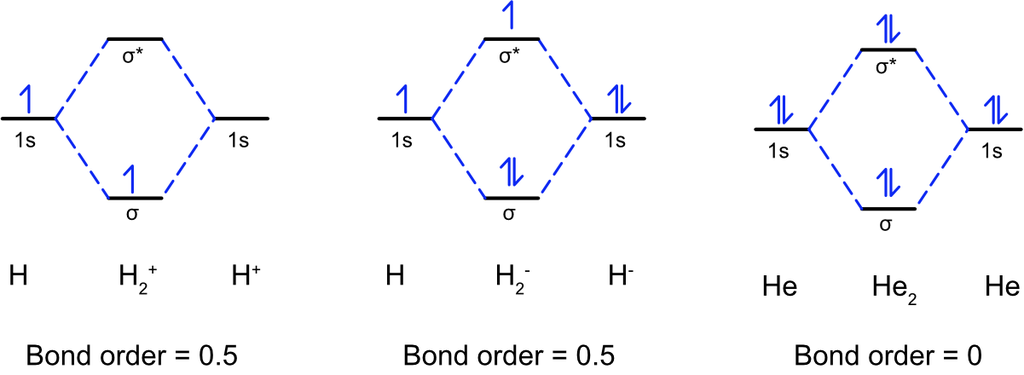
9. HYDROGEN BONDING
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
HYDROGEN BONDING
When highly electronegative elements like nitrogen, oxygen, flourine are attached to hydrogen to form covalent bond, the electrons of the covalent bond are shifted towards the more electronegative atom. Thus, partial positive charge develops on hydrogen atom which forms a bond with the other electronegative atom. This bond is known as hydrogen bond and it is weaker than the covalent bond. For example, in HF molecule, hydrogen bond exists between hydrogen atom of one molecule and fluorine atom of another molecule.
It can be depicted as
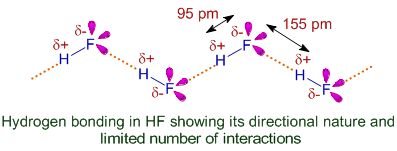
• Types of H-Bonds
(i) Intermolecular hydrogen bond (ii) Intramolecular hydrogen bond.
(i) Intermolecular hydrogen bond: It is formed between two different molecules of the same or different compounds. For Example, in HF molecules, water molecules etc.
(ii) Intramolecular hydrogen bond: In this type, hydrogen atom is in between the two highly electronegative F, N, O atoms present within the same molecule. For example, in o-nitrophenol, the hydrogen is in between the two oxygen atoms.
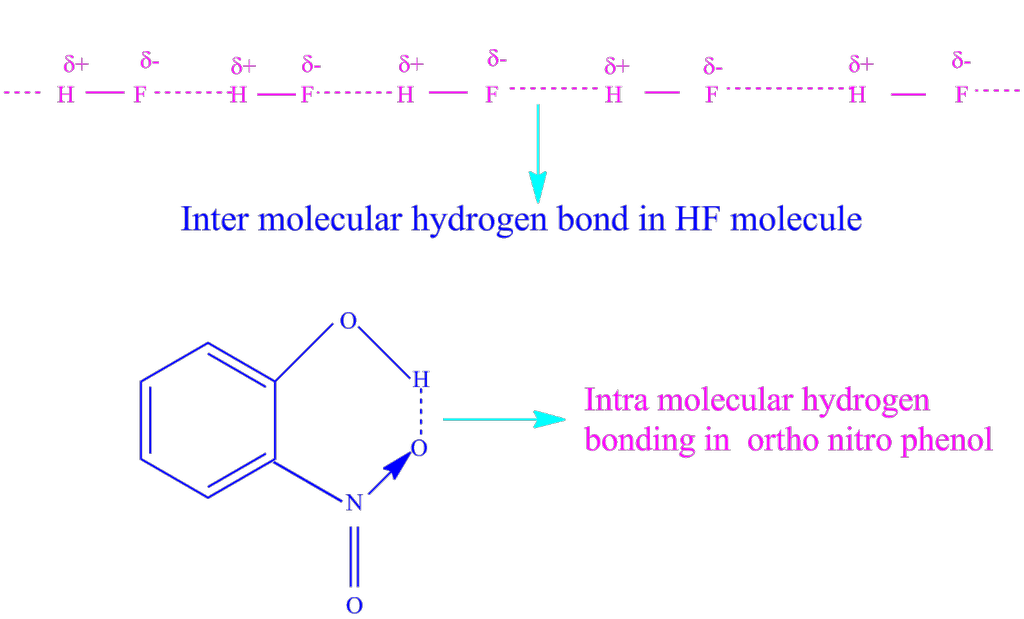
2. THERMAL ENERGY
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
THERMAL ENERGY
The energy arising due to molecular motion of the body is known as thermal energy. Since motion of the molecules is directly related to kinetic energy and kinetic energy is directly proportional to the temperature.
3. INTERMOLECULAR FORCES vs THERMAL INTERACTIONS
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
INTERMOLECULAR FORCES vs THERMAL INTERACTIONS
Intermolecular forces tend to keep the molecules together but thermal energy of the molecules tends to keep them apart. Three states of matter are the result of balance between intermolecular forces and the thermal energy of the molecules. When molecular interactions are very weak, molecules do not cling together to make liquid or solid unless thermal energy is reduced by lowering the temperature. Gases do not liquify on compression only, although molecules come very close to each other and intermolecular forces operate to the maximum. However, when thermal energy of molecules is reduced by lowering the temperature; the gases can be very easily liquified. Predominance of thermal energy and the molecular interaction energy of a substance in three states is depicted as follows
4. THE GASEOUS STATE
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
THE GASEOUS STATE
Physical Properties of Gaseous State
(i) ases have no definite volume and they do not have specific shape,
(ii) Gases mix evenly and completely in all proportions without any mechanical aid.
(iii) Their density is much lower than solids and liquids. :
(iv) They are highly compressible and exert pressure equally in all directions
5. THE GAS LAWS
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
THE GAS LAWS
• Boyle’s Law (Pressure-Volume Relationship)
At constant temperature, the volume of a given mass of gas is inversely proportional to its pressure. It states that, under isothermal conditions pressure of a given mass of a gas is inversely proportional to its volume.
According to this the volume of a given mass of gas is inversely proportional to pressure at constant temperature. This law is given by Robert Boyle.
P ∝ 1 …… (at constant T and n)
V
P = k 1
V
Where k is the proportionality constant.
If a fixed amount of gas at constant temperature T occupying volume V1 at pressure P1 undergoes expansion so that volume becomes V2 and pressure becomes P2, then according to Boyle’s law.
P1V1 = P2V2 = constant
∴ P1 = V2
P2 V1
• Charles’ law:
At constant pressure, the volume of a given mass of a gas is directly proportional to its absolute temperature.
V ∝ T
or, V = constant
T
Let V1 be the volume of a gas at temperature T1. Pressure remains constant.
If the temperature of the gas increased to T2, then the volume will also increase to V2.
Therefore, according to law,
V1 = V2
T1 T2
• Gay Lussac’s Law (Pressure-Temperature Relationship)
At constant volume, pressure of a given mass of a gas is directly proportional to the temperature.
Mathematically,
P ∝ T
∴ P = k (at constant volume, and mass)
T
Where, k is the proportionality constant.
If a fixed amount of gas at constant volume V occupying pressure P1 at temperature T1 undergoes expansion, so that pressure becomes P2 and temperature becomes T2 then according to lussac’s law
P = constant
T
P1 = P2
T1 T2
• Avogadro Law (Volume-Amount Relationship)
Avogadro’s law states that equal volumes of all gases under the same conditions of temperature and pressure contain equal number of molecules. V α n
Where n is the number of moles of the gas.
Avogadro constant: The number of molecules in one mole of a gas
= 6.022 x 1023
Ideal Gas: A gas that follows Boyle’s law, Charles’ law and Avogadro law strictly, is called an ideal gas.
Real gases follow these laws only under certain specific conditions. When forces of interaction are practically negligible.
6. IDEAL GAS EQUATION
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
IDEAL GAS EQUATION
This is the combined gas equation of three laws and is known as ideal gas equation.
At constant T and n : V ∝ 1
P Boyle’s law
At constant P and n : V ∝ T Charle’s law
At constant P and T : V ∝ n Avogadro law
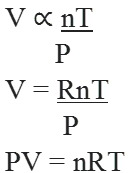
Where R is proportionality constant known as universal gas constant.
Numerical value or R
R = 0.0821 litre atm K-1 mol-1
R = 0.0831 litre bar K-1 mol-1
R = 8.314 J K-1mol-1
R = 1.987 ≈ 2 cal K-1 mol-1
R = 8.314 x 107 erg K-1 mol-1
If tempurature, volume and pressure of a fixed amount of gas vary from T1 , V1 and P1 to T2 , V2 and P2 then we can write,
![]()
This equation is also known as combined gas law.
• Dalton’s Law of Partial Pressure
When two or more non-reactive gases are enclosed in a vessel, the total pressure exerted by the gaseous mixture is equal to the sum of the partial pressure of individual gases.
Let P1 ,P2, and P3 be the pressure of three non reactive gases A, B, and C. When enclosed separately in the same volume and under same condition.
PTotal = P1+ P2 + P3
Where, PTotal = P is the total pressure exerted by the mixture of gases.
• Aqueous Tension
Pressure of non reacting gases are generally collected over water and therefore are moist. Pressure of dry gas can be calculated by substracting vapour pressure of water from total pressure of moist gas.
P2Dry gas = PTotal – Aqueous Tension
• Partial Pressure in terms of Mole Fraction
Let at the temperature T, three gases enclosed in the volume V, exert partial pressure P1 , P2 and P3 respectively, then
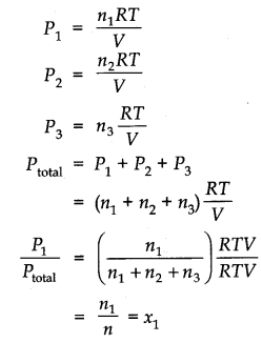
Where, (n = n1 + n2 + n3)
∴ P1 = n1 Ptotal
7. KINETIC ENERGY AND MOLECULAR SPEEDS
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
KINETIC ENERGY AND MOLECULAR SPEEDS
Molecules of gases remain in continuous motion. While moving they collide with each other and with the walls of the container. This results in change of their speed and redistribution of energy.
So the speed and energy of all the molecules of the gas at any instant are not the same. Thus, we can obtain only average value of speed of molecules.
If there are n number of molecules in a sample and their individual speeds are u1, u2,…….un, then average speed of molecules uav can be calculated as follows:
uav = (u 1 + u 2 + .........u n) / n
Maxwell and Boltzmann have shown that actual distribution of molecular speeds depends on temperature and molecular mass of a gas. Maxwell derived a formula for calculating the number of molecules possessing a particular speed.
Fig. shows schematic plot of number of molecules vs. molecular speed at two different temperatures T1 and T 2 (T 2 is higher than T 1 ) . The distribution of speeds shown in the plot is called Maxwell-Boltzmann distribution of speeds.
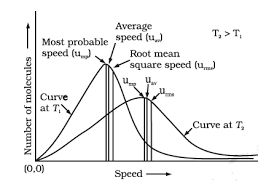
The graph shows that number of molecules possessing very high and very low speed is very small. The maximum in the curve represents speed possessed by maximum number of molecules .
This speed is called most probable speed, ump. This is very close to the average speed of the molecules . On increasing the temperature most probable speed increases. Also, speed distribution curve broadens at higher temperature.
Broadening of the curve shows that number of molecules moving at higher speed increases. Speed distribution also depends upon mass of molecules. At the same temperature, gas molecules with heavier mass have slower speed than lighter gas molecules .
For example, at the same temperature lighter nitrogen molecules move faster than heavier chlorine molecules. Hence, at any given temperature, nitrogen molecules have higher value of most probable speed than the chlorine molecules. We know that kinetic energy of a particle is given by the expression:
Kinetic Energy = (1/2)mu2
Therefore, if we want to know average translational kinetic energy, for the movement of a gas particle in a straight line, we require the value of mean of square of speeds, of all molecules.
The mean square speed is the direct measure of the average kinetic energy of gas molecules. If we take the square root of the mean of the square of speeds then we get a value of speed which is different from most probable speed and average speed. This speed is called root mean square speed and is given by the expression as follows:
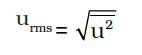
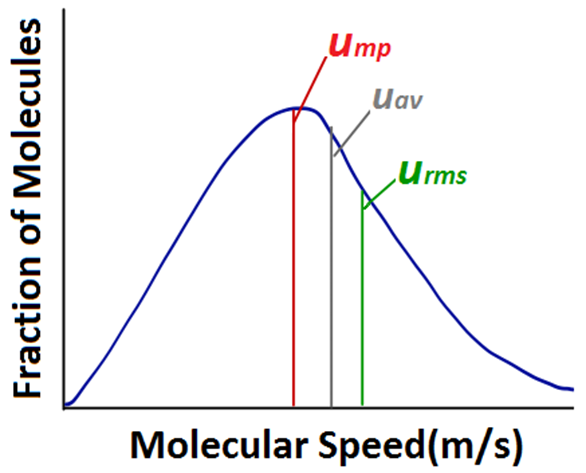
8. KINETIC MOLECULAR THEORY OF GASES
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
KINETIC MOLECULAR THEORY OF GASES
(i) Gases consist of large number of very small identical particles (atoms or molecules),
(ii) Actual volume occupied by the gas molecule is negligible in comparison to empty space between them.
(iii) Gases can occupy all the space available to them. This means they do not have any force of attraction between their particles.
(iv) Particles of a gas are always in constant random motion.
(v) When the particles of a gas are in random motion, pressure is exerted by the gas due to collision of the particles with the walls of the container.
(vi) Collision of the gas molecules are perfectly elastic. This means there is no loss of energy after collision. There may be only exchange of energy between colliding molecules.
(vii) At a particular temperature distribution of speed between gaseous particles remains constant.
(viii) Average kinetic energy of the gaseous molecule is directly proportional to the absolute temperature.
9. BEHAVIOUR OF REAL GASES
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
DEVIATION FROM IDEAL GAS BEHAVIOUR
Real Gas: A gas which does not follow ideal gas behaviour under all conditions of temperature and pressure, is called real gas. Deviation with respect to pressure can be studied by plotting pressure Vs volume curve at a given temperature. (Boyle’s law)
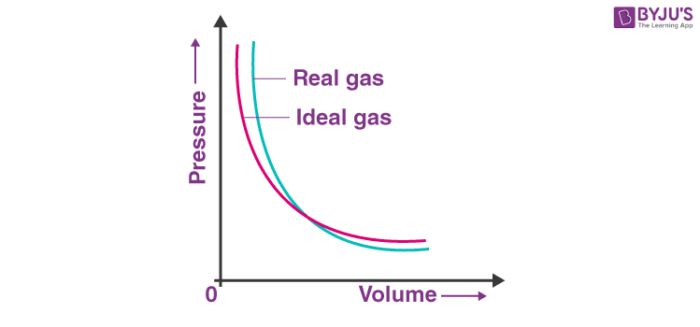
Compressibility factor (Z): Deviation from ideal behaviour can be measured in terms of compressibility factor, Z.
![]()
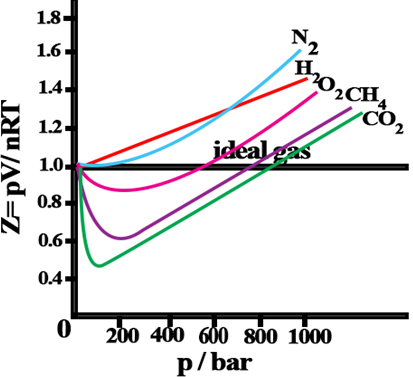
• van der Waals Equation
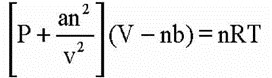
Where V is a constant for molecular attraction while ‘V is a constant for molecular volume.
(a) There is no force of attraction between the molecules of a gas.
(b) Volume occupied by the gas molecule is negligible in comparison to the total volume of the gas.
Above two assumptions of the kinetic theory of gas was found to be wrong at very high pressure and low temperature.
10. LIQUEFACTION OF GASES
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
LIQUIFACTION OF GASES
Liquifaction of gases can be achieved either by lowering the temperature or increasing the pressure of the gas simultaneously.
Thomas Andrews plotted isotherms of C02 at various temperatures shown in figure.
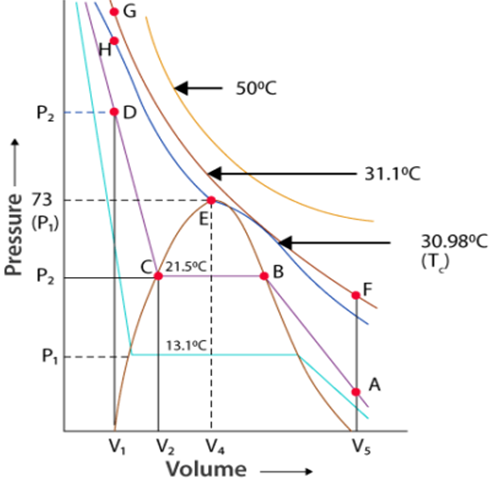
Critical Temperature (Tc): It is defined as that temperature above which a gas cannot be liquified however high pressure may be applied on the gas.
Tc = 8a/27bR
(Where a and b are van der Waals constants)
Critical Pressure (Pc): It is the pressure required to Liquify the gas at the critical temperature.
Pc = a/27b2
The volume occupied by one mole of the gas at the critical temperature and the critical pressure is called the critical volume (Vc).
For Example. For C02 to Liquify.
Tc = 30.98°C
Pc = 73,9 atm.
Vc = 95-6 cm3/mole
All the three are collectively called critical constants.
11. LIQUID STATE
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
LIQUID STATE
Characteristics of Liquid State
(i) In liquid, intermolecular forces are strong in comparison to gas.
(ii) They have definite volume but irregular shapes or we can say that they can take the shape of the container.
(iii) Molecules of liquids are held together by attractive intermolecular forces.
Vapour Pressure: The pressure exerted by the vapour of a liquid, at a particular temperature in a state of dynamic equilibrium, is called the vapour pressure of that liquid at that temperature.
Vapour Pressure depends upon two factors:
(i) Nature of Liquid
(ii) Temperature
• Surface Tension
It is defined as the force acting per unit length perpendicular to the line drawn on the surface of liquid.
S.I. unit of Surface Tension = Nm-1
Surface Tension decreases with increase in temperature, because force acting per unit length decreases due to increase in kinetic energy of molecules.
• Viscosity
It is defined as the internal resistance to flow possessed by a liquid.
The liquids which flow slowly have very high internal resistance, which is due to strong intermolecular forces and hence are said to be more viscous.
This force is proportional to the area of contact of layers and velocity gradient
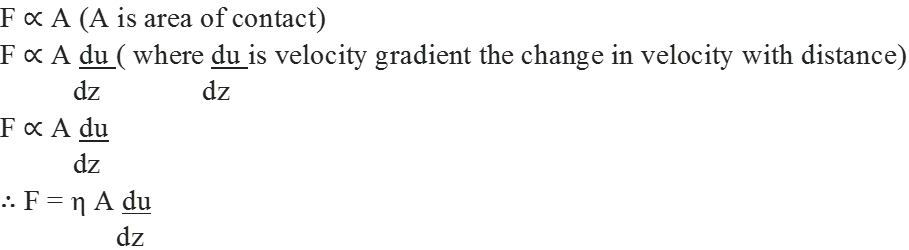
where ‘ η’ is proportionality constant and is called coefficient of viscosity. It is expressed in Nm-2s or poise
1 poise = 0.1 Nm-2s
When liquid flows, the layer immediately below it tries to retard its flow while the one above tries to accelerate.
Thus, force is required to maintain the flow of layers.

Effect of Temp, on Viscosity: Viscosity of liquids decreases as the temperature rises because at high temperature, molecules have high kinetic energy and can overcome the intermolecular forces to slip past one another.
2. APPLICATIONS
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
APPLICATIONS
• Work (Pressure-volume Work)
Let us consider a cylinder which contains one mole of an ideal gas in which a frictionless piston is fitted.
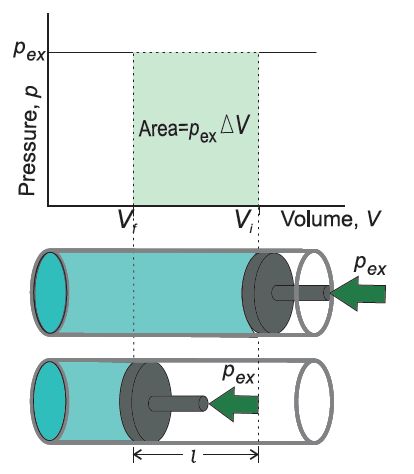
• Work Done in Isothermal and Reversible Expansion of Ideal Gas
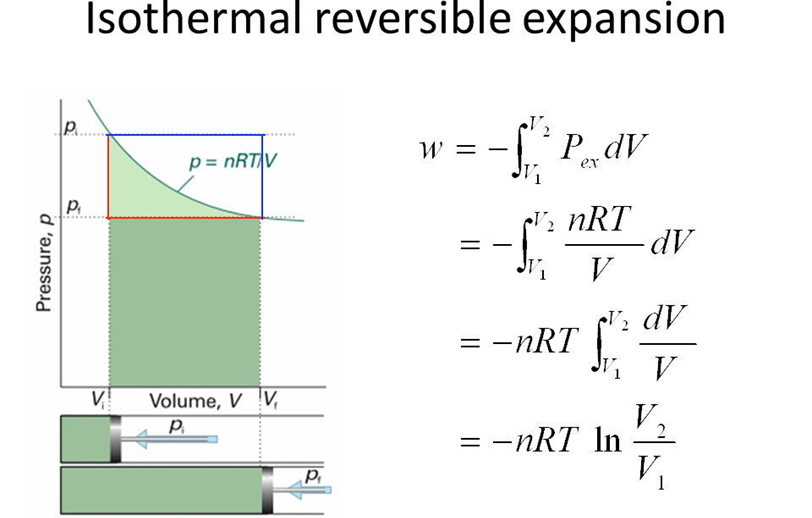
• Isothermal and Free Expansion of an Ideal Gas
For isothermal (T = constant) expansion of an
ideal gas into vacuum ; w = 0 since pex = 0.
Also, Joule determined experimentally that
q = 0; therefore, ∆U = 0
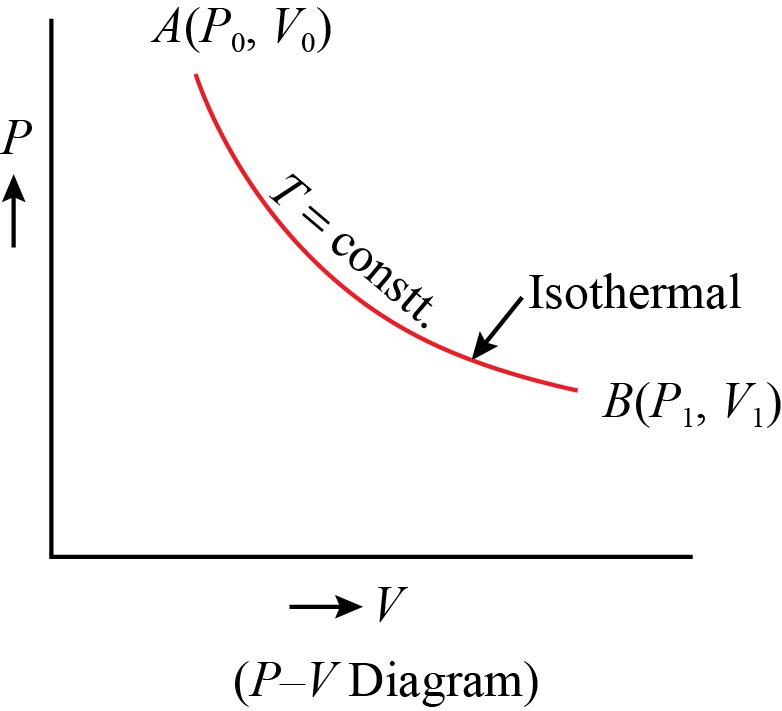
• Enthalpy (H)
It is defined as total heat content of the system. It is equal to the sum of internal energy and pressure-volume work.
Mathematically, H = U + PV
Change in enthalpy: Change in enthalpy is the heat absorbed or evolved by the system at constant pressure.
ΔH = qp
For exothermic reaction (System loses energy to Surroundings),
ΔH and qp both are -Ve.
For endothermic reaction (System absorbs energy from the Surroundings).
ΔH and qp both are +Ve.
Relation between ΔH and Δu.
![]() B
B
Let HA be the enthalpy of reactant A and HB be that of the products.
∴ HA = UA + PVA
HB = UB + PVB
ΔH = HB - HA
= (UB + PVB) – (UA + PVA)
ΔH = ΔU + PΔV (HB – HA)
ΔH = ΔU + PΔV
At constant pressure and temperature using ideal gas law,
PVA = nA RT (for reactant A)
PVB = nB RT (for reactant B)
Thus, PVB – PVA = nB RT - nA RT
= ( nB – nA) RT
PΔV = Δng RT
∴ ΔH = ΔU + Δng RT
• Extensive property
An extensive property is a property whose value depends on the quantity or size of matter present in the system.
For example: Mass, volume, enthalpy etc. are known as extensive property.
• Intensive property
Intensive properties do not depend upon the size of the matter or quantity of the matter present in the system.
For example: temperature, density, pressure etc. are called intensive properties.
• Heat capacity
The increase in temperature is proportional to the heat transferred.
q = coeff. x ΔT
q = CΔT
Where, coefficient C is called the heat capacity.
C is directly proportional to the amount of substance.
Cm = C/n
It is the heat capacity for 1 mole of the substance.
• Molar heat capacity
It is defined as the quantity of heat required to raise the temperature of a substance by 1° (kelvin or Celsius).
• Specific Heat Capacity
It is defined as the heat required to raise the temperature of one unit mass of a substance by 1° (kelvin or Celsius).
q = C x m x ΔT
where m = mass of the substance
ΔT = rise in temperature.
• Relation Between Cp and Cv for an Ideal Gas
At constant volume heat capacity = Cv
At constant pressure heat capacity = Cp
At constant volume qv= CvΔT = ΔU
At constant pressure qp = Cp ΔT = ΔH
For one mole of an ideal gas
ΔH = ΔU + Δ (PV) = ΔU + Δ (RT)
ΔH = ΔU + RΔT
On substituting the values of ΔH and Δu, the equation is modified as
Cp ΔT = CvΔT + RΔT
or Cp-Cv = R
3. MEASUREMENT OF ∆U AND ∆H: CALORIMETRY
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
MEASUREMENT OF ΔU AND ΔH—CALORIMETRY
Determination of ΔU: ΔU is measured in a special type of calorimeter, called bomb calorimeter.
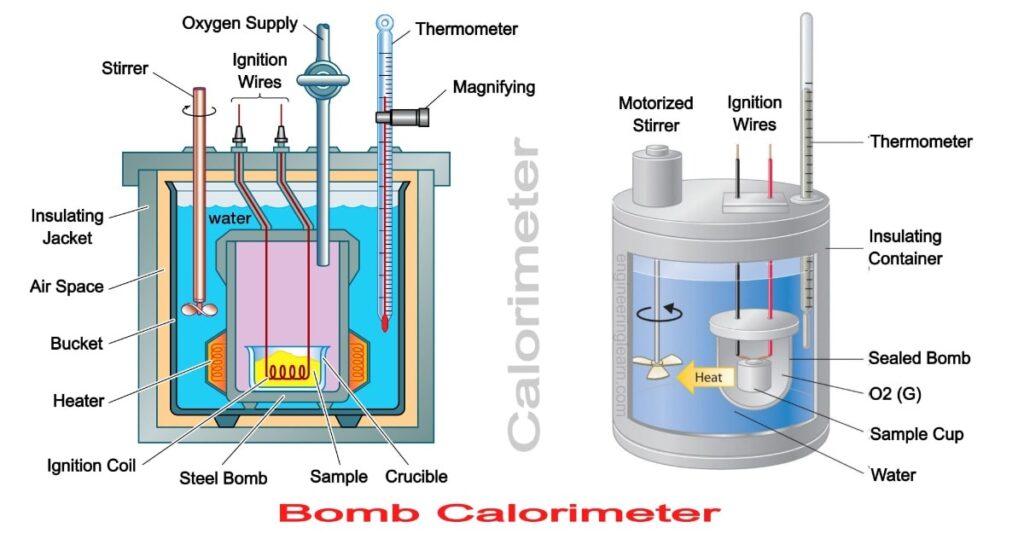
Working with calorimeter. The calorimeter consists of a strong vessel called (bomb) which can withstand very high pressure. It is surrounded by a water bath to ensure that no heat is lost to the surroundings.
Procedure: A known mass of the combustible substance is burnt in the pressure of pure dioxygen in the steel bomb. Heat evolved during the reaction is transferred to the water and its temperature is monitored.
4. ENTHALPY CHANGE, ∆rH OF A REACTION – REACTION ENTHALPY
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
ENTHALPY CHANGE, ∆rH OF A REACTION – REACTION ENTHALPY
• Enthalpy Changes During Phase Transformation
Enthalpy of fusion: Enthalpy of fusion is the heat energy or change in enthalpy when one mole of a solid at its melting point is converted into liquid state.
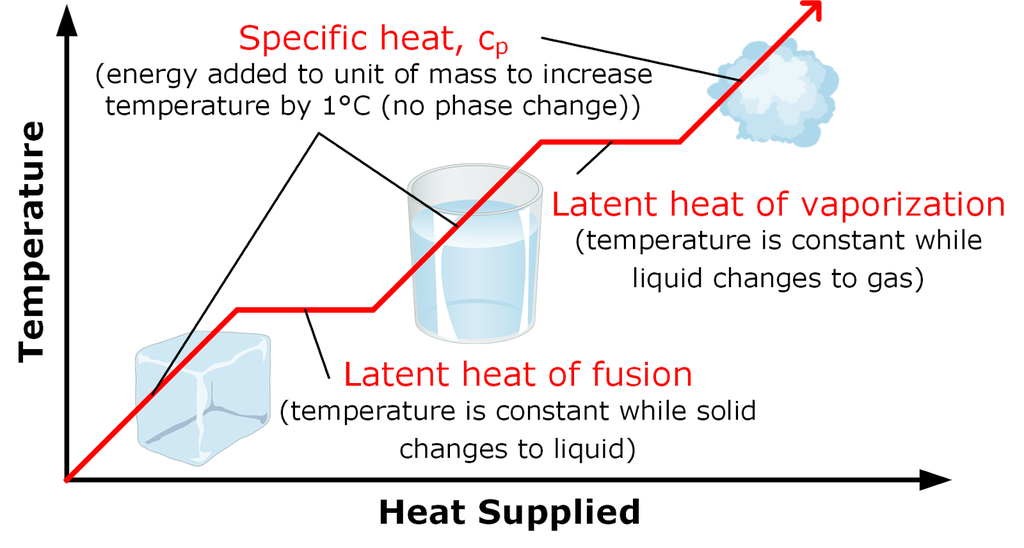
Enthalpy of vaporisation: It is defined as the heat energy or change in enthalpy when one mole of a liquid at its boiling point changes to gaseous state.
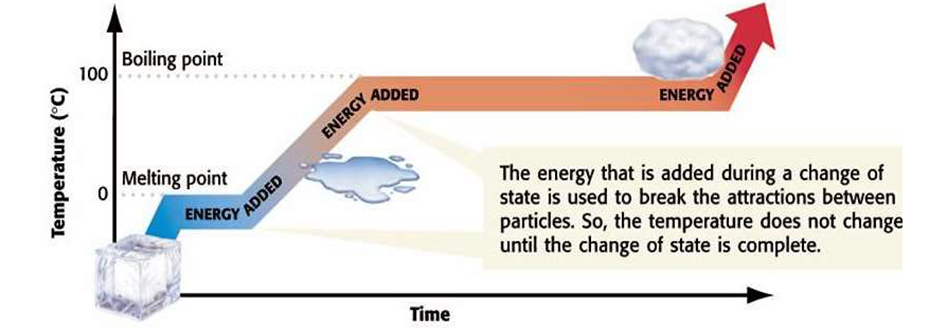
Enthalpy of Sublimation: Enthalpy of sublimation is defined as the change in heat energy or change in enthalpy when one mole of solid directly changes into gaseous state at a temperature below its melting point.
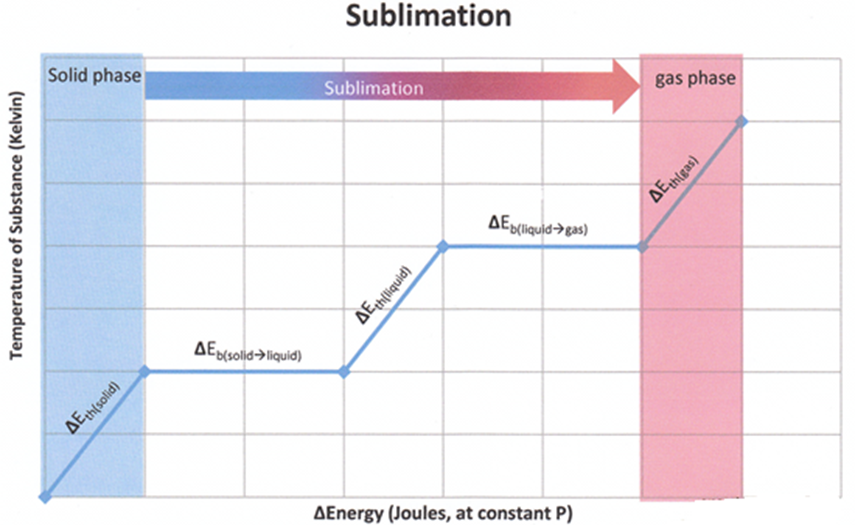
5. ENTHALPIES FOR DIFFERENT TYPES OF REACTIONS
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
ENTHALPIES FOR DIFFERENT TYPES OF REACTIONS
• Standard Enthalpy of Formation
Enthalpy of formation is defined as the change in enthalpy in the formation of 1 mole of a substance from its constituting elements under standard conditions of temperature at 298K and 1 atm pressure.
ΔHrº (298.15 K) and ΔGrº (298.15 K)
ΔGrº (T)
ΔHrº (T) and Kp (298.15 K)
Kp (T1) and Kp (T2) where T1, T2 ≠ T
ΔHrº (T) and ΔGrº (298.15 K)
Enthalpy of Combustion: It is defined as the heat energy or change in enthalpy that accompanies the combustion of 1 mole of a substance in excess of air or oxygen.
CO(g) + ½ O2(g) ![]() CO2(g) ΔHº = -283 kJ
CO2(g) ΔHº = -283 kJ
• Thermochemical Equation
A balanced chemical equation together with the value of ΔrH and the physical state of reactants and products is known as thermochemical equation.
Thermochemical equations
- A typical chemical equation is
![]() SO2
SO2
- It is called a thermochemical equation when we add information about ΔH…
![]() SO2 ΔH = -296.9 kJ
SO2 ΔH = -296.9 kJ
- If we change the equation, then the ΔH also changes…
![]() S + O2 ΔH = +296.9 kJ
S + O2 ΔH = +296.9 kJ
- If the reaction is reversed the sign is reversed
- Also, if numbers in the equation change, so will the amount of energy produced/absorbed:
![]() 2SO2 ΔH = -593.8 kJ
2SO2 ΔH = -593.8 kJ
Conventions regarding thermochemical equations
1. The coefficients in a balanced thermochemical equation refer to the number of moles of reactants and products involved in the reaction.
If the coefficients of the chemical equation are multiplied by some factor, the enthalpy change must also be multiplied by the same factor (ΔH is an extensive property).
H2(g) + ½ O2(g) ![]() H2O(l) ΔH = -286 kJ
H2O(l) ΔH = -286 kJ
Multiply by a factor of two:
2H2(g) + O2(g) ![]() 2H2O(l) ΔH = 2 x (-286kJ) = -572kJ
2H2O(l) ΔH = 2 x (-286kJ) = -572kJ
Multiply by a factor of one-half:
½ H2(g) + ¼ O2(g) ![]() ½ H2O(l) ΔH = ½ x (-286kJ) = -134kJ
½ H2O(l) ΔH = ½ x (-286kJ) = -134kJ
• Hess’s Law of Constant Heat Summation
The total amount of heat evolved or absorbed in a reaction is same whether the reaction takes place in one step or in number of steps.
The law stats that the change in enthalpy for a reaction is the same whether the reaction takes place in one or a series of step. The Hess’s law can also be states as the enthalpy change for a chemical reaction is the same regardless of the path by which the reaction occurs.
For example, consider following two paths for the preparation of methylene chloride
Path I:
CH4 (g) + 2 Cl2(g) ![]() CH2Cl2(g) + 2HCl(g) ΔH1º = - 202.3kJ
CH2Cl2(g) + 2HCl(g) ΔH1º = - 202.3kJ
Path II:
CH4 (g) + Cl2(g) ![]() CH3Cl2(g) + HCl(g) ΔH2º = - 98.3kJ
CH3Cl2(g) + HCl(g) ΔH2º = - 98.3kJ
CH3Cl(g) + Cl2(g) ![]() CH2Cl2(g) + HCl(g) ΔH3º = - 104.0kJ
CH2Cl2(g) + HCl(g) ΔH3º = - 104.0kJ
Adding two steps
CH4(g) + 2Cl2(g) ![]() CH2Cl2(g) + 2HCl(g) ΔHº = - 202.3kJ
CH2Cl2(g) + 2HCl(g) ΔHº = - 202.3kJ
Thus whether we follow path 1 or path 2 the enthalpy change of the reaction is same.
ΔH1º = ΔH2º + ΔH3º = - 202.3kJ
• Born-Haber Cycle
It is not possible to determine the Lattice enthalpy of ionic compound by direct experiment. Thus, it can be calculated by following steps. The diagrams which show these steps is known as Born-Haber Cycle.
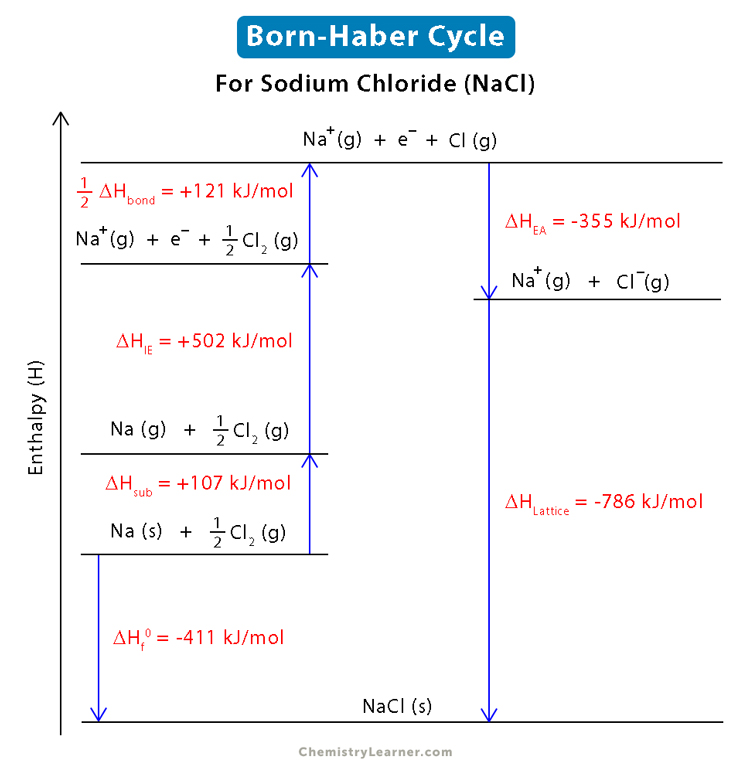
6. SPONTANEITY
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
SPONTANEITY
Spontaneous Process: A process which can take place by itself or has a tendency to take place is called spontaneous process.
Spontaneous process need not be instantaneous. Its actual speed can vary from very slow to quite fast.
A few examples of spontaneous process are:
(i) Common salt dissolves in water of its own.
(ii) Carbon monoxide is oxidised to carbon dioxide of its own.
• Entropy (S)
The entropy is a measure of degree of randomness or disorder of a system. Entropy of a substance is minimum in solid state while it is maximum in gaseous state.
The change in entropy in a spontaneous process is expressed as ΔS
ΔS = ΔSsystem + ΔSsurroundings
ΔS = Overall change in entropy
ΔSsystem = Change in entropy of the system
ΔSsurroundings =Change in entropy of the surroundings
ΔS > 0, + entropy change, reaction is spontaneous
ΔS < 0, - entropy change, reaction is nonspontaneous
Equation for the total change in entropy
• Gibbs Energy and Spontaneity
A new thermodynamic function, the Gibbs energy or Gibbs function G, can be defined as G = H-TS
ΔG = ΔH – TΔS
Gibbs energy change = enthalpy change – temperature x entropy change ΔG gives a criteria for spontaneity at constant pressure and temperature, (i) If ΔG is negative (< 0) the process is spontaneous.
(ii) If ΔG is positive (> 0) the process is non-spontaneous.
• Free Energy Change in Reversible Reaction
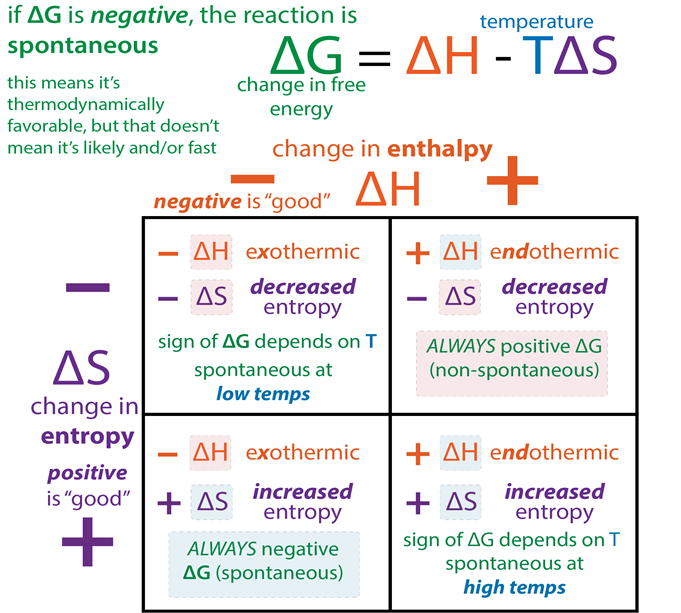
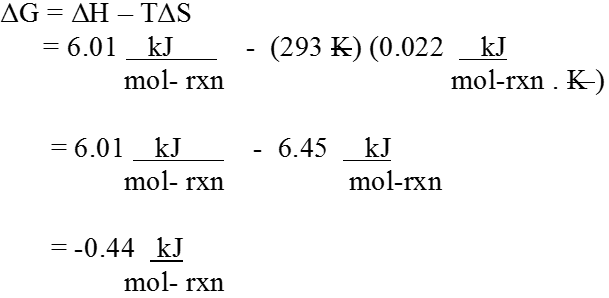
qualitative relationship between the change in standard free energy and the equilibrium constant for a given relation

7. GIBBS ENERGY CHANGE AND EQUILIBRIUM
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
GIBBS ENERGY CHANGE AND EQUILIBRIUM
At equilibrium, i.e., ΔG = 0, the process is neither spontaneous nor non-spontaneous because it is balanced between spontaneous and non-spontaneous behavior. (+ΔH)
So,
ΔG = ΔH – T ΔS = 0
Hence,
ΔH = TΔS or T = ΔH / ΔS
T is the temperature at which the transition from spontaneous to non-spontaneous behaviour happens. T is calculated on the assumption that ΔH and ΔS are temperature independent. In reality, ΔH and ΔS change with temperature. However, for modest temperature changes, the variance in them will not add considerable mistakes.
ΔG and Equilibrium constant
All of the substances (reactants and products) in a chemical reaction may not be in their normal forms. As a result of the connection, the change in Gibbs energy of a reaction is related to the change in standard Gibbs energy.
ΔG = ΔG° + RT ln Q
where:
ΔG° is the standard Gibbs energy change (change in Gibbs energy when all the substances are in their standard state).
Q is the reaction quotient.
The expression of the reaction quotient is similar to that of the equilibrium constant, but there is one single difference between them, i.e., Equilibrium concentrations or partial pressures of products and reactants are included in the equilibrium constant. Whereas Q is expressed in terms of reactant beginning concentration partial pressures and product final concentrations or pressures.
For Example, consider the below example:
aA +bB ⇢ cC + dD
For the above reaction, the reaction Quotient is given by

When the values of concentration or partial pressure are other than equilibrium values. When the reaction reaches equilibrium, the concentrations and partial pressure reach their equilibrium values and at this stage, Q = K. At equilibrium, ΔG = 0 and Q = K, then the standard Gibbs energy equation becomes,
0 = ΔG° + RT ln K
Hence,
ΔG° = -RT ln K = -2.303RT log10K
This equation gives the relationship between standard Gibbs energy change for the reaction and its equilibrium constant.
2. EQUILIBRIUM IN CHEMICAL PROCESSES – DYNAMIC EQUILIBRIUM
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
EQUILIBRIUM IN CHEMICAL PROCESSES
Like equilibria in physical systems it can also be achieved in chemical process involving reversible chemical reactions carried in closed container. A + B ↔ C + D
The dynamic nature of chemical equilibrium can be demonstrated in the synthesis of ammonia by Haber’s process. Haber started his experiment with the known amounts of N2 and H2 at high temperature and pressure. At regular intervals of time he determined the amount of ammonia present. He also found out concentration of unreacted N2 and H2.
After a certain time he found that the composition of mixture remains the same even though some of the reactants are still present. This constancy indicates the attainment of equilibrium. In general, for a o can be shown by
According to the equilibrium law,
![]()
Where Kc is called equilibrium constant.
For a general reaction,
aA + bB ↔ cC + dD
![]()
For the reactio H2 + I2 ↔ 2HI ;
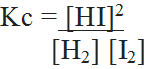
For the reaction N2 + 3H2 ↔ 2NH3
![]()
After a certain time the two reactions occur at the same rate and the system reaches a state of equilibrium. This can be shown by the given figure.
Equilibrium constant for the reverse reaction is the inverse of that for the forward reaction.
If the equilibrium constant for the reaction H2 + I2 ↔ 2HI is Kc, then that for the reverse reaction 2HI ↔ H2 + I2 is 1/Kc
3. LAW OF CHEMICAL EQUILIBRIUM AND EQUILIBRIUM CONSTANT
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
LAW OF CHEMICAL EQUILIBRIUM
At a constant temperature, the rate of a chemical reaction is directly proportional to the product of the molar concentrations of the reactants each raised to a power equal to the corresponding stoichiometric coefficients as represented by the balanced chemical equation. Let us consider the reaction,
![]()
Chemical equilibrium is defined as a state where both products along with reactants are present in the concentration and have no tendency to change further with time. There will be no observable changes in the properties of any particular system in the present. The equilibrium rates of forward and backward reactions are equal.
For example, the mixture of products and the reactants are in the equilibrium state.
In equilibrium, two opposite reactions act in equal rules or velocities, and therefore there are no changes in the substances involved. At this particular point, the reaction must be considered complete. The quantitative formulation is a reversible reaction A ⇋ B + C of equilibrium, the reaction’s velocity to its right, r1, which mathematical expression gives is based on the law of mass action. In “r1 = k1 (A)”, here the k1 is ratio rate.
A catalyst addition can affect both the backward & forward reaction in the same way and do not affect the equilibrium constant. Both the reactions will speed up with the help of a catalyst and increase the speed from which the equilibrium rate can be reached.
The law of chemical equilibrium helps to properly understand the rate of forward as well as backward reaction and rate of change in a chemical reaction.
The rate of forwarding reaction = rate of backward reaction.
The formula mentioned above is known as the Law of chemical equilibrium. Here K is considered an equilibrium constant, and it defines the molar concentration of the product. By the statement of the law of chemical equilibrium, we get to understand the ratio between the product’s concentration and the reactant’s concentration which are both raised to a power of stoichiometric coefficient that is said to be constant, provided that the temperature does not vary. This is called an equilibrium constant. This ratio defines the amount of reactant and product used to understand and analyze the chemical behaviour. This is the law of chemical equilibrium and equilibrium constant.
This constant can be presented as the partial pressures of the products along with reactants for gas-phase reactions. If this is expressed by partial pressure, then the K is represented as Kp.
Here, Pa, Pb, Pc, Pd are the partial pressures of a,b,c,d in the mixture of reactions.
●Examples of chemical equilibrium
To understand the law of chemical equilibrium better, let us analyze an experiment on hydrogen and iodine. The vapor of these two products is kept on a closed vessel at a constant temperature. The reaction starts to proceed and then stops after some time by converting some portion of iodine and hydrogen to hydrogen iodide. The reason for stopping the process was that the two constants reached the equilibrium level after reaching a particular point of dynamism.
Similarly, let us take some amount of hydrogen iodide in the closed vessel and keep it at the same constant temperature after some time. It will be converted into hydrogen molecules and iodine molecules. Therefore, the rest of the product will remain unchanged. However, two constants will remain the same and be fixed in both the experiment and reaction. This reaching of the dynamic stage is called the equilibrium.
Chemical equation: H2 (gas) + I2 (gas) ⇌ 2HI (gas)
4. HOMOGENEOUS EQUILIBRIA
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
HOMOGENEOUS EQUILIBRIUM
Homogeneous equilibrium is more straightforward and less complex when compared to Heterogeneous equilibrium. The most common examples are reactions that involve components in the gaseous state or solution reactions.
e.g.: Reaction of Nitrogen and Hydrogen to form Ammonia (Haber’s process)
N2(g)+ 3H2(g) ⇔ 2NH3(g)
The Esterification reaction between an alcohol and an organic acid is the best example of a liquid phase homogeneous reaction.
CH3COOH(l) + CH3CH2OH(l) ⇔ CH3COOCH2CH3(l) +H2O(l)
The equilibrium constant is a number that expresses the relationship between the concentration of products and the reactants in an equilibrium reaction at a given temperature. It is expressed as ‘Kc’. To derive the expression of Kc, let us consider the homogenous equilibrium equation,
aA + bB ⇔ cC + dD
Note that the products of the reaction are always written on the right side and the reactants are on the left side. The Equilibrium constant Kc for this reaction would consist of a ratio where the products with their coefficient as exponent forms the numerator and similarly the reactants form the denominator.
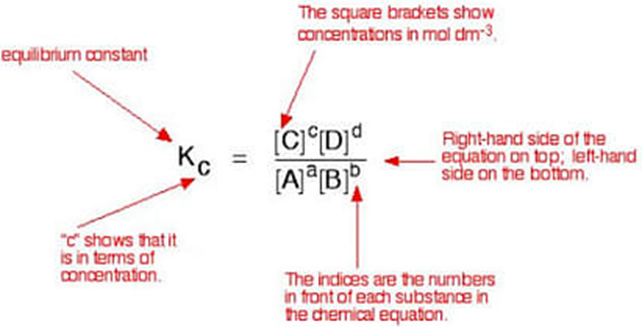
Example: Let us write the Equilibrium Constant expression Kc for the Haber’s process of Ammonia production
N2(g)+ 3H2(g) ⇔ 2NH3(g)
Kc is written as:
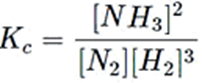
Note that for components that have only one molecule such as for N2, the exponential power of 1 need not be written. The concentration of only the gaseous and aqueous components in the reactions are taken into account.
Equilibrium Constant in Gaseous Systems
For an equilibrium reaction that involves gases, equilibrium constants should be expressed in terms of partial pressure. Thus the ideal gas equation is taken into account.
pV = nRT ……(Ideal gas equation)
→ p = n/V x RT
p → Pressure in Pa
n → Number of moles of gas
V → Volume in cu.m
T → Temperature in K
Here n/V expresses the concentration in moles/m³
Thus, p = c RT
Where c is the concentration in moles/lit
We can also write,
p = [gas] RT
Therefore, at a constant temperature, the pressure of a gas is directly proportional to its concentration.
Consider the reaction
aA + bB ⇔ cC + dD
Kc is written as,
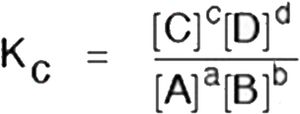
In terms of partial pressure, Kp is written as
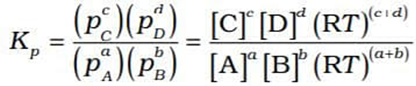 ( as p = [gas] RT)
( as p = [gas] RT)
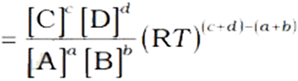
On substitution, we get the relation between Kc and Kp
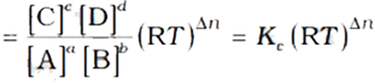
Where, Δn → (number of moles of gaseous products) - (number of moles of gaseous reactants)
5. HETEROGENEOUS EQUILIBRIA
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
HETEROGENEOUS EQUILIBRIA
The equilibrium reactions in which the reactants and the products are not present in the same phase are called heterogeneous equilibrium reactions. Such equilibria in which the reactants and products are not all in the same phase are called heterogeneous equilibria. Heterogeneous equilibrium is demonstrated by the breakdown of calcium carbonate into calcium oxide and carbon dioxide when heated. The following equilibrium is obtained if the reaction is carried out in a closed vessel.
CaCO3(s)⇌CaO(s) + CO2(g)CaCO3(s)⇌CaO(s) + CO2(g)
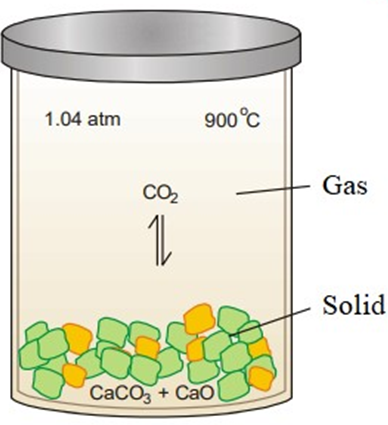
Some other examples of heterogeneous equilibria are:
NH4Cl(s)⇌NH3(g) + HCl(g)
3Fe(s) + 4H2O(g)⇌Fe3O4(s) + 4H2(g)
●Quantitative Characteristics of Heterogeneous Equilibria
An important point to note is that in the case of heterogeneous equilibria, the expression for equilibrium constant does not include the concentrations of pure solids and pure liquids as their concentrations remain constant. In other words, the concentration (moles per unit volume) of a pure solid (or liquid) is fixed and cannot vary. Thus, the concentrations of pure solids or liquids are not included in the equilibrium constant expression. For example, consider the following heterogeneous reaction,
CaCO3(s)⇌CaO(s) + CO2(g)
The equilibrium constant expression for this reaction is:
Kc = [CO2][CaO][CaCO3] CO2
But CaCO3 and CaO are pure solids. So, their concentrations may be assumed to be constant and can be ignored in the equilibrium constant expression. So the equilibrium constant expression for this reaction can be written as
Kc = [CO2]
Since the partial pressure of a gaseous component is proportional to its concentration,
Kp = pco2
As a result, we can deduce that when CaCO3 decomposes at a specific temperature, the equilibrium partial pressure of carbon dioxide gas equals its equilibrium constant in terms of partial pressure. In other words, there is constant pressure of carbon dioxide gas in equilibrium with calcium carbonate and calcium oxide at a particular temperature. So, it gives us a very easy method to find the value of Kp. For this, we need to measure the pressure of carbon dioxide gas in equilibrium with calcium carbonate and calcium oxide at a particular temperature.
Similarly, consider the following reaction:
2H2O(l)⇌2H2(g) + O2(g)
After ignoring the concentration for liquid water, its equilibrium constant expression becomes:
Kc = [H2]2[O2]
Kp = (pH2)2(pO2)
●Some Important Points Regarding Heterogeneous Equilibria
For heterogeneous chemical reactions, the concentration of pure solids and pure liquids are not included in the expression for the equilibrium constant. By convention
[solid]=1 and [liquid]=1
When the substance occurs in the liquid solutions, their concentrations are variable, and therefore their concentrations are given in the expression for the equilibrium constant.
It must be noted that pure substances must be present (however small it may be) for the equilibrium to exist, but they do not appear in the expression for the equilibrium constant.
The concentration of the solvent is considered constant because it is present in large quantities and will not change appreciably.
6. APPLICATIONS OF EQUILIBRIUM CONSTANTS
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
APPLICATION OF EQUILIBRIUM CONSTANT
The knowledge of equilibrium constant helps us to
1. predict the direction in which the net reaction will take place
2. predict the extent of the reaction and
3. calculate the equilibrium concentrations of the reactants and products.
It is to be noted that these constants do not provide any information regarding the rates of the forward or reverse reactions.
1. Predicting the extent of a reaction
The value of equilibrium constant, Kc tells us the extent of a reaction, i.e., it indicates how far the reaction has proceeded towards product formation at a given temperature. A large value of Kc indicates that the reaction reaches equilibrium with high product yield. On the other hand, a low value of Kc indicates that the reaction reaches equilibrium with low product formed. In general, if the Kc is greater than the 103, the reaction proceeds nearly to completion. If it is less than 10-3, the reaction rarely proceeds. If the Kc is in the range 10-3 to103, significant amount of both reactants and products are present at equilibrium.
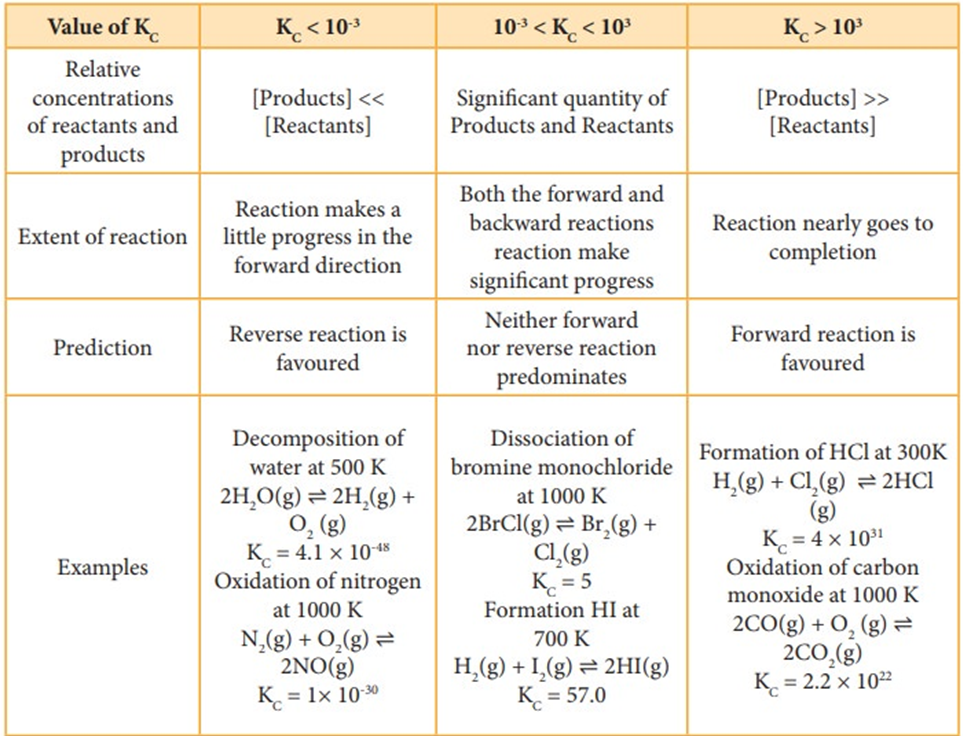
Example
Consider the following equilibrium reactions and relate their equilibrium, constants

2. Predicting the direction of a reaction
From the knowledge of equilibrium constant, it is possible to predict the direction in which the net reaction is taking place for a given concentration or partial pressure of reactants and products.
Consider a general homogeneous reversible reaction,
xA + yB ⇌ lC + mD
For the above reaction under non-equilibrium conditions, reaction quotient ‘Q’ is defined as the ratio of the product of active masses of reaction products raised to the respective stoichiometric coefficients in the balanced chemical equation to that of the reactants.
Under non-equilibrium conditions, the reaction quotient Q can be calculated using the following expression.
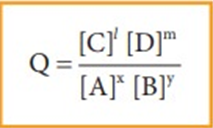
As the reaction proceeds, there is a continuous change in the concentration of reactants and products and also the Q value until the reaction reaches the equilibrium. At equilibrium Q is equal to Kc at a particular temperature. Once the equilibrium is attained, there is no change in the Q value. By knowing the Q value, we can predict the direction of the reaction by comparing it with Kc.
· If Q = Kc, the reaction is in equilibrium state.
· If Q > Kc, the reaction will proceed in the reverse direction i.e., formation of reactants.
· If Q < Kc, the reaction will proceed in the forward direction i.e., formation of products.
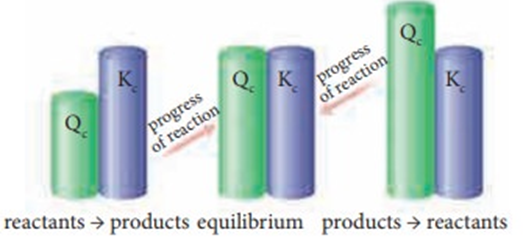
Example 1
The value of Kc for the following reaction at 717 K is 48.
H2(g) + I2(g) ⇌ 2HI(g)
At a particular instant, the concentration of H2, I2and HI are found to be 0.2 mol L-1, 0.2 mol L-1 and 0.6 mol L-1 respectively. From the above information we can predict the direction of reaction as follows.
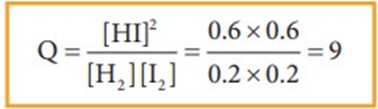
Since Q< Kc, the reaction will proceed in the forward direction.
Example 2
The value of Kc for the reaction
N2O4 (g) ⇌ 2NO2(g)
Kc = 0.21 at 373 K. The concentrations N2O4 and NO2 are found to be 0.125 mol dm-3 and 0.5 mol dm-3 respectively at a given time. From the above information we can predict the direction of reaction as follows
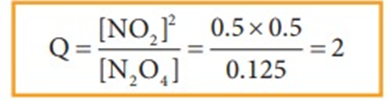
The Q value is greater than Kc. Hence, the reaction will proceed in the reverse direction until the Q value reaches 0.21
3. Calculation of concentration of reactants and products at equilibrium
If the equilibrium concentrations of reactants and products are known for a reaction, then the equilibrium constant can be calculated and vice versa.
Let us consider the formation of HI in which, ‘a’ moles of hydrogen and ‘b’ moles of iodine gas are allowed to react in a container of volume V. Let ‘x’ moles of each of H2 and I2 react together to form 2x moles of HI.
H2 (g)+ I2 (g) ⇌ 2HI2(g)

Applying law of mass action,

The equilibrium constant Kp can also be calculated as follows:
We know the relationship between the Kc and Kp

Solved Problem
One mole of H2 and one mole of I2 are allowed to attain equilibrium. If the equilibrium mixture contains 0.4 mole of HI. Calculate the equilibrium constant.
Given data:
[H2] = 1 mole [I2] = 1 mole
At equilibrium, [HI] = 0.4 mole Kc= ?
Solution:
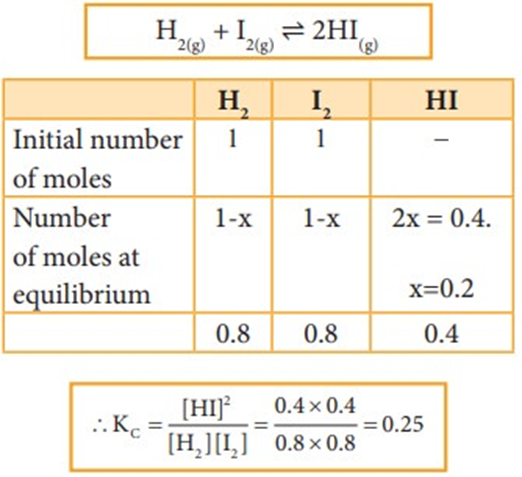
Dissociation of PCl5:
Consider that ‘a’ moles of PCl5 is taken in a container of volume V. Let ‘x’ moles of PCl5 be dissociated into x moles of PCl3 and x moles of Cl2.
PCl5(g) ⇌ PCl3(g) + Cl2(g)
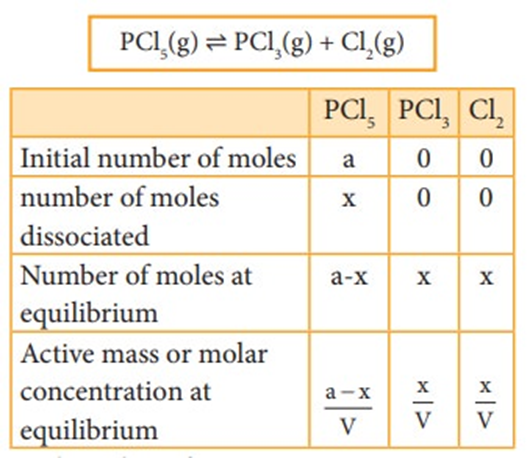
Applying law of mass action,
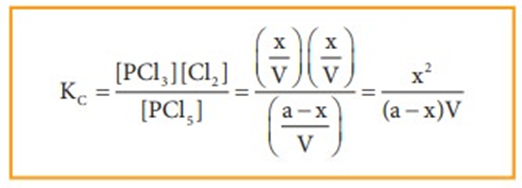
The equilibrium constant Kp can also be calculated as follows:
We know the relationship between the Kc and Kp

Where n is the total number of moles at equilibrium.
n = (a-x) + x + x = (a+x)
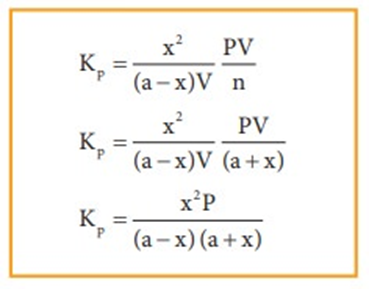
Synthesis of ammonia:
Let us consider the formation of ammonia in which, ‘a’ moles nitrogen and ‘b’ moles hydrogen gas are allowed to react in a container of volume V. Let ‘x’ moles of nitrogen react with 3x moles of hydrogen to give 2x moles of ammonia.
N2(g) + 3H2(g) ⇌ 2NH3(g)
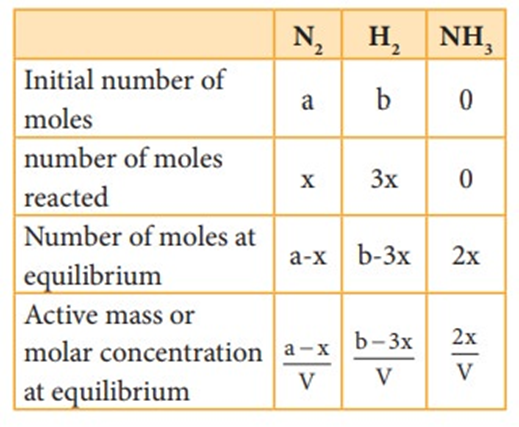
Applying law of mass action,
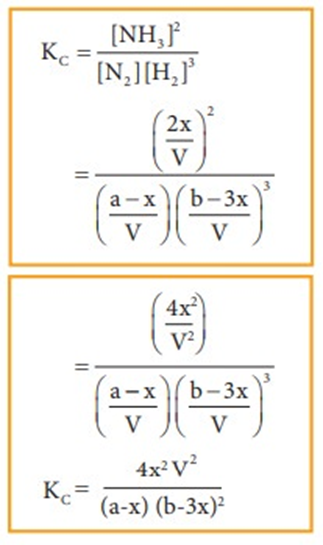
The equilibrium constant Kp can also be calculated as follows:

Total number of moles at equilibrium,
n= a-x + b-3x+ 2x = a+b-2x

Solved Problems:
The equilibrium concentrations of NH3, N2 and H2 are 1.8 × 10-2 M, 1.2 × 10-2 M and 3 × 10-2 M respectively. Calculate the equilibrium constant for the formation of NH3 from N2 and H2. [Hint: M= mol lit-1]
Given data:
[NH3] = 1.8 × 10-2 M
[N2] = 1.2 × 10-2 M
[H2] = 3 × 10-2 M
Kc = ?
Solution:
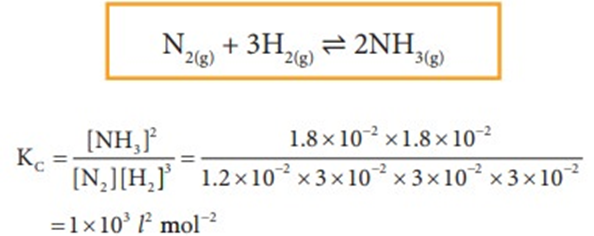
2. The equilibrium constant at 298 K for a reaction is 100.
A + B ⇌ C + D
If the initial concentration of all the four species is 1 M, the equilibrium concentration of D (in mol lit-1) will be
Given data:
[A] = [B] = [C]= [D] =1 M
Kc = 100
[D]eq = ?
Solution:
Let x be the no moles of reactants reacted

7. RELATIONSHIP BETWEEN EQUILIBRIUM CONSTANT K, REACTION QUOTIENT Q AND GIBBS ENERGY G
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
RELATIONSHIP BETWEEN EQUILIBRIUM CONSTANT K, REACTION QUOTIENT Q AND GIBBS ENERGY G.
A mathematical expression of thermodynamic view of equilibrium can be described by tine equation.
ΔG = ΔGº + RT InQ
Where, ΔGº is standard Gibbs energy.
At equilibrium, ΔG = 0 and Q = Kc, so the equation becomes,
0 = ΔGº + RT In Kc
Or, ΔGº = - RT InKc
On changing the base we get ΔGº = -2.303RT log Kc
We know that for a spontaneous process ΔG should be negative. So the value of Kc should be positive.
8. FACTORS AFFECTING EQUILIBRIA
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
FACTORS AFFECTING EQUILIBRIA
Le Chatelier’s principle: If a system under equilibrium is subjected to a change in temperature, pressure or concentration, then the equilibrium shifts in such a manner as to reduce or to counteract the effect of change.
Effect of Change of Concentration: When the concentration of any of the reactants or products in a reaction at equilibrium is changed, the composition of the equilibrium changes so as to minimise the effect.
Effect of Pressure Change
If the number of moles of gaseous reactants and products are equal, there is no effect of pressure.
When the total number of moles of gaseous reactants and total number of moles of gaseous products are different.
On increasing pressure, total number of moles per unit volume increases, thus the equilibrium will shift in direction in which number of moles per unit volume will be less.
If the total number of moles of products are more than the total number of moles of reactants, low pressure will favour forward reaction.
If total number of moles of reactants are more than total number of moles of products, high pressure is favourable to forward reaction.
Effect of Inert Gas Addition
If the volume is kept constant there is no effect on equilibrium after the addition of an inert gas.
Reason: This is because the addition of an inert gas at constant volume does not change the partial pressure or the molar concentration.
The reaction quotient changes only if the added gas is involved in the reaction.
Effect of Temperature Change
When the temperature of the system is changed (increased or decreased), the equilibrium shifts in opposite direction in order to neutralize the effect of change. In exothermic reaction low temperature favours forward reaction e.g.,

but practically very low temperature slows down the reaction and thus a catalyst is used. In case of endothermic reaction, the increase in temperature will shift the equilibrium in the direction of the endothermic reaction.
Effect of a Catalyst
Catalyst has no effect on the equilibrium composition of a reaction mixture.
Reason: Since catalyst increases the speed of both the forward and backward reactions to the same extent in a reversible reaction.
9. IONIC EQUILIBRIUM IN SOLUTION
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
IONIC EQUILIBRIUM IN SOLUTION
Electrolytes: Substances which conduct electricity in their aqueous solution.
Strong Electrolytes: Those electrolytes which on dissolution in water are ionized almost completely are called strong electrolytes.
Weak electrolyte: Those electrolytes which on dissolution in water partially dissociated are called weak electrolyte.
Ionic Equilibrium: The equilibrium formed between ions and unionised substance is called ionic equilibrium, e.g.,
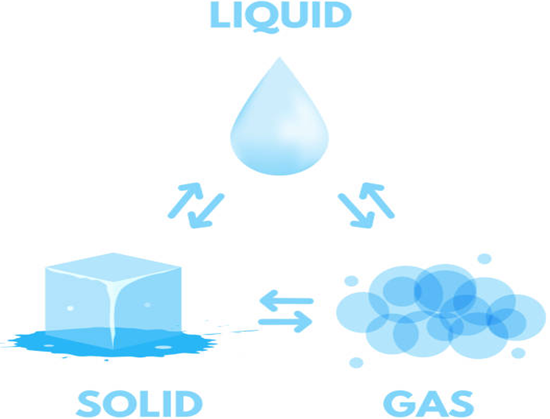
10. ACIDS, BASES AND SALTS
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
ACIDS, BASES AND SALTS
Acids: Acids are the substances which turn blue litmus paper to red and liberate dihydrogen on reacting with some metals.
Bases: Bases are the substances which turn red litmus paper blue. It is bitter in taste. Common Example: NaOH, Na2C03.
• Arrhenius Concept of Acids and Bases
Acids: According to Arrhenius theory, acids are substances that dissociates in water to give hydrogen ions H+(aq).
Bases: Bases are substances that produce OH–(aq) after dissociation in water.
CH3COOH + H2O ↔ CH3COO- + H3O+
• Limitations of the Arrhenius Concept
(i) According to the Arrhenius concept, an acid gives H+ ions in water but the H+ ions does not exist independently because of its very small size (~H-18 m radius) and intense electric field.
(ii) It does not account for the basicity of substances like, ammonia which does not possess a hydroxyl group
• The Bronsted-Lowry Acids and Bases
According to Bronsted-Lowry, an acid is a substance which is capable of donating a hydrogen ion H+ and bases are substances capable of accepting a hydrogen ion H+.
In other words, acids are proton donors and bases are proton acceptors. This can be explained by the following example.
e.g. HCL is an acid since it produces H3O+ in aqueous solution.
HCl(l) + H2O(l) ↔ H3O+(aq) + Cl-(aq)
e.g. for base is NaOH
NaOH(s) + H2O(l) ↔ Na+(aq) + OH-(aq)
Note : H+ ions exist in water as hydronium ions (H3O+)
H+ + H2O ↔ H3O+
• Acid and Base as Conjugate Pairs
The acid-base pair that differs only by one proton is called a conjugate acid-base pair.
Let us consider the example of ionization of HCl in water.
For example in the reaction : NH3(l) + H2O(l) ↔ NH4+(aq) + OH-(aq)
Here water acts as a base because it accepts the proton.
CL is a conjugate base of HCl and HCl is the conjugate acid of base CL. Similarly, H20 is conjugate base of an acid H30+ and H30+ is a conjugate acid of base H2O.
• Lewis Acids and Bases
According to Lewis, acid is a substance which accepts electron pair and base is a substance with donates an electron pair.
Electron deficient species like AlCl3, BH3, H+ etc. can act as Lewis acids while species like H20, NH3 etc. can donate a pair of electrons, can act as Lewis bases.
11. IONIZATION OF ACIDS AND BASES
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
IONIZATION OF ACIDS AND BASES
Strength of acid or base is determined with the help of extent of ionization in aqueous solution.
pH Scale: Hydrogen-ion concentration are measured as the number of gram ions of hydrogen ions present per litre of solution. Since these concentrations are usually small, the concentration is generally expressed as the pH of the solution. pH being the logarithm of the reciprocal of the hydrogen ion concentration.
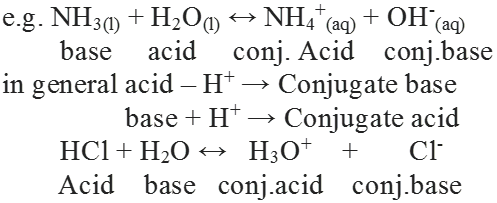
• Di and Polybasic Acids
Acids which contain more than one ionizable proton per molecule are called Dibasic acids or polybasic acids or polyprotic acids.
Common examples are oxalic acid, sulphuric acid, phosphoric acid etc.
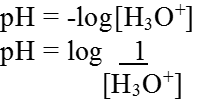
The pH range at 25º C is taken as 0 to 14.
pH = 7 Neutral
pH > 7 Basic
pH < 7 Acidic
The ionization reaction for a dibasic acid can be represented as:
H2X (aq) ↔ H+(aq) + HX-(aq)
HX-(aq) ↔ H+(aq) + X2-(aq)
Their equilibrium constant can be written as
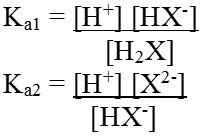
Ka1 and Ka2 are called first and second ionization constants respectively
For dibasic acid Ka1 > Ka2
Factors Affecting Acid Strength
When the strength of H-A bond decreases

The energy required to break the bond decreases, H-A becomes a stronger acid.
As the size of A increases down the group, H-A bond strength decreases and so the acid strength increases.
In a period, as the electronegativity of A increases, the strength of the acid increases.

• Common Ion Effect
If in a aqueous solution of a weak electrolyte, a strong electrolyte is added having an ion common with the weak electrolyte, then the dissociation of the weak electrolyte is decreased or suppressed. The effect by which the dissociation of weak electrolyte is suppresed is known as common ion effect.
CH3COOH(aq) ↔ CH3COO-(aq) + H+(aq)
• Hydrolysis of Salts and the pH of their Solutions
As per the hydrolysis formula,
For the salt of weak acid and weak base like CH3COONa
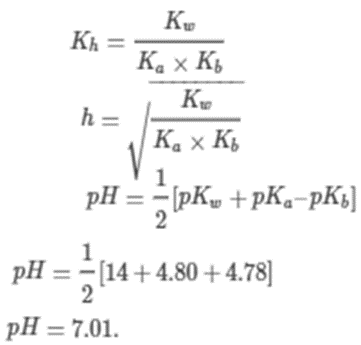
CH3COO- + Na+ H2O ↔ CH3COOH + Na+ + OH-
CH3COO- + H2O ↔ CH3COOH + OH-
Or,
After hydrolysis solution will be basic pH > 7
In this type of hydrolysis only anions of salt take part in the hydrolysis it is known as anionic hydrolysis.
Hydrolysis of weak acid and weak base
Salts belong to this type are CH3COONH4, (NH4)2CO3 etc.
CH3COONH4 + H2O ↔ CH3COOH + NH4OH
Or, CH3COO- + NH4+ + H2O ↔ CH3COOH + NH4OH
pH of the solution depends upon the relative strengths of acid and base.
12. BUFFER SOLUTIONS
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
BUFFER SOLUTIONS
The solutions which resist charge in pH on dilution or with addition of small amounts of acid or alkali are called buffer solutions.
e.g. CH3COOH + CH3COONa
H2CO3 + HCl
Acidic Buffer: Weak acid and its salt with strong base are known as acidic buffer pH < 7.
e.g CH3COOH and CH3COONa, H2CO3 and HCl
Basic Buffer: Weak base and its salt with strong acid are known as basic buffer. pH > 7
e.g. NH4Cl and NH4OH
- pOH of a basic buffer = pKb + log ([salt]/[acid])
- pH of a basic buffer = pKa – log ([salt]/[acid])

13. SOLUBILITY EQUILIBRIA OF SPARINGLY SOLUBLE SALTS
- Books Name
- Ritan Sheth Chemistry Book
- Publication
- Ritan Sheth
- Course
- CBSE Class 11
- Subject
- Chemistry
SOLUBILITY EQUILIBRIA OF SPARINGLY SOLUBLE SALTS
The solubility of a particular salt in a solvent is always a very significant fact to be taken into consideration when studying its properties and the properties of the solution it forms with a particular solvent. While salts like NaCl,KCl and others such as potassium dichromate are completely soluble in water, there are some salts that do not dissolve at all or dissolve only to a very minimal extent. These salts form a special case when defining the solubility equilibria and are called sparingly soluble salts.
Such sparingly soluble salts present solubility equilibria which are measured using an entity called a solubility product. This article will discuss the solubility product and how it can be applied to the solubility equilibria of sparingly soluble salts.
Salts are classified on the basis of their solubility in the following table.

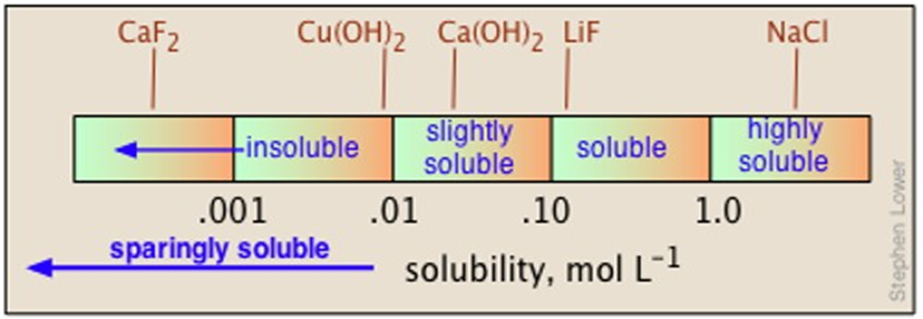
• Solubility Products
A sparingly soluble salt is so-called because when it is stirred into water or mixed with water, only a very small amount of the salt goes into the solution, and most of it remains undissolved. The solution becomes saturated with that little amount of salt dissolved, and the salt immediately dissociates into its ions. For example, when a sparingly soluble salt like AgCl goes into the solution, it dissociates as Ag+ and Cl− ions immediately. So, a dynamic equilibrium exists between the two entities: the undissolved salt and the dissolved ions which are in the solution.
At equilibrium, the dissolving of solid AgCl and precipitation of undissolved AgCl will take place at the same rate. Hence, the equilibrium between the two opposite processes can be given by a reversible equation:
AgCl(s) Dissolution/Precipitation ⇔ AgCl(aq) ↔ Ag+(aq) + Cl-(aq)
The equation can also be written as: AgCl(aq) ↔ Ag+(aq) + Cl–(aq)
When the law of chemical equilibrium is applied to the above equation, it can be written as: K = [Ag+][Cl–][AgCl]
The concentration of the undissolved solid AgCl usually remains constant, and hence, the above equation can be written as: [Ag+][Cl−]= K∗[AgCl] = Ksp
The Ksp is the solubility product and is equal to the ionic product: [Ag+][Cl−] in the saturated solution.
So, for any sparingly soluble salt solution, AxBy the equilibrium of the reaction can be represented as: AxBy ↔ xAy+ + yBx–
The solubility product for AxBy can be written as: Ksp = [Ay+]x ∗ [Bx–]y
The x and y represent the number of ions present in the formula of the sparingly soluble salt.
Hence, the solubility product at a specified temperature for an electrolyte can be defined as the product of the molar concentrations of the ions present in its saturated solution, with each concentration raised to the power equal to the number of ions produced on the dissociation of one molecule of the electrolyte.
Difference between Solubility Product and Ionic Product
As we know, the solubility product and the ionic product of an electrolyte is represented by the product of their concentrations, raised to a power that is equal to the number of ions present on its dissociation. So, how do we differentiate between the two of them? Here is how:
a. Ionic product is used for all types of solutions, both saturated and unsaturated. However, the solubility product is only used for saturated solutions, where a dynamic equilibrium exists between the undissolved salt and the dissolved ions present in the solution. So, one can call the solubility product the ionic product in saturated solutions.
b. For any salt, its solubility product is constant at a constant temperature. The ionic product, however, will depend upon the number of ions present at that particular time.
Solubility products of any sparingly soluble salt can be determined using the value of its solubility product in water at that temperature.
Significance of Solubility Product
The solubility product value can be applied in various aspects and, therefore, is very useful. Below are some of the applications of the solubility product of salts.
a. To Calculate the Solubility of Sparingly Soluble Salt: The solubility of a sparingly soluble salt is very difficult to measure. However, the knowledge of its solubility product can help in determining its solubility at any temperature.
The relationship between solubility (inmol/L) and solubility product (Ksp) depends upon the nature of the salt.
(i) Salts of type AB: (Example: PbSO4,AgCl,AgBr etc.)
AB ↔ A+ + B–
Ksp = [A+][B–] = s ∗ s = s2
(ii) Salts of type AB2:(PbCl2,SrF2)
AB2 ↔ A+ + 2B–
Ksp = [A+][B−] = s ∗ (2s)2 = s∗4 s2 = 4 s3
Similarly, it can be calculated for all other salts with different types to determine the relationship between solubility and solubility product.
b. To Predict Precipitation Reactions: We know that the solubility product of salt is its maximum saturation point at a particular temperature. So, it represents the upper limit in the ionic product of a sparingly soluble salt.
What that means is that if the ionic product is equal to Ksp then no more solute can go into that solution at that particular temperature. This can help in predicting the precipitation.
When the ionic product or the product of the concentration of ions in any solution is more than that of the value of its solubility product of that sparingly soluble salt, then the excess ions will result as a precipitate or precipitation will occur.
So, when two solutions containing known concentrations of ions are mixed together, the knowledge of their solubility product can help predict whether the precipitation will occur or not.
c. In Qualitative Analysis: The separation and identification of basic radicals are made based upon the principles of common ion effect and solubility product principle in qualitative analysis.
d. Precipitation of Soluble Salts: The use of solubility product and common ion effect explains the phenomenon of precipitation when a saturated solution is mixed with a suitable electrolyte containing a common ion. The increase in the ionic product over the solubility product results in precipitation. This phenomenon is used in the purification of common salt, salting out of soap and also in the manufacture of baking soda or sodium bicarbonate.
It is applicable to sparingly soluble salt. There is equilibrium between ions and unionised solid substance.
AgCl ↔ Ag+ + Cl-
Ksp = [Ag+] [Cl-]
Ksp is called solubility product
In pure water,
Ksp = [Ag+] [Cl-]
Ksp = S2 { ∵ S = [Ag+] = [Cl-] }
S = √Ksp
• Equilibrium: It can be established for both physical and chemical processes. At the state of equilibrium rate of forward and backward reactions are equal.
• Equilibrium constant: Kc is expressed as the concentration of products divided by reactants each term raised to the stoichiometric coefficients. For reactions,
aA + bB ↔ cC + dD
Kc = [C]ceq [D]deq
[A]aeq [B]beq
Kc >> 1 : Mixture contains mostly product
Kc << 1 : Mixture contains mostly reactants
• Le Chatelier’s principle: It states that the change in any factor such as temperature, pressure, concentration etc., will cause the equilibrium to shift in such a direction so as to reduce the effect of the change.
• Electrolytes: Substances that conduct electricity in aqueous solutions are called electrolytes.
• Arrhenius Concept: According to Arrhenius, acids give hydrogeneous while bases produce hydroxyl ions in their aqueous solution.
• Bronsted-Lowry concept: Bronsted-Lowry defined acid as proton donor and a base as a proton acceptor.
• Conjugate base and Conjugate acid: When a Bronsted-Lowry acid reacts with a base it produces its conjugate base and conjugate acid.
• Conjugate pair of acid and base: Conjugate pair of acid and base differs only by one proton.
• Lewis acids: Define acid as an electron pair acceptor and a base as an electron pair donor.
• pH Scale: Hydronium ion concentration in molarity is more conveniently expressed on a logarithmic scale known as the pH scale. The pH of pure water is 7.
• Buffer solution: It is the solution whose pH does not change by addition of small amount of strong acid or base.
For example: CH3COOH + CH3COONa.
• Solubility product (Ksp): For a sparingly soluble salt, it is defined as the product of molar concentration of the ions raised to the power equal to the number of times each ion occurs in the equation for solubilities.
BaSO4 ↔ Ba2+(aq) + SO42-(aq)
This equilibrium system may be described by the mass action expression

 Ritan Sheth
Ritan Sheth
