1. Inequalities and Algebraic Solutions of Linear Inequalities in One Variable and their Graphical Representation
- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
Chapter-6
Linear Inequalities
Inequalities and Algebraic Solutions of Linear Inequalities in One Variable and their Graphical Representation:
What is inequalities
- In mathematics, an inequality is a relation that holds between two values when they are different
- Solving linear inequalities is very similar to solving linear equations, except for one small but important detail: you flip the inequality sign whenever you multiply or divide the inequality by a negative
- Two real numbers or two algebraic expressions related by the symbol ‘<’, ‘>’, ‘£’ or ‘³’ form an inequality.
Symbols used in inequalities
- The symbol < means less than. The symbol > means greater than.
- The symbol < with a bar underneath means less than or equal to. Usually this is written as ≤
- The symbol > with a bar underneath means greater than or equal to. Usually this is written as ≥
- The symbol ≠ means the quantities on left and right side are not equal
Examples
- a < b means a is less then b or b is greater a
- a≤b means a is less then or equal to b
- a > b means a is greater than b
- a≥b means a is greater or equal to b
Types of inequalities:
- Numerical inequalities :
Example:
3 < 5(read as 3 is less than 5)
7 > 5 (read as 7 is greater than 5)
- Literal inequalities:
Inequalities which involve variables are called literal inequalities
Example: x < 5; y > 2
x ³5; y £ 2;
- Double inequalities:
The inequality is said to be a double inequality if the statement shows the double relation of the expressions or the numbers..
Example: 3 < 5 < 7 (read as 5 is greater than 3 and less than 7),
3 £ x < 5 (read as x is greater than or equal to 3 and less than 5)
And 2 < y £ 4(read as y is less than or equal to 4 and greater than 2)
- Open Sentence :
The inequality is said to be an open sentence if it has only one variable.
Example: x < 6 (x is less than 6),
x > 8
- Strict inequalities:
A relation that expresses the comparison between the unequal quantities is called strict inequality.
Example: ax + b < 0,
ax + b > 0,
ax + by < c,
ax + by > c,
ax2 + bx + c > 0
- Slack inequalities:
Inequalities involving the symbol '≥' or '≤' are called slack inequalities.
Example: ax + by +c,
ax + by +c,
3x – y ≥ 5
- Linear inequalities:
When two expressions are connected by “greater than” or “less than” sign, we get an inequality. Also, the linear inequation is similar to a linear equation, where the equal to sign is replaced by the inequality sign.
Example: ax + b < 0,
ax + b > 0,
x - 5 > 3x – 10,
- Quadratic inequalities:
A quadratic inequality is an inequality that contains a quadratic expression.
Example: ax2+bx+c<0,
ax2 + bx + c > 0
ax2 + bx + c £ 0
Things are which are safe to do in inequality which does not change in direction:
- Addition of same number on both sides
a>b
=> a+c > b+c - Subtraction of same number on both sides
a>b
=> a−c > b−c - Multiplication/Division by same positive number on both sides
a>b
if c is positive number then
ac > bc
if c is positive number (non zero) then
a/c > b/c
Things which changes the direction of the inequality:
- Swapping the left and right sides
- Multiplication/Division by negative number on both sides
If a > b and c is negative number then ac < bc
If a < b and c is negative number then ac > bc
- Don’t multiple by variable whose values you dont know as you don’t know the nature of the variable
Concept Of Number line:
- A number line is a horizontal line that has points which correspond to numbers. The points are spaced according to the value of the number they correspond to; in a number line containing only whole numbers or integers, the points are equally spaced.
- It is very useful in solving problem related to inequalities and also representing it
Suppose x >2(1/ 3), this can represent this on number line like that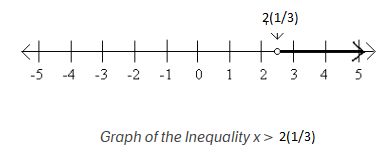
Linear Inequation in One Variable:
A inequation of the form
ax+b>0
or
ax+b≥0
or
ax+b<0
or
ax+b≤0
are called the linear equation in One Variable
Example:
x−2<0,
3x+10>0,
10x−17≥0
Linear Inequations in Two Variable:
A inequation of the form
ax+by>c
or
ax+by≥c
or
ax+by<c
or
ax+by≤c
are called the linear equation in two Variable
Example:
- x−2y<0
- 3x+10y>0
- 10x−17y≥0
How to solve the linear inequalities in one variable?:
Steps to solve the Linear inequalities in one variable:
- Obtain the linear inequation
- Pull all the terms having variable on one side and all the constant term on another side of the inequation
- Simplify the equation in the form given above
ax>b
or
ax≥b
or
ax<b
or ax≤b - Divide the coefficent of the variable on the both side.If the coefficent is positive,direction of the inequality does not changes,but if it is negative, direction of the inequation changed
- Put the result of this equation on number line and get the solution set in interval form
Example:
x−2 > 2x+15
Solution
x−2 > 2x+15
Subtract x from both the side x−2−x > 2x+15−x
−2>x+15
Subtract 15 from both the sides −17 > x
Solution set (−∞,−17)
Example: Find all pairs of consecutive odd natural numbers, both of which are larger
than 10, such that their sum is less than 40.
Solution: Let x be the smaller of the two consecutive odd natural number, so that the
other one is x +2. Then, we should have
x > 10 ... (1)
and x + ( x + 2) < 40 ... (2)
Solving (2), we get
2x + 2 < 40
i.e., x < 19 ... (3)
From (1) and (3), we get
10 < x < 19
Since x is an odd number, x can take the values 11, 13, 15, and 17. So, the required
possible pairs will be
(11, 13), (13, 15), (15, 17), (17, 19)
Steps to solve the linear inequality of the fraction form
[(ax+b)/(cx+d)]>k or similar type
- Take k on the LHS
- Simplify LHS to obtain the inequation in the form
[(px+q)/(ex+f)]>0
Make the coefficent positive if not - Find out the end points solving the equatoon px+q=0 and ex+f=0
- Plot these numbers on the Number line. This divide the number into three segment
- Start from LHS side of the number and Substitute some value in the equation in all the three segments to find out which segments satisfy the equation
- Write down the solution set in interval form
Or there is more method to solves these
- Take k on the LHS
- Simplify LHS to obtain the inequation in the form
[(px+q)/(ex+f)]>0
Make the coefficent positive if not
- For the equation to satisfy both the numerator and denominator must have the same sign
- So taking both the part +, find out the variable x interval
- So taking both the part -, find out the variable x interval
- Write down the solution set in interval form
Lets take one example to clarify the points
Lets take one example to clarify the points
Question
1. Solve X−3x+5>0
Solution:
Method A
- Lets find the end points of the equation
Here it is clearly
x=3 and x=-5 - Now plots them on the Number line
- Now lets start from left part of the most left number
i.e
Case 1
x<−5 ,Let takes x=-6 then −6−3−6+5>0
3>0
So it is good
Case 2
Now take x=-5
as x+5 becomes zero and we cannot have zero in denominator,it is not the solution
Case 3
Now x > -5 and x < 3, lets take x=1 then 1−31+5>0
−16>0
Which is not true
Case 4
Now take x =3,then
0> 0 ,So this is also not true
case 5
x> 3 ,Lets x=4
4−34+5>0
19>0
So this is good - So the solution is
x < -5 or x > 3
or
(−∞,−5)∪(3,∞)
Method B
- the numerator and denominator must have the same sign. Therefore, either
1) x−3>0 and x+5>0,or 2) x - 3 < 0 and x + 5 < 0$ - Now, 1) implies x > 3 and x > -5.
Which numbers are these that are both greater than 3 and greater than -5?
Clearly, any number greater than 3 will also be greater than -5. Therefore, 1) has the solution
x > 3. - Next, 2) implies
x < 3 and x < -5.
Which numbers are these that are both less than 3 and less than -5?
Clearly, any number less than -5 will also be less than 3. Therefore, 2) has the solution
x < -5. - The solution, therefore, is
x < -5 or x > 3
Quadratic Inequality:
A inequation of the form
so for a ≠ 0
ax2+bx+c>0
or
ax2+bx+c<0
or
ax2+bx+c≥0
or
ax2+bx+c≤0
are called Quadratic Inequation in one Variable
Steps to solve Quadratic or polynomial inequalities:
ax2+bx+c>0,
or
ax2+bx+c<0,
or
ax2+bx+c≥0,
ax2+bx+c≤0
- Obtain the Quadratic inequation
- Pull all the terms having on one side and Simplify the equation in the form given above
- Find the roots(0 points) of the Quadratic equation using any of the method and write in this form
(x-a)(x-b) - Plot these roots on the number line .This divide the number into three segment
- Start from LHS side of the number and Substitute some value in the equation in all the three segments to find out which segments satisfy the equation
- Write down the solution set in interval form
Solved Example
Question 1
x2-5x+6>0
Solution
1) Simplify or factorize the inequality which means factorizing the equation in case of quadratic equalities
Which can be simplified as
x2−5x+6>0
=> x2−2x−3x+6>0
=> (x−2)(x−3)>0
2) Now plot those points on Number line clearly
3) Now start from left of most left point on the Number line and look out the if inequalities looks good or not. Check for greater ,less than and equalities at all the end points
So in above case of x2−5x+6>0
We have two ends points 2 ,3
Case 1
So for x<2 ,Let take x=1,then (1−2)(1−3)>0
=> 2>0
So it is good
So This inequalities is good for x < 2
Case 2
Now for x =2,it makes it zero, so not true. Now takes the case of 2<x<3. Lets takes x= 2.5
(2.5−2)(2.5−3)>0
=> −0.25>0
Which is not true so this solution is not good
Case 3
Now lets take the right most part i.e x>3
Lets take x=4
(4−2)(4−3)>0
=> 2>0
So it is good.
Now the solution can either be represented on number line or we can say like this
(−∞,2)∪(3,∞)
Question: Solve y < 2 graphically
Graph of y = 2 is given in the Figure.
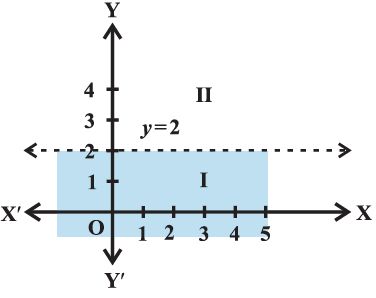
Let us select a point, (0, 0) in lower half plane I and putting y = 0 in the given inequality, we see that
1 × 0 < 2 or 0 < 2 which is true.
Thus, the solution region is the shaded region below the line y = 2.
Hence, every point below the line (excluding all the points on the line) determines the solution of the given inequality.
2. Graphical methods and Solution of Linear Inequalities in Two Variables
- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
Graphical methods and Solution of Linear Inequalities in Two Variables
Graph of Linear inequalities in Two Variable
A linear equation in two variable is of the form
ax+by+c=0
We have already studied in Coordinate geometry that this can be represented by a straight line in xy- plane. All the points on the straight line are the solutions of this linear equation.
we can similarly find the solution set graphically for the linear inequalities in the below form
ax+by+c<0
ax+by+c>0
ax+by+c≥0
ax+by+c≤0
How to find the solution graphically for Linear inequalities in Two Variable.:
- Draw the graph of the equation obtained for the given inequality by replacing the inequality sign with an equal sign.
ax+by+c=0
- This can be done easily by Point on the x-axis( x,0) and point on the y axis ( 0,y)
- Point on x-axis given by ax+b(0)+c=0 or x=−c/a or (−c/a,0)
- Point on y-axis given by a(0)+by+c=0 or y=−c/b or (0,−c/b)
- Locate these point on cartesian plane and join them to find the line
- Use a dashed or dotted line if the problem involves a strict inequality, < or >.
- Otherwise, use a solid line to indicate that the line itself constitutes part of the solution.
- Pick a point lying in one of the half-planes determined by the line sketched in step 1 and substitute the values of x and y into the given inequality.
Use the origin whenever possible. - If the inequality is satisfied, the graph of the inequality includes the half-plane containing the test point.
Otherwise, the solution includes the half-plane not containing the test point
Example
Determine the solution set for the inequality
x+y>1
Solution
1) Draw the graph of the equation obtained for the given inequality by replacing the inequality sign with an equal sign.
i.e x+y=1
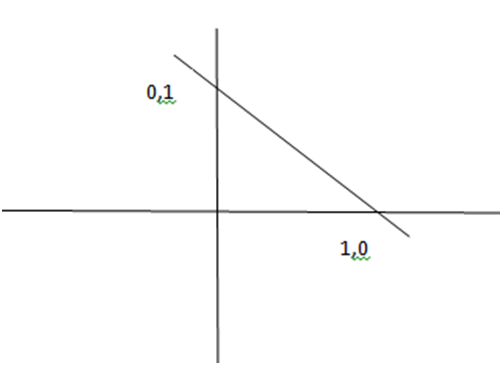
2) Pick the test point as origin (0,0), and put into the inequality
0+0>1
0>1
Which is false
So the solution set is other half plane of the line
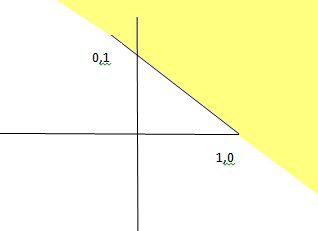
How to find the solution graphically for pair of Linear inequalities in Two Variable.
ax+by+c<0
px+qy+c<0
The solution set of a system of linear inequalities in two variables x and y is the set of all points (x, y) that satisfy each inequality of the system.
Step
- Find the graphical solution for each inequality independently using the technique described above
- Now determine the region in common with each solution set
Example
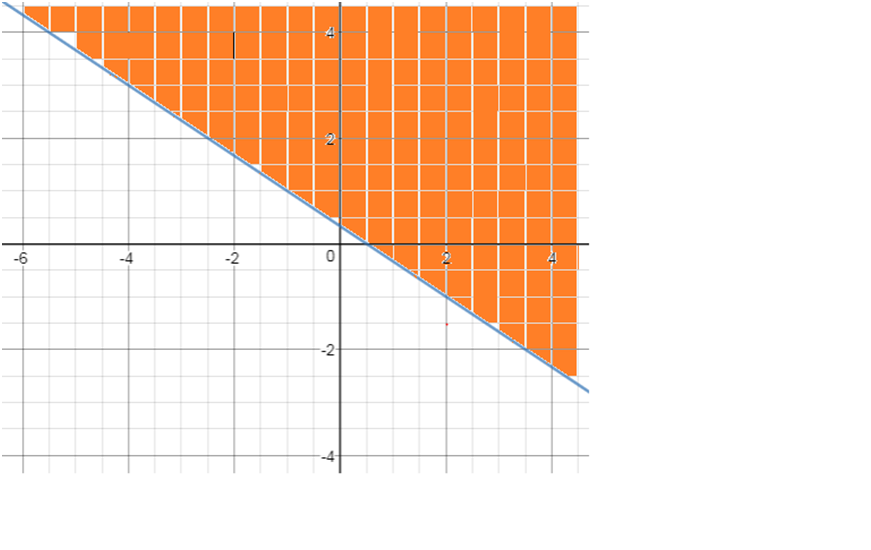
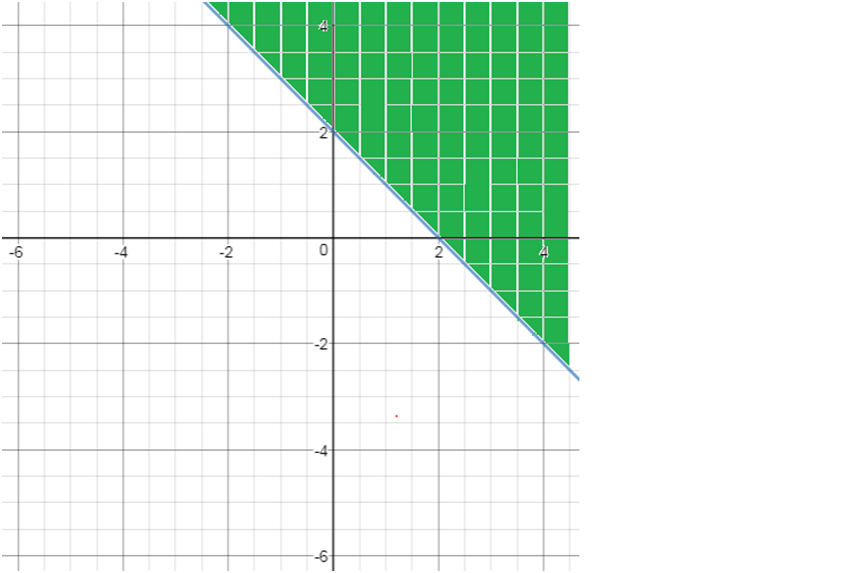
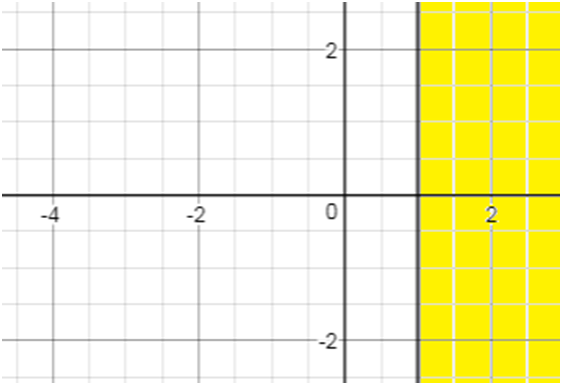
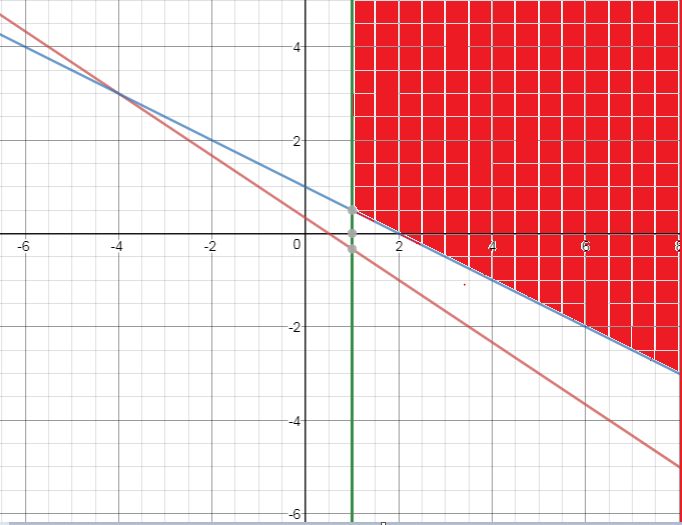
Find the solution of the below system of inequalities
2x+3y>1
x+2y>2
x>1
Solution
1) for 2x+3y>1, Solving using the above method solution is
2) for x+2y>2, Solving using the above method solution is
3) for x>1, Solving using the above method solution is
4) Now we draw these on the single graph and can determine the common region
Example:
Solve the following system of inequalities
8x + 3y £ 100 ......... (1)
x ³ 0 ......... (2)
y ³ 0 ... …. (3)
Ans:
Let 8x + 3y = 100
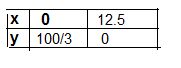
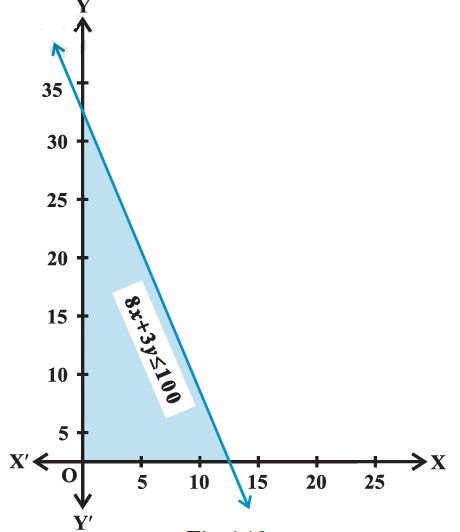
The inequality 8x + 3y £ 100 represents the shaded region below the line, including the
points on the line 8x +3y =100.
Since x ³ 0, y ³ 0, every point in the shaded region in the first quadrant, including the points on the line and the axes, represents the solution of the given system of inequalities.
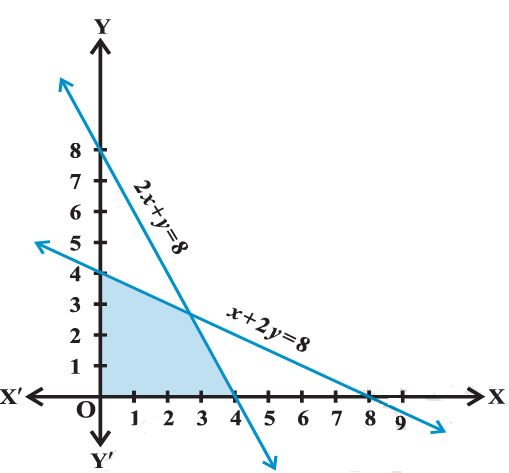
Question: Solve the following system of inequalities graphically
x + 2y £ 8 ... (1)
2x + y £ 8 ... (2)
x > 0 ... (3)
y > 0 ... (4)
Solution:
We draw the graphs of the lines
x + 2y = 8

and
2x + y = 8.
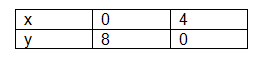
The inequality (1) and (2) represent the region below the two lines, including the point on the respective lines.
Since x ³ 0, y ³ 0, every point in the shaded region in the first quadrant represent
a solution of the given system of inequalities.
Note:
1 The region containing all the solutions of an inequality is called thesolution region.
2. In order to identify the half plane represented by an inequality, it is just sufficient to take any point (a, b) (not online) and check whether it satisfies the inequality or not. If it satisfies, then the inequality represents the half plane and shade the region which contains the point, otherwise, the inequality represents that half plane which does not contain the point within it. For convenience, the point (0, 0) is preferred.
3. If an inequality is of the type ax + by ³ c or ax + by £ c, then the points on the line ax + by = c are also included in the solution region. So draw a dark line in the solution region.
4. If an inequality is of the form ax + by > c or ax + by < c, then the points on the line ax + by = c are not to be included in the solution region. So draw a broken ordotted line in the solution region.
Example: Solve – 8 £ 5x – 3 < 7.
Solution : In this case, we have two inequalities,
– 8 £ 5x – 3 and 5x – 3 < 7,
which we will solve simultaneously.
We have – 8 £ 5x –3 < 7
or –5 £ 5x < 10 or –1 £ x < 2
Example:
A manufacturer has 600 litres of a 12% solution of acid. How many litres
of a 30% acid solution must be added to it so that acid content in the resulting mixture
will be more than 15% but less than 18%?
Solution: Let x litres of 30% acid solution is required to be added. Then
Total mixture = (x + 600) litres
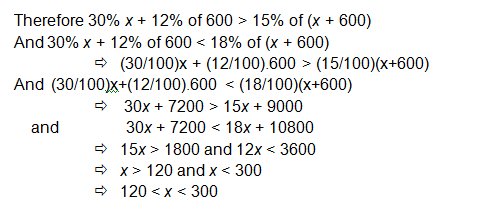

 KRISHNA PUBLICATIONS
KRISHNA PUBLICATIONS
