1. Sequences and Series

Chapter 9

Sequences and Series

Sequences and Series:

A sequence can be regarded as a function whose domain is the set of natural numbers or some subset of it. Sometimes, we use the functional notation a(n) for a_n.

The different numbers occurring in any particular sequence are known as terms. The terms of a sequence are denoted by

a₁, a₂, a₃,….,a_n

If a sequence has a finite number of terms then it is known as a finite sequence. A sequence is termed as infinite if it is not having a definite number of terms.

Series: Let a1, a2, a3,…,an, be a given sequence. Then, the expression

a1 + a2 + a3 +,…+ an + ...

is called the series associated with the given sequence .The series is finite or infinite according as the given sequence is finite or infinite. Series are often represented in compact form, called sigma notation, using the Greek letter å (sigma) as means of indicating the summation involved. Thus, the series a1 + a2 + a3 + ... + an is abbreviated as

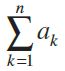
 Sequence relates to the organization of terms in a particular order (i.e. related terms follow each other) and series is the summation of the elements of a sequence.

Examples

Example: Write the first three terms in each of the following sequences defined by

the following:  an = 2n + 5,

Ans.: (i) Here an = 2n + 5

Substituting n = 1, 2, 3, we get

a1 = 2(1) + 5 = 7, a2 = 9, a3 = 11

Therefore, the required terms are 7, 9 and 11.

Example  Let the sequence an be defined as follows:

a1 = 1, an = an – 1 + 2 for n 2.

Find first five terms and write corresponding series.

Solution We have

a1 = 1, a2 = a1 + 2 = 1 + 2 = 3, a3 = a2 + 2 = 3 + 2 = 5,

a4 = a3 + 2 = 5 + 2 = 7, a5 = a4 + 2 = 7 + 2 = 9.

Hence, the first five terms of the sequence are 1,3,5,7 and 9. The corresponding series

is 1 + 3 + 5 + 7 + 9 +...

Examples

Q.1: If a_n = 2ⁿ, then find the first five terms of the series.

Solution: Given: a_n = 2ⁿ

On substituting n = 1, 2, 3, 4, 5, we get

a₁ = 2¹ = 2

a₂ = 2² = 4

a₃ = 2³ = 8

a₄ = 2⁴ = 16

a₅ = 2⁵ = 32

Therefore, the required terms are 2, 4, 8, 16, and 32.

Q.2: Find the sum of odd integers from 1 to 2001.

Solution:

The odd integers from 1 to 2001 are 1, 3, 5, …1999, 2001.

It clearly forms a sequence in A.P.

Where, the first term, a = 1

Common difference, d = 2

Now,

a + (n -1)d = 2001

1 + (n-1)(2) = 2001

2n – 2 = 2000

2n = 2000 + 2 = 2002

n = 1001

We know,

S_n = n/2 [2a + (n-1)d]

S_n = 1001/2[2×1+(1001-1)2]

S_n = 1001/2[2+1000×2]

S_n = 1001/2[2002]

S_n = 1001 x 1001

S_n = 1002001