5. Square Root and Cube Root Of Complex Numbers

Square Root and Cube Root Of Complex Numbers:

Square roots of a complex number

Let the square root of a + ib be x + iy

That is = √[a+ib] = x + iy where x, y ∈ R

a + ib =  ( x + iy )²  = x²  - y²  + i2xy

Equating real and imaginary parts, we get 

x² - y² = a and 2xy = b

(x²  + y² )² =  (x² - y² ) ²  + 4x² y²  = a²  + b²

x²  + y² =  √[a²+b²], since x² + y² is positive 

Solving x² + y² = a  and  x²+ y² =√[a²+b²], we get

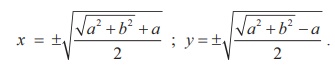
Since 2xy = b  it is clear that both x and y will have the same sign when b is positive, and x and y have different signs when b is negative.

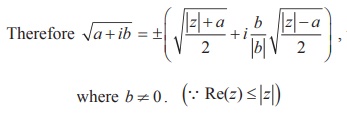
Formula for finding square root of a complex number

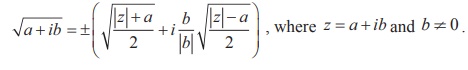
Note

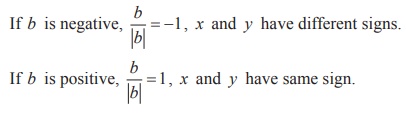
Example 1.

Find the square root of 6 - 8i.

Solution

We compute |6 - 8i| = √[6² + (-8)²] = 10

and applying the formula for square root, we get

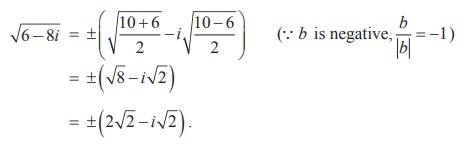
Example 2: Determine the square root of complex number 3 + 4i.

Solution: To determine the square root of 3 + 4i, we will determine its magnitude and compare with a + ib.

|3 + 4i| = √(3² + 4²) = √(9 + 16) = √25 = 5; a = 3 and b = 4 > 0

Therefore, using formula for square root of complex numbers, we have

√(3 + 4i) = ± (√[√(5 + 3)/2] + i√[√(5 - 3)/2] )

= ± (√(8/2) + i √(2/2))

= ±(√4 + i√1)

= ± (2 + i)

Answer: Hence, √(3 + 4i) = ± (2 + i)

Cube Root of Unity Values:

Suppose the cube root of 1 is “x”,

i .e  .,  ³√1 = x.

According to the general cube roots definition,

                            x³ = 1

• •  x³ – 1 = 0

since (a³ – b³) = (a – b) ( a² + ab + b²)

Now, (x³ – 1³) = 0

• • (x – 1)( x² + x + 1) = 0

Therefore,

 x = 1  Or   ( x² + x + 1) = 0

• • x=1  or  x = [(-1) ± √(1²-4.1.1)]/2
  • x=1 or x= [-1 ± √-3]/2
  • x=1 or  x= -1/2 ± i√(3)/2

Therefore, the three cube roots of unity are:

1,  ω= -1/2+i√(3)/2,  ω²= -1/2 – i√(3)/2

Properties of Cube roots of unity

1) One imaginary cube roots of unity is the square of the other imaginary cube root.

= ¼ [(-1)² – 2 × 1 × √3 i + ( √3 i)²] = ¼(1 – 2√ 3i – 3) = (-1-√ 3 i) /2

And

= ¼ [(-1)² + 2 × 1 × √3 i + ( √3 i)²] = ¼(1 + 2√ 3i – 3) = (-1+ √ 3 i) /2

i.e., ω²= (ω²)²

2) If two imaginary cube roots are multiplied then the product we get is equal to 1.

Let’s take ω = (-1 + √3 i ) /2

ω² = (-1 – √3 i ) /2

Now we will get the product of two imaginary cube roots as ω x ω² = [(-1 + √3 i ) / 2]x [(-1 – √3 i ) /2]

Or ω³ = ¼[(-1)² – (√3 i)²]

= ¼[( 1 – 3i²) = ¼ x 4 = 1.

3) As there are three cube roots of unity, their sum is zero, let’s see how

= 1 + [(-1 + √3 i ) /2] + [(-1 – √3 i ) /2]

Or

1 + ω + ω² = 1 – ½ + (√3 i ) /2 – ½ – (√3 i ) /2

= 0

4) conjugate of One imaginary cube roots of unity is equal to the other imaginary cube root.

Euler’s form of a Complex Number

e^iƟ = cos Ɵ + i sin Ɵ

This form makes the study of complex numbers and its properties simple. Any complex number can be expressed as

z = x + iy (Cartesian form)

= |z| [cos Ɵ + I sin Ɵ] (polar form)

= |z| e^iƟ

De Moivre’s Theorem and its Applications

(a) De Moivre’s Theorem for integral index. If n is a integer, then (cos Ɵ + i sin Ɵ)ⁿ = cos (nƟ) + i sin (nƟ)

(b) De Moivre’s Theorem for rational index. If n is a rational number, then the value of or one of the values of

(cosƟ + isinƟ)ⁿ is cos (nƟ) + i sin (nƟ).

In fact, if n = p/q where p, q ϵ I, q > 0 and p,q have no factors in common, then (cos Ɵ + i sin Ɵ)ⁿ has q distinct values, one of which is cos (nƟ) + i sin (nƟ)

The nth Roots of Unity

By an nth root of unity we mean any complex number z which satisfies the equation zⁿ = 1 (1)

Since an equation of degree n has n roots, there are n values of z which satisfy the equation (1). To obtain these n values of z, we write 1 = cos (2kπ) + I sin (2kπ)

Where k ϵ I and

[using the De Moivre’s Theorem]

Where k = 0, 1, 2, …., n -1.

Note

The values of (cos Ɵ + I sin Ɵ)^p/q where p, q ϵ I, q ≠ 0, hcf (p,q) = 1 are given by

Where k = 0, 1, 2, ….., q -1.