3. Geometric Progression (GP) and Geometric Mean (GM)

Geometric Progression (GP) and Geometric Mean (GM)

A sequence a1, a2, a3,…, an,… is called Geometric sequence or Geometric progression

if an + 1 / an = r, n ΠN, where a1 is called the first term and the constant term r is called

 the common ratio of the G.P.

It is represented by:

a, ar, ar², ar³, ar⁴, and so on.

Where a is the first term and r is the common ratio.

The nth term of a GP is a_n=T_n = ar^n-1

a = the first term, r = the common ratio, l = the last term,

n = the numbers of terms,

S_n = the sum of first n terms.

Suppose a, ar, ar², ar³,……ar^n-1 is the given Geometric Progression.

Then the sum of n terms of GP is given by:

S_n = a + ar + ar² + ar³ +…+ ar^n-1

• S_n = a[(rⁿ – 1)/(r – 1)] if r ≠ 1 and r > 1

Types  of GP:

1. Finite geometric progression (Finite GP)
2. Infinite geometric progression (Infinite GP)

Finite Geometric Progression

The terms of a finite G.P. can be written as a, ar, ar², ar³,……ar^n-1

a, ar, ar², ar³,……ar^n-1 is called finite geometric series.

The sum of finite Geometric series is S_n = a[(rⁿ – 1)/(r – 1)] if r ≠ 1 and r > 1

Infinite Geometric Progression

Terms of an infinite G.P. can be written as a, ar, ar², ar³, ……ar^n-1,…….

a, ar, ar², ar³, ……ar^n-1,……. is called infinite geometric series.

The sum of infinite geometric series is S_n =

Properties of GP:

• Three non-zero terms a, b, c are in GP if and only if b² = ac
• In a GP,
  Three consecutive terms can be taken as a/r, a, ar
  Four consecutive terms can be taken as a/r³, a/r, ar, ar³
  Five consecutive terms can be taken as a/r², a/r, a, ar, ar²
• In a finite GP, the product of the terms equidistant from the beginning and the end is the same
  That means, t₁.t_n = t₂.t_n-1 = t₃.t_n-2 = …..
• If each term of a GP is multiplied or divided by a non-zero constant, then the resulting sequence is also a GP with the same common ratio
• The product and quotient of two GP’s is again a GP
• If each term of a GP is raised to the power by the same non-zero quantity, the resultant sequence is also a GP
• If a₁, a₂, a₃,… is a GP of positive terms then log a₁, log a₂, log a₃,… is an AP (arithmetic progression) and vice versa

Geometric Mean (G .M.) : The geometric mean of two positive numbers a and b is the

Number √(ab).

Therefore, the geometric mean of 2 and 8 is 4.

 We observe that the three numbers 2,4,8 are consecutive terms of a G.P.

Let G1, G2,…, Gn be n numbers between positive numbers a and b such that

a,G1,G2,G3,…,Gn,b is a G.P.

Thus, b being the (n + 2)th term,

we have b= arⁿ⁺¹

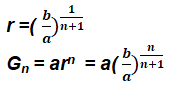
Example: Insert three numbers between 1 and 256 so that the resulting sequence

is a G.P.

Solution Let G1, G2,G3 be three numbers between 1 and 256 such that

1, G1,G2,G3 ,256 is a G.P.

Therefore 256 = r⁴ giving r = ± 4 (Taking real roots only)

For r = 4, we have G1 = ar = 4, G2 = ar² = 16, G3 = ar³ = 64

Similarly, for r = – 4, numbers are – 4,16 and – 64.

Hence, we can insert 4, 16, 64 between 1 and 256 so that the resulting sequences are in G.P.

Relationship Between A.M. and G.M.:

Let A and G be A.M. and G.M. of two given positive real numbers a and b, respectively.

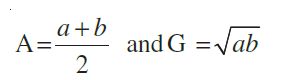
Thus, we have

 

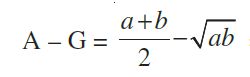
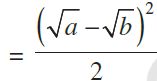
• A – B ³  0

we obtain the relationship A G.

Example 1. We know the sum of the interior angles of a triangle is 180°. Show that the sums of the interior angles of polygons with 3, 4, 5, 6, … sides form an arithmetic progression. Find the sum of the interior angles for a 21-sided polygon.

Solution:

Given the sum of interior angles of a polygon having ‘n’ sides is given by (n – 2) × 180°

Sum of angles with three sides that is n = 3 is (3 – 2) × 180° = 180°

Sum of angles with four sides that is n = 4 is (4 – 2) × 180° = 360°

Sum of angles with five sides that is n = 5 is (5 – 2) × 180° = 540°

Sum of angles with six sides that is n = 6 is (6 – 2) × 180° = 720°

As seen as the number of sides increases by 1 the sum of interior angles increases by 180°

Hence the sequence of sum of angles as number of sides’ increases is 180°, 360°, 540°, 720° …

The sequence is AP with first term as a = 180° and common difference as d = 180°

We have to find sum of angles of polygon with 21 sides

Using (n – 2) × 180°

⇒ Sum of angles of polygon having 21 sides = (21 – 2) × 180°

⇒ Sum of angles of polygon having 21 sides = 19 × 180°

⇒ Sum of angles of polygon having 21 sides = 3420°

Example 2. A side of an equilateral triangle is 20cm long. A second equilateral triangle is inscribed in it by joining the mid points of the sides of the first triangle. The process is continued as shown in the accompanying diagram. Find the perimeter of the sixth inscribed equilateral triangle.

Solution:

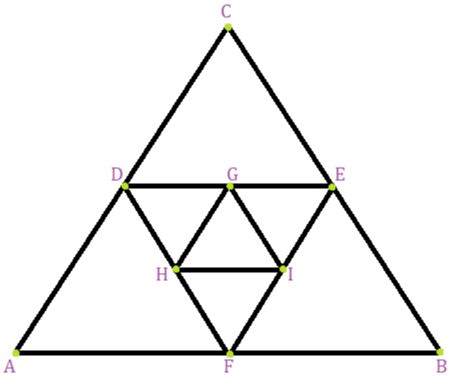
Let ABC be the triangle with AB = BC = AC = 20 cm

Let D, E and F be midpoints of AC, CB and AB respectively which are joined to form an equilateral triangle DEF

Now we have to find the length of side of ΔDEF

Consider ΔCDE

CD = CE = 10 cm … D and E are midpoints of AC and CB

Hence ΔCDE is isosceles

⇒ ∠CDE = ∠CED … base angles of isosceles triangle

But ∠DCE = 60° …∠ABC is equilateral

Hence ∠CDE = ∠CED = 60°

Hence ΔCDE is equilateral

Hence DE = 10 cm

Similarly, we can show that GH = 5 cm

Hence the series of sides of equilateral triangle will be 20, 10, 5 …

The series is GP with first term a = 20 and common ratio r = ½

To find the perimeter of 6^th triangle inscribed we first have to find the side of 6^th triangle that is the 6^th term in the series

n^th term in GP is given by t_n = ar^n-1

⇒ t₆ = (20) (1/2)^6-1

⇒ t₆ = 20/ 2⁵

= 20/ (4 × 2³)

⇒ t₆ = 5/8

Hence the side of 6^th equilateral triangle is 5/8 cm and hence its perimeter would be thrice its side length because it’s an equilateral triangle

Perimeter of 6^th equilateral triangle inscribed is 3 × 5/8 = 15/8 cm  

Example 3: Find the sum of GP: 10, 30, 90, 270 and 810, using formula.

Solution: Given GP is 10, 30, 90, 270 and 810

First term, a = 10

Common ratio, r = 30/10 = 3 > 1

Number of terms, n = 5

Sum of GP is given by;

S_n = a[(rⁿ – 1)/(r – 1)]

S₅ = 10[(3⁵ – 1)/(3 – 1)]

= 10[(243 – 1)/2]

= 10[242/2]

= 10 × 121

= 1210

Check: 10 + 30 + 90 + 270 + 810 = 1210

Example 4: If 2, 4, 8,…., is the GP, then find its 10th term.

Solution: The nth term of GP is given by:

2, 4, 8,….

Here, a = 2 and r = 4/2 = 2

a_n = ar^n-1

Therefore,

a₁₀ = 2 x 2^{10 – 1}

= 2 × 2⁹

= 1024

Example 5. Find the sum of the following series up to n terms:

(i) 5 + 55 + 555 + … (ii) .6 + .66 + . 666 + …

Solution:

(i) Given, 5 + 55 + 555 + …

Let S_n = 5 + 55 + 555 + ….. up to n terms

(ii) Given, .6 + .66 + . 666 + …

Let S_n = 06. + 0.66 + 0.666 + … up to n terms

The Geometric Mean (G.M.) of a set of n observations is the nth root of their product. If x1, x2, ... , xn are n observations then

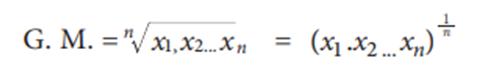
Example: If AM and HM of the data sets are 4 and 25 respectively, then find the GM.

Ans:

Given that, AM = 4
HM = 25.
We know that the relation between AM, GM and HM is

 GM = √[ AM × HM]
Now, substitute AM and HM in the relation,

we get;
GM = √[4 × 25]
GM = √100 = 10
Hence, GM = 10.