- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
The Modulus and the Conjugate of a Complex Numbers
Modulus of a complex number gives the distance of the complex number from the origin in the argand plane, whereas the conjugate of a complex number gives the reflection of the complex number about the real axis in the argand plane.
The product of two complex conjugate numbers is real. = a - ib. , which is real. Thus, the modulus of any complex number is equal to the positive square root of the product of the complex number and its conjugate complex number.
Conjugate of a Complex Number
Conjugate of a complex number z = x + iy is denoted by
![]() = x – iy. It is the reflection of the complex number about the real axis on Argand’s plane or the image of the complex number about the real axis on Argand’s plane. If we replace the ‘i’ with ‘- i’, we get conjugate of the complex number.
= x – iy. It is the reflection of the complex number about the real axis on Argand’s plane or the image of the complex number about the real axis on Argand’s plane. If we replace the ‘i’ with ‘- i’, we get conjugate of the complex number.
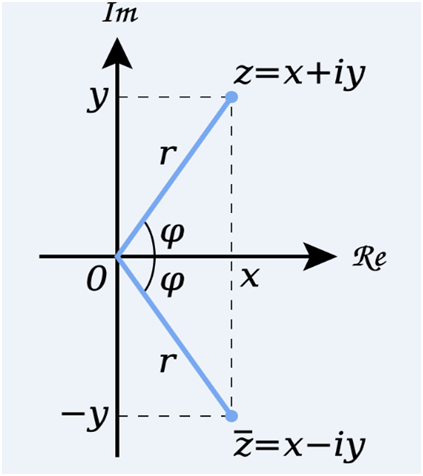
Geometrical representation of the complex number is shown in the figure given below:
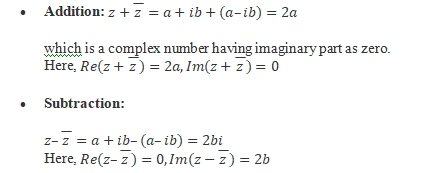
Properties of conjugate of a complex number:
If z, z1 and z2 are complex number, then
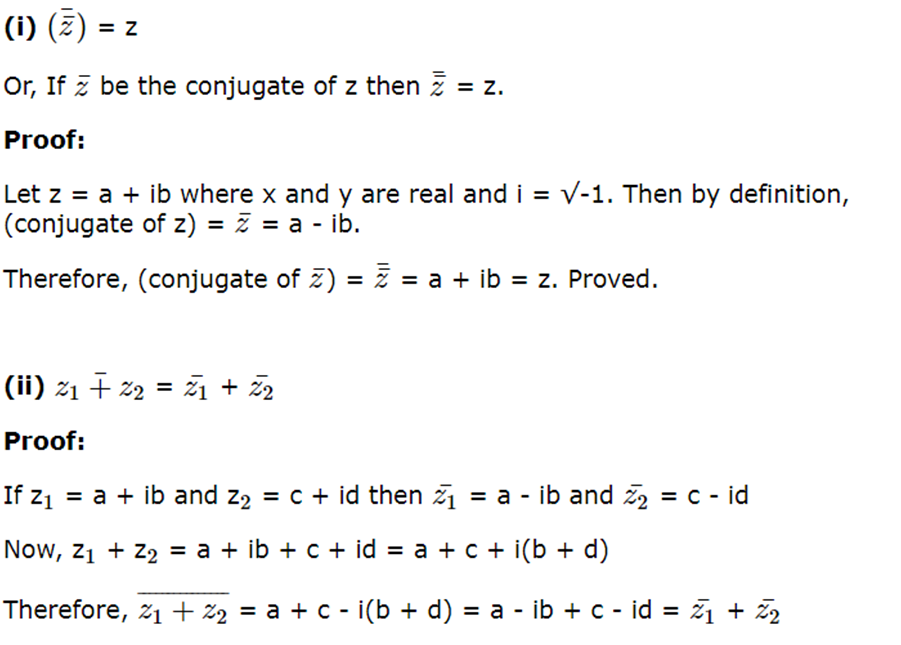
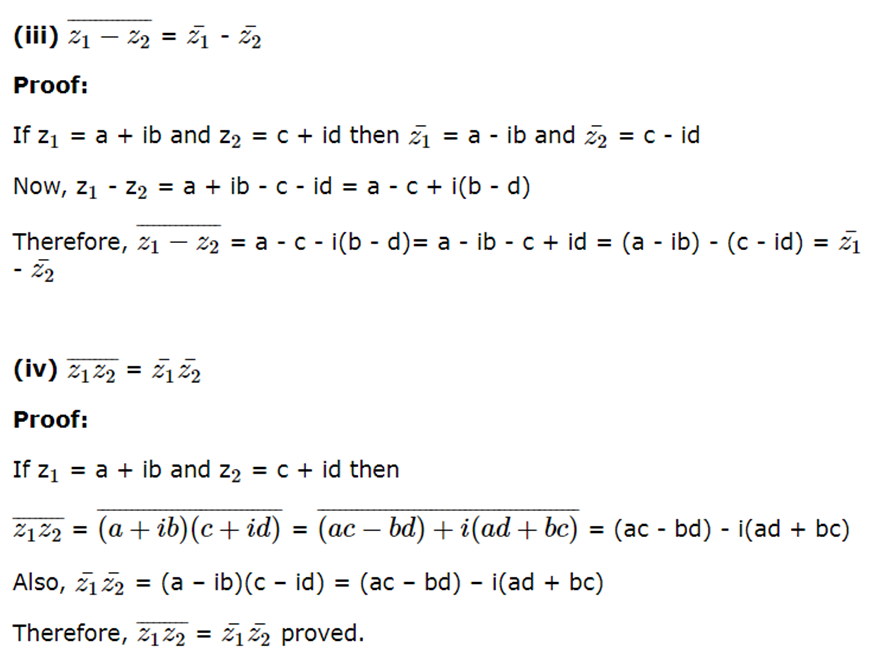

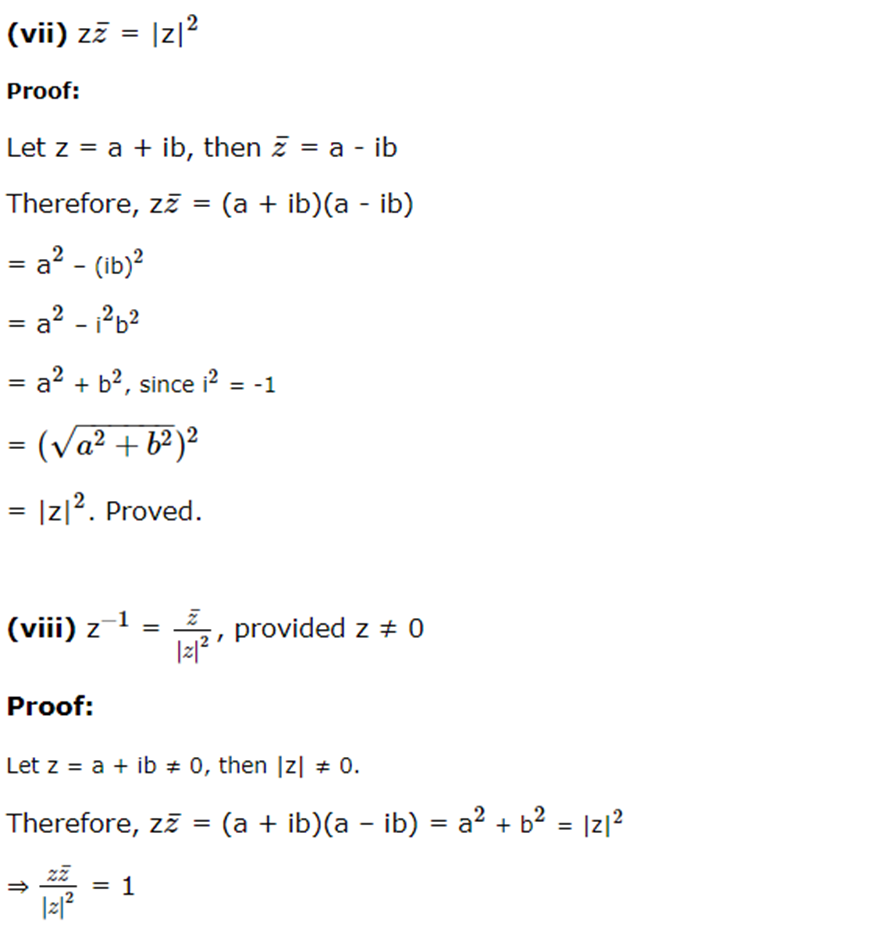

Modulus of Complex Number
Modulus of the complex number is the distance of the point on the argand plane representing the complex number z from the origin.
Let P is the point that denotes the complex number z = x + iy.
Then OP = |z| = r = √(x2 + y2 ).
Properties of Modulus of Complex Number:
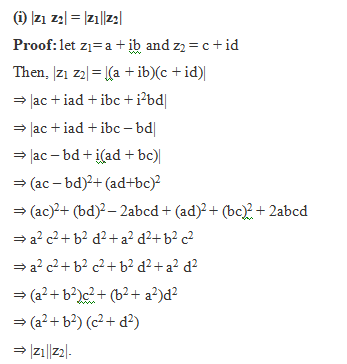
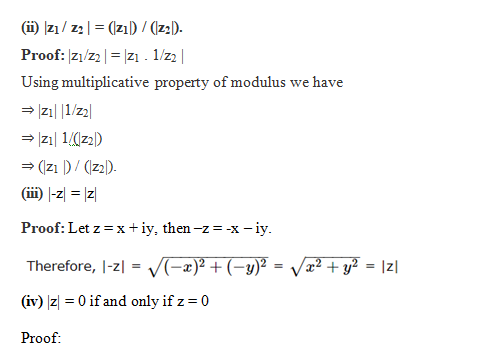
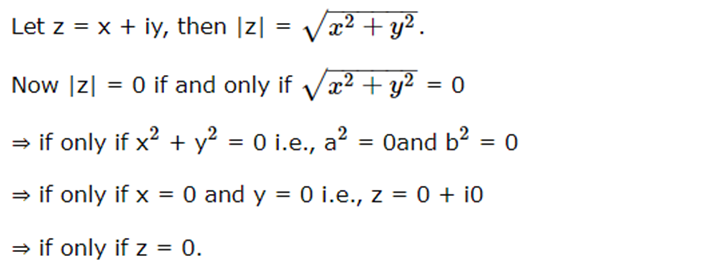
(v) For any two complex numbers z1 and z2, we have |z1 + z2| ≤ |z1| + |z2|.
Proof

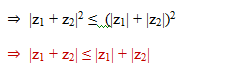
The distance between the two points z1 and z2 in complex plane is | z1 - z2 |
If we consider origin, z1 and z2 as vertices of a triangle, by the similar argument we have
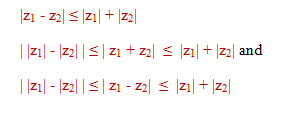
Geometrical interpretation
Now consider the triangle shown in figure with vertices O, z1 or z2 , and z1 + z2. We know from geometry that the length of the side of the triangle corresponding to the vector z1 + z2 cannot be greater than the sum of the lengths of the remaining two sides. This is the reason for calling the property as "Triangle Inequality".

It can be generalized by means of mathematical induction to finite number of terms:
|z1 + z2 + z3 + …. + zn | ≤ |z1| + |z2| + |z3| + … + |zn| for n = 2,3,….
Note:
1. |z| > 0.
2. All the complex number with same modulus lie on the circle with centre origin and radius r = |z|.
Application:
Spectrum Analyzer

Those cool displays you see when music is playing? Yes, Complex Numbers are used to calculate them! Using something called "Fourier Transforms".
In fact many clever things can be done with sound using Complex Numbers, like filtering out sounds, hearing whispers in a crowd and so on.
It is part of a subject called "Signal Processing".
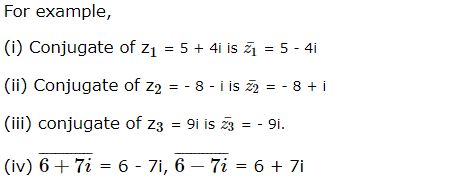
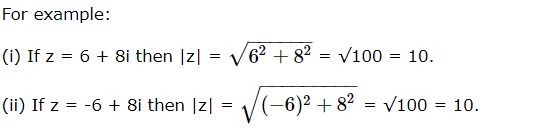
Example 1: Find the conjugate of the complex number z = (1 + 2i)/(1 – 2i).
Solution: z = (1 + 2i)/(1 – 2i)
Rationalising given complex number we have
⇒ z = ((1 + 2i)/(1 – 2i) )× (1 + 2i)/(1 + 2i)
⇒ z = (1 + 2i)2/(12 – (2i)2)
⇒ z = (1 + 4i2 + 4i)/(1 + 4)
⇒ z = (1 – 4 + 4i)/(1 + 4)
⇒ z = (-3 + 4i)/5
⇒![]() = (- 3 – 4i)/5.
= (- 3 – 4i)/5.
Example 2: Find the modulus of the complex number z = (3 – 2i)/2i
Solution: z = (3 – 2i)/2i
⇒ z = (3 )/2i – 2i/2i
⇒ z = 3/2i – 1
⇒ z = 3i/(2i2 ) – 1
⇒ z = (-3i/2) – 1
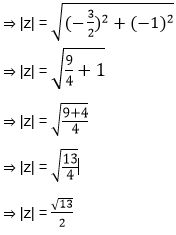
Example 3: If z + |z| = 1 + 4i, then find the value of |z|.
Solution: Let z = x + iy
⇒ z + |z| = 1 + 4i
⇒ x + iy + |x + iy| = 1 + 4i
⇒ x + iy + √(x2 + y2 ) = 1 + 4i
⇒ y = 4 and x + √(x2 + y2 ) = 1
⇒ x + √(x2 + 42 ) = 1
⇒ √(x2 + 42 ) = 1 – x
Squaring both side we have
⇒ x2 + 42 = 1 + x2 – 2x
⇒ 2x = -15
or x = -15/2
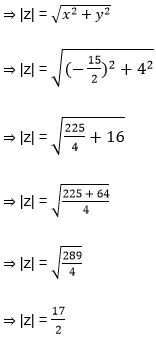
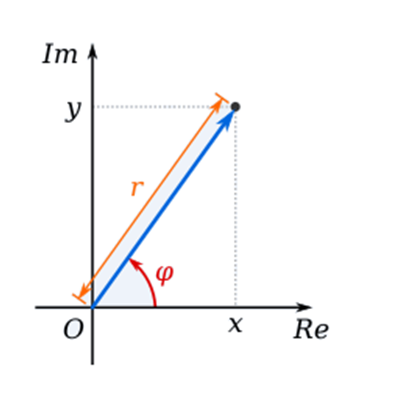
Argand Plane and Polar Representation
The plane having a complex number assigned to each of its point is called the
complex plane or the Argand plane.
Argument of Complex Numbers
The argument of a complex number is defined as the angle inclined from the real axis in the direction of the complex number represented on the complex plane. It is denoted by “θ” or “φ”. It is measured in the standard unit called “radians”.
The real and complex components of coordinates are found in terms of r and θ where r is the length of the vector, and θ is the angle made with the real axis.
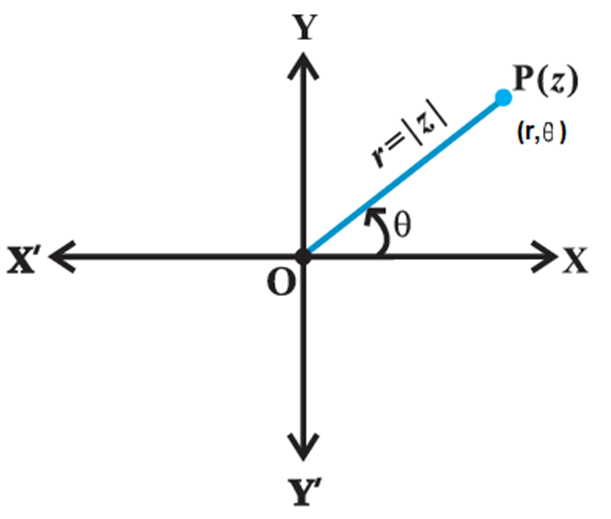
The point P is uniquely determined by the ordered pair of real numbers (r, ), called the polar
coordinates of the point P.
Polar Form of Complex Numbers
The argument of a complex number is defined as the angle inclined from the real axis in the direction of the complex number represented on the complex plane. It is denoted by “θ” or “φ”. It is measured in the standard unit called “radians”.
The real and complex components of coordinates are found in terms of r and θ where r is the length of the vector, and θ is the angle made with the real axis.
We have, x = r cos q, y = r sin q and therefore, z = r (cos q + i sin q).
The latter is said to be the polar form of the complex number.
q is called the argument (or amplitude) of z which is denoted by arg z. and
r = |z| =√(x2 + y2) is the modulus of z
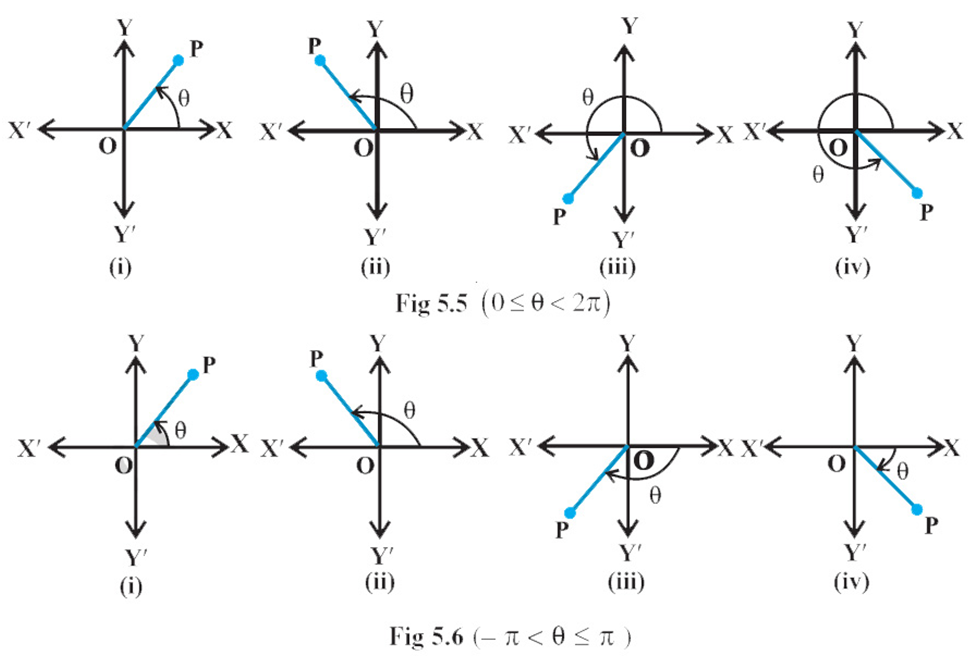
For any complex number z ¹ 0, there corresponds only one value of q in 0 £ q < 2p.
The value of q such that – p < q £ p, called principal argument of z and is denoted by arg z.

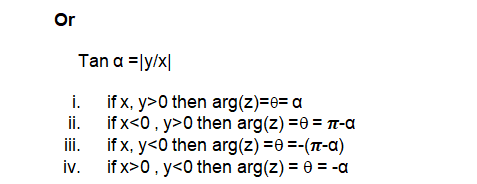
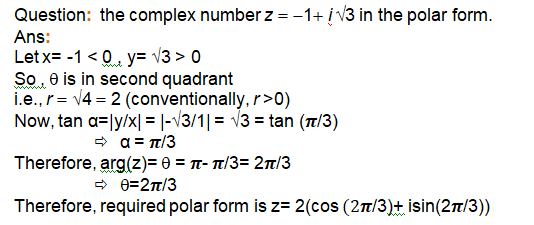
Properties of Argument of Complex Numbers
Suppose that z be a nonzero complex number and n be some integer, then
![]()
Let us assume, z1 and z2 be the two complex numbers, the following identities are:
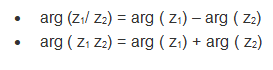

 KRISHNA PUBLICATIONS
KRISHNA PUBLICATIONS
