2. Arithmetic Progression (AP) and Arithmetic Mean (AM)

Arithmetic Progression (AP) and Arithmetic Mean (AM)

A sequence a1, a2, a3,…, an,… is called arithmetic sequence or arithmetic progression

if an + 1 = an + d, n ΠN, where a1 is called the first term and the constant term d is called

 the common difference of the A.P.

Let us consider an A.P. (in its standard form) with first term a and common

difference d, i.e., a, a + d, a + 2d, ...

The nth term of an AP is given by

n^th term = a_n= a + (n-1) d.

a = the first term, l = the last term, d = common difference,

n = the number of terms.

Sum of nth term:

Sn= the sum to n terms of A.P.

Let a, a + d, a + 2d, …, a + (n – 1) d be an A.P.

Then

l = a + (n – 1) d

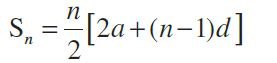
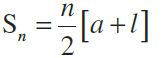
Arithmetic mean: Given two numbers a and b. We can insert a number A between them

so that a, A, b is an A.P. Such a number A is called the arithmetic mean (A.M.) of the numbers

 a and b. Note that, in this case, we have

        A – a = b – A

• A =(a+b)/2

Between any two numbers ‘a’ and ‘b’, n numbers can be inserted such that the resulting sequence is an Arithmetic Progression. A_1, A_2, A_3,……,A_n be n numbers between a and b such that a, A_1 , A_2 , A_3,……,A_n, b is in A.P.

Here, a is the 1st term and b is (n+2)th term. Therefore,

b = a + d[(n + 2) – 1] = a + d (n + 1).

Hence, common difference (d) = (b-a)/(n+1)

Now, A₁= a+d= a+((b-a)/(n+1))

A₂= a+2d = a + ((2(b-a)/(n+1))

A_n = a+nd= a + ((n(b-a)/(n+1))}

The nth term of a geometric progression is given by a_n = ar^n-1

Example: Insert 6 numbers between 3 and 24 such that the resulting sequence is

an A.P.

Solution: Let A1, A2, A3, A4, A5 and A6 be six numbers between 3 and 24 such that

3, A1, A2, A3, A4, A5, A6, 24 are in A.P. Here, a = 3, b = 24, n = 8.

Therefore, 24 = 3 + (8 –1) d, so that d = 3.

Thus A1 = a + d = 3 + 3 = 6; A2 = a + 2d = 3 + 2 × 3 = 9;

A3 = a + 3d = 3 + 3 × 3 = 12; A4 = a + 4d = 3 + 4 × 3 = 15;

A5 = a + 5d = 3 + 5 × 3 = 18; A6 = a + 6d = 3 + 6 × 3 = 21.

Hence, six numbers between 3 and 24 are 6, 9, 12, 15, 18 and 21.

simple properties of an A.P. :

(i) If a constant is added to each term of an A.P., the resulting sequence is

also an A.P.

(ii) If a constant is subtracted from each term of an A.P., the resulting

sequence is also an A.P.

(iii) If each term of an A.P. is multiplied by a constant, then the resulting

sequence is also an A.P.

(iv) If each term of an A.P. is divided by a non-zero constant then the

resulting sequence is also an A.P.

Example 1. Show that the sum of (m + n)^th and (m – n)^th terms of an A.P. is equal to twice the m^th term.

Solution:

Let’s take a and d to be the first term and the common difference of the A.P. respectively.

We know that, the k^th term of an A. P. is given by

a_k = a + (k –1) d

So, a_m + n = a + (m + n –1) d

And, a_m – n = a + (m – n –1) d

a_m = a + (m –1) d

Thus,

a_m + n + a_m – n  = a + (m + n –1) d + a + (m – n –1) d

= 2a + (m + n –1 + m – n –1) d

= 2a + (2m – 2) d

= 2a + 2 (m – 1) d

=2 [a + (m – 1) d]

= 2a_m

Therefore, the sum of (m + n)^th and (m – n)^th terms of an A.P. is equal to twice the m^th term

Example 2. If the sum of three numbers in A.P., is 24 and their product is 440, find the numbers.

Solution:

Let’s consider the three numbers in A.P. as a – d, a, and a + d.

Then, from the question we have

(a – d) + (a) + (a + d) = 24 … (i)

3a = 24

∴ a = 8

And,

(a – d) a (a + d) = 440 … (ii)

(8 – d) (8) (8 + d) = 440

(8 – d) (8 + d) = 55

64 – d² = 55

d² = 64 – 55 = 9

∴ d = ± 3

Thus,

When d = 3, the numbers are 5, 8, and 11 and

When d = –3, the numbers are 11, 8, and 5.

Therefore, the three numbers are 5, 8, and 11.