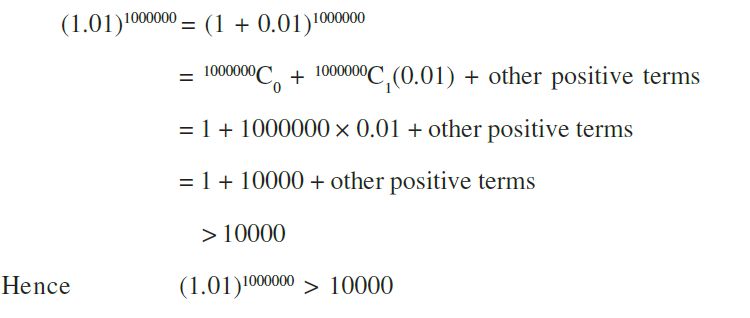1. Motivation and Process of proof by induction
- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
Chapter 4
Principles of Mathematical induction
The Principle of Mathematical Induction
What is principle of mathematical induction ?
Mathematical Induction is a technique of proving a statement, theorem or formula which is thought to be true, for each and every natural number n. By generalizing this in form of a principle which we would use to prove any mathematical statement is 'Principle of Mathematical Induction'.
Steps:
- Let the given statement be P(n)
- The statement is true for n = 1 i.e., P(1) is true, and.
- If the statement is true for n=k, where k is a positive integer, then the statement is also true for all cases of. n= k+1 i.e., P(k) leads to the truth of P(k+1).
- Hence P(n) is true for all n Î N
Motivation and Process of proof by induction:
Mathematical Induction gets motivated by the real life examples like if we have a ladder to reach to the roof then how will you prove that you will reach at the top using these ladders.
- First thing we need to assure that can we reach to the first step of that ladder, as if we reach to the first step then only you can go to the second, third and so on. And if you will not reach to the first one then you cannot reach to the top.
- Second thing is if we count the steps of the ladder then if we assume that we can reach to the 4th step then we can reach to the 5th one also.
Let’s understand it in terms of numbers:
Let’s give the numbers to the ladders as number 1, 2, and so on. Let p (n) is the proposition to reach to the nth number of step. Now we have to prove that if we move to the any step then we can reach to the nth step.
This statement in mathematical term is the same as “for any k ≥ 0, if P (k) is true then P (k + 1) is also true.”
For this first we have to reach to the first step so in mathematical term, If P (1) is true, then only we can say that “if P (k) is true then P (k + 1) is also true” for k = 1 and then we get that P(2) is also true, which then indicates that P(3) is true, and so on, which shows that P(n) is true for all n ≥ 1. But if P (1) is not true, then P (n) also may not be true for any n ≥ 2.
Principle of Mathematical Induction
The above concept derives the principle of mathematical induction which is used to directly prove the statements given in terms of n natural numbers.
- Base Case: The given statement is correct for first n natural number that is, for n = 1, p (1) is true.
- Inductive Step: If the given statement is correct for any natural number like n = k then it will be correct for n = k + 1 also that is, if p (k) is true then p (k+1) is also true.
This principle says that if both the above steps are proven then p (n) is true for all natural numbers.
Example
Let’s take the example of the formula for the sum of the first n squares, for n ≥ 0. We will find a pattern in the sum of squares of n natural numbers:
02 = 0
02 + 12 = 1
02 + 12 + 22 = 5
02 + 12 + 22 + 32 = 14
If we will follow this pattern we can see that the sum of the first n squares could be n (n + 1) (2n + 1)/6. Now we have to prove that this formula works for every number n ≥ 0, that is, we have to prove an infinite number of equalities.
When can we use Mathematical Induction?
Mathematical induction can be used for so many statements where we want to show, that statement is true. Every statement cannot be proved by this new technique.
- First, in induction we need to find our statement P (n) for all integers n ≥ 0, so induction works only for the statements with the whole numbers. So, the statements like “For all x ∈ R, x2 ≥ 0” will not be able to prove with induction as the set of real numbers is not easy to calculate.
- Secondly, for our induction proof we have to follow the inductive step that is, statements where the P (k+ 1) case is true assuming that the P (k) case is true are particularly well-suited for induction. For Example, statements involving sums are suitable as it is easy to write the left-hand side of our statement P (k + 1) in terms of the left-hand side of the statement P (k).
1. Imaginary Numbers and Powers
- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
Chapter 5
Complex Numbers and Quadratic Equations
Imaginary Numbers and Powers
It is a solution to the quadratic equation or expression, x2+1 = 0, such as;
x2 = 0 – 1
x2 = -1
x = √-1
x = i
Therefore, an imaginary number is the part of complex number which we can write like a real number multiplied by the imaginary unit i, where i2 = -1. The imaginary number, when multiplied by itself, gives a negative value.
Value of Powers of i
We know, i2 = -1, let us calculate the value of ‘i’ raised to the power other imaginary numbers.
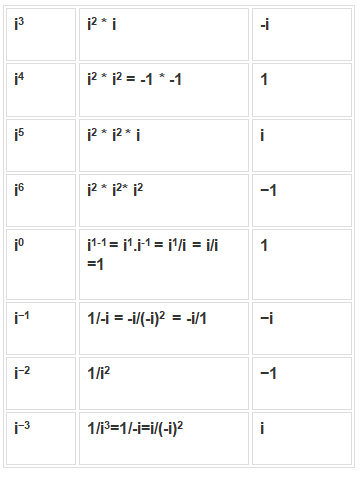
i4n = 1
i4n+1 = i
i4n+2= -1
i4n+3=-i
1. Inequalities and Algebraic Solutions of Linear Inequalities in One Variable and their Graphical Representation
- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
Chapter-6
Linear Inequalities
Inequalities and Algebraic Solutions of Linear Inequalities in One Variable and their Graphical Representation:
What is inequalities
- In mathematics, an inequality is a relation that holds between two values when they are different
- Solving linear inequalities is very similar to solving linear equations, except for one small but important detail: you flip the inequality sign whenever you multiply or divide the inequality by a negative
- Two real numbers or two algebraic expressions related by the symbol ‘<’, ‘>’, ‘£’ or ‘³’ form an inequality.
Symbols used in inequalities
- The symbol < means less than. The symbol > means greater than.
- The symbol < with a bar underneath means less than or equal to. Usually this is written as ≤
- The symbol > with a bar underneath means greater than or equal to. Usually this is written as ≥
- The symbol ≠ means the quantities on left and right side are not equal
Examples
- a < b means a is less then b or b is greater a
- a≤b means a is less then or equal to b
- a > b means a is greater than b
- a≥b means a is greater or equal to b
Types of inequalities:
- Numerical inequalities :
Example:
3 < 5(read as 3 is less than 5)
7 > 5 (read as 7 is greater than 5)
- Literal inequalities:
Inequalities which involve variables are called literal inequalities
Example: x < 5; y > 2
x ³5; y £ 2;
- Double inequalities:
The inequality is said to be a double inequality if the statement shows the double relation of the expressions or the numbers..
Example: 3 < 5 < 7 (read as 5 is greater than 3 and less than 7),
3 £ x < 5 (read as x is greater than or equal to 3 and less than 5)
And 2 < y £ 4(read as y is less than or equal to 4 and greater than 2)
- Open Sentence :
The inequality is said to be an open sentence if it has only one variable.
Example: x < 6 (x is less than 6),
x > 8
- Strict inequalities:
A relation that expresses the comparison between the unequal quantities is called strict inequality.
Example: ax + b < 0,
ax + b > 0,
ax + by < c,
ax + by > c,
ax2 + bx + c > 0
- Slack inequalities:
Inequalities involving the symbol '≥' or '≤' are called slack inequalities.
Example: ax + by +c,
ax + by +c,
3x – y ≥ 5
- Linear inequalities:
When two expressions are connected by “greater than” or “less than” sign, we get an inequality. Also, the linear inequation is similar to a linear equation, where the equal to sign is replaced by the inequality sign.
Example: ax + b < 0,
ax + b > 0,
x - 5 > 3x – 10,
- Quadratic inequalities:
A quadratic inequality is an inequality that contains a quadratic expression.
Example: ax2+bx+c<0,
ax2 + bx + c > 0
ax2 + bx + c £ 0
Things are which are safe to do in inequality which does not change in direction:
- Addition of same number on both sides
a>b
=> a+c > b+c - Subtraction of same number on both sides
a>b
=> a−c > b−c - Multiplication/Division by same positive number on both sides
a>b
if c is positive number then
ac > bc
if c is positive number (non zero) then
a/c > b/c
Things which changes the direction of the inequality:
- Swapping the left and right sides
- Multiplication/Division by negative number on both sides
If a > b and c is negative number then ac < bc
If a < b and c is negative number then ac > bc
- Don’t multiple by variable whose values you dont know as you don’t know the nature of the variable
Concept Of Number line:
- A number line is a horizontal line that has points which correspond to numbers. The points are spaced according to the value of the number they correspond to; in a number line containing only whole numbers or integers, the points are equally spaced.
- It is very useful in solving problem related to inequalities and also representing it
Suppose x >2(1/ 3), this can represent this on number line like that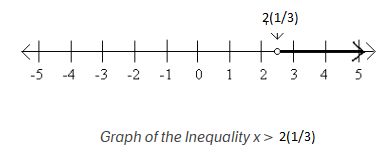
Linear Inequation in One Variable:
A inequation of the form
ax+b>0
or
ax+b≥0
or
ax+b<0
or
ax+b≤0
are called the linear equation in One Variable
Example:
x−2<0,
3x+10>0,
10x−17≥0
Linear Inequations in Two Variable:
A inequation of the form
ax+by>c
or
ax+by≥c
or
ax+by<c
or
ax+by≤c
are called the linear equation in two Variable
Example:
- x−2y<0
- 3x+10y>0
- 10x−17y≥0
How to solve the linear inequalities in one variable?:
Steps to solve the Linear inequalities in one variable:
- Obtain the linear inequation
- Pull all the terms having variable on one side and all the constant term on another side of the inequation
- Simplify the equation in the form given above
ax>b
or
ax≥b
or
ax<b
or ax≤b - Divide the coefficent of the variable on the both side.If the coefficent is positive,direction of the inequality does not changes,but if it is negative, direction of the inequation changed
- Put the result of this equation on number line and get the solution set in interval form
Example:
x−2 > 2x+15
Solution
x−2 > 2x+15
Subtract x from both the side x−2−x > 2x+15−x
−2>x+15
Subtract 15 from both the sides −17 > x
Solution set (−∞,−17)
Example: Find all pairs of consecutive odd natural numbers, both of which are larger
than 10, such that their sum is less than 40.
Solution: Let x be the smaller of the two consecutive odd natural number, so that the
other one is x +2. Then, we should have
x > 10 ... (1)
and x + ( x + 2) < 40 ... (2)
Solving (2), we get
2x + 2 < 40
i.e., x < 19 ... (3)
From (1) and (3), we get
10 < x < 19
Since x is an odd number, x can take the values 11, 13, 15, and 17. So, the required
possible pairs will be
(11, 13), (13, 15), (15, 17), (17, 19)
Steps to solve the linear inequality of the fraction form
[(ax+b)/(cx+d)]>k or similar type
- Take k on the LHS
- Simplify LHS to obtain the inequation in the form
[(px+q)/(ex+f)]>0
Make the coefficent positive if not - Find out the end points solving the equatoon px+q=0 and ex+f=0
- Plot these numbers on the Number line. This divide the number into three segment
- Start from LHS side of the number and Substitute some value in the equation in all the three segments to find out which segments satisfy the equation
- Write down the solution set in interval form
Or there is more method to solves these
- Take k on the LHS
- Simplify LHS to obtain the inequation in the form
[(px+q)/(ex+f)]>0
Make the coefficent positive if not
- For the equation to satisfy both the numerator and denominator must have the same sign
- So taking both the part +, find out the variable x interval
- So taking both the part -, find out the variable x interval
- Write down the solution set in interval form
Lets take one example to clarify the points
Lets take one example to clarify the points
Question
1. Solve X−3x+5>0
Solution:
Method A
- Lets find the end points of the equation
Here it is clearly
x=3 and x=-5 - Now plots them on the Number line
- Now lets start from left part of the most left number
i.e
Case 1
x<−5 ,Let takes x=-6 then −6−3−6+5>0
3>0
So it is good
Case 2
Now take x=-5
as x+5 becomes zero and we cannot have zero in denominator,it is not the solution
Case 3
Now x > -5 and x < 3, lets take x=1 then 1−31+5>0
−16>0
Which is not true
Case 4
Now take x =3,then
0> 0 ,So this is also not true
case 5
x> 3 ,Lets x=4
4−34+5>0
19>0
So this is good - So the solution is
x < -5 or x > 3
or
(−∞,−5)∪(3,∞)
Method B
- the numerator and denominator must have the same sign. Therefore, either
1) x−3>0 and x+5>0,or 2) x - 3 < 0 and x + 5 < 0$ - Now, 1) implies x > 3 and x > -5.
Which numbers are these that are both greater than 3 and greater than -5?
Clearly, any number greater than 3 will also be greater than -5. Therefore, 1) has the solution
x > 3. - Next, 2) implies
x < 3 and x < -5.
Which numbers are these that are both less than 3 and less than -5?
Clearly, any number less than -5 will also be less than 3. Therefore, 2) has the solution
x < -5. - The solution, therefore, is
x < -5 or x > 3
Quadratic Inequality:
A inequation of the form
so for a ≠ 0
ax2+bx+c>0
or
ax2+bx+c<0
or
ax2+bx+c≥0
or
ax2+bx+c≤0
are called Quadratic Inequation in one Variable
Steps to solve Quadratic or polynomial inequalities:
ax2+bx+c>0,
or
ax2+bx+c<0,
or
ax2+bx+c≥0,
ax2+bx+c≤0
- Obtain the Quadratic inequation
- Pull all the terms having on one side and Simplify the equation in the form given above
- Find the roots(0 points) of the Quadratic equation using any of the method and write in this form
(x-a)(x-b) - Plot these roots on the number line .This divide the number into three segment
- Start from LHS side of the number and Substitute some value in the equation in all the three segments to find out which segments satisfy the equation
- Write down the solution set in interval form
Solved Example
Question 1
x2-5x+6>0
Solution
1) Simplify or factorize the inequality which means factorizing the equation in case of quadratic equalities
Which can be simplified as
x2−5x+6>0
=> x2−2x−3x+6>0
=> (x−2)(x−3)>0
2) Now plot those points on Number line clearly
3) Now start from left of most left point on the Number line and look out the if inequalities looks good or not. Check for greater ,less than and equalities at all the end points
So in above case of x2−5x+6>0
We have two ends points 2 ,3
Case 1
So for x<2 ,Let take x=1,then (1−2)(1−3)>0
=> 2>0
So it is good
So This inequalities is good for x < 2
Case 2
Now for x =2,it makes it zero, so not true. Now takes the case of 2<x<3. Lets takes x= 2.5
(2.5−2)(2.5−3)>0
=> −0.25>0
Which is not true so this solution is not good
Case 3
Now lets take the right most part i.e x>3
Lets take x=4
(4−2)(4−3)>0
=> 2>0
So it is good.
Now the solution can either be represented on number line or we can say like this
(−∞,2)∪(3,∞)
Question: Solve y < 2 graphically
Graph of y = 2 is given in the Figure.
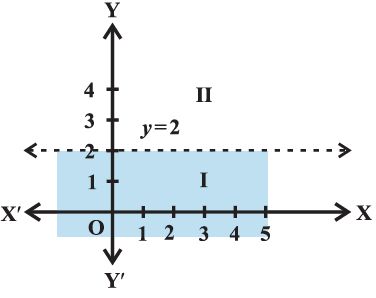
Let us select a point, (0, 0) in lower half plane I and putting y = 0 in the given inequality, we see that
1 × 0 < 2 or 0 < 2 which is true.
Thus, the solution region is the shaded region below the line y = 2.
Hence, every point below the line (excluding all the points on the line) determines the solution of the given inequality.
1. Fundamental Principle of Counting
- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
Chapter 7
Permutation and Combinations
Fundamental Principle of Counting:
If one experiment has n possible outcomes and another experiment has m possible outcomes, then there are m × n possible outcomes when both of these experiments are performed simultaneously.
In other words, suppose a job has n parts and the job will be completed only when each part is completed. Further, it is known that the first part can be completed in a1 ways, the second part can be completed in a2 ways and so on ...... the nth part can be completed in an ways. Then the total number of ways of doing the job is a1a2a3 ... an. This is also known as the rule of product.
Note:
- Fundamental Principal of Counting (FPC) is used to calculate the possibilities of an event without actually counting them.
- Basic steps to be used while applying the FPC:
1. Try to identify the independent events involved in a given problem.
2. Find the number of ways of performing or possibilities of occurrence of an event.
3. Multiply these numbers to get the total number of ways of occurrence of these events.
Example 1:
Suppose you have 33 shirts (call them A , B , and C ), and 44 pairs of pants (call them w , x , y , and z ).
Ans.: Then you have
3×4=12
possible outfits:
Aw, Ax, Ay, Az, Bw, Bx, By, Bz, Cw, Cx, Cy, Cz
Example 2:
Suppose you roll a 6 -sided die and draw a card from a deck of 52 cards. There are 6 possible outcomes on the die, and 52 possible outcomes from the deck of cards.
Ans.:
So, there are a total of
6×52=312
possible outcomes of the experiment.
Generalisation of the Addition and the Product Rule
In general, if there are several mutually exclusive events P1, P2, P3, P4……Pn…etc. with the respective number of ways given as n (P1), n(P2), n(P3), n(P4)….n(Pn), then the number of ways in which either P1 and P2 and ….. … Pn can occur is given by,
n(E) = n(P1) + n(P2) …….. + n(Pn)
Similarly, if there are several mutually independent events P1, P2, P3, P4……Pn…etc. with the respective number of ways given as n (P1), n(P2), n(P3), n(P4)….n(Pn), then the number of ways in which P1 and P2 and ….. … Pn can occur is given by,
n(E) = n(P1) × n(P2) …….. × n(Pn)
We must note that all the possible number of ways derived thus, all of them will represent the unique and distinct ways in which the event E will take place.
Event and Its Trials
Suppose we have an event E with ‘m’ possible outcomes. If we conduct this event n number of times, then the number of outcomes of ‘n trials of the event’ will be, mn
Clearly, this is only valid when all the outcomes of the experiment/event E are independent of each other. This would ensure that everytime the event takes place, any of its outcomes are possible.
Question : A coin is tossed 50 times. What is the number of possible outcomes of this experiment?
Answer : A coin toss has two possible outcomes: ‘A heads’ or ‘A tails’. Every toss of the coin is independent of every other toss of the coin, since whenever you toss the coin; there would be two possible outcomes with equal probability. Thus, the no. of possible outcomes of the experiment = 250
Question :
How many 3-digit numbers can be formed from the digits 1, 2, 3, 4 and 5 assuming that
(i) repetition of the digits is allowed?
(ii) repetition of the digits is not allowed?
ANSWER:
(i)
There will be as many ways as there are ways of filling 3 vacant places


 in succession by the given five digits. In this case, repetition of digits is allowed. Therefore, the units place can be filled in by any of the given five digits. Similarly, tens and hundreds digits can be filled in by any of the given five digits.
in succession by the given five digits. In this case, repetition of digits is allowed. Therefore, the units place can be filled in by any of the given five digits. Similarly, tens and hundreds digits can be filled in by any of the given five digits.
Thus, by the multiplication principle, the number of ways in which three-digit numbers can be formed from the given digits is 5 × 5 × 5 = 125
(ii)
In this case, repetition of digits is not allowed. Here, if units place is filled in first, then it can be filled by any of the given five digits. Therefore, the number of ways of filling the units place of the three-digit number is 5.
Then, the tens place can be filled with any of the remaining four digits and the hundreds place can be filled with any of the remaining three digits.
Thus, by the multiplication principle, the number of ways in which three-digit numbers can be formed without repeating the given digits is 5 × 4 × 3 = 60
Question :
A coin is tossed 3 times and the outcomes are recorded. How many possible outcomes are there?
ANSWER:
When a coin is tossed once, the number of outcomes is 2 (Head and tail) i.e., in each throw, the number of ways of showing a different face is 2.
Thus, by multiplication principle, the required number of possible outcomes is 2 × 2 × 2 = 8
1. Binomial Theorem for Positive Integral Indices
- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
Chapter 8
Binomial Theorem
Binomial Theorem for Positive Integral Indices:
The Binomial Theorem is the method of expanding an Binomial expression that has been raised to any finite power.
Binomial Expression: A binomial expression is an algebraic expression that contains two dissimilar terms. Ex: a + b, a3 + b3,a-b, etc.
The binomial theorem states a formula for the expression of the powers of sums.
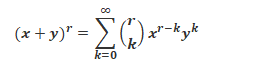
From the above representation, we can expand (a + b)n as given below:
(a + b)n = nC0 an + nC1 an-1 b + nC2 an-2 b2 + … + nCn-1 a bn-1 + nCn bn
This is the binomial theorem formula for any positive integer n.
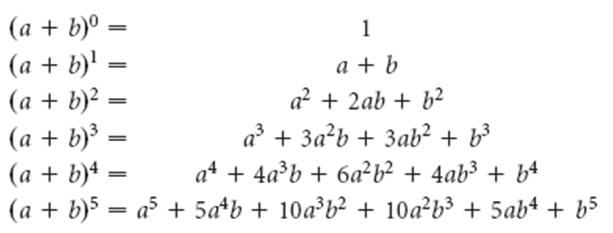
Some special cases from the binomial theorem can be written as:
- (x + y)n = nC0 xn + nC1 xn-1 by+ nC2 xn-2 y2 + … + nCn-1 x yn-1 + nCn xn
- (x – y)n = nC0 xn – nC1 xn-1 by + nC2 xn-2 y2 + … + (-1)n nCn xn
- (1 – x)n = nC0 – nC1 x + nC2 x2 – …. (-1)n nCn xn
Also, nC0 = nCn = 1
However, there will be (n + 1) terms in the expansion of (a + b)n.
Example: (√2 + 1)5 + (√2 − 1)5
Sol:
We have
(x + y)5 + (x – y)5 = 2[5C0 x5 + 5C2 x3 y2 + 5C4 xy4]
= 2(x5 + 10 x3 y2 + 5xy4)
Now (√2 + 1)5 + (√2 − 1)5 = 2[(√2)5 + 10(√2)3(1)2 + 5(√2)(1)4]
=58√2
Properties:
- The total number of terms in the expansion of (x+y)n are (n+1)
- The sum of exponents of x and y is always n.
- nC0, nC1, nC2, … .., nCn are called binomial coefficients and also represented by C0, C1, C2, ….., Cn
- The binomial coefficients which are equidistant from the beginning and from the ending are equal i.e. nC0 = nCn, nC1 = nCn-1 , nC2 = nCn-2 ,….. etc.
Some other expansions:
- (x + y)n + (x−y)n = 2[C0 xn + C2 xn-1 y2 + C4 xn-4 y4 + …]
- (x + y)n – (x−y)n = 2[C1 xn-1 y + C3 xn-3 y3 + C5 xn-5 y5 + …]
- (1 + x)n = nΣr-0 nCr . xr = [C0 + C1 x + C2 x2 + … Cn xn]
- (1+x)n + (1 − x)n = 2[C0 + C2 x2+C4 x4 + …]
- (1+x)n − (1−x)n = 2[C1 x + C3 x3 + C5 x5 + …]
- The number of terms in the expansion of (x + a)n + (x−a)n are (n+2)/2 if “n” is even or (n+1)/2 if “n” is odd.
- The number of terms in the expansion of (x + a)n − (x−a)n are (n/2) if “n” is even or (n+1)/2 if “n” is odd.
Question: Find the 4th term in the expansion of (x – 2y)12.
Solution:
The general term Tr+1 in the binomial expansion is given by Tr+1 = n C r an-r br
Here a= x, n =12, r= 3 and b = -2y
By substituting the values we get
T4 = 12C3 x9 (-2y)3
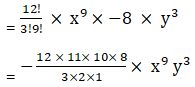
= -1760 x9 y3
1. Sequences and Series
- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
Chapter 9
Sequences and Series
Sequences and Series:
A sequence can be regarded as a function whose domain is the set of natural numbers or some subset of it. Sometimes, we use the functional notation a(n) for an.
The different numbers occurring in any particular sequence are known as terms. The terms of a sequence are denoted by
a1, a2, a3,….,an
If a sequence has a finite number of terms then it is known as a finite sequence. A sequence is termed as infinite if it is not having a definite number of terms.
Series: Let a1, a2, a3,…,an, be a given sequence. Then, the expression
a1 + a2 + a3 +,…+ an + ...
is called the series associated with the given sequence .The series is finite or infinite according as the given sequence is finite or infinite. Series are often represented in compact form, called sigma notation, using the Greek letter å (sigma) as means of indicating the summation involved. Thus, the series a1 + a2 + a3 + ... + an is abbreviated as
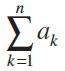
Sequence relates to the organization of terms in a particular order (i.e. related terms follow each other) and series is the summation of the elements of a sequence.
Examples
Example: Write the first three terms in each of the following sequences defined by
the following: an = 2n + 5,
Ans.: (i) Here an = 2n + 5
Substituting n = 1, 2, 3, we get
a1 = 2(1) + 5 = 7, a2 = 9, a3 = 11
Therefore, the required terms are 7, 9 and 11.
Example Let the sequence an be defined as follows:
a1 = 1, an = an – 1 + 2 for n ![]() 2.
2.
Find first five terms and write corresponding series.
Solution We have
a1 = 1, a2 = a1 + 2 = 1 + 2 = 3, a3 = a2 + 2 = 3 + 2 = 5,
a4 = a3 + 2 = 5 + 2 = 7, a5 = a4 + 2 = 7 + 2 = 9.
Hence, the first five terms of the sequence are 1,3,5,7 and 9. The corresponding series
is 1 + 3 + 5 + 7 + 9 +...
Examples
Q.1: If an = 2n, then find the first five terms of the series.
Solution: Given: an = 2n
On substituting n = 1, 2, 3, 4, 5, we get
a1 = 21 = 2
a2 = 22 = 4
a3 = 23 = 8
a4 = 24 = 16
a5 = 25 = 32
Therefore, the required terms are 2, 4, 8, 16, and 32.
Q.2: Find the sum of odd integers from 1 to 2001.
Solution:
The odd integers from 1 to 2001 are 1, 3, 5, …1999, 2001.
It clearly forms a sequence in A.P.
Where, the first term, a = 1
Common difference, d = 2
Now,
a + (n -1)d = 2001
1 + (n-1)(2) = 2001
2n – 2 = 2000
2n = 2000 + 2 = 2002
n = 1001
We know,
Sn = n/2 [2a + (n-1)d]
Sn = 1001/2[2×1+(1001-1)2]
Sn = 1001/2[2+1000×2]
Sn = 1001/2[2002]
Sn = 1001 x 1001
Sn = 1002001
2. Principles of Mathematical induction and simple applications
- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
Principles of Mathematical induction and simple applications
Question 1: Prove that m≥ 1 prove that, 12+ 22 + 32 +42 +……+ m2 = m(m + 1)(2m + 1)/6
Solution: Let the given statement be
P(n) : 12+ 22 + 32 +42 +……+n2 = n(n + 1) (2n + 1) / 6
Let n= 1 , then P(1) : LHS=12 =1 and RHS=1(1 + 1) (2 × 1 + 1) /6
= 1 × 2 × 3 / 6 = 1
Now LHS=RHS
So, P(1) is true.
Now, let n=k, and assume X(P) to be true
i.e.,P(k): 12+ 22 + 32 +42 +……+k2 = k(k+1) (2k+1) / 6 (1)
We shall now prove that P(k+1) is also true,
so now we have,
Let n=k+1 , then P(k+1) : LHS=
12+ 22 + 32 +42 +……+k2 + (+1)2
= k(k+1)(2k+1) / 6 + (k+1)2
= k(k+1)(2k+1)+6(k+1)2 / 6
= (k+1) {( 2k2 + k) + 6(k+1)} /6
= (k+1) (2k2 +7k+6)/6
= (k+1) (k+1+1) {2(k+1) +1 }/6
So, P(k + 1) is true, whenever P(k) is true for all natural numbers.
Thus, P(n) is true for all n ÎN
Question 2: Prove that the sum of cubes of n natural numbers is equal to ( n(n+1)2)2 for all n natural numbers.
Solution:
Let P(n):
13+23+33+⋯+n3 = (n(n+1)2)2
Step 1: Let n=1 then P(1): LHS=13=1
RHS=(1(1+1)2)2 = 1
So P(1) is true.
Step 2: Let n=k, then Assume P(k) is true
i.e.,
P(k): 13+23+33+⋯+k3= (k(k+1)2)2 .
Step 3: Let n=k+1, then P(k+1) : LHS=
13+23+33+⋯+k3+(k+1)3 = (k(k+1)2)2+(k+1)3
⇒13+23+33+⋯+k3+(k+1)3=k2(k+1)4+(k+1)3
= k2(k+1)2+4((k+1)3)4
=(k+1)2(k2+4(k+1))4
=(k+1)2(k2+4k+4)4
= (k+1)2((k+2)2)4
=(k+1)2(k+1+1)2)4
=(k+1)2((k+1)+1)2)4
=RHS
So, P(k + 1) is true, whenever P(k) is true for all natural numbers.
Thus, P(n) is true for all n ÎN
Question3: Show that 1 + 3 + 5 + … + (2n−1) = n2
Solution:
Step 1: Result is true for n = 1
That is 1 = (1)2 (True)
Step 2: Assume that result is true for n = k
1 + 3 + 5 + … + (2k−1) = k2
Step 3: Check for n = k + 1
i.e. 1 + 3 + 5 + … + (2(k+1)−1) = (k+1)2
We can write the above equation as,
1 + 3 + 5 + … + (2k−1) + (2(k+1)−1) = (k+1)2
Using step 2 result, we get
k2 + (2(k+1)−1) = (k+1)2
k2 + 2k + 2 −1 = (k+1)2
k2 + 2k + 1 = (k+1)2
(k+1)2 = (k+1)2
L.H.S. and R.H.S. are same.
So, P(k + 1) is true, whenever P(k) is true for all natural numbers.
Thus, P(n) is true for all n ÎN
Question4: Show that 22n-1 is divisible by 3 using the principles of mathematical induction.
To prove: 22n-1 is divisible by 3
Assume that the given statement be P(k)
Thus, the statement can be written as P(k) = 22n-1 is divisible by 3, for every natural number
Step 1: In step 1, assume n= 1, so that the given statement can be written as
P(1) = 22(1)-1 = 4-1 = 3. So 3 is divisible by 3. (i.e.3/3 = 1)
Step 2: Now, assume that P(n) is true for all the natural number, say k
Hence, the given statement can be written as
P(k) = 22k-1 is divisible by 3.
It means that 22k-1 = 3a (where a belongs to natural number)
Now, we need to prove the statement is true for n= k+1
Hence,
P(k+1) = 22(k+1)-1
P(k+1)= 22k+2-1
P(k+1)= 22k. 22 – 1
P(k+1)= (22k. 4)-1
P(k+1) =3.2k +(22k-1)
The above expression can be written as
P(k+1) =3.22k + 3a
Now, take 3 outside, we get
P(k+1) = 3(22k + a)= 3b, where “b” belongs to natural number
So, P(k + 1) is true, whenever P(k) is true for all natural numbers.
Thus, P(n) is true for all n ÎN
Question5. n (n + 1) (n + 5) is a multiple of 3
Solution:
We can write the given statement as
P (n): n (n + 1) (n + 5), which is a multiple of 3
If n = 1 we get
1 (1 + 1) (1 + 5) = 12, which is a multiple of 3
Which is true.
Consider P (k) be true for some positive integer k
k (k + 1) (k + 5) is a multiple of 3
k (k + 1) (k + 5) = 3m, where m ∈ N …… (1)
Now let us prove that P (k + 1) is true.
Here
(k + 1) {(k + 1) + 1} {(k + 1) + 5}
We can write it as
= (k + 1) (k + 2) {(k + 5) + 1}
By multiplying the terms
= (k + 1) (k + 2) (k + 5) + (k + 1) (k + 2)
So we get
= {k (k + 1) (k + 5) + 2 (k + 1) (k + 5)} + (k + 1) (k + 2)
Substituting equation (1)
= 3m + (k + 1) {2 (k + 5) + (k + 2)}
By multiplication
= 3m + (k + 1) {2k + 10 + k + 2}
On further calculation
= 3m + (k + 1) (3k + 12)
Taking 3 as common
= 3m + 3 (k + 1) (k + 4)
We get
= 3 {m + (k + 1) (k + 4)}
= 3 × q where q = {m + (k + 1) (k + 4)} is some natural number
(k + 1) {(k + 1) + 1} {(k + 1) + 5} is a multiple of 3
P (k + 1) is true whenever P (k) is true.
Therefore, P (n) is true for all natural numbers n.
Question 6. (2n +7) < (n + 3)2
Solution:
We can write the given statement as
P(n): (2n +7) < (n + 3)2
If n = 1 we get
2.1 + 7 = 9 < (1 + 3)2 = 16
Which is true.
Consider P (k) be true for some positive integer k
(2k + 7) < (k + 3)2 … (1)
Now let us prove that P (k + 1) is true.
Here
{2 (k + 1) + 7} = (2k + 7) + 2
We can write it as
= {2 (k + 1) + 7}
From equation (1) we get
(2k + 7) + 2 < (k + 3)2 + 2
By expanding the terms
2 (k + 1) + 7 < k2 + 6k + 9 + 2
On further calculation
2 (k + 1) + 7 < k2 + 6k + 11
Here k2 + 6k + 11 < k2 + 8k + 16
We can write it as
2 (k + 1) + 7 < (k + 4)2
2 (k + 1) + 7 < {(k + 1) + 3}2
P (k + 1) is true for n=k+1 whenever P (k) is true.
Therefore, P (n) is true for all natural numbers n.
2. Complex Numbers and Algebra of Complex Numbers
- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
Complex Numbers and Algebra of Complex Numbers
Example 1: Solve the complex number √-4?
Solution: √-4 = √(-1 * 4) = 2√-1 = 2i
Example 2: Solve y2+1 = 0
Solution: y2+1 = 0
y2 = -1
y = √-1 = i
Check:
L.H.S = y2+1 = i2 + 1 = -1 + 1 = 0 (R.H.S)
Example 3: Find the value of √-3 + 1.
Solution: √-3 + 1
= √-1 √3 + 1
i√3 + 1
Example 4: Solve x2+16 = 0
Solution: x2+16 = 0
x2= -16
x =√-16
x = i √16
x = i4
Check:
L.H.S = x2+16 = (i4)2 + 16 = i242 + 16 = -16 +16 = 0 (R.H.S)
Example 5 : Simplify.
(2i)(−6i)(−7i)(2i)(−6i)(−7i)
Rewrite the expression grouping the real and imaginary parts.
(2i)(−6i)(−7i)=(2)⋅(−6)⋅(−7)⋅i⋅i⋅i
=84⋅i⋅i⋅i(2i)(−6i)(−7i)
=(2)⋅(−6)⋅(−7)⋅i⋅i⋅i=84⋅i⋅i⋅i
Simplify the imaginary part using the property of multiplying powers.
=84i3=84i2i1=84i3=84i2i1
Recall the definition of i.
Since i2=−1:
=84(−1)i=−84i=84(−1)i=−84i
Example 6:Simplify the principal square root of √−64
Ans:
√−64
Taking the square root and substituting √-1= i
=(√−1). √64=√(−1)⋅ √64=i√64
=8i
3. The Modulus and the Conjugate of a Complex Numbers
- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
The Modulus and the Conjugate of a Complex Numbers
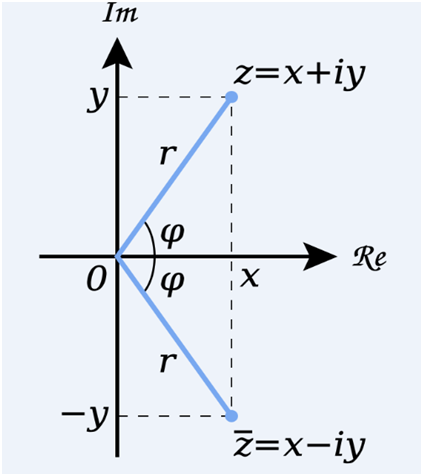
Modulus of a complex number gives the distance of the complex number from the origin in the argand plane, whereas the conjugate of a complex number gives the reflection of the complex number about the real axis in the argand plane.
The product of two complex conjugate numbers is real. = a - ib. , which is real. Thus, the modulus of any complex number is equal to the positive square root of the product of the complex number and its conjugate complex number.
Conjugate of a Complex Number
Conjugate of a complex number z = x + iy is denoted by
![]() = x – iy. It is the reflection of the complex number about the real axis on Argand’s plane or the image of the complex number about the real axis on Argand’s plane. If we replace the ‘i’ with ‘- i’, we get conjugate of the complex number.
= x – iy. It is the reflection of the complex number about the real axis on Argand’s plane or the image of the complex number about the real axis on Argand’s plane. If we replace the ‘i’ with ‘- i’, we get conjugate of the complex number.
Geometrical representation of the complex number is shown in the figure given below:
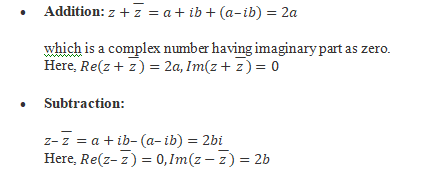
Properties of conjugate of a complex number:
If z, z1 and z2 are complex number, then
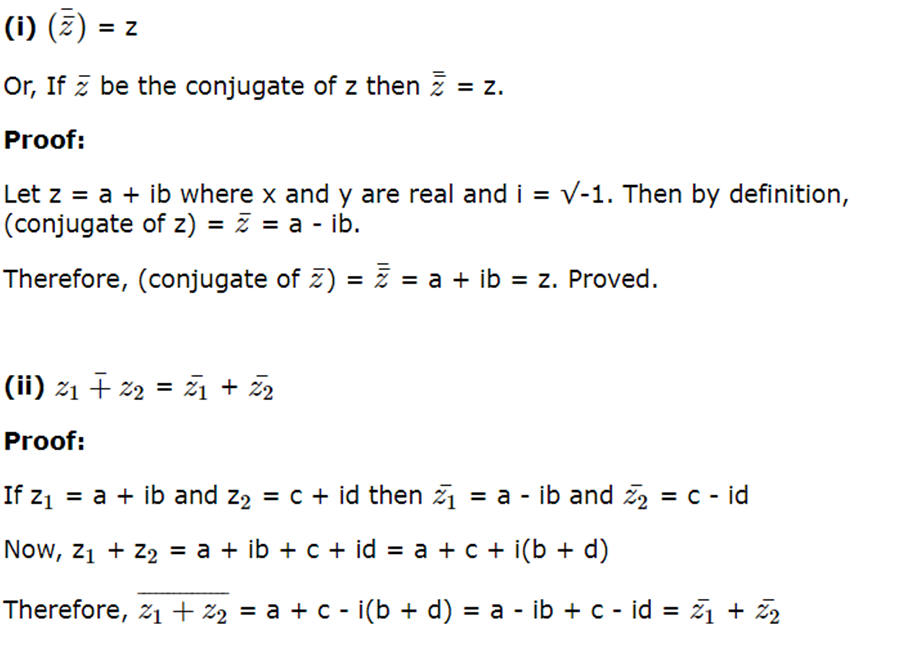
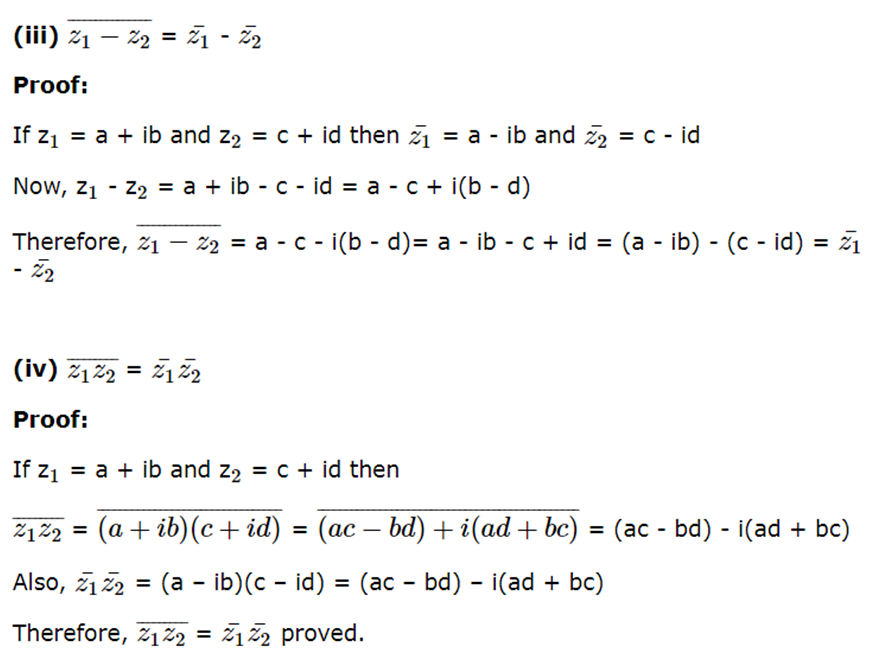

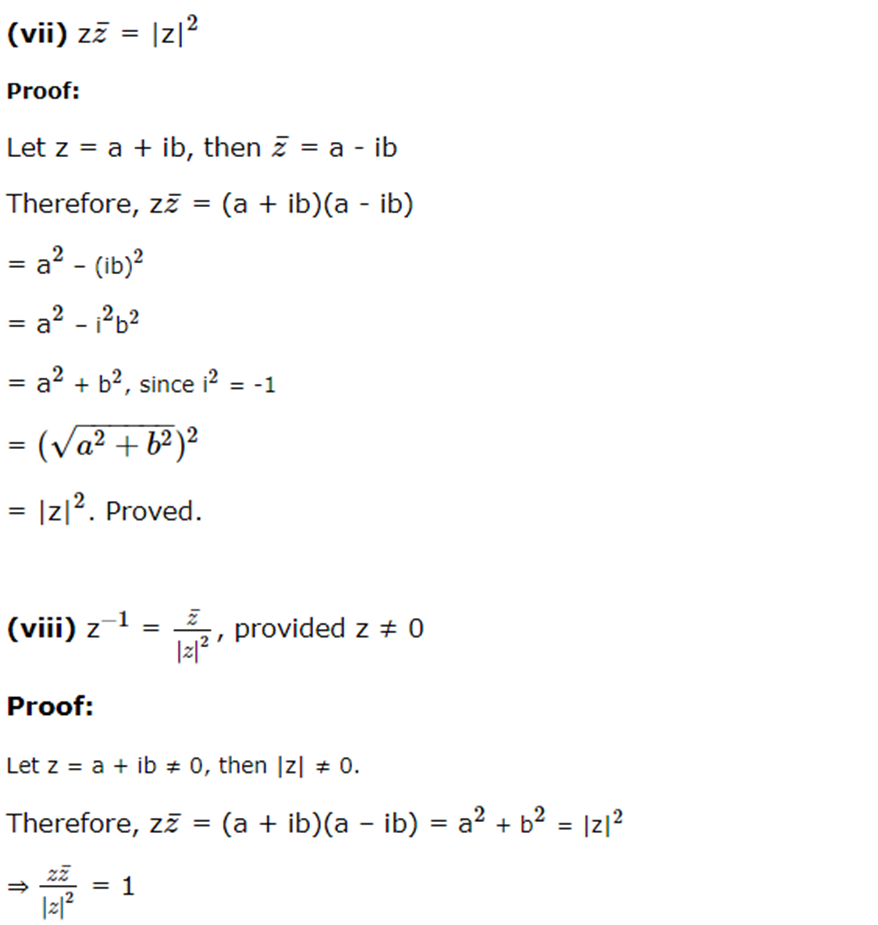

Modulus of Complex Number
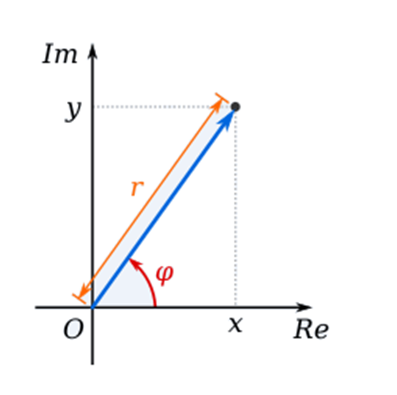
Modulus of the complex number is the distance of the point on the argand plane representing the complex number z from the origin.
Let P is the point that denotes the complex number z = x + iy.
Then OP = |z| = r = √(x2 + y2 ).
Properties of Modulus of Complex Number:
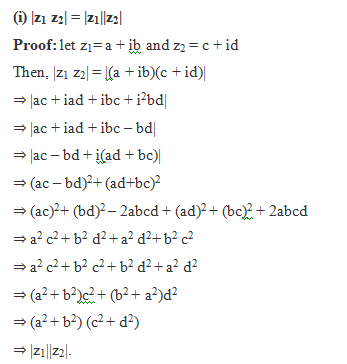
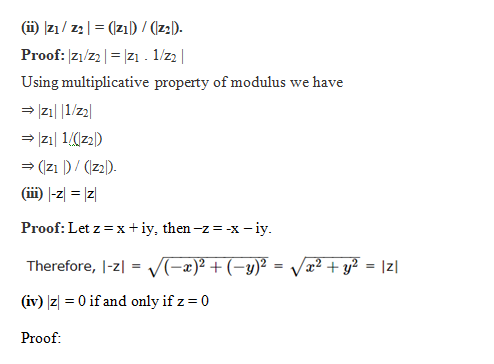
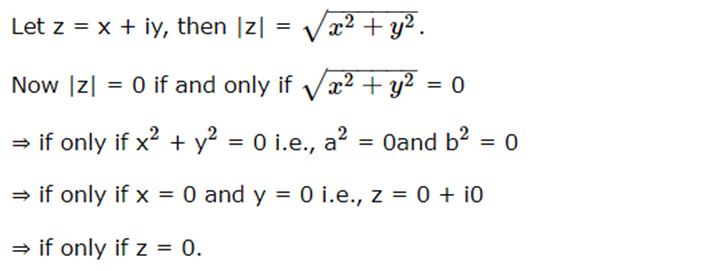
(v) For any two complex numbers z1 and z2, we have |z1 + z2| ≤ |z1| + |z2|.
Proof
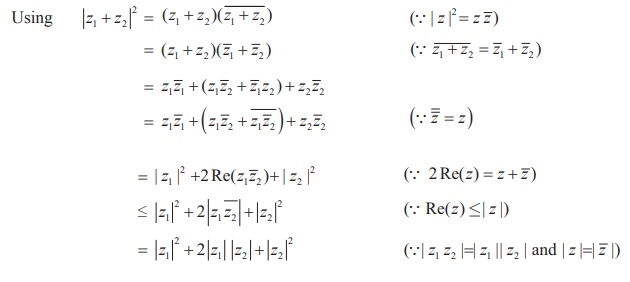
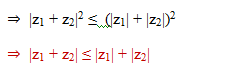
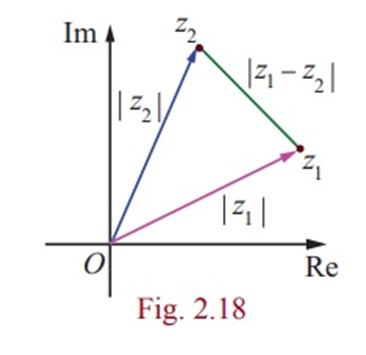
The distance between the two points z1 and z2 in complex plane is | z1 - z2 |
If we consider origin, z1 and z2 as vertices of a triangle, by the similar argument we have
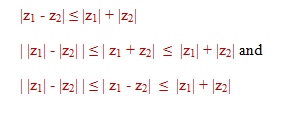
Geometrical interpretation
Now consider the triangle shown in figure with vertices O, z1 or z2 , and z1 + z2. We know from geometry that the length of the side of the triangle corresponding to the vector z1 + z2 cannot be greater than the sum of the lengths of the remaining two sides. This is the reason for calling the property as "Triangle Inequality".
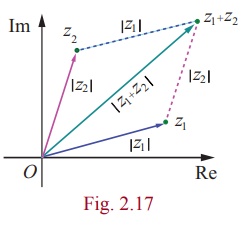
It can be generalized by means of mathematical induction to finite number of terms:
|z1 + z2 + z3 + …. + zn | ≤ |z1| + |z2| + |z3| + … + |zn| for n = 2,3,….
Note:
1. |z| > 0.
2. All the complex number with same modulus lie on the circle with centre origin and radius r = |z|.
Application:
Spectrum Analyzer

Those cool displays you see when music is playing? Yes, Complex Numbers are used to calculate them! Using something called "Fourier Transforms".
In fact many clever things can be done with sound using Complex Numbers, like filtering out sounds, hearing whispers in a crowd and so on.
It is part of a subject called "Signal Processing".
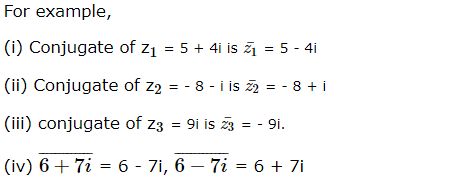
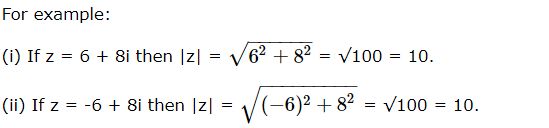
Example 1: Find the conjugate of the complex number z = (1 + 2i)/(1 – 2i).
Solution: z = (1 + 2i)/(1 – 2i)
Rationalising given complex number we have
⇒ z = ((1 + 2i)/(1 – 2i) )× (1 + 2i)/(1 + 2i)
⇒ z = (1 + 2i)2/(12 – (2i)2)
⇒ z = (1 + 4i2 + 4i)/(1 + 4)
⇒ z = (1 – 4 + 4i)/(1 + 4)
⇒ z = (-3 + 4i)/5
⇒![]() = (- 3 – 4i)/5.
= (- 3 – 4i)/5.
Example 2: Find the modulus of the complex number z = (3 – 2i)/2i
Solution: z = (3 – 2i)/2i
⇒ z = (3 )/2i – 2i/2i
⇒ z = 3/2i – 1
⇒ z = 3i/(2i2 ) – 1
⇒ z = (-3i/2) – 1
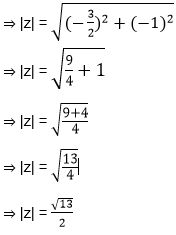
Example 3: If z + |z| = 1 + 4i, then find the value of |z|.
Solution: Let z = x + iy
⇒ z + |z| = 1 + 4i
⇒ x + iy + |x + iy| = 1 + 4i
⇒ x + iy + √(x2 + y2 ) = 1 + 4i
⇒ y = 4 and x + √(x2 + y2 ) = 1
⇒ x + √(x2 + 42 ) = 1
⇒ √(x2 + 42 ) = 1 – x
Squaring both side we have
⇒ x2 + 42 = 1 + x2 – 2x
⇒ 2x = -15
or x = -15/2
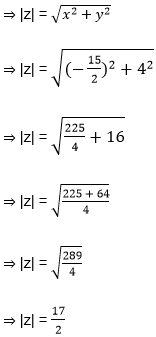
Argand Plane and Polar Representation
The plane having a complex number assigned to each of its point is called the
complex plane or the Argand plane.
Argument of Complex Numbers
The argument of a complex number is defined as the angle inclined from the real axis in the direction of the complex number represented on the complex plane. It is denoted by “θ” or “φ”. It is measured in the standard unit called “radians”.
The real and complex components of coordinates are found in terms of r and θ where r is the length of the vector, and θ is the angle made with the real axis.
The point P is uniquely determined by the ordered pair of real numbers (r, ), called the polar
coordinates of the point P.
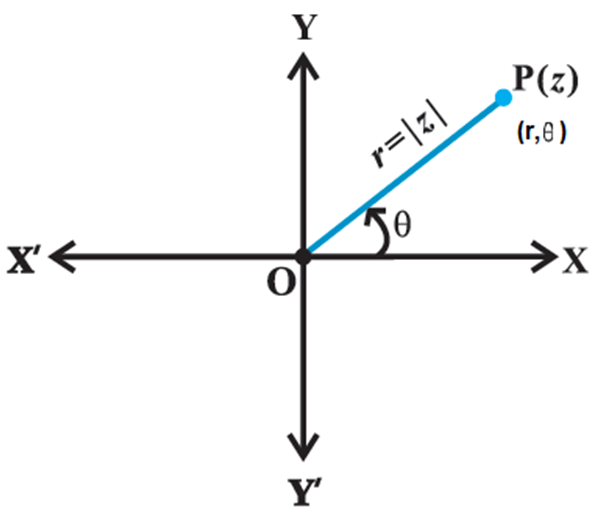
Polar Form of Complex Numbers
The argument of a complex number is defined as the angle inclined from the real axis in the direction of the complex number represented on the complex plane. It is denoted by “θ” or “φ”. It is measured in the standard unit called “radians”.
The real and complex components of coordinates are found in terms of r and θ where r is the length of the vector, and θ is the angle made with the real axis.
We have, x = r cos q, y = r sin q and therefore, z = r (cos q + i sin q).
The latter is said to be the polar form of the complex number.
q is called the argument (or amplitude) of z which is denoted by arg z. and
r = |z| =√(x2 + y2) is the modulus of z
For any complex number z ¹ 0, there corresponds only one value of q in 0 £ q < 2p.
The value of q such that – p < q £ p, called principal argument of z and is denoted by arg z.

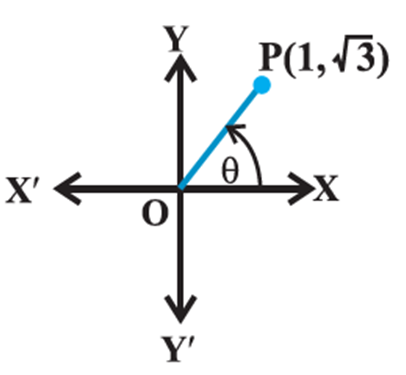
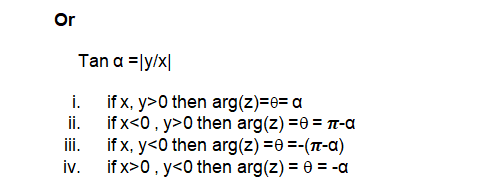
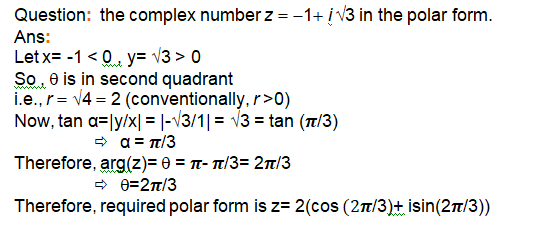
Properties of Argument of Complex Numbers
Suppose that z be a nonzero complex number and n be some integer, then
![]()
Let us assume, z1 and z2 be the two complex numbers, the following identities are:
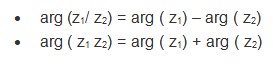
4. Solving Quadratic equations in complex numbers
- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
Solving Quadratic equations in complex numbers
We can solve quadratic equations with complex coefficients using the quadratic formula. If the discriminant is zero, the equation has one repeated root. If all the coefficients are real, the root will be real. A general quadratic with complex coefficients can have any combination of real and nonreal roots.
The Quadratic Formula is ![]() The expression under the radical,
The expression under the radical, ![]() is called the discriminant. You can use the discriminant to determine the number and type of solutions an equation has.
is called the discriminant. You can use the discriminant to determine the number and type of solutions an equation has.
Using the discriminant, we identify the three different cases of quadratic equations as follows.
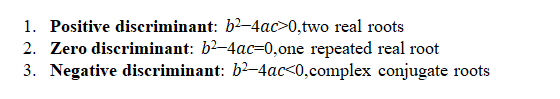

Solving Equations with Different Types of Solutions
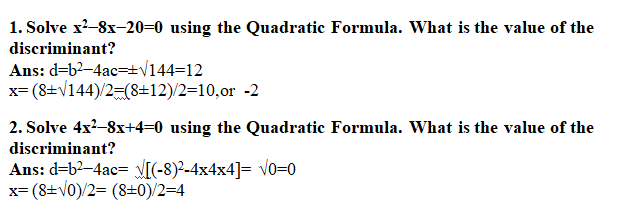

4. Nonreal Quadratic Equations with Real Negative Discriminants

5. Square Root and Cube Root Of Complex Numbers
- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
Square Root and Cube Root Of Complex Numbers:
Square roots of a complex number
Let the square root of a + ib be x + iy
That is = √[a+ib] = x + iy where x, y ∈ R
a + ib = ( x + iy )2 = x2 - y2 + i2xy
Equating real and imaginary parts, we get
x2 - y2 = a and 2xy = b
(x2 + y2 )2 = (x2 - y2 ) 2 + 4x2 y2 = a2 + b2
x2 + y2 = √[a2+b2], since x2 + y2 is positive
Solving x2 + y2 = a and x2+ y2 =√[a2+b2], we get
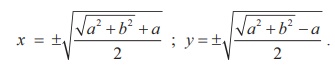
Since 2xy = b it is clear that both x and y will have the same sign when b is positive, and x and y have different signs when b is negative.
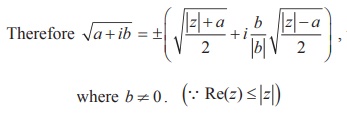
Formula for finding square root of a complex number
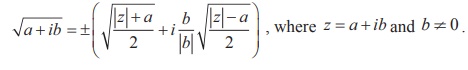
Note
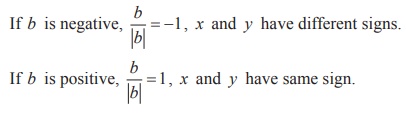
Example 1.
Find the square root of 6 - 8i.
Solution
We compute |6 - 8i| = √[62 + (-8)2] = 10
and applying the formula for square root, we get
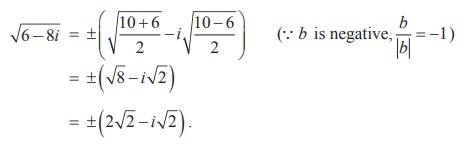
Example 2: Determine the square root of complex number 3 + 4i.
Solution: To determine the square root of 3 + 4i, we will determine its magnitude and compare with a + ib.
|3 + 4i| = √(32 + 42) = √(9 + 16) = √25 = 5; a = 3 and b = 4 > 0
Therefore, using formula for square root of complex numbers, we have
√(3 + 4i) = ± (√[√(5 + 3)/2] + i√[√(5 - 3)/2] )
= ± (√(8/2) + i √(2/2))
= ±(√4 + i√1)
= ± (2 + i)
Answer: Hence, √(3 + 4i) = ± (2 + i)

Cube Root of Unity Values:
Suppose the cube root of 1 is “x”,
i .e ., 3√1 = x.
According to the general cube roots definition,
x3 = 1
-
- x3 – 1 = 0
since (a3 – b3) = (a – b) ( a2 + ab + b2)
Now, (x3 – 13) = 0
-
- (x – 1)( x2 + x + 1) = 0
Therefore,
x = 1 Or ( x2 + x + 1) = 0
-
- x=1 or x = [(-1) ± √(12-4.1.1)]/2
- x=1 or x= [-1 ± √-3]/2
- x=1 or x= -1/2 ± i√(3)/2
Therefore, the three cube roots of unity are:
1, ω= -1/2+i√(3)/2, ω2= -1/2 – i√(3)/2
Properties of Cube roots of unity
1) One imaginary cube roots of unity is the square of the other imaginary cube root.
= ¼ [(-1)2 – 2 × 1 × √3 i + ( √3 i)2] = ¼(1 – 2√ 3i – 3) = (-1-√ 3 i) /2
And
= ¼ [(-1)2 + 2 × 1 × √3 i + ( √3 i)2] = ¼(1 + 2√ 3i – 3) = (-1+ √ 3 i) /2
i.e., ω2= (ω2)2
2) If two imaginary cube roots are multiplied then the product we get is equal to 1.
Let’s take ω = (-1 + √3 i ) /2
ω2 = (-1 – √3 i ) /2
Now we will get the product of two imaginary cube roots as ω x ω2 = [(-1 + √3 i ) / 2]x [(-1 – √3 i ) /2]
Or ω3 = ¼[(-1)2 – (√3 i)2]
= ¼[( 1 – 3i2) = ¼ x 4 = 1.
3) As there are three cube roots of unity, their sum is zero, let’s see how
= 1 + [(-1 + √3 i ) /2] + [(-1 – √3 i ) /2]
Or
1 + ω + ω2 = 1 – ½ + (√3 i ) /2 – ½ – (√3 i ) /2
= 0
4) conjugate of One imaginary cube roots of unity is equal to the other imaginary cube root.
Euler’s form of a Complex Number
eiƟ = cos Ɵ + i sin Ɵ
This form makes the study of complex numbers and its properties simple. Any complex number can be expressed as
z = x + iy (Cartesian form)
= |z| [cos Ɵ + I sin Ɵ] (polar form)
= |z| eiƟ
De Moivre’s Theorem and its Applications
(a) De Moivre’s Theorem for integral index. If n is a integer, then (cos Ɵ + i sin Ɵ)n = cos (nƟ) + i sin (nƟ)
(b) De Moivre’s Theorem for rational index. If n is a rational number, then the value of or one of the values of
(cosƟ + isinƟ)n is cos (nƟ) + i sin (nƟ).
In fact, if n = p/q where p, q ϵ I, q > 0 and p,q have no factors in common, then (cos Ɵ + i sin Ɵ)n has q distinct values, one of which is cos (nƟ) + i sin (nƟ)
The nth Roots of Unity
By an nth root of unity we mean any complex number z which satisfies the equation zn = 1 (1)
Since an equation of degree n has n roots, there are n values of z which satisfy the equation (1). To obtain these n values of z, we write 1 = cos (2kπ) + I sin (2kπ)
Where k ϵ I and ![]()
[using the De Moivre’s Theorem]
Where k = 0, 1, 2, …., n -1.
Note
The values of (cos Ɵ + I sin Ɵ)p/q where p, q ϵ I, q ≠ 0, hcf (p,q) = 1 are given by
![]()
Where k = 0, 1, 2, ….., q -1.
2. Graphical methods and Solution of Linear Inequalities in Two Variables
- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
Graphical methods and Solution of Linear Inequalities in Two Variables
Graph of Linear inequalities in Two Variable
A linear equation in two variable is of the form
ax+by+c=0
We have already studied in Coordinate geometry that this can be represented by a straight line in xy- plane. All the points on the straight line are the solutions of this linear equation.
we can similarly find the solution set graphically for the linear inequalities in the below form
ax+by+c<0
ax+by+c>0
ax+by+c≥0
ax+by+c≤0
How to find the solution graphically for Linear inequalities in Two Variable.:
- Draw the graph of the equation obtained for the given inequality by replacing the inequality sign with an equal sign.
ax+by+c=0
- This can be done easily by Point on the x-axis( x,0) and point on the y axis ( 0,y)
- Point on x-axis given by ax+b(0)+c=0 or x=−c/a or (−c/a,0)
- Point on y-axis given by a(0)+by+c=0 or y=−c/b or (0,−c/b)
- Locate these point on cartesian plane and join them to find the line
- Use a dashed or dotted line if the problem involves a strict inequality, < or >.
- Otherwise, use a solid line to indicate that the line itself constitutes part of the solution.
- Pick a point lying in one of the half-planes determined by the line sketched in step 1 and substitute the values of x and y into the given inequality.
Use the origin whenever possible. - If the inequality is satisfied, the graph of the inequality includes the half-plane containing the test point.
Otherwise, the solution includes the half-plane not containing the test point
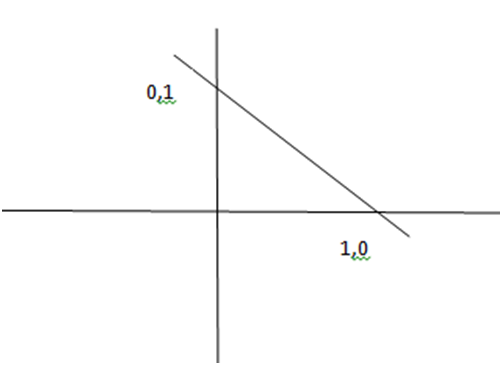
Example
Determine the solution set for the inequality
x+y>1
Solution
1) Draw the graph of the equation obtained for the given inequality by replacing the inequality sign with an equal sign.
i.e x+y=1
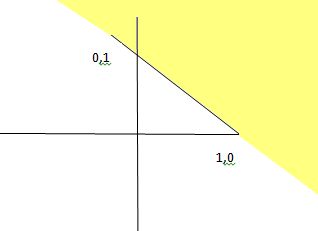
2) Pick the test point as origin (0,0), and put into the inequality
0+0>1
0>1
Which is false
So the solution set is other half plane of the line
How to find the solution graphically for pair of Linear inequalities in Two Variable.
ax+by+c<0
px+qy+c<0
The solution set of a system of linear inequalities in two variables x and y is the set of all points (x, y) that satisfy each inequality of the system.
Step
- Find the graphical solution for each inequality independently using the technique described above
- Now determine the region in common with each solution set
Example
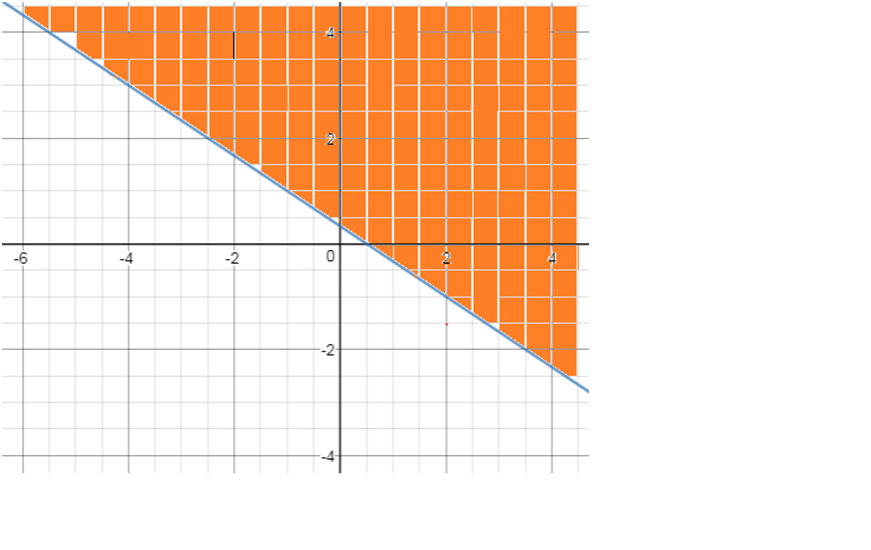
Find the solution of the below system of inequalities
2x+3y>1
x+2y>2
x>1
Solution
1) for 2x+3y>1, Solving using the above method solution is
2) for x+2y>2, Solving using the above method solution is
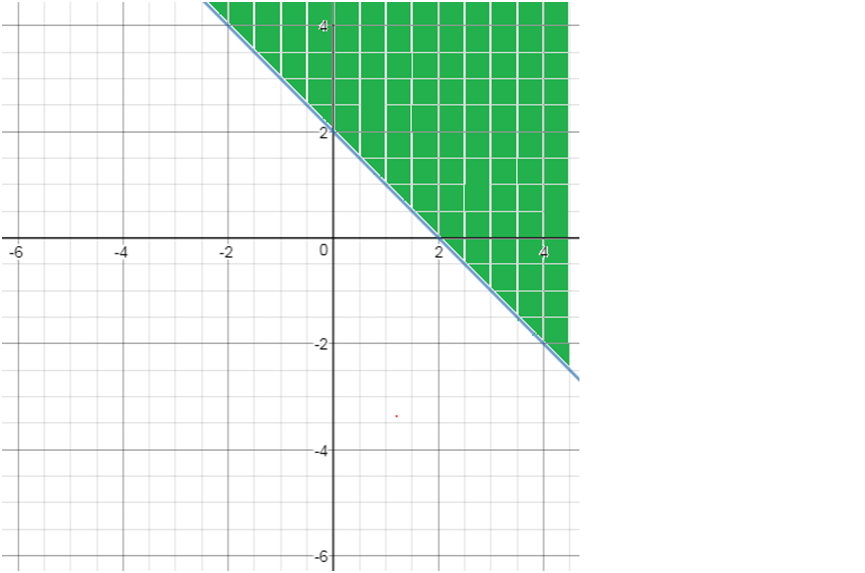
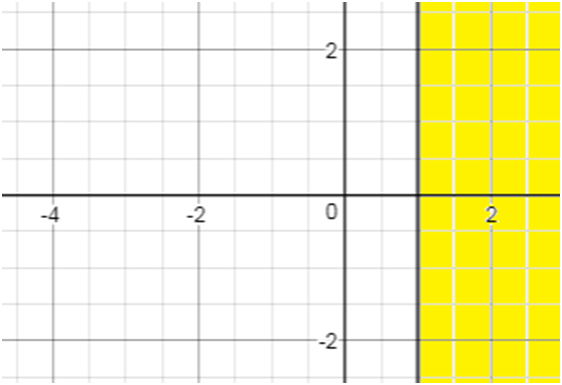
3) for x>1, Solving using the above method solution is
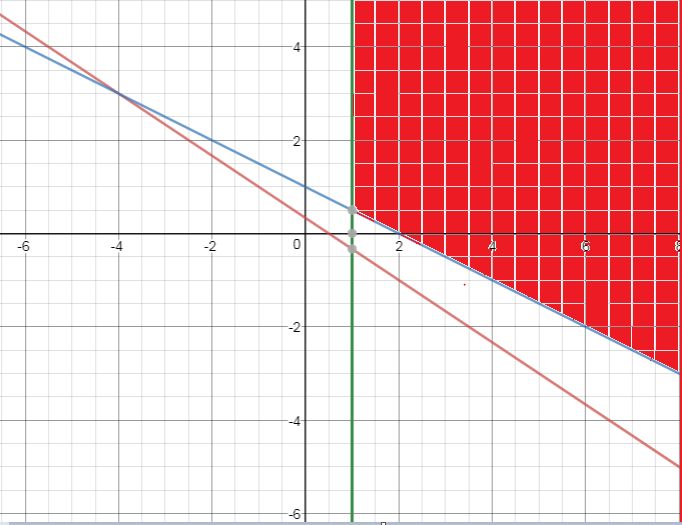
4) Now we draw these on the single graph and can determine the common region
Example:
Solve the following system of inequalities
8x + 3y £ 100 ......... (1)
x ³ 0 ......... (2)
y ³ 0 ... …. (3)
Ans:
Let 8x + 3y = 100
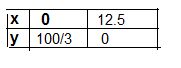
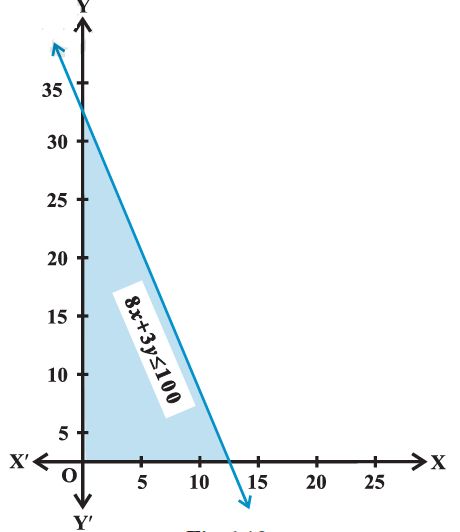
The inequality 8x + 3y £ 100 represents the shaded region below the line, including the
points on the line 8x +3y =100.
Since x ³ 0, y ³ 0, every point in the shaded region in the first quadrant, including the points on the line and the axes, represents the solution of the given system of inequalities.
Question: Solve the following system of inequalities graphically
x + 2y £ 8 ... (1)
2x + y £ 8 ... (2)
x > 0 ... (3)
y > 0 ... (4)
Solution:
We draw the graphs of the lines
x + 2y = 8

and
2x + y = 8.
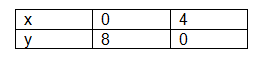
The inequality (1) and (2) represent the region below the two lines, including the point on the respective lines.
Since x ³ 0, y ³ 0, every point in the shaded region in the first quadrant represent
a solution of the given system of inequalities.
Note:
1 The region containing all the solutions of an inequality is called thesolution region.
2. In order to identify the half plane represented by an inequality, it is just sufficient to take any point (a, b) (not online) and check whether it satisfies the inequality or not. If it satisfies, then the inequality represents the half plane and shade the region which contains the point, otherwise, the inequality represents that half plane which does not contain the point within it. For convenience, the point (0, 0) is preferred.
3. If an inequality is of the type ax + by ³ c or ax + by £ c, then the points on the line ax + by = c are also included in the solution region. So draw a dark line in the solution region.
4. If an inequality is of the form ax + by > c or ax + by < c, then the points on the line ax + by = c are not to be included in the solution region. So draw a broken ordotted line in the solution region.
Example: Solve – 8 £ 5x – 3 < 7.
Solution : In this case, we have two inequalities,
– 8 £ 5x – 3 and 5x – 3 < 7,
which we will solve simultaneously.
We have – 8 £ 5x –3 < 7
or –5 £ 5x < 10 or –1 £ x < 2
Example:
A manufacturer has 600 litres of a 12% solution of acid. How many litres
of a 30% acid solution must be added to it so that acid content in the resulting mixture
will be more than 15% but less than 18%?
Solution: Let x litres of 30% acid solution is required to be added. Then
Total mixture = (x + 600) litres
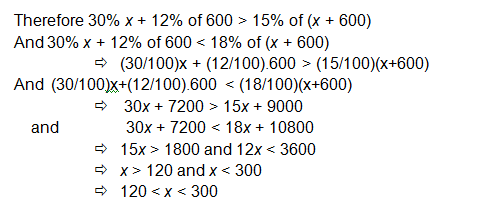
2. Permutations and Factorial notation
- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
Permutations and Factorial notation
Factorial notation:
n! = n(n-1)(n-2) (n-3) …….2x1
n! = n(n-1)! = n(n-1)(n-2)!
0! = 1
1! = 1
5! = 4! x 5 = 3 ! x 4x 5
Question 1: Evaluate (i) 8! (ii) 4! – 3!
ANSWER:
(i) 8! = 1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 = 40320
(ii) 4! = 1 × 2 × 3 × 4 = 24
3! = 1 × 2 × 3 = 6
∴4! – 3! = 24 – 6 = 18
Question 2: Is 3! + 4! = 7!?
ANSWER:
3! = 1 × 2 × 3 = 6
4! = 1 × 2 × 3 × 4 = 24
∴3! + 4! = 6 + 24 = 30
7! = 1 × 2 × 3 × 4 × 5 × 6 × 7 = 5040
∴ 3! + 4! ≠ 7!
Question 3: Compute 
ANSWER:

Question 4: If  , find x.
, find x.
ANSWER:

Question 4. How many 5-digit telephone numbers can be constructed using the digits 0 to 9 if each number starts with 67 and no digit appears more than once?
Solution:
Let the five-digit number be ABCDE. Given that first 2 digits of each number is 67. Therefore, the number is 67CDE.
As the repetition is not allowed and 6 and 7 are already taken, the digits available for place C are 0,1,2,3,4,5,8,9. The number of possible digits at place C is 8. Suppose one of them is taken at C, now the digits possible at place D is 7. And similarly, at E the possible digits are 6.
∴The total five-digit numbers with given conditions = 8 × 7 × 6 = 336.
Question 5. A coin is tossed 3 times and the outcomes are recorded. How many possible outcomes are there?
Solution:
Given A coin is tossed 3 times and the outcomes are recorded
The possible outcomes after a coin toss are head and tail.
The number of possible outcomes at each coin toss is 2.
∴The total number of possible outcomes after 3 times = 2 × 2 × 2 = 8.
Question 6. Given 5 flags of different colours, how many different signals can be generated if each signal requires the use of 2 flags, one below the other?
Solution:
Given 5 flags of different colours
We know the signal requires 2 flags.
The number of flags possible for upper flag is 5.
Now as one of the flag is taken, the number of flags remaining for lower flag in the signal is 4.
The number of ways in which signal can be given = 5 × 4 = 20.
Question 7. Evaluate
(i) 8!
(ii) 4! – 3!
Solution:
(i) Consider 8!
We know that 8! = 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1
= 40320
(ii) Consider 4!-3!
4!-3! = (4 × 3!) – 3!
Above equation can be written as
= 3! (4-1)
= 3 × 2 × 1 × 3
= 18
2. Is 3! + 4! = 7!?
Solution:
Consider LHS 3! + 4!
Computing left hand side, we get
3! + 4! = (3 × 2 × 1) + (4 × 3 × 2 × 1)
= 6 + 24
= 30
Again consider RHS and computing we get
7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040
Therefore LHS ≠ RHS
Therefore 3! + 4! ≠ 7!
Permutations:
A permutation is an arrangement in a definite order of a number of objects taken some or all at a time.
Permutations when all the objects are distinct:
Theorem 1: The number of permutations of n different objects taken r at a time,
where 0 < r n and the objects do not repeat is n ( n – 1) ( n – 2). . .( n – r + 1),
which is denoted by nPr.
Proof There will be as many permutations as there are ways of filling in r vacant places
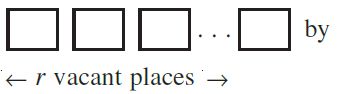
the n objects. The first place can be filled in n ways; following which, the second placecan be filled in (n – 1) ways, following which the third place can be filled in (n – 2)ways,..., the rth place can be filled in (n – (r – 1)) ways. Therefore, the number of ways of filling in r vacant places in succession is n(n – 1) (n – 2) . . . (n – (r – 1)) or n ( n – 1) (n – 2) ... (n – r + 1)
= [n ( n – 1) (n – 2) ... (n – r + 1)(n-r)! ] / (n-r)! = npr = p(n,r)
npr =![]() , where 0 < r n
, where 0 < r n
npn =![]() =1
=1
np0 =![]() =n!
=n!
Theorem 2 : The number of permutations of n different objects taken r at a time,
where repetition is allowed, is nr.
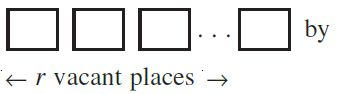
i.e., n x n x n x n x n x…r times….x n= nr
Example: Find the number of 4 letter words, with or without meaning, which can be
formed out of the letters of the word ROSE.
Ans:
The required number of words = 4P4 = 4! = 24. Here repetition is not allowed.
If repetition is allowed, the required number of words would be 44 = 256.
Example: The number of 3-letter words which can be formed by the letters of the word
NUMBER =6P3 = 6!/3!= 4 × 5 × 6 = 120.
Here, in this case also, the repetition is not allowed.
If the repetition is allowed, the required number of words would be 63 = 216.
Example:
The number of ways in which a Chairman and a Vice-Chairman can be chosen
from amongst a group of 12 persons assuming that one person can not hold more than
one position, clearly 12P2= 12!/10! =11x12=132
Permutations when all the objects are not distinct objects:
Example:
Suppose we have to find the number of ways of rearranging the letters of the word ROOT.
Therefore, the required number of permutations = 4!/2! =3x4= 12
Theorem 3: The number of permutations of n objects, where p objects are of the same kind and rest are all different = n!/p!
Theorem 4: The number of permutations of n objects, where p1 objects are of one
kind, p2 are of second kind, ..., pk are of kth kind and the rest, if any, are of different kind is 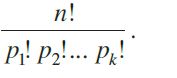
Example Find the number of permutations of the letters of the word ALLAHABAD.
Solution Here, there are 9 objects (letters) of which there are 4A’s, 2 L’s and rest are
all different.
Therefore, the required number of arrangements =9!/(4!x2!)= 5x 6 x 7 x 8 x 9 / 2 =7560
Example: ![]()
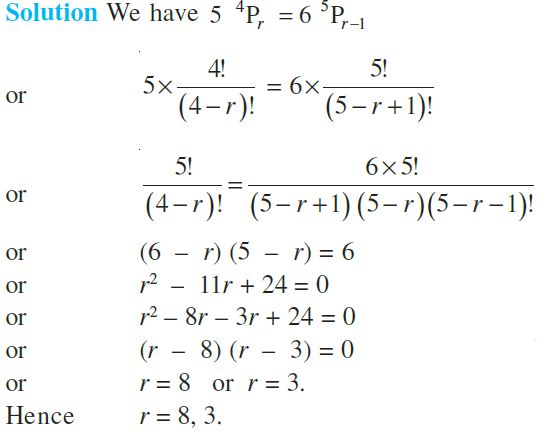
Example: How many words, with or without meaning can be made from the letters of the word MONDAY, assuming that no letter is repeated, if
(i) 4 letters are used at a time,
(ii) all letters are used at a time,
(iii) all letters are used but the first letter is a vowel?
Solution:
Given word: MONDAY
(i) Number of letters to be used = 4
Number of permutations = 6P4 = 6!/(6 – 4)! = 6!/2! = 720/2 = 360
Therefore, we can form 350 words with 4 letters from the word MONDAY.
(ii) Number of letters to be used = 6
Number of permutations = 6P6 = 6!/(6 – 6)! = 6!/0! = 720/1 = 720
Therefore, we can form 720 words using all the letters from the word MONDAY.
(iii) Number of vowels in the word MONDAY = 2 (O and A)
Number of ways that the first letter is a vowel = 2P1 = 2!/(2 – 1)! = 2!/1! = 2
Now, the remaining places = 5
Remaining letters = 5
These can be arranged in 5! ways, i.e. 120
Therefore, the total number of words can be formed with the first letter as vowel = 2 × 120 = 240.
N.B.:
- Almost all permutation questions involve putting things in order from a line where the order matters. For example ABC is a different permutation to ACB.
- The number of permutations of n distinct objects when a particular object is not to be considered in the arrangement is given by n-1Pr.
- The number of permutations of n distinct objects when a specific object is to be always included in the arrangement is given by r.n-1Pr-1.
- If we need to compute the number of permutations of n different objects, out of which r have to be selected and each object has the probability of occurring once, twice or thrice… up to r times in any arrangement is given by (n)r.
- Circular permutation is used when some arrangement is to be made in the form of a ring or circle.
- When ‘n’ different or unlike objects are to be arranged in a ring in such a way that the clockwise and anticlockwise arrangements are different, then the number of such arrangements is given by (n – 1)!
- If r things are taken at a time out of n distinct things and arranged along a circle, then the number of ways of doing this is given by nCr(r-1)!.
- If clockwise and anti-clockwise are considered to be the same, then the total number of circular permutations is given by (n-1)!/2.
- If n persons are to be seated around a round table in such a way that no person has similar neighbor then it is given by ½ (n – 1)!
- The number of necklaces formed with n beads of different colors = ½ (n – 1)!
3. Combinations and Simple applications
- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
Combinations and Simple applications
Combinations:
Let us now assume that there is a group of 3 lawn tennis players X, Y, Z. A team consisting of 2 players is to be formed. In how many ways can we do so? Is the team of X and Y different from the team of Y and X ? Here, order is not important.
These are XY, YZ and ZX.
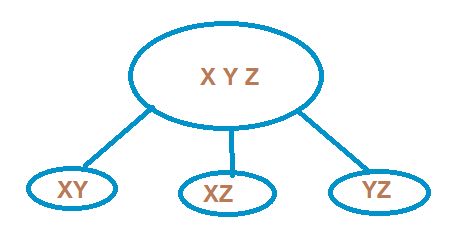
Here, each selection is called a combination of 3 different objects taken 2 at a time.
Definition:
The combination is a selection of a part of a set of objects or a selection of all objects when the order doesn't matter.
or
The number of combinations/selection of n different objects taken r at a time, denoted by nCr
Theorem: nPr= r! . nCr , 0 < r ![]() n
n
Proof: Corresponding to each combination of nCr, we have r ! permutations, because r objects in every combination can be rearranged in r ! ways.
Hence, the total number of permutations of n different things taken r at a time is nPr= r! . nCr .
Properties:
1. nCr = nCn-r
2. If nCr = nCk, then r = k or n-r = k
3. nCr + nCr-1 = n+1Cr
4. nCr = n/r n-1Cr-1
5. nCr/nCr-1 = (n-r+1)/ r
6. If n is even nCr is greatest for r = n/2
7. If n is odd, nCr is greatest for r = (n-1)/2,(n+1)/2
Example; nC9 = nC8 then n=? and nC17=?
Ans: n = a+b = 9+8 =17
nC17= 17C17=1
Question. In how many ways can a football team of 11 players be selected from 16 players? How many of them will
(i) include 2 particular players?
(ii) exclude 2 particular players?
Solution:
We know that,
nCr ![]()
According to the question,
11 players can be selected out of 16 = 16C11
(i) include 2 particular players = 14C9
(ii) exclude 2 particular players = 14C11
Question : Find the number of ways of choosing 4 cards from a pack of 52 playing cards? In how many of these
(i) four cards are of the same suit,
(ii) four cards belong to four different suits,
(iii) are face cards,
(iv) two are red and two are black cards,
(v) cards are of the same colour?
Solution :
There will be a number of possible ways for choosing 4 cards from 52 cards as there are combinations of 52 different things when we take 4 at a time.
Therefore, the required number of ways = 52C4
= 52! / (4! 48!) = (49x50x51x52) / (2x3x4)
= 270725
(i) Four cards of the same suit:
There are four suits: Spade, heart, Club, diamond. Totally, there are 13 cards of each suit
Therefore, the required number of ways are given by 13C4 + 13C4 + 13C4 + 13C4
= 4(13! / (4! 9! )) = 2860
(ii) four cards belong to four different suits:
Since there are 13 cards in each suit. Therefore choosing 1 card from 13 cards of each suit, it becomes
= 13C1 + 13C1 + 13C1 + 13C1 = 134
(iii) Face cards :
There are 12 face cards and 4 cards are selected from these 12 cards, it becomes
= 12C4
Therefore, the required number of ways = 12! / ( 4! 8!) = 495
(iv) Two red cards and two black cards:
There are 26 red and 26 black cards in a pack of52 cards.
Therefore, the required number of ways = 26C2 x 26C2
= ![]()
= (325)2
=105625
(v) Cards of the same color:
Out of 26 red cards and 26 black cards, 4 red and black cards are selected in 26C4 ways. So, the required number of ways = 26C4 + 26C4
= 2 (26! / 4! 22! )
=29900.
Question: If the different permutations of all the letter of the word EXAMINATION are listed as in a dictionary, how many words are there in this list before the first word starting with E?
Solution:
In dictionary words are listed alphabetically, so to find the words
Listed before E should start with letter either A, B, C or D
But the word EXAMINATION doesn`t have B, C or D
Hence the words should start with letter A
The remaining 10 places are to be filled by the remaining letters of the word EXAMINATION which are E, X, A, M, 2N, T, 2I, 0
Since the letters are repeating the formula used would be
![]()
Where n is remaining number of letters p1 and p2 are number of times the repeated terms occurs.
![]()
The number of words in the list before the word starting with E
= words starting with letter A = 907200
N.B.:
- The number of ways of selecting r objects from n different objects subject to certain condition like:
1. k particular objects are always included = n-kCr-k
2. k particular objects are never included = n-kCr
- The number of arrangement of n distinct objects taken r at a time so that k particular objects are
(i) Always included = n-kCr-k.r!,
(ii) Never included = n-kCr.r!.
- In order to compute the combination of n distinct items taken r at a time wherein, the chances of occurrence of any item are not fixed and may be one, twice, thrice, …. up to r times is given by n+r-1Cr
- If there are m men and n women (m > n) and they have to be seated or accommodated in a row in such a way that no two women sit together then total no. of such arrangements = m+1Cn. m! This is also termed as the Gap Method.
- If we have n different things taken r at a time in form of a garland or necklace, then the required number of arrangements is given by nCr(r-1)!/2.
- If there is a problem that requires n number of persons to be accommodated in such a way that a fixed number say ‘p’ are always together, then that particular set of p persons should be treated as one person. Hence, the total number of people in such a case becomes (n-m+1). Therefore, the total number of possible arrangements is (n-m+1)! m! This is also termed as the String Method.
- Let there be n types of objects with each type containing at least r objects. Then the number of ways of arranging r objects in a row is nr.
- The number of selections from n different objects, taking at least one = nC1 + nC2 + nC3 + ... + nCn = 2n - 1.
- Total number of selections of zero or more objects from n identical objects is n+1.
- Selection when both identical and distinct objects are present:
The number of selections, taking at least one out of a1 + a2 + a3 + ... an + k objects, where a1 are alike (of one kind), a2 are alike (of second kind) and so on ... an are alike (of nth kind), and k are distinct = {[(a1 + 1)(a2 + 1)(a3 + 1) ... (an + 1)]2k} - 1.
- Combination of n different things taken some or all of n things at a time is given by 2n – 1.
- Combination of n things taken some or all at a time when p of the things are alike of one kind, q of the things are alike and of another kind and r of the things are alike of a third kind = [(p + 1) (q + 1)(r + 1)….] – 1.
- The number of ways to select some or all out of (p+q+t) things where p are alike of first kind, q are alike of second kind and the remaining t are different is = (p+1)(q+1)2t – 1.
- Combination of selecting s1 things from a set of n1 objects and s2 things from a set of n2 objects where combination of s1 things and s2 things are independent is given by n1Cs1 x n2Cs2
- Total number of ways in which n identical items which can be distributed among p persons so that each person may get any number of items is n+p-1Cp-1.
- Total number of ways in which n identical items can be distributed among p persons such that each them receive at least one item n-1Cp-1
2. Pascal’s triangle
- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
Pascal’s triangle
An expression consisting of two terms, connected by + or – sign is called binomial expression. Binomial Theorem. If a and b are real numbers and n is a positive integer, then. The general term of (r + 1)th term in the expression is given by. Tr+1 = nCr an-r br.
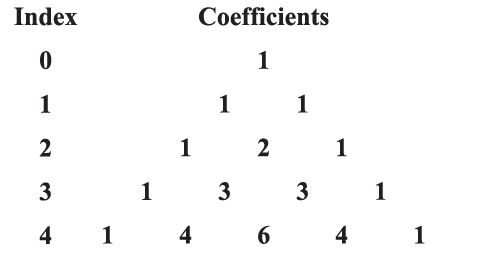

Example: (a + b)7 = 7C0 a7+ 7C1a6b + 7C2a5b2 + 7C3a4b3 + 7C4a3b4 + 7C5a2b5 + 7C6ab6 + 7C7b7
2. Arithmetic Progression (AP) and Arithmetic Mean (AM)
- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
Arithmetic Progression (AP) and Arithmetic Mean (AM)
A sequence a1, a2, a3,…, an,… is called arithmetic sequence or arithmetic progression
if an + 1 = an + d, n Î N, where a1 is called the first term and the constant term d is called
the common difference of the A.P.
Let us consider an A.P. (in its standard form) with first term a and common
difference d, i.e., a, a + d, a + 2d, ...
The nth term of an AP is given by
nth term = an= a + (n-1) d.
a = the first term, l = the last term, d = common difference,
n = the number of terms.
Sum of nth term:
Sn= the sum to n terms of A.P.
Let a, a + d, a + 2d, …, a + (n – 1) d be an A.P.
Then
l = a + (n – 1) d
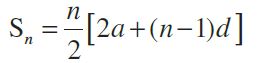
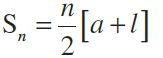
Arithmetic mean: Given two numbers a and b. We can insert a number A between them
so that a, A, b is an A.P. Such a number A is called the arithmetic mean (A.M.) of the numbers
a and b. Note that, in this case, we have
A – a = b – A
- A =(a+b)/2
Between any two numbers ‘a’ and ‘b’, n numbers can be inserted such that the resulting sequence is an Arithmetic Progression. A1, A2, A3,……,An be n numbers between a and b such that a, A1 , A2 , A3,……,An, b is in A.P.
Here, a is the 1st term and b is (n+2)th term. Therefore,
b = a + d[(n + 2) – 1] = a + d (n + 1).
Hence, common difference (d) = (b-a)/(n+1)
Now, A1= a+d= a+((b-a)/(n+1))
A2= a+2d = a + ((2(b-a)/(n+1))
An = a+nd= a + ((n(b-a)/(n+1))}
The nth term of a geometric progression is given by an = arn-1
Example: Insert 6 numbers between 3 and 24 such that the resulting sequence is
an A.P.
Solution: Let A1, A2, A3, A4, A5 and A6 be six numbers between 3 and 24 such that
3, A1, A2, A3, A4, A5, A6, 24 are in A.P. Here, a = 3, b = 24, n = 8.
Therefore, 24 = 3 + (8 –1) d, so that d = 3.
Thus A1 = a + d = 3 + 3 = 6; A2 = a + 2d = 3 + 2 × 3 = 9;
A3 = a + 3d = 3 + 3 × 3 = 12; A4 = a + 4d = 3 + 4 × 3 = 15;
A5 = a + 5d = 3 + 5 × 3 = 18; A6 = a + 6d = 3 + 6 × 3 = 21.
Hence, six numbers between 3 and 24 are 6, 9, 12, 15, 18 and 21.
simple properties of an A.P. :
(i) If a constant is added to each term of an A.P., the resulting sequence is
also an A.P.
(ii) If a constant is subtracted from each term of an A.P., the resulting
sequence is also an A.P.
(iii) If each term of an A.P. is multiplied by a constant, then the resulting
sequence is also an A.P.
(iv) If each term of an A.P. is divided by a non-zero constant then the
resulting sequence is also an A.P.
Example 1. Show that the sum of (m + n)th and (m – n)th terms of an A.P. is equal to twice the mth term.
Solution:
Let’s take a and d to be the first term and the common difference of the A.P. respectively.
We know that, the kth term of an A. P. is given by
ak = a + (k –1) d
So, am + n = a + (m + n –1) d
And, am – n = a + (m – n –1) d
am = a + (m –1) d
Thus,
am + n + am – n = a + (m + n –1) d + a + (m – n –1) d
= 2a + (m + n –1 + m – n –1) d
= 2a + (2m – 2) d
= 2a + 2 (m – 1) d
=2 [a + (m – 1) d]
= 2am
Therefore, the sum of (m + n)th and (m – n)th terms of an A.P. is equal to twice the mth term
Example 2. If the sum of three numbers in A.P., is 24 and their product is 440, find the numbers.
Solution:
Let’s consider the three numbers in A.P. as a – d, a, and a + d.
Then, from the question we have
(a – d) + (a) + (a + d) = 24 … (i)
3a = 24
∴ a = 8
And,
(a – d) a (a + d) = 440 … (ii)
(8 – d) (8) (8 + d) = 440
(8 – d) (8 + d) = 55
64 – d2 = 55
d2 = 64 – 55 = 9
∴ d = ± 3
Thus,
When d = 3, the numbers are 5, 8, and 11 and
When d = –3, the numbers are 11, 8, and 5.
Therefore, the three numbers are 5, 8, and 11.
3. Geometric Progression (GP) and Geometric Mean (GM)
- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
Geometric Progression (GP) and Geometric Mean (GM)
A sequence a1, a2, a3,…, an,… is called Geometric sequence or Geometric progression
if an + 1 / an = r, n Î N, where a1 is called the first term and the constant term r is called
the common ratio of the G.P.
It is represented by:
a, ar, ar2, ar3, ar4, and so on.
Where a is the first term and r is the common ratio.
The nth term of a GP is an=Tn = arn-1
a = the first term, r = the common ratio, l = the last term,
n = the numbers of terms,
Sn = the sum of first n terms.
Suppose a, ar, ar2, ar3,……arn-1 is the given Geometric Progression.
Then the sum of n terms of GP is given by:
Sn = a + ar + ar2 + ar3 +…+ arn-1
- Sn = a[(rn – 1)/(r – 1)] if r ≠ 1 and r > 1
Types of GP:
- Finite geometric progression (Finite GP)
- Infinite geometric progression (Infinite GP)
Finite Geometric Progression
The terms of a finite G.P. can be written as a, ar, ar2, ar3,……arn-1
a, ar, ar2, ar3,……arn-1 is called finite geometric series.
The sum of finite Geometric series is Sn = a[(rn – 1)/(r – 1)] if r ≠ 1 and r > 1
Infinite Geometric Progression
Terms of an infinite G.P. can be written as a, ar, ar2, ar3, ……arn-1,…….
a, ar, ar2, ar3, ……arn-1,……. is called infinite geometric series.
The sum of infinite geometric series is Sn = ![]()
Properties of GP:
- Three non-zero terms a, b, c are in GP if and only if b2 = ac
- In a GP,
Three consecutive terms can be taken as a/r, a, ar
Four consecutive terms can be taken as a/r3, a/r, ar, ar3
Five consecutive terms can be taken as a/r2, a/r, a, ar, ar2 - In a finite GP, the product of the terms equidistant from the beginning and the end is the same
That means, t1.tn = t2.tn-1 = t3.tn-2 = ….. - If each term of a GP is multiplied or divided by a non-zero constant, then the resulting sequence is also a GP with the same common ratio
- The product and quotient of two GP’s is again a GP
- If each term of a GP is raised to the power by the same non-zero quantity, the resultant sequence is also a GP
- If a1, a2, a3,… is a GP of positive terms then log a1, log a2, log a3,… is an AP (arithmetic progression) and vice versa
Geometric Mean (G .M.) : The geometric mean of two positive numbers a and b is the
Number √(ab).
Therefore, the geometric mean of 2 and 8 is 4.
We observe that the three numbers 2,4,8 are consecutive terms of a G.P.
Let G1, G2,…, Gn be n numbers between positive numbers a and b such that
a,G1,G2,G3,…,Gn,b is a G.P.
Thus, b being the (n + 2)th term,
we have b= arn+1
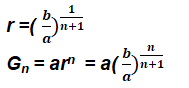
Example: Insert three numbers between 1 and 256 so that the resulting sequence
is a G.P.
Solution Let G1, G2,G3 be three numbers between 1 and 256 such that
1, G1,G2,G3 ,256 is a G.P.
Therefore 256 = r4 giving r = ± 4 (Taking real roots only)
For r = 4, we have G1 = ar = 4, G2 = ar2 = 16, G3 = ar3 = 64
Similarly, for r = – 4, numbers are – 4,16 and – 64.
Hence, we can insert 4, 16, 64 between 1 and 256 so that the resulting sequences are in G.P.
Relationship Between A.M. and G.M.:
Let A and G be A.M. and G.M. of two given positive real numbers a and b, respectively.
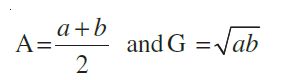
Thus, we have
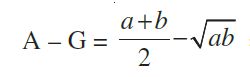
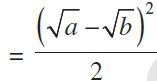
- A – B ³ 0
we obtain the relationship A ![]() G.
G.
Example 1. We know the sum of the interior angles of a triangle is 180°. Show that the sums of the interior angles of polygons with 3, 4, 5, 6, … sides form an arithmetic progression. Find the sum of the interior angles for a 21-sided polygon.
Solution:
Given the sum of interior angles of a polygon having ‘n’ sides is given by (n – 2) × 180°
Sum of angles with three sides that is n = 3 is (3 – 2) × 180° = 180°
Sum of angles with four sides that is n = 4 is (4 – 2) × 180° = 360°
Sum of angles with five sides that is n = 5 is (5 – 2) × 180° = 540°
Sum of angles with six sides that is n = 6 is (6 – 2) × 180° = 720°
As seen as the number of sides increases by 1 the sum of interior angles increases by 180°
Hence the sequence of sum of angles as number of sides’ increases is 180°, 360°, 540°, 720° …
The sequence is AP with first term as a = 180° and common difference as d = 180°
We have to find sum of angles of polygon with 21 sides
Using (n – 2) × 180°
⇒ Sum of angles of polygon having 21 sides = (21 – 2) × 180°
⇒ Sum of angles of polygon having 21 sides = 19 × 180°
⇒ Sum of angles of polygon having 21 sides = 3420°
Example 2. A side of an equilateral triangle is 20cm long. A second equilateral triangle is inscribed in it by joining the mid points of the sides of the first triangle. The process is continued as shown in the accompanying diagram. Find the perimeter of the sixth inscribed equilateral triangle.
Solution:
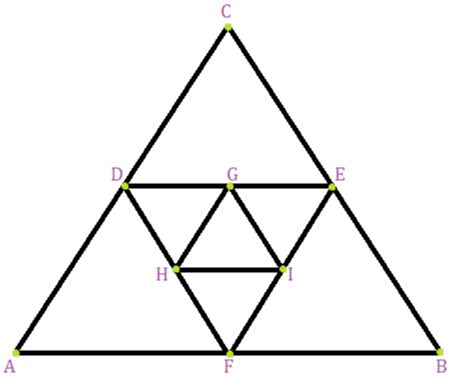
Let ABC be the triangle with AB = BC = AC = 20 cm
Let D, E and F be midpoints of AC, CB and AB respectively which are joined to form an equilateral triangle DEF
Now we have to find the length of side of ΔDEF
Consider ΔCDE
CD = CE = 10 cm … D and E are midpoints of AC and CB
Hence ΔCDE is isosceles
⇒ ∠CDE = ∠CED … base angles of isosceles triangle
But ∠DCE = 60° …∠ABC is equilateral
Hence ∠CDE = ∠CED = 60°
Hence ΔCDE is equilateral
Hence DE = 10 cm
Similarly, we can show that GH = 5 cm
Hence the series of sides of equilateral triangle will be 20, 10, 5 …
The series is GP with first term a = 20 and common ratio r = ½
To find the perimeter of 6th triangle inscribed we first have to find the side of 6th triangle that is the 6th term in the series
nth term in GP is given by tn = arn-1
⇒ t6 = (20) (1/2)6-1
⇒ t6 = 20/ 25
= 20/ (4 × 23)
⇒ t6 = 5/8
Hence the side of 6th equilateral triangle is 5/8 cm and hence its perimeter would be thrice its side length because it’s an equilateral triangle
Perimeter of 6th equilateral triangle inscribed is 3 × 5/8 = 15/8 cm
Example 3: Find the sum of GP: 10, 30, 90, 270 and 810, using formula.
Solution: Given GP is 10, 30, 90, 270 and 810
First term, a = 10
Common ratio, r = 30/10 = 3 > 1
Number of terms, n = 5
Sum of GP is given by;
Sn = a[(rn – 1)/(r – 1)]
S5 = 10[(35 – 1)/(3 – 1)]
= 10[(243 – 1)/2]
= 10[242/2]
= 10 × 121
= 1210
Check: 10 + 30 + 90 + 270 + 810 = 1210
Example 4: If 2, 4, 8,…., is the GP, then find its 10th term.
Solution: The nth term of GP is given by:
2, 4, 8,….
Here, a = 2 and r = 4/2 = 2
an = arn-1
Therefore,
a10 = 2 x 210 – 1
= 2 × 29
= 1024
Example 5. Find the sum of the following series up to n terms:
(i) 5 + 55 + 555 + … (ii) .6 + .66 + . 666 + …
Solution:
(i) Given, 5 + 55 + 555 + …
Let Sn = 5 + 55 + 555 + ….. up to n terms

(ii) Given, .6 + .66 + . 666 + …
Let Sn = 06. + 0.66 + 0.666 + … up to n terms

The Geometric Mean (G.M.) of a set of n observations is the nth root of their product. If x1, x2, ... , xn are n observations then
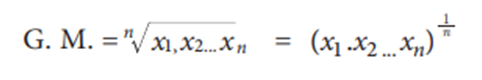
Example: If AM and HM of the data sets are 4 and 25 respectively, then find the GM.
Ans:
Given that, AM = 4
HM = 25.
We know that the relation between AM, GM and HM is
GM = √[ AM × HM]
Now, substitute AM and HM in the relation,
we get;
GM = √[4 × 25]
GM = √100 = 10
Hence, GM = 10.
4. Sum to n Terms of Special Series
- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
Sum to n Terms of Special Series
sum of first n terms of some special series,
(i) 1 + 2 + 3 +… + n (sum of first n natural numbers)
(ii) 12 + 22 + 32 +… + n2 (sum of squares of the first n natural numbers)
(iii) 13 + 23 + 33 +… + n3 (sum of cubes of the first n natural numbers).
Proof:
(i) 1 + 2 + 3 +… + n (sum of first n natural numbers)
Sum of First n Natural Numbers
Natural numbers are: 1, 2, 3, 4,….
Sum of these natural numbers can be written as: 1 + 2 + 3 + 4 +….
This is an AP with first term 1 and common difference 1.
i.e. a = 1 and d = 2 – 1 = 1
Sum of first n terms of an AP = n/2 [2a + (n – 1)d]
Now,
Sn = 1 + 2 + 3 + 4 + ….. + n
Sn = n/2 [2a + (n – 1)d]
Substituting a = 1 and d = 1,
Sn = (n/2) [2(1) + (n – 1)(1)]
= (n/2) [2 + n – 1]
= n(n + 1)/2
Therefore, the sum of first n natural numbers = n(n + 1)/2
Sum of Squares of The First n Natural Numbers
(ii) 12 + 22 + 32 +… + n2 (sum of squares of the first n natural numbers)
The squares of natural numbers are: 12, 22, 32, 42,…
Or
1, 4, 9, 16, ….
We can express the sum of n terms as: 12 + 22 + 32 +…+ n2
This is neither AP nor GP since either the difference between two consecutive numbers is not constant or the ratio of two consecutive numbers is constant.
Let’s find the sum of this series by considering an expression given below:
k3 – (k – 1)3 = 3k2 – 3k + 1
Substituting k = 1,
13 – (1 – 1)3 = 3(1)2 – 3(1) + 1
13 – 03 = 3(1)2 – 3(1) + 1….(i)
Substituting k = 2,
23 – (2 – 1)3 = 3(2)2 – 3(2) + 1
23 – 13 = 3(2)2 – 3(2) + 1….(ii)
Substituting k = 3,
33 – (3 – 1)3 = 3(3)2 – 3(3) + 1
33 – 23 = 3(3)2 – 3(3) + 1….(iii)
Substituting k = 4,
43 – (4 – 1)3 = 3(4)2 – 3(4) + 1
43 – 33 = 3(4)2 – 3(4) + 1….(iv)
Substituting k = n,
n3 – (n – 1)3 = 3(n)2 – 3(n) + 1
Now, adding both sides of these equations together, we get;
13 – 03 + 23 – 13 + 33 – 23 + … + n3 – (n – 1)3 = 3(12 + 22 + 32 + 42 + … + n2) – 3(1 + 2 + 3 + 4 + … + n) + n(1)
n3 – 03 = 3(12 + 22+ 32 + 42 + … + n2) – 3(1 + 2 + 3 + 4 + … + n) + n
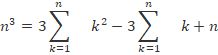
Here, ![]()
represents the sum of first n natural numbers and is equal to n(n + 1)/2.
So, ![]()
Rearranging the terms, ![]()
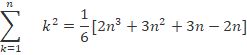
= (1/6) (2n3 + 3n2 + n)
= (1/6) [n(2n2 + 3n + 1)]
= (1/6)[n(n + 1)(2n + 1)]
Therefore, the sum of squares of first n natural numbers = [n(n + 1)(2n + 1)]/6
Sum of Cubes of The First n Natural Numbers
(iii) 13 + 23 + 33 +… + n3 (sum of cubes of the first n natural numbers).
The squares of natural numbers are: 13, 23, 33, 43,…
Or
1, 8, 27, 64,….
We can express the sum of n terms as: 13 + 23 + 33 +…+ n3
This is neither AP nor GP since either the difference between two consecutive numbers is not constant or the ratio of two consecutive numbers is constant.
Let’s find the sum of this series by considering an expression given below:
(k + 1)4 – k4 = 4k3 + 6k2 + 4k + 1
Substituting k = 1, 2, 3, …, n
24 – 14 = 4(1)3 + 6(1)2 + 4(1) + 1
34 – 24 = 4(2)3 + 6(2)2 + 4(2) + 1
44 – 34 = 4(3)3 + 6(3)2 + 4(3) + 1
(n – 1)4 – (n – 2)4 = 4(n – 2)3 + 6(n – 2)2 + 4(n – 2) + 1
n4 – (n – 1)4 = 4(n – 1)3 + 6(n – 1)2 + 4(n – 1) + 1
(n + 1)4 – n4 = 4n3 + 6n2 + 4n + 1
By adding both sides of these equations, we get;
24 – 14 + 34 – 24 + 44 – 34 + …. + (n + 1)4 – n4 = 4(1)3 + 6(1)2 + 4(1) + 1 + 4(2)3 + 6(2)2 + 4(2) + 1 + 4(3)3 + 6(3)2 + 4(3) + 1 + …. + 4n3 + 6n2 + 4n + 1
(n + 1)4 – 14 = 4(13 + 23 + 33 +…+ n3) + 6(12 + 22 + 32 + …+ n2) + 4(1 + 2 + 3 +…+ n) + n
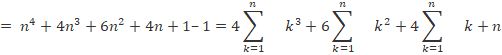
We know that, ![]()
And ![]()
Thus, ![]()
By rearranging the terms,
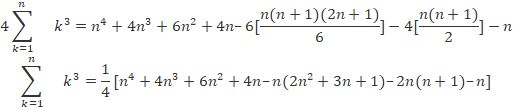
= (1/4) [n4 + 4n3 + 6n2 + 4n – 2n3 – 3n2 – n – 2n2 – 2n – n]
= (1/4) [n4 + 2n3 + n2]
= (1/4)[n2(n2 + 2n + 1)]
= (1/4)[n2(n + 1)2]
Therefore, the sum of cubes of first n natural numbers = [n(n + 1)]2/4
Question:
Find the sum to n terms of the series: 2 + 5 + 14 + 41 +….
Solution:
2 + 5 + 14 + 41 +….
The difference between two consecutive terms of this series is: 3, 9, 27, ….
Let Sn be the sum of its n terms and an be its nth term. Then,
Sn =2 + 5 + 14 + 41 + … + an….(i)
And
Sn = 2 + 5+ 14 + 41 + … + an – 1 + an….(ii)
Subtracting equation (ii) from (i), we get
0 = 2 + [3 + 9 + 27 + … + (n – 1) term] – an
⇒ an = 2 + [3 + 9 + 27 +… + (n- 1) term]
Here, 3 + 9 + 27 + … is a geometric series.
So, an = 2 + [3(3n-1 – 1)/2]
= [4 + 3n – 3]/2
= (1 + 3n)/2
Now, we need to find the sum of the series whose general term is (1 + 3n)/2
Sn = [(1 + 3)/2] + [(1 + 32)/2] + [(1 + 33)/2] + …. + (1 + 3n)/2
= (1/2) [(3 + 32 + 33 + …. + 3n) + (1 + 1 + 1 + … + n)]
= (1/2) {[3(3n – 1)/(3 – 1)] + n}
= (1/2) [(3/2)(3n – 1) + n]
= [(3n+1 – 3 + 2n)/4]
Therefore, the sum of the given series = (3n+1 + 2n – 3)/4
5. Infinite GM and its sum
- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
Infinite GM and its sum
The sum of an infinite Geometric Progression whose first term 'a' and common ratio 'r' (-1 < r < 1 i.e., |r| < 1) is
S = a/(1−r)
Proof:
A series of the form a + ar + ar22 + ...... + arnn + ............... ∞ is called an infinite geometric series.
Let us consider an infinite Geometric Progression with first term a and common ratio r, where -1 < r < 1 i.e., |r| < 1. Therefore, the sum of n terms of this Geometric Progression in given by
![]()
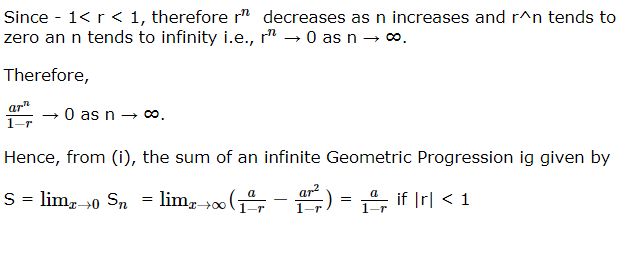
Example: Find the sum to infinity of the Geometric Progression
![]()
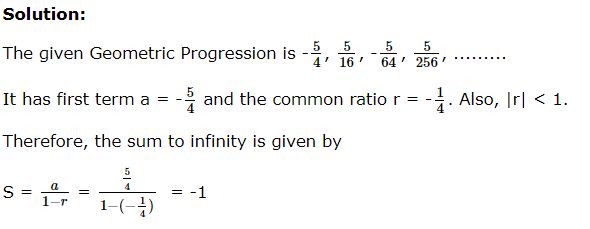
Example:. If the pth and qth terms of a G.P. are q and p respectively, show that its (p + q)th term is
Solution:

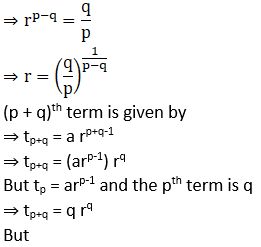
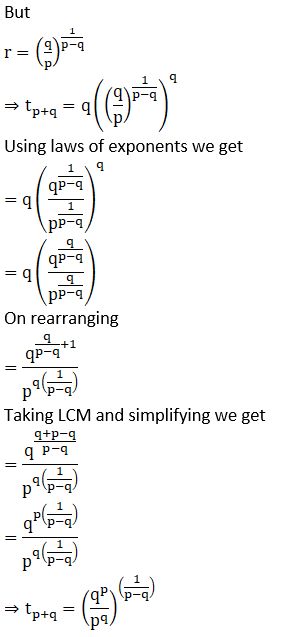
Hence the proof.
3. General and Middle Terms
- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
General and Middle Terms
General Term in binomial expansion:
We have (x + y)n = nC0 xn + nC1 xn-1 . y + nC2 xn-2 . y2 + … + nCn yn
General Term = Tr+1 = nCr xn-r . yr
- General Term in (1 + x)n is nCr xr
- In the binomial expansion of (x + y)n , the rth term from end is (n – r + 2)th .
Example: Find the number of terms in (1 + 2x +x2)50
Sol:
(1 + 2x + x2)50 = [(1 + x)2]50 = (1 + x)100
The number of terms = (100 + 1) = 101
Example: Find the fourth term from the end in the expansion of (2x – 1/x2)10
Sol:
Required term =T10 – 4 + 2 = T8 = 10C7 (2x)3 (−1/x2)7 = −960x-11
Middle Term(S) in the expansion of (x+y) n
- If n is even then (n/2 + 1) Term is the middle Term.
- If n is odd then [(n+1)/2]th and [(n+3)/2)th terms are the middle terms.
![]()
Example: Find the middle term of (1 −3x + 3x2 – x3)2n
Sol:
(1 − 3x + 3x2 – x3)2n = [(1 − x)3]2n = (1 − x)6n
Middle Term = [(6n/2) + 1] term = 6nC3n (−x)3n
Determining a Particular Term:
- In the expansion of(axp + b/xq)n the coefficient of xm is the coefficient of Tr+1 where r = [(np−m)/(p+q)]
- In the expansion of (x + a)n, Tr+1/Tr = (n – r + 1)/r . a/x
Independent Term
The term Independent of in the expansion of [axp + (b/xq)]n is
Tr+1 = nCr an-r br, where r = (np/p+q) (integer)
Example: Find the independent term of x in (x+1/x)6
Sol:
r = [6(1)/1+1] = 3
The independent term is 6C3 = 20
Example :In the expansion of (1 + a)m+n, prove that coefficients of am and an are equal.
Solution:
We know that the general term Tr+1 in the binomial expansion is given by Tr+1 = nCr an-r br
Here n= m+n, a = 1 and b= a
Substituting the values in the general form
Tr+1 = m+n Cr 1m+n-r ar
= m+n Cr ar…………. (i)
Now we have that the general term for the expression is,
Tr+1 = m+n Cr ar
Now, For coefficient of am
Tm+1 = m+n Cm am
Hence, for coefficient of am, value of r = m
So, the coefficient is m+n C m
Similarly, Coefficient of an is m+n C n
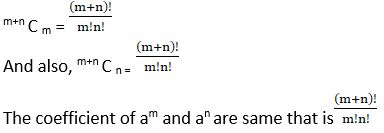
Example: Write the general term in the expansion of (x2 – y x)12, x ≠ 0.
Solution:
The general term Tr+1 in the binomial expansion is given by Tr+1 = n C r an-r br
Here n = 12, a= x2 and b = -y x
Substituting the values we get
Tn+1 =12Cr × x2(12-r) (-1)r yr xr
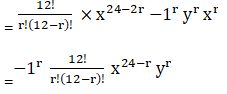
= -1r 12cr .x24 –2r. yr
Example: Which is larger (1.01)1000000 or 10,000?
Ans.:
Numerically greatest term in the expansion of (1+x)n:
- If [(n+1)|x|]/[|x|+1] = P, is a positive integer then Pth term and (P+1)th terms are numerically the greatest terms in the expansion of (1+x)n
- If[(n+1)|x|]/[|x|+1] = P + F, where P is a positive integer and 0 < F < 1 then (P+1)th term is numerically the greatest term in the expansion of (1+x)n.
Example: Find the numerically greatest term in (1-3x)10 when x = (1/2)
Sol:
[(n + 1)|α|] / [|α| + 1] = (11 × 3/2)/(3/2+1) = 33/5 = 6.6
Therefore, T7 is the numerically greatest term.
T6 + 1 = 10C6 . (−3x)6 = 10C6 . (3/2)6
Ratio of Consecutive Terms/Coefficients:
Coefficients of xr and xr + 1 are nCr – 1 and nCr respectively.
(nCr / nCr – 1) = (n – r + 1) / r
Example: If the coefficients of three consecutive terms in the expansion of (1+x)n are in the ratio 1:7:42 then find the value of n.
Sol:
Let (r – 1)th, (r)th and (r + 1)th be the three consecutive terms.
Then, the given ratio is 1:7:42
Now (nCr-2 / nCr – 1) = (1/7)
(nCr-2 / nCr – 1) = (1/7) ⇒ [(r – 1)/(n − r+2)] = (1/7) ⇒ n−8r+9=0 → (1)
And,
(nCr-1 / nCr) = (7/42) ⇒ [(r)/(n – r +1)] =(1/6) ⇒ n−7r +1=0 → (2)
From (1) & (2), n = 55
Applications of Binomial Theorem
Binomial theorem has a wide range of applications in Mathematics like finding the remainder, finding digits of a number, etc. The most common binomial theorem applications are:
Finding Remainder using Binomial Theorem
Example: Find the remainder when 7103 is divided by 25
Sol:
(7103 / 25) = [7(49)51 / 25)] = [7(50 − 1)51 / 25]
= [7(25K − 1) / 25] = [(175K – 25 + 25−7) / 25]
= [(25(7K − 1) + 18) / 25]
∴ The remainder = 18.
Example: If the fractional part of the number (2403 / 15) is (K/15), then find K.
Sol:
(2403 / 15) = [23 (24)100 / 15]
= 8/15 (15 + 1)100 = 8/ 15 (15λ + 1) = 8λ + 8/15
∵ 8λ is an integer, fractional part = 8/15
So, K = 8.
Finding Digits of a Number
Example: Find the last two digits of the number (13)10
Sol:
(13)10 = (169)5 = (170 − 1)5
= 5C0 (170)5 − 5C1 (170)4 + 5C2 (170)3 − 5C3 (170)2 + 5C4 (170) − 5C5
= 5C0 (170)5 − 5C1 (170)4 + 5C2 (170)3 − 5C3 (170)2 + 5(170) − 1
A multiple of 100 + 5(170) – 1 = 100K + 849
∴ The last two digits are 49.
Relation Between two Numbers
Example: Find the larger of 9950 + 10050 and 10150
Sol:
10150 = (100 + 1)50 = 10050 + 50 . 10049 + 25 . 49 . 10048 + …
⇒ 9950 = (100 − 1)50 = 10050 – 50 . 10049 + 25 . 49 . 10048 − ….
⇒ 10150 – 9950 = 2[50 . 10049 + 25(49) (16) 10047 + …]
= 10050 + 50 . 49 . 16 . 10047 + … >10050
∴ 10150 – 9950 > 10050
⇒ 10150 > 10050 + 9950
Divisibility Test
Example: Show that 119 + 911 is divisible by 10.
Sol:
119 + 911 = (10 + 1)9 + (10 − 1)11
= (9C0 . 109 + 9C1 . 108 + … 9C9) + (11C0 . 1011 − 11C1 . 1010 + … −11C11)
= 9C0 . 109 + 9C1 . 108 + … + 9C8 . 10 + 1 + 1011 − 11C1 . 1010 + … + 11C10 . 10−1
= 10[9C0 . 108 + 9C1 . 107 + … + 9C8 + 11C0 . 1010 − 11C1 . 109 + … + 11C10]
= 10K, which is divisible by 10.
Formulae:
- The number of terms in the expansion of (x1 + x2 + … xr)n is (n + r − 1)Cr – 1
- Sum of the coefficients of (ax + by)n is (a + b)n
If f(x) = (a0 + a1x + a2x2 + …. + amxm)n then
- (a) Sum of coefficients = f(1)
- (b) Sum of coefficients of even powers of x is: [f(1) + f(−1)] / 2
- (c) Sum of coefficients of odd powers of x is [f(1) − f(−1)] / 2
Multinomial Theorem
Using binomial theorem, we have
(x + a)n
=n∑r = 0nCr xn – r ar, n∈N
= n∑r = 0 [n! / (n − r)!r!] xn – rar
= n∑r + s =n [n! / r!s!] xs ar, where s = n – r.
This result can be generalized in the following form:
(x1 + x2 + … +xk)n
= ∑r1 + r2 + …. + rk = n [n! / r1!r2!…rk!] x1r1 x2r2 …xkrk
The general term in the above expansion is
[(n!) / (r1! r2! r3! … rk!)] x1r1 x2r2 x3r3… xkrk
The number of terms in the above expansion is equal to the number of non-negative integral solution of the equation.
r1+r2 + … + rk = n, because each solution of this equation gives a term in the above expansion. The number of such solutions is n + k – 1Ck −1.
PARTICULAR CASES
Case-1:
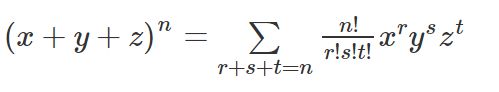
The above expansion has n+3-1C3-1 = n + 2C2 terms.
Case-2:
There are n + 4 – 1C4 – 1 = n + 3C3 terms in the above expansion.
REMARK: The greatest coefficient in the expansion of (x1 + x2 + … + xm)n is [(n!) / (q!)m – r{(q+1)!}r], where q and r are the quotient and remainder, respectively when n is divided by m.
Multinomial Expansions
Consider the expansion of (x + y + z)10. In the expansion, each term has different powers of x, y, and z and the sum of these powers is always 10.
One of the terms is λx2y3z5. Now, the coefficient of this term is equal to the number of ways 2x′s, 3y′s, and 5z′s are arranged, i.e., 10! (2! 3! 5!). Thus,
(x+y+z)10 = ∑(10!) / (P1! P2! P3!) xP1 yP2 zP3
Where P1 + P2 + P3 = 10 and 0 ≤ P1, P2, P3 ≥ 10
In general,
(x1 + x2 + … xr)n = ∑ (n!) / (P1! P2! … Pr!) xP1 xP2 … xPr
Where P1 + P2 + P3 + … + Pr = n and 0 ≤ P1, P2, … Pr ≥ n
Number of Terms in the Expansion of (x1 + x2 + … + xr)n
From the general term of the above expansion, we can conclude that the number of terms is equal to the number of ways different powers can be distributed to x1, x2, x3 …., xn such that the sum of powers is always “n”.
Number of non-negative integral solutions of x1 + x2 + … + xr = n is n +r – 1Cr – 1.
For example, number of terms in the expansion of (x + y + z)3 is 3 + 3 -1C3 – 1 = 5C2 = 10
As in the expansion, we have terms such as
As x0 y0 z0, x0 y1 z2, x0 y2 z1, x0 y3 z0, x1 y0 z2, x1 y1 z1, x1 y2 z0, x2 y0 z1, x2 y1 z0, x3 y0 z0.
Number of terms in (x + y + z)n is n + 3 – 1C3 – 1 = n + 2C2.
Number of terms in (x + y + z + w)n is n + 4 – 1C4 – 1 = n + 3C3 and so on.
Example. Show that 9n+1 – 8n – 9 is divisible by 64, whenever n is a positive integer.
Solution:
In order to show that 9n+1 – 8n – 9 is divisible by 64, it has to be show that 9n+1 – 8n – 9 = 64 k, where k is some natural number
Using binomial theorem,
(1 + a)m = mC0 + mC1 a + mC2 a2 + …. + m C m am
For a = 8 and m = n + 1 we get
(1 + 8)n+1 = n+1C0 + n+1C1 (8) + n+1C2 (8)2 + …. + n+1 C n+1 (8)n+1
9n+1 = 1 + (n + 1) 8 + 82 [n+1C2 + n+1C3 (8) + …. + n+1 C n+1 (8)n-1]
9n+1 = 9 + 8n + 64 [n+1C2 + n+1C3 (8) + …. + n+1 C n+1 (8)n-1]
9n+1 – 8n – 9 = 64 k
Where k = [n+1C2 + n+1C3 (8) + …. + n+1 C n+1 (8)n-1] is a natural number
Thus, 9n+1 – 8n – 9 is divisible by 64, whenever n is positive integer.
Hence the proof
Example. Find the expansion of (3x2 – 2ax + 3a2)3 using binomial theorem.
Solution:
We know that (a + b)3 = a3 + 3a2b + 3ab2 + b3
Putting a = 3x2 & b = -a (2x-3a), we get
[3x2 + (-a (2x-3a))]3
= (3x2)3+3(3x2)2(-a (2x-3a)) + 3(3x2) (-a (2x-3a))2 + (-a (2x-3a))3
= 27x6 – 27ax4 (2x-3a) + 9a2x2 (2x-3a)2 – a3(2x-3a)3
= 27x6 – 54ax5 + 81a2x4 + 9a2x2 (4x2-12ax+9a2) – a3 [(2x)3 – (3a)3 – 3(2x)2(3a) + 3(2x)(3a)2]
= 27x6 – 54ax5 + 81a2x4 + 36a2x4 – 108a3x3 + 81a4x2 – 8a3x3 + 27a6 + 36a4x2 – 54a5x
= 27x6 – 54ax5+ 117a2x4 – 116a3x3 + 117a4x2 – 54a5x + 27a6
Thus, (3x2 – 2ax + 3a2)3
= 27x6 – 54ax5+ 117a2x4 – 116a3x3 + 117a4x2 – 54a5x + 27a6

 KRISHNA PUBLICATIONS
KRISHNA PUBLICATIONS