Chapter 7: Permutation and Combinations

Chapter 7

Permutation and Combinations

Fundamental Principle of Counting:

If one experiment has n possible outcomes and another experiment has m possible outcomes, then there are m × n possible outcomes when both of these experiments are performed simultaneously. 

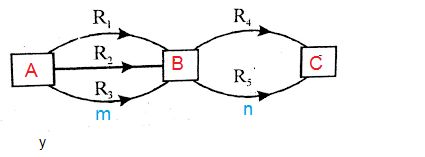
In other words, suppose a job has n parts and the job will be completed only when each part is completed. Further, it is known that the first part can be completed in a₁ ways, the second part can be completed in a₂ ways and so on ...... the nth part can be completed in a_n ways. Then the total number of ways of doing the job is a₁a₂a₃ ... a_n. This is also known as the rule of product.

Note:

• Fundamental Principal of Counting (FPC) is used to calculate the possibilities of an event without actually counting them.
• Basic steps to be used while applying the FPC:

1. Try to identify the independent events involved in a given problem.

2. Find the number of ways of performing or possibilities of occurrence of an event.

3. Multiply these numbers to get the total number of ways of occurrence of these events.

Example 1:

Suppose you have 33 shirts (call them A , B , and C ), and 44 pairs of pants (call them w , x , y , and z ).

Ans.: Then you have

3×4=12

possible outfits:

Aw, Ax, Ay, Az, Bw, Bx, By, Bz, Cw, Cx, Cy, Cz

Example 2:

Suppose you roll a 6 -sided die and draw a card from a deck of 52 cards. There are 6 possible outcomes on the die, and 52 possible outcomes from the deck of cards.

Ans.:

So, there are a total of

6×52=312

possible outcomes of the experiment.

Generalisation of the Addition and the Product Rule

In general, if there are several mutually exclusive events P₁, P₂, P₃, P₄……P_n…etc. with the respective number of ways given as n (P₁), n(P₂), n(P₃), n(P₄)….n(P_n),  then the number of ways in which either P₁ and P₂ and ….. … P_n can occur is given by,

n(E) = n(P₁) + n(P₂) …….. + n(P_n)

Similarly, if there are several mutually independent events P₁, P₂, P₃, P₄……P_n…etc. with the respective number of ways given as n (P₁), n(P₂), n(P₃), n(P₄)….n(P_n), then the number of ways in which  P₁ and P₂ and ….. … P_n  can occur is given by,

n(E) = n(P₁) × n(P₂) …….. × n(P_n)

We must note that all the possible number of ways derived thus, all of them will represent the unique and distinct ways in which the event E will take place.

Event and Its Trials

Suppose we have an event E with ‘m’ possible outcomes. If we conduct this event n number of times, then the number of outcomes of ‘n trials of the event’ will be, mⁿ

Clearly, this is only valid when all the outcomes of the experiment/event E are independent of each other. This would ensure that everytime the event takes place, any of its outcomes are possible.

Question : A coin is tossed 50 times. What is the number of possible outcomes of this experiment?

Answer : A coin toss has two possible outcomes: ‘A heads’ or ‘A tails’. Every toss of the coin is independent of every other toss of the coin, since whenever you toss the coin; there would be two possible outcomes with equal probability. Thus, the no. of possible outcomes of the experiment = 2⁵⁰

Question :

How many 3-digit numbers can be formed from the digits 1, 2, 3, 4 and 5 assuming that

(i) repetition of the digits is allowed?

(ii) repetition of the digits is not allowed?

ANSWER:

(i)

There will be as many ways as there are ways of filling 3 vacant places

 in succession by the given five digits. In this case, repetition of digits is allowed. Therefore, the units place can be filled in by any of the given five digits. Similarly, tens and hundreds digits can be filled in by any of the given five digits.

Thus, by the multiplication principle, the number of ways in which three-digit numbers can be formed from the given digits is 5 × 5 × 5 = 125

(ii)

In this case, repetition of digits is not allowed. Here, if units place is filled in first, then it can be filled by any of the given five digits. Therefore, the number of ways of filling the units place of the three-digit number is 5.

Then, the tens place can be filled with any of the remaining four digits and the hundreds place can be filled with any of the remaining three digits.

Thus, by the multiplication principle, the number of ways in which three-digit numbers can be formed without repeating the given digits is 5 × 4 × 3 = 60

Question :

A coin is tossed 3 times and the outcomes are recorded. How many possible outcomes are there?

ANSWER:

When a coin is tossed once, the number of outcomes is 2 (Head and tail) i.e., in each throw, the number of ways of showing a different face is 2.

Thus, by multiplication principle, the required number of possible outcomes is 2 × 2 × 2 = 8

Permutations and Factorial notation

Factorial notation:    

n! = n(n-1)(n-2) (n-3) …….2x1

n! = n(n-1)! = n(n-1)(n-2)!

0! = 1

1! = 1

5! = 4! x 5  = 3 ! x 4x 5

Question 1: Evaluate  (i) 8! (ii) 4! – 3!

ANSWER:

(i) 8! = 1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 = 40320

(ii) 4! = 1 × 2 × 3 × 4 = 24

3! = 1 × 2 × 3 = 6

∴4! – 3! = 24 – 6 = 18
Question 2: Is 3! + 4! = 7!?

ANSWER:

3! = 1 × 2 × 3 = 6

4! = 1 × 2 × 3 × 4 = 24

∴3! + 4! = 6 + 24 = 30

7! = 1 × 2 × 3 × 4 × 5 × 6 × 7 = 5040

∴ 3! + 4! ≠ 7!

Question 3:  Compute 

ANSWER:

Question 4: If , find x.

ANSWER:

Question 4. How many 5-digit telephone numbers can be constructed using the digits 0 to 9 if each number starts with 67 and no digit appears more than once?

Solution:

Let the five-digit number be ABCDE. Given that first 2 digits of each number is 67. Therefore, the number is 67CDE.

As the repetition is not allowed and 6 and 7 are already taken, the digits available for place C are 0,1,2,3,4,5,8,9. The number of possible digits at place C is 8. Suppose one of them is taken at C, now the digits possible at place D is 7. And similarly, at E the possible digits are 6.

∴The total five-digit numbers with given conditions = 8 × 7 × 6 = 336.

Question 5. A coin is tossed 3 times and the outcomes are recorded. How many possible outcomes are there?

Solution:

Given A coin is tossed 3 times and the outcomes are recorded

The possible outcomes after a coin toss are head and tail.

The number of possible outcomes at each coin toss is 2.

∴The total number of possible outcomes after 3 times = 2 × 2 × 2 = 8.

Question 6. Given 5 flags of different colours, how many different signals can be generated if each signal requires the use of 2 flags, one below the other?

Solution:

Given 5 flags of different colours

We know the signal requires 2 flags.

The number of flags possible for upper flag is 5.

Now as one of the flag is taken, the number of flags remaining for lower flag in the signal is 4.

The number of ways in which signal can be given = 5 × 4 = 20.

Question 7. Evaluate
(i) 8!

(ii) 4! – 3!

Solution:

(i) Consider 8!

We know that 8! = 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1

= 40320

(ii) Consider 4!-3!

4!-3! = (4 × 3!) – 3!

Above equation can be written as

= 3! (4-1)

= 3 × 2 × 1 × 3

= 18

2. Is 3! + 4! = 7!?

Solution:

Consider LHS 3! + 4!

Computing left hand side, we get

3! + 4! = (3 × 2 × 1) + (4 × 3 × 2 × 1)

= 6 + 24

= 30

Again consider RHS and computing we get

7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040

Therefore LHS ≠ RHS

Therefore 3! + 4! ≠ 7!

Permutations:

A permutation is an arrangement in a definite order of a number of objects taken some or all at a time.

Permutations when all the objects are distinct:

Theorem 1: The number of permutations of n different objects taken r at a time,

where 0 < r n and the objects do not repeat is n ( n – 1) ( n – 2). . .( n – r + 1),

which is denoted by nPr.

Proof There will be as many permutations as there are ways of filling in r vacant places

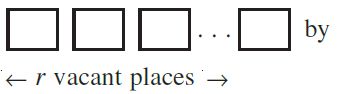
the n objects. The first place can be filled in n ways; following which, the second placecan be filled in (n – 1) ways, following which the third place can be filled in (n – 2)ways,..., the rth place can be filled in (n – (r – 1)) ways. Therefore, the number of ways of filling in r vacant places in succession is n(n – 1) (n – 2) . . . (n – (r – 1)) or n ( n – 1) (n – 2) ... (n – r + 1)

= [n ( n – 1) (n – 2) ... (n – r + 1)(n-r)! ] / (n-r)!  = ⁿp_r = p(n,r)

ⁿp_r =n!n-r! , where 0 < r n

ⁿp_n =n!n!=1

ⁿp₀ =n!0! =n!

Theorem 2 : The number of permutations of n different objects taken r at a time,

where repetition is allowed, is n^r.

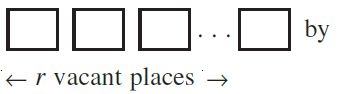
i.e., n x n x n x n x n x…r times….x n= n^r

Example: Find the number of 4 letter words, with or without meaning, which can be

formed out of the letters of the word ROSE.

Ans:

The required number of words = ⁴P4 = 4! = 24. Here repetition is not allowed.

If repetition is allowed, the required number of words would be 4⁴ = 256.

Example: The number of 3-letter words which can be formed by the letters of the word

NUMBER =⁶P₃ = 6!/3!= 4 × 5 × 6 = 120.

Here, in this case also, the repetition is not allowed.

 If the repetition is allowed, the required number of words would be 6³ = 216.

Example:

The number of ways in which a Chairman and a Vice-Chairman can be chosen

from amongst a group of 12 persons assuming that one person can not hold more than

one position, clearly ¹²P₂= 12!/10! =11x12=132

Permutations when all the objects are not distinct objects:

Example:

Suppose we have to find the number of ways of rearranging the letters of the word ROOT.

Therefore, the required number of permutations = 4!/2! =3x4= 12

Theorem 3: The number of permutations of n objects, where p objects are of the same kind and rest are all different = n!/p!

Theorem 4: The number of permutations of n objects, where p1 objects are of one

kind, p2 are of second kind, ..., p_k are of k^th kind and the rest, if any, are of different kind is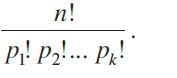  

Example  Find the number of permutations of the letters of the word ALLAHABAD.

Solution Here, there are 9 objects (letters) of which there are 4A’s, 2 L’s and rest are

all different.

Therefore, the required number of arrangements =9!/(4!x2!)= 5x 6 x 7 x 8 x 9  / 2 =7560

Example: 

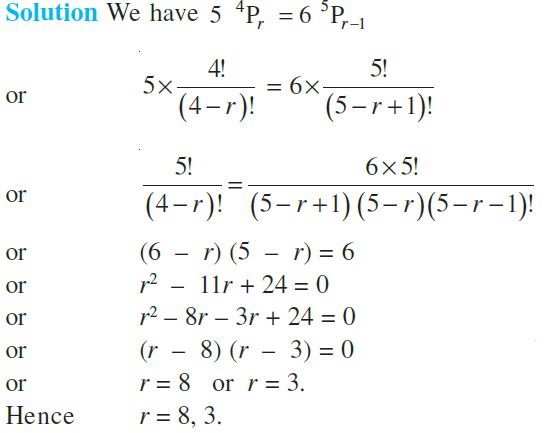
Example: How many words, with or without meaning can be made from the letters of the word MONDAY, assuming that no letter is repeated, if

(i) 4 letters are used at a time, 

(ii) all letters are used at a time, 

(iii) all letters are used but the first letter is a vowel?

Solution:

Given word: MONDAY

(i) Number of letters to be used = 4

Number of permutations = ⁶P₄ = 6!/(6 – 4)! = 6!/2! = 720/2 = 360

Therefore, we can form 350 words with 4 letters from the word MONDAY.

(ii) Number of letters to be used = 6

Number of permutations = ⁶P₆ = 6!/(6 – 6)! = 6!/0! = 720/1 = 720

Therefore, we can form 720 words using all the letters from the word MONDAY.

(iii) Number of vowels in the word MONDAY = 2 (O and A)

Number of ways that the first letter is a vowel = ²P₁ = 2!/(2 – 1)! = 2!/1! = 2

Now, the remaining places = 5

Remaining letters  = 5

These can be arranged in 5! ways, i.e. 120

Therefore, the total number of words can be formed with the first letter as vowel = 2 × 120 = 240.

N.B.:

• Almost all permutation questions involve putting things in order from a line where the order matters. For example ABC is a different permutation to ACB.
• The number of permutations of n distinct objects when a particular object is not to be considered in the arrangement is given by ^n-1P_r.
• The number of permutations of n distinct objects when a specific object is to be always included in the arrangement is given by r.^n-1P_r-1.
• If we need to compute the number of permutations of n different objects, out of which r have to be selected and each object has the probability of occurring once, twice or thrice… up to r times in any arrangement is given by (n)^r.
• Circular permutation is used when some arrangement is to be made in the form of a ring or circle.
• When ‘n’ different or unlike objects are to be arranged in a ring in such a way that the clockwise and anticlockwise arrangements are different, then the number of such arrangements is given by (n – 1)!
• If r things are taken at a time out of n distinct things and arranged along a circle, then the number of ways of doing this is given by ⁿC_r(r-1)!.
• If clockwise and anti-clockwise are considered to be the same, then the total number of circular permutations is given by (n-1)!/2.
• If n persons are to be seated around a round table in such a way that no person has similar neighbor then it is given by ½ (n – 1)!
• The number of necklaces formed with n beads of different colors = ½ (n – 1)!

Combinations and Simple applications

Combinations:

Let us now assume that there is a group of 3 lawn tennis players X, Y, Z. A team consisting of 2 players is to be formed. In how many ways can we do so? Is the team of X and Y different from the team of Y and X ? Here, order is not important.

These are XY, YZ and ZX.

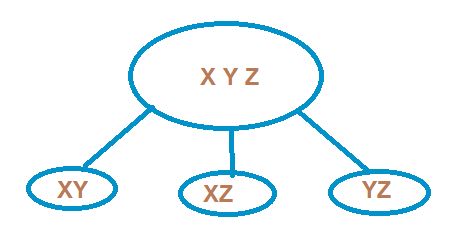
Here, each selection is called a combination of 3 different objects taken 2 at a time.

Definition:

The combination is a selection of a part of a set of objects or a selection of all objects when the order doesn't matter.

or

The number of combinations/selection of n different objects taken r at a time, denoted by ⁿC_r

^{Theorem:   n}P_r= r! . ⁿC_r  , 0 < r  n

Proof: Corresponding to each combination of nCr, we have r ! permutations, because r objects in every combination can be rearranged in r ! ways.

Hence, the total number of permutations of n different things taken r at a time is ⁿP_r= r! . ⁿC_r  .

Properties:

1. ⁿC_r = ⁿC_n-r

2. If ⁿC_r = ⁿC_k, then r = k or n-r = k

3. ⁿC_r + ⁿC_r-1 = ⁿ⁺¹C_r

4. ⁿC_r = n/r  ^n-1C_r-1

5. ⁿC_r/ⁿC_r-1 = (n-r+1)/ r

6. If n is even ⁿC_r is greatest for r = n/2

7. If n is odd, ⁿC_r is greatest for r = (n-1)/2,(n+1)/2

Example; ⁿC₉ = ⁿC₈ then n=?  and ⁿC₁₇=?

Ans: n = a+b = 9+8 =17

ⁿC₁₇= ¹⁷C₁₇=1

Question. In how many ways can a football team of 11 players be selected from 16 players? How many of them will
(i) include 2 particular players?
(ii) exclude 2 particular players?

Solution:

We know that,

ⁿC_r 

According to the question,

11 players can be selected out of 16 = ¹⁶C₁₁

(i) include 2 particular players = ¹⁴C₉

(ii) exclude 2 particular players = ¹⁴C₁₁

Question : Find the number of ways of choosing 4 cards from a pack of 52 playing cards? In how many of these

(i) four cards are of the same suit,

(ii) four cards belong to four different suits,

(iii) are face cards,

(iv) two are red and two are black cards,

(v) cards are of the same colour?

Solution :

There will be a number of possible ways for choosing 4 cards from 52 cards as there are combinations of 52 different things when we take 4 at a time.

Therefore, the required number of ways = ⁵²C₄

= 52! / (4! 48!) = (49x50x51x52) / (2x3x4)

= 270725

(i) Four cards of the same suit:

There are four suits: Spade, heart, Club, diamond. Totally, there are 13 cards of each suit

Therefore, the required number of ways are given by ¹³C₄ + ¹³C₄ + ¹³C₄ + ¹³C₄

= 4(13! / (4! 9! )) = 2860

(ii) four cards belong to four different suits:

Since there are 13 cards in each suit. Therefore choosing 1 card from 13 cards of each suit, it becomes

= ¹³C₁ + ¹³C₁ + ¹³C₁ + ¹³C₁ = 13⁴

(iii) Face cards :

There are 12 face cards and 4 cards are selected from these 12 cards, it becomes

= ¹²C₄

Therefore, the required number of ways = 12! / ( 4! 8!) = 495

(iv) Two red cards and two black cards:

There are 26 red and 26 black cards in a pack of52 cards.

Therefore, the required number of ways = ²⁶C₂ x ²⁶C₂

=

= (325)²

=105625

(v) Cards of the same color:

Out of 26 red cards and 26 black cards, 4 red and black cards are selected in ²⁶C₄ ways. So, the required number of ways = ²⁶C₄ + ²⁶C₄

= 2 (26! / 4! 22! )

=29900.

Question: If the different permutations of all the letter of the word EXAMINATION are listed as in a dictionary, how many words are there in this list before the first word starting with E?

Solution:

In dictionary words are listed alphabetically, so to find the words

Listed before E should start with letter either A, B, C or D

But the word EXAMINATION doesn`t have B, C or D

Hence the words should start with letter A

The remaining 10 places are to be filled by the remaining letters of the word EXAMINATION which are E, X, A, M, 2N, T, 2I, 0

Since the letters are repeating the formula used would be

Where n is remaining number of letters p₁ and p₂ are number of times the repeated terms occurs.

The number of words in the list before the word starting with E

= words starting with letter A = 907200

N.B.:

• The number of ways of selecting r objects from n different objects subject to certain condition like:

1. k particular objects are always included =  ^n-kC_r-k

2. k particular objects are never included =  ^n-kC_r

• The number of arrangement of n distinct objects taken r at a time so that k particular objects are

        (i) Always included = ^n-kC_r-k.r!,

        (ii) Never included = ^n-kC_r.r!.

• In order to compute the combination of n distinct items taken r at a time wherein, the chances of occurrence of any item are not fixed and may be one, twice, thrice, …. up to r times is given by ^n+r-1C_r
• If there are m men and n women (m > n) and they have to be seated or accommodated in a row in such a way that no two women sit together then total no. of such arrangements = ^m+1C_n. m! This is also termed as the Gap Method. 
• If we have n different things taken r at a time in form of a garland or necklace, then the required number of arrangements is given by ⁿC_r(r-1)!/2.
• If there is a problem that requires n number of persons to be accommodated in such a way that a fixed number say ‘p’ are always together, then that particular set of p persons should be treated as one person. Hence, the total number of people in such a case becomes (n-m+1). Therefore, the total number of possible arrangements is (n-m+1)! m! This is also termed as the String Method.  
• Let there be n types of objects with each type containing at least r objects. Then the number of ways of arranging r objects in a row is n^r. 
• The number of selections from n different objects, taking at least one =  ⁿC₁ + ⁿC₂ + ⁿC₃ + ... + ⁿC_n = 2ⁿ - 1.  
• Total number of selections of zero or more objects from n identical objects is n+1.
• Selection when both identical and distinct objects are present: 

The number of selections, taking at least one out of a₁ + a₂ + a₃ + ... a_n + k objects, where a₁ are alike (of one kind), a₂ are alike (of second kind) and so on ... a_n are alike (of nth kind), and k are distinct = {[(a₁ + 1)(a₂ + 1)(a₃ + 1) ... (a_n + 1)]2^k} - 1.

• Combination of n different things taken some or all of n things at a time is given by 2ⁿ – 1. 
• Combination of n things taken some or all at a time when p of the things are alike of one kind, q of the things are alike and of another kind and r of the things are alike of a third kind = [(p + 1) (q + 1)(r + 1)….] – 1.
• The number of ways to select some or all out of (p+q+t) things where p are alike of first kind, q are alike of second kind and the remaining t are different is = (p+1)(q+1)2^t – 1.
• Combination of selecting s₁ things from a set of n₁ objects and s₂ things from a set of n₂ objects where combination of s₁ things and s₂ things are independent is given by ⁿ₁C_s1 x ⁿ₂C_s2  
• Total number of ways in which n identical items which can be distributed among p persons so that each person may get any number of items is ^n+p-1C_p-1.
• Total number of ways in which n identical items can be distributed among p persons such that each them receive at least one item ^n-1C_p-1