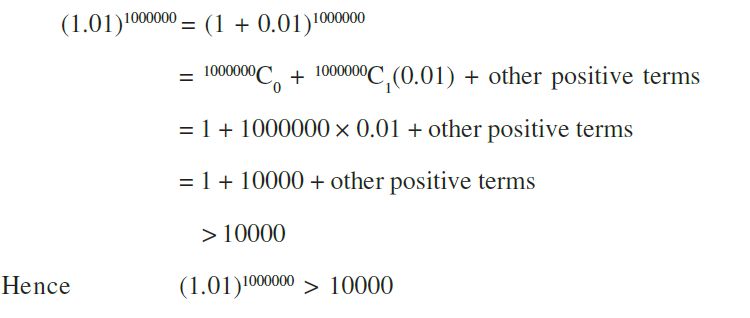Chapter 8: Binomial Theorem

Chapter 8

Binomial Theorem

Binomial Theorem for Positive Integral Indices:

The Binomial Theorem is the method of expanding an Binomial expression that has been raised to any finite power.

Binomial Expression: A binomial expression is an algebraic expression that contains two dissimilar terms. Ex: a + b, a³ + b³,a-b, etc.

The binomial theorem states a formula for the expression of the powers of sums.

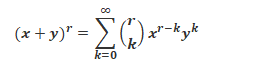
From the above representation, we can expand (a + b)ⁿ as given below:

(a + b)ⁿ = ⁿC₀ aⁿ + ⁿC₁ a^n-1 b + ⁿC₂ a^n-2 b² + … + ⁿC_n-1 a b^n-1 + ⁿC_n bⁿ

This is the binomial theorem formula for any positive integer n.

 

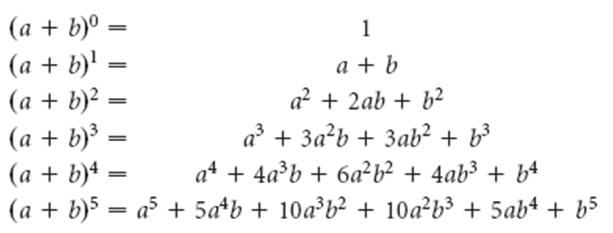
Some special cases from the binomial theorem can be written as:

• (x + y)ⁿ = ⁿC₀ xⁿ + ⁿC₁ x^n-1 by+ ⁿC₂ x^n-2 y² + … + ⁿC_n-1 x y^n-1 + ⁿC_n xⁿ
• (x – y)ⁿ = ⁿC₀ xⁿ – ⁿC₁ x^n-1 by + ⁿC₂ x^n-2 y² + … + (-1)^n nC_n xⁿ
• (1 – x)ⁿ = ⁿC₀ – ⁿC₁ x + ⁿC₂ x² – …. (-1)^n nC_n xⁿ

Also, ⁿC₀ = ⁿC_n = 1

However, there will be (n + 1) terms in the expansion of (a + b)ⁿ.

Example: (√2 + 1)⁵ + (√2 − 1)⁵

Sol:

We have

(x + y)⁵ + (x – y)⁵ = 2[5C₀  x⁵ + 5C₂  x³ y²  +  5C₄ xy⁴]

= 2(x⁵ + 10 x³ y² + 5xy⁴)

Now (√2 + 1)⁵ + (√2 − 1)⁵ = 2[(√2)⁵ + 10(√2)³(1)² + 5(√2)(1)⁴]

=58√2

 

Properties:

• The total number of terms in the expansion of (x+y)ⁿ  are (n+1)
• The sum of exponents of x and y is always n.
• ⁿC₀, ⁿC₁, ⁿC₂, … .., ⁿC_n are called binomial coefficients and also represented by C₀, C₁, C₂, ….., C_n
• The binomial coefficients which are equidistant from the beginning and from the ending are equal i.e. ⁿC₀ = ⁿC_n, ⁿC₁ = ⁿC_n-1 , ⁿC₂ = ⁿC_n-2 ,….. etc.

Some other  expansions:

• (x + y)ⁿ + (x−y)ⁿ = 2[C₀ xⁿ + C₂ x^n-1 y² + C₄ x^n-4 y⁴ + …]
• (x + y)ⁿ – (x−y)ⁿ = 2[C₁ x^n-1 y + C₃ x^n-3 y³ + C₅ x^n-5 y⁵ + …]
• (1 + x)ⁿ  = ⁿΣ_r-0 ⁿC_r . x^r = [C₀ + C₁ x + C₂ x² + … C_n x_n]
• (1+x)ⁿ + (1 − x)ⁿ = 2[C₀ + C₂ x²+C₄ x⁴ + …]
• (1+x)ⁿ − (1−x)ⁿ = 2[C₁ x + C₃ x³ + C₅ x⁵ + …]
• The number of terms in the expansion of (x + a)ⁿ + (x−a)ⁿ are (n+2)/2 if “n” is even or (n+1)/2 if “n” is odd.
• The number of terms in the expansion of (x + a)ⁿ − (x−a)ⁿ  are (n/2) if “n” is even or (n+1)/2 if “n” is odd.

Question: Find the 4th term in the expansion of (x – 2y)¹².

Solution:

The general term T_r+1 in the binomial expansion is given by T_r+1 = ⁿ C _r a^n-r b^r

Here a= x, n =12, r= 3 and b = -2y

By substituting the values we get

T₄ = ¹²C₃ x⁹ (-2y)³

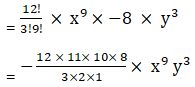
= -1760 x⁹ y³

Pascal’s triangle

An expression consisting of two terms, connected by + or – sign is called binomial expression. Binomial Theorem. If a and b are real numbers and n is a positive integer, then. The general term of (r + 1)^th term in the expression is given by. T_r+1 = ⁿC_r a^n-r b^r.

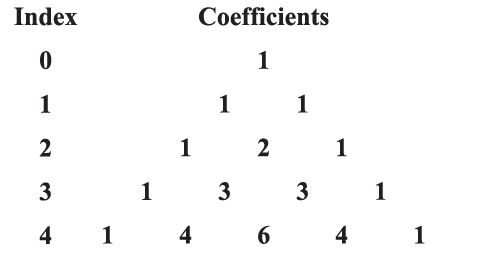
Example: (a + b)⁷ = ⁷C₀ a⁷+ ⁷C₁a⁶b + ⁷C₂a⁵b² + ⁷C₃a⁴b³ + ⁷C₄a³b⁴ + ⁷C₅a²b⁵ + ⁷C₆ab⁶ + ⁷C₇b⁷

General and Middle Terms

General Term in binomial expansion:

We have (x + y)ⁿ = ⁿC₀ xⁿ + ⁿC₁ x^n-1 . y + ⁿC₂ x^n-2 . y² + … + ⁿC_n yⁿ

General Term = T_r+1 = ⁿC_r x^n-r . y^r

• General Term in (1 + x)ⁿ is nC_r x^r
• In the binomial expansion of (x + y)ⁿ , the r^th term from end is (n – r + 2)^th .

Example: Find the number of terms in (1 + 2x +x²)⁵⁰

Sol:

(1 + 2x + x²)⁵⁰ = [(1 + x)²]⁵⁰ = (1 + x)¹⁰⁰

The number of terms = (100 + 1) = 101

Example: Find the fourth term from the end in the expansion of (2x – 1/x²)¹⁰

Sol:

Required term =T_{10 – 4 + 2} = T₈ = ¹⁰C₇ (2x)³ (−1/x²)⁷ = −960x^-11

 

Middle Term(S) in the expansion of (x+y^) n

• If n is even then (n/2 + 1) Term is the middle Term.
• If n is odd then [(n+1)/2]^th and [(n+3)/2)^th terms are the middle terms.

i.e., (n+12)thterm and (n+12+1)thterm

Example: Find the middle term of (1 −3x + 3x² – x³)²ⁿ

Sol:

(1 − 3x + 3x² – x³)²ⁿ = [(1 − x)³]²ⁿ = (1 − x)⁶ⁿ

Middle Term = [(6n/2) + 1] term = 6nC_3n (−x)³ⁿ

Determining a Particular Term:

• In the expansion of(ax^p + b/x^q)ⁿ the coefficient of x^m is the coefficient of T_r+1 where r = [(np−m)/(p+q)]
• In the expansion of (x + a)ⁿ, T_r+1/T_r = (n – r + 1)/r . a/x

Independent Term

The term Independent of in the expansion of [ax^p + (b/x^q)]ⁿ is

T_r+1 = ⁿC_r a^n-r b^r, where r = (np/p+q) (integer)

Example: Find the independent term of x in (x+1/x)⁶

Sol:

r = [6(1)/1+1] = 3

The independent term is 6C₃ = 20

Example :In the expansion of (1 + a)^m+n, prove that coefficients of a^m and aⁿ are equal.

Solution:

We know that the general term T_r+1 in the binomial expansion is given by T_r+1 = ⁿC_r a^n-r b^r

Here n= m+n, a = 1 and b= a

Substituting the values in the general form

T_r+1 = ^m+n C_r 1^m+n-r a^r

= ^m+n C_r a^r…………. (i)

Now we have that the general term for the expression is,

T_r+1 =  ^m+n C_r a^r

Now, For coefficient of a^m

T_m+1 =  ^m+n C_m a^m

Hence, for coefficient of a^m, value of r = m

So, the coefficient is ^m+n C _m

Similarly, Coefficient of aⁿ is ^m+n C _n

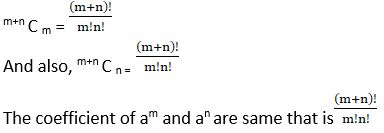
Example: Write the general term in the expansion of (x² – y x)¹², x ≠ 0.

Solution:

The general term T_r+1 in the binomial expansion is given by T_r+1 = ⁿ C _r a^n-r b^r

Here n = 12, a= x² and b = -y x

Substituting the values we get

T_n+1 =¹²C_r × x^2(12-r) (-1)^r y^r x^r

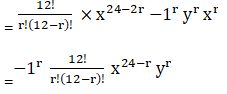
= -1^{r 12}c_r .x^{24 –2r}. y^r

Example: Which is larger (1.01)^1000000 or 10,000?

Ans.:

Numerically greatest term in the expansion of (1+x)ⁿ:

• If [(n+1)|x|]/[|x|+1] = P, is a positive integer then P^th term and (P+1)^th terms are numerically the greatest terms in the expansion of (1+x)ⁿ
• If[(n+1)|x|]/[|x|+1] = P + F, where P is a positive integer and 0 < F < 1 then (P+1)^th term is numerically the greatest term in the expansion of (1+x)ⁿ.

Example: Find the numerically greatest term in (1-3x)¹⁰ when x = (1/2)

Sol:

[(n + 1)|α|] / [|α| + 1] = (11 × 3/2)/(3/2+1) = 33/5 = 6.6

Therefore, T₇ is the numerically greatest term.

T_{6 + 1} = 10C₆ . (−3x)⁶ = 10C₆ . (3/2)⁶

Ratio of Consecutive Terms/Coefficients:

Coefficients of x^r and x^{r + 1} are ⁿC_{r – 1} and nC_r respectively.

(ⁿC_r / ⁿC_{r – 1}) = (n – r + 1) / r

Example: If the coefficients of three consecutive terms in the expansion of (1+x)ⁿ are in the ratio 1:7:42 then find the value of n.

Sol:

Let (r – 1)^th, (r)^th and (r + 1)^th be the three consecutive terms.

Then, the given ratio is 1:7:42

Now (ⁿC_r-2 / ⁿC_{r – 1}) = (1/7)

(ⁿC_r-2 / ⁿC_{r – 1}) = (1/7) ⇒ [(r – 1)/(n − r+2)] = (1/7) ⇒ n−8r+9=0 → (1)

And,

(ⁿC_r-1 / ⁿC_r) = (7/42) ⇒ [(r)/(n – r +1)] =(1/6) ⇒ n−7r +1=0 → (2)

From (1) & (2), n = 55

Applications of Binomial Theorem

Binomial theorem has a wide range of applications in Mathematics like finding the remainder, finding digits of a number, etc. The most common binomial theorem applications are:

Finding Remainder using Binomial Theorem

Example: Find the remainder when 7¹⁰³ is divided by 25

Sol:

(7¹⁰³ / 25) = [7(49)⁵¹ / 25)] = [7(50 − 1)⁵¹ / 25]

= [7(25K − 1) / 25] = [(175K – 25 + 25−7) / 25]

= [(25(7K − 1) + 18) / 25]

∴ The remainder = 18.

Example: If the fractional part of the number (2⁴⁰³ / 15) is (K/15), then find K.

Sol:

(2⁴⁰³ / 15) = [2³ (2⁴)¹⁰⁰ / 15]

= 8/15 (15 + 1)¹⁰⁰ = 8/ 15 (15λ + 1) = 8λ + 8/15

∵ 8λ is an integer, fractional part = 8/15

So, K = 8.

Finding Digits of a Number

Example: Find the last two digits of the number (13)¹⁰

Sol:

(13)¹⁰ = (169)⁵ = (170 − 1)⁵

= 5C₀ (170)⁵ − 5C₁ (170)⁴ + 5C₂ (170)³ − 5C₃ (170)² + 5C₄ (170) − 5C₅

= 5C₀ (170)⁵ − 5C₁ (170)⁴ + 5C₂ (170)³ − 5C₃ (170)² + 5(170) − 1

A multiple of 100 + 5(170) – 1 = 100K + 849

∴ The last two digits are 49.

Relation Between two Numbers

Example: Find the larger of 99⁵⁰ + 100⁵⁰ and 101⁵⁰

Sol:

101⁵⁰ = (100 + 1)⁵⁰ = 100⁵⁰ + 50 . 100⁴⁹ + 25 . 49 . 100⁴⁸ + …

⇒ 99⁵⁰ = (100 − 1)⁵⁰ = 100⁵⁰ – 50 . 100⁴⁹ + 25 . 49 . 100⁴⁸ − ….

⇒ 101⁵⁰ – 99⁵⁰ = 2[50 . 100⁴⁹ + 25(49) (16) 100⁴⁷ + …]

= 100⁵⁰ + 50 . 49 . 16 . 100⁴⁷ + … >100⁵⁰

∴ 101⁵⁰ – 99⁵⁰ > 100⁵⁰

⇒ 101⁵⁰ > 100⁵⁰ + 99⁵⁰

Divisibility Test

Example: Show that 11⁹ + 9¹¹ is divisible by 10.

Sol:

11⁹ + 9¹¹ = (10 + 1)⁹ + (10 − 1)¹¹

= (9C₀ . 10⁹ + 9C₁ . 10⁸ + … 9C₉) + (11C₀ . 10¹¹ − 11C₁ . 10¹⁰ + … −11C₁₁)

= 9C₀ . 10⁹ + 9C₁ . 10⁸ + … + 9C₈ . 10 + 1 + 10¹¹ − 11C₁ . 10¹⁰ + … + 11C₁₀ . 10−1

= 10[9C₀ . 10⁸ + 9C₁ . 10⁷ + … + 9C₈ + 11C₀ . 10¹⁰ − 11C₁ . 10⁹ + … + 11C₁₀]

= 10K, which is divisible by 10.

Formulae:

• The number of terms in the expansion of (x₁ + x₂ + … x_r)ⁿ is (n + r − 1)C_{r – 1}
• Sum of the coefficients of (ax + by)ⁿ is (a + b)ⁿ

If f(x) = (a₀ + a₁x + a₂x² + …. + a_mx^m)ⁿ then

• (a) Sum of coefficients = f(1)
• (b) Sum of coefficients of even powers of x is: [f(1) + f(−1)] / 2
• (c) Sum of coefficients of odd powers of x is [f(1) − f(−1)] / 2

Multinomial Theorem

Using binomial theorem, we have

(x + a)ⁿ

=ⁿ∑_{r = 0}nC_r x^{n – r} a^r, n∈N

= ⁿ∑_{r = 0} [n! / (n − r)!r!] x^{n – r}a^r

= ⁿ∑_{r + s =n} [n! / r!s!] x^s a^r, where s = n – r.

This result can be generalized in the following form:

(x₁ + x₂ + … +x_k)ⁿ

= ∑_{r1 + r2 + …. + rk = n} [n! / r1!r2!…rk!] x₁^r1 x₂^r2 …x_k^rk

The general term in the above expansion is

[(n!) / (r₁! r₂! r₃! … r_k!)] x₁^r1 x₂^r2 x₃^r3… x_k^rk

The number of terms in the above expansion is equal to the number of non-negative integral solution of the equation.

r₁+r₂ + … + r_k = n, because each solution of this equation gives a term in the above expansion. The number of such solutions is ^{n + k – 1}C_k −1.

PARTICULAR CASES

Case-1:

 

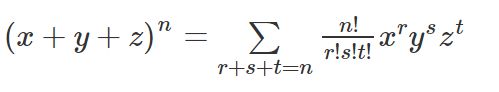
The above expansion has ^n+3-1C_3-1 = ^{n + 2}C₂ terms.

Case-2: 

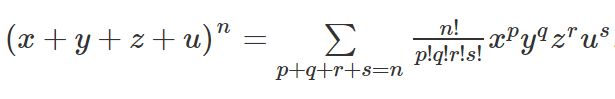
There are ^{n + 4 – 1}C_{4 – 1} = ^{n + 3}C₃ terms in the above expansion.

REMARK: The greatest coefficient in the expansion of (x₁ + x₂ + … + x_m)ⁿ is [(n!) / (q!)^{m – r}{(q+1)!}^r], where q and r are the quotient and remainder, respectively when n is divided by m.

Multinomial Expansions

Consider the expansion of (x + y + z)¹⁰. In the expansion, each term has different powers of x, y, and z and the sum of these powers is always 10.

One of the terms is λx²y³z⁵. Now, the coefficient of this term is equal to the number of ways 2x′s, 3y′s, and 5z′s are arranged, i.e., 10! (2! 3! 5!). Thus,

(x+y+z)¹⁰ = ∑(10!) /  (P1! P2! P3!) x^P1 y^P2 z^P3

Where P1 + P2 + P3 = 10 and 0 ≤ P1, P2, P3 ≥ 10

In general,

(x₁ + x₂ + … x_r)ⁿ = ∑ (n!) / (P1! P2! … Pr!) x^P1 x^P2 … x^Pr

Where P1 + P2 + P3 + … + Pr = n and 0 ≤ P1, P2, … Pr ≥ n

Number of Terms in the Expansion of (x₁ + x₂ + … + x_r)ⁿ

From the general term of the above expansion, we can conclude that the number of terms is equal to the number of ways different powers can be distributed to x₁, x₂, x₃ …., x_n such that the sum of powers is always “n”.

Number of non-negative integral solutions of x₁ + x₂ + … + x_r = n is ^{n +r – 1}C_{r – 1}.

For example, number of terms in the expansion of (x + y + z)³ is ^{3 + 3 -1}C_{3 – 1} =  ⁵C₂ = 10

As in the expansion, we have terms such as

As x⁰ y⁰ z⁰, x⁰ y¹ z², x⁰ y² z¹, x⁰ y³ z⁰, x¹ y⁰ z², x¹ y¹ z¹, x¹ y² z⁰, x² y⁰ z¹, x² y¹ z⁰, x³ y⁰ z⁰.

Number of terms in (x + y + z)ⁿ is ^{n + 3 – 1}C_{3 – 1} = ^{n + 2}C₂.

Number of terms in (x + y + z + w)ⁿ is ^{n + 4 – 1}C_{4 – 1} = ^{n + 3}C₃ and so on.

Example. Show that 9ⁿ⁺¹ – 8n – 9 is divisible by 64, whenever n is a positive integer.

Solution:

In order to show that 9ⁿ⁺¹ – 8n – 9 is divisible by 64, it has to be show that 9ⁿ⁺¹ – 8n – 9 = 64 k, where k is some natural number

Using binomial theorem,

(1 + a)^m = ^mC₀ + ^mC₁ a + ^mC₂ a² + …. + ^m C _m a^m

For a = 8 and m = n + 1 we get

(1 + 8)ⁿ⁺¹ = ⁿ⁺¹C₀ + ⁿ⁺¹C₁ (8) + ⁿ⁺¹C₂ (8)² + …. + ⁿ⁺¹ C _n+1 (8)ⁿ⁺¹

9ⁿ⁺¹ = 1 + (n + 1) 8 + 8² [ⁿ⁺¹C₂ + ⁿ⁺¹C₃ (8) + …. + ⁿ⁺¹ C _n+1 (8)^n-1]

9ⁿ⁺¹ = 9 + 8n + 64 [ⁿ⁺¹C₂ + ⁿ⁺¹C₃ (8) + …. + ⁿ⁺¹ C _n+1 (8)^n-1]

9ⁿ⁺¹ – 8n – 9 = 64 k

Where k = [ⁿ⁺¹C₂ + ⁿ⁺¹C₃ (8) + …. + ⁿ⁺¹ C _n+1 (8)^n-1] is a natural number

Thus, 9ⁿ⁺¹ – 8n – 9 is divisible by 64, whenever n is positive integer.

Hence the proof

Example. Find the expansion of (3x² – 2ax + 3a²)³ using binomial theorem.

Solution:

We know that (a + b)³ = a³ + 3a²b + 3ab² + b³

Putting a = 3x² & b = -a (2x-3a), we get

[3x² + (-a (2x-3a))]³

= (3x²)³+3(3x²)²(-a (2x-3a)) + 3(3x²) (-a (2x-3a))² + (-a (2x-3a))³

= 27x⁶ – 27ax⁴ (2x-3a) + 9a²x² (2x-3a)² – a³(2x-3a)³

= 27x⁶ – 54ax⁵ + 81a²x⁴ + 9a²x² (4x²-12ax+9a²) – a³ [(2x)³ – (3a)³ – 3(2x)²(3a) + 3(2x)(3a)²]

= 27x⁶ – 54ax⁵ + 81a²x⁴ + 36a²x⁴ – 108a³x³ + 81a⁴x² – 8a³x³ + 27a⁶ + 36a⁴x² – 54a⁵x

= 27x⁶ – 54ax⁵+ 117a²x⁴ – 116a³x³ + 117a⁴x² – 54a⁵x + 27a⁶

Thus, (3x² – 2ax + 3a²)³

= 27x⁶ – 54ax⁵+ 117a²x⁴ – 116a³x³ + 117a⁴x² – 54a⁵x + 27a⁶