Circles and its related terms
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Circles and its related terms
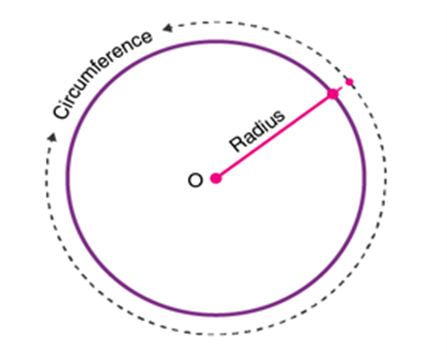
In Maths or Geometry, a circle is a special kind of ellipse in which the eccentricity is zero and the two foci are coincident. A circle is also termed as the locus of the points drawn at an equidistant from the center. The distance from the center of the circle to the outer line is its radius. Diameter is the line that divides the circle into two equal parts and is also equal to twice the radius.
A circle is a basic 2D shape that is measured in terms of its radius. The circles divide the plane into two regions as interior and exterior regions. It is similar to the type of line segment. Imagine that the line segment is bent around till its ends join. Arrange the loop until it is precisely circular.
The circle is a two-dimensional figure, which has its area and perimeter. The perimeter of the circle is also called the circumference, which is the distance around the circle. The area of the circle is the region bounded by it in a 2D plane. Let us discuss here circle definition, formulas, and important terms with examples in detail.
Circle Definition
A circle is a closed two-dimensional figure in which the set of all the points in the plane is equidistant from a given point called the “center”. Every line that passes through the circle forms the line of reflection symmetry. Also, it has rotational symmetry around the center for every angle. The circle formula in the plane is given as:
(x-h)2 + (y-k)2 = r2
where (x,y) are the coordinate points (h,k) is the coordinate of the center of a circle
and r is the radius of a circle.
Circle Shaped Objects
There are many objects we have seen in the real world that are circular in shape. Some of the examples are:
- Ring
- CD/Disc
- Bangles
- Coins
- Wheels
- Button
- Dartboard
- Hula hoop
We can observe many such examples in our day-to-day life.
How to Draw a Circle?
In maths projects for class 10 on circles, the construction of a circle, all the properties and terminologies are explained in detail. To understand what circles are in simple terms, go through circles for class 10, and also try the following exercise –
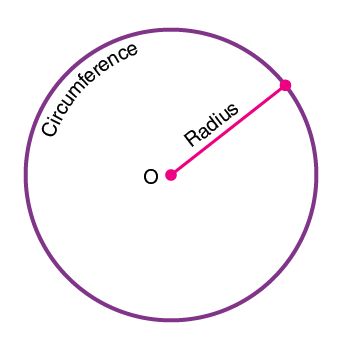
- Take an empty sheet of paper and mark a single point on the sheet, somewhere in the middle of the sheet, and name it point O.
- Select a random length for radius, for example, 3 cm.
- Using a ruler, keep the reference zero mark on point O and randomly mark 3 cm away from point O in all the directions.
- Mark as many points as you want away from point O, but all of them should be exactly 3 cm away from point O.
If you’ve selected sufficient points, you may notice that the shape is starting to resemble a circle and this is exactly what the definition of a circle is.
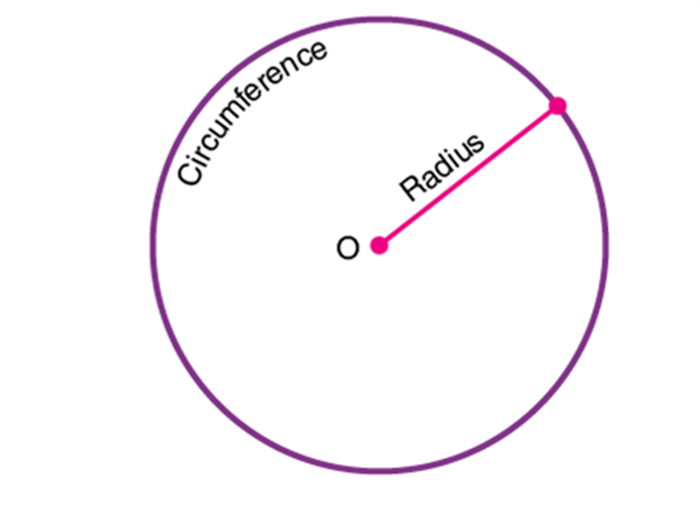
Parts of Circle
A circle has different parts based on its positions and their properties. The different parts of a circle are explained below in detail.
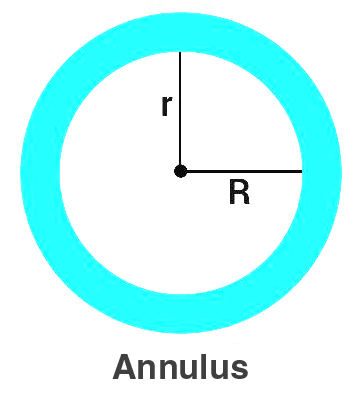
- Annulus-The region bounded by two concentric circles. It is basically a ring-shaped object. See the figure below.
- Arc – It is basically the connected curve of a circle.
- Sector – A region bounded by two radii and an arc.
- Segment- A region bounded by a chord and an arc lying between the chord’s endpoints. It is to be noted that segments do not contain the center.
See the figure below explaining the arc, sector and segment of a circle.
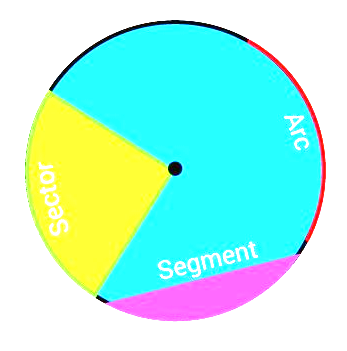
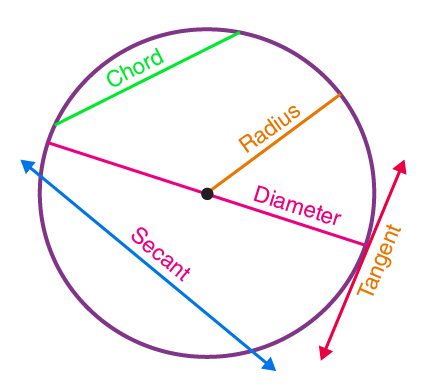
- Centre – It is the midpoint of a circle.
- Chord- A line segment whose endpoints lie on the circle.
- Diameter- A line segment having both the endpoints on the circle and is the largest chord of the circle.
- Radius- A line segment connecting the center of a circle to any point on the circle itself.
- Secant- A straight line cutting the circle at two points. It is also called an extended chord.
- Tangent- A coplanar straight line touching the circle at a single point.
See the figure below representing the center, chord, diameter, radius, secant and tangent of a circle.
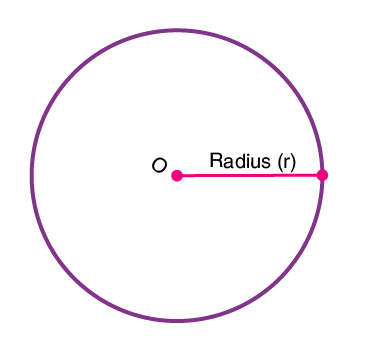
Radius of Circle (r)
A line segment connecting the center of a circle to any point on the circle itself “. The radius of the circle is denoted by “R” or “r”.
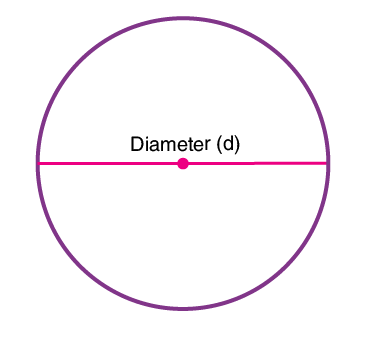
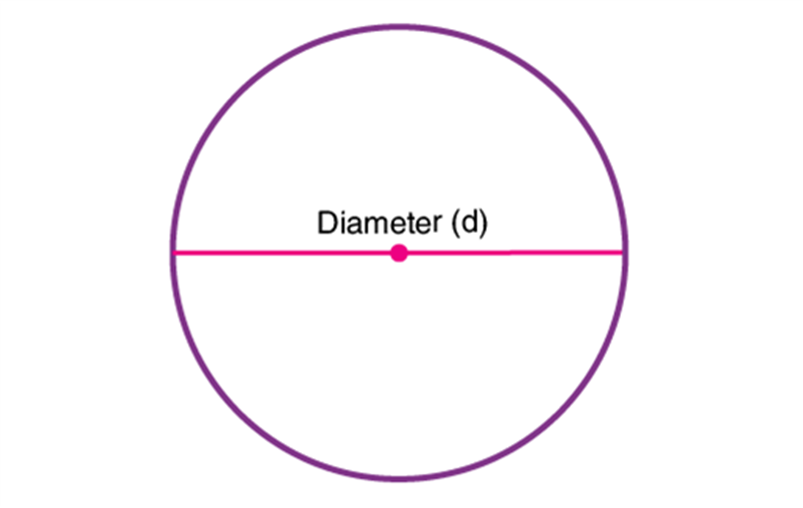
Diameter (d) of Circle
A line segment has both endpoints on the circle. It is twice the length of radius i.e. d = 2r. From the diameter, the radius of the circle formula is obtained as r= d/2.
Circle Formulas
We know that a circle is a two-dimensional curve-shaped figure, and the two different parameters used to measure the circle are:
- Area of circle
- Circumference of a circle
Let us discuss here the general formulas for the area and perimeter/circumference of a circle.
Area and Circumference of a Circle
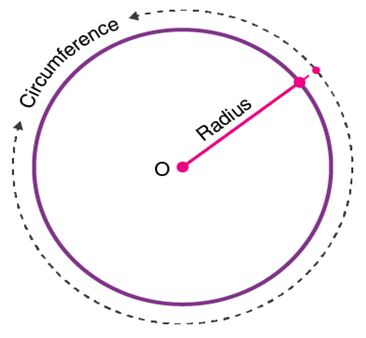
Circumference (C)
The circumference of a circle is defined as the
distance around the circle. The word ‘perimeter’
is also sometimes used, although this usually
refers to the distance around polygons, figures made up of the straight line segment.
A circle circumference formula is given by
C = πd = 2 π r
Where, π = 3.1415
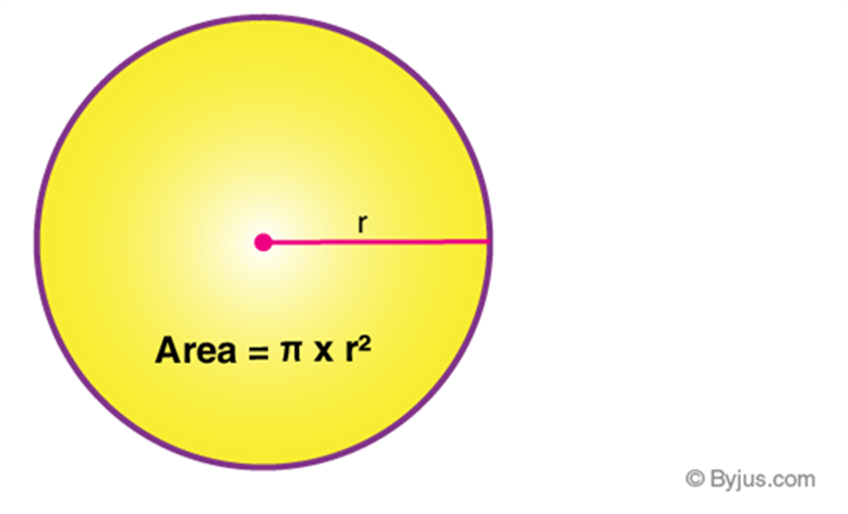
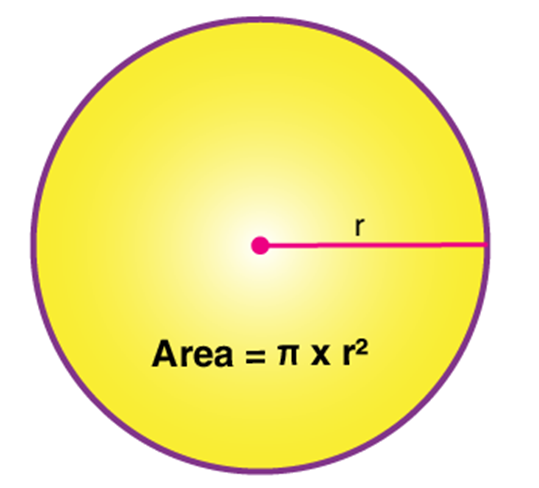
Area (A)
Area of a circle is the amount of space occupied by the circle.
The circle formula to find the area is given by
Area of a circle = πr2
Circle Area Proof
We know that Area is the space occupied by the circle.
Consider a concentric circle having an external circle radius to be ‘r.’
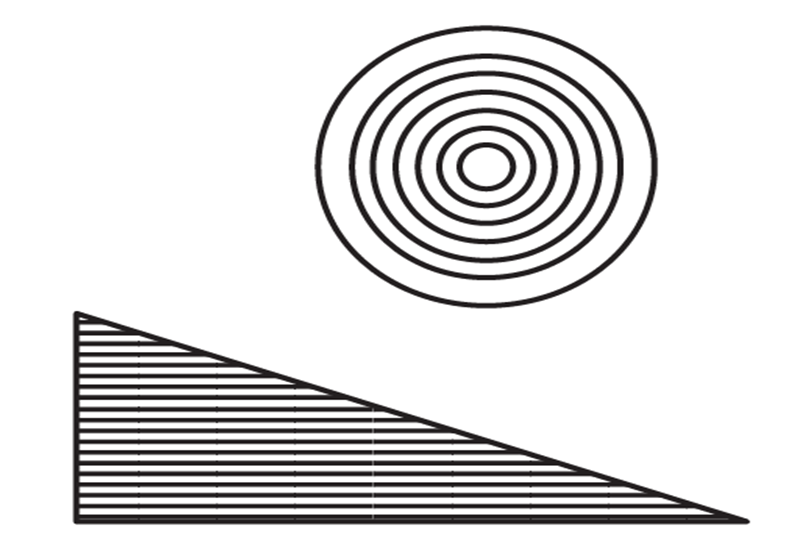
Open all the concentric circles to form a right-angled triangle.
The outer circle would form a line having a length of 2πr forming the base.
The height would be ‘r’
Therefore the area of the right-angled triangle formed would be equal to the area of a circle.
Area of a circle = Area of triangle = (1/2) ×b ×h
= (1/2) × 2π r × r
Therefore, the Area of a circle = πr2
Properties of Circles
The important basic properties of circles are as follows:
- The outer line of a circle is equidistant from the center.
- The diameter of the circle divides it into two equal parts.
- Circles which have equal radii are congruent to each other.
- Circles that are different in size or have different radii are similar.
- The diameter of the circle is the largest chord and is double the radius.
Solved Examples
Example 1:
Find the area and the circumference of a circle whose radius is 10 cm. (Take the value of π = 3.14)
Solution:
Given: Radius = 10 cm.
Area =π r2
= 3.14 × 102
A= 314 cm2
Circumference, C = 2πr
C= 2 ×3.14× 10
Circumference= 62.8 cm
Example 2:
Find the area of a circle whose circumference is 31.4 cm.
Solution:
Given:
Circumference = 31.4 cm
To find the area of a circle, we need to find the radius.
From the circumference, the radius can be calculated:
2 π r = 31.4
(2)(3.14)r = 31.4
r = 31.4 /(2)(3.14)
r=10/2
r= 5
Therefore, the radius of the circle is 5 cm.
The area of a circle is πr2 square units
Now, substitute the radius value in the area of a circle formula, we get
A = π(5)2
A = 3.14 x 25
A = 78.5 cm2
Therefore, the area of a circle is 78.5 cm2.
Circles and its related terms
Chapter 10 - Circles
Circles and its related terms
In Maths or Geometry, a circle is a special kind of ellipse in which the eccentricity is zero and the two foci are coincident. A circle is also termed as the locus of the points drawn at an equidistant from the centre. The distance from the centre of the circle to the outer line is its radius. Diameter is the line which divides the circle into two equal parts and is also equal to twice of the radius.
A circle is a basic 2D shape which is measured in terms of its radius. The circles divide the plane into two regions such as interior and exterior region. It is similar to the type of line segment. Imagine that the line segment is bent around till its ends join. Arrange the loop until it is precisely circular.
The circle is a two-dimensional figure, which has its area and perimeter. The perimeter of the circle is also called the circumference, which is the distance around the circle. The area of the circle is the region bounded by it in a 2D plane. Let us discuss here circle definition, formulas, important terms with examples in detail.
Circle Definition
A circle is a closed two-dimensional figure in which the set of all the points in the plane is equidistant from a given point called “centre”. Every line that passes through the circle forms the line of reflection symmetry. Also, it has rotational symmetry around the centre for every angle. The circle formula in the plane is given as:
(x-h)2 + (y-k)2 = r2
where (x,y) are the coordinate points
(h,k) is the coordinate of the centre of a circle
and r is the radius of a circle.
Circle Shaped Objects
There are many objects we have seen in the real world that are circular in shape. Some of the examples are:
- Ring
- CD/Disc
- Bangles
- Coins
- Wheels
- Button
- Dartboard
- Hula hoop
We can observe many such examples in our day to day life.
How to Draw a Circle?
In maths projects for class 10 on circles, the construction of a circle, all the properties and terminologies are explained in detail. To understand what circles are in simple terms, go through circles for class 10, and also try the following exercise –
- Take an empty sheet of paper and mark a single point on the sheet, somewhere in the middle of the sheet, and name it to point O.
- Select a random length for radius, for example, 3 cm.
- Using a ruler, keep the reference zero mark on point O and randomly mark 3 cm away from point O in all the direction.
- Mark as many points as you want away from point O, but all of them should be exactly 3 cm away from point O.
If you’ve selected sufficient points, you may notice that the shape is starting to resemble a circle and this is exactly what the definition of a circle is.
Parts of Circle
A circle has different parts based on the positions and their properties. The different parts of a circle are explained below in detail.
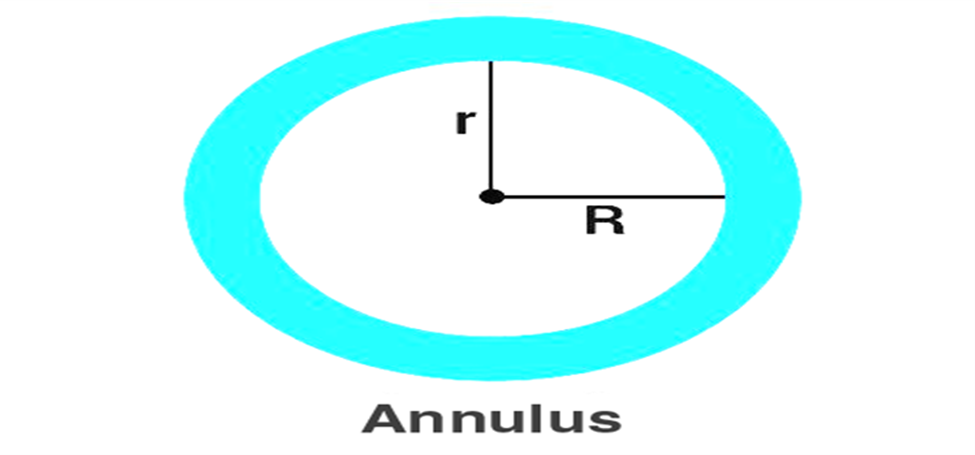
- Annulus-The region bounded by two concentric circles. It is basically a ring-shaped object. See the figure below.
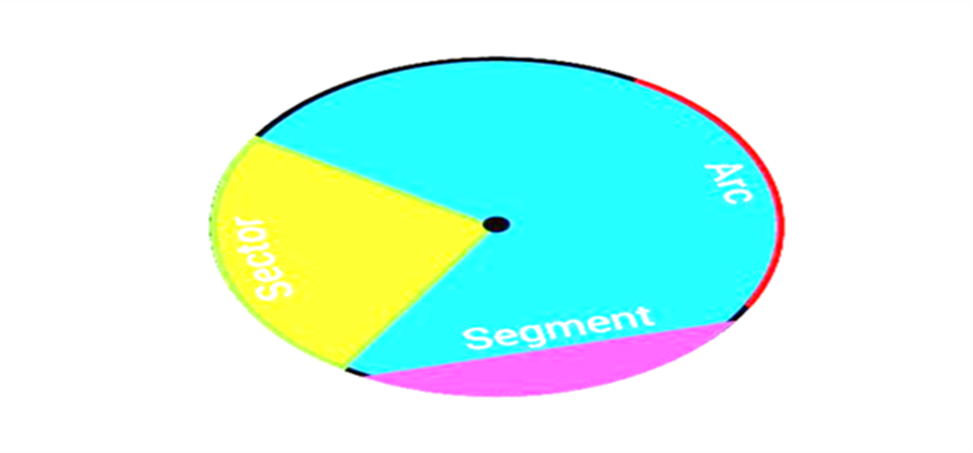
- Arc – It is basically the connected curve of a circle.
- Sector – A region bounded by two radii and an arc.
- Segment- A region bounded by a chord and an arc lying between the chord’s endpoints. It is to be noted that segments do not contain the centre.
See the figure below explaining the arc, sector and segment of a circle.
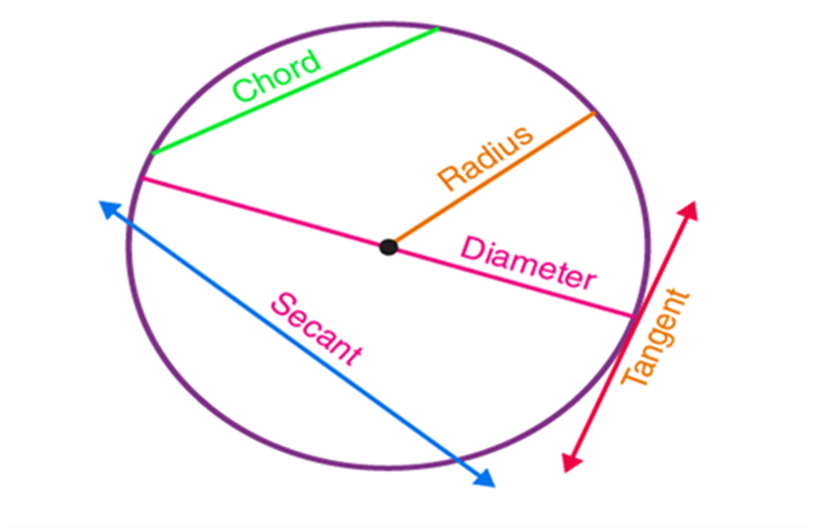
- Centre – It is the midpoint of a circle.
- Chord- A line segment whose endpoints lie on the circle.
- Diameter- A line segment having both the endpoints on the circle and is the largest chord of the circle.
- Radius- A line segment connecting the centre of a circle to any point on the circle itself.
- Secant- A straight line cutting the circle at two points. It is also called an extended chord.
- Tangent- A coplanar straight line touching the circle at a single point.
See the figure below-representing the centre, chord, diameter, radius, secant and tangent of a circle.
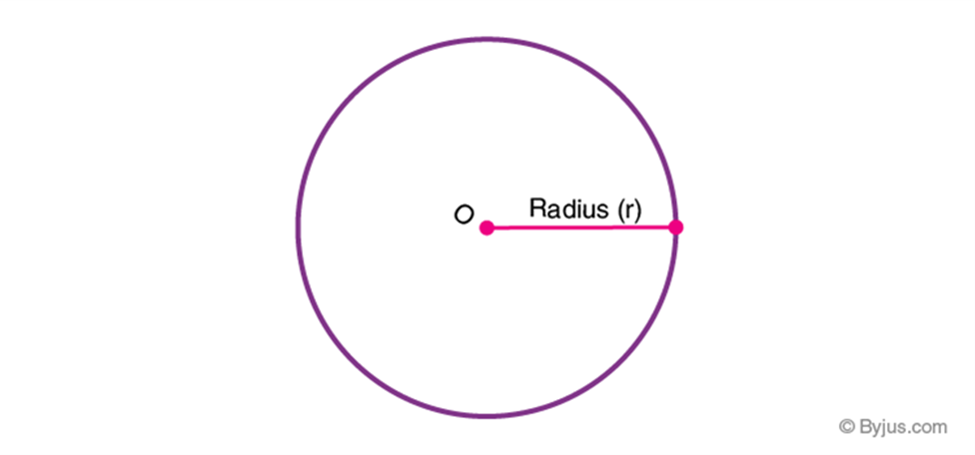
A line segment connecting the centre of a circle to any point on the circle itself “. The radius of the circle is denoted by “R” or “r”.
A line segment having both the endpoints on the circle. It is twice the length of radius i.e. d = 2r. From the diameter, the radius of the circle formula is obtained as r= d/2.
Circle Formulas
We know that a circle is a two-dimensional curve-shaped figure, and the two different parameters used to measure the circle are:
- Area of circle
- Circumference of a circle
Let us discuss here the general formulas for area and perimeter/circumference of a circle.
Area and Circumference of a Circle
|
Circumference (C) |
The circumference of a circle is defined as the distance around the circle. The word ‘perimeter’ is also sometimes used, although this usually refers to the distance around polygons, figures made up of the straight line segment. A circle circumference formula is given by C = πd = 2 π r Where, π = 3.1415 |
|
|
Area (A) |
Area of a circle is the amount of space occupied by the circle. The circle formula to find the area is given by Area of a circle = πr2 |
|
Circle Area Proof
We know that Area is the space occupied by the circle.
Consider a concentric circle having an external circle radius to be ‘r.’
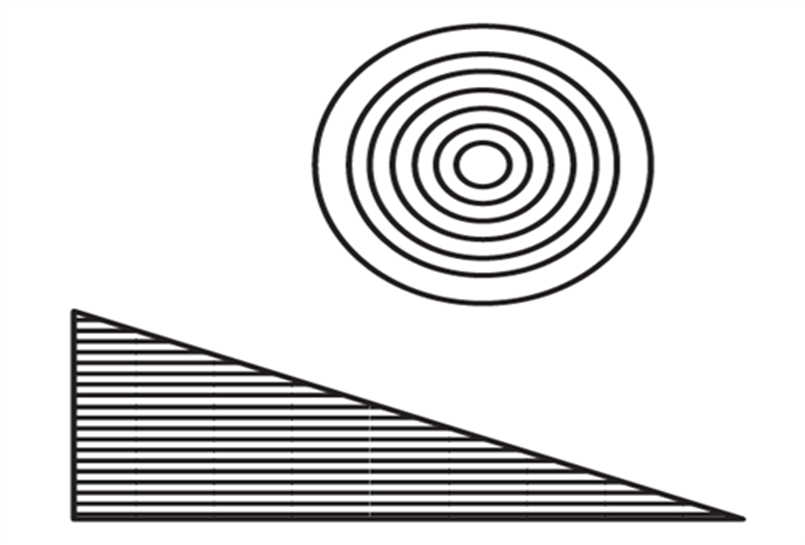
Open all the concentric circles to form a right-angled triangle.
The outer circle would form a line having length 2πr forming the base.
The height would be ‘r’
Therefore the area of the right-angled triangle formed would be equal to the area of a circle.
Area of a circle = Area of triangle = (1/2) ×b ×h
= (1/2) × 2π r × r
Therefore, Area of a circle = πr2
Properties of Circles
The important basic properties of circles are as follows:
- The outer line of a circle is at equidistant from the centre.
- The diameter of the circle divides it into two equal parts.
- Circles which have equal radii are congruent to each other.
- Circles which are different in size or having different radii are similar.
- The diameter of the circle is the largest chord and is double the radius.
Solved Examples
Example 1:
Find the area and the circumference of a circle whose radius is 10 cm. (Take the value of π = 3.14)
Solution:
Given: Radius = 10 cm.
Area =π r2
= 3.14 × 102
A= 314 cm2
Circumference, C = 2πr
C= 2 ×3.14× 10
Circumference= 62.8 cm
Example 2:
Find the area of a circle whose circumference is 31.4 cm.
Solution:
Given:
Circumference = 31.4 cm
To find the area of a circle, we need to find the radius.
From the circumference, the radius can be calculated:
2 π r = 31.4
(2)(3.14)r = 31.4
r = 31.4 /(2)(3.14)
r=10/2
r= 5
Therefore, the radius of the circle is 5 cm.
The area of a circle is πr2 square units
Now, substitute the radius value in the area of a circle formula, we get
A = π(5)2
A = 3.14 x 25
A = 78.5 cm2
Therefore, the area of a circle is 78.5 cm2.
Angle subtended by a Chord at a Point
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Angle Subtended by a Chord at a Point
In Mathematics, a circle is a two-dimensional geometrical figure, where all the points on the surface of a circle are equidistant from the center point called the radius. The chord of a circle is the line segment that joins two points on the circumference of a circle. If you draw two or more equal chords of a circle and determine the angles subtended by them at the center, you will observe that the angles subtended by them at the center are equal. In this article, we will learn the theorems related to the angle subtended by a chord at a point in detail.
Angle Subtended by a Chord at a Point – Theorem
Theorem: Equal chords of a circle subtend equal angles at the center.
Proof - Consider a circle and draw two equal chords AB and CD of a circle with center “O” as shown in the figure.
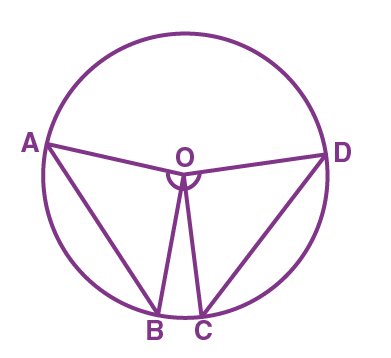
To prove: ∠ AOB = ∠ COD.
From the triangles, AOB and COD, we get
OA = OC (Radii of a circle)
OB = OD (Radii of a circle)
AB = CD (Equal chords)
By, using Side-Side-Side (SSS Rule), we can write:
∆ AOB ≅ ∆ COD
As the triangles are congruent, the angles should be of equal measurement.
Therefore, ∠ AOB = ∠ COD [Using Corresponding parts of the congruent triangle (CPCT)]
Hence, the theorem “Equal chords of a circle subtend equal angles at the center” is proved.
Converse Theorem
If the angles subtended by the chords of a circle at the center are equal, then the chords are equal.
In the converse theorem, if ∠AOB is equal to ∠COD, we need to prove that the chord AB = CD.
This can be again proved with the help of CPCT and SSS rules.
Angle subtended by a Chord at a Point
Angle Subtended by a Chord at a Point
In Mathematics, a circle is a two-dimensional geometrical figure, where all the points on the surface of a circle are equidistant from the center point called the radius. The chord of a circle is the line segment that joins two points on the circumference of a circle. If you draw two or more equal chords of a circle and determine the angles subtended by them at the center, you will observe that the angles subtended by them at the center are equal. In this article, we will learn the theorems related to the angle subtended by a chord at a point in detail.
Angle Subtended by a Chord at a Point – Theorem
Theorem: Equal chords of a circle subtend equal angles at the center.
Proof
Consider a circle and draw two equal chords AB and CD of a circle with center “O” as shown in the figure.
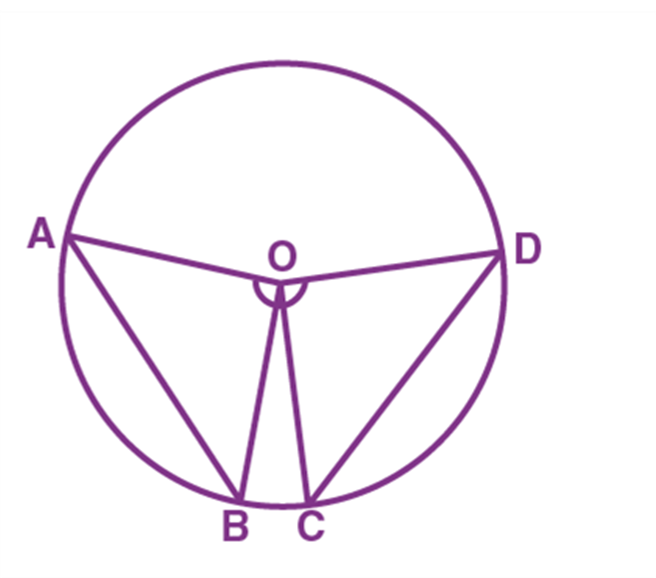
To prove: ∠ AOB = ∠ COD.
From the triangles, AOB and COD, we get
OA = OC (Radii of a circle)
OB = OD (Radii of a circle)
AB = CD (Equal chords)
By, using Side-Side-Side (SSS Rule), we can write:
∆ AOB ≅ ∆ COD
As the triangles are congruent, the angles should be of equal measurement.
Therefore, ∠ AOB = ∠ COD [Using Corresponding parts of the congruent triangle (CPCT)]
Hence, the theorem “Equal chords of a circle subtend equal angles at the center” is proved.
Converse Theorem
If the angles subtended by the chords of a circle at the center are equal, then the chords are equal.
In the converse theorem, if ∠AOB is equal to ∠COD, we need to prove that the chord AB = CD.
This can be again proved with the help of CPCT and SSS rules.
Perpendicular from the centre to a Chord
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Perpendicular from the Centre to a Chord
In Mathematics, a chord is a line segment that joins two points on the circumference of a circle. We know that the longest chord of a circle is a diameter that passes through the center of a circle. In this article, we will discuss the theorem related to the perpendicular from the center to a circle and its proof, and the converse of this theorem in detail.
Perpendicular from the Centre to a Chord – Theorem and Proof
Theorem: The perpendicular from the center of a circle to a chord bisects the chord.
Proof: Consider a circle with the center “O”.
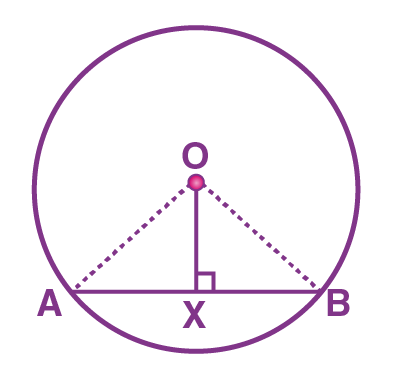
AB is a chord such that the line OX is perpendicular to the chord AB.
(i.e) OX ⊥ AB
Now, we need to prove: AX = BX
To prove AX = BX, consider two triangles OAX and OBX.
∠OXA = ∠OXB (∠X = 90°)
OX = OX (Common side)
OA = OB (Radii)
By using the RHS rule, we can prove that the triangle OAX is congruent to OBX.
Therefore,
∆OAX ≅ ∆OBX
Hence, we can say that AX = BX ( Using CPCT)
Thus, the perpendicular from the center of a circle to a chord bisects the chord, is proved.
The Converse of this Theorem:
The line drawn through the center of a circle to bisect a chord is perpendicular to the chord
Proof: Consider the same figure, as given above.
Assume that AB is the chord of a circle with a center “O”.
The center “O” is joined to the midpoint “X” of the chord AB.
Now, we need to prove OX ⊥ AB.
Join OA and OB, and the two triangles formed are OAX and OAB.
Here, OA = OB (Radii)
OX = OX (Common side)
AX = BX (As, X is the midpoint of AB)
Therefore, we can say that ∆OAX ≅ ∆OBX.
Thus, by using the RHS rule, we get
∠OMA = ∠OMB = 90°
This proves that the line drawn through the center of a circle to bisect a chord is perpendicular to the chord.
Hence, the converse of this theorem is proved.
Perpendicular from the centre to a Chord
Perpendicular from the Centre to a Chord
In Mathematics, a chord is a line segment that joins two points on the circumference of a circle. We know that the longest chord of a circle is a diameter that passes through the centre of a circle. In this article, we will discuss the theorem related to the perpendicular from the centre to a circle and its proof, and the converse of this theorem in detail.
Perpendicular from the Centre to a Chord – Theorem and Proof
Theorem:
The perpendicular from the centre of a circle to a chord bisects the chord.
Proof:
Consider a circle with centre “O”.
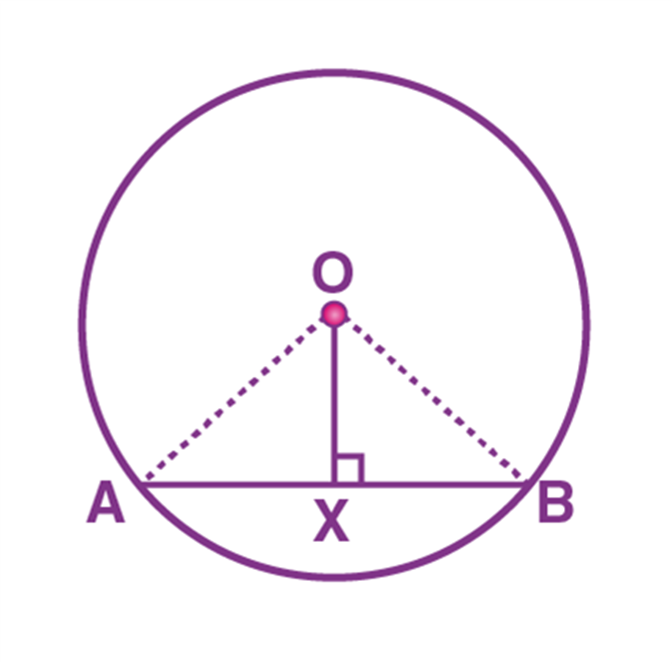
AB is a chord such that the line OX is perpendicular to the chord AB.
(i.e) OX ⊥ AB
Now, we need to prove: AX = BX
To prove AX = BX, consider two triangles OAX and OBX.
∠OXA = ∠OXB (∠X = 90°)
OX = OX (Common side)
OA = OB (Radii)
By using the RHS rule, we can prove that the triangle OAX is congruent to OBX.
Therefore,
∆OAX ≅ ∆OBX
Hence, we can say that AX = BX ( Using CPCT)
Thus, the perpendicular from the centre of a circle to a chord bisects the chord, is proved.
The Converse of this Theorem:
The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord
Proof:
Consider the same figure, as given above.
Assume that AB is the chord of a circle with centre “O”.
The centre “O” is joined to the midpoint “X” of the chord AB.
Now, we need to prove OX ⊥ AB.
Join OA and OB, and the two triangles formed are OAX and OAB.
Here,
OA = OB (Radii)
OX = OX (Common side)
AX = BX (As, X is the midpoint of AB)
Therefore, we can say that ∆OAX ≅ ∆OBX.
Thus, by using the RHS rule, we get
∠OMA = ∠OMB = 90°
This proves that the line drawn through the centre of a circle to bisect a chord is perpendicular to the chord.
Hence, the converse of this theorem is proved.
Circle through three points
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Circle through three points
To draw a straight line, the minimum number of points required is two. That means we can draw a straight line with the given two points. How many minimum points are sufficient to draw a unique circle? Is it possible to draw a circle passing through 3 points? In how many ways can we draw a circle that passes through three points? Well, let’s try to find answers to all these queries.
Learn: Circle Definition
Before drawing a circle passing through 3 points, let’s have a look at the circles that have been drawn through one and two points respectively.
Circle Passing Through a Point
Let us consider a point and try to draw a circle passing through that point.
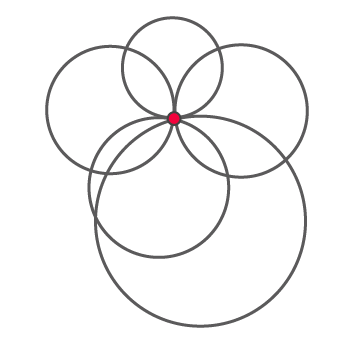
As given in the figure, through a single point P, we can draw infinite circles passing through it.
Circle Passing Through Two Points
Now, let us take two points, P and Q and see what happens?
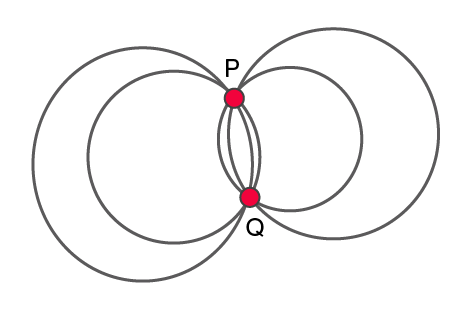
Again we see that an infinite number of circles passing through points P and Q can be drawn.
Circle Passing Through Three Points (Collinear or Non-Collinear)
Let us now take 3 points. For a circle passing through 3 points, two cases can arise.
- Three points can be collinear
- Three points can be non-collinear
Let us study both cases individually.
Case 1: A circle passing through 3 points: Points are collinear
Consider three points, P, Q and R, which are collinear.
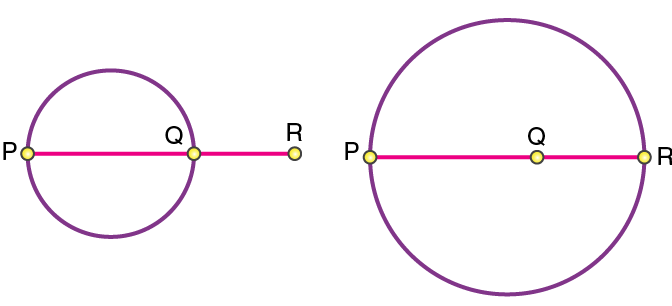
If three points are collinear, any one of the points either lies outside the circle or inside it. Therefore, a circle passing through 3 points, where the points are collinear, is not possible.
Case 2: A circle passing through 3 points: Points are non-collinear
To draw a circle passing through three non-collinear points, we need to locate the center of a circle passing through 3 points and its radius. Follow the steps given below to understand how we can draw a circle in this case.
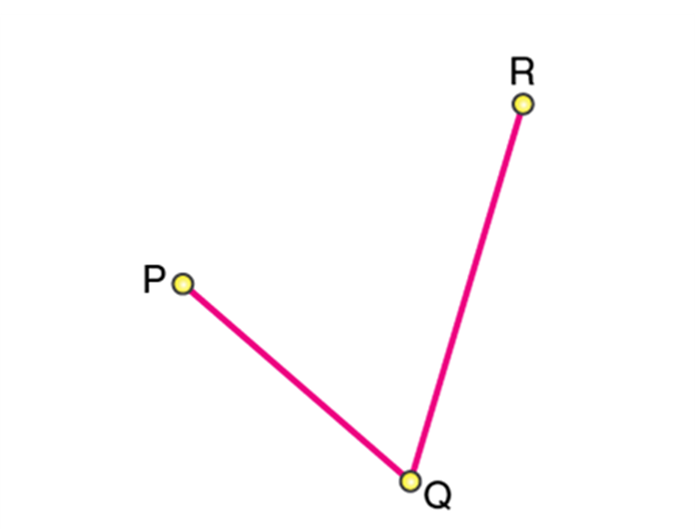
Step 1: Take three points P, Q, R and join the points as shown below:
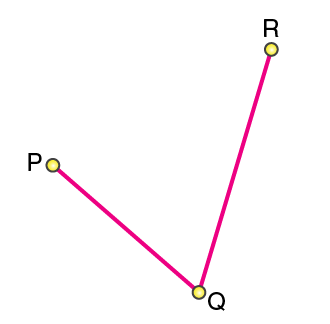
Step 2: Draw perpendicular bisectors of PQ and RQ. Let the bisectors AB and CD meet at O such that the point O is called the center of the circle.
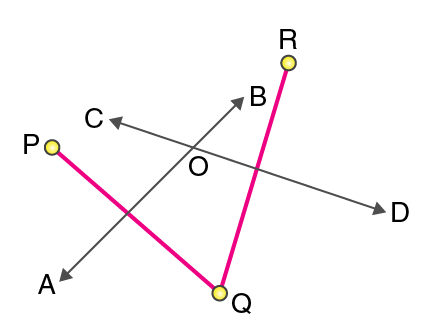
Step 3: Draw a circle with O as the center and radius OP or OQ or OR. We get a circle passing through 3 points P, Q, and R.

It is observed that only a unique circle will pass through all three points. It can be stated as a theorem and the proof is explained as follows.
It is observed that only a unique circle will pass through all three points. It can be stated as a theorem, and the proof of this is explained below.
Given:
Three non-collinear points P, Q and R
To prove:
Only one circle can be drawn through P, Q and R
Construction:
Join PQ and QR.
Draw the perpendicular bisectors of PQ and QR such that these perpendiculars intersect each other at O.
Proof:
|
S. No |
Statement |
Reason |
|
1 |
OP = OQ |
Every point on the perpendicular bisector of a line segment is equidistant from the endpoints of the line segment. |
|
2 |
OQ = OR |
Every point on the perpendicular bisector of a line segment is equidistant from the endpoints of the line segment. |
|
3 |
OP = OQ = OR |
From (i) and (ii) |
|
4 |
O is equidistant from P, Q and R |
|
If a circle is drawn with O as center and OP as radius, then it will also pass through Q and R.
O is the only point that is equidistant from P, Q and R as the perpendicular bisectors of PQ and QR intersect at O only.
Thus, O is the center of the circle to be drawn.
OP, OQ and OR will be radii of the circle.
From the above, it follows that a unique circle passing through 3 points can be drawn given that the points are non-collinear.
Till now, you learned how to draw a circle passing through 3 non-collinear points. Now, you will learn how to find the equation of a circle passing through 3 points. For this, we need to take three non-collinear points.
Circle Equation Passing Through 3 Points
Let’s derive the equation of the circle passing through the 3 points formula.
Let P(x1, y1), Q(x2, y2) and R(x3, y3) be the coordinates of three non-collinear points.
We know that,
The general form of equation of a circle is: x2 + y2 + 2gx + 2fy + c = 0….(1)
Now, we need to substitute the given points P, Q and R in this equation and simplify to get the value of g, f and c.
Substituting P(x1, y1) in equ(1),
x12 + y12 + 2gx1 + 2fy1 + c = 0….(2)
x22 + y22 + 2gx2 + 2fy2 + c = 0….(3)
x32 + y32 + 2gx3 + 2fy3 + c = 0….(4)
From (2) we get,
2gx1 = -x12 – y12 – 2fy1 – c….(5)
Again from (2) we get,
c = -x12 – y12 – 2gx1 – 2fy1….(6)
From (4) we get,
2fy3 = -x32 – y32 – 2gx3 – c….(7)
Now, subtracting (3) from (2),
2g(x1 – x2) = (x22 -x12) + (y22 – y12) + 2f (y2 – y1)….(8)
Substituting (6) in (7),
2fy3 = -x32 – y32 – 2gx3 + x12 + y12 + 2gx1 + 2fy1….(9)
Now, substituting equ(8), i.e. 2g in equ(9),
2f = [(x12 – x32)(x1 – x2) + (y12 – y32 )(x1 – x2) + (x22 – x12)(x1 – x3) + (y22 – y12)(x1 – x3)] / [(y3 – y1)(x1 – x2) – (y2 – y1)(x1 – x3)]
Similarly, we can get 2g as:
2g = [(x12 – x32)(y1 – x2) + (y12 – y32)(y1 – y2) + (x22 – x12)(y1 – y3) + (y22 – y12)(y1 – y3)] / [(x3 – x1)(y1 – y2) – (x2 – x1)(y1 – y3)]
Using these 2g and 2f values we can get the value of c.
Thus, by substituting g, f and c in (1) we will get the equation of the circle passing through the given three points.
Solved Example
Question: What is the equation of the circle passing through the points A(2, 0), B(-2, 0) and C(0, 2)?
Solution: Consider the general equation of circle:
x2 + y2 + 2gx + 2fy + c = 0….(i)
Substituting A(2, 0) in (i),
(2)2 + (0)2 + 2g(2) + 2f(0) + c = 0
4 + 4g + c = 0….(ii)
Substituting B(-2, 0) in (i),
(-2)2 + (0)2 + 2g(-2) + 2f(0) + c = 0
4 – 4g + c = 0….(iii)
Substituting C(0, 2) in (i),
(0)2 + (2)2 + 2g(0) + 2f(2) + c = 0
4 + 4f + c = 0….(iv)
Adding (ii) and (iii),
4 + 4g + c + 4 – 4g + c = 0
2c + 8 = 0
2c = -8
c = -4
Substituting c = -4 in (ii),
4 + 4g – 4 = 0
4g = 0
g = 0
Substituting c = -4 in (iv),
4 + 4f – 4 = 0
4f = 0
f = 0
Now, substituting the values of g, f and c in (i),
x2 + y2 + 2(0)x + 2(0)y + (-4) = 0
x2 + y2 – 4 = 0
Or
x2 + y2 = 4
This is the equation of the circle passing through the given three points A, B and C
Circle through three points
Circle through three points
To draw a straight line, the minimum number of points required is two. That means we can draw a straight line with the given two points. How many minimum points are sufficient to draw a unique circle? Is it possible to draw a circle passing through 3 points? In how many ways can we draw a circle that passes through three points? Well, let’s try to find answers to all these queries.
Learn: Circle Definition
Before drawing a circle passing through 3 points, let’s have a look at the circles that have been drawn through one and two points respectively.
Circle Passing Through a Point
Let us consider a point and try to draw a circle passing through that point.
As given in the figure, through a single point P, we can draw infinite circles passing through it.
Circle Passing Through Two Points
Now, let us take two points, P and Q and see what happens?
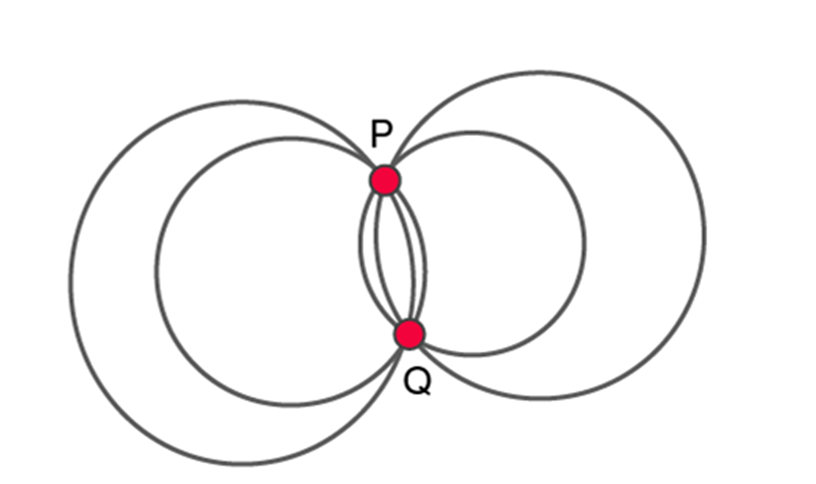
Again we see that an infinite number of circles passing through points P and Q can be drawn.
Circle Passing Through Three Points (Collinear or Non-Collinear)
Let us now take 3 points. For a circle passing through 3 points, two cases can arise.
- Three points can be collinear
- Three points can be non-collinear
Let us study both cases individually.
Case 1: A circle passing through 3 points: Points are collinear
Consider three points, P, Q and R, which are collinear.
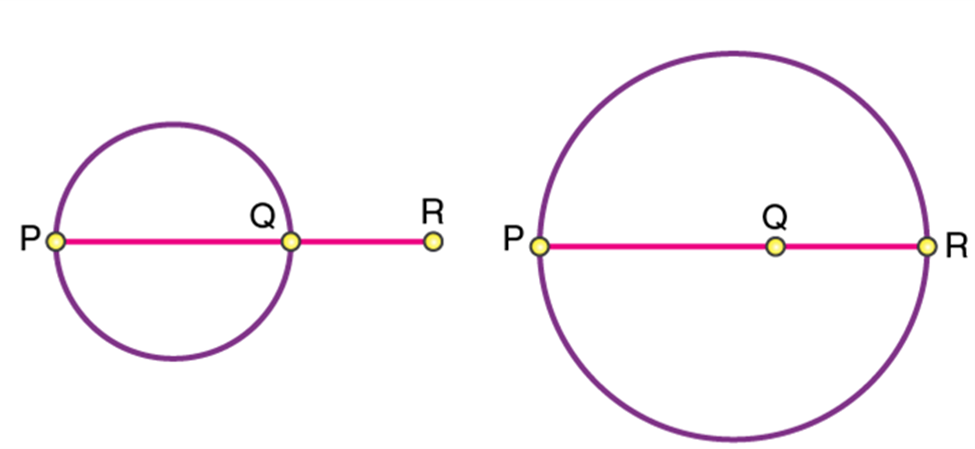
If three points are collinear, any one of the points either lie outside the circle or inside it. Therefore, a circle passing through 3 points, where the points are collinear, is not possible.
Case 2: A circle passing through 3 points: Points are non-collinear
To draw a circle passing through three non-collinear points, we need to locate the centre of a circle passing through 3 points and its radius. Follow the steps given below to understand how we can draw a circle in this case.
Step 1: Take three points P, Q, R and join the points as shown below:
Step 2: Draw perpendicular bisectors of PQ and RQ. Let the bisectors AB and CD meet at O such that the point O is called the centre of the circle.
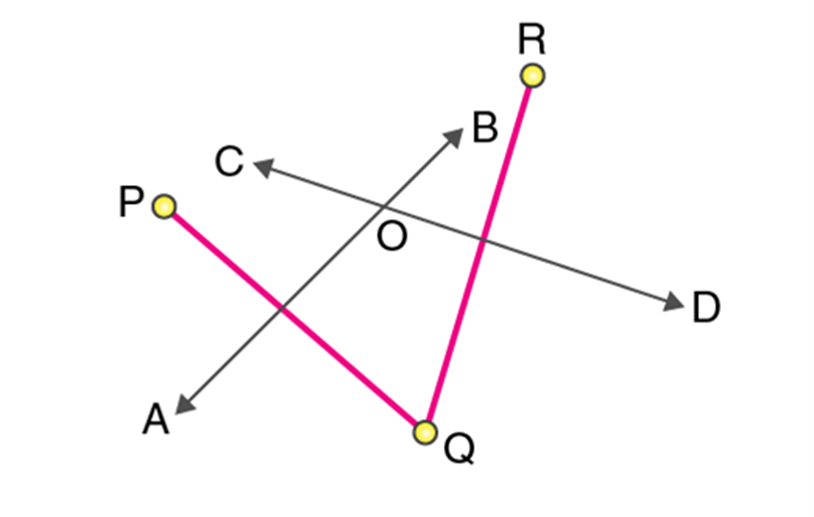
Step 3: Draw a circle with O as the centre and radius OP or OQ or OR. We get a circle passing through 3 points P, Q, and R.
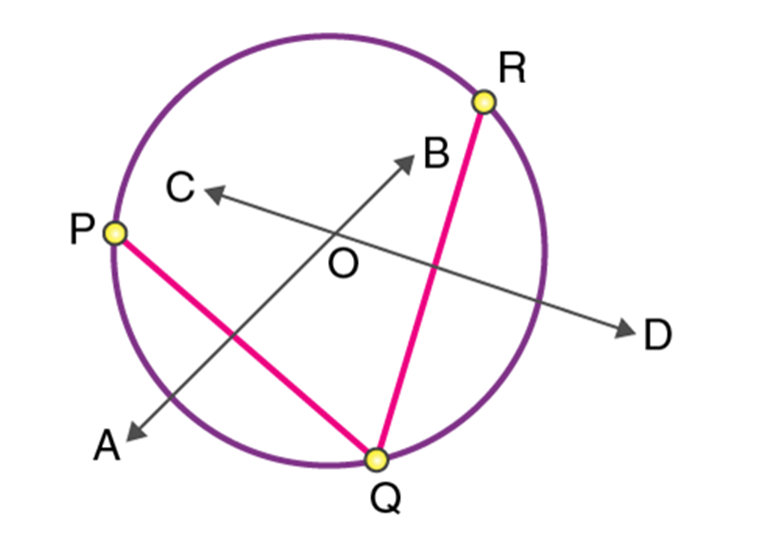
It is observed that only a unique circle will pass through all three points. It can be stated as a theorem and the proof is explained as follows.
It is observed that only a unique circle will pass through all three points. It can be stated as a theorem, and the proof of this is explained below.
Given:
Three non-collinear points P, Q and R
To prove:
Only one circle can be drawn through P, Q and R
Construction:
Join PQ and QR.
Draw the perpendicular bisectors of PQ and QR such that these perpendiculars intersect each other at O.
Proof:
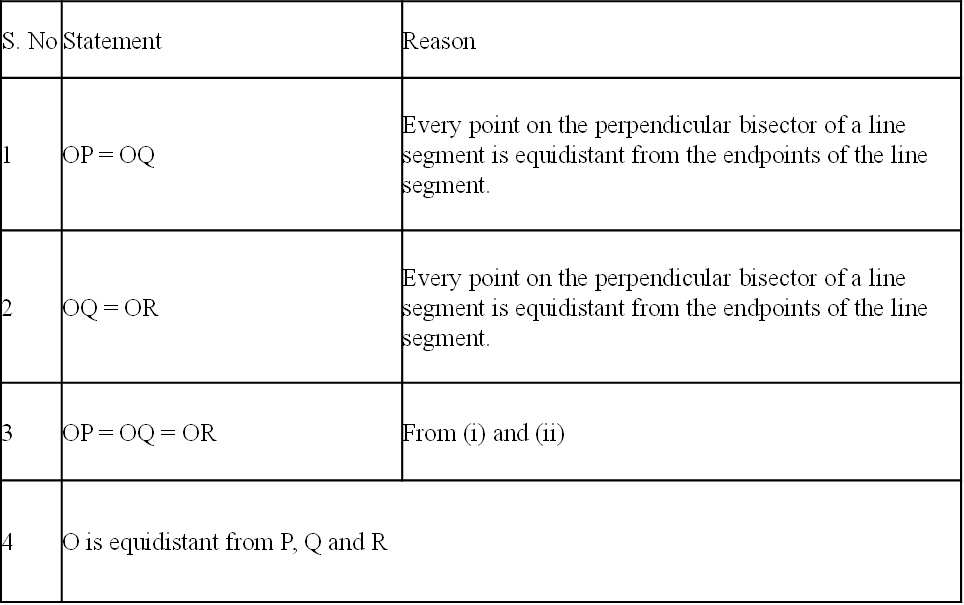
If a circle is drawn with O as centre and OP as radius, then it will also pass through Q and R.
O is the only point which is equidistant from P, Q and R as the perpendicular bisectors of PQ and QR intersect at O only.
Thus, O is the centre of the circle to be drawn.
OP, OQ and OR will be radii of the circle.
From above it follows that a unique circle passing through 3 points can be drawn given that the points are non-collinear.
Till now, you learned how to draw a circle passing through 3 non-collinear points. Now, you will learn how to find the equation of a circle passing through 3 points. For this we need to take three non-collinear points.
Circle Equation Passing Through 3 Points
Let’s derive the equation of the circle passing through the 3 points formula.
Let P(x1, y1), Q(x2, y2) and R(x3, y3) be the coordinates of three non-collinear points.
We know that,
The general form of equation of a circle is: x2 + y2 + 2gx + 2fy + c = 0….(1)
Now, we need to substitute the given points P, Q and R in this equation and simplify to get the value of g, f and c.
Substituting P(x1, y1) in equ(1),
x12 + y12 + 2gx1 + 2fy1 + c = 0….(2)
x22 + y22 + 2gx2 + 2fy2 + c = 0….(3)
x32 + y32 + 2gx3 + 2fy3 + c = 0….(4)
From (2) we get,
2gx1 = -x12 – y12 – 2fy1 – c….(5)
Again from (2) we get,
c = -x12 – y12 – 2gx1 – 2fy1….(6)
From (4) we get,
2fy3 = -x32 – y32 – 2gx3 – c….(7)
Now, subtracting (3) from (2),
2g(x1 – x2) = (x22 -x12) + (y22 – y12) + 2f (y2 – y1)….(8)
Substituting (6) in (7),
2fy3 = -x32 – y32 – 2gx3 + x12 + y12 + 2gx1 + 2fy1….(9)
Now, substituting equ(8), i.e. 2g in equ(9),
2f = [(x12 – x32)(x1 – x2) + (y12 – y32 )(x1 – x2) + (x22 – x12)(x1 – x3) + (y22 – y12)(x1 – x3)] / [(y3 – y1)(x1 – x2) – (y2 – y1)(x1 – x3)]
Similarly, we can get 2g as:
2g = [(x12 – x32)(y1 – x2) + (y12 – y32)(y1 – y2) + (x22 – x12)(y1 – y3) + (y22 – y12)(y1 – y3)] / [(x3 – x1)(y1 – y2) – (x2 – x1)(y1 – y3)]
Using these 2g and 2f values we can get the value of c.
Thus, by substituting g, f and c in (1) we will get the equation of the circle passing through the given three points.
Solved Example
Question:
What is the equation of the circle passing through the points A(2, 0), B(-2, 0) and C(0, 2)?
Solution:
Consider the general equation of circle:
x2 + y2 + 2gx + 2fy + c = 0….(i)
Substituting A(2, 0) in (i),
(2)2 + (0)2 + 2g(2) + 2f(0) + c = 0
4 + 4g + c = 0….(ii)
Substituting B(-2, 0) in (i),
(-2)2 + (0)2 + 2g(-2) + 2f(0) + c = 0
4 – 4g + c = 0….(iii)
Substituting C(0, 2) in (i),
(0)2 + (2)2 + 2g(0) + 2f(2) + c = 0
4 + 4f + c = 0….(iv)
Adding (ii) and (iii),
4 + 4g + c + 4 – 4g + c = 0
2c + 8 = 0
2c = -8
c = -4
Substituting c = -4 in (ii),
4 + 4g – 4 = 0
4g = 0
g = 0
Substituting c = -4 in (iv),
4 + 4f – 4 = 0
4f = 0
f = 0
Now, substituting the values of g, f and c in (i),
x2 + y2 + 2(0)x + 2(0)y + (-4) = 0
x2 + y2 – 4 = 0
Or
x2 + y2 = 4
This is the equation of the circle passing through the given three points A, B and C
Angle subtended by an arc of a circle
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
We know that the endpoints of a chord other than the diameter of a circle divide it into two arcs, namely the major arc and the minor arc. If we take two equal chords, we can say that equal chords make congruent arcs and conversely, congruent arcs make equal chords of a circle. In this article, we will discuss the theorem related to the angle subtended by an arc of a circle and its proof with a complete explanation.
Angle Subtended by an Arc of a Circle – Theorem and Proof
Theorem: The angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.
Proof: Consider a circle with center “O”. Here the arc PQ of the circle subtends angle POQ at Centre O and ∠PAQ at a point A on the remaining part of the circle.
To prove: ∠POQ = 2∠PAQ.
To prove this, join AO and extend it to point B.
There are two general cases while proving this theorem.
Case 1:
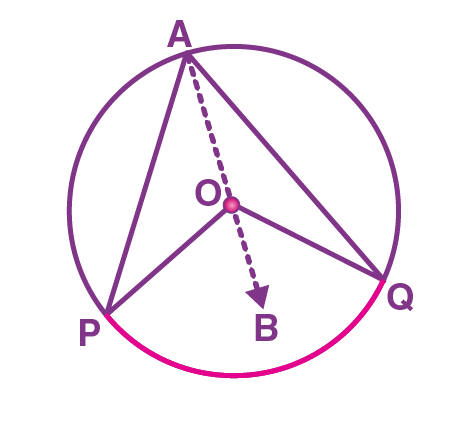
Consider a triangle APO,
Here, OA = OP (Radii)
Since, the angles opposite to the equal sides are equal,
∠OPA = ∠OAP …(1)
Also, by using the exterior angle property (exterior angle is the sum of interior opposite angles),
We can write,
∠BOP = ∠OAP + ∠OPA
By using (1),
∠BOP = ∠OAP + ∠OAP
∠BOP = 2∠OAP… (2)
Similarly, consider another triangle AQO,
OA = OQ (Radii)
As the angles opposite to the equal sides are equal,
∠OQA = ∠OAQ … (3)
Similarly, by using the exterior angle property, we get
∠BOQ = ∠OAQ + ∠OQA
∠BOQ = ∠OAQ + ∠OAQ (using (3))
∠BOQ = 2∠OAQ …(4)
Adding (2) and (4) we get,
∠BOP + ∠BOQ = 2∠OAP + 2∠OAQ
∠POQ = 2(∠OAP + ∠OAQ)
∠POQ = 2∠PAQ.
Hence, case (1) is proved.
Case 2:
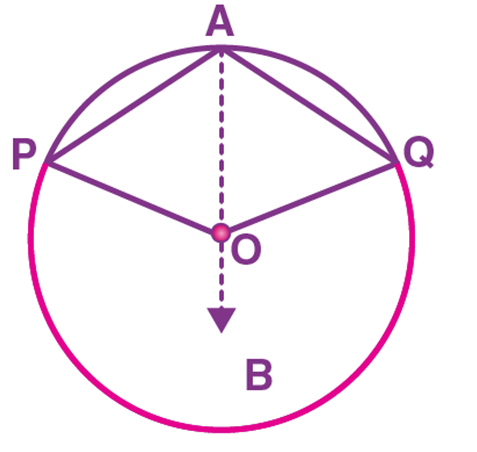
To prove ∠POQ = 2∠PAQ for this case, we can follow the steps as same as for case (1). But while adding (2) and (4), we have to follow the below steps.
∠BOP + ∠BOQ = 2∠OAP + 2∠OAQ
Reflex angle ∠POQ = 2(∠OAP + ∠OAQ) (Since, PQ is a Major arc)
Reflex angle ∠POQ = 2∠PAQ.
Hence, proved.
Theorem: Angle subtended by a diameter/ semicircle on any point of a circle is 90°
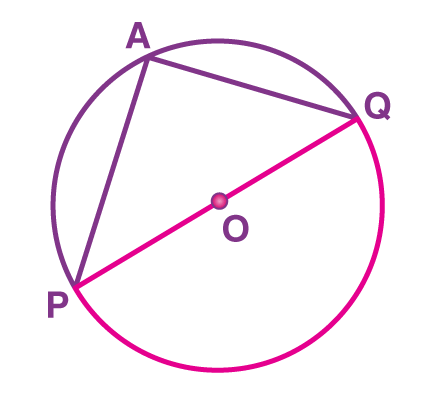
Consider a circle with center “O” and PQ be its diameter, subtending ∠PAQ at a point A on the circle.
Now, we need to prove that ∠PAQ = 90°.
Here, POQ is a straight line that passes through the center “O” of the circle.
Therefore, the angle subtended by arc PQ at O is
∠POQ = 180° (Since, POQ is a straight line) ….(5)
Now, by using the theorem, “The angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle”, we can write
∠POQ = 2 ∠PAQ
∠PAQ = ∠POQ/2
By using (5),
∠PAQ = 180°/2
∠PAQ = 90°
Therefore, the angle subtended by a diameter/ semicircle on any point of a circle is 90°.
Hence, proved.
Angle subtended by an arc of a circle
Angle Subtended by an Arc of a Circle
We know that the end points of a chord other than the diameter of a circle divides it into two arcs, namely the major arc and the minor arc. If we take two equal chords, we can say that equal chords make congruent arcs and conversely, congruent arcs make equal chords of a circle. In this article, we will discuss the theorem related to the angle subtended by an arc of a circle and its proof with complete explanation.
Angle Subtended by an Arc of a Circle – Theorem and Proof
Theorem:
The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
Proof:
Consider a circle with centre “O”. Here the arc PQ of the circle subtends angle POQ at Centre O and ∠PAQ at a point A on the remaining part of the circle.
To prove: ∠POQ = 2∠PAQ.
To prove this, join AO and extend it to point B.
There are two general cases while proving this theorem.
Case 1:
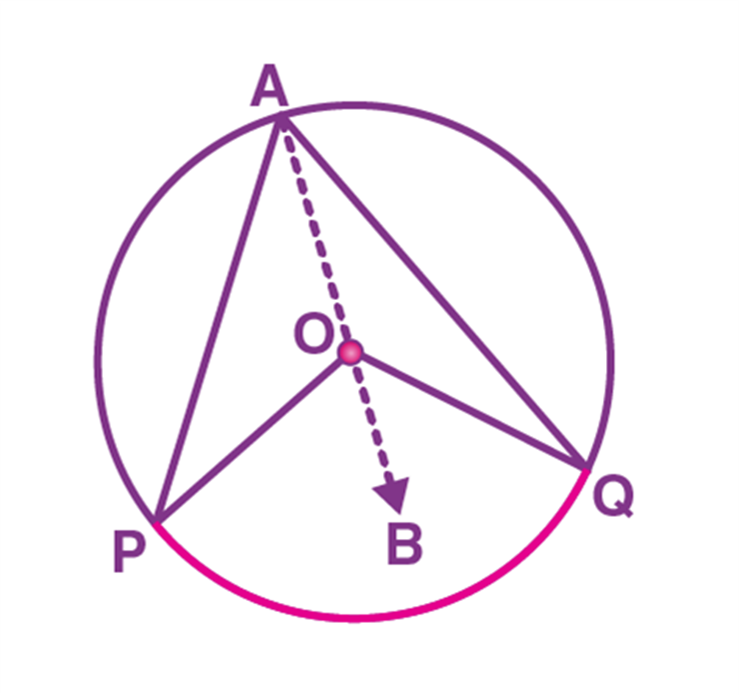
Consider a triangle APO,
Here, OA = OP (Radii)
Since, the angles opposite to the equal sides are equal,
∠OPA = ∠OAP …(1)
Also, by using the exterior angle property (exterior angle is the sum of interior opposite angles),
We can write,
∠BOP = ∠OAP + ∠OPA
By using (1),
∠BOP = ∠OAP + ∠OAP
∠BOP = 2∠OAP… (2)
Similarly, consider another triangle AQO,
OA = OQ (Radii)
As the angles opposite to the equal sides are equal,
∠OQA = ∠OAQ … (3)
Similarly, by using the exterior angle property, we get
∠BOQ = ∠OAQ + ∠OQA
∠BOQ = ∠OAQ + ∠OAQ (using (3))
∠BOQ = 2∠OAQ …(4)
Adding (2) and (4) we get,
∠BOP + ∠BOQ = 2∠OAP + 2∠OAQ
∠POQ = 2(∠OAP + ∠OAQ)
∠POQ = 2∠PAQ.
Hence, case (1) is proved.
Case 2:
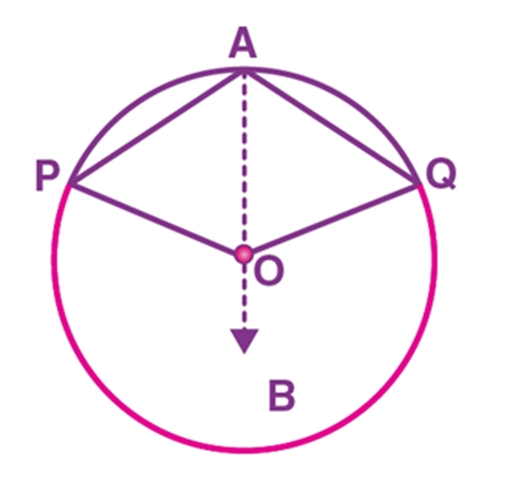
To prove ∠POQ = 2∠PAQ for this case, we can follow the steps as same as for case (1). But while adding (2) and (4), we have to follow the below steps.
∠BOP + ∠BOQ = 2∠OAP + 2∠OAQ
Reflex angle ∠POQ = 2(∠OAP + ∠OAQ) (Since, PQ is a Major arc)
Reflex angle ∠POQ = 2∠PAQ.
Hence, proved.
Theorem: Angle subtended by a diameter/ semicircle on any point of a circle is 90°
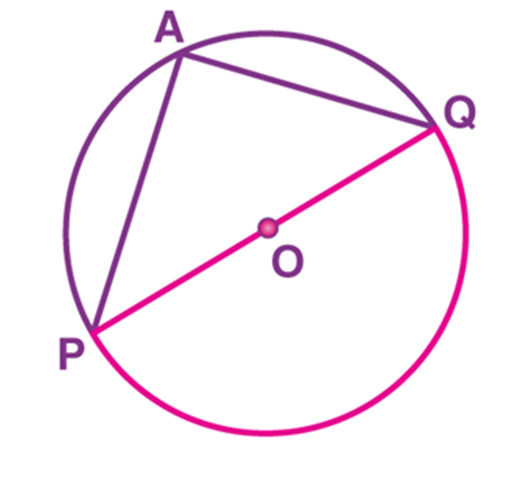
Consider a circle with centre “O” and PQ be its diameter, subtending ∠PAQ at a point A on the circle.
Now, we need to prove that ∠PAQ = 90°.
Here, POQ is a straight line that passes through the centre “O” of the circle.
Therefore, the angle subtended by arc PQ at O is
∠POQ = 180° (Since, POQ is a straight line) ….(5)
Now, by using the theorem, “The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle”, we can write
∠POQ = 2 ∠PAQ
∠PAQ = ∠POQ/2
By using (5),
∠PAQ = 180°/2
∠PAQ = 90°
Therefore, the angle subtended by a diameter/ semicircle on any point of a circle is 90°.
Hence, proved.
Cyclic Quadrilaterals
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Cyclic Quadrilateral
A cyclic quadrilateral is a quadrilateral that has all its four vertices lying on a circle. It is also sometimes called inscribed quadrilateral. The circle which consists of all the vertices of any polygon on its circumference is known as the circumcircle or circumscribed circle.
A quadrilateral is a 4 sided polygon bounded by 4 finite line segments. The word ‘quadrilateral’ is composed of two Latin words, Quadri meaning ‘four ‘and latus meaning ‘side’. It is a two-dimensional figure having four sides (or edges) and four vertices. A circle is the locus of all points in a plane that are equidistant from a fixed point.
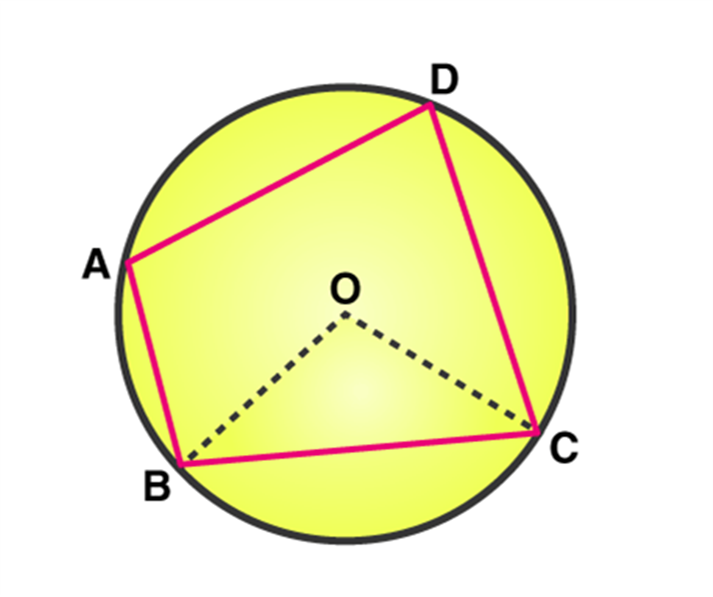
If all the four vertices of a quadrilateral ABCD lie on the circumference of the circle, then ABCD is a cyclic quadrilateral. In other words, if any four points on the circumference of a circle are joined, they form the vertices of a cyclic quadrilateral. It can be visualized as a quadrilateral that is inscribed in a circle, i.e. all four vertices of the quadrilateral lie on the circumference of the circle.
Cyclic Quadrilateral Definition
The definition states that a quadrilateral that is circumscribed in a circle is called a cyclic quadrilateral. It means that all the four vertices of the quadrilateral lie in the circumference of the circle. Let us understand with a diagram.
In the figure given below, the quadrilateral ABCD is cyclic.
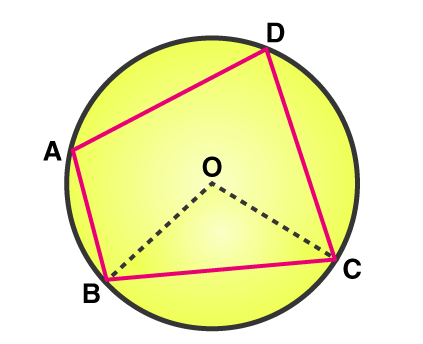
Let us do an activity. Take a circle and choose any 4 points on the circumference of the circle. Join these points to form a quadrilateral. Now measure the angles formed at the vertices of the cyclic quadrilateral. It is noted that the sum of the angles formed at the vertices is always 360o and the sum of angles formed at the opposite vertices is always supplementary.
Cyclic Quadrilateral Angles
The sum of the opposite angles of a cyclic quadrilateral is supplementary.
Let ∠A, ∠B, ∠C and ∠D are the four angles of an inscribed quadrilateral. Then,
∠A + ∠C = 180°
∠B + ∠D = 180°
Therefore, an inscribed quadrilateral also meets the angle sum property of a quadrilateral, according to which, the sum of all the angles equals 360 degrees. Hence,
∠A + ∠B + ∠C + ∠D= 360°
Radius of Cyclic Quadrilateral
If a, b, c and d are the successive sides of a cyclic quadrilateral, and s is the semi perimeter, then the radius is given by,
Diagonals of Cyclic Quadrilaterals
Suppose a,b,c and d are the sides of a cyclic quadrilateral and p & q are the diagonals, then we can find the diagonals of it using the below given formulas:
Area of Cyclic Quadrilateral
If a,b,c and d are the sides of an inscribed quadrilateral, then its area is given by:
Where s is the semiperimeter.
s = ½(a+b+c+d)
Cyclic Quadrilateral Theorems
There are two important theorems that prove the cyclic quadrilateral.
Theorem 1 - In a cyclic quadrilateral, the sum of either pair of opposite angles is supplementary.
Proof: Let us now try to prove this theorem.
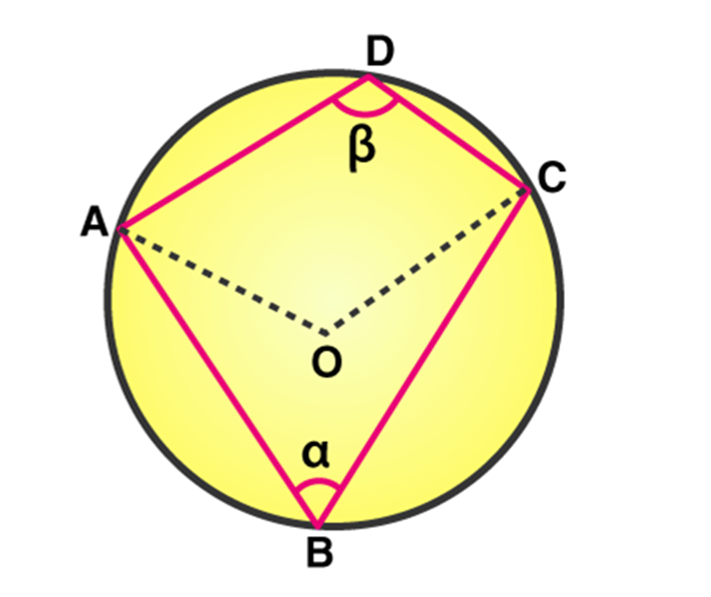
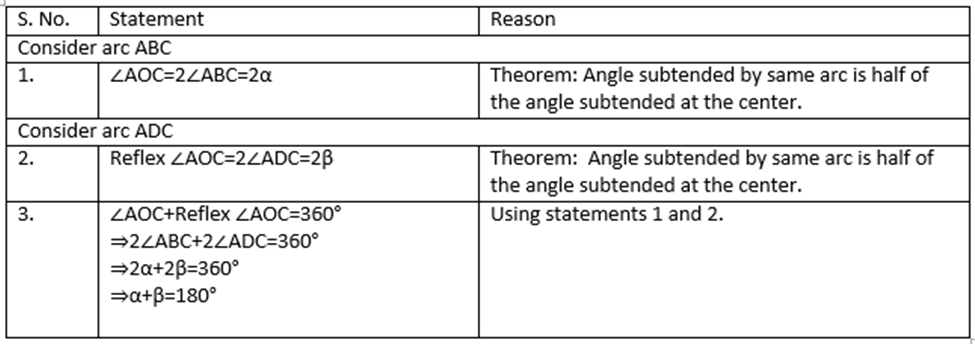
Given: Acyclic quadrilateral ABCD inscribed in a circle with center O.
Construction: Join the vertices A and C with center O.
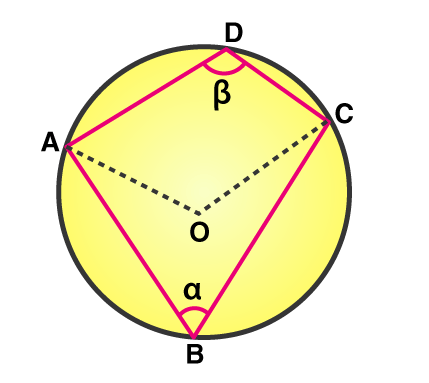
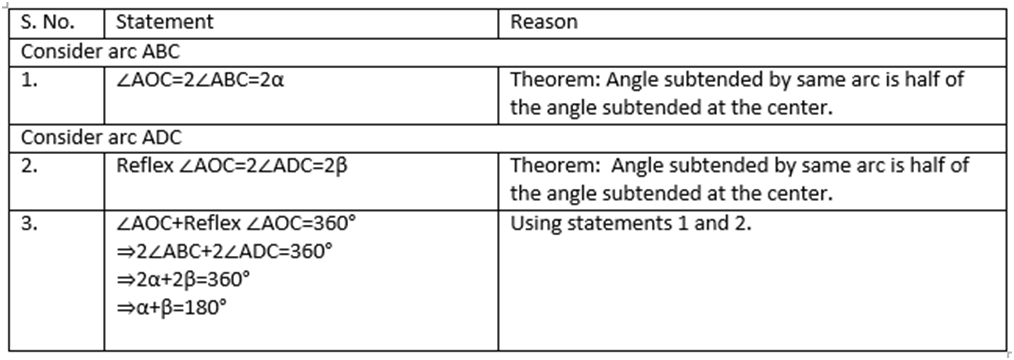
The converse of this theorem is also true, which states that if opposite angles of a quadrilateral are supplementary, then the quadrilateral is cyclic.
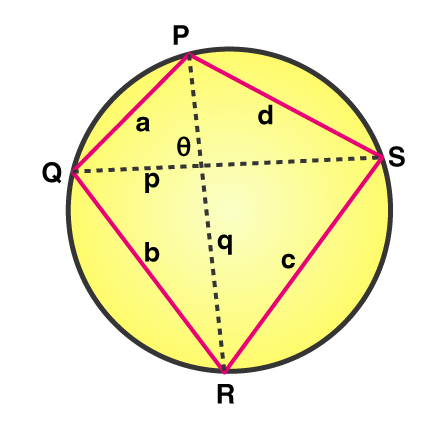
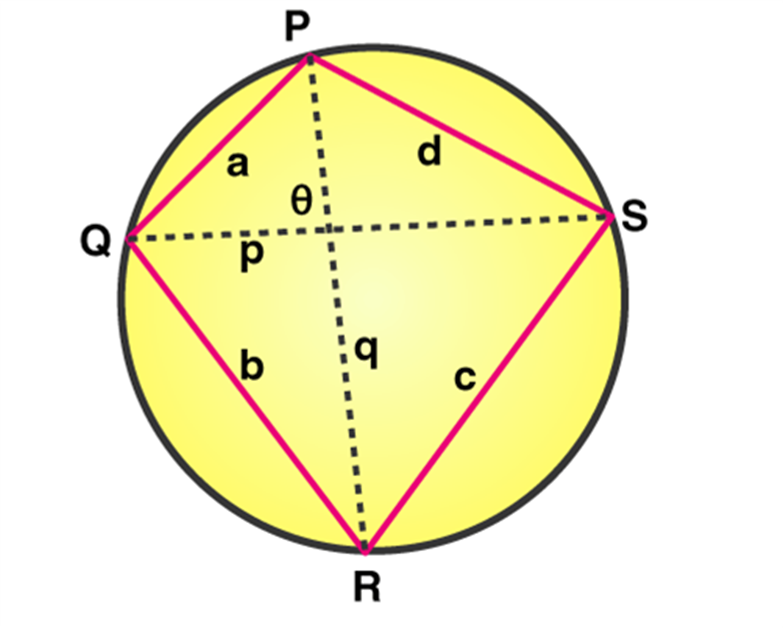
Theorem 2 - The ratio between the diagonals and the sides can be defined and is known as the Cyclic quadrilateral theorem. If there’s a quadrilateral that is inscribed in a circle, then the product of the diagonals is equal to the sum of the product of its two pairs of opposite sides.
If PQRS is a cyclic quadrilateral, PQ and RS, and QR and PS are opposite sides. PR and QS are the diagonals.
(PQ x RS) + ( QR x PS) = PR x QS
Properties of Cyclic Quadrilateral
• In a cyclic quadrilateral, the sum of a pair of opposite angles is 1800(supplementary).
• If the sum of two opposite angles is supplementary, then it’s a cyclic quadrilateral.
• The area of a cyclic quadrilateral is where a, b, c, and d are the four sides of the quadrilateral.
• The four vertices of a cyclic quadrilateral lie on the circumference of the circle.
• To get a rectangle or a parallelogram, just join the midpoints of the four sides in order.
• If PQRS is a cyclic quadrilateral, then ∠SPR = ∠SQR, ∠QPR = ∠QSR, ∠PQS = ∠PRS, ∠QRP = ∠QSP.
• If T is the point of intersection of the two diagonals, PT X TR = QT X TS.
• The exterior angle formed if any one side of the cyclic quadrilateral produced is equal to the interior angle opposite to it.
• In a given cyclic quadrilateral, d1 / d2 = sum of the product of opposite sides, which shares the diagonals endpoints.
• If it is a cyclic quadrilateral, then the perpendicular bisectors will be concurrent compulsorily.
• In a cyclic quadrilateral, the four perpendicular bisectors of the given four sides meet at the center O.
Problems and Solutions
Question: Find the value of angle D of a cyclic quadrilateral, if angle B is 60o.
Solution:
If ABCD is a cyclic quadrilateral, so the sum of a pair of two opposite angles will be 180°.
∠B + ∠ D = 180°
60° + ∠D = 180°
∠D = 180° – 60°
∠D = 120°
The value of angle D is 120°.
Question: Find the value of angle D of a cyclic quadrilateral, if angle B is 80°.
Solution:
If ABCD is a cyclic quadrilateral, so the sum of a pair of two opposite angles will be 180°.
∠B + ∠ D = 180°
80° + ∠D = 180°
∠D = 180° – 80°
∠D = 100°
The value of angle D is 100°.
Cyclic Quadrilaterals
Cyclic Quadrilateral
A cyclic quadrilateral is a quadrilateral which has all its four vertices lying on a circle. It is also sometimes called inscribed quadrilateral. The circle which consists of all the vertices of any polygon on its circumference is known as the circumcircle or circumscribed circle.
A quadrilateral is a 4 sided polygon bounded by 4 finite line segments. The word ‘quadrilateral’ is composed of two Latin words, Quadri meaning ‘four ‘and latus meaning ‘side’. It is a two-dimensional figure having four sides (or edges) and four vertices. A circle is the locus of all points in a plane which are equidistant from a fixed point.
If all the four vertices of a quadrilateral ABCD lie on the circumference of the circle, then ABCD is a cyclic quadrilateral. In other words, if any four points on the circumference of a circle are joined, they form the vertices of a cyclic quadrilateral. It can be visualized as a quadrilateral which is inscribed in a circle, i.e. all four vertices of the quadrilateral lie on the circumference of the circle.
Cyclic Quadrilateral Definition
The definition states that a quadrilateral which is circumscribed in a circle is called a cyclic quadrilateral. It means that all the four vertices of quadrilateral lie in the circumference of the circle. Let us understand with a diagram.
In the figure given below, the quadrilateral ABCD is cyclic.
Let us do an activity. Take a circle and choose any 4 points on the circumference of the circle. Join these points to form a quadrilateral. Now measure the angles formed at the vertices of the cyclic quadrilateral. It is noted that the sum of the angles formed at the vertices is always 360o and the sum of angles formed at the opposite vertices is always supplementary.
Cyclic Quadrilateral Angles
The sum of the opposite angles of a cyclic quadrilateral is supplementary.
Let ∠A, ∠B, ∠C and ∠D are the four angles of an inscribed quadrilateral. Then,
∠A + ∠C = 180°
∠B + ∠D = 180°
Therefore, an inscribed quadrilateral also meets the angle sum property of a quadrilateral, according to which, the sum of all the angles equals 360 degrees. Hence,
∠A + ∠B + ∠C + ∠D= 360°
Radius of Cyclic Quadrilateral
If a, b, c and d are the successive sides of a cyclic quadrilateral, and s is the semi perimeter, then the radius is given by,
Diagonals of Cyclic Quadrilaterals
Suppose a,b,c and d are the sides of a cyclic quadrilateral and p & q are the diagonals, then we can find the diagonals of it using the below given formulas:
If a,b,c and d are the sides of a inscribed quadrialteral, then its area is given by:
Where s is the semiperimeter.
s = ½(a+b+c+d)
Cyclic Quadrilateral Theorems
There are two important theorems which prove the cyclic quadrilateral.
Theorem 1
In a cyclic quadrilateral, the sum of either pair of opposite angles is supplementary.
Proof: Let us now try to prove this theorem.
Given: A cyclic quadrilateral ABCD inscribed in a circle with center O.
Construction: Join the vertices A and C with center O.
The converse of this theorem is also true, which states that if opposite angles of a quadrilateral are supplementary, then the quadrilateral is cyclic.
Theorem 2
The ratio between the diagonals and the sides can be defined and is known as Cyclic quadrilateral theorem. If there’s a quadrilateral which is inscribed in a circle, then the product of the diagonals is equal to the sum of the product of its two pairs of opposite sides.
If PQRS is a cyclic quadrilateral, PQ and RS, and QR and PS are opposite sides. PR and QS are the diagonals.
(PQ x RS) + ( QR x PS) = PR x QS
Properties of Cyclic Quadrilateral
|
|
where a, b, c, and d are the four sides of the quadrilateral. |
|
|
|
|
|
|
|
|
Problems and Solutions
Question: Find the value of angle D of a cyclic quadrilateral, if angle B is 60o.
Solution:
If ABCD is a cyclic quadrilateral, so the sum of a pair of two opposite angles will be 180°.
∠B + ∠ D = 180°
60° + ∠D = 180°
∠D = 180° – 60°
∠D = 120°
The value of angle D is 120°.
Question: Find the value of angle D of a cyclic quadrilateral, if angle B is 80°.
Solution:
If ABCD is a cyclic quadrilateral, so the sum of a pair of two opposite angles will be 180°.
∠B + ∠ D = 180°
80° + ∠D = 180°
∠D = 180° – 80°
∠D = 100°
The value of angle D is 100°.
You should practise more examples using cyclic quadrilateral formulas to understand the concept better.
Equal Chords and their distances from the centre
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
In Mathematics, a chord is the line segment that joins two points on the circumference of a circle. In general, a circle can have infinitely many chords. The distance of the line from a point is defined as the perpendicular distance from a point to a line. If you draw infinite chords to a circle, the longer chord is close to the center of the circle, than the smaller chord of a circle. In this article, we will discuss the theorem and proof related to the equal chords and their distance from the center and also its converse theorem in detail.
Equal Chords and their Distance from the Centre – Theorem and Proof
Theorem: Equal chords of a circle (or of congruent circles) are equidistant from the center (or centers).
Proof: Consider a circle with “O”.
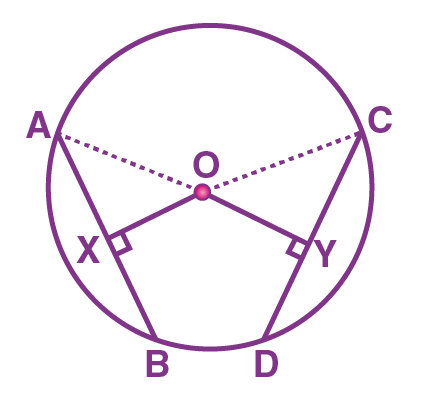
AB and CD are the equal chords of a circle.
(i.e) AB = CD
The line OX is perpendicular to the chord AB and OY is perpendicular to the chord CD.
We have to prove OX = OY.
Also, the line OX is perpendicular to AB.
As the perpendicular from the center of the circle to a chord, bisects the chord, we can write it as
AX = BX = AB/2 …(1)
Similarly, the line OY is perpendicular to CD,
CY = DY = CD/2 ….(2) [Since, the perpendicular from the center of the circle to a chord, bisects the chord)
Given that, AB = CD
AB/2 = CD/2
Therefore, AX = CY …(3) [Using (1) and (2)]
Now, by using the triangles AOX and COY,
∠ OXA = ∠ OYC (Both are 90°)
OA = OC (Radii)
AX = CY (From equation (3))
From the RHS rule, we can write it as
∆ AOX ≅ ∆ COY
Hence, we can conclude that OX = OY (Using CPCT)
Therefore, the theorem “equal chords of a circle (or of congruent circles) are equidistant from the center (or centers)”, is proved.
Converse of this Theorem
The converse of the above-mentioned theorem is “chords equidistant from the center of a circle are equal in length”.
Example
Question: Two intersecting chords of a circle make equal angles with the diameter that passes through their point of intersection. Prove that the chords are equal.
Solution: Given that AB and CD are the two chords of a circle with a center “O” and it intersects at the point “E” as shown in the figure.
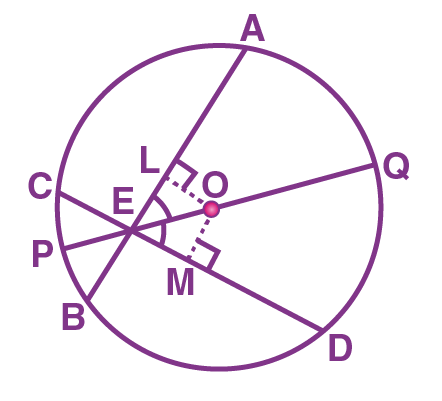
PQ is the diameter of a circle (longest chord of a circle), that passes through the point of intersection E, such that it makes an angle ∠ AEQ = ∠ DEQ.
Now, we need to prove that AB = CD.
Now, draw the perpendicular OL to the chord AB and the perpendicular line OM to the chord CD.
By using the angle sum property of a triangle, we can write it as:
∠ LOE = 180° – 90° – ∠ LEO
∠ LOE = 90° – ∠ LEO
= 90° – ∠ AEQ = 90° – ∠ DEQ
= 90° – ∠ MEO = ∠ MOE
Therefore,
∠ LOE = ∠ MOE
From the triangles, OLE and OME, we observe that
∠ LOE = ∠ MOE
Also, ∠ LEO = ∠ MEO
EO = EO (Common side)
Therefore, we will say that the triangles OLE and OME are congruent with each other.
(i.e) ∆ OLE ≅ ∆ OME
Thus, by using the CPCT rule,
OL = OM
By using equal chords and their distance from the center theorem, we can say,
AB = CD.
So, the chords AB and CD are equal.
Hence, proved.
Practice Problems
Solve the following problems.
- Find the length of the common chord, if two circles of radii 5 cm and 3 cm intersect at two points and the distance between the centers is 4 cm.
- The two equal chords of a circle intersect within a circle. Prove that the segments of one chord are equal to the corresponding segments of the other chord.
Equal Chords and their distances from the centre
Equal Chords and their distances from the centre
In Mathematics, a chord is the line segment which joins two points on the circumference of a circle. In general, a circle can have infinitely many chords. The distance of the line from a point is defined as the perpendicular distance from a point to a line. If you draw infinite chords to a circle, the longer chord is close to the centre of the circle, than the smaller chord of a circle. In this article, we will discuss the theorem and proof related to the equal chords and their distance from the centre and also its converse theorem in detail.
Equal Chords and their Distance from the Centre – Theorem and Proof
Theorem:
Equal chords of a circle (or of congruent circles) are equidistant from the centre (or centres).
Proof:
Consider a circle with “O”.
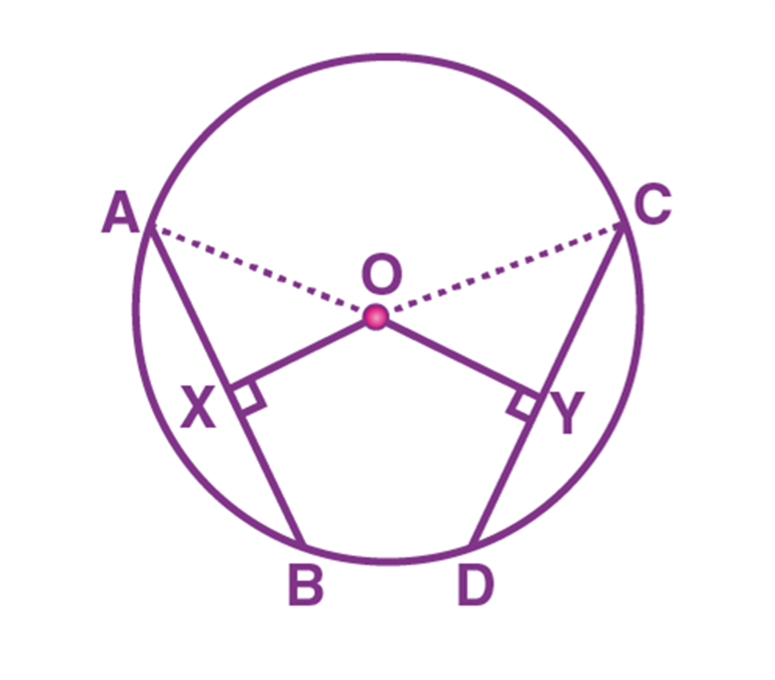
AB and CD are the equal chords of a circle.
(i.e) AB = CD
The line OX is perpendicular to the chord AB and OY is perpendicular to the chord CD.
We have to prove OX = OY.
Also, the line OX is perpendicular to AB.
As the perpendicular from the centre of the circle to a chord, bisects the chord, we can write it as
AX = BX = AB/2 …(1)
Similarly, the line OY is perpendicular to CD,
CY = DY = CD/2 ….(2) [Since, the perpendicular from the centre of the circle to a chord, bisects the chord)
Given that, AB = CD
AB/2 = CD/2
Therefore, AX = CY …(3) [Using (1) and (2)]
Now, by using the triangles AOX and COY,
∠ OXA = ∠ OYC (Both are 90°)
OA = OC (Radii)
AX = CY (From equation (3))
From the RHS rule, we can write it as
∆ AOX ≅ ∆ COY
Hence, we can conclude that OX = OY (Using CPCT)
Therefore, the theorem “equal chords of a circle (or of congruent circles) are equidistant from the centre (or centres)”, is proved.
Converse of this Theorem
The converse of the above-mentioned theorem is “chords equidistant from the centre of a circle are equal in length”.
Example
Question:
Two intersecting chords of a circle make equal angles with the diameter that passes through their point of intersection. Prove that the chords are equal.
Solution:
Given that AB and CD are the two chords of a circle with centre “O” and it intersects at the point “E” as shown in the figure.
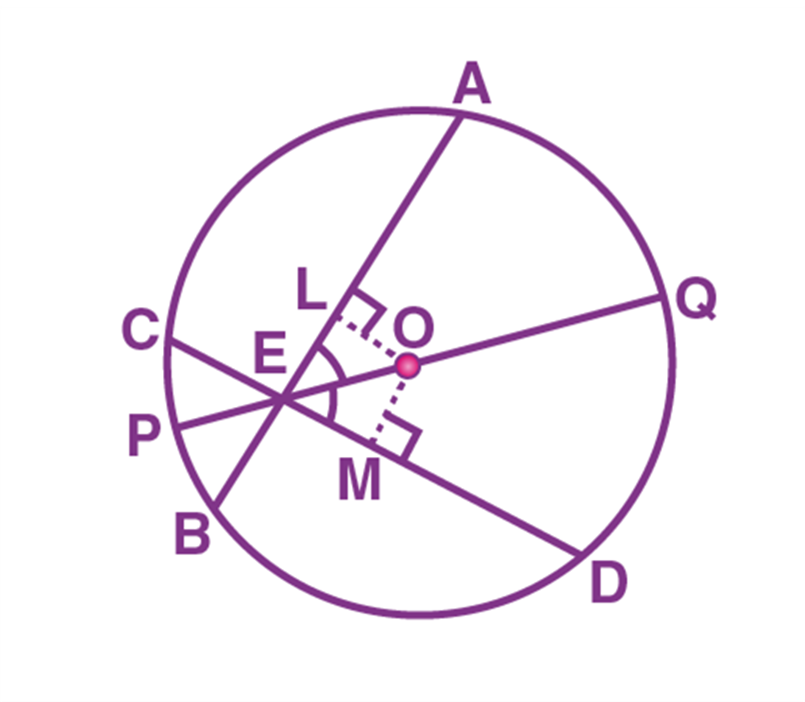
PQ is the diameter of a circle (longest chord of a circle), that passes through the point of intersection E, such that it makes an angle ∠ AEQ = ∠ DEQ.
Now, we need to prove that AB = CD.
Now, draw the perpendicular OL to the chord AB and the perpendicular line OM to the chord CD.
By using the angle sum property of a triangle, we can write it as:
∠ LOE = 180° – 90° – ∠ LEO
∠ LOE = 90° – ∠ LEO
= 90° – ∠ AEQ = 90° – ∠ DEQ
= 90° – ∠ MEO = ∠ MOE
Therefore,
∠ LOE = ∠ MOE
From the triangles, OLE and OME, we observe that
∠ LOE = ∠ MOE
Also, ∠ LEO = ∠ MEO
EO = EO (Common side)
Therefore, we will say that the triangles OLE and OME are congruent to each other.
(i.e) ∆ OLE ≅ ∆ OME
Thus, by using the CPCT rule,
OL = OM
By using equal chords and their distance from the centre theorem, we can say,
AB = CD.
So, the chords AB and CD are equal.
Hence, proved.
Practice Problems
Solve the following problems.
- Find the length of the common chord, if two circles of radii 5 cm and 3 cm intersect at two points and the distance between the centres is 4 cm.
- The two equal chords of a circle intersect within a circle. Prove that the segments of one chord are equal to the corresponding segments of the other chord.

 ABCD CLASSES
ABCD CLASSES