Construction
In Constructions class 9 chapter 11, explains how different shapes are drawn using the compass and ruler. In this chapter, you can learn how to construct the bisector of the given angle, construction of a perpendicular bisector of the given line segment is explained with construction steps and a clear diagram. Also, solve all the important questions for class 9 Maths Chapter 11 construction problems given in the textbook to score good marks.

Constructions Class 9 Concepts

The important topics and subtopics covered under constructions class 9 are:

• Introduction
• Basic constructions
• Some constructions of triangles
• Summary

Construction Class 9 Notes

For constructing the angle bisector of angle ABC, take B as a center and construct an arc (any radius) intersecting the rays BA and BC at D and E. Now take E and D as centers and a radius of more than ½ DE, construct arcs such that they intersect with each other at F.

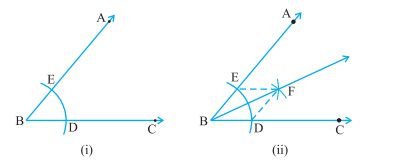
Join BF. This line is the required angle bisector of the given angle ABC.

Proof: Join EF and DF. Now, from triangle BEF and triangle BDF, BD = BE (Radius of the same arc), DF = EF (Arcs of equal radii) and BF are Common. Therefore, triangle BEF is congruent to triangle BDF by SSS congruence rule. Hence by CPCT, angle EBF is equal to angle DBF.

Constructions Class 9 Example

Go through the below example:

Example: Given that AB is a line segment. Construct the perpendicular bisector for the given line segment. 

Construction Steps:

1. Take A and B as centers and the radius should be more than 1/2 AB. Now, draw arcs on both sides of the line segment AB (the arc should intersect each other)
2. Assume that these arcs intersect each other at the points P and Q, and join the points PQ
3. Now, PQ intersect AB at the point M. Therefore, the line PMQ is the required perpendicular bisector of AB

Now, let us see how this method gives us the perpendicular bisector of AB.

To prove this, join A and B to both P and Q to form AP, AQ, BP and BQ.

From the triangles PAQ and PBQ

AP = BP and AQ = BQ (Arcs of equal radii)

PQ = PQ (Common)

Therefore, by using SSS Rule, ∆ PAQ ≅ ∆ PBQ

Thus, ∠ APM = ∠ BPM (CPCT)

Now in the triangles PMA and PMB,

AP = BP

PM = PM (Common)

∠ APM = ∠ BPM

Thus by using SAS rule, we get ∆ PMA ≅ ∆ PMB 

Hence, by using CPCT, AM = BM and ∠ PMA = ∠ PMB

From the linear pair axiom ∠ PMA + ∠ PMB = 180° 

∠ PMA = ∠ PMB = 90°

Therefore, the line PM, that is, PMQ is the perpendicular bisector of the line segment AB.

Practice Problems

Solve the practical problems given below for constructions class 9:

1. Construct an angle of 45° at the initial point of a given ray. And also, justify the construction. 
2. Construct a triangle ABC in which ∠B = 30°, ∠C = 90° and AB + BC+ CA = 11 cm.
3. Construct a triangle XYZ in which YZ = 8cm, ∠Y = 45° and XY – XZ= 3.5 cm
4. Construct the angle 105°, and verify that using the protractor.

Basic Constructions

Why do we learn constructions? Suppose a building needs to be constructed. One needs to know the accurate map of the building. Construction means drawing the lines and angles accurately. Also to draw the road maps, learning the basic constructions is of great importance. Let us now learn about the basic constructions in geometry.

Suggested Videos

Construction of segment of a circle

Some Constructions of Triangles I

Construct a perpendicular bisector of a line segment

Basic Constructions

1. Construction of a bisector of a given angle

Construction:

1. With A as a center and using compasses, draw an arc that cuts both rays of A.
2. Label the points of intersection as B and C.
3.  Now with B as a center, draw (in the interior of A) an arc whose radius is more than half the length BC.
4. With the same radius and with C as a center, draw another arc in the interior of A.
5. Let the two arcs intersect at D
6. So we get AD as the required bisector of A.

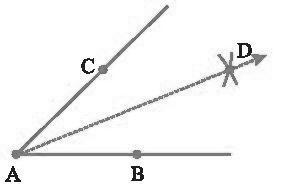
2. Construction of the perpendicular bisector of a given line segment.

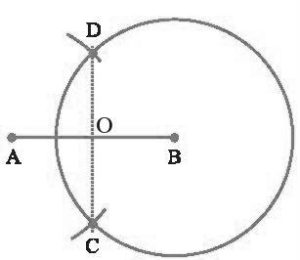
Construction:

1. Draw a line segment AB
2. Now take  A as a center, use compasses, and draw a circle.
3. The radius of your circle should be more than half the length of AB.
4. With the same radius and with B as a center, draw another circle using compasses.
5. Let it cut the previous circle at C and D.
6. Join CD so it cuts AB at O.
7. O is the midpoint of AB. Also, COA and COB are at right angles.
8. Therefore, the CD is the perpendicular bisector of AB.

3.  Construction of 60° Angle

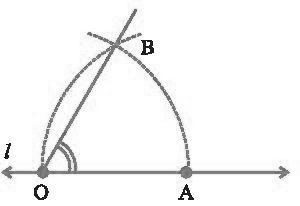
Construction:

1. Take a ruler and draw a line l and make a point O on it. Take a compass and put its one end at point O and draw an arc with any convenient radius.
2. We take the center O and draw an arc. We get to point A.
3. Now take the compass and with the same orientation taking the point A as the center draw an arc that passes through O. Draw an arc such that it intersects the existing arc.
4. Here OA and OB are nothing but the radius which is equal in length.
5. So actually we are trying to draw an equilateral triangle which means the angle we see in the above construction is 60 degrees.
6. We get ∠BOA which measures 60 degrees.

​​​​​​​Solved Examples for You on Basic Constructions

Question 1: To construct a perpendicular to a line L from a point P outside the line, steps are given in the jumbled form. Identify the second step from the following.

1) Draw line PQ
2) Draw a line L and consider point P outside the line.
3) Take  P as a center, draw 2 arcs on line L  and name it as points A and B respectively.
4) Taking A and B  as a center one by one and keeping the same distance in compass, draw the arcs on another side of the plane. The point where these arcs intersect name that point as Q

1. 4
2. 3
3. 2
4. 1

Solution: B is the correct option. 3 is the second step amongst all.

Question 2: While constructing a parallel line to a given line, we ______.

1. Copy a segment
2. Bisect a segment
3. Copy an angle
4. Construct a perpendicular

Solution: C is the correct option. While constructing a parallel line to a given line, we copy an angle.

Chapter 11 -  Construction

In Constructions class 9 chapter 11, explains how different shapes are drawn using the compass and ruler. In this chapter, you can learn how to construct the bisector of the given angle, construction of a perpendicular bisector of the given line segment are explained with construction steps and clear diagram. Also, solve all the important questions for class 9 Maths Chapter 11 construction problems given in the textbook to score good marks.

Constructions Class 9 Concepts

The important topics and subtopics covered under constructions class 9 are:

• Introduction
• Basic constructions
• Some constructions of triangles
• Summary

Construction Class 9 Notes

For constructing the angle bisector of angle ABC, take B as a centre construct an arc (any radius) intersecting the rays BA and BC at D and E. Now take E and D as centres and radius more than ½ DE, construct arcs such that they intersect with each other at F.

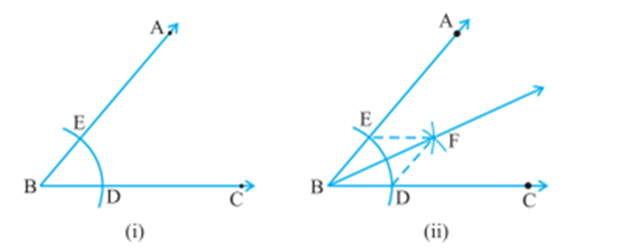
Join BF. This line is the required angle bisector of given angle ABC.

Proof:

Join EF and DF. Now, from triangle BEF and triangle BDF, BD = BE (Radius of the same arc), DF = EF (Arcs of equal radii) and BF is Common. Therefore, triangle BEF is congruent to triangle BDF by SSS congruence rule. Hence by CPCT, angle EBF is equal to angle DBF.

Constructions Class 9 Example

Go through the below example:

Example: 

Given that AB is a line segment. Construct the perpendicular bisector for the given line segment. 

Construction Steps:

1. Take A and B as centres and radius should be more than 1/2 AB. Now, draw arcs on both sides of the line segment AB (the arc should intersect each other)
2. Assume that these arcs intersect each other at the points P and Q, and join the points PQ
3. Now, PQ intersect AB at the point M. Therefore, the line PMQ is the required perpendicular bisector of AB

Now, let us see how this method gives us the perpendicular bisector of AB.

To prove this, join A and B to both P and Q to form AP, AQ, BP and BQ.

From the triangles PAQ and PBQ

AP = BP and AQ = BQ (Arcs of equal radii)

PQ = PQ (Common)

Therefore, by using SSS Rule, ∆ PAQ ≅ ∆ PBQ

Thus, ∠ APM = ∠ BPM (CPCT)

Now in the triangles PMA and PMB,

AP = BP

PM = PM (Common)

∠ APM = ∠ BPM

Thus by using SAS rule, we get ∆ PMA ≅ ∆ PMB 

Hence, by using CPCT, AM = BM and ∠ PMA = ∠ PMB

From the linear pair axiom ∠ PMA + ∠ PMB = 180° 

∠ PMA = ∠ PMB = 90°

Therefore, the line PM, that is, PMQ is the perpendicular bisector of the line segment AB.

Practice Problems

Solve the practical problems given below for constructions class 9:

1. Construct an angle of 45° at the initial point of a given ray. And also, justify the construction. 
2. Construct a triangle ABC in which ∠B = 30°, ∠C = 90° and AB + BC+ CA = 11 cm.
3. Construct a triangle XYZ in which YZ = 8cm, ∠Y = 45° and XY – XZ= 3.5 cm
4. Construct the angle 105°, and verify that using the protractor.

Basic Constructions

Why do we learn constructions? Suppose a building needs to be constructed. One needs to know the accurate map of the building. Construction means to draw the lines and angles accurately. Also to draw the road maps, learning the basic constructions is of great importance. Let us now learn about the basic constructions in geometry.

Suggested Videos

Construction of segment of circle

Some Constructions of Triangles I

Construct perpendicular bisector of a line segment

Basic Constructions

1. Construction of a bisector of a given angle

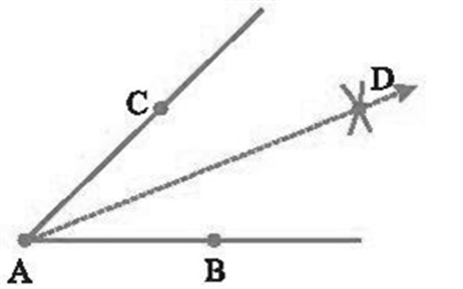
Construction:

1. With A as a centre and using compasses, draw an arc that cuts both rays of A.
2. Label the points of intersection as B and C.
3.  Now with B as a centre, draw (in the interior of A) an arc whose radius is more than half the length BC.
4. With the same radius and with C as a centre, draw another arc in the interior of A.
5. Let the two arcs intersect at D
6. So we get AD as the required bisector of A.

2. Construction of the perpendicular bisector of a given line segment.

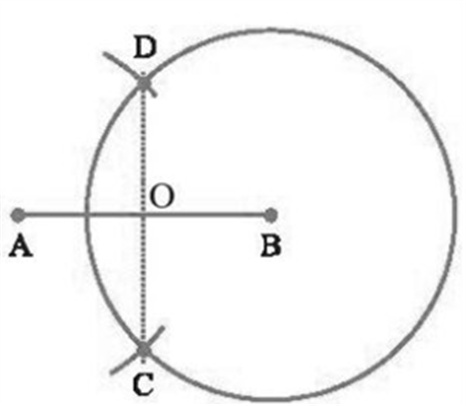
Construction:

1. Draw a line segment AB
2. Now take  A as a centre, using compasses, draw a circle.
3. The radius of your circle should be more than half the length of AB.
4. With the same radius and with B as a centre, draw another circle using compasses.
5. Let it cut the previous circle at C and D.
6. Join CD so it cuts AB at O.
7. O is the midpoint of AB. Also, COA and COB are right angles.
8. Therefore, the CD is the perpendicular bisector of AB.

3.  Construction of 60° Angle

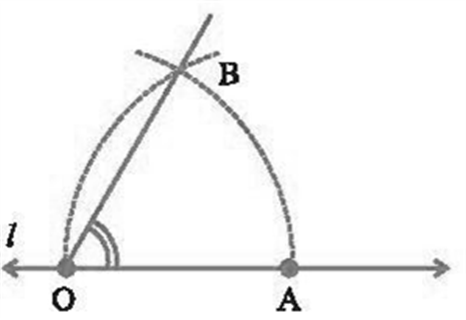
Construction:

1. Take a ruler and draw a line l and make a point O on it. Take a compass and put its one end at point O and draw an arc with any convenient radius.
2. We take the centre O and draw an arc. We get the point A.
3. Now take the compass and with the same orientation taking the point A as the centre draw an arc that passes through O. Draw an arc such that it intersects the existing arc.
4. Here OA and OB are nothing but the radius which is equal in length.
5. So actually we are trying to draw an equilateral triangle which means the angle we see in the above construction is 60 degree.
6. We get ∠BOA which measures 60 degrees.

Solved Examples for You on Basic Constructions

Question 1: To construct a perpendicular to a line L from a point P outside the line, steps are given in the jumbled form. Identify the second step from the following.

1)Draw line PQ
2)Draw a line L and consider point P outside the line.
3)Take  P as a centre, draw 2 arcs on line L  and name it as points A and B respectively.
4)Taking A and B  as a centre one by one and keeping the same distance in compass, draw the arcs on another side of the plane.The point where these arcs intersect name that point as Q

1. 4
2. 3
3. 2
4. 1

Solution: B is the correct option. 3 is the second step amongst all.

Question 2: While constructing a parallel line to a given line, we ______.

1. Copy a segment
2. Bisect a segment
3. Copy an angle
4. Construct a perpendicular

Solution: C is the correct option. While constructing a parallel line to a given line, we copy an angle.

Constructing Triangles

Constructing triangles will include the construction of different triangles using a protractor, a compass and a ruler. A triangle is a three-sided polygon. It has three sides, three vertices and three angles. Construction of triangles is easy when the measurements are given to us based on different properties such as SSS, SAS and ASA.

Let us learn here to construct a triangle with given measurements. Also, learn to draw triangles of some special cases.

How to Construct Triangles?

To construct a triangle one should know these properties and rules:

• All three sides are given (SSS – Side side side)
• Two sides and included angle are given (SAS – Side angle side)
• Two angles and the included side is given (ASA – Angle side angle)
• The measure of the hypotenuse and a side is given in the right triangle (RHS – Right angle hypotenuse side)

For constructing triangles from given data, we generally make use of the given congruency conditions and construct the required triangle.

Constructing triangle With SSS Property

When the length of three sides of the triangle is given, then follow the below steps to construct the required triangle.

• Draw a line segment AB, of length equal to the longest side of the triangle
• Now using a compass and ruler take the measure of the second side and draw an arc
• Again take the measure of the third side and cut the previous arc at a point C
• Now join the endpoints of the line segment to point C and get the required triangle ABC

Constructing triangle with SAS Property

When the length of the two sides and the angle included between them are given, then use the following steps to construct the triangle.

• Draw a line segment AB, of length equal to the longest side of the triangle, using a ruler
• Put the center of the protractor on one end of a line segment (say A) and measure the given angle. Join the points and construct a ray, such that the ray is nearer to the line segment AB
• Take the measure of another given side of the triangle using a compass and a ruler
• Put the compass at point A and cut the ray at another point, C
• Now join the other end of the line segment, i.e., B to the point C
• Hence, the triangle ABC is constructed

Constructing triangle with ASA Property

When the measures of two angles and the side included between them are given of a triangle, then it is said to be ASA congruency. Follow the given steps to draw a triangle with ASA property.

• Draw a line segment AB, of length equal to the given side of the triangle, using a ruler
• At one endpoint of a line segment (say A) measure one of the given angles and draw a ray AR
• At another endpoint of a line segment (i.e., B) measure the other angle using a protractor and draw the ray BQ, such that it cuts the previous ray at a point P
• Join the previous point P, with both the endpoints A and B of the line segment AB, to get the required triangle

Construction triangle with RHS Property

When the hypotenuse side and any one of the other two sides of a right triangle are given, then it is RHS property. Follow the given steps to draw a triangle with RHS property.

• Draw the line segment AB, equal to the measure of the hypotenuse side
• At one endpoint, say A, of line-segment measure the angle equal to 90 degrees and draw a ray, AR
• Measure the length of another given side and draw an arc to cut the ray AR at a point P
• Now join the points P and B to get the required right triangle

Special Cases of Constructing Triangles

There are a few special cases of constructing triangles that are discussed here.

Construction of Triangles – Case 1

Given the base of a triangle, its base angle and the sum of the other two sides

For constructing ∆ABC such that base BC, base angle ∠B and the sum of the other two sides, i.e. AB + AC are given, the following steps of construction are followed:

Steps of Construction of a Triangle

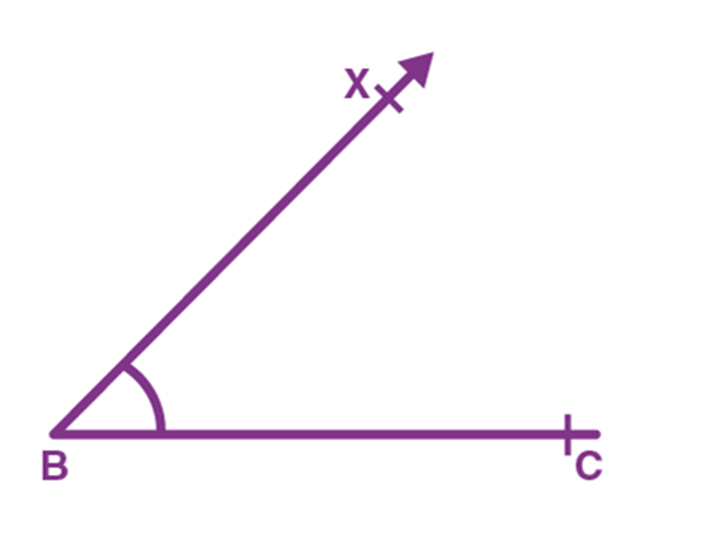
Step 1. Draw the base BC of ∆ABC as given and construct ∠XBC of the given measure at B as shown.

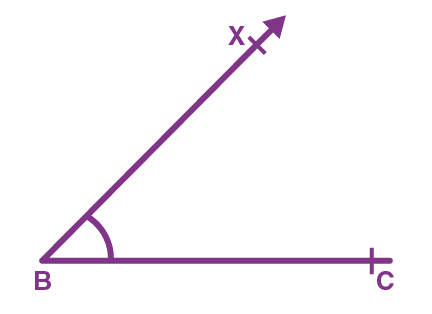
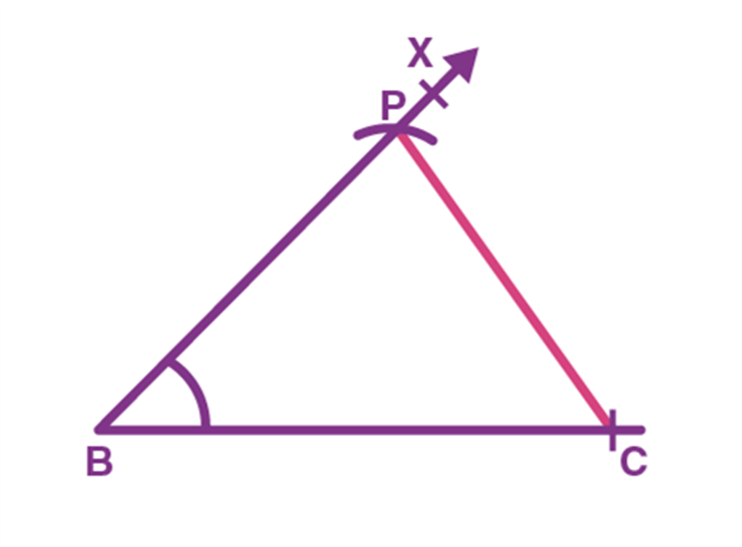
Step 2. Keeping the compass at point B cut an arc from the ray BX such that its length equals AB + AC at point P and join it to C as shown in the figure.

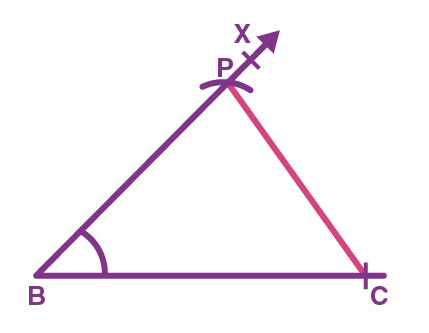
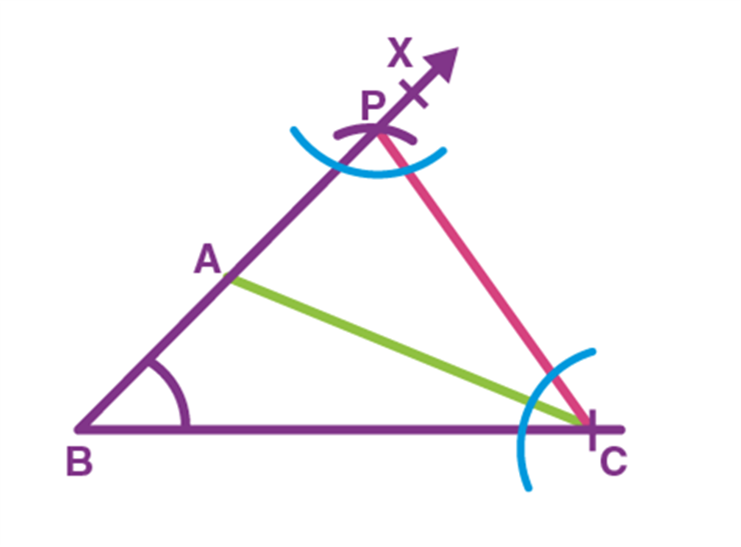
Step 3. Now measure ∠BPC and from C, draw an angle equal to ∠BPC as shown in the figure.

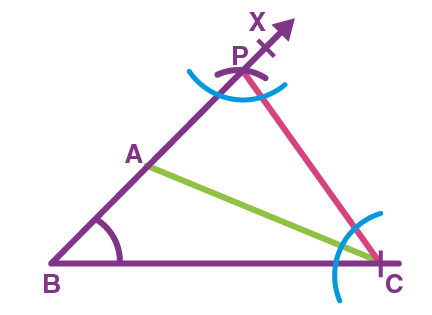
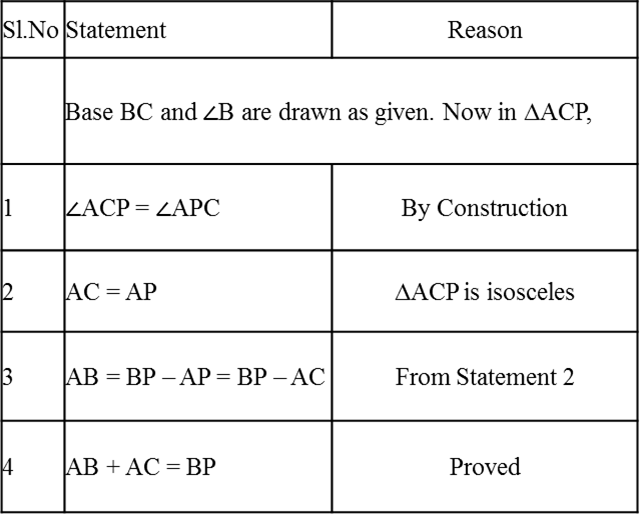
∆ABC is the required triangle. This can be proved as follows:

Base BC and ∠B are drawn as given. Now in ∆ACP,

Sl.No	Statement	Reason
1	∠ACP = ∠APC	By Construction
2	AC = AP	∆ACP is isosceles
3	AB = BP – AP = BP – AC	From Statement 2
4	AB + AC = BP	Proved

Construction of Triangles – Case 2

Given the base of a triangle, its base angle and the difference between the other two sides

For constructing ∆ABC such that base BC, base angle∠B and difference of the other two sides, i.e. AB – AC or  AC-AB is given, then for constructing triangles such as these two cases can arise:

1. AB > AC
2. AC > AB

The following steps of construction are followed for the two cases:

Steps of Construction if AB > AC:

Step 1. Draw the base BC of ∆ABC as given and construct ∠XBC of the required measure at B as shown.

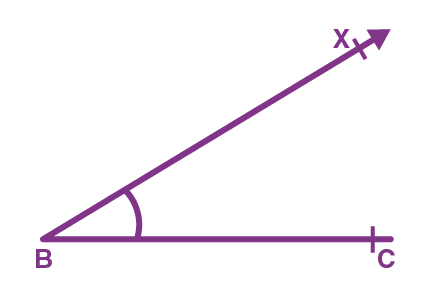
Step 2. From the ray, BX cut an arc equal to AB – AC at point P and join it to C as shown

Step 3. Draw the perpendicular bisector of PC and let it intersect BX at point A as shown:

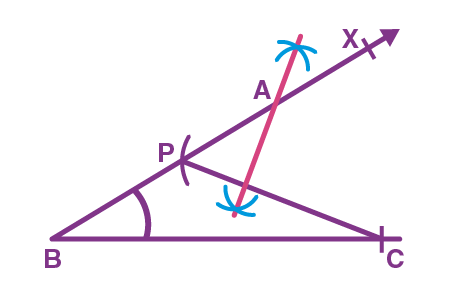
Step 4. Join AC, ∆ABC is the required triangle.

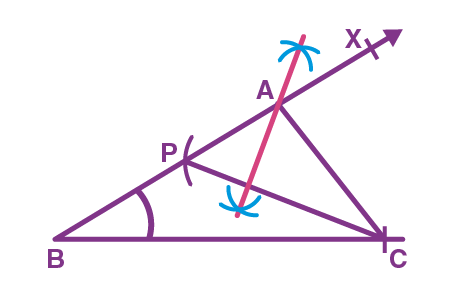
Steps of Construction if AC > AB:

Step 1. Draw the base BC of ∆ABC as given and construct ∠XBC of the required measure at B as shown.

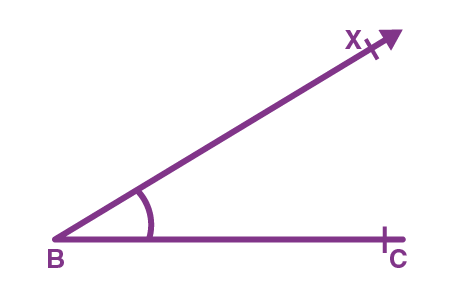
Step 2. On the ray, BX cut an arc equal to AB – AC at point P and join it to C. In this case, P will lie on the opposite side to the ray BX. Draw the perpendicular bisector of PC and let it intersect BX at point A as shown

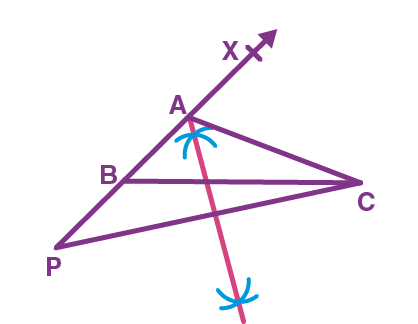
Step 3. Join the points A and C, and hence ∆ABC is the required triangle.

Constructing Triangles

Constructing triangles will include the construction of different triangles using a protractor, a compass and a ruler. A triangle is a three-sided polygon. It has three sides, three vertices and three angles. Construction of triangles is easy when the measurements are given to us based on different properties such as SSS, SAS and ASA.

Let us learn here to construct a triangle with given measurements. Also, learn to draw triangles of some special cases.

How to Construct Triangles?

To construct a triangle one should know these properties and rules:

• All three sides are given (SSS – Side side side)
• Two sides and included angle are given (SAS – Side angle side)
• Two angles and the included side is given (ASA – Angle side angle)
• The measure of the hypotenuse and a side is given in the right triangle (RHS – Right angle hypotenuse side)

For constructing triangles from given data, we generally make use of the given congruency conditions and construct the required triangle.

Constructing triangle With SSS Property

When the length of three sides of the triangle is given, then follow the below steps to construct the required triangle.

• Draw a line segment AB, of length equal to the longest side of the triangle
• Now using a compass and ruler take the measure of the second side and draw an arc
• Again take the measure of the third side and cut the previous arc at a point C
• Now join the endpoints of the line segment to point C and get the required triangle ABC

Constructing triangle with SAS Property

When the length of two sides and the angle included between them are given, then use the following steps to construct the triangle.

• Draw a line segment AB, of length equal to the longest side of the triangle, using a ruler
• Put the center of protractor on one end of a line segment (say A) and measure the given angle. Join the points and construct a ray, such that the ray is nearer to the line segment AB
• Take the measure of another given side of the triangle using a compass and a ruler
• Put the compass at point A and cut the ray at another point, C
• Now join the other end of the line segment, i.e., B to the point C
• Hence, the triangle ABC is constructed

Constructing triangle with ASA Property

When the measures of two angles and the side included between them are given of a triangle, then it is said to be ASA congruency. Follow the given steps to draw a triangle with ASA property.

• Draw a line segment AB, of length equal to the given side of the triangle, using a ruler
• At one endpoint of line segment (say A) measure one of the given angles and draw a ray AR
• At another endpoint of line segment (i.e.,B) measure the other angle using a protractor and draw the ray BQ, such that it cuts the previous ray at a point P
• Join the previous point P, with both the endpoints A and B of the line segment AB, to get the required triangle

Construction triangle with RHS Property

When the hypotenuse side and any one of the other two sides of right triangle are given, then it is RHS property. Follow the given steps to draw a triangle with RHS property.

• Draw the line segment AB, equal to the measure of hypotenuse side
• At one endpoint, say A, of line-segment measure the angle equal to 90 degrees and draw a ray, AR
• Measure the length of another given side and draw an arc to cut the ray AR at a point P
• Now join the point P and B to get the required right triangle

Special Cases of Constructing Triangles

There are few special cases of constructing triangles that are discussed here.

Construction of Triangles – Case 1

Given the base of a triangle, its base angle and the sum of other two sides

For constructing ∆ABC such that base BC, base angle ∠B and the sum of other two sides, i.e. AB + AC are given, the following steps of construction is followed:

Steps of Construction of a Triangle

Step 1. Draw the base BC of ∆ABC as given and construct ∠XBC of the given measure at B as shown.

Step 2. Keeping the compass at point B cut an arc from the ray BX such that its length equals AB + AC at point P and join it to C as shown in the figure.

Step 3. Now measure ∠BPC and from C, draw an angle equal to ∠BPC as shown in the figure.

∆ABC is the required triangle. This can be proved as follows:

Construction of Triangles – Case 2

Given the base of a triangle, its base angle and the difference between the other two sides

For constructing ∆ABC such that base BC, base angle∠B and difference of the other two sides, i.e. AB – AC or  AC-AB is given, then for constructing triangles such as these two cases can arise:

1. AB > AC
2. AC > AB

The following steps of construction are followed for the two cases:

Steps of Construction if AB > AC:

Step 1. Draw the base BC of ∆ABC as given and construct ∠XBC of the required measure at B as shown.

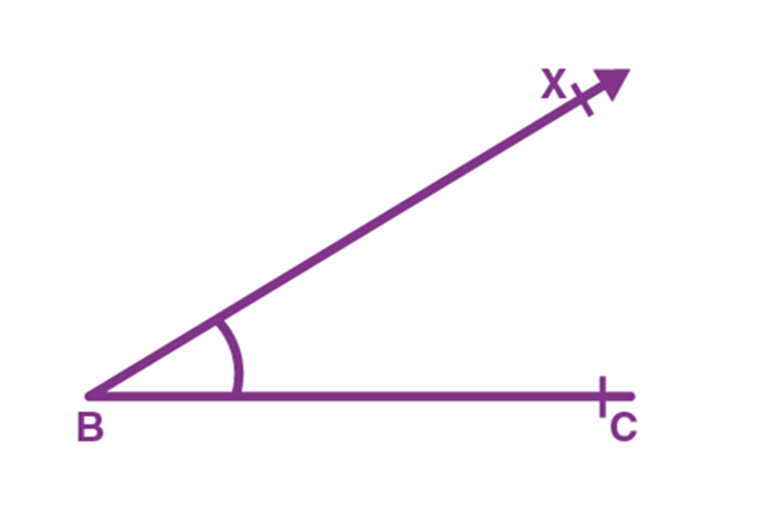
Step 2. From the ray, BX cut an arc equal to AB – AC at point P and join it to C as shown

Step 3. Draw the perpendicular bisector of PC and let it intersect BX at point A as shown:

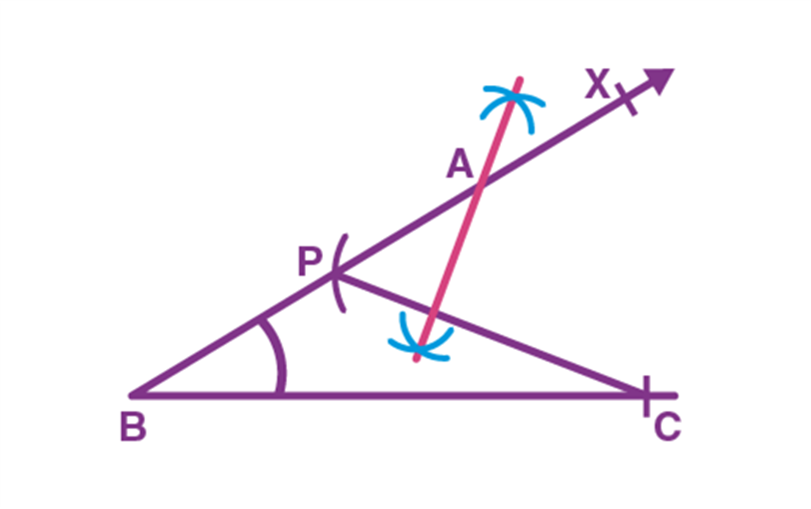
Step 4. Join AC, ∆ABC is the required triangle.

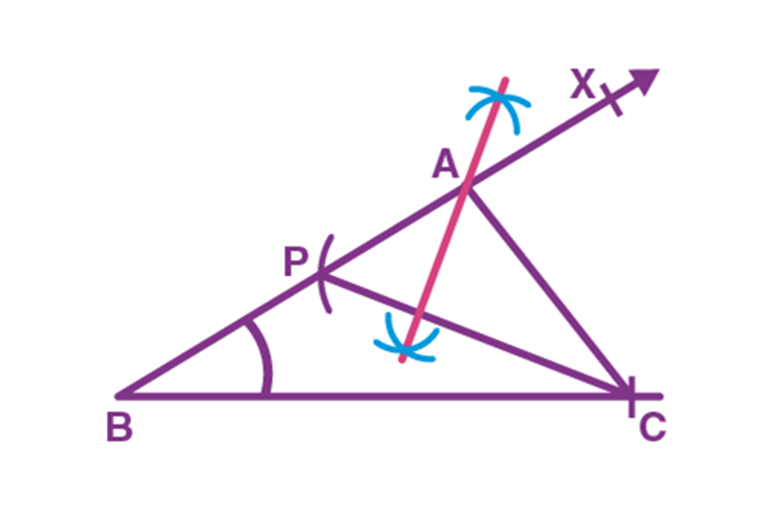
Steps of Construction if AC > AB:

Step 1. Draw the base BC of ∆ABC as given and construct ∠XBC of the required measure at B as shown.

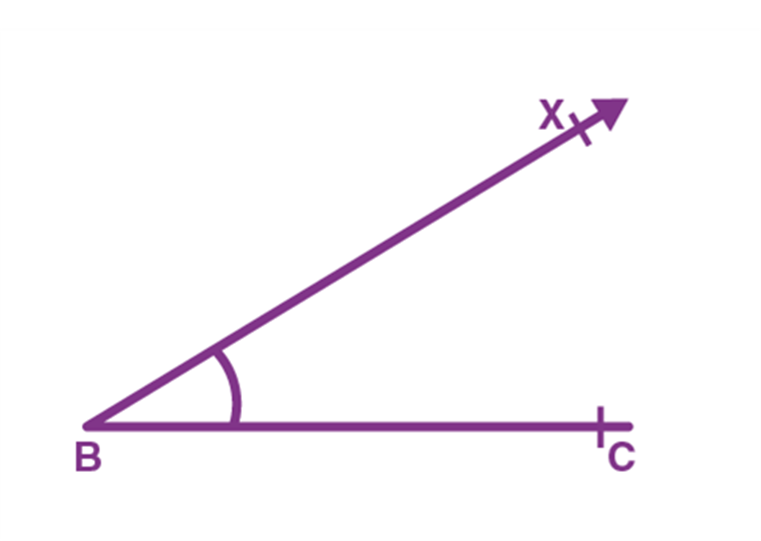
Step 2. On the ray BX cut an arc equal to AB – AC at point P and join it to C. In this case P will lie on the opposite side to the ray BX. Draw the perpendicular bisector of PC and let it intersect BX at point A as shown

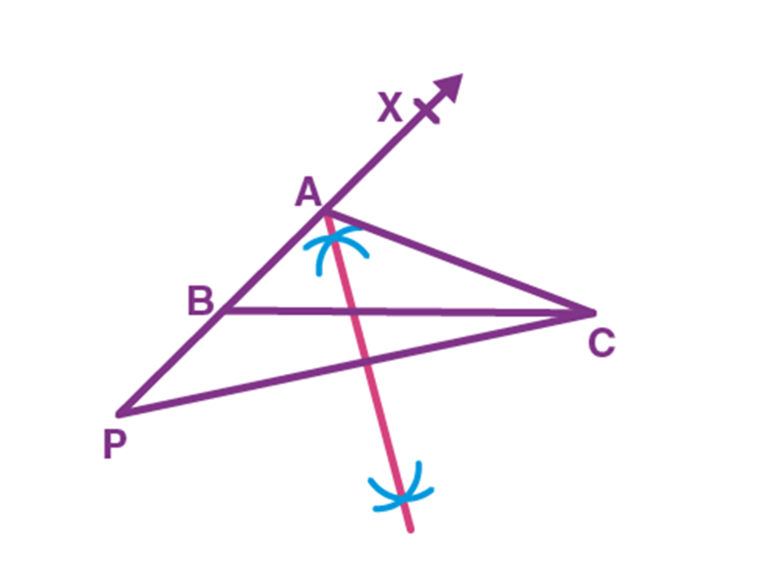
Step 3. Join the points A and C, and hence ∆ABC is the required triangle.