Euclid's Definitions, Axioms and Postulates
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Introduction to Euclid's Geometry
Euclid's Definitions, Axioms, and Postulates
Euclid's Geometry, also known as Euclidean Geometry, is considered the study of plane and solid shapes based on different axioms and theorems. The word Geometry comes from the Greek words 'geo’, meaning the ‘earth’, and ‘metrein’, meaning ‘to measure’. Euclid's Geometry was introduced by the Greek mathematician Euclid, where Euclid defined a basic set of rules and theorems for a proper study of geometry. In this section, we are going to learn more about the concept of Euclid's Geometry, the axioms and solve a few examples.
What is Euclid's Geometry?
Euclid's Geometry was introduced by the Father of Geometry i.e. Euclid and is also called Euclidean Geometry. Geometry was originated from the need for measuring land and was studied in various forms in every ancient civilization such as Egypt, Babylonia, India, etc. Euclid's geometry came into play when Euclid accumulated all the concepts and fundamentals of geometry into a book called 'Elements'. This book spoke about the definitions, the axioms, the theorems, and the proof of various shapes. Euclid specifically spoke about the shape, size, and position of solid shapes and various terms associated with them such as the surface, straight or curved lines, points, etc. Some of his fundamentals about solid shapes are :
- A point has no parts.
- A line is a breadthless length.
- The ends of a line are points.
- A straight line is a line that lies evenly with the points on itself.
- A surface has a length and breadth only.
- The edges of a surface are lines.
- A plane surface is a surface that lies evenly with the straight lines on itself.
Definition of Euclid's Geometry
Euclid's geometry or the euclidean geometry is the study of Geometry based on the undefined terms such as points, lines, and planes of flat spaces. In other words, it is the study of geometrical shapes both plane shapes and solid shapes and the relationship between these shapes in terms of lines, points, and surfaces. Euclid introduced axioms and postulates for these solid shapes in his book elements that help in defining geometric shapes. Euclid's geometry deals with two main aspects - plane geometry and solid geometry. The table below mentions the theorems that were proved by Euclid.
|
Plane Geometry |
Theorem Proved |
|
Congruence of Triangles |
Two triangles are congruent if they are similar in shape and size. |
|
Similarity of Triangles |
Two triangles are similar in shape but differ in size. |
|
Areas |
Area of a plane shape can be measured by comparing it with a unit square. |
|
Pythagorean Theorem |
Pythagorean theorem helps in calculating the distance in different situations for Geometric shapes. |
|
Circles |
Equal chord determines equal angles and vice versa in a circle. |
|
Regular Polygons |
Regular Polygons are equal in sides and angles. |
|
Conic Section |
Conic sections include Ellipse, Parabola, and Hyperbola. |
|
Solid Geometry |
Theorem Proved |
|
Volume |
Volume of a shape can be calculated. |
|
Regular Solids |
The existence of Platonic Solids. |
Euclid's Axioms
Euclid's axioms or common notions are the assumptions of the obvious universal truths that have not been proven. But in his book, Elements, Euclid wrote a few axioms or common notions related to geometric shapes. Let us take a look:
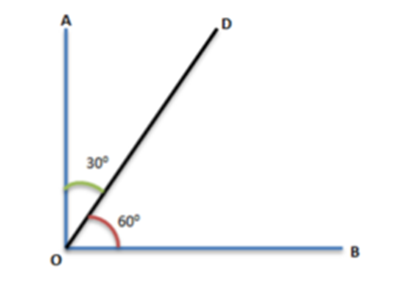
Axiom 1: Things that are equal to the same thing are equal to one another.
Suppose the area of a rectangle is equal to the area of a triangle and the area of that triangle is equal to the area of a square. After applying the first axiom, we can say that that the area of the triangle and the square are equal. For example, if p = q and q = r, then we can say p = r.
Axiom 2: If equals are added to equals, the wholes are equal.
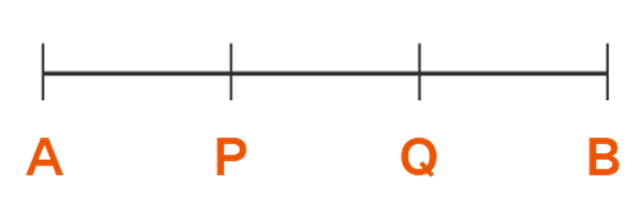
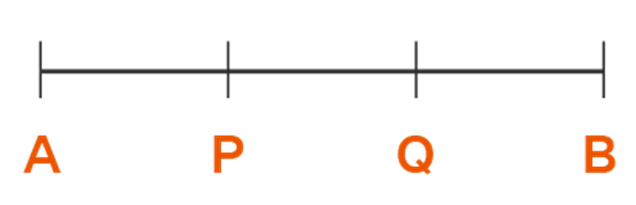
Let us look at the line segment AB, where AP = QB. When PQ is added to both sides, then according to axiom 2, AP + PQ = QB + PQ i.e AQ = PB.
Axiom 3: If equals are subtracted from equals, the remainders are equal.
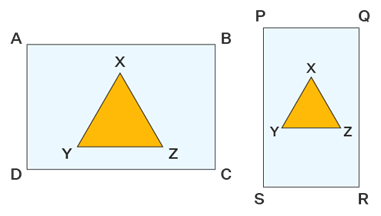
Consider rectangles ABCD and PQRS, where the areas are equal. If the triangle XYZ is removed from both the rectangles then according to axiom 3, the areas of the remaining portions of the two triangles are equal.
Axiom 4: Things that coincide with one another are equal to one another.
Consider line segment AB with C in the center. AC + CB coincides with the line segment AB. Thus by axiom 4, we can say that AC + CB = AB.
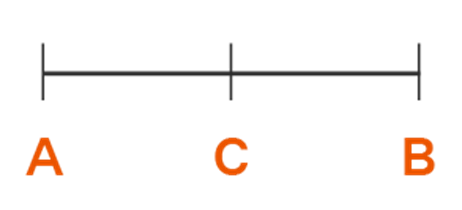
Axiom 5: The whole is greater than the part.
Using the same figure as above, AC is a part of AB. Thus according to axiom 5, we can say that AB > AC.
Axiom 6 and Axiom 7: Things that are double of the same things are equal to one another. Things that are halves of the same things are equal to one another.
Axiom 6 and 7 are interrelated. Consider two identical circles with radii (r)1(r)1 and (r)2(r)2 with diameters as (d)1(d)1 and (d)2(d)2 respectively. Since the circles are identical, using both axioms 6 and 7, we can say that
(r)1(r)1 = (r)2(r)2 and (d)1(d)1 = (d)2(d)2.
Euclid's Postulate
For discussing Euclid's postulate, there are a few terms that we need to get familiarized with. Euclid talks about a three-step process from solids to points which is solids-surface-lines-points. At each step, one dimension is lost from the shape. Therefore, a solid is a 3D shape, a surface is a 2D shape, a line is a one dimension shape, and points are dimensions. The term surface means something that has length and breadth only. Whereas a point has no part, has a long length, etc. These terms will help in understanding the postulate better. There is 5 Euclid's postulate, let us take a look:
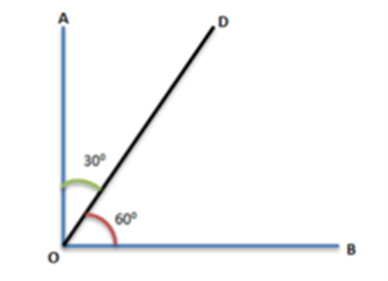
Postulate 1: A straight line segment can be drawn for any two given points.
This postulate shows us that at least one straight line passes through two distinct points, but it does not say that there cannot be more than one such line. Look at the line below, only one line passes through P and Q which is PQ that passes through both Q and P respectively.

Postulate 2: A line segment can be extended in either direction to form a line.
A line segment can be extended in either direction to form a line is the second postulate.
Postulate 3: To describe a circle with any center and radius.
A circle is considered as a plane figure that consists of a set of points that are equidistant from a reference point and can be drawn with its center and radius. According to the third postulate, the shape of a circle does not change when the radius is different. What changes is the size of the circle?
Postulate 4: All right angles are equal to one another.
A right-angle measures at exactly 90° irrespective of the lengths of their arms. Hence according to postulate 4, all right angles are equal to each other. This holds good only for right-angled triangles and not acute angle triangles or obtuse angle triangles.
Postulate 5: If two lines are intersected by a third in such a way that the sum of the inner angles on one side is less than two right angles, then the two lines will intersect each other on that side if produced indefinitely.
When there are two lines cut by a third line, if the sum of the interior angles is less than 180°, then the two lines will meet when extended on that side.
In the image given below, ∠1+∠2<180∘∠1+∠2<180∘. Therefore, Line mm and nn will meet when extended on the side of 1 and 2
Non-Euclidean Geometry
There is a branch of geometry known as Non-Euclidean geometry. Basically, it is everything that does not fall under Euclidean geometry. However, it is commonly used to describe spherical geometry and hyperbolic geometry. Since spherical geometry comes under non-euclidean geometry, to convert it to euclidean or Euclid's geometry or basic geometry we need to change actual distances, location of points, area of the regions, and actual angles.
Examples of Euclid's Geometry
- Example 1: Bella marked three points A, B, and C on a line such that, B lies between A and C. Help Bella prove that AB + BC = AC.
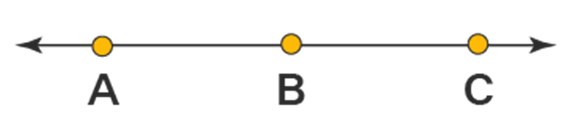
Solution
AC coincides with AB + BC.
Euclid’s Axiom (4) says that things that coincide with one another are equal to one another. So, it can be deduced that AB + BC = AC
It has been assumed that there is a unique line passing through two points.
- Example 2: Prove that an equilateral triangle can be constructed on any given line segment.
Solution:
A line segment of any length is given, say AB. Using Euclid’s postulate 3, first, draw an arc with point A as the center and AB as the radius. Similarly, draw another arc with point B as the center and BA as the radius. Mark the meeting point of the arcs as C. Now, draw the line segments AC and BC to form △ABC△ABC.
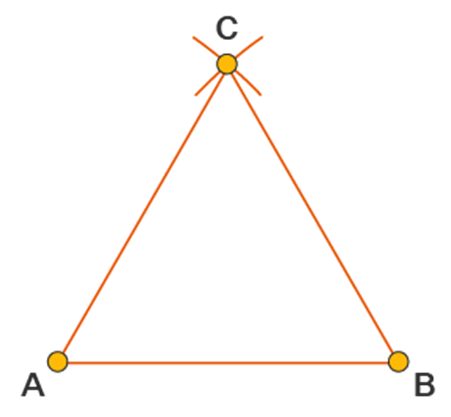
AB = AC; Arcs of same length. AB = BC; Arcs of same length.
Euclid’s axiom says that things which are equal to the same things are equal to one another. Hence, AB = BC = AC. Therefore, △ABC△ABC is an equilateral triangle.
Example 3: Prove that things that are equal to the same thing are equal to one another.
Solution: According to Euclid's axiom 1, if the area of a triangle is equal to the area of a rectangle and the area of the rectangle is equal to the area of the square, we can say that the area of the triangle is also equal to the area of a square. Hence it is proved that things that are equal to the same thing are equal to one another.
Euclid's Definitions, Axioms and Postulates
CHAPTER -5
Introduction to Euclid's Geometry
Euclid's Definitions, Axioms and Postulates
Euclid's Geometry, also known as Euclidean Geometry, is considered the study of plane and solid shapes based on different axioms and theorems. The word Geometry comes from the Greek words 'geo’, meaning the ‘earth’, and ‘metrein’, meaning ‘to measure’. Euclid's Geometry was introduced by the Greek mathematician Euclid, where Euclid defined a basic set of rules and theorems for a proper study of geometry. In this section, we are going to learn more about the concept of Euclid's Geometry, the axioms and solve a few examples.
What is Euclid's Geometry?
Euclid's Geometry was introduced by the Father of Geometry i.e. Euclid and is also called Euclidean Geometry. Geometry was originated from the need for measuring land and was studied in various forms in every ancient civilization such as Egypt, Babylonia, India, etc. Euclid's geometry came into play when Euclid accumulated all the concepts and fundamentals of geometry into a book called 'Elements'. This book spoke about the definitions, the axioms, the theorems, and the proof of various shapes. Euclid specifically spoke about the shape, size, and position of solid shapes and various terms associated with them such as the surface, straight or curved lines, points, etc. Some of his fundamentals about solid shapes are :
- A point has no parts.
- A line is a breadthless length.
- The ends of a line are points.
- A straight line is a line that lies evenly with the points on itself.
- A surface has a length and breadth only.
- The edges of a surface are lines.
- A plane surface is a surface that lies evenly with the straight lines on itself.
Definition of Euclid's Geometry
Euclid's geometry or the euclidean geometry is the study of Geometry based on the undefined terms such as points, lines, and planes of flat spaces. In other words, it is the study of geometrical shapes both plane shapes and solid shapes and the relationship between these shapes in terms of lines, points, and surfaces. Euclid introduced axioms and postulates for these solid shapes in his book elements that help in defining geometric shapes. Euclid's geometry deals with two main aspects - plane geometry and solid geometry. The table below mentions the theorems that were proved by Euclid.
|
Plane Geometry |
Theorem Proved |
|
Two triangles are congruent if they are similar in shape and size. |
|
|
Two triangles are similar in shape but differ in size. |
|
|
Area of a plane shape can be measured by comparing it with a unit square. |
|
|
Pythagorean theorem helps in calculating the distance in different situations for Geometric shapes. |
|
|
Equal chord determines equal angles and vice versa in a circle. |
|
|
Regular Polygons |
Regular Polygons are equal in sides and angles. |
|
Conic Section |
|
Solid Geometry |
Theorem Proved |
|
Volume of a shape can be calculated. |
|
|
Regular Solids |
The existence of Platonic Solids. |
Euclid's Axioms
Euclid's axioms or common notions are the assumptions of the obvious universal truths that have not been proven. But in his book, Elements, Euclid wrote a few axioms or common notions related to geometric shapes. Let us take a look:
Axiom 1: Things that are equal to the same thing are equal to one another.
Suppose the area of a rectangle is equal to the area of a triangle and the area of that triangle is equal to the area of a square. After applying the first axiom, we can say that that the area of the triangle and the square are equal. For example, if p = q and q = r, then we can say p = r.
Axiom 2: If equals are added to equals, the wholes are equal.
Let us look at the line segment AB, where AP = QB. When PQ is added to both sides, then according to axiom 2, AP + PQ = QB + PQ i.e AQ = PB.
Axiom 3: If equals are subtracted from equals, the remainders are equal.
Consider rectangles ABCD and PQRS, where the areas are equal. If the triangle XYZ is removed from both the rectangles then according to axiom 3, the areas of the remaining portions of the two triangles are equal.
Axiom 4: Things that coincide with one another are equal to one another.
Consider line segment AB with C in the center. AC + CB coincides with the line segment AB. Thus by axiom 4, we can say that AC + CB = AB.

Axiom 5: The whole is greater than the part.
Using the same figure as above, AC is a part of AB. Thus according to axiom 5, we can say that AB > AC.
Axiom 6 and Axiom 7: Things that are double of the same things are equal to one another. Things that are halves of the same things are equal to one another.
Axiom 6 and 7 are interrelated. Consider two identical circles with radii (r)1(r)1 and (r)2(r)2 with diameters as (d)1(d)1 and (d)2(d)2 respectively. Since the circles are identical, using both axioms 6 and 7, we can say that
(r)1(r)1 = (r)2(r)2 and (d)1(d)1 = (d)2(d)2.
Euclid's Postulate
For discussing Euclid's postulate, there are a few terms that we need to get familiarized with. Euclid talks about a three-step process from solids to points which is solids-surface-lines-points. At each step, one dimension is lost from the shape. Therefore, a solid is a 3D shape, a surface is a 2D shape, a line is a one dimension shape, and points are dimensions. The term surface means something that has length and breadth only. Whereas a point has no part, has a long length, etc. These terms will help in understanding the postulate better. There is 5 Euclid's postulate, let us take a look:
Postulate 1: A straight line segment can be drawn for any two given points.
This postulate shows us that at least one straight line passes through two distinct points, but it does not say that there cannot be more than one such line. Look at the line below, only one line passes through P and Q which is PQ that passes through both Q and P respectively.

Postulate 2: A line segment can be extended in either direction to form a line.
A line segment can be extended in either direction to form a line is the second postulate.
Postulate 3: To describe a circle with any center and radius.
A circle is considered as a plane figure that consists of a set of points that are equidistant from a reference point and can be drawn with its center and radius. According to the third postulate, the shape of a circle does not change when the radius is different. What changes is the size of the circle.
Postulate 4: All right angles are equal to one another.
A right-angle measures at exactly 90° irrespective of the lengths of their arms. Hence according to postulate 4, all right angles are equal to each other. This holds good only for right-angled triangles and not acute angle triangles or obtuse angle triangles.
Postulate 5: If two lines are intersected by a third in such a way that the sum of the inner angles on one side is less than two right angles, then the two lines will intersect each other on that side if produced indefinitely.
When there are two lines cut by a third line, if the sum of the interior angles is less than 180°, then the two lines will meet when extended on that side.
In the image given below, ∠1+∠2<180∘∠1+∠2<180∘. Therefore, Line mm and nn will meet when extended on the side of 1 and 2
Non-Euclidean Geometry
There is a branch of geometry known as Non-Euclidean geometry. Basically, it is everything that does not fall under Euclidean geometry. However, it is commonly used to describe spherical geometry and hyperbolic geometry. Since spherical geometry comes under non-euclidean geometry, to convert it to euclidean or Euclid's geometry or basic geometry we need to change actual distances, location of points, area of the regions, and actual angles.
Examples on Euclid's Geometry
Example 1: Bella marked three points A, B, and C on a line such that, B lies between A and C. Help Bella prove that AB + BC = AC.

Solution
AC coincides with AB + BC.
Euclid’s Axiom (4) says that things that coincide with one another are equal to one another. So, it can be deduced that AB + BC = AC
It has been assumed that there is a unique line passing through two points.
Example 2: Prove that an equilateral triangle can be constructed on any given line segment.
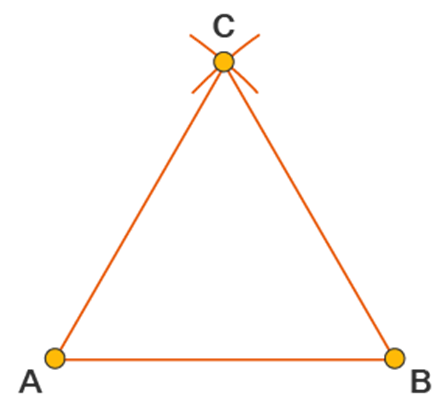
Solution:
A line segment of any length is given, say AB. Using Euclid’s postulate 3, first, draw an arc with point A as the center and AB as the radius. Similarly, draw another arc with point B as the center and BA as the radius. Mark the meeting point of the arcs as C. Now, draw the line segments AC and BC to form △ABC△ABC.
AB = AC; Arcs of same length. AB = BC; Arcs of same length.
Euclid’s axiom says that things which are equal to the same things are equal to one another. Hence, AB = BC = AC. Therefore, △ABC△ABC is an equilateral triangle.
Example 3: Prove that things that are equal to the same thing are equal to one another.
Solution: According to Euclid's axiom 1, if the area of a triangle is equal to the area of a rectangle and the area of the rectangle is equal to the area of the square, we can say that the area of the triangle is also equal to the area of a square. Hence it is proved that things that are equal to the same thing are equal to one another.
Equivalent Versions of Euclid's Fifth Postulate
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Equivalent versions of Euclid’s Fifth Postulate: Diagrams, Example
Equivalent versions of Euclid’s Fifth Postulate is very significant in the history of mathematics. We see that, by implication, no intersection of lines will occur when the sum of the measures of the interior angles on the same side of the falling line is exactly ({180^ circ }). There are several equivalent versions of this postulate. One of them is ‘Playfair’s Axiom’ (given by a Scottish mathematician John Playfair in (1729)), as stated below:
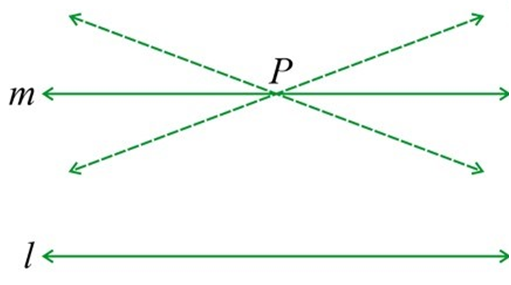
“For every line (l) and every point (P) not lying on (l,) there exists a unique line (m) passing through (P) and parallel to ( l.”)
Of all the lines passing through the point (P,) only line (m) is parallel to line (l,) as shown in the diagram below.
What is the Equivalent Version?
Geometry has been taken from a variety of civilisations. Almost every significant civilisation has studied and used geometry in its prime. The Egyptian and the Indian civilisations were more focused on using geometry as a tool. Then Euclid came and changed the way people used to think of geometry. So instead of making it the tool, he thought of geometry as an abstract model of the world in which Euclid lived.
Five Basic Postulates of Euclidean Geometry
Below you can see Euclid’s five postulates:
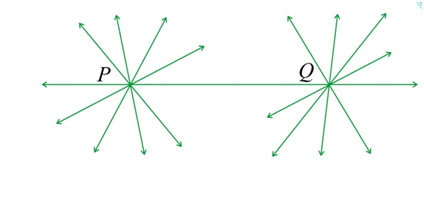
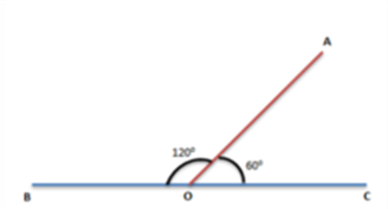
Postulate 1: A straight line can be drawn from any point to any other point.
This postulate tells you that at least one straight line crosses two distinct points, but it does not say that there cannot be more than one line. However, without mentioning it, Euclid frequently assumed that there is a unique line connecting two distinct points in his work. You can state this result in the form of an axiom as follows:
Axiom: Given two distinct points, there is a unique line that passes through them.
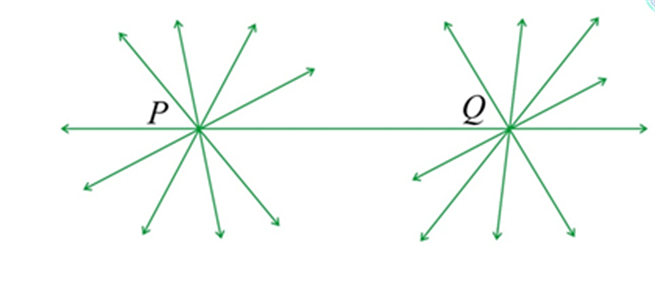
How many lines passing through (P) also pass through (Q) on the given diagram. Only one, that is, the line (PQ.) How many lines passing through (Q) also pass through (P?) Only one, that is, the line (PQ.) Hence, the statement that is given above is self-evident, and it is considered as an axiom.
Postulate 2: A terminated line can be produced indefinitely.
Note that what you call the line segment nowadays is what Euclid called a terminated line. So, according to the present-day terms, the second postulate says that a line segment can be extended on either side to form a line in the given diagram.

Postulate 3: A circle can be drawn with any centre and radius.
Postulate 4: All the right angles are similar (equal) to one another.
Postulate 5: If the straight line that is falling on two straight lines makes the interior angles on the same side of it is taken together less than two right angles, then the two straight lines, if it is produced indefinitely, they meet on the side on which the sum of the angles is less than the two right angles.
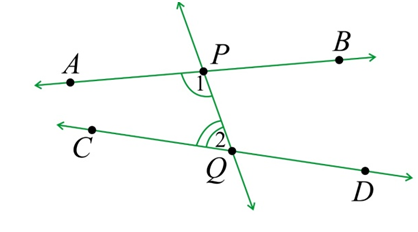
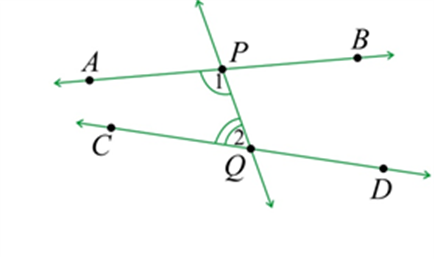
Example: The line (PQ) in the given diagram falls on lines (AB) and (CD) such that the sum of the interior angles (1) and (2) is less than ({180^ circ }) on the left side of (PQ.) Therefore, the lines (AB) and (CD) will eventually intersect on the left side of (PQ.)
Difference Between an Axiom and a Postulate
An axiom is a statement that is usually considered self-evident and assumed to be true without proof. It is used as the starting point in math proof for reducing other facts.
The axioms were considered different from the postulates. An axiom would mention a self-evident assumption common to many areas of the inquiry. In contrast, the postulate mentioned a hypothesis specific to a certain line of the inquiry that was approved without proof.
Example: In Euclid’s Elements, we can compare “common notions” (axioms) with the postulates.
There is generally no difference between what was classically referred to as the “axioms” and the “postulates” in modern mathematics. Modern mathematics distinguishes between the logical axioms and the non-logical axioms, with the latter sometimes referred to as the postulates.
What Does Euclid’s Fifth Postulate Imply?
Euclid’s fifth postulate states that if a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two right angles, then both straight lines, if produced indefinitely, will meet on the other side on which the sum of angles is less than two right angles. First, you have to use this postulate and then prove it by using graphs and angles.
Complete step by step answer:
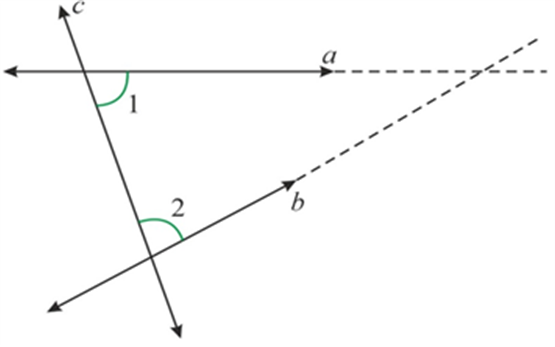
We know that Euclid’s fifth postulate states that if (angle 1 + angle 2 < {180^ circ },), the line (a) and (b) meet on the right side of line (c.)
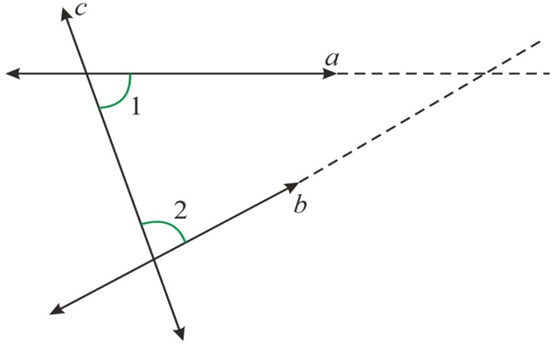
Now, since you know that (a) and (b) are parallel, then (angle 1 + angle 2 = {180^ circ }), you get to see the below diagram:
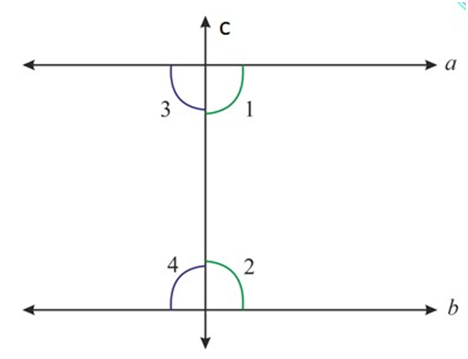
Hence, by Euclid’s fifth postulate, lines (a) and (b) will not meet on the right side of (c) as the sum is not less than ({180^ circ })
In the same way, you can see (angle 3 + angle 4 = {180^ circ })
Therefore, by Euclid’s fifth postulate, lines (a) and (b) will not meet on the left side of (c) as the sum is not less than ({180^ circ })
Thus, Euclid’s postulate implies the existence of parallel lines.
Equivalent Versions of Euclid's Fifth Postulate
Equivalent versions of Euclid’s Fifth Postulate: Diagrams, Example
Equivalent versions of Euclid’s Fifth Postulate is very significant in the history of mathematics. We see that, by implication, no intersection of lines will occur when the sum of the measures of the interior angles on the same side of the falling line is exactly \({180^ \circ }\). There are several equivalent versions of this postulate. One of them is ‘Playfair’s Axiom’ (given by a Scottish mathematician John Playfair in \(1729)\), as stated below:
“For every line \(l\) and every point \(P\) not lying on \(l,\) there exists a unique line \(m\) passing through \(P\) and parallel to \( l.”\)
Of all the lines passing through the point \(P,\) only line \(m\) is parallel to line \(l,\) as shown in the diagram below.

What is the Equivalent Version?
Geometry has been taken from a variety of civilisations. Almost every significant civilisation has studied and used geometry in its prime. The Egyptian and the Indian civilisations were more focused on using geometry as a tool. Then Euclid came and changed the way people used to think of geometry. So instead of making it the tool, he thought of geometry as an abstract model of the world in which Euclid lived.
Five Basic Postulates of Euclidean Geometry
Below you can see Euclid’s five postulates:
Postulate 1: A straight line can be drawn from any point to any other point.
This postulate tells you that at least one straight line crosses two distinct points, but it does not say that there cannot be more than one line. However, without mentioning it, Euclid frequently assumed that there is a unique line connecting two distinct points in his work. You can state this result in the form of an axiom as follows:
Axiom: Given two distinct points, there is a unique line that passes through them.
How many lines passing through \(P\) also pass through \(Q\) on the given diagram. Only one, that is, the line \(PQ.\) How many lines passing through \(Q\) also pass through \(P?\) Only one, that is, the line \(PQ.\) Hence, the statement that is given above is self-evident, and it is considered as an axiom.
Postulate 2: A terminated line can be produced indefinitely.
Note that what you call the line segment nowadays is what Euclid called a terminated line. So, according to the present-day terms, the second postulate says that a line segment can be extended on either side to form a line in the given diagram.

Postulate 3: A circle can be drawn with any centre and radius.
Postulate 4: All the right angles are similar (equal) to one another.
Postulate 5: If the straight line that is falling on two straight lines makes the interior angles on the same side of it is taken together less than two right angles, then the two straight lines, if it is produced indefinitely, they meet on the side on which the sum of the angles is less than the two right angles.
Example: The line \(PQ\) in the given diagram falls on lines \(AB\) and \(CD\) such that the sum of the interior angles \(1\) and \(2\) is less than \({180^ \circ }\) on the left side of \(PQ.\) Therefore, the lines \(AB\) and \(CD\) will eventually intersect on the left side of \(PQ.\)
Difference Between an Axiom and a Postulate
An axiom is a statement that is usually considered self-evident and assumed to be true without proof. It is used as the starting point in math proof for reducing other facts.
The axioms were considered different from the postulates. An axiom would mention a self-evident assumption common to many areas of the inquiry. In contrast, the postulate mentioned a hypothesis specific to a certain line of the inquiry that was approved without proof.
Example: In Euclid’s Elements, we can compare “common notions” (axioms) with the postulates.
There is generally no difference between what was classically referred to as the “axioms” and the “postulates” in modern mathematics. Modern mathematics distinguishes between the logical axioms and the non-logical axioms, with the latter sometimes referred to as the postulates.
What Does Euclid’s Fifth Postulate Imply?
Euclid’s fifth postulate states that if a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two right angles, then both straight lines, if produced indefinitely, will meet on the other side on which the sum of angles is less than two right angles. First, you have to use this postulate and then prove it by using graphs and angles.
Complete step by step answer:
We know that Euclid’s fifth postulate states that if \(\angle 1 + \angle 2 < {180^ \circ },\), the line \(a\) and \(b\) meet on the right side of line \(c.\)
Now, since you know that \(a\) and \(b\) are parallel, then \(\angle 1 + \angle 2 = {180^ \circ }\), you get to see the below diagram:
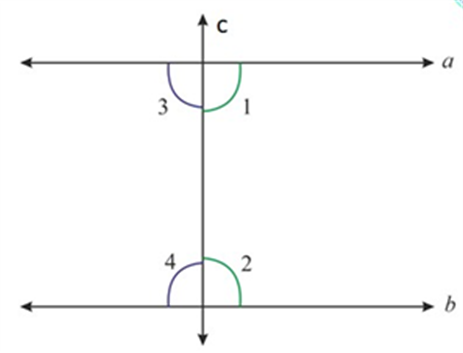
Hence, by Euclid’s fifth postulate, lines \(a\) and \(b\) will not meet on the right side of \(c\) as the sum is not less than \({180^ \circ }\)
In the same way, you can see \(\angle 3 + \angle 4 = {180^ \circ }\)
Therefore, by Euclid’s fifth postulate, lines \(a\) and \(b\) will not meet on the left side of \(c\) as the sum is not less than \({180^ \circ }\)
Thus, Euclid’s postulate implies the existence of parallel lines.
Solved Examples
Q.1. If \(A, B\) and \(C\) are three points on a line, and \(B\) lies between \(A\) and \(C\) in the given diagram, then prove that \(AB+BC=AC.\)

Ans: In the given diagram above, \(AC\) coincides with \(AB+BC\)
Also, Euclid’s Axiom \((4)\) says that things that coincide with one another are equal. So, it can be deduced that
\(AB+BC=AC\)
Note that in the given solution, it has been considered that there is a unique line that is passing through two points.
Q.2. Prove that an equilateral triangle may be constructed on any of the given line segments.
Ans: In the segment above, a line segment of any length is given, say AB in the given diagram.
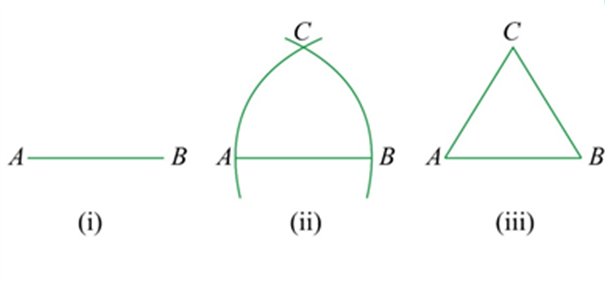
Here, you have to do some construction. Using Euclid’s postulate \(3,\) you can draw a circle with point \(A\) as the centre and \(AB\) as the radius in the given diagram. Similarly, you draw another circle with point \(B\) as the centre and \(BA\) as the radius. The two circles that meet at a point say \(C.\)
Now, draw the line segments \(AC\) and \(BC\) to form \(\Delta A B C\) in the given diagram.
So, you have to show that this triangle is the equilateral triangle, i.e., \(AB=AC=BC.\)
Now, \(AB=AC\), since they are the radii of the same circle (1)
Similarly, \(AB=BC\) (Radii of the same circle) (2)
From the given two facts, and Euclid’s axiom that things that are equal to the same thing are equal, you can conclude that \(AB=BC=AC\)
So, \(\Delta A B C\) is an equilateral triangle.
Q.3. Prove that the two lines that are both parallel to the same line are parallel to each other.
Ans: Three lines, \(l, m\) and \(n\) in a plane such that \(m||l\) and \(n||l.\)
Prove: \(m||n\)
If possible, let \(m\) be not parallel to \(n\). Then, \(m\) and \(n\) intersect in a unique point, say \(P.\)

Thus, through a point \(P\) outside \(l,\) two lines \(m\) and \(n,\) both parallel to \(l.\) This is a contradiction to the parallel axiom. So, the supposition is wrong.
Hence, \(m||n.\)
Q.4. Prove that two distinct lines cannot have more than one point in common.
Ans: Here, we are given two lines \(l\) and \(m.\) You need to prove that they have only a single point in common. Let us assume that the two lines intersect in two distinct points, say \(P\) and \(Q.\) So, you have two lines that are passing through two distinct points \(P\) and \(Q.\)
But this assumption clashes with the axiom that only one line can pass through two distinct points. So, the assumption that we started with that two lines can pass through two distinct points is wrong.
From this, we understand that we are forced to conclude that two distinct lines cannot have more than one point in common.
Q.5. Prove that if lines \(AB, AC, AD\) and \(AE\) are parallel to line \(l,\) then points \(A, B, C, D\) and \(E\) are collinear.
Ans: Lines \(AB, AC, AD\) and \(AE\) are parallel to a line \(l.\)
Prove: \(A,B,C, D\) and \(E\) are collinear.
Since lines \(AB, AC, AD\) and \(AE\) are parallel to a line \(l.\)
Therefore, point \(A\) lies outside \(l\) and through \(A\) lines \(AB, AC, AD\) and \(AE\) are drawn parallel to \(l.\) But, by parallel axiom, only one line can be drawn parallel to \(l, \) through a point outside it.
Therefore, the points \(A, B, C, D, E\) lie on the same line.
Hence, points \(A, B, C, D\) and \(E\) are collinear points.
Q.1. What is the equivalent version?
Ans: Geometry has taken from a variety of civilisations. Almost every significant civilisation has studied and used geometry in its prime. The Egyptian and the Indian civilisations were more focused on using geometry as a tool. Then Euclid came and changed the way people use to think in geometry. So instead of making it the tool, he thought of geometry as an abstract model of the world in which Euclid lived.
Q.2. Which of the five postulates is equivalent to Playfair’s postulate?
Ans: The definition of the fifth postulate is taken so that the parallel lines are the lines that do not intersect or have some line that is intersecting them in the same angles. Playfair’s axiom is contextually equivalent to Euclid’s fifth postulate and is thus logically independent of the first four postulates.
Q.3. How would you rewrite Euclid’s fifth postulate?
Ans: This postulate can be rewritten in reference to the given below diagram: You can consider a straight line \(PQ\) that falls on both straight lines \(AB\) and \(CD\) in such a way that the total sum of the interior angles \(\angle 1\) and \(\angle 2\) is less than \(180\) degrees on the left side of the straight line \(PQ.\) In this case, \(AB\) and \(CD,\) if produced, will meet at the left side of \(PQ.\)
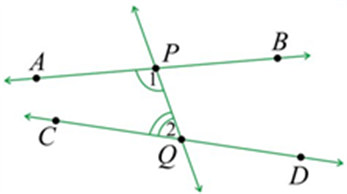
Q 4. Who proved Euclid’s fifth postulate?
Ans: The Persian mathematician, astronomer, philosopher, and poet Omar Khayyam \((1050-1153)\) attempted to prove the fifth postulate.
Q.5. What is the equivalent of the fifth postulate?
Ans: If the straight line that is falling on two straight lines makes the interior angles on the same side of it is taken together less than two right angles, then the two straight lines, if it is produced indefinitely, they meet on the side on which the sum of the angles is less than the two right angles.
Basic terms and definitions
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Lines and Angles
Lines And Angles are the basic shapes in geometry. Lines are figures that are made up of infinite points extending indefinitely in both directions. Lines are straight and have negligible depth or width. There are a variety of lines you will learn about, such as perpendicular lines, intersecting lines, transversal lines, etc. An angle is a figure in which two rays emerge from a common point. You may also come across alternate and corresponding angles in this field. Geometry shapes and their properties are the most practical branch of mathematics. Mostly this concept has been taught in Class 7 and Class 9.
Definition of Lines and Angles
As we have discussed, both lines and angles form the base for any shape in geometry. We cannot draw a two-dimensional to three-dimensional shape without using lines and angles. Thus, it is very necessary to learn the definitions of both terms.
Here, the basic definitions and properties of lines and also for angles are given. It will give the students a basic knowledge of these geometrical terms.
What are Lines?
A line is a straight one-dimensional figure, that extends in the opposite directions infinitely. A line can be horizontal or vertical. It can be drawn from left to right or top to bottom.
What are Angles?
Angles are the shape that is formed when the endpoints of two rays meet at a single point. They are measured in degrees (°) or radians. A complete rotation is equal to an angle of 360 degrees. It is represented by the symbol ‘∠’.
Types of Lines and Angles
There are various types of lines and angles in geometry based on the measurements and different scenarios. Let us learn here all those lines and angles along with their definitions.
Types of Lines
Lines are basically categorized as:
- Line segment
- Ray
Based on concepts or operations performed on lines, they are;
- Parallel Lines
- Perpendicular Lines
- Transversal
Line Segment - A line segment is a part of a line with two end-points. It is the shortest distance between two points and has a fixed length.

Ray - A ray is a part of a line, which has a starting point and extends infinitely in one direction.

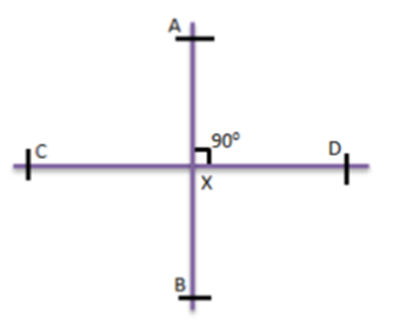
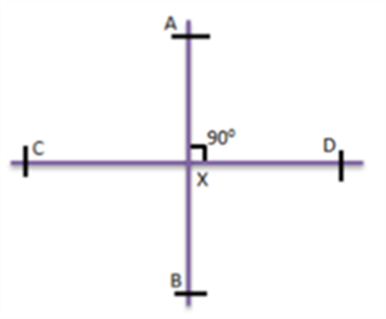
Perpendicular Lines - When two lines form a right angle with each other, by meeting at a single point, are called perpendicular lines. In the figure, you can see, lines AB and CD are perpendicular to each other.
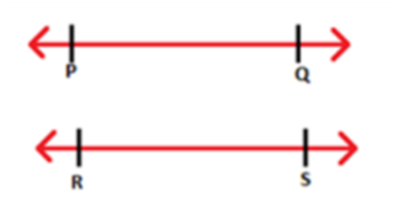
Parallel Lines - Two lines are said to be parallel when they do not meet at any point in a plane or which do not intersects each other. In the figure, lines PQ and RS are parallel to each other.
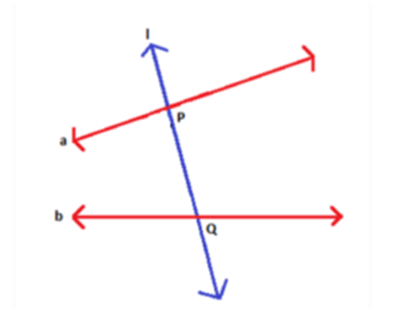
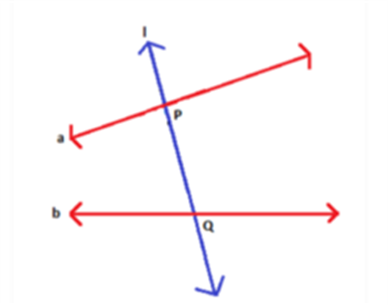
Transversal Line - When a line intersects two lines at distinct points, it is called a transversal. In the figure, a transversal l is intersecting two lines at point P and Q.
Types of Angles
Angles are basically classified as:
- Acute Angle(<90°)
- Right Angle(=90°)
- Obtuse Angle(>90°)
- Straight Angle(=180°)
And based on the relation between two angles, conceptual wise, they are;
- Supplementary Angles
- Complementary Angles
- Adjacent Angles
- Vertically Opposite Angles
Acute Angle
If the inclination between the arms is less than a right angle, it is called an acute angle.
Obtuse Angle
If the inclination between the arms is more than a right angle, it is called an obtuse angle.
Right Angle
If the arms form an angle of 90 degrees between them, it is called a right angle.
Straight Angle
If the arms form an angle of 180 degrees between them, it is called a straight angle.
Complementary Angles
Two angles that sum up to 90 degrees are called complementary angles.
Supplementary Angles - Two angles that sum up to 180 degrees are called supplementary angles.
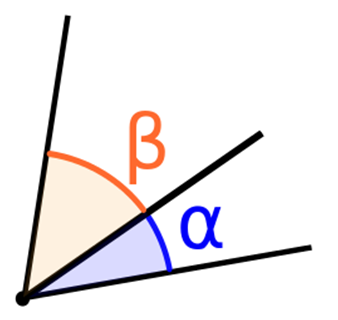
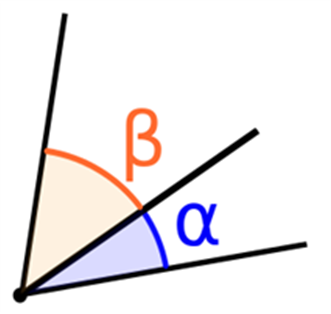
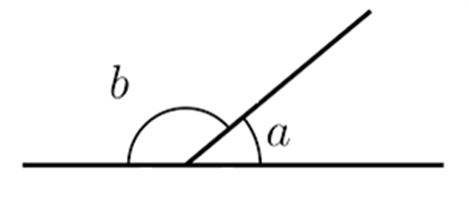
Adjacent Angles - Two angles that have a common side and a common vertex are called adjacent angles. In the following figure, ∠α and ∠β are adjacent angles.
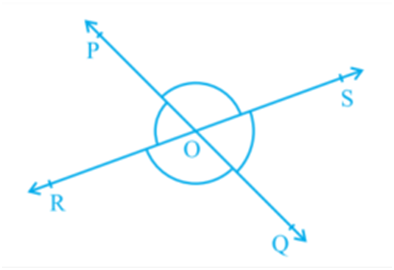
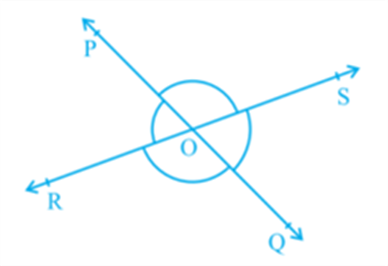
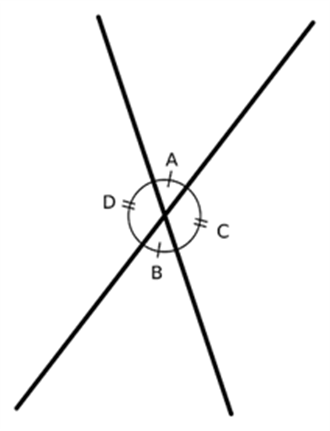
Vertically Opposite Angles - Two angles which are formed, opposite to each other, when two lines intersect at a common point or vertex, are called vertically opposite angles. In the figure, given below;
∠POR = ∠SOQ and ∠POS = ∠ROQ
Properties of Lines and Angles
Similar to other shapes and sizes in geometry, lines and angles also have their own properties. Let us see what are they.
Properties of Lines
- Collinear points are a set of three or more points that lie on the same line.
- The points which do not lie on the same line are called non-collinear points.
Note: Three points can be either collinear or non-collinear, but not both together at the same time.
Properties of Angles
- An angle is a figure in which two rays emerge from a common point. This point is called the vertex of the angle and the two rays forming the angle are called its arms or sides.
- An angle that is greater than 180 degrees but less than 360 degrees is called a reflex angle.
- If two adjacent angles add up to 180 degrees, they form a linear pair of angles. In the following figure, ∠a and ∠b form a linear pair.
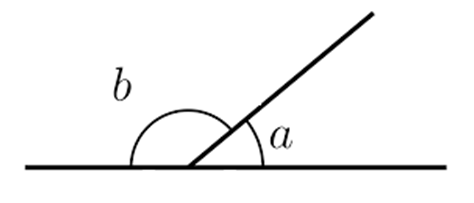
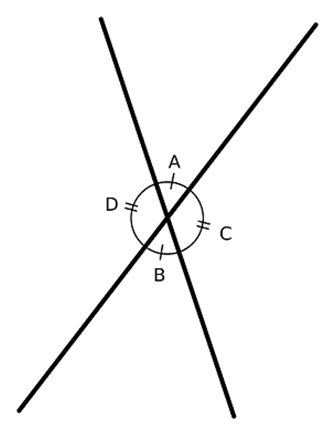
- When two lines intersect each other, the two opposite pairs of angles formed are called vertically opposite angles. In the following figure, ∠A and ∠B are vertically opposite angles. Another pair is ∠C and ∠D.
What are the five types of Angles?
The five types of angles are:
- Acute Angle
- Right Angle
- Obtuse Angle
- Straight Angle
- Reflex Angle
What are the properties of Lines and Angles?
If two parallel lines are intersected by a transversal then:
- Its vertically opposite angles are always equal
- Its corresponding angles are equal
- Its alternate exterior and interior angles are equal
What are Lines and its types?
Lines are figures that are made up of infinite points extending indefinitely in both directions. The types of lines are:
- Horizontal lines
- Vertical lines
- Parallel lines
- Perpendicular lines
Basic terms and definitions
Chapter 6 - Lines and Angles
Lines And Angles are the basic shapes in geometry. Lines are figures that are made up of infinite points extending indefinitely in both directions. Lines are straight and have negligible depth or width. There are a variety of lines you will learn about, such as perpendicular lines, intersecting lines, transversal lines, etc. An angle is a figure in which two rays emerge from a common point. You may also come across alternate and corresponding angles in this field. Geometry shapes and their properties are the most practical branch of mathematics. Mostly this concept has been taught in Class 7 and Class 9.
Definition of Lines and Angles
As we have discussed, both lines and angles form the base for any shape in geometry. We cannot draw a two-dimensional to three-dimensional shape without using lines and angles. Thus, it is very necessary to learn the definitions of both terms.
Here, the basic definitions and properties of lines and also for angles are given. It will give the students a basic knowledge of these geometrical terms.
What are Lines?
A line is a straight one-dimensional figure, that extends in the opposite directions infinitely. A line can be horizontal or vertical. It can be drawn from left to right or top to bottom.
What are Angles?
Angles are the shape that is formed when the endpoints of two rays meet at a single point. They are measured in degrees (°) or radians. A complete rotation is equal to an angle of 360 degrees. It is represented by the symbol ‘∠’.
Types of Lines and Angles
There are various types of lines and angles in geometry based on the measurements and different scenarios. Let us learn here all those lines and angles along with their definitions.
Types of Lines
Lines are basically categorized as:
- Line segment
- Ray
Based on concepts or operations performed on lines, they are;
- Parallel Lines
- Perpendicular Lines
- Transversal
Line Segment
A line segment is a part of a line with two end-points. It is the shortest distance between two points and has a fixed length.

Ray
A ray is a part of a line, which has a starting point and extends infinitely in one direction.

Perpendicular Lines
When two lines form a right angle with each other, by meeting at a single point, are called perpendicular lines. In the figure, you can see, lines AB and CD are perpendicular to each other.
Parallel Lines
Two lines are said to be parallel when they do not meet at any point in a plane or which do not intersects each other. In the figure, lines PQ and RS are parallel to each other.

Transversal Line
When a line intersects two lines at distinct points, it is called a transversal. In the figure, a transversal l is intersecting two lines at point P and Q.
Types of Angles
Angles are basically classified as:
- Acute Angle(<90°)
- Right Angle(=90°)
- Obtuse Angle(>90°)
- Straight Angle(=180°)
And based on the relation between two angles, conceptual wise, they are;
- Supplementary Angles
- Complementary Angles
- Adjacent Angles
- Vertically Opposite Angles
Acute Angle
If the inclination between the arms is less than a right angle, it is called an acute angle.
Obtuse Angle
If the inclination between the arms is more than a right angle, it is called an obtuse angle.
Right Angle
If the arms form an angle of 90 degrees between them, it is called a right angle.
Straight Angle
If the arms form an angle of 180 degrees between them, it is called a straight angle.
Complementary Angles
Two angles which sum up to 90 degrees are called complementary angles.
Supplementary Angles
Two angles which sum up to 180 degrees are called supplementary angles.
Adjacent Angles
Two angles which have a common side and a common vertex are called adjacent angles. In the following figure, ∠α and ∠β are adjacent angles.
Vertically Opposite Angles
Two angles which are formed, opposite to each other, when two lines intersect at a common point or vertex, are called vertically opposite angles. In the figure, given below;
∠POR = ∠SOQ and ∠POS = ∠ROQ
Video Lesson on Lines
For More Information On Lines, Watch The Below Video:
10,432
Video Lessons on Types and Parts of Angles
Types of angles
1,36,490
Parts of Angles
14,976
Properties of Lines and Angles
Similar to other shapes and sizes in geometry, lines and angles also have their own properties. Let us see what are they.
Properties of Lines
- Collinear points are a set of three or more points which lie on the same line.
- The points which do not lie on the same line are called non-collinear points.
Note: Three points can be either collinear or non-collinear, but not both together at the same time.
Properties of Angles
- An angle is a figure in which two rays emerge from a common point. This point is called the vertex of the angle and the two rays forming the angle are called its arms or sides.
- An angle which is greater than 180 degrees but less than 360 degrees is called a reflex angle.
- If two adjacent angles add up to 180 degrees, they form a linear pair of angles. In the following figure, ∠a and ∠b form a linear pair.
- When two lines intersect each other, the two opposite pairs of angles formed are called vertically opposite angles. In the following figure, ∠A and ∠B are vertically opposite angles. Another pair is ∠C and ∠D.
What are the five types of Angles?
The five types of angles are:
- Acute Angle
- Right Angle
- Obtuse Angle
- Straight Angle
- Reflex Angle
What are the properties of Lines and Angles?
If two parallel lines are intersected by a transversal then:
- Its vertically opposite angles are always equal
- Its corresponding angles are equal
- Its alternate exterior and interior angles are equal
What are Lines and its types?
Lines are figures that are made up of infinite points extending indefinitely in both directions. The types of lines are:
- Horizontal lines
- Vertical lines
- Parallel lines
- Perpendicular lines
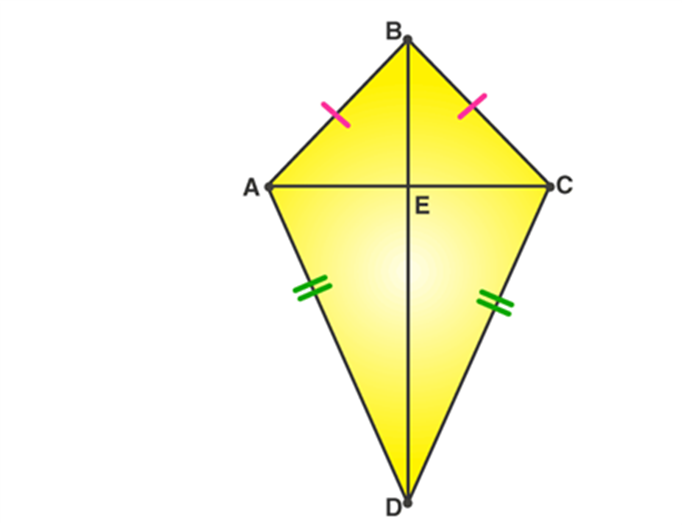
Congruence of Triangles
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Congruence of Triangles
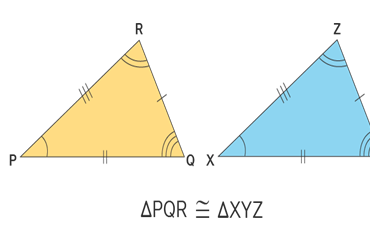
Congruence of triangles: Two triangles are said to be congruent if all three corresponding sides are equal and all the three corresponding angles are equal in measure. These triangles can be slides, rotated, flipped and turned to be looked identical. If repositioned, they coincide with each other. The symbol of congruence is’ ≅’.
The corresponding sides and angles of congruent triangles are equal. There are basically four congruency rules that proves if two triangles are congruent. But it is necessary to find all six dimensions. Hence, the congruence of triangles can be evaluated by knowing only three values out of six. The meaning of congruence in Maths is when two figures are similar to each other based on their shape and size. Also, learn about Congruent Figures here.
Congruence is the term used to define an object and its mirror image. Two objects or shapes are said to be congruent if they superimpose on each other. Their shape and dimensions are the same. In the case of geometric figures, line segments with the same length are congruent and angles with the same measure are congruent.
|
Conditions for Congruence of Triangles:
|
CPCT is the term, we come across when we learn about the congruent triangle. Let’s see the condition for triangles to be congruent with proof.
Congruent meaning in Maths
The meaning of congruent in Maths is addressed to those figures and shapes that can be repositioned or flipped to coincide with the other shapes. These shapes can be reflected to coincide with similar shapes.
Two shapes are congruent if they have the same shape and size. We can also say if two shapes are congruent, then the mirror image of one shape is same as the other.
Congruent Triangles
A polygon made of three line segments forming three angles is known as a Triangle.
Two triangles are said to be congruent if their sides have the same length and angles have same measure. Thus, two triangles can be superimposed side to side and angle to angle.
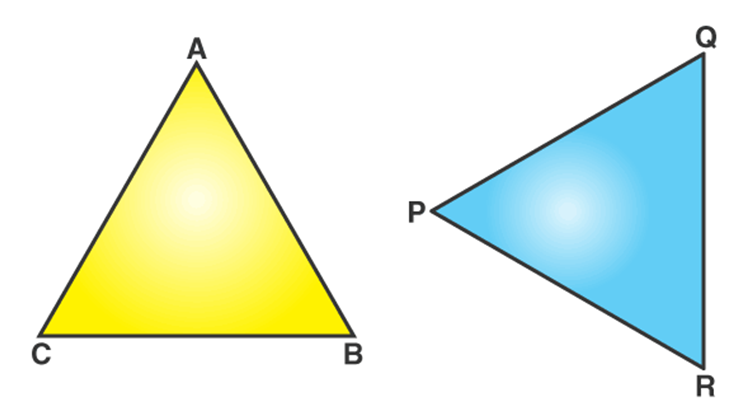
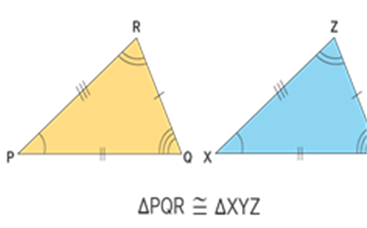
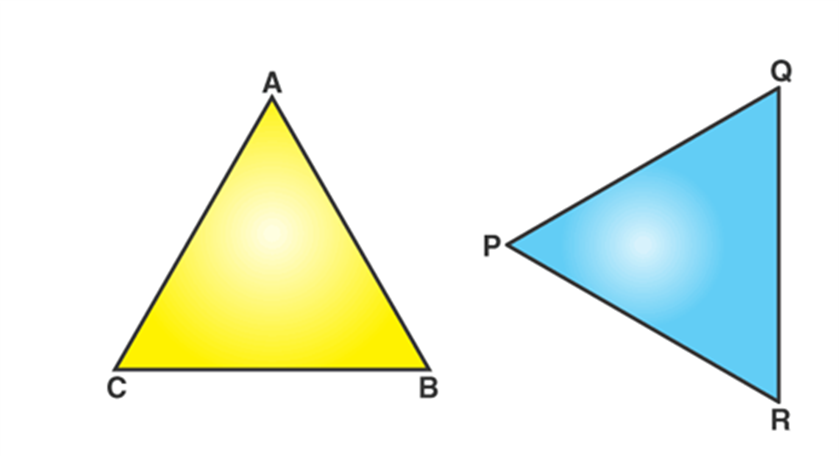
In the above figure, Δ ABC and Δ PQR are congruent triangles. This means,
Vertices: A and P, B and Q, and C and R are the same.
Sides: AB=PQ, QR= BC and AC=PR;
Angles: ∠A = ∠P, ∠B = ∠Q, and ∠C = ∠R.
Congruent triangles are triangles having corresponding sides and angles to be equal. Congruence is denoted by the symbol “≅”. They have the same area and the same perimeter.
CPCT Full Form - CPCT is the term we come across when we learn about the congruent triangle. CPCT means “Corresponding Parts of Congruent Triangles”. As we know that the corresponding parts of congruent triangles are equal. While dealing with the concepts related to triangles and solving questions, we often make use of the abbreviation cpct in short words instead of full form.
CPCT Rules in Maths
The full form of CPCT is Corresponding parts of Congruent triangles. Congruence can be predicted without actually measuring the sides and angles of a triangle. Different rules of congruency are as follows.
- SSS (Side-Side-Side)
- SAS (Side-Angle-Side)
- ASA (Angle-Side-Angle)
- AAS (Angle-Angle-Side)
- RHS (Right angle-Hypotenuse-Side)
Let us learn them all in detail.
SSS (Side-Side-Side)
If all the three sides of one triangle are equivalent to the corresponding three sides of the second triangle, then the two triangles are said to be congruent by SSS rule.
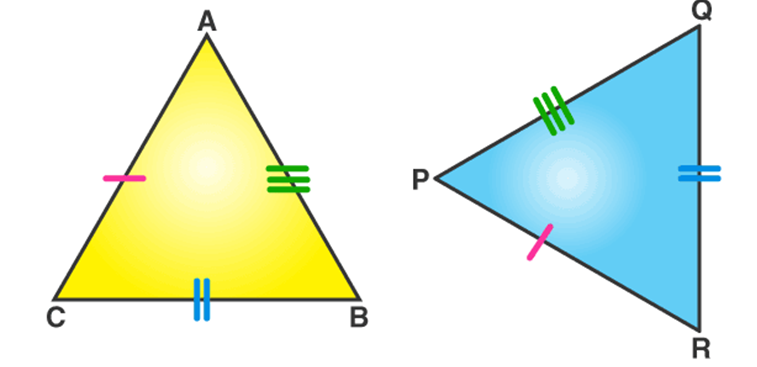
In the above-given figure, AB= PQ, QR= BC and AC=PR, hence Δ ABC ≅ Δ PQR.
SAS (Side-Angle-Side)
If any two sides and the angle included between the sides of one triangle are equivalent to the corresponding two sides and the angle between the sides of the second triangle, then the two triangles are said to be congruent by SAS rule.
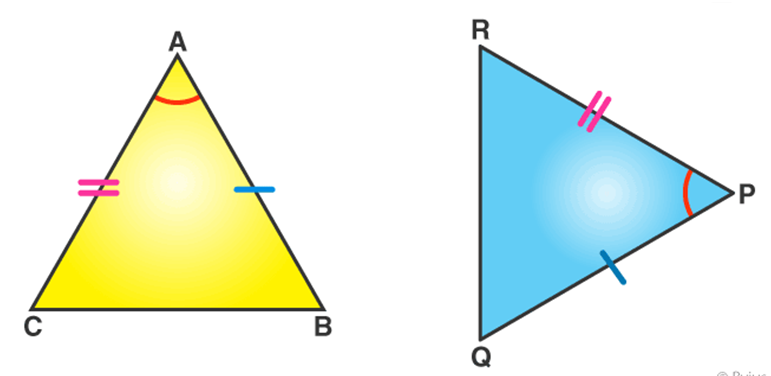
In above given figure, sides AB= PQ, AC=PR and angle between AC and AB equal to angle between PR and PQ i.e. ∠A = ∠P. Hence, Δ ABC ≅ Δ PQR.
ASA (Angle-Side- Angle)
If any two angles and the side included between the angles of one triangle are equivalent to the corresponding two angles and side included between the angles of the second triangle, then the two triangles are said to be congruent by ASA rule.
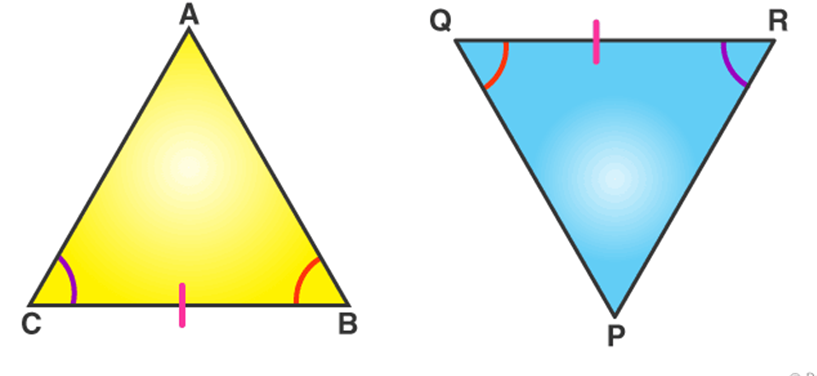
In above given figure, ∠ B = ∠ Q, ∠ C = ∠ R and sides between ∠B and ∠C , ∠Q and ∠ R are equal to each other i.e. BC= QR. Hence, Δ ABC ≅ Δ PQR.
AAS (Angle-Angle-Side) [Application of ASA]
AAS stands for Angle-angle-side. When two angles and a non-included side of a triangle are equal to the corresponding angles and sides of another triangle, then the triangles are said to be congruent.
AAS congruency can be proved in easy steps. Suppose we have two triangles ABC and DEF, where,
∠B = ∠E [Corresponding sides] ∠C = ∠F [Corresponding sides] And
AC = DF [Adjacent sides]
By angle sum property of triangle, we know that;
∠A + ∠B + ∠C = 180 ………(1)
∠D + ∠E + ∠F = 180 ……….(2)
From equation 1 and 2 we can say;
∠A + ∠B + ∠C = ∠D + ∠E + ∠F
∠A + ∠E + ∠F = ∠D + ∠E + ∠F [Since, ∠B = ∠E and ∠C = ∠F] ∠A = ∠D
Hence, in triangle ABC and DEF,
∠A = ∠D
AC = DF
∠C = ∠F
Hence, by ASA congruency,
Δ ABC ≅ Δ DEF
RHS (Right angle- Hypotenuse-Side)
If the hypotenuse and a side of a right- angled triangle is equivalent to the hypotenuse and a side of the second right- angled triangle, then the two right triangles are said to be congruent by RHS rule.
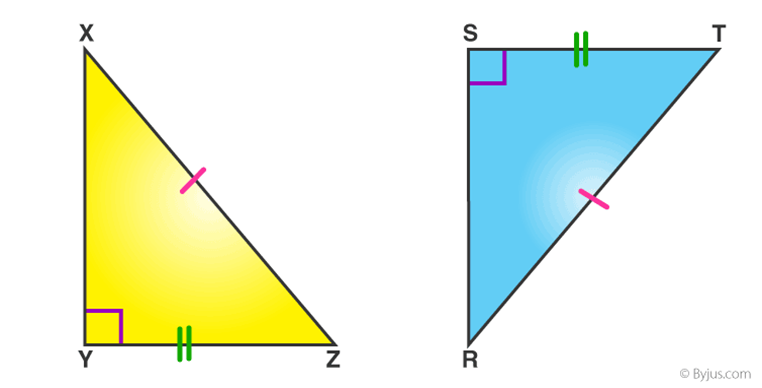
In above figure, hypotenuse XZ = RT and side YZ=ST, hence triangle XYZ ≅ triangle RST.
Congruence of Triangles
Chapter 7 - Triangles
Congruence of Triangles
Congruence of triangles: Two triangles are said to be congruent if all three corresponding sides are equal and all the three corresponding angles are equal in measure. These triangles can be slides, rotated, flipped and turned to be looked identical. If repositioned, they coincide with each other. The symbol of congruence is’ ≅’.
The corresponding sides and angles of congruent triangles are equal. There are basically four congruency rules that proves if two triangles are congruent. But it is necessary to find all six dimensions. Hence, the congruence of triangles can be evaluated by knowing only three values out of six. The meaning of congruence in Maths is when two figures are similar to each other based on their shape and size. Also, learn about Congruent Figures here.
Congruence is the term used to define an object and its mirror image. Two objects or shapes are said to be congruent if they superimpose on each other. Their shape and dimensions are the same. In the case of geometric figures, line segments with the same length are congruent and angles with the same measure are congruent.
|
Conditions for Congruence of Triangles: |
CPCT is the term, we come across when we learn about the congruent triangle. Let’s see the condition for triangles to be congruent with proof.
Congruent meaning in Maths
The meaning of congruent in Maths is addressed to those figures and shapes that can be repositioned or flipped to coincide with the other shapes. These shapes can be reflected to coincide with similar shapes.
Two shapes are congruent if they have the same shape and size. We can also say if two shapes are congruent, then the mirror image of one shape is same as the other.
Congruent Triangles
A polygon made of three line segments forming three angles is known as a Triangle.
Two triangles are said to be congruent if their sides have the same length and angles have same measure. Thus, two triangles can be superimposed side to side and angle to angle.
In the above figure, Δ ABC and Δ PQR are congruent triangles. This means,
Vertices: A and P, B and Q, and C and R are the same.
Sides: AB=PQ, QR= BC and AC=PR;
Angles: ∠A = ∠P, ∠B = ∠Q, and ∠C = ∠R.
Congruent triangles are triangles having corresponding sides and angles to be equal. Congruence is denoted by the symbol “≅”. They have the same area and the same perimeter.
7,728
CPCT Full Form
CPCT is the term we come across when we learn about the congruent triangle. CPCT means “Corresponding Parts of Congruent Triangles”. As we know that the corresponding parts of congruent triangles are equal. While dealing with the concepts related to triangles and solving questions, we often make use of the abbreviation cpct in short words instead of full form.
CPCT Rules in Maths
The full form of CPCT is Corresponding parts of Congruent triangles. Congruence can be predicted without actually measuring the sides and angles of a triangle. Different rules of congruency are as follows.
- SSS (Side-Side-Side)
- SAS (Side-Angle-Side)
- ASA (Angle-Side-Angle)
- AAS (Angle-Angle-Side)
- RHS (Right angle-Hypotenuse-Side)
Let us learn them all in detail.
SSS (Side-Side-Side)
If all the three sides of one triangle are equivalent to the corresponding three sides of the second triangle, then the two triangles are said to be congruent by SSS rule.
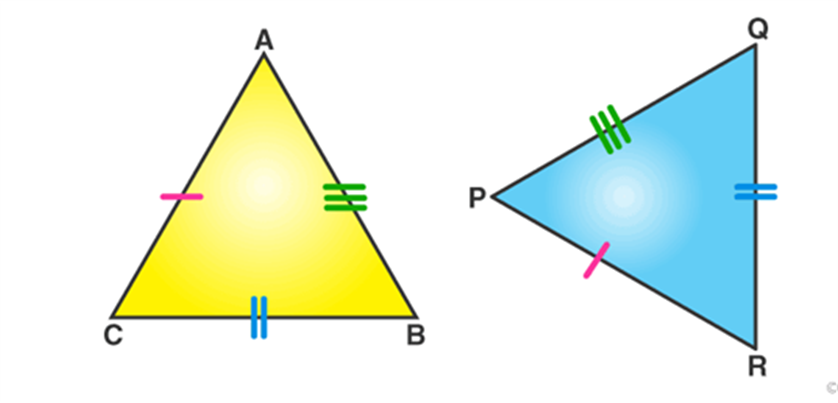
In the above-given figure, AB= PQ, QR= BC and AC=PR, hence Δ ABC ≅ Δ PQR.
SAS (Side-Angle-Side)
If any two sides and the angle included between the sides of one triangle are equivalent to the corresponding two sides and the angle between the sides of the second triangle, then the two triangles are said to be congruent by SAS rule.
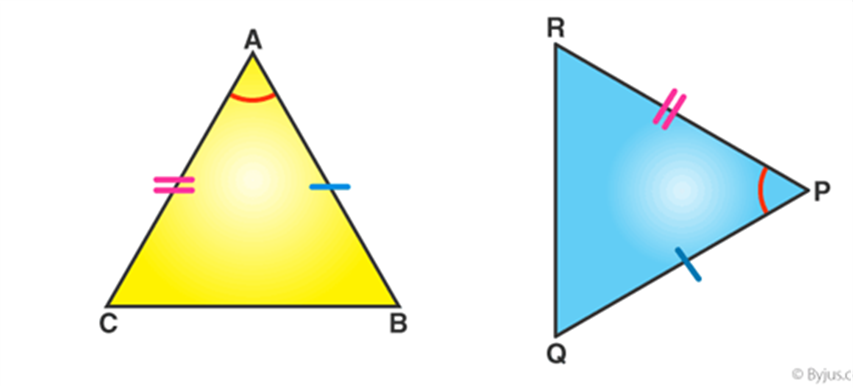
In above given figure, sides AB= PQ, AC=PR and angle between AC and AB equal to angle between PR and PQ i.e. ∠A = ∠P. Hence, Δ ABC ≅ Δ PQR.
ASA (Angle-Side- Angle)
If any two angles and the side included between the angles of one triangle are equivalent to the corresponding two angles and side included between the angles of the second triangle, then the two triangles are said to be congruent by ASA rule.
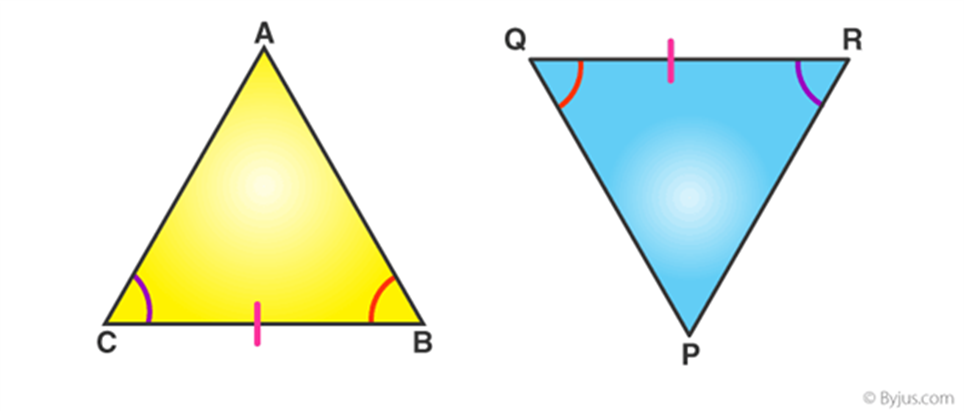
In above given figure, ∠ B = ∠ Q, ∠ C = ∠ R and sides between ∠B and ∠C , ∠Q and ∠ R are equal to each other i.e. BC= QR. Hence, Δ ABC ≅ Δ PQR.
For More Information On SAS And ASA Congruency Rules, Watch The Below Video:
10,184
AAS (Angle-Angle-Side) [Application of ASA]
AAS stands for Angle-angle-side. When two angles and a non-included side of a triangle are equal to the corresponding angles and sides of another triangle, then the triangles are said to be congruent.
AAS congruency can be proved in easy steps. Suppose we have two triangles ABC and DEF, where,
∠B = ∠E [Corresponding sides] ∠C = ∠F [Corresponding sides] And
AC = DF [Adjacent sides]
By angle sum property of triangle, we know that;
∠A + ∠B + ∠C = 180 ………(1)
∠D + ∠E + ∠F = 180 ……….(2)
From equation 1 and 2 we can say;
∠A + ∠B + ∠C = ∠D + ∠E + ∠F
∠A + ∠E + ∠F = ∠D + ∠E + ∠F [Since, ∠B = ∠E and ∠C = ∠F] ∠A = ∠D
Hence, in triangle ABC and DEF,
∠A = ∠D
AC = DF
∠C = ∠F
Hence, by ASA congruency,
Δ ABC ≅ Δ DEF
RHS (Right angle- Hypotenuse-Side)
If the hypotenuse and a side of a right- angled triangle is equivalent to the hypotenuse and a side of the second right- angled triangle, then the two right triangles are said to be congruent by RHS rule.
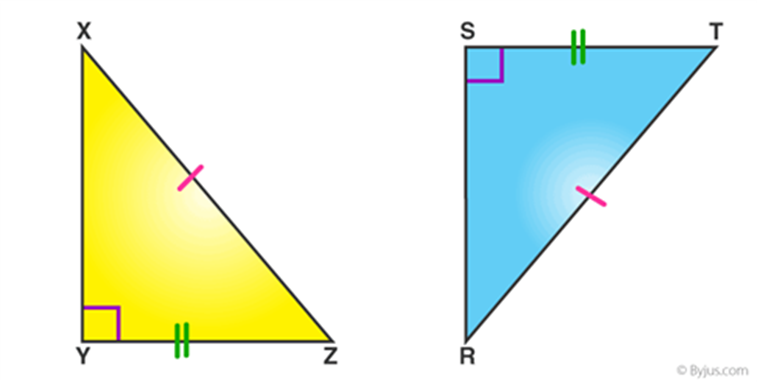
In above figure, hypotenuse XZ = RT and side YZ=ST, hence triangle XYZ ≅ triangle RST.
Solved Example
|
Let’s Work Out:
Solution: We are required to prove ∠BEA = ∠BEC = 90° and AE = EC.Consider ∆ABD and ∆CBD,AB = BC (Given)AD = CD (Given) BD = BD (Common) Therefore, ∆ABD ≅ ∆CBD (By SSS congruency) ∠ABD = ∠CBD (CPCTC) Now, consider ∆ABE and ∆CBE, AB = BC (Given) ∠ABD = ∠CBD (Proved above) BE = BE (Common) Therefore, ∆ABE≅ ∆CBE (By SAS congruency) ∠BEA = ∠BEC (CPCTC) And ∠BEA +∠BEC = 180° (Linear pair) 2∠BEA = 180° (∠BEA = ∠BEC) ∠BEA = 180°/2 = 90° = ∠BEC AE = EC (CPCTC) Hence, BD is a perpendicular bisector of AC. Example 2: In a Δ ABC, if AB = AC and ∠ B = 70°, find ∠ A. Solution: Given: In a Δ ABC, AB = AC and ∠B = 70° ∠ B = ∠ C [Angles opposite to equal sides are equal] Therefore, ∠ B = ∠ C = 70° Sum of angles in a triangle = 180° ∠ A + ∠ B + ∠ C = 180° ∠ A + 70° + 70° = 180° ∠ A = 180° – 140° ∠ A = 40° |
Angle sum property of a quadrilateral
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Quadrilateral: Angle Sum Property
Before talking about the quadrilaterals angle sum property, let us recall what angles and quadrilateral is. The angle is formed when two line segment joins at a single point. An angle is measured in degrees (°). Quadrilateral angles are the angles formed inside the shape of a quadrilateral. The quadrilateral is four-sided polygon that can have or not have equal sides. It is a closed figure in two-dimension and has non-curved sides. A quadrilateral is a polygon that has 4 vertices and 4 sides enclosing 4 angles and the sum of all the angles is 360°. When we draw draw the diagonals to the quadrilateral, it forms two triangles. Both these triangles have an angle sum of 180°. Therefore, the total angle sum of the quadrilateral is 360°. Angle sum is one of the properties of quadrilaterals. In this article, w will learn the rules of angle sum property.
Angle Sum Property of a Quadrilateral
According to the angle sum property of a Quadrilateral, the sum of all the four interior angles is 360 degrees.
Proof: In the quadrilateral ABCD,
- ∠ABC, ∠BCD, ∠CDA, and ∠DAB are the internal angles.
- AC is a diagonal
- AC divides the quadrilateral into two triangles, ∆ABC and ∆ADC
We have learned that the sum of internal angles of a quadrilateral is 360°, that is, ∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°.
let’s prove that the sum of all the four angles of a quadrilateral is 360 degrees.
- We know that the sum of angles in a triangle is 180°.
- Now consider triangle ADC,
∠D + ∠DAC + ∠DCA = 180° (Sum of angles in a triangle)
- Now consider triangle ABC,
∠B + ∠BAC + ∠BCA = 180° (Sum of angles in a triangle)
- On adding both the equations obtained above we have,
(∠D + ∠DAC + ∠DCA) + (∠B + ∠BAC + ∠BCA) = 180° + 180°
∠D + (∠DAC + ∠BAC) + (∠BCA + ∠DCA) + ∠B = 360°
- We see that (∠DAC + ∠BAC) = ∠DAB and (∠BCA + ∠DCA) = ∠BCD.
- Replacing them we have,
∠D + ∠DAB + ∠BCD + ∠B = 360°
- That is,
∠D + ∠A + ∠C + ∠B = 360°.
Or, the sum of angles of a quadrilateral is 360°. This is the angle sum property of quadrilaterals.
Quadrilateral Angles
A quadrilateral has 4 angles. The sum of its interior angles is 360 degrees. We can find the angles of a quadrilateral if we know 3 angles or 2 angles or 1 angle and 4 lengths of the quadrilateral. In the image given below, a Trapezoid (also a type of Quadrilateral) is shown.
The sum of all the angles ∠A +∠B + ∠C + ∠D = 360°
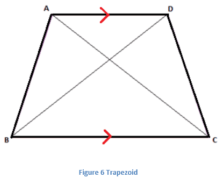
In the case of square and rectangle, the value of all the angles is 90 degrees. Hence, ∠A = ∠B = ∠C = ∠D = 90°
A quadrilateral, in general, has sides of different lengths and angles of different measures. However, squares, rectangles, etc. are special types of quadrilaterals with some of their sides and angles being equal.
Do the Opposite side in a Quadrilateral equals 180 Degrees?
There is no relationship between the opposite side and the angle measures of a quadrilateral. To prove this, the scalene trapezium has the side length of different measure, which does not have opposite angles of 180 degrees. But in case of some cyclic quadrilateral, such as square, isosceles trapezium, rectangle, the opposite angles are supplementary angles. It means that the angles add up to 180 degrees. One pair of opposite quadrilateral angles are equal in the kite and two pair of the opposite angles are equal in the quadrilateral such as rhombus and parallelogram. It means that the sum of the quadrilateral angles is equal to 360 degrees, but it is not necessary that the opposite angles in the quadrilateral should be of 180 degrees.
Types of Quadrilaterals
There are basically five types of quadrilaterals. They are;
- Parallelogram: Which has opposite sides as equal and parallel to each other.
- Rectangle: Which has equal opposite sides but all the angles are at 90 degrees.
- Square: Which all its four sides as equal and angles at 90 degrees.
- Rhombus: Its a parallelogram with all its sides as equal and its diagonals bisects each other at 90 degrees.
- Trapezium: Which has only one pair of sides as parallel and the sides may not be equal to each other.
Example
1. Find the fourth angle of a quadrilateral whose angles are 90°, 45° and 60°.
Solution: By the angle sum property we know;
Sum of all the interior angles of a quadrilateral = 360°
Let the unknown angle be x So,
90° + 45° + 60° + x = 360°
195° + x = 360°
x = 360° – 195°
x = 165°
Angle sum property of a quadrilateral
Chapter 8 - Quadrilaterals
Quadrilateral: Angle Sum Property
Before talking about the quadrilaterals angle sum property, let us recall what angles and quadrilateral is. The angle is formed when two line segment joins at a single point. An angle is measured in degrees (°). Quadrilateral angles are the angles formed inside the shape of a quadrilateral. The quadrilateral is four-sided polygon which can have or not have equal sides. It is a closed figure in two-dimension and has non-curved sides. A quadrilateral is a polygon which has 4 vertices and 4 sides enclosing 4 angles and the sum of all the angles is 360°. When we draw a draw the diagonals to the quadrilateral, it forms two triangles. Both these triangles have an angle sum of 180°. Therefore, the total angle sum of the quadrilateral is 360°. Angle sum is one of the properties of quadrilaterals. In this article, w will learn the rules of angle sum property.
Angle Sum Property of a Quadrilateral
According to the angle sum property of a Quadrilateral, the sum of all the four interior angles is 360 degrees.
Proof: In the quadrilateral ABCD,
- ∠ABC, ∠BCD, ∠CDA, and ∠DAB are the internal angles.
- AC is a diagonal
- AC divides the quadrilateral into two triangles, ∆ABC and ∆ADC
We have learned that the sum of internal angles of a quadrilateral is 360°, that is, ∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°.
let’s prove that the sum of all the four angles of a quadrilateral is 360 degrees.
- We know that the sum of angles in a triangle is 180°.
- Now consider triangle ADC,
∠D + ∠DAC + ∠DCA = 180° (Sum of angles in a triangle)
- Now consider triangle ABC,
∠B + ∠BAC + ∠BCA = 180° (Sum of angles in a triangle)
- On adding both the equations obtained above we have,
(∠D + ∠DAC + ∠DCA) + (∠B + ∠BAC + ∠BCA) = 180° + 180°
∠D + (∠DAC + ∠BAC) + (∠BCA + ∠DCA) + ∠B = 360°
- We see that (∠DAC + ∠BAC) = ∠DAB and (∠BCA + ∠DCA) = ∠BCD.
- Replacing them we have,
∠D + ∠DAB + ∠BCD + ∠B = 360°
- That is,
∠D + ∠A + ∠C + ∠B = 360°.
Or, the sum of angles of a quadrilateral is 360°. This is the angle sum property of quadrilaterals.
Quadrilateral Angles
A quadrilateral has 4 angles. The sum of its interior angles is 360 degrees. We can find the angles of a quadrilateral if we know 3 angles or 2 angles or 1 angle and 4 lengths of the quadrilateral. In the image given below, a Trapezoid (also a type of Quadrilateral) is shown.
The sum of all the angles ∠A +∠B + ∠C + ∠D = 360°
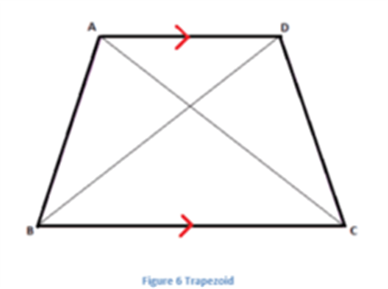
In the case of square and rectangle, the value of all the angles is 90 degrees. Hence,
∠A = ∠B = ∠C = ∠D = 90°
A quadrilateral, in general, has sides of different lengths and angles of different measures. However, squares, rectangles, etc. are special types of quadrilaterals with some of their sides and angles being equal.
Do the Opposite side in a Quadrilateral equals 180 Degrees?
There is no relationship between the opposite side and the angle measures of a quadrilateral. To prove this, the scalene trapezium has the side length of different measure, which does not have opposite angles of 180 degrees. But in case of some cyclic quadrilateral, such as square, isosceles trapezium, rectangle, the opposite angles are supplementary angles. It means that the angles add up to 180 degrees. One pair of opposite quadrilateral angles are equal in the kite and two pair of the opposite angles are equal in the quadrilateral such as rhombus and parallelogram. It means that the sum of the quadrilateral angles is equal to 360 degrees, but it is not necessary that the opposite angles in the quadrilateral should be of 180 degrees.
Types of Quadrilaterals
There are basically five types of quadrilaterals. They are;
- Parallelogram: Which has opposite sides as equal and parallel to each other.
- Rectangle: Which has equal opposite sides but all the angles are at 90 degrees.
- Square: Which all its four sides as equal and angles at 90 degrees.
- Rhombus: Its a parallelogram with all its sides as equal and its diagonals bisects each other at 90 degrees.
- Trapezium: Which has only one pair of sides as parallel and the sides may not be equal to each other.
Example
1. Find the fourth angle of a quadrilateral whose angles are 90°, 45° and 60°.
Solution: By the angle sum property we know;
Sum of all the interior angles of a quadrilateral = 360°
Let the unknown angle be x
So,
90° + 45° + 60° + x = 360°
195° + x = 360°
x = 360° – 195°
x = 165°
Figures on the same base and between the same parallels
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
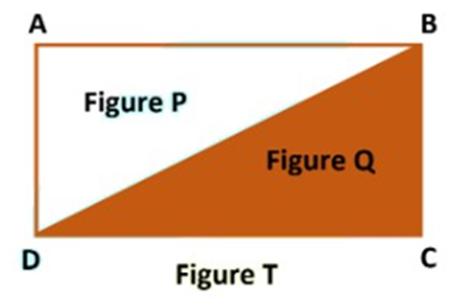
Figures on the same base and between the same parallels
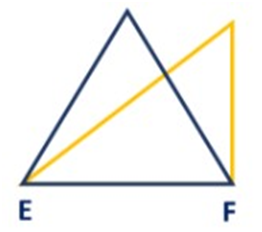
Two triangles with common base EF.
Two figures are between two parallels AB & CD but have different bases’ lengths.

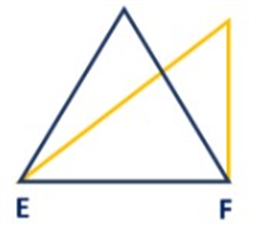
Two figures with common base XY and between two parallels XY & PQ.

“So, two figures are said to be on the same base and between the same parallels, if they have a common base (side) and the vertices (or the vertex) opposite to the common base of each figure lie on a line parallel to the base”. [As shown in the figure above]
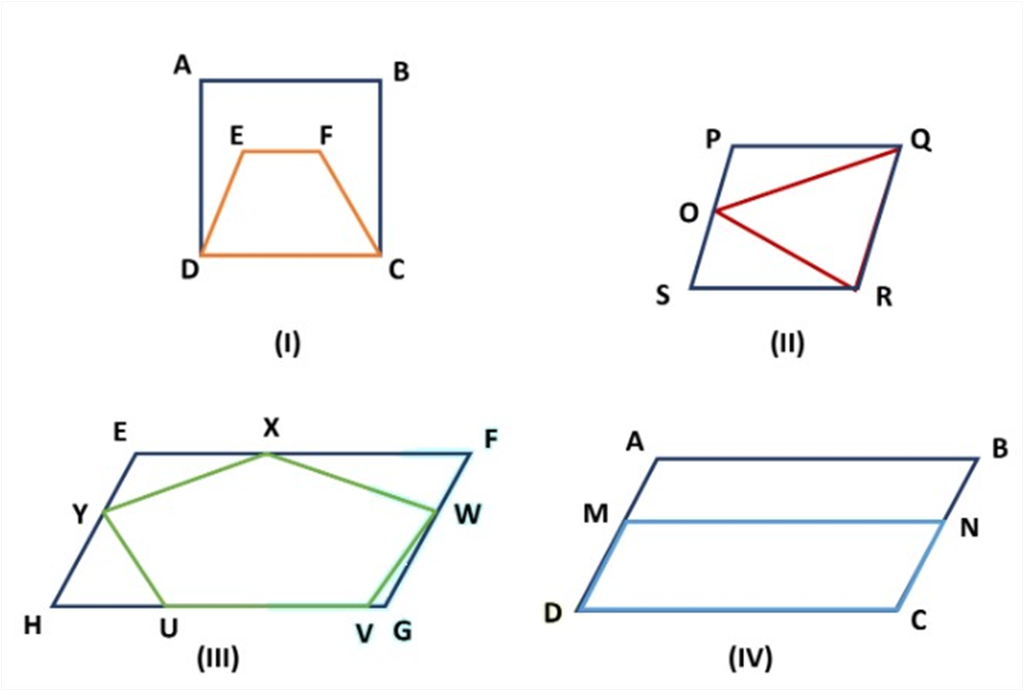
Example: Choose which of the following figures lie on the same base and between the same parallels. For such a figure, write the common base and the two parallels.
Solution:
I. Rectangle ABCD and trapezium EFCD are on the same base CD but they are not between the same parallels.
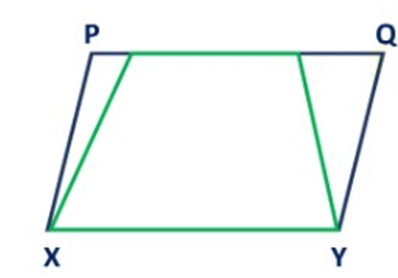
II. Parallelogram PQRS and ∆ ROQ are on the same base RQ and between the same parallel lines PS and QR.
III. Parallelogram EFGH and pentagon UVWXY are between the same parallel EF and HG but they are not on the same base.
IV. Parallelogram ABCD and parallelogram MNCD lie between the same parallels AB and CD and they have a common base CD.
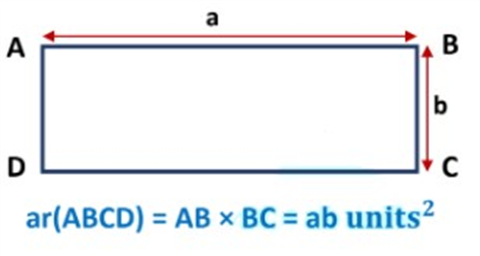
RECTANGLE AREA AXIOM
If ABCD is a rectangular region such that AB = a units and BC = b units in length, then

CONGRUENT AREA AXIOM
Consider two ∆ ABC and ∆ DEF which are congruent to each other.

Now, we calculate the area of ∆ ABC, then we get
ar(∆ABC) = 1/2× base × height.
![]() × 3 cm × 4 cm.
× 3 cm × 4 cm.
= 3 cm × 2 cm.
= 6 cm2.
Also, we calculate the area of ∆ DEF, then we get
ar(∆DEF) = ![]() × base × height.
× base × height.
= ![]() × 3 cm × 4 cm.
× 3 cm × 4 cm.
= 3 cm × 2 cm.
= 6 cm2.
Here, we also see that the area of triangles ABC and DEF are equal.
Therefore, we conclude that if two figures are congruent with each other, they must have equal areas.
Now, consider a rectangle ABCD and square PQRS which are equal in area.

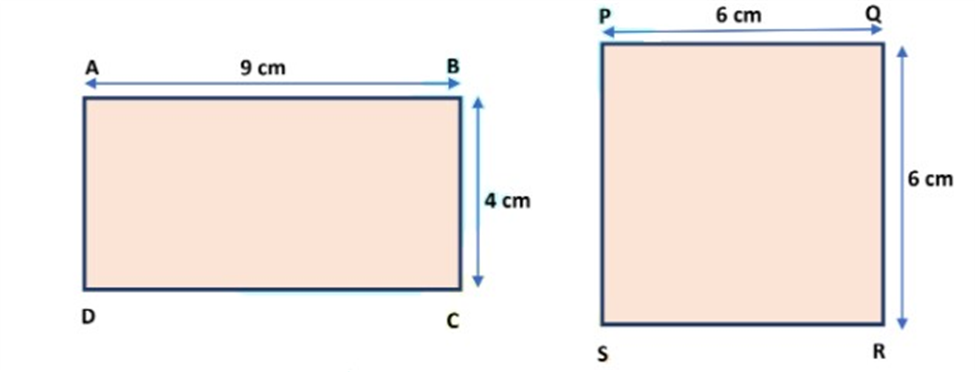
We calculate the area of rectangle ABCD, then we get ar(ABCD) = Length × Breath.
= 9 cm × 4 cm.
= 36 cm2
Also, we calculate the area of square PQRS, then we get
ar(PQRS) = Side × Side.
= 6 cm × 6 cm.
= 36 cm2.
Here, we see that areas of triangles ABC and DEF are equal. Rectangles ABCD and square PQRS are not congruent, but still, they have equal areas. Therefore, we can conclude that if two figures are congruent, they will have equal areas whereas, if two figures have equal areas, they need not be congruent with each other.
AREA MONOTONE AXIOM:
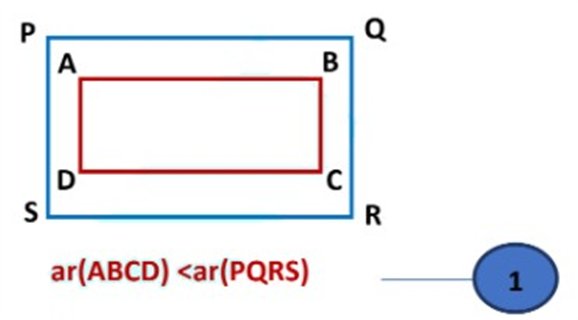
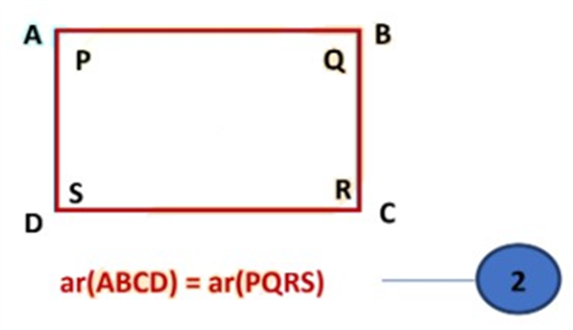
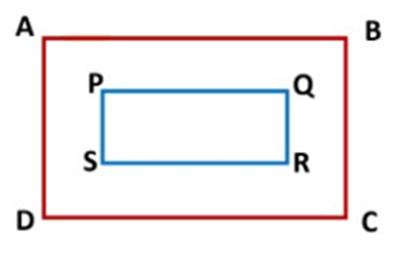
If R1, R2 are two polygonal regions such that R1 is a part of R2, then
ar(R1 ) ≤ ar(R2)
i.e. In the given figure region, ABCD is the part of region PQRS, which means

In the next figure (below) the region, the vertices A, B, C, D of parallelogram ABCD coincide with the vertices P, Q, R, S of the parallelogram PQRS.

The third possibility for figure ABCD and PQRS is

But in this case, ar(ABCD) >ar(PQRS) and PQRS is the part of ABCD which is not held by the statement of the axiom. So, this case shall not be considered.
AREA ADDITION AXIOM:
If a planer region formed by a figure T is made up of two non-overlapping planar regions formed by figures P and Q, then ar (T)=ar (P)+ar (Q).

In the figure above, ar(ABCD) = ar(∆ADB) + ar(∆BCD
Figures on the same base and between the same parallels
Chapter 9 - Areas of parallelograms and triangles
Figures on the same base and between the same parallels
Figures on the same base and between the same parallels
Two triangles with common base EF.
Two figures are between two parallels AB & CD but have different bases’ length.
Two figures with common base XY and between two parallels XY & PQ.
“So, two figures are said to be on the same base and between same parallels, if they have a common base (side) and the vertices (or the vertex) opposite to the common base of each figure lie on a line parallel to the base”. [As shown in the figure above]
Example: Choose which of the following figures lie on the same base and between the same parallels. For such a figure, write the common base and the two parallels.
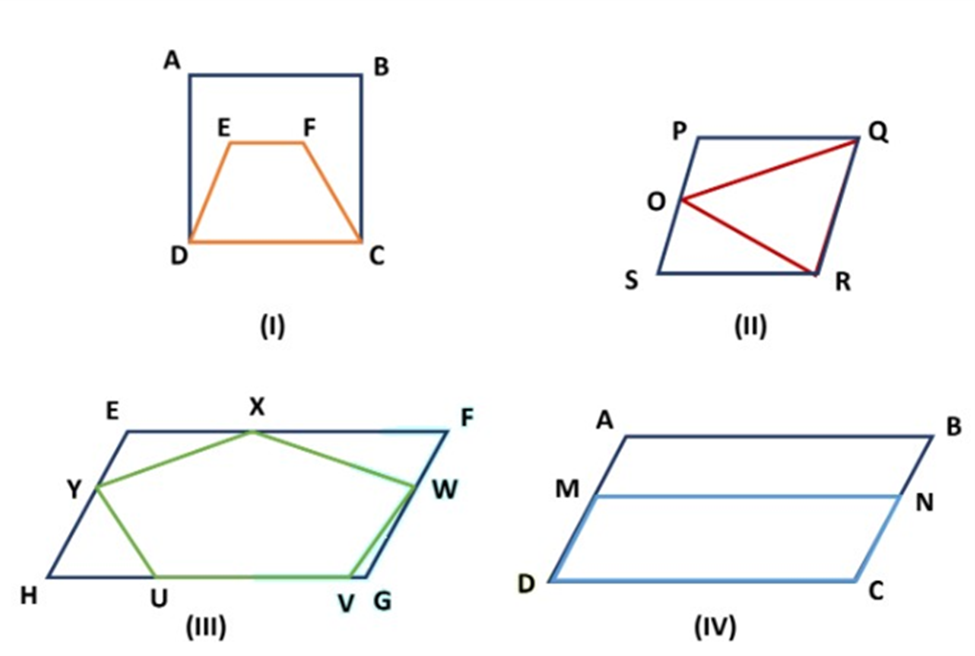
Solution:
I. Rectangle ABCD and trapezium EFCD are on the same base CD but they are not between the same parallels.
II. Parallelogram PQRS and ∆ ROQ are on the same base RQ and between the same parallel lines PS and QR.
III. Parallelogram EFGH and pentagon UVWXY are between the same parallel EF and HG but they are not on the same base.
IV. Parallelogram ABCD and parallelogram MNCD lie between the same parallels AB and CD and they have common base CD.
RECTANGLE AREA AXIOM
If ABCD is a rectangular region such that AB = a units and BC = b units in length, then
CONGRUENT AREA AXIOM
Consider two ∆ ABC and ∆ DEF which are congruent to each other.
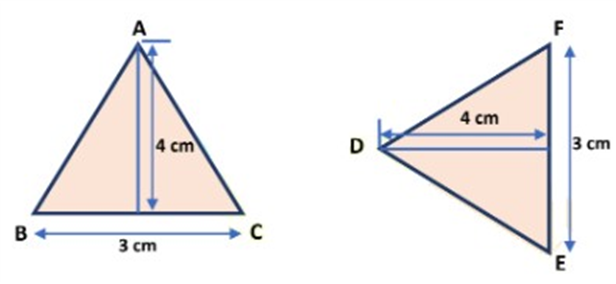
Now, we calculate the area of ∆ ABC, then we get
ar(∆ABC) = 1/2× base × height.
=  × 3 cm × 4 cm.
× 3 cm × 4 cm.
= 3 cm × 2 cm.
= 6 cm2.
Also, we calculate the area of ∆ DEF, then we get
ar(∆DEF) =  × base × height.
× base × height.
=  × 3 cm × 4 cm.
× 3 cm × 4 cm.
= 3 cm × 2 cm.
= 6 cm2.
Here, we also see that the area of triangles ABC and DEF are equal.
Therefore, we conclude that if two figures are congruent with each other, they must have equal areas.
Now, consider a rectangle ABCD and square PQRS which are equal in area.
We calculate the area of rectangle ABCD, then we get ar(ABCD) = Length × Breath.
= 9 cm × 4 cm.
= 36 cm2
Also, we calculate the area of square PQRS, then we get
ar(PQRS) = Side × Side.
= 6 cm × 6 cm.
= 36 cm2.
Here, we see that areas of triangles ABC and DEF are equal. Rectangles ABCD and square PQRS are not congruent, but still, they have equal areas. Therefore, we can conclude that if two figures are congruent, they will have equal areas whereas, if two figures have equal areas, they need not be congruent with each other.
AREA MONOTONE AXIOM:
If R1, R2 are two polygonal regions such that R1 is a part of R2, then
ar(R1 ) ≤ ar(R2)
i.e. In the given figure region, ABCD is the part of region PQRS, that means
In the next figure (below) the region, the vertices A, B, C, D of parallelogram ABCD coincide with the vertices P, Q, R, S of the parallelogram PQRS.
The third possibility for figure ABCD and PQRS is
But in this case, ar(ABCD) >ar(PQRS) and PQRS is the part of ABCD which is not held by the statement of the axiom. So, this case shall not be considered.
AREA ADDITION AXIOM:
If a planer region formed by a figure T is made up of two non-overlapping planar regions formed by figures P and Q, then ar (T)=ar (P)+ar (Q).
In the figure above, ar(ABCD) = ar(∆ADB) + ar(∆BCD)
Circles and its related terms
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Circles and its related terms
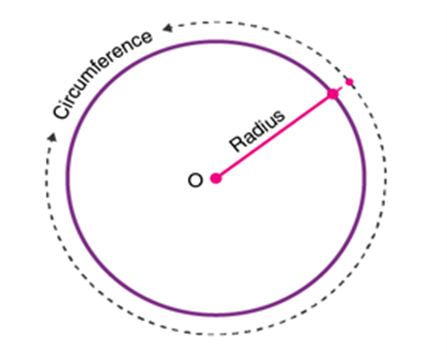
In Maths or Geometry, a circle is a special kind of ellipse in which the eccentricity is zero and the two foci are coincident. A circle is also termed as the locus of the points drawn at an equidistant from the center. The distance from the center of the circle to the outer line is its radius. Diameter is the line that divides the circle into two equal parts and is also equal to twice the radius.
A circle is a basic 2D shape that is measured in terms of its radius. The circles divide the plane into two regions as interior and exterior regions. It is similar to the type of line segment. Imagine that the line segment is bent around till its ends join. Arrange the loop until it is precisely circular.
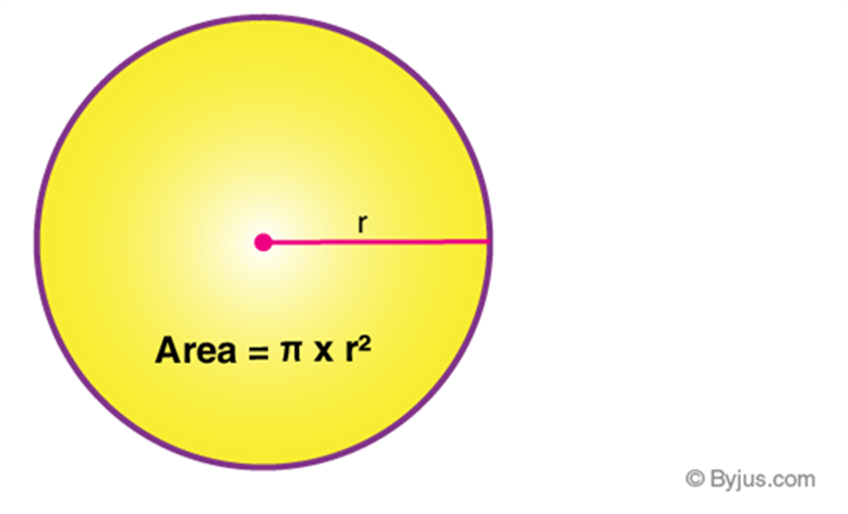
The circle is a two-dimensional figure, which has its area and perimeter. The perimeter of the circle is also called the circumference, which is the distance around the circle. The area of the circle is the region bounded by it in a 2D plane. Let us discuss here circle definition, formulas, and important terms with examples in detail.
Circle Definition
A circle is a closed two-dimensional figure in which the set of all the points in the plane is equidistant from a given point called the “center”. Every line that passes through the circle forms the line of reflection symmetry. Also, it has rotational symmetry around the center for every angle. The circle formula in the plane is given as:
(x-h)2 + (y-k)2 = r2
where (x,y) are the coordinate points (h,k) is the coordinate of the center of a circle
and r is the radius of a circle.
Circle Shaped Objects
There are many objects we have seen in the real world that are circular in shape. Some of the examples are:
- Ring
- CD/Disc
- Bangles
- Coins
- Wheels
- Button
- Dartboard
- Hula hoop
We can observe many such examples in our day-to-day life.
How to Draw a Circle?
In maths projects for class 10 on circles, the construction of a circle, all the properties and terminologies are explained in detail. To understand what circles are in simple terms, go through circles for class 10, and also try the following exercise –
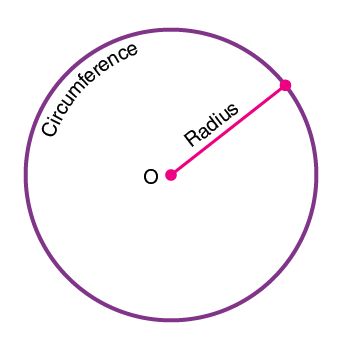
- Take an empty sheet of paper and mark a single point on the sheet, somewhere in the middle of the sheet, and name it point O.
- Select a random length for radius, for example, 3 cm.
- Using a ruler, keep the reference zero mark on point O and randomly mark 3 cm away from point O in all the directions.
- Mark as many points as you want away from point O, but all of them should be exactly 3 cm away from point O.
If you’ve selected sufficient points, you may notice that the shape is starting to resemble a circle and this is exactly what the definition of a circle is.
Parts of Circle
A circle has different parts based on its positions and their properties. The different parts of a circle are explained below in detail.
- Annulus-The region bounded by two concentric circles. It is basically a ring-shaped object. See the figure below.
- Arc – It is basically the connected curve of a circle.
- Sector – A region bounded by two radii and an arc.
- Segment- A region bounded by a chord and an arc lying between the chord’s endpoints. It is to be noted that segments do not contain the center.
See the figure below explaining the arc, sector and segment of a circle.
- Centre – It is the midpoint of a circle.
- Chord- A line segment whose endpoints lie on the circle.
- Diameter- A line segment having both the endpoints on the circle and is the largest chord of the circle.
- Radius- A line segment connecting the center of a circle to any point on the circle itself.
- Secant- A straight line cutting the circle at two points. It is also called an extended chord.
- Tangent- A coplanar straight line touching the circle at a single point.
See the figure below representing the center, chord, diameter, radius, secant and tangent of a circle.
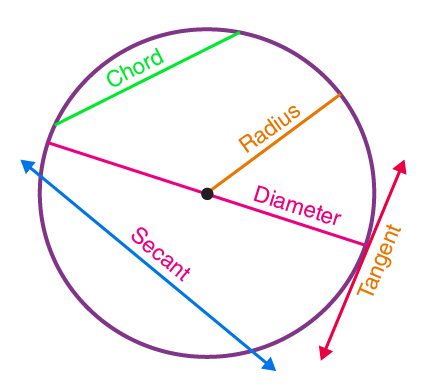
Radius of Circle (r)
A line segment connecting the center of a circle to any point on the circle itself “. The radius of the circle is denoted by “R” or “r”.
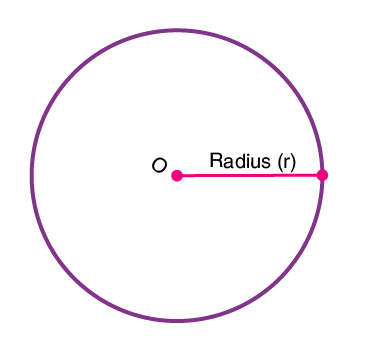
Diameter (d) of Circle
A line segment has both endpoints on the circle. It is twice the length of radius i.e. d = 2r. From the diameter, the radius of the circle formula is obtained as r= d/2.
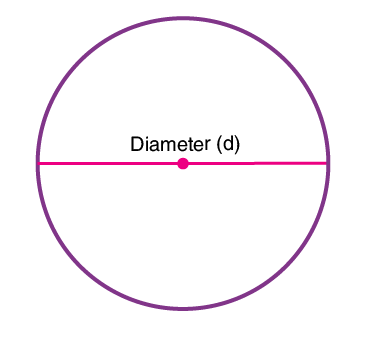
Circle Formulas
We know that a circle is a two-dimensional curve-shaped figure, and the two different parameters used to measure the circle are:
- Area of circle
- Circumference of a circle
Let us discuss here the general formulas for the area and perimeter/circumference of a circle.
Area and Circumference of a Circle
Circumference (C)
The circumference of a circle is defined as the
distance around the circle. The word ‘perimeter’
is also sometimes used, although this usually
refers to the distance around polygons, figures made up of the straight line segment.
A circle circumference formula is given by
C = πd = 2 π r
Where, π = 3.1415
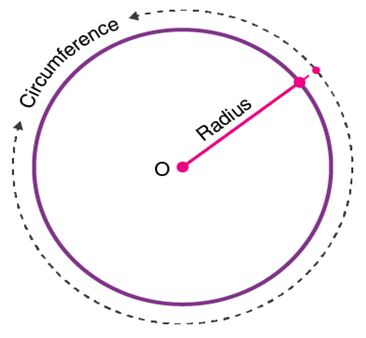
Area (A)
Area of a circle is the amount of space occupied by the circle.
The circle formula to find the area is given by
Area of a circle = πr2
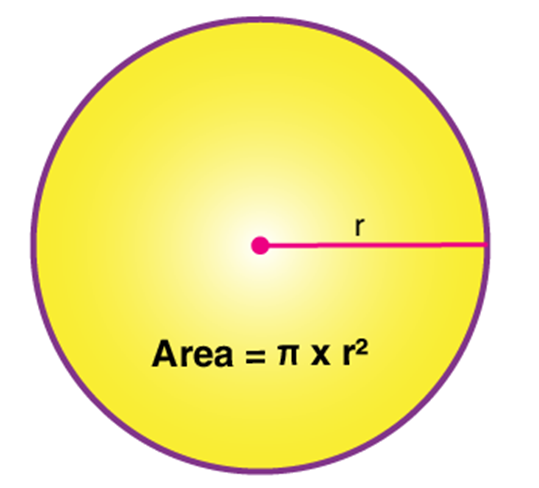
Circle Area Proof
We know that Area is the space occupied by the circle.
Consider a concentric circle having an external circle radius to be ‘r.’
Open all the concentric circles to form a right-angled triangle.
The outer circle would form a line having a length of 2πr forming the base.
The height would be ‘r’
Therefore the area of the right-angled triangle formed would be equal to the area of a circle.
Area of a circle = Area of triangle = (1/2) ×b ×h
= (1/2) × 2π r × r
Therefore, the Area of a circle = πr2
Properties of Circles
The important basic properties of circles are as follows:
- The outer line of a circle is equidistant from the center.
- The diameter of the circle divides it into two equal parts.
- Circles which have equal radii are congruent to each other.
- Circles that are different in size or have different radii are similar.
- The diameter of the circle is the largest chord and is double the radius.
Solved Examples
Example 1:
Find the area and the circumference of a circle whose radius is 10 cm. (Take the value of π = 3.14)
Solution:
Given: Radius = 10 cm.
Area =π r2
= 3.14 × 102
A= 314 cm2
Circumference, C = 2πr
C= 2 ×3.14× 10
Circumference= 62.8 cm
Example 2:
Find the area of a circle whose circumference is 31.4 cm.
Solution:
Given:
Circumference = 31.4 cm
To find the area of a circle, we need to find the radius.
From the circumference, the radius can be calculated:
2 π r = 31.4
(2)(3.14)r = 31.4
r = 31.4 /(2)(3.14)
r=10/2
r= 5
Therefore, the radius of the circle is 5 cm.
The area of a circle is πr2 square units
Now, substitute the radius value in the area of a circle formula, we get
A = π(5)2
A = 3.14 x 25
A = 78.5 cm2
Therefore, the area of a circle is 78.5 cm2.
Circles and its related terms
Chapter 10 - Circles
Circles and its related terms
In Maths or Geometry, a circle is a special kind of ellipse in which the eccentricity is zero and the two foci are coincident. A circle is also termed as the locus of the points drawn at an equidistant from the centre. The distance from the centre of the circle to the outer line is its radius. Diameter is the line which divides the circle into two equal parts and is also equal to twice of the radius.
A circle is a basic 2D shape which is measured in terms of its radius. The circles divide the plane into two regions such as interior and exterior region. It is similar to the type of line segment. Imagine that the line segment is bent around till its ends join. Arrange the loop until it is precisely circular.
The circle is a two-dimensional figure, which has its area and perimeter. The perimeter of the circle is also called the circumference, which is the distance around the circle. The area of the circle is the region bounded by it in a 2D plane. Let us discuss here circle definition, formulas, important terms with examples in detail.
Circle Definition
A circle is a closed two-dimensional figure in which the set of all the points in the plane is equidistant from a given point called “centre”. Every line that passes through the circle forms the line of reflection symmetry. Also, it has rotational symmetry around the centre for every angle. The circle formula in the plane is given as:
(x-h)2 + (y-k)2 = r2
where (x,y) are the coordinate points
(h,k) is the coordinate of the centre of a circle
and r is the radius of a circle.
Circle Shaped Objects
There are many objects we have seen in the real world that are circular in shape. Some of the examples are:
- Ring
- CD/Disc
- Bangles
- Coins
- Wheels
- Button
- Dartboard
- Hula hoop
We can observe many such examples in our day to day life.
How to Draw a Circle?
In maths projects for class 10 on circles, the construction of a circle, all the properties and terminologies are explained in detail. To understand what circles are in simple terms, go through circles for class 10, and also try the following exercise –
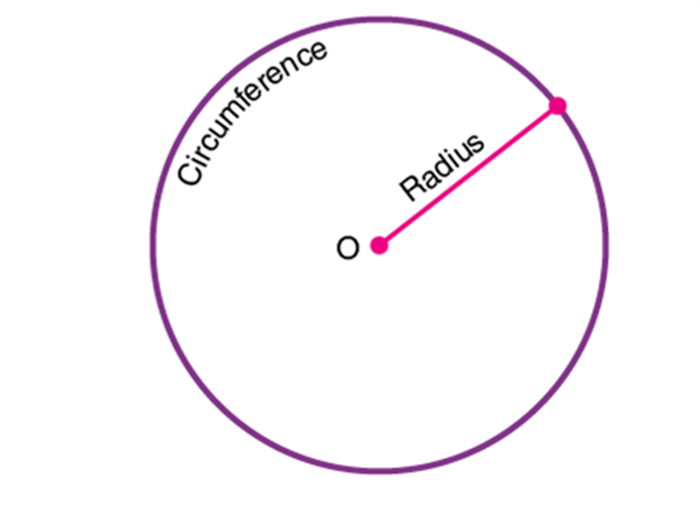
- Take an empty sheet of paper and mark a single point on the sheet, somewhere in the middle of the sheet, and name it to point O.
- Select a random length for radius, for example, 3 cm.
- Using a ruler, keep the reference zero mark on point O and randomly mark 3 cm away from point O in all the direction.
- Mark as many points as you want away from point O, but all of them should be exactly 3 cm away from point O.
If you’ve selected sufficient points, you may notice that the shape is starting to resemble a circle and this is exactly what the definition of a circle is.
Parts of Circle
A circle has different parts based on the positions and their properties. The different parts of a circle are explained below in detail.
- Annulus-The region bounded by two concentric circles. It is basically a ring-shaped object. See the figure below.
- Arc – It is basically the connected curve of a circle.
- Sector – A region bounded by two radii and an arc.
- Segment- A region bounded by a chord and an arc lying between the chord’s endpoints. It is to be noted that segments do not contain the centre.
See the figure below explaining the arc, sector and segment of a circle.
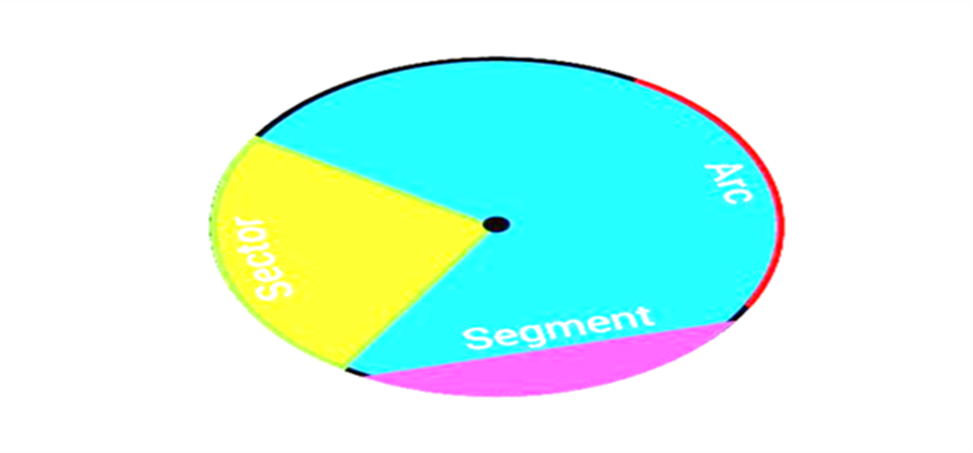
- Centre – It is the midpoint of a circle.
- Chord- A line segment whose endpoints lie on the circle.
- Diameter- A line segment having both the endpoints on the circle and is the largest chord of the circle.
- Radius- A line segment connecting the centre of a circle to any point on the circle itself.
- Secant- A straight line cutting the circle at two points. It is also called an extended chord.
- Tangent- A coplanar straight line touching the circle at a single point.
See the figure below-representing the centre, chord, diameter, radius, secant and tangent of a circle.
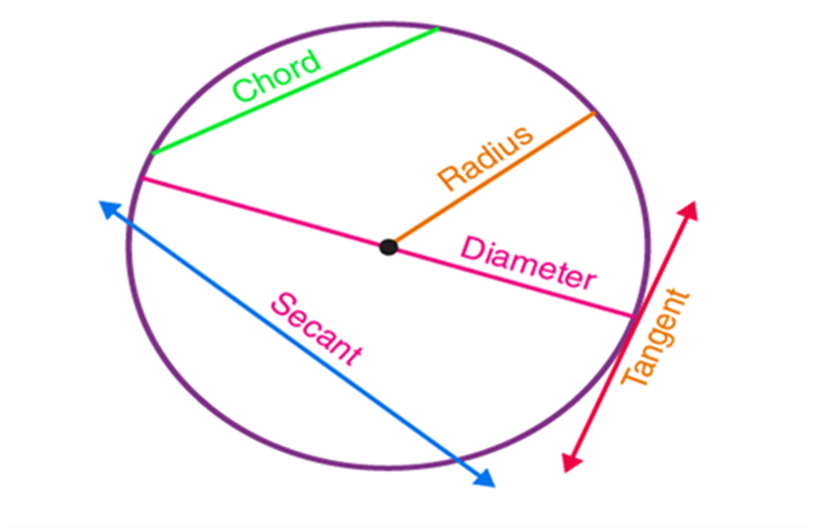
A line segment connecting the centre of a circle to any point on the circle itself “. The radius of the circle is denoted by “R” or “r”.
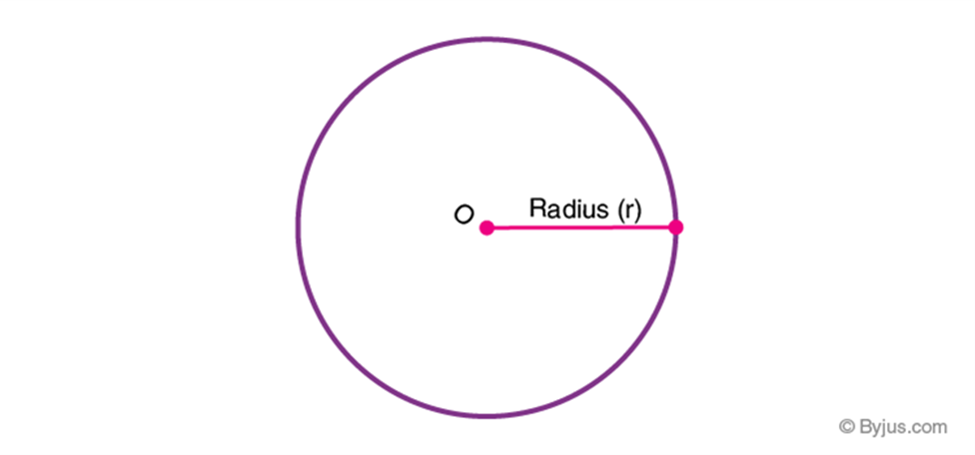
A line segment having both the endpoints on the circle. It is twice the length of radius i.e. d = 2r. From the diameter, the radius of the circle formula is obtained as r= d/2.
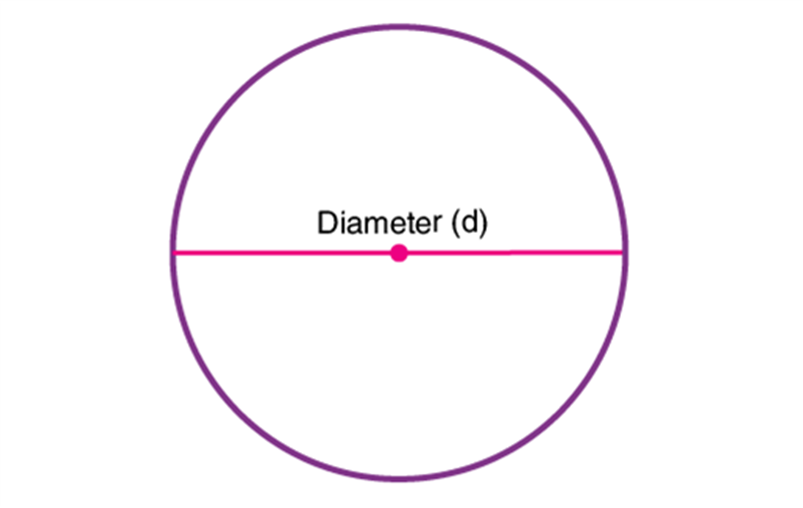
Circle Formulas
We know that a circle is a two-dimensional curve-shaped figure, and the two different parameters used to measure the circle are:
- Area of circle
- Circumference of a circle
Let us discuss here the general formulas for area and perimeter/circumference of a circle.
Area and Circumference of a Circle
|
Circumference (C) |
The circumference of a circle is defined as the distance around the circle. The word ‘perimeter’ is also sometimes used, although this usually refers to the distance around polygons, figures made up of the straight line segment. A circle circumference formula is given by C = πd = 2 π r Where, π = 3.1415 |
|
|
Area (A) |
Area of a circle is the amount of space occupied by the circle. The circle formula to find the area is given by Area of a circle = πr2 |
|
Circle Area Proof
We know that Area is the space occupied by the circle.
Consider a concentric circle having an external circle radius to be ‘r.’
Open all the concentric circles to form a right-angled triangle.
The outer circle would form a line having length 2πr forming the base.
The height would be ‘r’
Therefore the area of the right-angled triangle formed would be equal to the area of a circle.
Area of a circle = Area of triangle = (1/2) ×b ×h
= (1/2) × 2π r × r
Therefore, Area of a circle = πr2
Properties of Circles
The important basic properties of circles are as follows:
- The outer line of a circle is at equidistant from the centre.
- The diameter of the circle divides it into two equal parts.
- Circles which have equal radii are congruent to each other.
- Circles which are different in size or having different radii are similar.
- The diameter of the circle is the largest chord and is double the radius.
Solved Examples
Example 1:
Find the area and the circumference of a circle whose radius is 10 cm. (Take the value of π = 3.14)
Solution:
Given: Radius = 10 cm.
Area =π r2
= 3.14 × 102
A= 314 cm2
Circumference, C = 2πr
C= 2 ×3.14× 10
Circumference= 62.8 cm
Example 2:
Find the area of a circle whose circumference is 31.4 cm.
Solution:
Given:
Circumference = 31.4 cm
To find the area of a circle, we need to find the radius.
From the circumference, the radius can be calculated:
2 π r = 31.4
(2)(3.14)r = 31.4
r = 31.4 /(2)(3.14)
r=10/2
r= 5
Therefore, the radius of the circle is 5 cm.
The area of a circle is πr2 square units
Now, substitute the radius value in the area of a circle formula, we get
A = π(5)2
A = 3.14 x 25
A = 78.5 cm2
Therefore, the area of a circle is 78.5 cm2.
Basic Construction
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Construction
In Constructions class 9 chapter 11, explains how different shapes are drawn using the compass and ruler. In this chapter, you can learn how to construct the bisector of the given angle, construction of a perpendicular bisector of the given line segment is explained with construction steps and a clear diagram. Also, solve all the important questions for class 9 Maths Chapter 11 construction problems given in the textbook to score good marks.
Constructions Class 9 Concepts
The important topics and subtopics covered under constructions class 9 are:
- Introduction
- Basic constructions
- Some constructions of triangles
- Summary
Construction Class 9 Notes
For constructing the angle bisector of angle ABC, take B as a center and construct an arc (any radius) intersecting the rays BA and BC at D and E. Now take E and D as centers and a radius of more than ½ DE, construct arcs such that they intersect with each other at F.
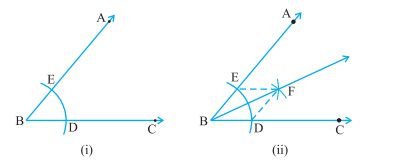
Join BF. This line is the required angle bisector of the given angle ABC.
Proof: Join EF and DF. Now, from triangle BEF and triangle BDF, BD = BE (Radius of the same arc), DF = EF (Arcs of equal radii) and BF are Common. Therefore, triangle BEF is congruent to triangle BDF by SSS congruence rule. Hence by CPCT, angle EBF is equal to angle DBF.
Constructions Class 9 Example
Go through the below example:
Example: Given that AB is a line segment. Construct the perpendicular bisector for the given line segment.
Construction Steps:
- Take A and B as centers and the radius should be more than 1/2 AB. Now, draw arcs on both sides of the line segment AB (the arc should intersect each other)
- Assume that these arcs intersect each other at the points P and Q, and join the points PQ
- Now, PQ intersect AB at the point M. Therefore, the line PMQ is the required perpendicular bisector of AB
Now, let us see how this method gives us the perpendicular bisector of AB.
To prove this, join A and B to both P and Q to form AP, AQ, BP and BQ.
From the triangles PAQ and PBQ
AP = BP and AQ = BQ (Arcs of equal radii)
PQ = PQ (Common)
Therefore, by using SSS Rule, ∆ PAQ ≅ ∆ PBQ
Thus, ∠ APM = ∠ BPM (CPCT)
Now in the triangles PMA and PMB,
AP = BP
PM = PM (Common)
∠ APM = ∠ BPM
Thus by using SAS rule, we get ∆ PMA ≅ ∆ PMB
Hence, by using CPCT, AM = BM and ∠ PMA = ∠ PMB
From the linear pair axiom ∠ PMA + ∠ PMB = 180°
∠ PMA = ∠ PMB = 90°
Therefore, the line PM, that is, PMQ is the perpendicular bisector of the line segment AB.
Practice Problems
Solve the practical problems given below for constructions class 9:
- Construct an angle of 45° at the initial point of a given ray. And also, justify the construction.
- Construct a triangle ABC in which ∠B = 30°, ∠C = 90° and AB + BC+ CA = 11 cm.
- Construct a triangle XYZ in which YZ = 8cm, ∠Y = 45° and XY – XZ= 3.5 cm
- Construct the angle 105°, and verify that using the protractor.
Basic Constructions
Why do we learn constructions? Suppose a building needs to be constructed. One needs to know the accurate map of the building. Construction means drawing the lines and angles accurately. Also to draw the road maps, learning the basic constructions is of great importance. Let us now learn about the basic constructions in geometry.
Suggested Videos
Construction of segment of a circle
Some Constructions of Triangles I
Construct a perpendicular bisector of a line segment
Basic Constructions
1. Construction of a bisector of a given angle
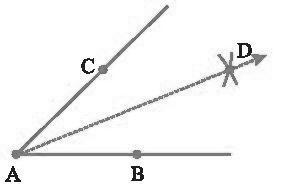
Construction:
- With A as a center and using compasses, draw an arc that cuts both rays of A.
- Label the points of intersection as B and C.
- Now with B as a center, draw (in the interior of A) an arc whose radius is more than half the length BC.
- With the same radius and with C as a center, draw another arc in the interior of A.
- Let the two arcs intersect at D
- So we get AD as the required bisector of A.
2. Construction of the perpendicular bisector of a given line segment.
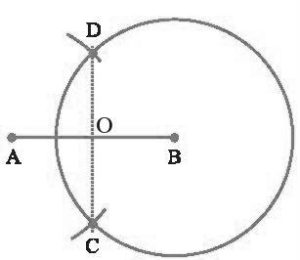
Construction:
- Draw a line segment AB
- Now take A as a center, use compasses, and draw a circle.
- The radius of your circle should be more than half the length of AB.
- With the same radius and with B as a center, draw another circle using compasses.
- Let it cut the previous circle at C and D.
- Join CD so it cuts AB at O.
- O is the midpoint of AB. Also, COA and COB are at right angles.
- Therefore, the CD is the perpendicular bisector of AB.
3. Construction of 60° Angle
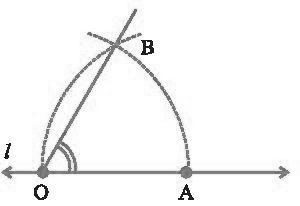
Construction:
- Take a ruler and draw a line l and make a point O on it. Take a compass and put its one end at point O and draw an arc with any convenient radius.
- We take the center O and draw an arc. We get to point A.
- Now take the compass and with the same orientation taking the point A as the center draw an arc that passes through O. Draw an arc such that it intersects the existing arc.
- Here OA and OB are nothing but the radius which is equal in length.
- So actually we are trying to draw an equilateral triangle which means the angle we see in the above construction is 60 degrees.
- We get ∠BOA which measures 60 degrees.
Solved Examples for You on Basic Constructions
Question 1: To construct a perpendicular to a line L from a point P outside the line, steps are given in the jumbled form. Identify the second step from the following.
1) Draw line PQ
2) Draw a line L and consider point P outside the line.
3) Take P as a center, draw 2 arcs on line L and name it as points A and B respectively.
4) Taking A and B as a center one by one and keeping the same distance in compass, draw the arcs on another side of the plane. The point where these arcs intersect name that point as Q
- 4
- 3
- 2
- 1
Solution: B is the correct option. 3 is the second step amongst all.
Question 2: While constructing a parallel line to a given line, we ______.
- Copy a segment
- Bisect a segment
- Copy an angle
- Construct a perpendicular
Solution: C is the correct option. While constructing a parallel line to a given line, we copy an angle.
Basic Construction
Chapter 11 - Construction
In Constructions class 9 chapter 11, explains how different shapes are drawn using the compass and ruler. In this chapter, you can learn how to construct the bisector of the given angle, construction of a perpendicular bisector of the given line segment are explained with construction steps and clear diagram. Also, solve all the important questions for class 9 Maths Chapter 11 construction problems given in the textbook to score good marks.
Constructions Class 9 Concepts
The important topics and subtopics covered under constructions class 9 are:
- Introduction
- Basic constructions
- Some constructions of triangles
- Summary
Construction Class 9 Notes
For constructing the angle bisector of angle ABC, take B as a centre construct an arc (any radius) intersecting the rays BA and BC at D and E. Now take E and D as centres and radius more than ½ DE, construct arcs such that they intersect with each other at F.
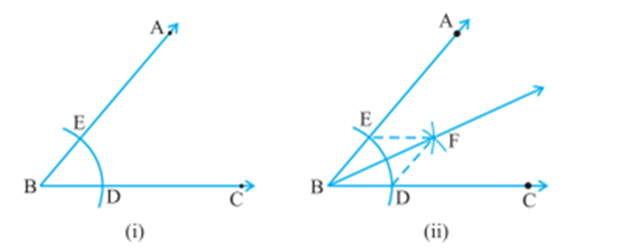
Join BF. This line is the required angle bisector of given angle ABC.
Proof:
Join EF and DF. Now, from triangle BEF and triangle BDF, BD = BE (Radius of the same arc), DF = EF (Arcs of equal radii) and BF is Common. Therefore, triangle BEF is congruent to triangle BDF by SSS congruence rule. Hence by CPCT, angle EBF is equal to angle DBF.
Constructions Class 9 Example
Go through the below example:
Example:
Given that AB is a line segment. Construct the perpendicular bisector for the given line segment.
Construction Steps:
- Take A and B as centres and radius should be more than 1/2 AB. Now, draw arcs on both sides of the line segment AB (the arc should intersect each other)
- Assume that these arcs intersect each other at the points P and Q, and join the points PQ
- Now, PQ intersect AB at the point M. Therefore, the line PMQ is the required perpendicular bisector of AB
Now, let us see how this method gives us the perpendicular bisector of AB.
To prove this, join A and B to both P and Q to form AP, AQ, BP and BQ.
From the triangles PAQ and PBQ
AP = BP and AQ = BQ (Arcs of equal radii)
PQ = PQ (Common)
Therefore, by using SSS Rule, ∆ PAQ ≅ ∆ PBQ
Thus, ∠ APM = ∠ BPM (CPCT)
Now in the triangles PMA and PMB,
AP = BP
PM = PM (Common)
∠ APM = ∠ BPM
Thus by using SAS rule, we get ∆ PMA ≅ ∆ PMB
Hence, by using CPCT, AM = BM and ∠ PMA = ∠ PMB
From the linear pair axiom ∠ PMA + ∠ PMB = 180°
∠ PMA = ∠ PMB = 90°
Therefore, the line PM, that is, PMQ is the perpendicular bisector of the line segment AB.
Practice Problems
Solve the practical problems given below for constructions class 9:
- Construct an angle of 45° at the initial point of a given ray. And also, justify the construction.
- Construct a triangle ABC in which ∠B = 30°, ∠C = 90° and AB + BC+ CA = 11 cm.
- Construct a triangle XYZ in which YZ = 8cm, ∠Y = 45° and XY – XZ= 3.5 cm
- Construct the angle 105°, and verify that using the protractor.
Basic Constructions
Why do we learn constructions? Suppose a building needs to be constructed. One needs to know the accurate map of the building. Construction means to draw the lines and angles accurately. Also to draw the road maps, learning the basic constructions is of great importance. Let us now learn about the basic constructions in geometry.
Suggested Videos
Construction of segment of circle
Some Constructions of Triangles I
Construct perpendicular bisector of a line segment
Basic Constructions
1. Construction of a bisector of a given angle
Construction:
- With A as a centre and using compasses, draw an arc that cuts both rays of A.
- Label the points of intersection as B and C.
- Now with B as a centre, draw (in the interior of A) an arc whose radius is more than half the length BC.
- With the same radius and with C as a centre, draw another arc in the interior of A.
- Let the two arcs intersect at D
- So we get AD as the required bisector of A.
2. Construction of the perpendicular bisector of a given line segment.
Construction:
- Draw a line segment AB
- Now take A as a centre, using compasses, draw a circle.
- The radius of your circle should be more than half the length of AB.
- With the same radius and with B as a centre, draw another circle using compasses.
- Let it cut the previous circle at C and D.
- Join CD so it cuts AB at O.
- O is the midpoint of AB. Also, COA and COB are right angles.
- Therefore, the CD is the perpendicular bisector of AB.
3. Construction of 60° Angle
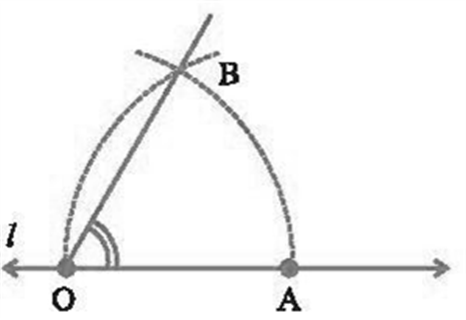
Construction:
- Take a ruler and draw a line l and make a point O on it. Take a compass and put its one end at point O and draw an arc with any convenient radius.
- We take the centre O and draw an arc. We get the point A.
- Now take the compass and with the same orientation taking the point A as the centre draw an arc that passes through O. Draw an arc such that it intersects the existing arc.
- Here OA and OB are nothing but the radius which is equal in length.
- So actually we are trying to draw an equilateral triangle which means the angle we see in the above construction is 60 degree.
- We get ∠BOA which measures 60 degrees.
Solved Examples for You on Basic Constructions
Question 1: To construct a perpendicular to a line L from a point P outside the line, steps are given in the jumbled form. Identify the second step from the following.
1)Draw line PQ
2)Draw a line L and consider point P outside the line.
3)Take P as a centre, draw 2 arcs on line L and name it as points A and B respectively.
4)Taking A and B as a centre one by one and keeping the same distance in compass, draw the arcs on another side of the plane.The point where these arcs intersect name that point as Q
- 4
- 3
- 2
- 1
Solution: B is the correct option. 3 is the second step amongst all.
Question 2: While constructing a parallel line to a given line, we ______.
- Copy a segment
- Bisect a segment
- Copy an angle
- Construct a perpendicular
Solution: C is the correct option. While constructing a parallel line to a given line, we copy an angle.
Intersecting lines and non-intersecting lines
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Intersecting Lines And Non-intersecting Lines
Before talking about what intersecting lines and non-intersecting lines are, let us recall the basic definition of a line. In geometry, a line is something that is made up of infinite points extending indefinitely in both directions. It is straight and has negligible depth or width. It is illustrated by little arrows on the two sides. A line has no ends. In case, if the line has an endpoint, then it is called a line segment.

Any two points can be taken and a line can be drawn which passes through them and extends in both directions. For example, the line in the figure above is denoted by
.In this article, you will learn about two types of lines:
- Intersecting lines
- Non-intersecting lines
Intersecting Lines
Two or more lines which share exactly one common point are called intersecting lines. This common point exists on all these lines and is called the point of intersection. It is to be noted that:
- The intersecting lines meet at one, and only one point, no matter at what angle they meet.
- No two straight lines can meet at more than one point.
- The lines that meet at more than one point are not straight lines. At least one of them is a curve.
Let us take a few examples.
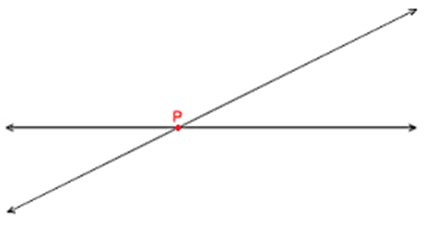
Consider these lines. They are two intersecting lines. The point of intersection is P.
The figure above also shows intersecting lines at different angles.
The figure shows an example of 4 intersecting lines.
Non-intersecting Lines
Two or more lines that do not intersect each other are called non-intersecting lines. It is to be noted that:
- Non-intersecting lines can never meet.
- They are also known as the parallel lines.
- They are always at the same distance from one another. This is called the distance between two parallel lines.

The figures above show non-intersecting or parallel lines.

Intersecting lines and non-intersecting lines
Intersecting Lines And Non-intersecting Lines
Before talking about what intersecting lines and non-intersecting lines are, let us recall the basic definition of a line. In geometry, a line is something that is made up of infinite points extending indefinitely in both directions. It is straight and has negligible depth or width. It is illustrated by little arrows on the two sides. A line has no ends. In case, if the line has an endpoint, then it is called a line segment.
![]()
Any two points can be taken and a line can be drawn which passes through them and extends in both directions. For example, the line in the figure above is denoted by
In this article, you will learn about two types of lines:
- Intersecting lines
- Non-intersecting lines
Intersecting Lines
Two or more lines which share exactly one common point are called intersecting lines. This common point exists on all these lines and is called the point of intersection. It is to be noted that:
- The intersecting lines meet at one, and only one point, no matter at what angle they meet.
- No two straight lines can meet at more than one point.
- The lines that meet at more than one point are not straight lines. At least one of them is a curve.
Let us take a few examples.
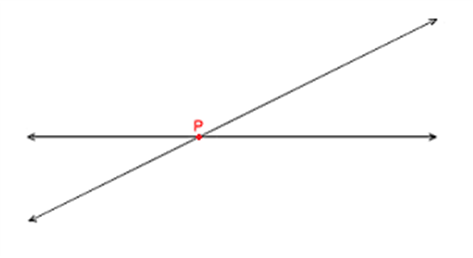
Consider these lines. They are two intersecting lines. The point of intersection is P.
The figure above also shows intersecting lines at different angles.
The figure shows an example of 4 intersecting lines.
8,288
Non-intersecting Lines
Two or more lines that do not intersect each other are called non-intersecting lines. It is to be noted that:
- Non-intersecting lines can never meet.
- They are also known as the parallel lines.
- They are always at the same distance from one another. This is called the distance between two parallel lines.

The figures above show non-intersecting or parallel lines.
Pairs of angles
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Linear Pair Of Angles
Linear pair of angles are formed when two lines intersect each other at a single point. The angles are said to be linear if they are adjacent to each other after the intersection of the two lines. The sum of angles of a linear pair is always equal to 180°. Such angles are also known as supplementary angles. The adjacent angles are the angles which have a common vertex. Hence, here as well the linear angles have a common vertex. Also, there will be a common arm which represents both the angles. A real-life example of a linear pair is a ladder which is placed against a wall, forms linear angles at the ground.
Linearity represents one which is straight. So here also, linear angles are the one which is formed into a straight line. The pair of adjacent angles here are constructed on a line segment, but not all adjacent angles are linear. Hence, we can also say, that linear pair of angles is the adjacent angles whose non-common arms are basically opposite rays.
Explanation for Linear Pair of Angles
When the angle between the two lines is 180°, they form a straight angle. A straight angle is just another way to represent a straight line. A straight line can be visualized as a circle with an infinite radius. A line segment is any portion of a line which has two endpoints. Also, a portion of any line with only one endpoint is called a ray. A line segment with A and B as two endpoints is represented as
The figure shown below represents a line segment AB and the two arrows at the end indicate a line.

If a point O is taken anywhere on the line segment AB as shown, then the angle between the two line segments AO and OB is a straight angle i.e. 180°.
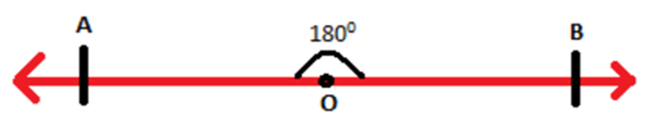
Consider a ray stand on the line segment as shown:
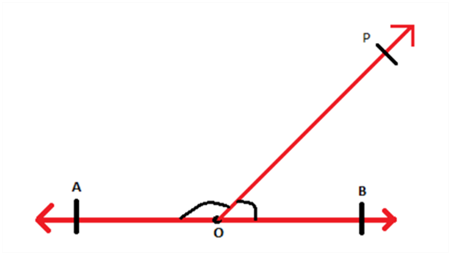
The angles which are formed at O are ∠POB and ∠POA. It is known that the angle between the two line segments AO and OB is 180°. therefore, the angles ∠POB and ∠POA add up to 180°.
Thus, ∠POB + ∠POA = ∠AOB = 180°
∠POB and ∠POA are adjacent to each other and when the sum of adjacent angles is 180° then such angles form linear pair of angles.
The above discussion can be stated as an axiom.
Axioms
Axiom 1: If a ray stands on a line then the adjacent angles form a linear pair of angles.
In the figure above, all the line segments pass through the point O as shown. As the ray OA lies on the line segment CD, angles ∠AOD and ∠AOC form a linear pair. Similarly, ∠QOD and ∠POD form a linear pair and so on.
The converse of the stated axiom is also true, which can also be stated as the following axiom.
Axiom 2: If two angles form a linear pair, then uncommon arms of both the angles form a straight line.
Figure 3 Adjacent angles with different measures
In the figure shown above, only the last one represents a linear pair, as the sum of the adjacent angles is 180°. Therefore, AB represents a line. The other two pairs of angles are adjacent but they do not form a linear pair. They do not form a straight line.
The two axioms mentioned above form the Linear Pair Axioms and are very helpful in solving various mathematical problems.
Example
Suppose two angles ∠AOC and ∠ BOC form a linear pair at point O in a line segment AB. If the difference between the two angles is 60°. Then find both the angles.
Solution: Given, ∠AOC and ∠ BOC form a linear pair
So, ∠AOC + ∠ BOC =180° ………(1)
Also given,
∠AOC – ∠ BOC = 60° ………(2)
Adding eq. 1 and 2, we get;
2∠AOC = 180° + 60° = 240°
∠AOC = 240°/2 = 120°
Now putting the value of ∠AOC in equation 1, we get;
∠BOC = 180° – ∠AOC = 180° – 120°
∠BOC = 60°
Pairs of angles
Linear Pair Of Angles
Linear pair of angles are formed when two lines intersect each other at a single point. The angles are said to be linear if they are adjacent to each other after the intersection of the two lines. The sum of angles of a linear pair is always equal to 180°. Such angles are also known as supplementary angles. The adjacent angles are the angles which have a common vertex. Hence, here as well the linear angles have a common vertex. Also, there will be a common arm which represents both the angles. A real-life example of a linear pair is a ladder which is placed against a wall, forms linear angles at the ground.
Linearity represents one which is straight. So here also, linear angles are the one which is formed into a straight line. The pair of adjacent angles here are constructed on a line segment, but not all adjacent angles are linear. Hence, we can also say, that linear pair of angles is the adjacent angles whose non-common arms are basically opposite rays.
Explanation for Linear Pair of Angles
When the angle between the two lines is 180°, they form a straight angle. A straight angle is just another way to represent a straight line. A straight line can be visualized as a circle with an infinite radius. A line segment is any portion of a line which has two endpoints. Also, a portion of any line with only one endpoint is called a ray. A line segment with A and B as two endpoints is represented as
. The figure shown below represents a line segment AB and the two arrows at the end indicate a line.

If a point O is taken anywhere on the line segment AB as shown, then the angle between the two line segments AO and OB is a straight angle i.e. 180°.
Consider a ray
stand on the line segment
as shown:
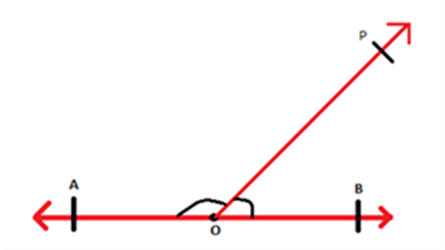
The angles which are formed at O are ∠POB and ∠POA. It is known that the angle between the two line segments AO and OB is 180°. therefore, the angles ∠POB and ∠POA add up to 180°.
Thus, ∠POB + ∠POA = ∠AOB = 180°
∠POB and ∠POA are adjacent to each other and when the sum of adjacent angles is 180° then such angles form linear pair of angles.
The above discussion can be stated as an axiom.
Axioms
Axiom 1: If a ray stands on a line then the adjacent angles form a linear pair of angles.
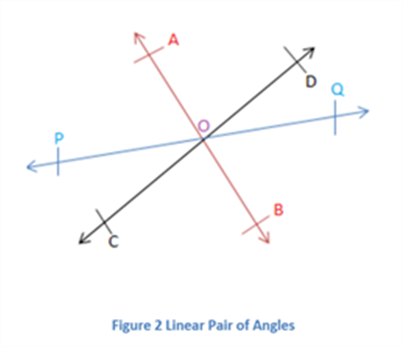
In the figure above, all the line segments pass through the point O as shown. As the ray OA lies on the line segment CD, angles ∠AOD and ∠AOC form a linear pair. Similarly, ∠QOD and ∠POD form a linear pair and so on.
The converse of the stated axiom is also true, which can also be stated as the following axiom.
Axiom 2: If two angles form a linear pair, then uncommon arms of both the angles form a straight line.
Figure 3 Adjacent angles with different measures
In the figure shown above, only the last one represents a linear pair, as the sum of the adjacent angles is 180°. Therefore, AB represents a line. The other two pairs of angles are adjacent but they do not form a linear pair. They do not form a straight line.
The two axioms mentioned above form the Linear Pair Axioms and are very helpful in solving various mathematical problems.
Example
Suppose two angles ∠AOC and ∠ BOC form a linear pair at point O in a line segment AB. If the difference between the two angles is 60°. Then find both the angles.
Solution: Given, ∠AOC and ∠ BOC form a linear pair
So, ∠AOC + ∠ BOC =180° ………(1)
Also given,
∠AOC – ∠ BOC = 60° ………(2)
Adding eq. 1 and 2, we get;
2∠AOC = 180° + 60° = 240°
∠AOC = 240°/2 = 120°
Now putting the value of ∠AOC in equation 1, we get;
∠BOC = 180° – ∠AOC = 180° – 120°
∠BOC = 60°
Parallel lines and a Transversal
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Parallel Lines & Transversal
In geometry, lines are classified into several types such as parallel, perpendicular, intersecting and non-intersecting lines, etc. For non-intersecting lines, we can draw a special line called transversal that intersects these lines at different points. In this article, you will learn about parallel lines, transversals and angle relationships with these lines along with suitable images and examples.
Parallel lines - Two lines are said to be parallel when they do not intersect each other. We can also say that two lines that run along and meet at infinity are called parallel lines.

Transversals - When a line intersects two lines at distinct points, it is called a transversal. In the below figure, line l intersects a and b at two distinct points, P and Q. Therefore, line l is the transversal line.
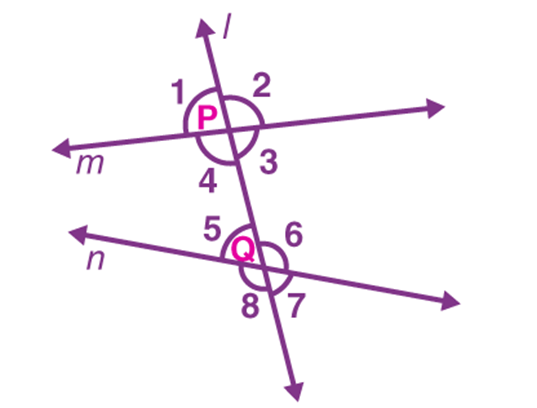
In the figure below, the line EF is not a transversal even if it intersects two lines AB and CD at O because it does not cut both lines at two distinct points. For a line to be transversal, it must cross two or more lines at separate points.
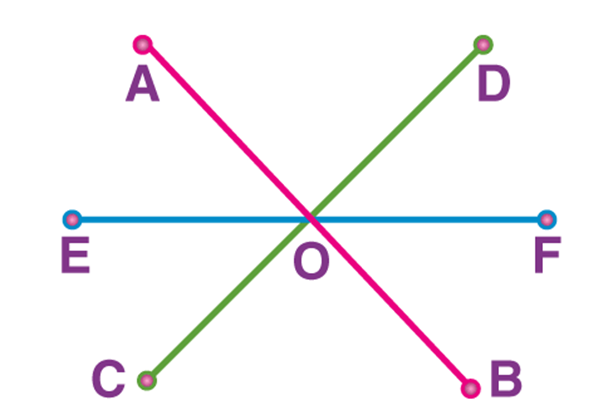
Angle Relationship Between the Parallel Lines and Transversal
Various angle pairs are formed when a transversal intersects two or more parallel lines. Let us quickly recapitulate the angle relationships for the parallel lines cut by a transversal. Let a and d be two parallel lines intersected by the transversal l at the points P and Q, as shown in the figure below.
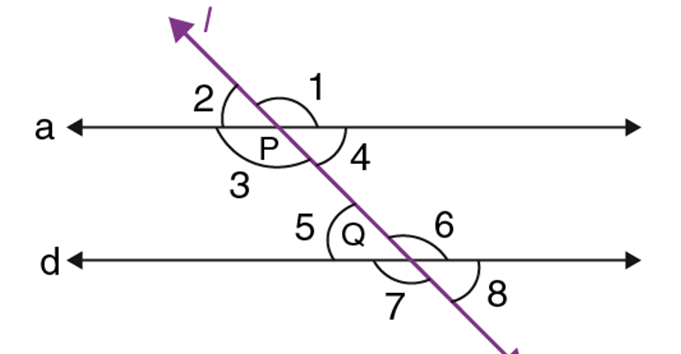
Now, we can write different pairs of angles and their corresponding relationships.
Corresponding Angles:
Corresponding angles are the angles which are formed in matching corners or corresponding corners with the transversal when two parallel lines and the transversal.
∠1 and ∠6
∠4 and ∠8
∠2 and ∠5
∠3 and ∠7
Also, if a transversal intersects two parallel lines, then each pair of corresponding angles is equal. Thus,
∠1 = ∠6
∠4 = ∠8
∠2 = ∠5
∠3 = ∠7
Alternate interior angles:
Alternate interior angles are the angles formed when a transversal intersects two coplanar lines.
∠4 and ∠5
∠3 and ∠6
However, if a transversal intersects two parallel lines, then each pair of alternate interior angles is equal.
∠4 = ∠5
∠3 = ∠6
Alternate exterior angles:
Alternate exterior angles are the pair of angles that are formed on the outer side of two lines but on the opposite side of the transversal.
∠1 and ∠7
∠2 and ∠8
If two parallel lines are cut by a transversal, then the resulting alternate exterior angles are congruent.
∠1 = ∠7
∠2 = ∠8
Interior angles on the same side of the transversal:
Interior angles on the same side of the transversal are also referred to as consecutive interior angles or allied angles or co-interior angles.
∠3 and ∠5
∠4 and ∠6
If a transversal intersects two parallel lines, then each pair of interior angles on the same side of the transversal is supplementary, i.e. they add up to 180°.
∠3 + ∠5 = 180°
∠4 + ∠6 = 180°
Vertically opposite angles
When two lines intersect each other, then the opposite angles, formed due to intersection, are called vertical angles or vertically opposite angles. Also, a pair of vertical angles are always congruent.
So,
∠1 = ∠3
∠2 = ∠4
∠7 = ∠6
∠8 = ∠5
The summary of angle relationships of parallel lines and transversal as given in the above figure is tabulated below:
|
Pair of angles formed |
Angle relationships |
|
Pairs of Corresponding angles |
∠1 = ∠6, ∠4 = ∠8, ∠2 = ∠5, ∠3 = ∠7 |
|
Pairs of Alternate interior angles |
∠4 = ∠5, ∠3 = ∠6 |
|
Pairs of Alternate exterior angles |
∠1 = ∠7, ∠2 = ∠8 |
|
Pairs of Interior angles on the same side of the transversal |
∠3 + ∠5 = 180°, ∠4 + ∠6 = 180° |
|
Pairs of Vertically opposite angles |
∠1 = ∠3, ∠2 = ∠4, ∠7 = ∠6, ∠8 = ∠5 |
Now, the question arises: how can we deduce if two lines are parallel or not? Is there any condition that demonstrates the parallel nature of two or more lines? Consider this situation.
His teacher asked Alan to draw two parallel lines. With the help of his set squares and ruler, he drew a straight line segment AB and then placed the set square on this line and drew two line segments XY and PQ, by changing the position of the set squares as shown.
He claimed that XY and PQ are parallel. Can you tell how? It’s simply right. The line segment AB serves as the transversal to XY and PQ, and angle X and angle Y are corresponding angles in this case which are in equal measure. Therefore, XY and PQ are parallel line segments.
Parallel lines and a Transversal
Parallel Lines & Transversal
In geometry, lines are classified into several types such as parallel, perpendicular, intersecting and non-intersecting lines, etc. For non-intersecting lines, we can draw a special line called transversal that intersects these lines at different points. In this article, you will learn about parallel lines, transversals and angle relationships with these lines along with suitable images and examples.
Parallel lines
Two lines are said to be parallel when they do not intersect each other. We can also say that two lines that run along and meet at infinity are called parallel lines.
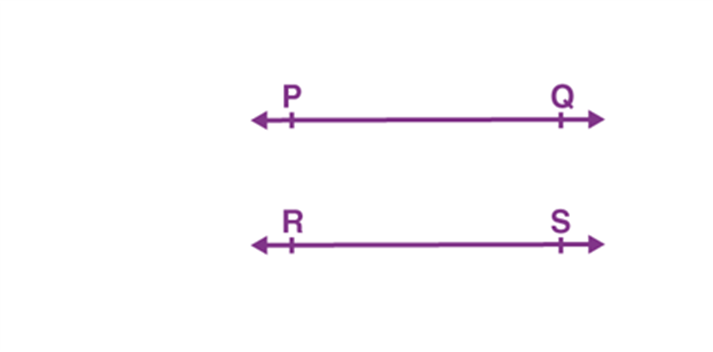
Transversals
When a line intersects two lines at distinct points, it is called a transversal. In the below figure, line l intersects a and b at two distinct points, P and Q. Therefore, line l is the transversal line.
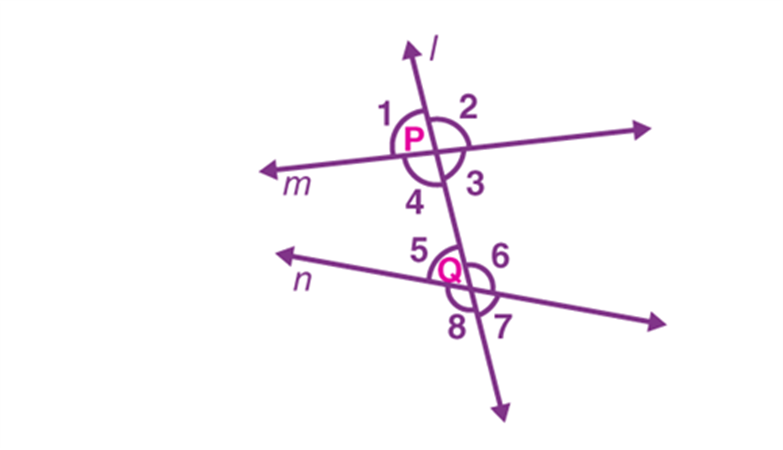
In the figure below, the line EF is not a transversal even if it intersects two lines AB and CD at O because it does not cut both lines at two distinct points. For a line to be transversal, it must cross two or more lines at separate points.
Angle Relationship Between the Parallel Lines and Transversal
Various angle pairs are formed when a transversal intersects two or more parallel lines. Let us quickly recapitulate the angle relationships for the parallel lines cut by a transversal. Let a and d be two parallel lines intersected by the transversal l at the points P and Q, as shown in the figure below.
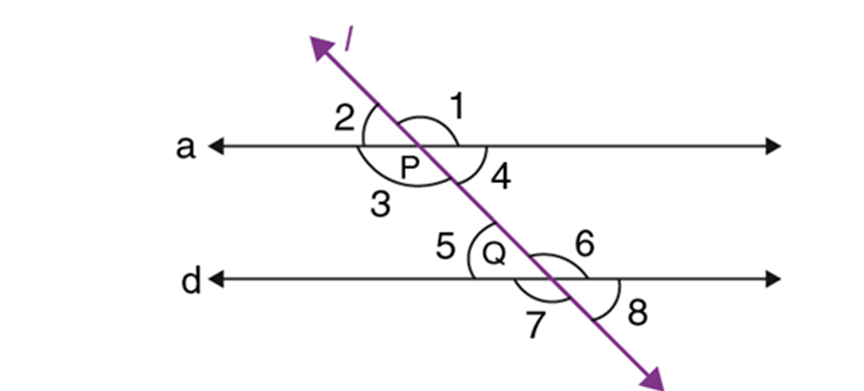
Now, we can write different pairs of angles and their corresponding relationships.
Corresponding Angles:
Corresponding angles are the angles which are formed in matching corners or corresponding corners with the transversal when two parallel lines and the transversal.
∠1 and ∠6
∠4 and ∠8
∠2 and ∠5
∠3 and ∠7
Also, if a transversal intersects two parallel lines, then each pair of corresponding angles is equal. Thus,
∠1 = ∠6
∠4 = ∠8
∠2 = ∠5
∠3 = ∠7
Alternate interior angles:
Alternate interior angles are the angles formed when a transversal intersects two coplanar lines.
∠4 and ∠5
∠3 and ∠6
However, if a transversal intersects two parallel lines, then each pair of alternate interior angles is equal.
∠4 = ∠5
∠3 = ∠6
Alternate exterior angles:
Alternate exterior angles are the pair of angles that are formed on the outer side of two lines but on the opposite side of the transversal.
∠1 and ∠7
∠2 and ∠8
If two parallel lines are cut by a transversal, then the resulting alternate exterior angles are congruent.
∠1 = ∠7
∠2 = ∠8
Interior angles on the same side of the transversal:
Interior angles on the same side of the transversal are also referred to as consecutive interior angles or allied angles or co-interior angles.
∠3 and ∠5
∠4 and ∠6
If a transversal intersects two parallel lines, then each pair of interior angles on the same side of the transversal is supplementary, i.e. they add up to 180°.
∠3 + ∠5 = 180°
∠4 + ∠6 = 180°
Vertically opposite angles
When two lines intersect each other, then the opposite angles, formed due to intersection, are called vertical angles or vertically opposite angles. Also, a pair of vertical angles are always congruent.
So,
∠1 = ∠3
∠2 = ∠4
∠7 = ∠6
∠8 = ∠5
The summary of angle relationships of parallel lines and transversal as given in the above figure is tabulated below:

Now, the question arises: how can we deduce if two lines are parallel or not? Is there any condition that demonstrates the parallel nature of two or more lines? Consider this situation.
His teacher asked Alan to draw two parallel lines. With the help of his set squares and ruler, he drew a straight line segment AB and then placed the set square on this line and drew two line segments XY and PQ, by changing the position of the set squares as shown.
He claimed that XY and PQ are parallel. Can you tell how? It’s simply right. The line segment AB serves as the transversal to XY and PQ, and angle X and angle Y are corresponding angles in this case which are in equal measure. Therefore, XY and PQ are parallel line segments.
Solved Example
Question:
Observe the figure given below:
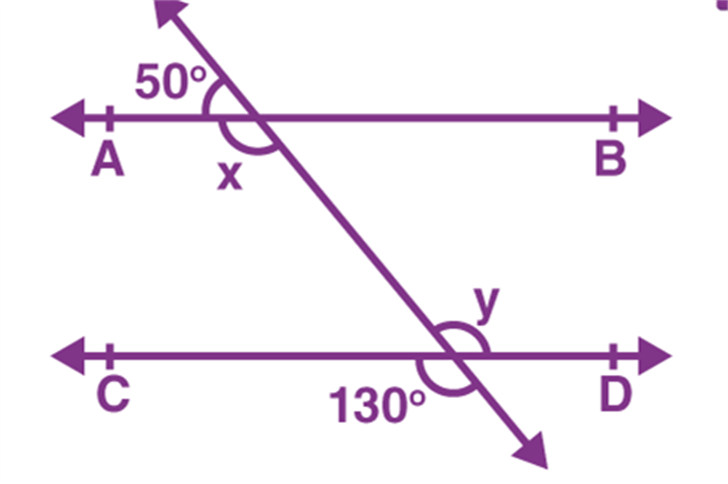
Find the missing angles.
Solution:
In the given figure, AB and CD are parallel lines and these are cut by a transversal line at two different points.
Here, x and 130° are the pair of corresponding angles.
So, x = 130°
Also, y and 130° are vertically opposite angles.
Thus, y = 130°
Lines parallel to the same line
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Lines Parallel to the Same Line
In Geometry, a line is defined as a one-dimensional geometric figure that extends infinitely in both directions. A line has no thickness. A line is generally made up of an infinite number of points. In this article, we will discuss the lines parallel to the same line and the theorem related to it with many solved examples.
What is Meant by Lines Parallel to the Same Line?
Theorem: Lines that are parallel to the same line are parallel to each other.
It means that if two lines are parallel to the same line, then they will be parallel to each other. Now, let us check this theorem with the help of the below figure.
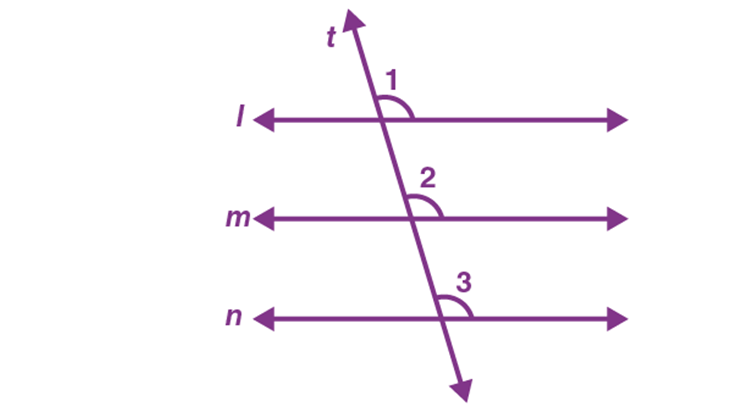
From the given figure, we can say that line m is parallel to line l and line n is parallel to line l. (i.e) line m || line l and line n || line l. Also, “t” is the transversal for the lines l, m and n.
Therefore, we can say that ∠1 = ∠2 and ∠1 = ∠3. (By corresponding angles axioms).
So, we can also say that ∠2 and ∠3 are corresponding and they are equal to each other.
Thus, ∠2 = ∠3
By using the converse of corresponding angle axioms, we conclude that line m is parallel to line n. (i.e) Line m || Line n.
Note: This property can be extended to more than two lines also.
Lines parallel to the same line
Lines Parallel to the Same Line
In Geometry, a line is defined as a one-dimensional geometric figure that extends infinitely in both directions. A line has no thickness. A line is generally made up of an infinite number of points. In this article, we will discuss the lines parallel to the same line and the theorem related to it with many solved examples.
What is Meant by Lines Parallel to the Same Line?
Theorem: Lines that are parallel to the same line are parallel to each other.
It means that if two lines are parallel to the same line, then they will be parallel to each other. Now, let us check this theorem with the help of the below figure.
From the given figure, we can say that line m is parallel to line l and line n is parallel to line l. (i.e) line m || line l and line n || line l. Also, “t” is the transversal for the lines l, m and n.
Therefore, we can say that ∠1 = ∠2 and ∠1 = ∠3. (By corresponding angles axioms).
So, we can also say that ∠2 and ∠3 are corresponding and they are equal to each other.
Thus, ∠2 = ∠3
By using the converse of corresponding angle axioms, we conclude that line m is parallel to line n.
(i.e) Line m || Line n.
Note: This property can be extended to more than two lines also.
Solved Example
Example:
From the given figure, AB is parallel to CD and CD is parallel to EF.
Also, given that EA is perpendicular to AB. Find the values of x, y and z, if ∠BEF = 55°.
Solution:
Given that AB|| CD, CD || EF, EA ⊥ AB, and ∠BEF = 55°.
Therefore, y+ 55° = 180° (Interior angles on the same side of transversal ED)
Hence, y = 180°-55°= 125°
By using the corresponding angles axiom, AB || CD, we can say that x = y.
Therefore, the value of x= 125°.
Since, AB || CD and CD || EF, therefore AB || EF.
So, we can write: ∠ FEA + ∠ EAB = 180° (Interior angles on the same side of transversal EA)
55° + z + 90° = 180°
z = 180° – 90° – 55°
z = 180° – 145°
z = 35°
Therefore, the values of x, y and z are 125°, 125° and 35°, respectively.
Solve the following problems:
1. From the given figure, AB ||CD and CD || EF and y:z = 3:7. Find the value of x.
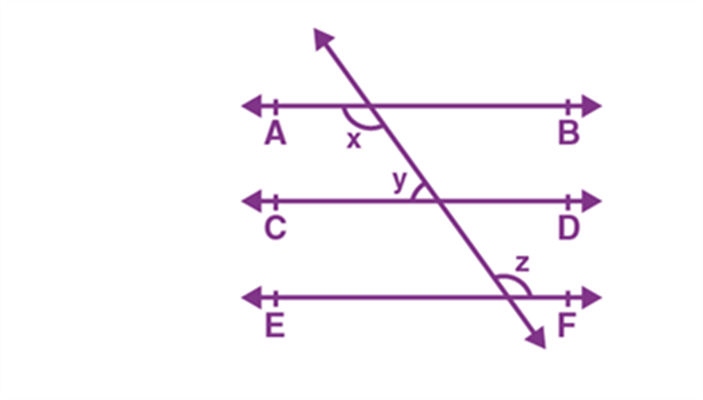
2. From the given figure, if PQ || RS and ∠MXQ = 135° and ∠MYR = 40°, then find the value of ∠XMY.
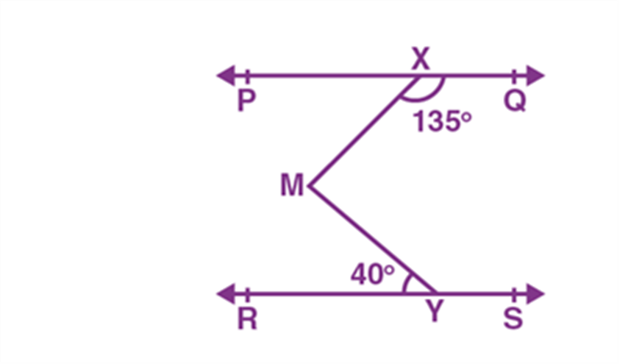
Angle sum property of a triangle
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Angle Sum Property Of A Triangle
A triangle is the smallest polygon which has three sides and three interior angles. In this article, we are going to discuss the angle sum property and the exterior angle theorem of a triangle with its statement and proof in detail.
Angle Sum Property of a Triangle Theorem
In the given triangle, ∆ABC, AB, BC, and CA represent three sides. A, B and C are the three vertices and ∠ABC, ∠BCA and ∠CAB are three interior angles of ∆ABC.
Theorem 1: Angle sum property of triangle states that the sum of interior angles of a triangle is 180°.
Proof: - Consider a ∆ABC, as shown in the figure below. To prove the above property of triangles, draw a line parallel to the side BC of the given triangle.
Since PQ is a straight line, it can be concluded that:
∠PAB + ∠BAC + ∠QAC = 180° ………(1)
Since PQ||BC and AB, AC are transversals,
Therefore, ∠QAC = ∠ACB (a pair of alternate angle)
Also, ∠PAB = ∠CBA (a pair of alternate angle)
Substituting the value of ∠QAC and∠PAB in equation (1),
∠ACB + ∠BAC + ∠CBA= 180°
Thus, the sum of the interior angles of a triangle is 180°.
Exterior Angle Property of a Triangle Theorem
Theorem 2: If any side of a triangle is extended, then the exterior angle so formed is the sum of the two opposite interior angles of the triangle.
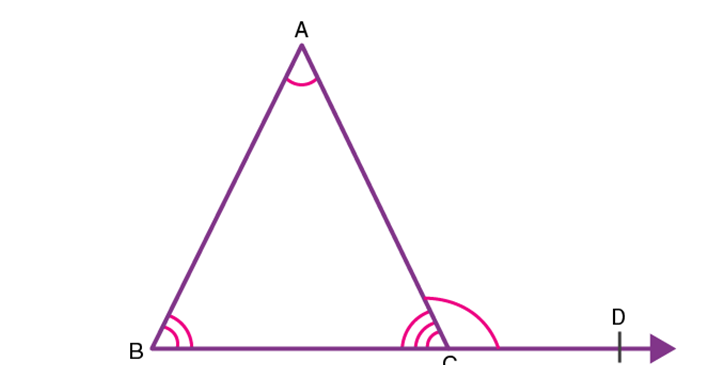
In the given figure, the side BC of ∆ABC is extended. The exterior angle ∠ACD so formed is the sum of measures of ∠ABC and ∠CAB.
Proof: - From figure 3, ∠ACB and ∠ACD form a linear pair since they represent the adjacent angles on a straight line.
Thus, ∠ACB + ∠ACD = 180° ……….(2)
Also, from the angle sum property, it follows that:
∠ACB + ∠BAC + ∠CBA = 180° ……….(3)
From equation (2) and (3) it follows that:
∠ACD = ∠BAC + ∠CBA
This property can also be proved using the concept of parallel lines as follows:
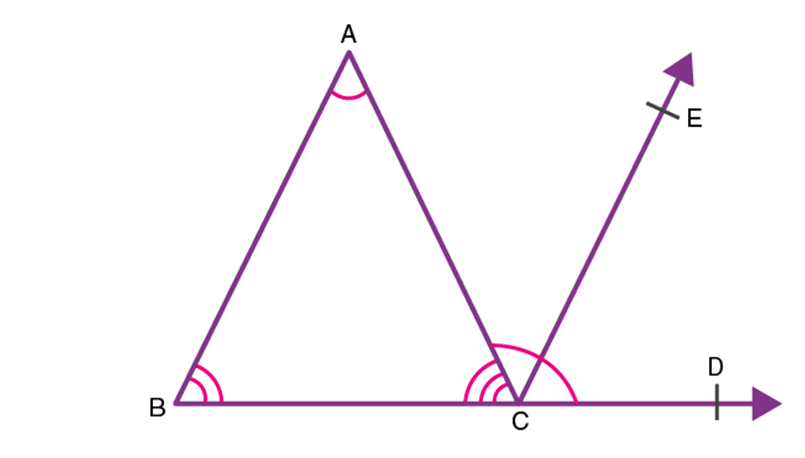
In the given figure, the side BC of ∆ABC is extended. A line parallel to the side AB is drawn, then: Since and is the transversal,
∠CAB = ∠ACE ………(4) (Pair of alternate angles)
Also, and is the transversal
Therefore, ∠ABC = ∠ECD ……….(5) (Corresponding angles)
We have, ∠ACB + ∠BAC + ∠CBA = 180° ………(6)
Since the sum of angles on a straight line is 180°
Therefore, ∠ACB + ∠ACE + ∠ECD = 180° ………(7)
Since, ∠ACE + ∠ECD = ∠ACD(From figure 4)
Substituting this value in equation (7);
∠ACB + ∠ACD = 180° ………(8)
From the equations (6) and (8) it follows that,
∠ACD = ∠BAC + ∠CBA
Hence, it can be seen that the exterior angle of a triangle equals the sum of its opposite interior angles.
Angle sum property of a triangle
Angle Sum Property Of A Triangle
A triangle is the smallest polygon which has three sides and three interior angles. In this article, we are going to discuss the angle sum property and the exterior angle theorem of a triangle with its statement and proof in detail.
Angle Sum Property of a Triangle Theorem
In the given triangle, ∆ABC, AB, BC, and CA represent three sides. A, B and C are the three vertices and ∠ABC, ∠BCA and ∠CAB are three interior angles of ∆ABC.
Theorem 1: Angle sum property of triangle states that the sum of interior angles of a triangle is 180°.
Proof:
Consider a ∆ABC, as shown in the figure below. To prove the above property of triangles, draw a line
parallel to the side BC of the given triangle.
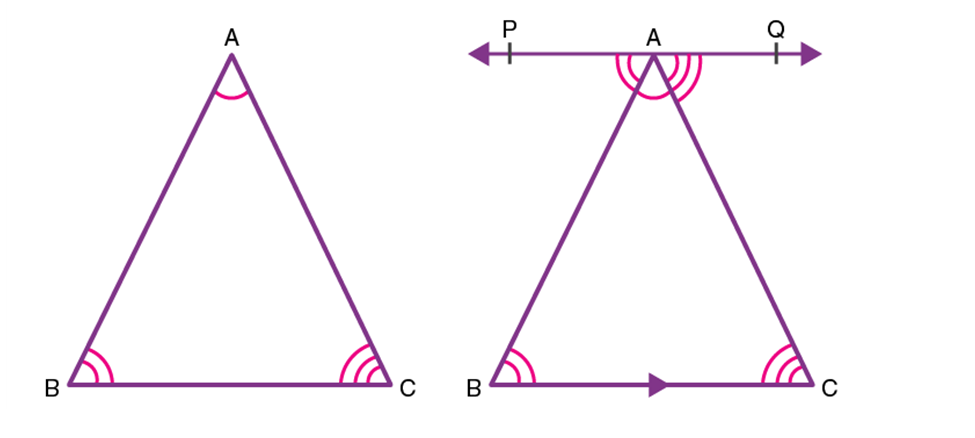
Since PQ is a straight line, it can be concluded that:
∠PAB + ∠BAC + ∠QAC = 180° ………(1)
Since PQ||BC and AB, AC are transversals,
Therefore, ∠QAC = ∠ACB (a pair of alternate angle)
Also, ∠PAB = ∠CBA (a pair of alternate angle)
Substituting the value of ∠QAC and∠PAB in equation (1),
∠ACB + ∠BAC + ∠CBA= 180°
Thus, the sum of the interior angles of a triangle is 180°.
Exterior Angle Property of a Triangle Theorem
Theorem 2: If any side of a triangle is extended, then the exterior angle so formed is the sum of the two opposite interior angles of the triangle.
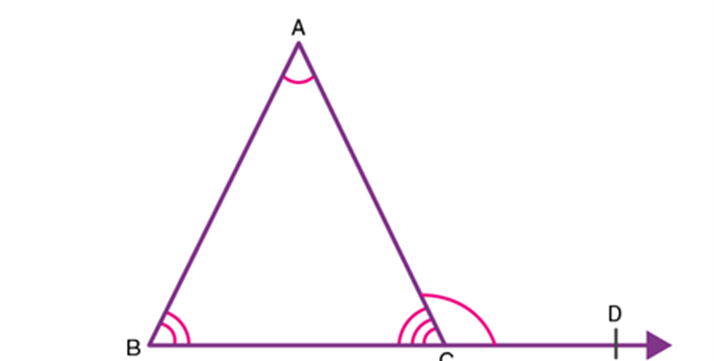
In the given figure, the side BC of ∆ABC is extended. The exterior angle ∠ACD so formed is the sum of measures of ∠ABC and ∠CAB.
Proof:
From figure 3, ∠ACB and ∠ACD form a linear pair since they represent the adjacent angles on a straight line.
Thus, ∠ACB + ∠ACD = 180° ……….(2)
Also, from the angle sum property, it follows that:
∠ACB + ∠BAC + ∠CBA = 180° ……….(3)
From equation (2) and (3) it follows that:
∠ACD = ∠BAC + ∠CBA
This property can also be proved using the concept of parallel lines as follows:
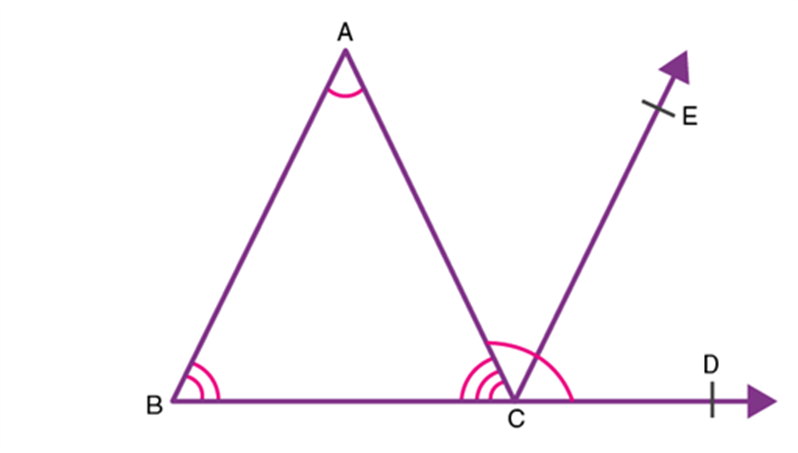
In the given figure, side BC of ∆ABC is extended. A line
parallel to the side AB is drawn, then: Since
and
is the transversal,
∠CAB = ∠ACE ………(4) (Pair of alternate angles)
Also,
and
is the transversal
Therefore, ∠ABC = ∠ECD ……….(5) (Corresponding angles)
We have, ∠ACB + ∠BAC + ∠CBA = 180° ………(6)
Since the sum of angles on a straight line is 180°
Therefore, ∠ACB + ∠ACE + ∠ECD = 180° ………(7)
Since, ∠ACE + ∠ECD = ∠ACD(From figure 4)
Substituting this value in equation (7);
∠ACB + ∠ACD = 180° ………(8)
From the equations (6) and (8) it follows that,
∠ACD = ∠BAC + ∠CBA
Hence, it can be seen that the exterior angle of a triangle equals the sum of its opposite interior angles.
12,333
Criteria for congruence of triangles
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Criteria For Congruent Triangles
Congruent triangles are triangles that have the same size and shape. This means that the corresponding sides are equal and the corresponding angles are equal.
Congruent Triangles do not have to be in the same orientation or position. They only have to be identical in size and shape.
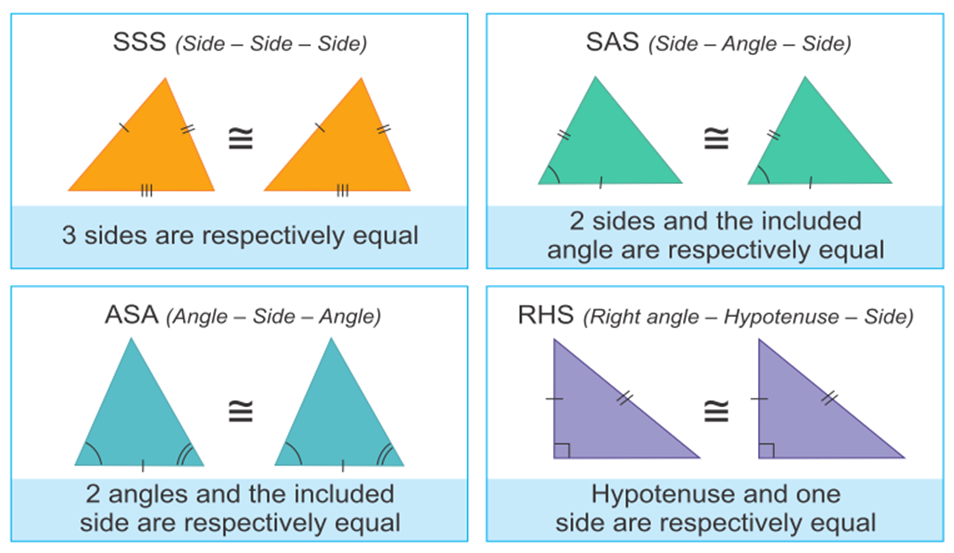
1. SSS (Side Side Side) Congruence Criteria (Condition):
Two triangles are congruent, if three sides of one triangle are equal to the corresponding three sides of the other triangle.
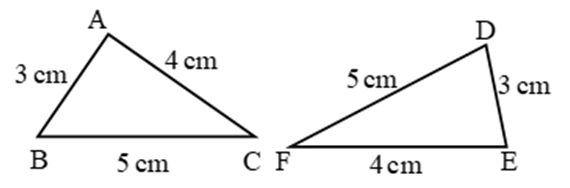
∴ By SSS criteria ∆ABC ∆EDF
∴ ∠A = ∠E, ∠B = ∠D, ∠C = ∠F (c.p.c.t.)
2. ASA (Angle Side Angle) Congruence Criteria (Condition):
Two triangles are congruent, if two angles and the included side of one is equal to the corresponding angles and side of the other.
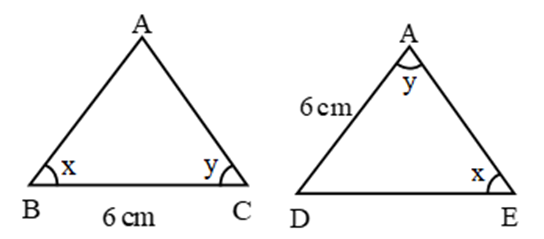
∴ By ASA criteria ∆ABC ≅ ∆DEF
∴ ∠A = ∠D, AB = DE, AC = DF (c.p.c.t.)
3. AAS (Angle Angle Side) Congruence Criteria (Condition):
∴ By AAS, ∆ABC ≅ ∆FDE
∴ ∠C = ∠E, AB = FD, AC = FE (c.p.c.t.)
4. SAS (Side Angle Side) Congruence Criteria (Condition):
When two sides and the included angle of one triangle is equal to the corresponding sides and the included angle of another triangle, the two triangles are congruent. This, condition of congruence is known as side-angle-side congruence. In short we write SAS condition.
By SAS, ∆ABC ≅ ∆QPR
∴ ∠A = ∠Q, ∠C = ∠R, AC = QR (c.p.c.t.)
5. RHS (Right Hypotenuse Side) Congruence Criteria (Condition):
Two right triangles are congruent, if the hypotenuse and one side of one triangle are respectively equal to the hypotenuse and a side of the other triangle.
∴ By RHS, ∆ABC ≅ ∆QPR
∴ ∠A = ∠Q, ∠C = ∠R, BC = PR (c.p.c.t.)
Example 1:
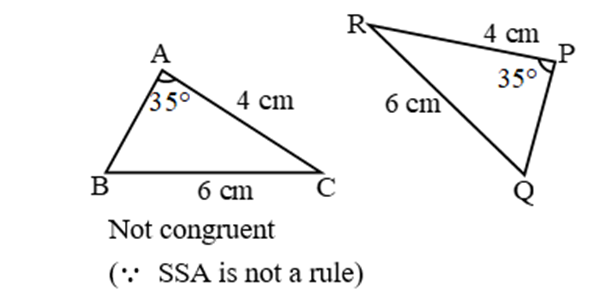
Example 2:
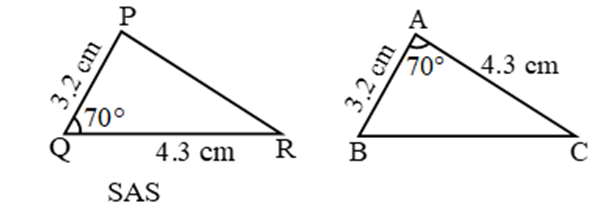
Example 3:
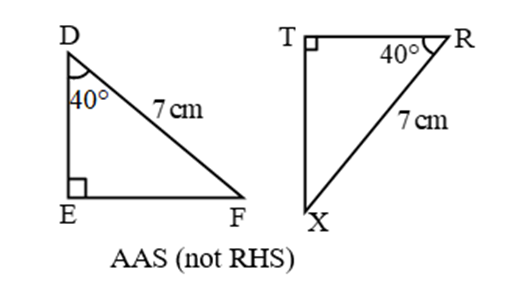
Example 4:
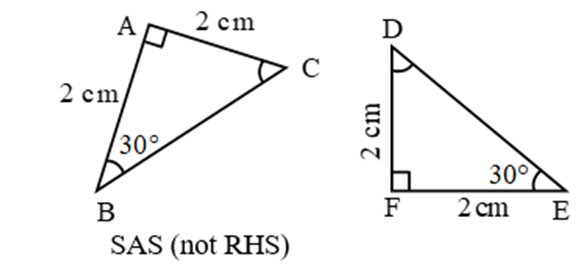
Theorem 1: If two angles and the included side of one triangle are equal to two angles and the included side of other triangle, then both triangles are congruent.
Proof:
Given: ∆ABC and ∆DEF in which
∠ABC = ∠DEF, ∠ACB = ∠DFE and BC = EF.
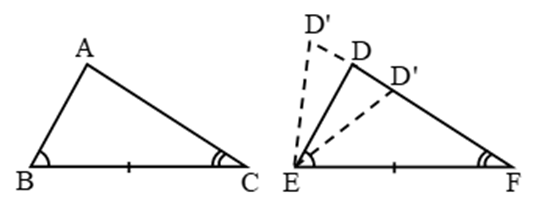
To Prove: ∆ABC ≅ ∆DEF.
Proof:
Case I:
Let AC = DF.
In this case, AC = DF, BC = EF and ∠C = ∠F.
∴ ∆ABC ≅ ∆DEF (SAS-criteria)
Case II:
If possible, let AC ≠ DF.
Then, construct D’ F = AC. Join D’ E.
Now, in ∆ABC and ∆D’EF, we have AC = D’F, BC = EF and ∠C = ∠F.
∴ ∆ABC ∆D’EF (SAS-criteria)
∴ ∠ABC = ∠D’EF (c.p.c.t)
But, ∠ABC = ∠DEF (given)
∴ ∠D’EF = ∠DEF.
This is possible only when D and D’ coincide.
∴ ∆ABC ≅ ∆DEF.
Theorem 2: Two right-angled triangles are congruent if one side and the hypotenuse of the one are respectively equal to the corresponding side and the hypotenuse of the other. (i.e. RHS)
Given: Two right-angled triangles ∆ABC & ∆DEF in which ∠B = ∠E = 90°, BC = EF and AC = DF.
To Prove: ∆ABC ≅ ∆DEF.
Construction: Produce DE to G such that
GE = AB. Join GF.
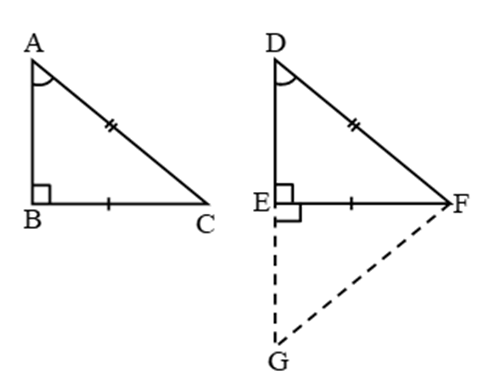
Proof: In ∆ABC and ∆GEF, we have:
AB = GE (construction),
BC = EF (given),
∠B = ∠FEG = 90°
⇒ ∆ABC ∆GEF (SAS-criteria)
⇒ ∠A = ∠G and AC = GF (c.p.c.t.)
Now, AC = GF and AC = DF ⇒GF = DF
⇒ ∠G = ∠D ⇒ ∠A = ∠D [∵ ∠G = ∠A]
Now, ∠A = ∠D, ∠B = ∠E ⇒ 3rd ∠C = 3rd ∠F.
Thus, in ∆ABC and ∆DEF, we have:
BC = EF, AC = DF and ∠C = ∠F.
∴ ∆ABC ≅ ∆DEF (SAS-criteria).
Criteria For Congruent Triangles Example Problems With Solutions
Example 1: Prove that diagonal of a parallelogram divides it into two congruent triangles.
Solution: Let ABCD is a parallelogram and AC is a diagonal.
(By SSS): In ∆ABC and ∆ADC
AB = CD (opp. sides of ||gm)
BC = AD (opp. sides of ||gm)
AC = AC (common)
∴ By SSS, ∆ABC ≅ ∆CDA proved
{other results : ∠1 = ∠2, ∠3 = ∠4, ∠B = ∠D (c.p.c.t.)}
(By ASA): In ∆ABC and ∆ADC
∠1 = ∠2 (alternate)
AC = AC (common)
∠3 = ∠4 (alternate)
∴ By ASA, ∆ABC ≅ ∆CDA
{other results: ∠B = ∠D, AB = CD, BC = AD (c.p.c.t.)}
(By AAS): In ∆ABC and ∆ADC
∠1 = ∠2 (alternate)
∠3 = ∠4 (alternate)
BC = AD (opp. sides)
∴ ∆ABC ≅ ∆CDA
{other results : AB = CD, ∠B = ∠D, AC = AC (c.p.c.t.)}
(By SAS): In ∆ABC and ∆ADC
AB = CD (opp. sides of ||gm)
∠1 = ∠2 (alternate)
AC = AC (common)
∴ ∆ABC ≅ ∆CDA
{other results: ∠3 = ∠4, BC = AD, ∠B = ∠D (c.p.c.t.)
We can not use ‘RHS’ for this proof.
Note: ASS or SSA criteria for congruency is not valid.
Example 2: In Fig. it is given that AB = CF, EF = BD and ∠AFE = ∠DBC. Prove that ∆AFE ∆CBD.
Solution: We have, AB = CF
⇒ AB + BF = CF + BF
⇒ AF = CB …. (i)
In ∆s AFE and CBD, we have AF = CB [From (i)]
∠AFE = ∠DBC [Given]
and EF = BD [Given]
So, by SAS criterion of congruence, we have ∆AFE ≅ ∆CBD
Example 3: In Fig. X and Y are two points on equal sides AB and AC of a ∆ABC such that AX = AY. Prove that XC = YB.
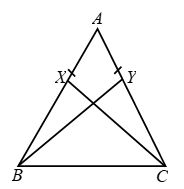
Solution: In ∆s AXC and AYB, we have
AX = AY [Given]
∠A = ∠A [Common angle]
AC = AB [Given]
So, by SAS criterion of congruene
∆AXC ≅ ∆AYB ⇒ XC = YB (c.p.c.t.)
Example 4: In Fig. PQRS is a quadrilateral and T and U are respectively points on PS and RS such PQ = RQ, ∠PQT = ∠RQU and ∠TQS = ∠UQS. Prove that QT = QU.
Solution: We have, ∠PQT = ∠RQU
and, ∠TQS = ∠UQS
∴ ∠PQT + ∠TQS = ∠RQU + ∠UQS
⇒ ∠PQS = ∠RQS …. (i)
Thus, in triangles PQS and RQS, we have
PQ = RQ [Given]
∠PQS = ∠RQS [From (i)]
and, QS = QS [Common side]
Therefore, by SAS congruence criterion, we have
∆PQS ≅ ∆RQS
⇒ ∠QPS = ∠QRS (c.p.c.t.)
⇒ ∠QPT = ∠QRU …. (ii)
Now, consider triangles QPT and QRS. In these two triangles, we have
QP = QR [Given]
∠PQT = ∠RQU [Given]
∠QPT = ∠QRU [From (ii)]
Therefore, by ASA congruence criterion, we get
∆QPT ≅ ∆QRU ⇒ QT = QU.
Example 5: In Fig. PS = QR and ∠SPQ = ∠RQP.
Prove that PR = QS and ∠QPR = ∠PQS.
Solution: In ∆SPQ and ∆RQP, we have
PS = QR [Given]
∠SPQ = ∠RQP [Given]
PQ = PQ [Common]
Therefore, by SAS criterion of congruence, we have
∆SPQ ∆RQP ⇒ SQ = RP and ∠QPR = ∠PQS
Example 6: ∆ABC is an isosceles triangle with AB = AC. Side BA is produced to D such that
AB = AD. Prove that ∠BCD is a right angle.
Solution: Given : A ∆ABC such that AB = AC. Side BA is produced to D such that AB = AD.
Construction : Join CD.
To prove : ∠BCD = 90º
Proof : In ∆ABC, we have AB = AC
⇒ ∠ACB = ∠ABC …(i) [∵ Angles opp. to equal sides are equal]
Now, AB = AD [Given]
∴ AD = AC [∴ AB = AC]
Thus, in ∆ADC, we have AD = AC
⇒ ∠ACD = ∠ADC …(ii)
[∵ Angles opp. to equal sides are equal]
Adding (i) and (ii), we get
∠ACB + ∠ACD = ∠ABC + ∠ADC
⇒ ∠BCD = ∠ABC + ∠BDC
[∵ ∠ADC = ∠BDC, ∠ABC = ∠DBC]
⇒ ∠BCD + ∠BCD = ∠DBC + ∠BCD + ∠BDC
[adding ∠BCD on both sides ]
⇒ 2 ∠BCD = 180º
[∵ Sum of the angles of a ∆ is 180º]
Hence, ∠BCD is a right angle.
Example 7: In Fig. AC = BC, ∠DCA = ∠ECB and ∠DBC = ∠EAC.
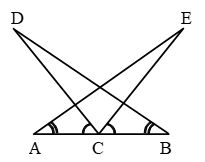
Prove that triangles DBC and EAC are congruent, and hence DC = EC.
Solution: We have, ∠DCA = ∠ECB
⇒ ∠DCA + ∠ECD = ∠ECB + ∠ECD
⇒ ∠ECA = ∠DCB …. (i)
Now, in ∆s DBC and EAC, we have
∠DCB = ∠ECA [From (i)]
BC = AC [Given]
and ∠DBC = ∠EAC [Given]
So, by ASA criterion of congruence
∆DBC ≅ ∠EAS ⇒ DC = EC (c.p.c.t.)
Example 8: If the altitudes from two vertices of a triangle to the opposite sides are equal, prove that the triangle is isosceles.
Solution: Given: A ∆ABC in which altitudes BE and CF from B and C respectively on AC and AB are equal.
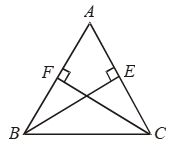
To prove: ∆ABC is isosceles i.e. AB = AC
Proof: In ∆s ABC and ACF, we have
∠AEB = ∠AFC [Each equal to 90º]
∠BAE = ∠CAF [Common angle]
and, BE = CF [Given]
So, by AAS criterion of congruence, we have
∆ABE ≅ ∆ACF
⇒ AB = AC [∵ Corresponding parts of congruent triangles are equal]
Hence, ∆ABC is isosceles.
Example 9: In ∆ABC, AB = AC and the bisectors of angles B and C intersect at point O. Prove that BO = CO and the ray AO is the bisector of angle BAC.
Solution: In ∆ABC, we have AB = AC

Now, in ∆ABO and ∆ACO, we have
AB = AC [Given]
∠OBC = ∠OCB [From (i)]
OB = OC [From (ii)]
So, by SAS criterion of congruence
∆ABO ≅ ∆ACO ⇒ ∠BAO = ∠CAO
[∵ Corresponding parts of congruent triangles are equal]
⇒ AO is the bisector of ∠BAC.
Example 10: In Fig. BM and DN are both perpendicular to the segments AC and BM = DN.
Prove that AC bisects BD.
Solution: In ∆s BMR and DNR, we have
∠BMR = ∠DNR
[Each equal to 90º ∵ BM ⊥ AC and DN ⊥ AC]
∠BRM = ∠DRN [Vert. opp. angles]
and, BM = DN [Given]
So, by AAS criterion of congruence
∆BMR ≅ ∆DNR ⇒ BR = DR
[∵ Corresponding parts of congruent triangles are equal]
⇒ R is the mid-point of BD.
Hence, AC bisects BD.
Example 11: In Fig. BD and CE are two altitudes of a ∆ABC such that BD = CE.
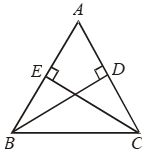
Prove that ∆ABC is isolceles.
Solution: In ∆ABD and ∆ACE, we have
∠ADB = ∠AEC = 90º [Given]
∠BAD = ∠CAE [Common]
and, BD = CE [Given]
So, by AAS congruence criterion, we have
∆ABD ≅ ∆ACE
⇒ AB = AC [∵ Corresponding parts of congruent triangles are equal]
Hence, ∆ABC is isosceles.
Example 12: If two isosceles triangles have a common base, the line joining their vertices bisects them at right angles.
Solution: Given: Two isosceles triangles ABC and DBC having the common base BC such that AB = AC and DB = DC.
To prove: AD (or AD produced) bisects BC at right angle.
Proof : In ∆s ABD and ACD, we have
AB = AC [Given]
BD = CD [Given]
AD = AD [Common side]
So, by SSS criterion of congruence
∆ABD ≅ ∆ACD
⇒ ∠1 = ∠2 …. (i)
[∵ Corresponding parts of congruent triangles are equal]
Now, in ∆s ABE and ACE, we have
AB = AC [Given]
∠1 = ∠2 [From (i)]
and, AE = AE [Commoni side]
So, by SAS criterion of congruence,
∆ABE ≅ ∆ACE ⇒ BE = CE
[∵ Corresponding parts of congruent triangles are equal]
and, ∠3 = ∠4
But, ∠3 + ∠4 = 180º
[∵ Sum of the angles of a linear pair is 180º]
⇒ 2 ∠3 = 180º [∵ ∠3 = ∠4]
⇒ ∠3 = 90º
∴ ∠3 = ∠4 = 90º
Hence, AD bisects BC at right angles.
Example 13: AD, BE and CF, the altitudes of ∆ABC are equal. Prove that ∆ABC is an equilateral triangle
Solution: In right triangles BCE and BFC, we have
Hyp. BC = Hyp. BC
BE = CF [Given]
So, by RHS criterion of congruence,
∆BCE ∆BFC.
⇒ ∠B = ∠C [∵ Corresponding parts of congruent triangles are equal]
⇒ AC = AB …. (i)
[∵ Sides opposite to equal angles are equal]
Similarly, ∆ABD ≅ ∆ABE ⇒ ∠B =∠A
[Corresponding parts of congruent triangles are equal]
⇒ AC = BC …. (ii)
[Sides opposite to equal angles are equal]
From (i) and (ii), we get AB = BC = AC
Hence, ∆ABC is an equilateral triangle.
Example 14: In Fig. AD = BC and BD = CA.
Prove that ∠ADB = ∠BCA and ∠DAB = ∠CBA.
Solution: In triangles ABD and ABC, we have
AD = BC [Given]
BD = CA [Given]
and AB = AB [Common]
So, by SSS congruence criterion, we have
∆ABD ∠CBA ⇒ ∠DAB = ∠ABC
[∵ Corresponding parts of congruent triangles are equal] ⇒ ∠DAB = ∠CBA
Example 15: Line-segment AB is parallel to another line-segment CD. O is the mid-point of AD (see figure). Show that (i) ∆AOB ≅ ∆DOC (ii) O is also the mid point of BC.
Solution: (i) Consider ∆AOB and ∆DOC ∠ABO = ∠DCO
(Alternate angles as AB || CD and BC is the transversal)
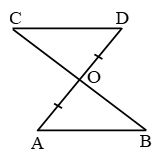
∠AOB = ∠DOC (Vertically opposite angles)
OA = OD (Given)
Therefore, ∆AOB ≅ ∆DOC (AAS rule)
(ii) OB = OC (c.p.c.t.)
So, O is the mid-point of BC.
Example 16: In quadrilateral ABCD, AC = AD and AB bisects ∠A. Show that ∆ABC ∆ABD. What can you say about BC and BD ?
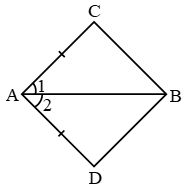
Solution: In ∆ABC & ∆ABD
AB = AB (common)
∠1 = ∠2 {∵ AB is bisector of ∠A}
AC = AD (Given)
∴ By SAS, ∆ABC ≅ ∆ABD Proved
also BC = BD (c.p.c.t.)
Example 17: AD and BC are equal perpendiculars to a line segment AB. Show that CD bisects AB.
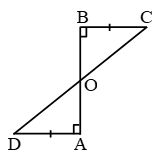
Solution: To show CD bisect AB i.e. AO = OB
∴ in ∆OAD and ∆OBC
∠O = ∠O (vertically opposite angles)
∠A = ∠B = 90° (Given)
AD = BC (Given)
∴ By AAS, ∆OAD ≅ ∆OBC
∴ OA = OB (c.p.c.t.)
∴ CD, bisects AB. Proved
Example 18: Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendicular from B to the arms of ∠A (see figure). Show that
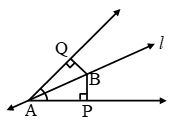
(i) ∆APB ≅ ∆AQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.
Solution: (i) In ∆APB and ∆AQB
∠P = ∠Q = 90° (Given)
∠PAB = ∠QAB (Given that ‘l’ bisect ∠A)
AB = AB (Common)
∴ By AAS, ∆APB ≅ ∆AQB. Proved
(ii) BP = BQ (c.p.c.t.) Proved.
Example 19: In given figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.
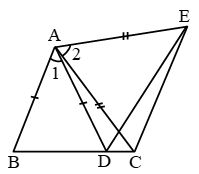
Solution: In ∆ABC and ∆ADE
Example 20: In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that:
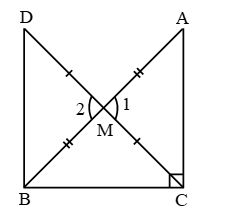
(i) ∆AMC ≅ ∆BMD
(ii) ∠DBC is a right angle
(iii) ∆DBC ≅ ∆ACB
(iv) CM = AB
Solution: (i) In ∆AMC and ∆BMD
AM = MB (M is mid point of AB)
∠1 = ∠2 (vertically opposite angles)
CM = MD (given)
∴ By SAS, ∆AMC ≅ ∆MBD Proved.
(ii) ∠ACM = ∠MDB (c.p.c.t. of (i))
These are alternate angles
∴ DB || AC
So ∠DBC + ∠ACB = 180°
(Cointerior angles)
⇒ ∠DBC + 90° = 180°
⇒ ∠DBC = 90° Proved.
(iii) In ∆DBC & ∆ACB
BC = BC ( common)
∠DBC = ∠ACB = 90°
DB = AC (c.p.c.t. of part (i))
∴ By SAS, ∆DBC ≅ ∆ACB. Proved
(iv) DC = AB (c.p.c.t. of part (iii))
But CM = DC (given)
∴ CM = AB Proved.
Criteria for congruence of triangles
Criteria For Congruent Triangles
Congruent triangles are triangles that have the same size and shape. This means that the corresponding sides are equal and the corresponding angles are equal.
Congruent Triangles do not have to be in the same orientation or position. They only have to be identical in size and shape.
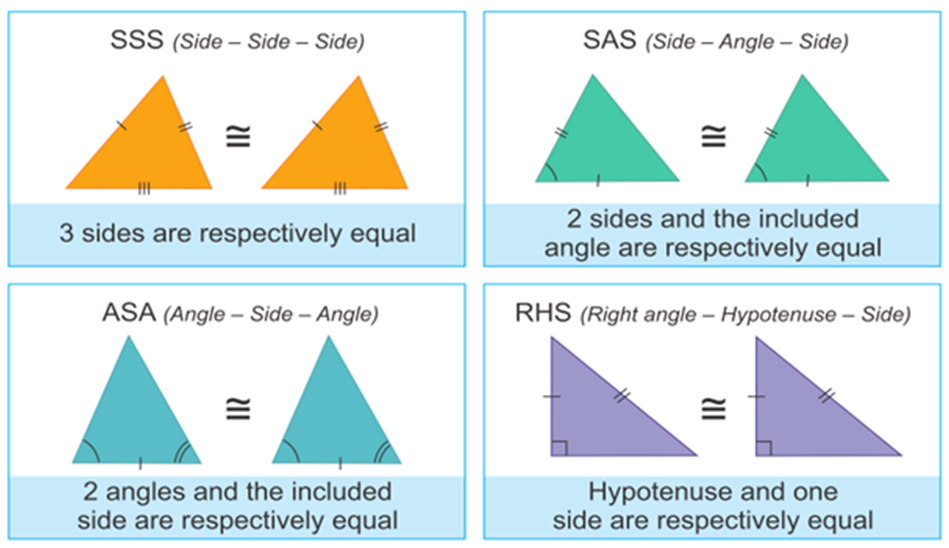
SSS (Side Side Side) Congruence Criteria (Condition):
Two triangles are congruent, if three sides of one triangle are equal to the corresponding three sides of the other triangle.
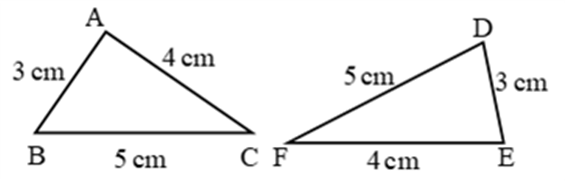
∴ By SSS criteria ∆ABC ∆EDF
∴ ∠A = ∠E, ∠B = ∠D, ∠C = ∠F (c.p.c.t.)
ASA (Angle Side Angle) Congruence Criteria (Condition):
Two triangles are congruent, if two angles and the included side of one is equal to the corresponding angles and side of the other.
∴ By ASA criteria ∆ABC ≅ ∆DEF
∴ ∠A = ∠D, AB = DE, AC = DF (c.p.c.t.)
AAS (Angle Angle Side) Congruence Criteria (Condition):
∴ By AAS, ∆ABC ≅ ∆FDE
∴ ∠C = ∠E, AB = FD, AC = FE (c.p.c.t.)
SAS (Side Angle Side) Congruence Criteria (Condition):
When two sides and the included angle of one triangle is equal to the corresponding sides and the included angle of another triangle, the two triangles are congruent. This, condition of congruence is known as side-angle-side congruence. In short we write SAS condition.
By SAS, ∆ABC ≅ ∆QPR
∴ ∠A = ∠Q, ∠C = ∠R, AC = QR (c.p.c.t.)
RHS (Right Hypotenuse Side) Congruence Criteria (Condition):
Two right triangles are congruent, if the hypotenuse and one side of one triangle are respectively equal to the hypotenuse and a side of the other triangle.
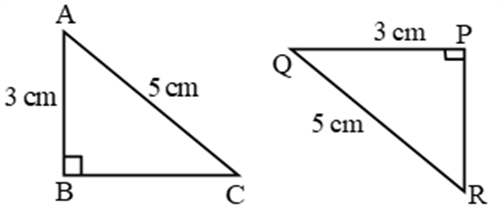
∴ By RHS, ∆ABC ≅ ∆QPR
∴ ∠A = ∠Q, ∠C = ∠R, BC = PR (c.p.c.t.)
Example 1:
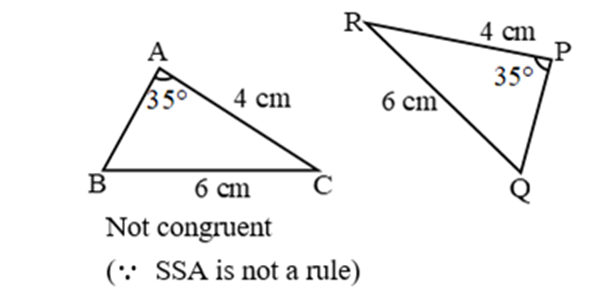
Example 2:
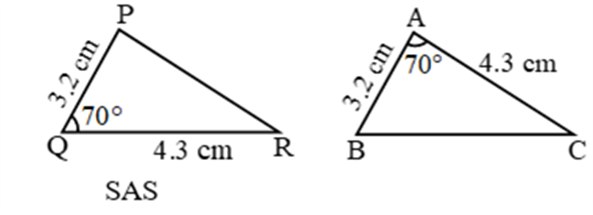
Example 3:
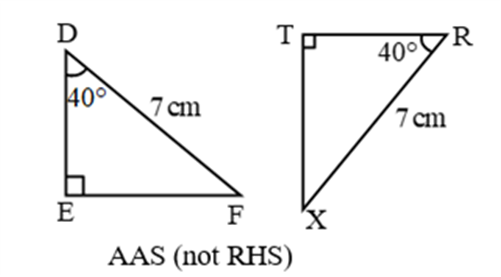
Example 4:
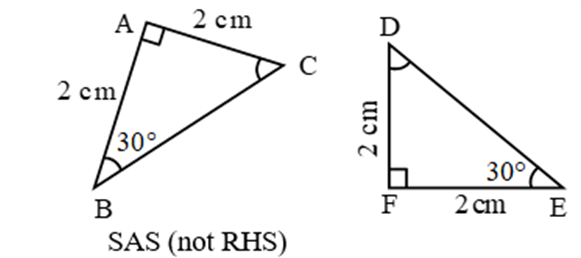
Theorem 1: If two angles and the included side of one triangle are equal to two angles and the included side of other triangle, then both triangles are congruent.
Proof:
Given: ∆ABC and ∆DEF in which
∠ABC = ∠DEF, ∠ACB = ∠DFE and BC = EF.
To Prove: ∆ABC ≅ ∆DEF.
Proof:
Case I:
Let AC = DF.
In this case, AC = DF, BC = EF and ∠C = ∠F.
∴ ∆ABC ≅ ∆DEF (SAS-criteria)
Case II:
If possible, let AC ≠ DF.
Then, construct D’ F = AC. Join D’ E.
Now, in ∆ABC and ∆D’EF, we have AC = D’F, BC = EF and ∠C = ∠F.
∴ ∆ABC ∆D’EF (SAS-criteria)
∴ ∠ABC = ∠D’EF (c.p.c.t)
But, ∠ABC = ∠DEF (given)
∴ ∠D’EF = ∠DEF.
This is possible only when D and D’ coincide.
∴ ∆ABC ≅ ∆DEF.
Theorem 2: Two right-angled triangles are congruent if one side and the hypotenuse of the one are respectively equal to the corresponding side and the hypotenuse of the other. (i.e. RHS)
Given: Two right-angled triangles ∆ABC & ∆DEF in which ∠B = ∠E = 90°, BC = EF and AC = DF.
To Prove: ∆ABC ≅ ∆DEF.
Construction: Produce DE to G such that
GE = AB. Join GF.
Proof: In ∆ABC and ∆GEF, we have:
AB = GE (construction),
BC = EF (given),
∠B = ∠FEG = 90°
⇒ ∆ABC ∆GEF (SAS-criteria)
⇒ ∠A = ∠G and AC = GF (c.p.c.t.)
Now, AC = GF and AC = DF ⇒GF = DF
⇒ ∠G = ∠D ⇒ ∠A = ∠D [∵ ∠G = ∠A]
Now, ∠A = ∠D, ∠B = ∠E ⇒ 3rd ∠C = 3rd ∠F.
Thus, in ∆ABC and ∆DEF, we have:
BC = EF, AC = DF and ∠C = ∠F.
∴ ∆ABC ≅ ∆DEF (SAS-criteria).
Criteria For Congruent Triangles Example Problems With Solutions
Example 1: Prove that diagonal of a parallelogram divides it into two congruent triangles.
Solution: Let ABCD is a parallelogram and AC is a diagonal.
(By SSS): In ∆ABC and ∆ADC
AB = CD (opp. sides of ||gm)
BC = AD (opp. sides of ||gm)
AC = AC (common)
∴ By SSS, ∆ABC ≅ ∆CDA proved
{other results : ∠1 = ∠2, ∠3 = ∠4, ∠B = ∠D (c.p.c.t.)}
(By ASA): In ∆ABC and ∆ADC
∠1 = ∠2 (alternate)
AC = AC (common)
∠3 = ∠4 (alternate)
∴ By ASA, ∆ABC ≅ ∆CDA
{other results: ∠B = ∠D, AB = CD, BC = AD (c.p.c.t.)}
(By AAS): In ∆ABC and ∆ADC
∠1 = ∠2 (alternate)
∠3 = ∠4 (alternate)
BC = AD (opp. sides)
∴ ∆ABC ≅ ∆CDA
{other results : AB = CD, ∠B = ∠D, AC = AC (c.p.c.t.)}
(By SAS): In ∆ABC and ∆ADC
AB = CD (opp. sides of ||gm)
∠1 = ∠2 (alternate)
AC = AC (common)
∴ ∆ABC ≅ ∆CDA
{other results: ∠3 = ∠4, BC = AD, ∠B = ∠D (c.p.c.t.)
We can not use ‘RHS’ for this proof.
Note: ASS or SSA criteria for congruency is not valid.
Example 2: In Fig. it is given that AB = CF, EF = BD and ∠AFE = ∠DBC. Prove that ∆AFE ∆CBD.
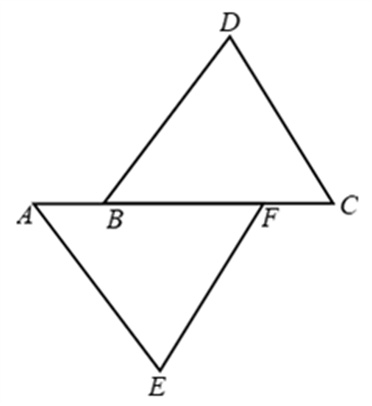
Solution: We have, AB = CF
⇒ AB + BF = CF + BF
⇒ AF = CB …. (i)
In ∆s AFE and CBD, we have
AF = CB [From (i)]
∠AFE = ∠DBC [Given]
and EF = BD [Given]
So, by SAS criterion of congruence, we have
∆AFE ≅ ∆CBD
Example 3: In Fig. X and Y are two points on equal sides AB and AC of a ∆ABC such that AX = AY. Prove that XC = YB.
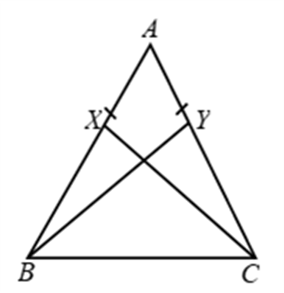
Solution: In ∆s AXC and AYB, we have
AX = AY [Given]
∠A = ∠A [Common angle]
AC = AB [Given]
So, by SAS criterion of congruene
∆AXC ≅ ∆AYB
⇒ XC = YB (c.p.c.t.)
Example 4: In Fig. PQRS is a quadrilateral and T and U are respectively points on PS and RS such PQ = RQ, ∠PQT = ∠RQU and ∠TQS = ∠UQS. Prove that QT = QU.
Solution: We have,
∠PQT = ∠RQU
and, ∠TQS = ∠UQS
∴ ∠PQT + ∠TQS = ∠RQU + ∠UQS
⇒ ∠PQS = ∠RQS …. (i)
Thus, in triangles PQS and RQS, we have
PQ = RQ [Given]
∠PQS = ∠RQS [From (i)]
and, QS = QS [Common side]
Therefore, by SAS congruence criterion, we have
∆PQS ≅ ∆RQS
⇒ ∠QPS = ∠QRS (c.p.c.t.)
⇒ ∠QPT = ∠QRU …. (ii)
Now, consider triangles QPT and QRS. In these two triangles, we have
QP = QR [Given]
∠PQT = ∠RQU [Given]
∠QPT = ∠QRU [From (ii)]
Therefore, by ASA congruence criterion, we get
∆QPT ≅ ∆QRU
⇒ QT = QU.
Example 5: In Fig. PS = QR and ∠SPQ = ∠RQP.
Prove that PR = QS and ∠QPR = ∠PQS.
Solution: In ∆SPQ and ∆RQP, we have
PS = QR [Given]
∠SPQ = ∠RQP [Given]
PQ = PQ [Common]
Therefore, by SAS criterion of congruence, we have
∆SPQ ∆RQP ⇒ SQ = RP and
∠QPR = ∠PQS
Example 6: ∆ABC is an isosceles triangle with AB = AC. Side BA is produced to D such that
AB = AD. Prove that ∠BCD is a right angle.
Solution: Given : A ∆ABC such that AB = AC. Side BA is produced to D such that AB = AD.
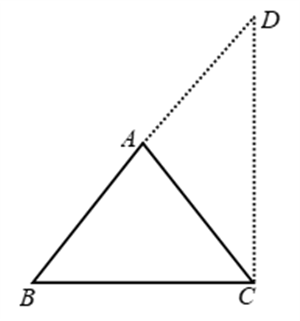
Construction : Join CD.
To prove : ∠BCD = 90º
Proof : In ∆ABC, we have AB = AC
⇒ ∠ACB = ∠ABC …(i) [∵ Angles opp. to equal sides are equal]
Now, AB = AD [Given]
∴ AD = AC [∴ AB = AC]
Thus, in ∆ADC, we have
AD = AC
⇒ ∠ACD = ∠ADC …(ii)
[∵ Angles opp. to equal sides are equal]
Adding (i) and (ii), we get
∠ACB + ∠ACD = ∠ABC + ∠ADC
⇒ ∠BCD = ∠ABC + ∠BDC
[∵ ∠ADC = ∠BDC, ∠ABC = ∠DBC]
⇒ ∠BCD + ∠BCD = ∠DBC + ∠BCD + ∠BDC
[adding ∠BCD on both sides ]
⇒ 2 ∠BCD = 180º
[∵ Sum of the angles of a ∆ is 180º]
Hence, ∠BCD is a right angle.
Example 7: In Fig. AC = BC, ∠DCA = ∠ECB and ∠DBC = ∠EAC.
Prove that triangles DBC and EAC are congruent, and hence DC = EC.
Solution: We have,
∠DCA = ∠ECB
⇒ ∠DCA + ∠ECD = ∠ECB + ∠ECD
⇒ ∠ECA = ∠DCB …. (i)
Now, in ∆s DBC and EAC, we have
∠DCB = ∠ECA [From (i)]
BC = AC [Given]
and ∠DBC = ∠EAC [Given]
So, by ASA criterion of congruence
∆DBC ≅ ∠EAS
⇒ DC = EC (c.p.c.t.)
Example 8: If the altitudes from two vertices of a triangle to the opposite sides are equal, prove that the triangle is isosceles.
Solution: Given: A ∆ABC in which altitudes BE and CF from B and C respectively on AC and AB are equal.
To prove: ∆ABC is isoceles i.e. AB = AC
Proof: In ∆s ABC and ACF, we have
∠AEB = ∠AFC [Each equal to 90º]
∠BAE = ∠CAF [Common angle]
and, BE = CF [Given]
So, by AAS criterion of congurence, we have
∆ABE ≅ ∆ACF
⇒ AB = AC [∵ Corresopnding parts of congruent triangles are equal]
Hence, ∆ABC is isosceles.
Example 9: In ∆ABC, AB = AC and the bisectors of angles B and C intersect at point O. Prove that BO = CO and the ray AO is the bisector of angle BAC.
Solution: In ∆ABC, we have
AB = AC
Now, in ∆ABO and ∆ACO, we have
AB = AC [Given]
∠OBC = ∠OCB [From (i)]
OB = OC [From (ii)]
So, by SAS criterion of congruence
∆ABO ≅ ∆ACO
⇒ ∠BAO = ∠CAO
[∵ Corresponding parts of congruent triangles are equal]
⇒ AO is the bisector of ∠BAC.
Example 10: In Fig. BM and DN are both perpendiculars to the segments AC and BM = DN.
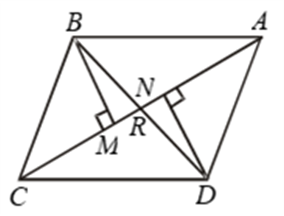
Prove that AC bisects BD.
Solution: In ∆s BMR and DNR, we have
∠BMR = ∠DNR
[Each equal to 90º ∵ BM ⊥ AC and DN ⊥ AC]
∠BRM = ∠DRN [Vert. opp. angles]
and, BM = DN [Given]
So, by AAS criterion of congruence
∆BMR ≅ ∆DNR
⇒ BR = DR
[∵ Corresponding parts of congruent triangles are equal]
⇒ R is the mid-point of BD.
Hence, AC bisects BD.
Example 11: In Fig. BD and CE are two altitudes of a ∆ABC such that BD = CE.
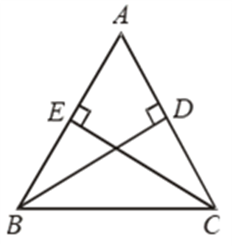
Prove that ∆ABC is isolceles.
Solution: In ∆ABD and ∆ACE, we have
∠ADB = ∠AEC = 90º [Given]
∠BAD = ∠CAE [Common]
and, BD = CE [Given]
So, by AAS congruence criterion, we have
∆ABD ≅ ∆ACE
⇒ AB = AC [∵ Corresponding parts of congruent triangles are equal]
Hence, ∆ABC is isosceles.
Example 12: If two isosceles triangles have a common base, the line joining their vertices bisects them at right angles.
Solution: Given: Two isosceles triangles ABC and DBC having the common base BC such that AB = AC and DB = DC.
To prove: AD (or AD produced) bisects BC at right angle.
Proof : In ∆s ABD and ACD, we have
AB = AC [Given]
BD = CD [Given]
AD = AD [Common side]
So, by SSS criterion of congruence
∆ABD ≅ ∆ACD
⇒ ∠1 = ∠2 …. (i)
[∵ Corresponding parts of congruent triangles are equal]
Now, in ∆s ABE and ACE, we have
AB = AC [Given]
∠1 = ∠2 [From (i)]
and, AE = AE [Commoni side]
So, by SAS criterion of congruence,
∆ABE ≅ ∆ACE
⇒ BE = CE
[∵ Corresponding parts of congruent triangles are equal]
and, ∠3 = ∠4
But, ∠3 + ∠4 = 180º
[∵ Sum of the angles of a linear pair is 180º]
⇒ 2 ∠3 = 180º [∵ ∠3 = ∠4]
⇒ ∠3 = 90º
∴ ∠3 = ∠4 = 90º
Hence, AD bisects BC at right angles.
Example 13: AD, BE and CF, the altitudes of ∆ABC are equal. Prove that ∆ABC is an equilateral triangle
Solution: In right triangles BCE and BFC, we have
Hyp. BC = Hyp. BC
BE = CF [Given]
So, by RHS criterion of congruence,
∆BCE ∆BFC.
⇒ ∠B = ∠C [∵ Corresponding parts of congruent triangles are equal]
⇒ AC = AB …. (i)
[∵ Sides opposite to equal angles are equal]
Similarly, ∆ABD ≅ ∆ABE
⇒ ∠B =∠A
[Corresponding parts of congruent triangles are equal]
⇒ AC = BC …. (ii)
[Sides opposite to equal angles are equal]
From (i) and (ii), we get
AB = BC = AC
Hence, ∆ABC is an equilateral triangle.
Example 14: In Fig. AD = BC and BD = CA.
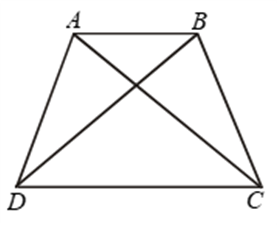
Prove that ∠ADB = ∠BCA and
∠DAB = ∠CBA.
Solution: In triangles ABD and ABC, we have
AD = BC [Given]
BD = CA [Given]
and AB = AB [Common]
So, by SSS congruence criterion, we have
∆ABD ∠CBA ⇒ ∠DAB = ∠ABC
[∵ Corresponding parts of congruent triangles are equal]
⇒ ∠DAB = ∠CBA
Example 15: Line-segment AB is parallel to another line-segment CD. O is the mid-point of AD (see figure). Show that (i) ∆AOB ≅ ∆DOC (ii) O is also the mid point of BC.
Solution: (i) Consider ∆AOB and ∆DOC
∠ABO = ∠DCO
(Alternate angles as AB || CD and BC is the transversal)
∠AOB = ∠DOC (Vertically opposite angles)
OA = OD (Given)
Therefore, ∆AOB ≅ ∆DOC (AAS rule)
(ii) OB = OC (c.p.c.t.)
So, O is the mid-point of BC.
Example 16: In quadrilateral ABCD, AC = AD and AB bisects ∠A. Show that ∆ABC ∆ABD. What can you say about BC and BD ?
Solution: In ∆ABC & ∆ABD
AB = AB (common)
∠1 = ∠2 {∵ AB is bisector of ∠A}
AC = AD (Given)
∴ By SAS, ∆ABC ≅ ∆ABD Proved
also BC = BD (c.p.c.t.)
Example 17: AD and BC are equal perpendiculars to a line segment AB. Show that CD bisects AB.
Solution: To show CD bisect AB i.e. AO = OB
∴ in ∆OAD and ∆OBC
∠O = ∠O (vertically opposite angles)
∠A = ∠B = 90° (Given)
AD = BC (Given)
∴ By AAS, ∆OAD ≅ ∆OBC
∴ OA = OB (c.p.c.t.)
∴ CD, bisects AB. Proved
Example 18: Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that
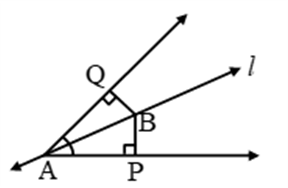
(i) ∆APB ≅ ∆AQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.
Solution: (i) In ∆APB and ∆AQB
∠P = ∠Q = 90° (Given)
∠PAB = ∠QAB (Given that ‘l’ bisect ∠A)
AB = AB (Common)
∴ By AAS, ∆APB ≅ ∆AQB. Proved
(ii) BP = BQ (c.p.c.t.) Proved.
Example 19: In given figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.
Solution: In ∆ABC and ∆ADE

Example 20: In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that:
(i) ∆AMC ≅ ∆BMD
(ii) ∠DBC is a right angle
(iii) ∆DBC ≅ ∆ACB
(iv) CM = AB
Solution: (i) In ∆AMC and ∆BMD
AM = MB (M is mid point of AB)
∠1 = ∠2 (vertically opposite angles)
CM = MD (given)
∴ By SAS, ∆AMC ≅ ∆MBD Proved.
(ii) ∠ACM = ∠MDB (c.p.c.t. of (i))
These are alternate angles
∴ DB || AC
So ∠DBC + ∠ACB = 180°
(Cointerior angles)
⇒ ∠DBC + 90° = 180°
⇒ ∠DBC = 90° Proved.
(iii) In ∆DBC & ∆ACB
BC = BC ( common)
∠DBC = ∠ACB = 90°
DB = AC (c.p.c.t. of part (i))
∴ By SAS, ∆DBC ≅ ∆ACB. Proved
(iv) DC = AB (c.p.c.t. of part (iii))
But CM = DC (given)
∴ CM = AB Proved.
Some properties of a triangle
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Properties of Triangle
All the properties of a triangle are based on its sides and angles. By the definition of triangle, we know that, it is a closed polygon that consists of three sides and three vertices. Also, the sum of all three internal angles of a triangle equal to 180°.
Depending upon the length of sides and measure of angles, the triangles are classified into different types of triangles. Triangle is an important concept which is taught in most of the classes like Class 7, Class 8, Class 9, Class 10 and in Class 11. You will learn the properties of triangles here along with its definitions, types and its significance in Maths.
In the beginning, we start from understanding the shape of triangles, its types and properties, theorems based on it such as Pythagoras theorem, etc. In higher classes, we deal with trigonometry, where the right-angled triangle is the base of the concept. Let us learn here some of the fundamentals of the triangle by knowing its properties.
Types of Triangle
|
Based on the Sides |
Based on the Angles |
|
Scalene Triangle |
Acute angled Triangle |
|
Isosceles Triangle |
Right angle Triangle |
|
Equilateral Triangle |
Obtuse-angled Triangle |
So before, discussing the properties of triangles, let us discuss types of triangles given above.
Scalene Triangle: All the sides and angles are unequal.
Isosceles Triangle: It has two equal sides. Also, the angles opposite these equal sides are equal.
Equilateral Triangle: All the sides are equal and all the three angles equal to 60°.
Acute Angled Triangle: A triangle having all its angles less than 90°.
Right Angled Triangle: A triangle having one of the three angles exactly 90°.
Obtuse Angled Triangle: A triangle having one of the three angles more than 90°.
Triangle Properties
The properties of the triangle are:
- The sum of all the angles of a triangle (of all types) is equal to 180°.
- The sum of the length of the two sides of a triangle is greater than the length of the third side.
- In the same way, the difference between the two sides of a triangle is less than the length of the third side.
- The side opposite the greater angle is the longest side of all the three sides of a triangle.
- The exterior angle of a triangle is always equal to the sum of the interior opposite angles. This property of a triangle is called an exterior angle property.
- Two triangles are said to be similar if the corresponding angles of both triangles are congruent and the lengths of their sides are proportional.
- Area of a triangle = ½ × Base × Height
- The perimeter of a triangle = sum of all its three sides
Triangle Formula
- Area of a triangle is the region occupied by a triangle in a two-dimensional plane. The dimension of the area is square units. The formula for area is given by;
Area = 1/2 x Base x Height
- The perimeter of a triangle is the length of the outer boundary of a triangle. To find the perimeter of a triangle we need to add the length of the sides of the triangle.
P = a + b + c
- Semi-perimeter of a triangle is half of the perimeter of the triangle. It is represented by s.
s = (a + b + c)/2
where a, b and c are the sides of the triangle.
- By Heron’s formula, the area of the triangle is given by:
A = √[s(s – a)(s – b)(s – c)]
where ‘s’ is the semi-perimeter of the triangle.
- By the Pythagorean theorem, the hypotenuse of a right-angled triangle can be calculated by the formula:
Hypotenuse2 = Base2 + Perpendicular2
Solved Examples
Example 1: If an equilateral triangle has lengths of sides as 5 cm and perpendicular is drawn from the vertex to the base of the triangle, then find its area and perimeter.
Solution: Given, side of the equilateral triangle, say AB = BC = CD = 5 cm
If we draw a perpendicular from the vertex of an equilateral triangle, A to the base at point O, it divides the base into two equal sides.
Such that, BO = OC = 2.5 cm
Now, the area of triangle = ½ × Base × Height
To find the height of the triangle, AOB, we have to use Pythagoras theorem.
That is, Hypotenuse2 = Base2 + Perpendicular2
Or Perpendicular =
Therefore, OA =
Or OA =
OA =
Area of triangle ABC = ½ × BC × OA
= ½ × 5 ×
= 2.5 × 4.33
Area of triangle ABC = 10.825 cm2
Perimeter of triangle ABC = sum of all its three sides
= 5 + 5 + 5 cm
= 15 cm
Example 2: If the sides of a triangle are given by 3 cm, 4 cm and 5 cm, where the base is 4cm and the altitude of the triangle is 3.2 cm, then find the area and perimeter of the triangle.
Solution: Let the given sides of the triangle be:
a = 3 cm, b = 4 cm and c = 5 cm
Altitude is the height of the triangle = 3.2 cm
By the formula of area of the triangle, we know;
Area = 1/2 x base x height
A = (1/2) x 4 x 3.2
A = 6.4 sq.cm.
Now, the perimeter of the triangle is given by;
P = a + b + c
P = 3 + 4 + 5
P = 12 cm.
Some properties of a triangle
Properties of Triangle
All the properties of a triangle are based on its sides and angles. By the definition of triangle, we know that, it is a closed polygon that consists of three sides and three vertices. Also, the sum of all three internal angles of a triangle equal to 180°.
Depending upon the length of sides and measure of angles, the triangles are classified into different types of triangles. Triangle is an important concept which is taught in most of the classes like Class 7, Class 8, Class 9, Class 10 and in Class 11. You will learn the properties of triangles here along with its definitions, types and its significance in Maths.
In the beginning, we start from understanding the shape of triangles, its types and properties, theorems based on it such as Pythagoras theorem, etc. In higher classes, we deal with trigonometry, where the right-angled triangle is the base of the concept. Let us learn here some of the fundamentals of the triangle by knowing its properties.
Types of Triangle
|
Based on the Sides |
Based on the Angles |
|
Scalene Triangle |
Acute angled Triangle |
|
Isosceles Triangle |
Right angle Triangle |
|
Equilateral Triangle |
Obtuse-angled Triangle |
So before, discussing the properties of triangles, let us discuss types of triangles given above.
Scalene Triangle: All the sides and angles are unequal.
Isosceles Triangle: It has two equal sides. Also, the angles opposite these equal sides are equal.
Equilateral Triangle: All the sides are equal and all the three angles equal to 60°.
Acute Angled Triangle: A triangle having all its angles less than 90°.
Right Angled Triangle: A triangle having one of the three angles exactly 90°.
Obtuse Angled Triangle: A triangle having one of the three angles more than 90°.
Triangle Properties
The properties of the triangle are:
- The sum of all the angles of a triangle (of all types) is equal to 180°.
- The sum of the length of the two sides of a triangle is greater than the length of the third side.
- In the same way, the difference between the two sides of a triangle is less than the length of the third side.
- The side opposite the greater angle is the longest side of all the three sides of a triangle.
- The exterior angle of a triangle is always equal to the sum of the interior opposite angles. This property of a triangle is called an exterior angle property.
- Two triangles are said to be similar if their corresponding angles of both triangles are congruent and the lengths of their sides are proportional.
- Area of a triangle = ½ × Base × Height
- The perimeter of a triangle = sum of all its three sides
Triangle Formula
- Area of a triangle is the region occupied by a triangle in a two-dimensional plane. The dimension of the area is square units. The formula for area is given by;
Area = 1/2 x Base x Height
- The perimeter of a triangle is the length of the outer boundary of a triangle. To find the perimeter of a triangle we need to add the length of the sides of the triangle.
P = a + b + c
- Semi-perimeter of a triangle is half of the perimeter of the triangle. It is represented by s.
s = (a + b + c)/2
where a, b and c are the sides of the triangle.
- By Heron’s formula, the area of the triangle is given by:
A = √[s(s – a)(s – b)(s – c)]
where ‘s’ is the semi-perimeter of the triangle.
- By the Pythagorean theorem, the hypotenuse of a right-angled triangle can be calculated by the formula:
Hypotenuse2 = Base2 + Perpendicular2
Solved Examples
Example 1: If an equilateral triangle has lengths of sides as 5 cm and perpendicular is drawn from the vertex to the base of the triangle, then find its area and perimeter.
Solution: Given, side of the equilateral triangle, say AB = BC = CD = 5 cm
If we draw a perpendicular from the vertex of an equilateral triangle, A to the base at point O, it divides the base into two equal sides.
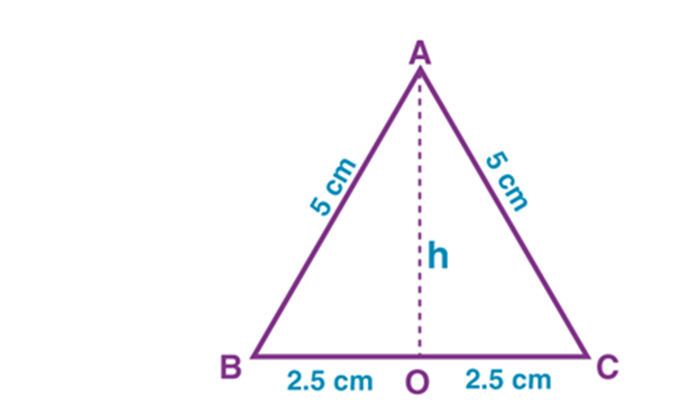
Such that, BO = OC = 2.5 cm
Now, the area of triangle = ½ × Base × Height
To find the height of the triangle, AOB, we have to use Pythagoras theorem.
That is, Hypotenuse2 = Base2 + Perpendicular2
Or Perpendicular =
Therefore, OA =
Or OA =
OA =
Area of triangle ABC = ½ × BC × OA
= ½ × 5 ×
= 2.5 × 4.33
Area of triangle ABC = 10.825 cm2
Perimeter of triangle ABC = sum of all its three sides
= 5 + 5 + 5 cm
= 15 cm
Example 2: If the sides of a triangle are given by 3 cm, 4 cm and 5 cm, where the base is 4cm and the altitude of the triangle is 3.2 cm, then find the area and perimeter of the triangle.
Solution: Let the given sides of the triangle be:
a = 3 cm, b = 4 cm and c = 5 cm
Altitude is the height of the triangle = 3.2 cm
By the formula of area of the triangle, we know;
Area = 1/2 x base x height
A = (1/2) x 4 x 3.2
A = 6.4 sq.cm.
Now, the perimeter of the triangle is given by;
P = a + b + c
P = 3 + 4 + 5
P = 12 cm.
Some more criteria for Congruence of Triangles
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Some More Criteria for Congruence of Triangles
Theorem 4 - SSS Congruence Rule
SSS Triangle Congruence
What if your parents were remodeling their kitchen so that measurements between the sink, refrigerator, and oven are in the picture at the left, below. Your neighbor’s kitchen has the measurements on the right, below. Are the two triangles congruent? After completing this Concept, you'll be able to determine whether or not two triangles are congruent given only their side lengths.
[Figure 1]
Side-Side-Side (SSS) Triangle Congruence Theorem: If three sides in one triangle are congruent to three sides in another triangle, then the triangles are congruent.
Now, we only need to show that all three sides in a triangle are congruent to the three sides in another triangle. We no longer have to show 3 sets of angles are congruent and 3 sets of sides are congruent in order to say that the two triangles are congruent.
Example A
Write a triangle congruence statement based on the diagram below:
[Figure 2]
From the tic marks, we know AB¯¯¯¯¯¯¯¯≅LM¯¯¯¯¯¯¯¯¯,AC¯¯¯¯¯¯¯¯≅LK¯¯¯¯¯¯¯¯,BC¯¯¯¯¯¯¯¯≅MK¯¯¯¯¯¯¯¯¯¯. Using the SSS Congruence rule we know the two triangles are congruent. Lining up the corresponding sides, we have △ABC≅△LMK.
Don’t forget ORDER MATTERS when writing triangle congruence statements. Here, we lined up the sides with one tic mark, then the sides with two tic marks, and finally the sides with three tic marks.
Example B
Write a two-column proof to show that the two triangles are congruent.
Given: AB¯¯¯¯¯¯¯¯≅DE¯¯¯¯¯¯¯¯
[Figure 3]
C is the midpoint of AE¯¯¯¯¯¯¯¯ and DB¯¯¯¯¯¯¯¯.
Prove: △ACB≅△ECD
|
Statement |
Reason |
|
1. AB¯¯¯¯¯¯¯¯≅DE¯¯¯¯¯¯¯¯ C is the midpoint of AE¯¯¯¯¯¯¯¯ and DB¯¯¯¯¯¯¯¯ |
Given |
|
2. AC¯¯¯¯¯¯¯¯≅CE¯¯¯¯¯¯¯¯,BC¯¯¯¯¯¯¯¯≅CD¯¯¯¯¯¯¯¯ |
Definition of a midpoint |
|
3. △ACB≅△ECD |
SSS Congruence rule |
Make sure that you clearly state the three sets of congruent sides BEFORE stating that the triangles are congruent.
Feel free to mark the picture with the information you are given as well as information that you can infer (vertical angles, information from parallel lines, midpoints, angle bisectors, right angles).
Concept Problem Revisited
From what we have learned in this section, the two triangles are not congruent because the distance from the fridge to the stove in your house is 4 feet and in your neighbor’s it is 4.5 ft. The SSS Congruence rule tells us that all three sides have to be congruent.
Vocabulary
Two figures are congruent if they have exactly the same size and shape. By definition, two triangles are congruent if the three corresponding angles and sides are congruent. The symbol ≅ means congruent. There are shortcuts for proving that triangles are congruent. The SSS Triangle Congruence Rule states that if three sides in one triangle are congruent to three sides in another triangle, then the triangles are congruent.
Theorem 5 - RHS Congruence Rule
HL Triangle Congruence
What if you were given two right triangles and provided with only the measure of their hypotenuses and one of their legs? How could you determine if the two right triangles were congruent? After completing this Concept, you'll be able to use the Hypotenuse-Leg (HL) shortcut to prove right triangles are congruent.
Guidance
Recall that a right triangle has exactly one right angle. The two sides adjacent to the right angle are called legs and the side opposite the right angle is called the hypotenuse.
[Figure 13]
The Pythagorean Theorem says, for any right triangle, (leg)2+(leg)2=(hypotenuse)2. What this means is that if you are given two sides of a right triangle, you can always find the third. Therefore, if you know that two sides of a right triangle are congruent to two sides of another right triangle, you can conclude that third sides are also congruent.
RHS Congruence Theorem: If the hypotenuse and leg in one right triangle are congruent to the hypotenuse and leg in another right triangle, then the two triangles are congruent.
The markings in the picture are enough to say △ABC≅△XYZ.
[Figure 14]
Notice that this theorem is only used with a hypotenuse and a leg. If you know that the two legs of a right triangle are congruent to two legs of another triangle, the two triangles would be congruent by SAS, because the right angle would be between them.
Example A
What information would you need to prove that these two triangles are congruent using the RHS Congruence Theorem?
[Figure 15]
For RHS Congruence condition, we need the hypotenuses to be congruent. So, AC¯¯¯¯¯¯¯¯≅MN¯¯¯¯¯¯¯¯¯¯.
Example B
Determine if the triangles are congruent. If they are, write the congruence statement and which congruence postulate or theorem you used.
[Figure 16]
We know the two triangles are right triangles. The have one pair of legs that is congruent and their hypotenuses are congruent. This means that △ABC≅△RQP by RHS Congruence theorem.
Example C
Determine the additional piece of information needed to show the two triangles are congruent by RHS Congruence theorem.
[Figure 17]
We already know one pair of legs is congruent and that they are right triangles. The additional piece of information we need is that the two hypotenuses are congruent, UT¯¯¯¯¯¯¯≅FG¯¯¯¯¯¯¯¯.
Vocabulary
Two figures are congruent if they have exactly the same size and shape. By definition, two triangles are congruent if the three corresponding angles and sides are congruent. The symbol ≅ means congruent. There are shortcuts for proving that triangles are congruent. The RHS Congruence Theorem states that if the hypotenuse and leg in one right triangle are congruent to the hypotenuse and leg in another right triangle, then the two triangles are congruent. A right triangle has exactly one right (90∘) angle. The two sides adjacent to the right angle are called legs and the side opposite the right angle is called the hypotenuse.
Some more criteria for Congruence of Triangles
Some More Criteria for Congruence of Triangles
Theorem 4 - SSS Congruence Rule
SSS Triangle Congruence
What if your parents were remodeling their kitchen so that measurements between the sink, refrigerator, and oven are in the picture at the left, below. Your neighbor’s kitchen has the measurements on the right, below. Are the two triangles congruent? After completing this Concept, you'll be able to determine whether or not two triangles are congruent given only their side lengths.
[Figure 1]
Side-Side-Side (SSS) Triangle Congruence Theorem: If three sides in one triangle are congruent to three sides in another triangle, then the triangles are congruent.
Now, we only need to show that all three sides in a triangle are congruent to the three sides in another triangle. We no longer have to show 3 sets of angles are congruent and 3 sets of sides are congruent in order to say that the two triangles are congruent.
Example A
Write a triangle congruence statement based on the diagram below:
[Figure 2]
From the tic marks, we know AB¯¯¯¯¯¯¯¯≅LM¯¯¯¯¯¯¯¯¯,AC¯¯¯¯¯¯¯¯≅LK¯¯¯¯¯¯¯¯,BC¯¯¯¯¯¯¯¯≅MK¯¯¯¯¯¯¯¯¯¯. Using the SSS Congruence rule we know the two triangles are congruent. Lining up the corresponding sides, we have △ABC≅△LMK.
Don’t forget ORDER MATTERS when writing triangle congruence statements. Here, we lined up the sides with one tic mark, then the sides with two tic marks, and finally the sides with three tic marks.
Example B
Write a two-column proof to show that the two triangles are congruent.
Given: AB¯¯¯¯¯¯¯¯≅DE¯¯¯¯¯¯¯¯
[Figure 3]
C is the midpoint of AE¯¯¯¯¯¯¯¯ and DB¯¯¯¯¯¯¯¯.
Prove: △ACB≅△ECD
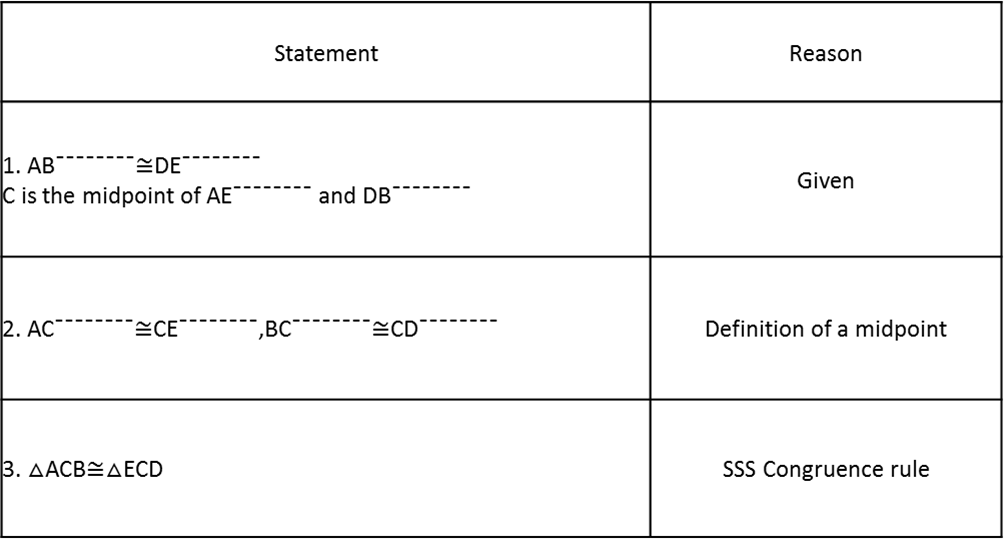
Make sure that you clearly state the three sets of congruent sides BEFORE stating that the triangles are congruent.
Feel free to mark the picture with the information you are given as well as information that you can infer (vertical angles, information from parallel lines, midpoints, angle bisectors, right angles).
Concept Problem Revisited
From what we have learned in this section, the two triangles are not congruent because the distance from the fridge to the stove in your house is 4 feet and in your neighbor’s it is 4.5 ft. The SSS Congruence rule tells us that all three sides have to be congruent.
Vocabulary
Two figures are congruent if they have exactly the same size and shape. By definition, two triangles are congruent if the three corresponding angles and sides are congruent. The symbol ≅ means congruent. There are shortcuts for proving that triangles are congruent. The SSS Triangle Congruence Rule states that if three sides in one triangle are congruent to three sides in another triangle, then the triangles are congruent.
Guided Practice
1. Fill in the blanks in the proof below.
Given: AB¯¯¯¯¯¯¯¯≅DC¯¯¯¯¯¯¯¯, AC¯¯¯¯¯¯¯¯≅DB¯¯¯¯¯¯¯¯
Prove: △ABC≅△DCB
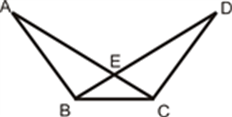
[Figure 4]
2. Is the pair of triangles congruent? If so, write the congruence statement and why.

[Figure 5]
Answers:
1
2. The triangles are congruent because they have three pairs of sides congruent. △DEF≅△IGH.
Practice
Are the pairs of triangles congruent? If so, write the congruence statement and why.
1
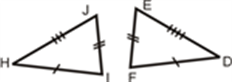
[Figure 6]
2.
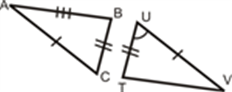
[Figure 7]
3.
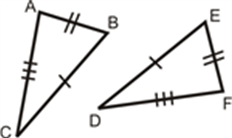
[Figure 8]
4.
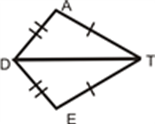
[Figure 9]
State the additional piece of information needed to show that each pair of triangles is congruent.
5. Use SSS
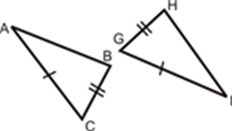
[Figure 10]
6. Use SSS
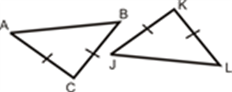
[Figure 11]
Fill in the blanks in the proofs below.
7. Given: B is the midpoint of DC¯¯¯¯¯¯¯¯, AD¯¯¯¯¯¯¯¯≅AC¯¯¯¯¯¯¯¯. Prove: △ABD≅△ABC
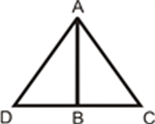
[Figure 12]

Theorem 5 - RHS Congruence Rule
HL Triangle Congruence
What if you were given two right triangles and provided with only the measure of their hypotenuses and one of their legs? How could you determine if the two right triangles were congruent? After completing this Concept, you'll be able to use the Hypotenuse-Leg (HL) shortcut to prove right triangles are congruent.
Guidance
Recall that a right triangle has exactly one right angle. The two sides adjacent to the right angle are called legs and the side opposite the right angle is called the hypotenuse.
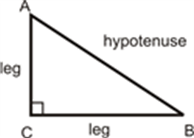
[Figure 13]
The Pythagorean Theorem says, for any right triangle, (leg)2+(leg)2=(hypotenuse)2. What this means is that if you are given two sides of a right triangle, you can always find the third. Therefore, if you know that two sides of a right triangle are congruent to two sides of another right triangle, you can conclude that third sides are also congruent.
RHS Congruence Theorem: If the hypotenuse and leg in one right triangle are congruent to the hypotenuse and leg in another right triangle, then the two triangles are congruent.
The markings in the picture are enough to say △ABC≅△XYZ.
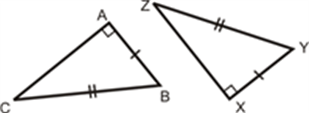
[Figure 14]
Notice that this theorem is only used with a hypotenuse and a leg. If you know that the two legs of a right triangle are congruent to two legs of another triangle, the two triangles would be congruent by SAS, because the right angle would be between them.
Example A
What information would you need to prove that these two triangles are congruent using the RHS Congruence Theorem?
[Figure 15]
For RHS Congruence condition, we need the hypotenuses to be congruent. So, AC¯¯¯¯¯¯¯¯≅MN¯¯¯¯¯¯¯¯¯¯.
Example B
Determine if the triangles are congruent. If they are, write the congruence statement and which congruence postulate or theorem you used.
[Figure 16]
We know the two triangles are right triangles. The have one pair of legs that is congruent and their hypotenuses are congruent. This means that △ABC≅△RQP by RHS Congruence theorem.
Example C
Determine the additional piece of information needed to show the two triangles are congruent by RHS Congruence theorem.
[Figure 17]
We already know one pair of legs is congruent and that they are right triangles. The additional piece of information we need is that the two hypotenuses are congruent, UT¯¯¯¯¯¯¯≅FG¯¯¯¯¯¯¯¯.
Watch this video for help with the examples above.
Vocabulary
Two figures are congruent if they have exactly the same size and shape. By definition, two triangles are congruent if the three corresponding angles and sides are congruent. The symbol ≅ means congruent. There are shortcuts for proving that triangles are congruent. The RHS Congruence Theorem states that if the hypotenuse and leg in one right triangle are congruent to the hypotenuse and leg in another right triangle, then the two triangles are congruent. A right triangle has exactly one right (90∘) angle. The two sides adjacent to the right angle are called legs and the side opposite the right angle is called the hypotenuse.
Guided Practice
1. Determine if the triangles are congruent. If they are, write the congruence statement and which congruence postulate or theorem you used.
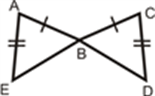
[Figure 18]
2. Fill in the blanks in the proof below.
Given:
SV¯¯¯¯¯¯¯⊥WU¯¯¯¯¯¯¯¯¯
T is the midpoint of SV¯¯¯¯¯¯¯ and WU¯¯¯¯¯¯¯¯¯
Prove: WS¯¯¯¯¯¯¯¯¯≅UV¯¯¯¯¯¯¯¯
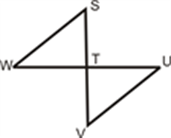
[Figure 19]

3. If two right triangles have congruent hypotenuses and one pair of non-right angles that are congruent, are the two right triangles definitively congruent?
Answers:
1. All we know is that two pairs of sides are congruent. Since we do not know if these are right triangles, we cannot use RHS Congruence theorem. We do not know if these triangles are congruent.
2
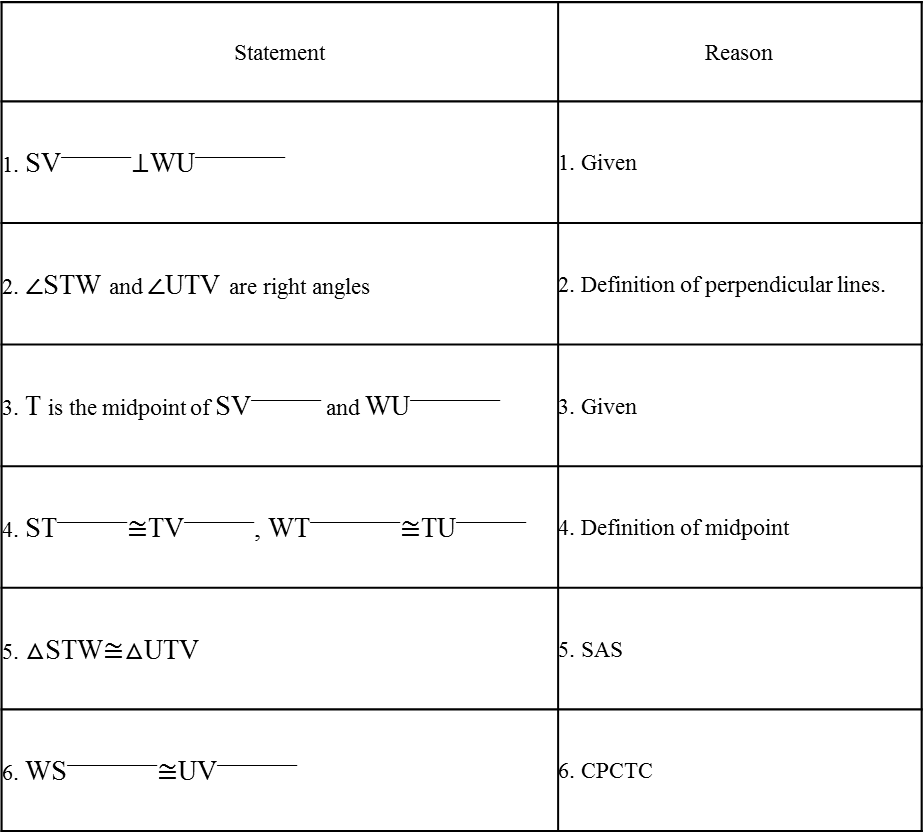
Note that even though these were right triangles, we did not use the RHS congruence theorem because we were not originally given that the two hypotenuses were congruent. The SAS congruence shortcut was quicker in this case.
3. Yes, by the AAS Congruence shortcut. One pair of congruent angles is the right angles, and another pair is given. The congruent pair of sides are the hypotenuses that are congruent. Note that just like in #2, even though the triangles are right triangles, it is possible to use a congruence shortcut other than RHS Congruence theorem to prove the triangles are congruent.
Practice
Using the RHS Congruence Theorem, what information do you need to prove the two triangles are congruent?
1.
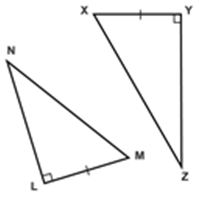
[Figure 20]
2.
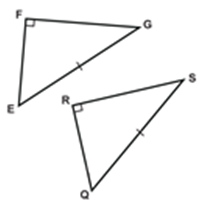
[Figure 21]
3.
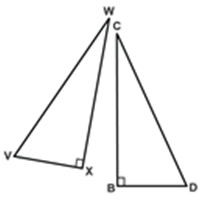
[Figure 22]
The triangles are formed by two parallel lines cut by a perpendicular transversal. C is the midpoint of AD¯¯¯¯¯¯¯¯. Complete the proof to show the two triangles are congruent.
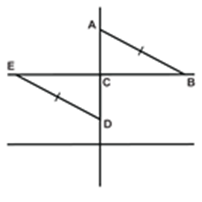
[Figure 23]
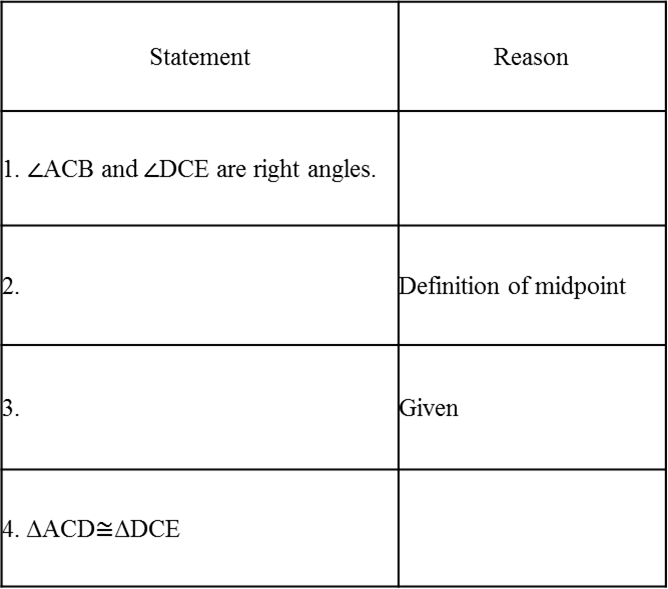
Based on the following details, are the two right triangles definitively congruent?
4. The hypotenuses of two right triangles are congruent.
5. Both sets of legs in the two right triangles are congruent.
6. One set of legs are congruent in the two right triangles.
7. The hypotenuses and one pair of legs are congruent in the two right triangles.
8. One of the non right angles of the two right triangles is congruent.
9. All of the angles of the two right triangles are congruent.
10. All of the sides of the two right triangles are congruent.
11. Both triangles have one leg that is twice the length of the other.
Inequalities in Triangle
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Triangle Inequality Theorem
According to triangle inequality theorem, for any given triangle, the sum of two sides of a triangle is always greater than the third side. A polygon bounded by three line segments is known as the Triangle. It is the smallest possible polygon. A triangle has three sides, three vertices, and three interior angles. The types of triangles are based on its angle measure and length of the sides. The inequality theorem is applicable for all types triangles such as equilateral, isosceles and scalene. Now let us learn this theorem in details with its proof.
Triangle Inequality Theorem Proof
The triangle inequality theorem describes the relationship between the three sides of a triangle. According to this theorem, for any triangle, the sum of lengths of two sides is always greater than the third side. In other words, this theorem specifies that the shortest distance between two distinct points is always a straight line.
Consider a ∆ABC as shown below, with a, b and c as the side lengths.
The triangle inequality theorem states that:
a < b + c,
b < a + c,
c < a + b
In any triangle, the shortest distance from any vertex to the opposite side is the Perpendicular. In figure below, XP is the shortest line segment from vertex X to side YZ.
Let us prove the theorem now for a triangle ABC.
Triangle ABC
To Prove: |BC|< |AB| + |AC|
Construction: Consider a ∆ABC. Extend the side AC to a point D such that AD = AB as shown in the fig. below.
Proof of triangle inequality theorem
|
S.No |
Statement |
Reason |
|
1. |
|CD|= |AC| + |AD| |
From figure 3 |
|
2. |
|CD|= |AC| + |AB| |
AB = AD, ∆ADB is an isosceles triangle |
|
3. |
∠DBA <∠DBC |
Since ∠DBC = ∠DBA+∠ABD |
|
4. |
∠ADB<∠DBC |
∆ADB is an isosceles triangle and ∠ADB = ∠DBA |
|
5. |
|BC|<|CD| |
Side opposite to greater angle is larger |
|
6. |
|BC|<|AC| + |AB| |
From statements 3 and 4 |
Thus, we can conclude that the sum of two sides of a triangle is greater than the third side.
Example Problems
Q.1. If 4cm, 8cm and 2cm are the measures of three lines segment. Can it be used to draw a triangle?
Solution: The triangle is formed by three line segments 4cm, 8cm and 2cm, then it should satisfy the inequality theorem.
Hence, let us check if the sum of two sides is greater than the third side.
4 + 8 > 2 ⇒ 12 > 2 ⇒ True
8 + 2 > 4 ⇒ 10 > 4 ⇒ True
4 + 2 > 8 ⇒ 6 > 8 ⇒ False
Therefore, the sides of the triangle do not satisfy the inequality theorem. So, we cannot construct a triangle with these three line segments.
Q.2: Could a triangle have side length as 6cm, 7cm and 5cm?
Solution: If 6cm, 7cm and 5cm are the sides of the triangle, then they should satisfy the inequality theorem.
Hence,
6 + 7 > 5 ⇒ 13 > 5 ⇒ True
7 + 5 > 6 ⇒ 12 > 6 ⇒ True
6 + 5 > 7 ⇒ 11 > 7 ⇒ True
All the three conditions are satisfied, therefore a triangle could have side length as 6cm, 7cm and 5cm
Q.3: If the two sides of a triangle are 2 and 7. Find all the possible lengths of the third side.
Solution: To find the possible values of the third side of the triangle we can use the formula:
A difference of two sides< Unknown side < Sum of the two sides
7 -2 < x < 7 + 2
5 < x <9
There could be any value for the third side between 5 and 9.
Inequalities in Triangle
Triangle Inequality Theorem
According to triangle inequality theorem, for any given triangle, the sum of two sides of a triangle is always greater than the third side. A polygon bounded by three line-segments is known as the Triangle. It is the smallest possible polygon. A triangle has three sides, three vertices, and three interior angles. The types of triangles are based on its angle measure and length of the sides. The inequality theorem is applicable for all types triangles such as equilateral, isosceles and scalene. Now let us learn this theorem in details with its proof.
Triangle Inequality Theorem Proof
The triangle inequality theorem describes the relationship between the three sides of a triangle. According to this theorem, for any triangle, the sum of lengths of two sides is always greater than the third side. In other words, this theorem specifies that the shortest distance between two distinct points is always a straight line.
Consider a ∆ABC as shown below, with a, b and c as the side lengths.
The triangle inequality theorem states that:
a < b + c,
b < a + c,
c < a + b
In any triangle, the shortest distance from any vertex to the opposite side is the Perpendicular. In figure below, XP is the shortest line segment from vertex X to side YZ.
Let us prove the theorem now for a triangle ABC.
Triangle ABC
To Prove: |BC|< |AB| + |AC|
Construction: Consider a ∆ABC. Extend the side AC to a point D such that AD = AB as shown in the fig. below.
Proof of triangle inequality theorem
|
S.No |
Statement |
Reason |
|
1. |
|CD|= |AC| + |AD| |
From figure 3 |
|
2. |
|CD|= |AC| + |AB| |
AB = AD, ∆ADB is an isosceles triangle |
|
3. |
∠DBA <∠DBC |
Since ∠DBC = ∠DBA+∠ABD |
|
4. |
∠ADB<∠DBC |
∆ADB is an isosceles triangle and ∠ADB = ∠DBA |
|
5. |
|BC|<|CD| |
Side opposite to greater angle is larger |
|
6. |
|BC|<|AC| + |AB| |
From statements 3 and 4 |
Thus, we can conclude that the sum of two sides of a triangle is greater than the third side.
Example Problems
Q.1. If 4cm, 8cm and 2cm are the measures of three lines segment. Can it be used to draw a triangle?
Solution: The triangle is formed by three line segments 4cm, 8cm and 2cm, then it should satisfy the inequality theorem.
Hence, let us check if the sum of two sides is greater than the third side.
4 + 8 > 2 ⇒ 12 > 2 ⇒ True
8 + 2 > 4 ⇒ 10 > 4 ⇒ True
4 + 2 > 8 ⇒ 6 > 8 ⇒ False
Therefore, the sides of the triangle do not satisfy the inequality theorem. So, we cannot construct a triangle with these three line-segments.
Q.2: Could a triangle have side length as 6cm, 7cm and 5cm?
Solution: If 6cm, 7cm and 5cm are the sides of the triangle, then they should satisfy inequality theorem.
Hence,
6 + 7 > 5 ⇒ 13 > 5 ⇒ True
7 + 5 > 6 ⇒ 12 > 6 ⇒ True
6 + 5 > 7 ⇒ 11 > 7 ⇒ True
All the three conditions are satisfied, therefore a triangle could have side length as 6cm, 7cm and 5cm
Q.3: If the two sides of a triangle are 2 and 7. Find all the possible lengths of the third side.
Solution: To find the possible values of the third side of the triangle we can use the formula:
A difference of two sides< Unknown side < Sum of the two sides
7 -2 < x < 7 + 2
5 < x <9
There could be any value for the third side between 5 and 9.
Types of Quadrilaterals
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Types of Quadrilaterals
Before talking about the types of quadrilaterals, let us recall what a quadrilateral is. A quadrilateral is a polygon that has the following properties
- 4 vertices and 4 sides enclosing 4 angles.
- The sum of all interior angles of a quadrilateral is 360 degrees.
- We can also derive the sum of interior angle from the formula of polygon i.e. (n -2) × 180, where n is equal to the number of sides of the polygon
A quadrilateral, in general, has sides of different lengths and angles of different measures. However, squares, rectangles, etc. are special types of quadrilaterals with some of their sides and angles being equal. This is the reason that the area of a quadrilateral depends on which type of quadrilateral it is. In this article, we will discuss the special types of quadrilaterals and their basic properties.
Different Types of Quadrilaterals
There are six basic types of quadrilaterals. They are:
- Trapezium
- Parallelogram
- Rectangle
- Rhombus
- Square
- Kite
Trapezium - It is a quadrilateral with one pair of opposite parallel sides. In the trapezium, ABCD, side AB is parallel to side CD.
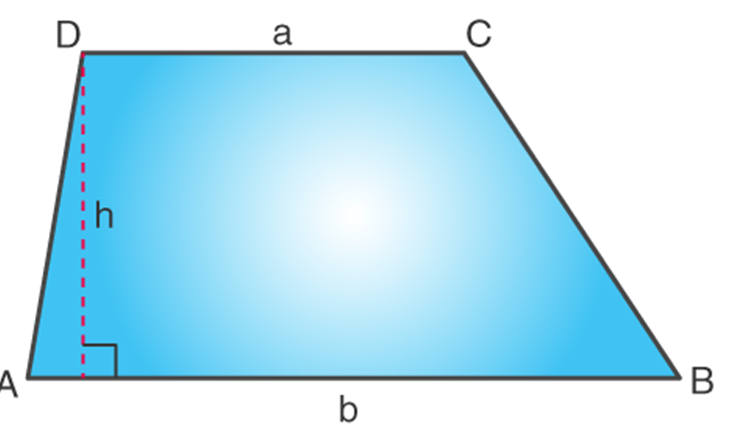
Parallelogram - It is a quadrilateral with two pairs of parallel sides. The opposite sides are parallel and equal in length. The opposite angles are equal in measure. In the parallelogram, ABCD, side AB is parallel to side CD and side AD is parallel to side BC.
Also, the two diagonals formed to intersect each other at the midpoints. As in the figure given below, E is the point where both the diagonals meet. So
Length AE = EC, & Length BE = ED
Rectangle - It is a quadrilateral with all the 4 angles of equal measure, that is, each of them is 90°. Both the pairs of opposite sides are parallel and equal in length.
Rhombus - It is a quadrilateral with all four sides having equal lengths. The Opposite sides of a rhombus are parallel and opposite angles are equal.
Square - It is a quadrilateral in which all the sides and angles are equal. Every angle is a right angle (i.e. 90° each). The pairs of opposite sides are parallel to each other.
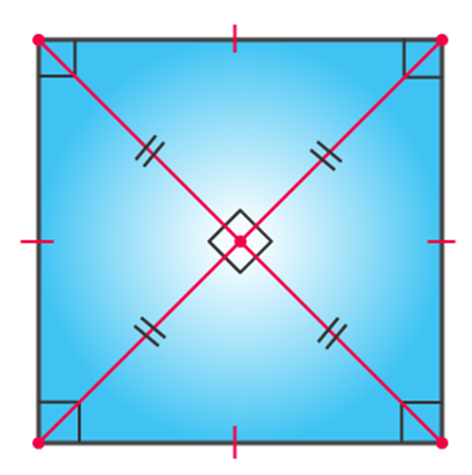
Kite - It is a quadrilateral that has 2 pairs of equal-length sides and these sides are adjacent to each other.
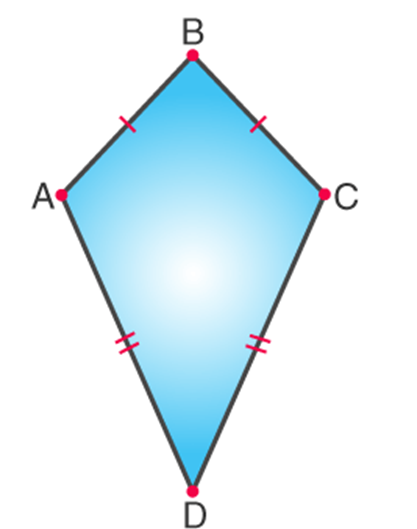
Some points about quadrilaterals to be kept in mind are:
- Square, rectangle, and rhombus are types of parallelograms.
- A square is a rectangle as well as a rhombus.
- Rectangle and rhombus are not a square.
- A parallelogram is a trapezium.
- A trapezium is not a parallelogram.
- Kite is not a parallelogram.
Types of Quadrilaterals
Types of Quadrilaterals
Before talking about the types of quadrilaterals, let us recall what a quadrilateral is. A quadrilateral is a polygon which has the following properties
- 4 vertices and 4 sides enclosing 4 angles.
- The sum of all interior angles of a quadrilateral is 360 degrees.
- We can also derive the sum of interior angle from the formula of polygon i.e. (n -2) × 180, where n is equal to the number of sides of the polygon
A quadrilateral, in general, has sides of different lengths and angles of different measures. However, squares, rectangles, etc. are special types of quadrilaterals with some of their sides and angles being equal. This is the reason that the area of quadrilateral depends on which type of quadrilateral it is. In this article, we will discuss the special types of quadrilaterals and their basic properties.
Different Types of Quadrilaterals
There are six basic types of quadrilaterals. They are:
- Trapezium
- Parallelogram
- Rectangle
- Rhombus
- Square
- Kite
Trapezium
It is a quadrilateral with one pair of opposite parallel sides. In the trapezium, ABCD, side AB is parallel to side CD.
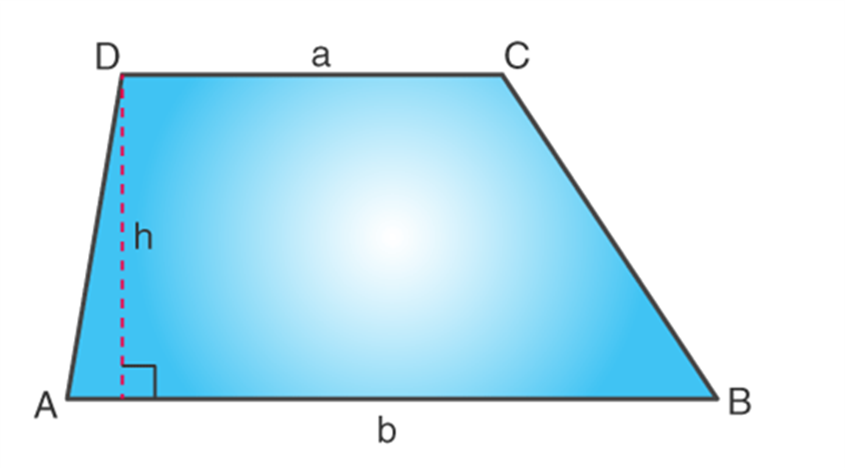
Parallelogram
It is a quadrilateral with two pairs of parallel sides. The opposite sides are parallel and equal in length. The opposite angles are equal in measure. In the parallelogram, ABCD, side AB is parallel to side CD and side AD is parallel to side BC.
Also, the two diagonals formed to intersect each other at the midpoints. As in the figure given below, E is the point where both the diagonals meet. So
Length AE = EC, & Length BE = ED
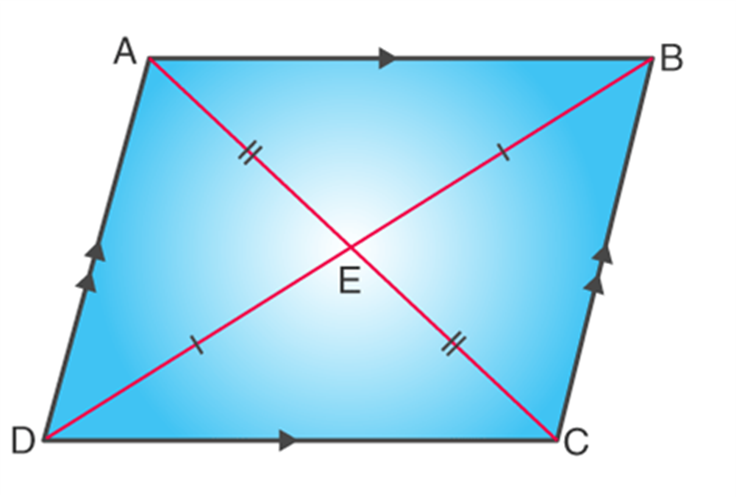
Rectangle
It is a quadrilateral with all the 4 angles of equal measure, that is, each of them is 90°. Both the pairs of opposite sides are parallel and equal in length.
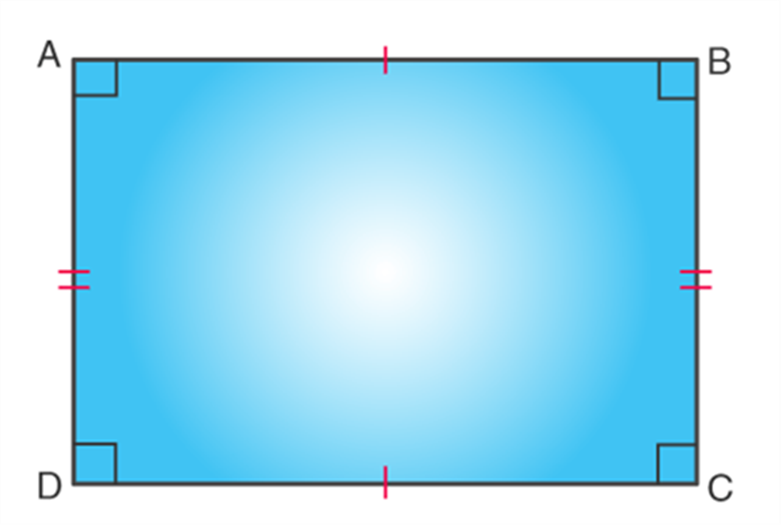
Rhombus
It is a quadrilateral with all the four sides having equal lengths. The Opposite sides of a rhombus are parallel and opposite angles are equal.
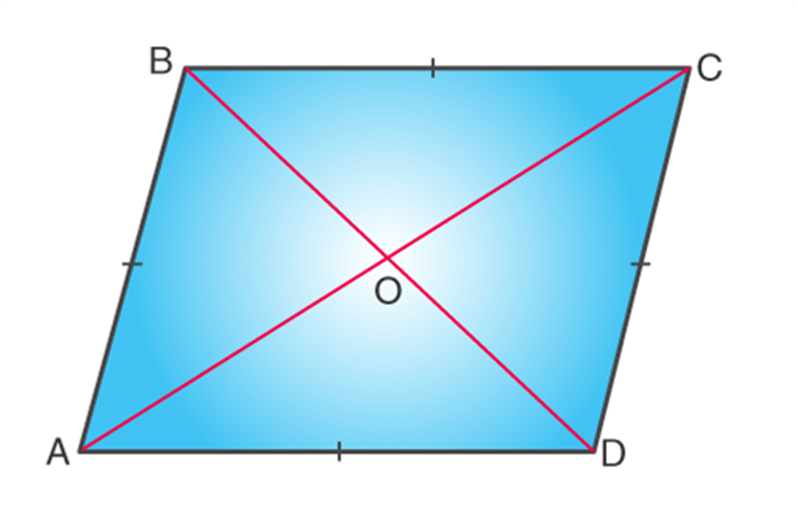
Square
It is a quadrilateral in which all the sides and angles are equal. Every angle is a right angle (i.e. 90° each). The pairs of opposite sides are parallel to each other.
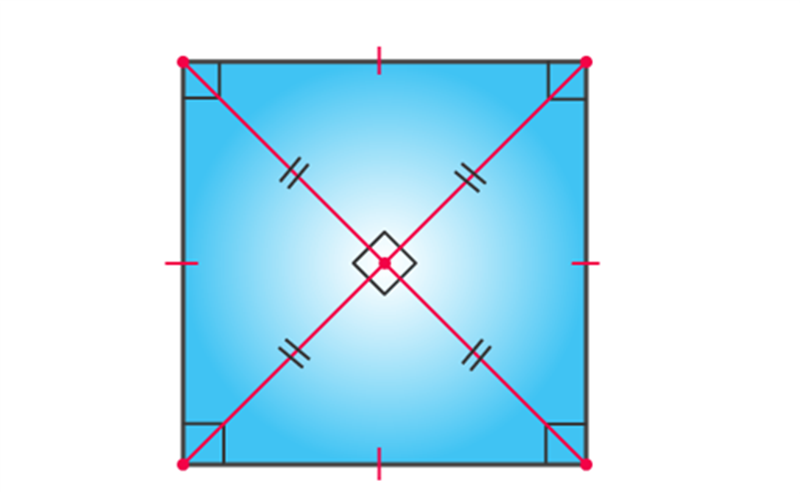
Kite
It is a quadrilateral that has 2 pairs of equal-length sides and these sides are adjacent to each other.
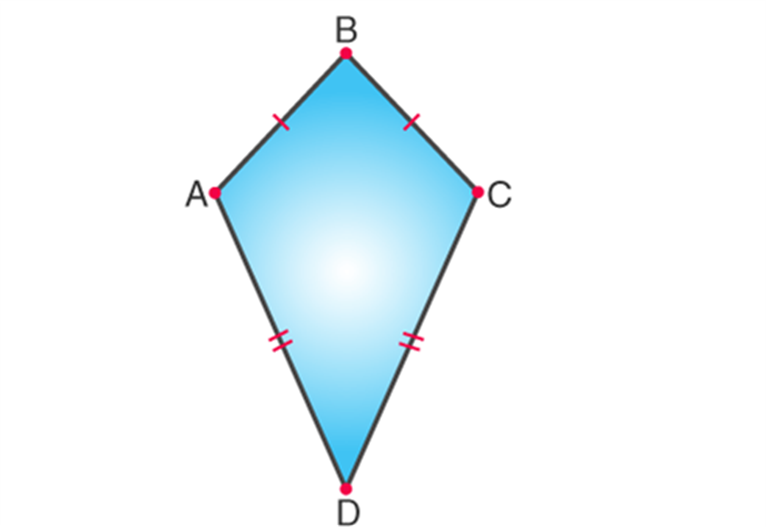
Some points about quadrilaterals to be kept in mind are:
- Square, rectangle, and rhombus are types of parallelograms.
- A square is a rectangle as well as a rhombus.
- Rectangle and rhombus are not a square.
- A parallelogram is a trapezium.
- A trapezium is not a parallelogram.
- Kite is not a parallelogram.
Properties of a Parallelogram
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Properties of a Parallelogram
A parallelogram is a two-dimensional geometrical shape, whose sides are parallel to each other. It is a type of polygon having four sides (also called quadrilateral), where the pair of parallel sides are equal in length. The Sum of adjacent angles of a parallelogram is equal to 180 degrees. In geometry, you must have learned about many 2D shapes and sizes such as circles, squares, rectangles, rhombus, etc. All of these shapes have a different set of properties. Also, the area and perimeter formulas of these shapes vary from each other and are used to solve many problems. Let us learn here the definition, formulas and properties of a parallelogram.
Parallelogram Definition
A parallelogram is a quadrilateral with two pairs of parallel sides. The opposite sides of a parallelogram are equal in length, and the opposite angles are equal in measure. Also, the interior angles on the same side of the transversal are supplementary. Sum of all the interior angles equals 360 degrees.
A three-dimensional shape that has its faces in a parallelogram shape, is called a parallelepiped. The area of the parallelogram depends on the base (one of its parallel sides) and the height (altitude drawn from top to bottom) of it. The perimeter of a parallelogram depends on the length of its four sides.
A square and a rectangle are two shapes that have similar properties to a parallelogram.
Rhombus: If all the sides of a parallelogram are congruent or equal to each other, then it is a rhombus.
If there is one parallel side and the other two sides are non-parallel, then it is a trapezium.
See the figure below:
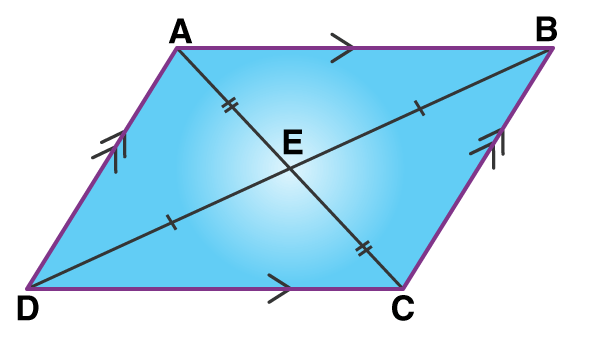
In the figure above, you can see, ABCD is a parallelogram, where AB || CD and AD || BC.
Also, AB = CD and AD = BC
And, ∠A = ∠C & ∠B = ∠D
Also, ∠A & ∠D are supplementary angles because these interior angles lie on the same side of the transversal. In the same way, ∠B & ∠C are supplementary angles.
Therefore,
∠A + ∠D = 180
∠B + ∠C = 180
|
Facts:
|
Shape of Parellelogram
A parallelogram is a two-dimensional shape. It has four sides, in which two pairs of sides are parallel. Also, the parallel sides are equal in length. If the length of the parallel sides is not equal in measurement, then the shape is not a parallelogram. Similarly, the opposite interior angles of parallelogram should always be equal. Otherwise, it is not a parallelogram.
Special Parallelograms
Square and Rectangle: A square and a rectangle are two shapes that have similar properties to a parallelogram. Both have their opposite sides equal and parallel to each other. Diagonals of both shapes bisect each other.
Rhombus: If all the sides of a parallelogram are congruent or equal to each other, then it is a rhombus.
Rhomboid: A special case of a parallelogram that has its opposite sides parallel to each other but adjacent sides are of unequal lengths. Also, the angles are equal to 90 degrees.
Trapezium: If there is one parallel side and the other two sides are non-parallel, then it is a trapezium.
Angles of Parallelogram
A parallelogram is a flat 2d shape that has four angles. The opposite interior angles are equal. The angles on the same side of the transversal are supplementary, which means they add up to 180 degrees. Hence, the sum of the interior angles of a parallelogram is 360 degrees.
Properties of Parallelogram
If a quadrilateral has a pair of parallel opposite sides, then it’s a special polygon called Parallelogram. The properties of a parallelogram are as follows:
- The opposite sides are parallel and congruent
- The opposite angles are congruent
- The consecutive angles are supplementary
- If any one of the angles is a right angle, then all the other angles will be at the right angle
- The two diagonals bisect each other
- Each diagonal bisects the parallelogram into two congruent triangles
- The Sum of squares of all the sides of a parallelogram is equal to the sum of squares of its diagonals. It is also called parallelogram law
Formulas (Area & Perimeter)
The formula for the area and perimeter of a parallelogram is covered here in this section. Students can use these formulas and solve problems based on them.
Area of Parallelogram
Area of a parallelogram is the region occupied by it in a two-dimensional plane. Below is the formula to find the parallelogram area:
Area = Base × Height
In the above figure, ||gramABCD, Area is given by;
|
Area = a b sin A = b a sin B |
where a is the slant length of the side of ||gramABCD and b is the base.
Check here: Area of a Parallelogram Formula
Perimeter of Parallelogram
The perimeter of any shape is the total distance covered around the shape or the total length of any shape. Similarly, the perimeter of a parallelogram is the total distance of the boundaries of the parallelogram. To calculate the perimeter value, we have to know the values of its length and breadth. The parallelogram has its opposite sides equal in length. Therefore, the formula to calculate the perimeter is written as;
|
Perimeter = 2 (a+b) units |
Where a and b are the length of the sides of the parallelogram.
Types of Parallelogram
There are mainly four types of Parallelogram, depending on various factors. The factors which distinguish between all of these different types of parallelograms are angles, sides etc.
- In a parallelogram, say PQRS
- If PQ = QR = RS = SP are the equal sides, then it’s a rhombus. All the properties are the same for rhombus as for parallelogram.
- Other two special types of a parallelogram are:
- Rectangle
- Square
Is Square a Parallelogram?
Square could be considered as a parallelogram since the opposite sides are parallel to each other, and the diagonals of the square bisect each other.
Is Rectangle a Parallelogram?
Yes, a rectangle is also a parallelogram, because it satisfies the conditions or meets the properties of a parallelogram such as the opposite sides are parallel and diagonals bisect each other.
Parallelogram Theorems
Theorem 1: Parallelograms on the same base and between the same parallel sides are equal in area.
Proof: Two parallelograms ABCD and ABEF, on the same base DC and between the same parallel line AB and FC.
To prove that area (ABCD) = area (ABEF).
Proof:
Consider the figure given below:
Parallelogram ABCD and rectangle ABML are on the same base and between the same parallels AB and LC.
area of parallelogram ABCD = area of parallelogram ABML
We know that area of a rectangle = length x breadth.
Therefore, area of parallelogram ABCD = AB x AL
Hence, the area of a parallelogram is the product of any base of it and the corresponding altitude.
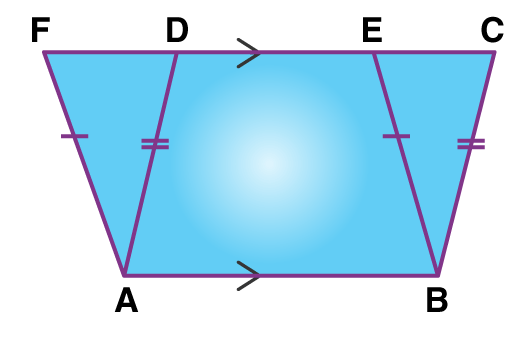
In ∆ADF and ∆BCE,
AD=BC (∴ABCD is a parallelogram ∴ AD=BC)
AF=BE (∴ABEF is a parallelogram ∴AF=BE)
∠ADF=∠BCE (Corresponding Angles)
∠AFD=∠BEC (Corresponding Angles)
∠DAF =∠CBE (Angle Sum Property)
∆ADE ≅ ∆BCF (From SAS-rule)
Area(ADF) = Area(BCE) (By congruence area axiom)
Area(ABCD)=Area(ABED) + Area(BCE)
Area(ABCD)=Area(ABED)+Area(ADF)
Area(ABCD)=Area(ABEF)
Hence, the area of parallelograms on the same base and between the same parallel sides is equal.
Corollary
A parallelogram and a rectangle on the same base and between the same parallels are equal in area.
Proof: Since a rectangle is also a parallelogram so, the result is a direct consequence of the above theorem.
Theorem: The area of a parallelogram is the product of its base and the corresponding altitude.
Given: In a parallelogram ABCD, AB is the base.
To prove that Area(||gmABCD) = AB×AL
Construction: Complete the rectangle ALMB by Drawing BM perpendicular to CD.
Difference Between Parallelogram and Rhombus
|
Parallelogram |
Rhombus |
|
A quadrilateral that has its opposite sides equal and parallel |
A quadrilateral that has all its sides congruent |
|
Diagonals bisect each other |
Diagonals bisect each other at 90 degrees |
|
Opposite angles are of equal measure |
All four angles are of equal measure |
Examples on Parallelogram
|
Example 1: Find the area of a parallelogram whose base is 5 cm and height is 8 cm. Solution-: Given, Base = 5 cm and Height = 8 cm. We know, Area = Base x Height Area = 5 × 8 Area = 40 Sq.cm Example 2: Find the area of a parallelogram having a length of diagonals to be 10 and 22 cm and an intersecting angle to be 65 degrees. Solution: We know that the diagonals of a parallelogram bisect each other. Hence, the length of half the diagonal will be 5 and 11 cm.
The angle opposite to the side b comes out to be 180 – 65 = 115° We use the law of cosines to calculate the base of the parallelogram – b² = 5² + 11² – 2(11)(5)cos(115°) b² = 25 + 121 – 110(-0.422) b² = 192.48 b = 13.87 cm.
After finding the base, we need to calculate the height of the given parallelogram. To find the height we have to calculate the value of θ, so we use sine law 5/sin(θ) = b/sin(115)
Now we extend the base and draw in the height of the figure and denote it as ‘h’. The right-angled triangle (marked with a red line) has the Hypotenuse to be 22 cm and the Perpendicular to be h. So sin θ = h/22 h = 7.184 cm Area = base × height A = 13.87 × 7.184 A = 99.645 sq.cm |
Properties of a Parallelogram
Properties of a Parallelogram
A parallelogram is a two-dimensional geometrical shape, whose sides are parallel to each other. It is a type of polygon having four sides (also called quadrilateral), where the pair of parallel sides are equal in length. The Sum of adjacent angles of a parallelogram is equal to 180 degrees. In geometry, you must have learned about many 2D shapes and sizes such as circle, square, rectangle, rhombus, etc. All of these shapes have a different set of properties. Also, the area and perimeter formulas of these shapes vary from each other and are used to solve many problems. Let us learn here the definition, formulas and properties of a parallelogram.
Parallelogram Definition
A parallelogram is a quadrilateral with two pairs of parallel sides. The opposite sides of a parallelogram are equal in length, and the opposite angles are equal in measure. Also, the interior angles on the same side of the transversal are supplementary. Sum of all the interior angles equals 360 degrees.
A three-dimensional shape that has its faces in parallelogram shape, is called a parallelepiped. The area of parallelogram depends on the base (one of its parallel sides) and height (altitude drawn from top to bottom) of it. The perimeter of a parallelogram depends on the length of its four sides.
A square and a rectangle are two shapes which have similar properties of a parallelogram.
Rhombus: If all the sides of a parallelogram are congruent or equal to each other, then it is a rhombus.
If there is one parallel side and the other two sides are non-parallel, then it is a trapezium.
See the figure below:
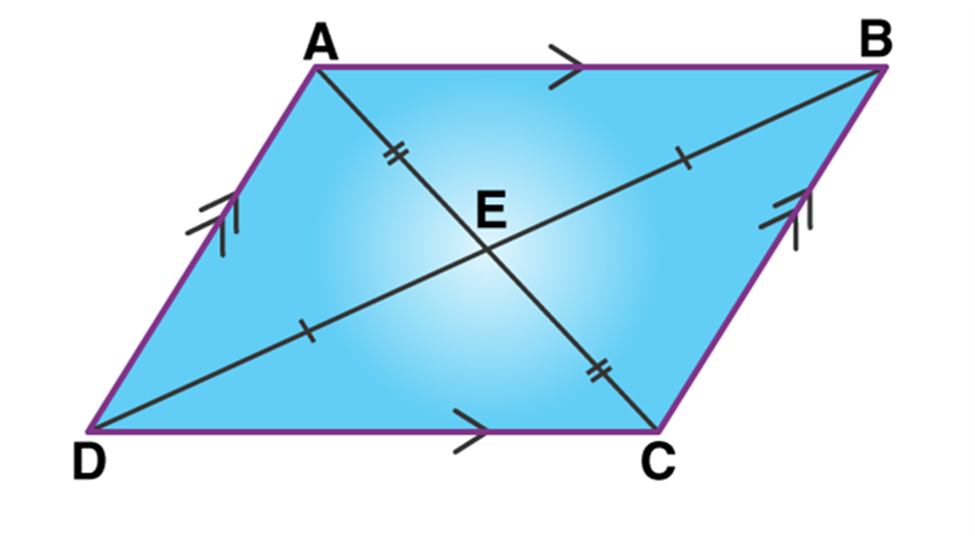
In the figure above, you can see, ABCD is a parallelogram, where AB || CD and AD || BC.
Also, AB = CD and AD = BC
And, ∠A = ∠C & ∠B = ∠D
Also, ∠A & ∠D are supplementary angles because these interior angles lie on the same side of the transversal. In the same way, ∠B & ∠C are supplementary angles.
Therefore,
∠A + ∠D = 180
∠B + ∠C = 180
Facts:
- Number of sides = 4
- Number of vertices = 4
- Mutually Parallel sides = 2 (in pair)
- Area = Base x Height
- Perimeter = 2 (Sum of adjacent sides length)
- Type of polygon = Quadrilateral
Shape of Parellelogram
A parallelogram is a two-dimensional shape. It has four sides, in which two pairs of sides are parallel. Also, the parallel sides are equal in length. If the length of the parallel sides is not equal in measurement, then the shape is not a parallelogram. Similarly, the opposite interior angles of parallelogram should always be equal. Otherwise, it is not a parallelogram.
Special Parallelograms
Square and Rectangle: A square and a rectangle are two shapes which have similar properties of a parallelogram. Both have their opposite sides equal and parallel to each other. Diagonals of both shapes bisect each other.
Rhombus: If all the sides of a parallelogram are congruent or equal to each other, then it is a rhombus.
Rhomboid: A special case of a parallelogram that has its opposite sides parallel to each other but adjacent sides are of unequal lengths. Also, the angles are equal to 90 degrees.
Trapezium: If there is one parallel side and the other two sides are non-parallel, then it is a trapezium.
Angles of Parallelogram
A parallelogram is a flat 2d shape which has four angles. The opposite interior angles are equal. The angles on the same side of the transversal are supplementary, that means they add up to 180 degrees. Hence, the sum of the interior angles of a parallelogram is 360 degrees.
Properties of Parallelogram
If a quadrilateral has a pair of parallel opposite sides, then it’s a special polygon called Parallelogram. The properties of a parallelogram are as follows:
- The opposite sides are parallel and congruent
- The opposite angles are congruent
- The consecutive angles are supplementary
- If any one of the angles is a right angle, then all the other angles will be at right angle
- The two diagonals bisect each other
- Each diagonal bisects the parallelogram into two congruent triangles
- The Sum of square of all the sides of parallelogram is equal to the sum of square of its diagonals. It is also called parallelogram law
Formulas (Area & Perimeter)
The formula for the area and perimeter of a parallelogram is covered here in this section. Students can use these formulas and solve problems based on them.
Area of Parallelogram
Area of a parallelogram is the region occupied by it in a two-dimensional plane. Below is the formula to find the parallelogram area:
Area = Base × Height
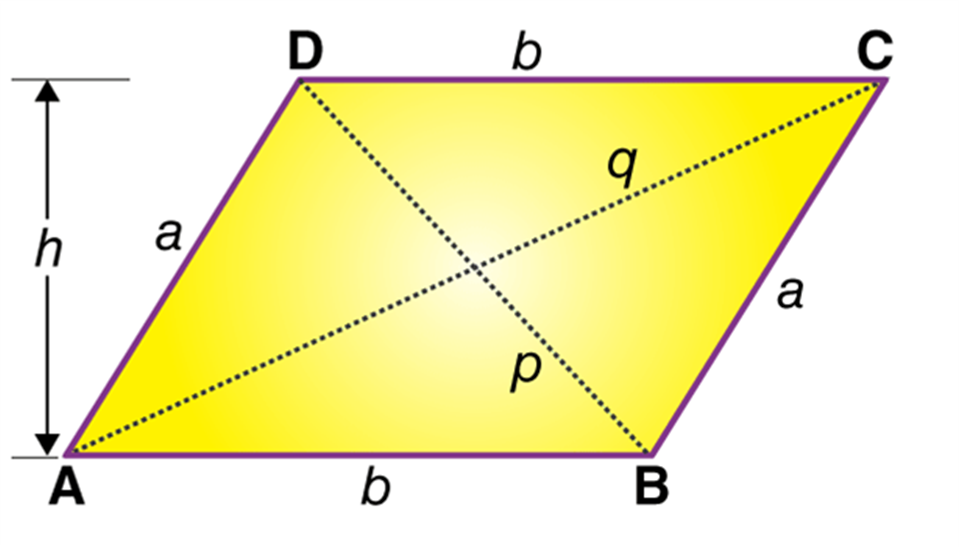
In the above figure, ||gramABCD, Area is given by;
Area = a b sin A = b a sin B
where a is the slant length of the side of ||gramABCD and b is the base.
Check here: Area of a Parallelogram Formula
Perimeter of Parallelogram
The perimeter of any shape is the total distance covered around the shape or the total length of any shape. Similarly, the perimeter of a parallelogram is the total distance of the boundaries of the parallelogram. To calculate the perimeter value, we have to know the values of its length and breadth. The parallelogram has its opposite sides equal in length. Therefore, the formula to calculate the perimeter is written as;
Perimeter = 2 (a+b) units
Where a and b are the length of the sides of the parallelogram.
Types of Parallelogram
There are mainly four types of Parallelogram, depending on various factors. The factors which distinguish between all of these different types of parallelogram are angles, sides etc.
- In a parallelogram, say PQRS
- If PQ = QR = RS = SP are the equal sides, then it’s a rhombus. All the properties are the same for rhombus as for parallelogram.
- Other two special types of a parallelogram are:
- Rectangle
- Square
Is Square a Parallelogram?
Square could be considered as a parallelogram since the opposite sides are parallel to each other, and the diagonals of the square bisect each other.
Is Rectangle a Parallelogram?
Yes, a rectangle is also a parallelogram, because it satisfies the conditions or meets the properties of parallelogram such as the opposite sides are parallel and diagonals bisect each other.
Parallelogram Theorems
Theorem 1: Parallelograms on the same base and between the same parallel sides are equal in area.
Proof: Two parallelograms ABCD and ABEF, on the same base DC and between the same parallel line AB and FC.
To prove that area (ABCD) = area (ABEF).
Proof:
Consider the figure given below:
Parallelogram ABCD and rectangle ABML are on the same base and between the same parallels AB and LC.
area of parallelogram ABCD = area of parallelogram ABML
We know that area of a rectangle = length x breadth.
Therefore, area of parallelogram ABCD = AB x AL
Hence, the area of a parallelogram is the product of any base of it and the corresponding altitude.
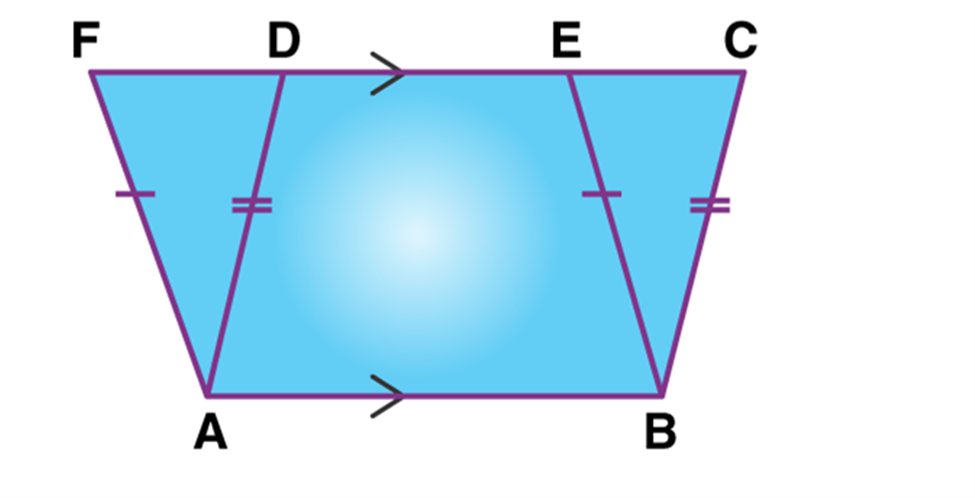
In ∆ADF and ∆BCE,
AD=BC (∴ABCD is a parallelogram ∴ AD=BC)
AF=BE (∴ABEF is a parallelogram ∴AF=BE)
∠ADF=∠BCE (Corresponding Angles)
∠AFD=∠BEC (Corresponding Angles)
∠DAF =∠CBE (Angle Sum Property)
∆ADE ≅ ∆BCF (From SAS-rule)
Area(ADF) = Area(BCE) (By congruence area axiom)
Area(ABCD)=Area(ABED) + Area(BCE)
Area(ABCD)=Area(ABED)+Area(ADF)
Area(ABCD)=Area(ABEF)
Hence, the area of parallelograms on the same base and between the same parallel sides is equal.
Corollary
A parallelogram and a rectangle on the same base and between the same parallels are equal in area.
Proof: Since a rectangle is also a parallelogram so, the result is a direct consequence of the above theorem.
Theorem: The area of a parallelogram is the product of its base and the corresponding altitude.
Given: In a parallelogram ABCD, AB is the base.
To prove that Area(||gmABCD) = AB×AL
Construction: Complete the rectangle ALMB by Drawing BM perpendicular to CD.
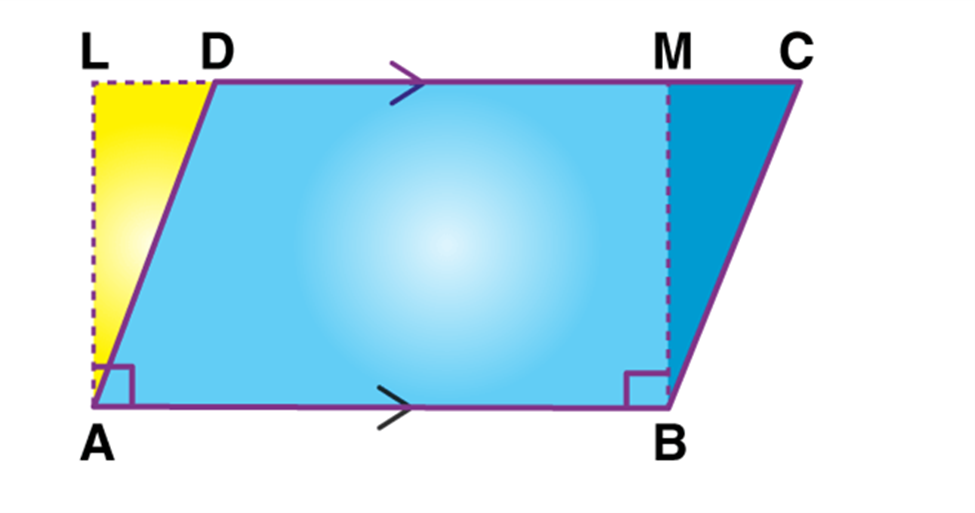
Difference Between Parallelogram and Rhombus
Examples on Parallelogram
Example 1:
Find the area of a parallelogram whose base is 5 cm and height is 8 cm.
Solution-:
Given, Base = 5 cm and Height = 8 cm.
We know, Area = Base x Height
Area = 5 × 8
Area = 40 Sq.cm
Example 2:
Find the area of a parallelogram having a length of diagonals to be 10 and 22 cm and an intersecting angle to be 65 degrees.
Solution:
We know that the diagonals of a parallelogram bisect each other. Hence, the length of half the diagonal will be 5 and 11 cm.
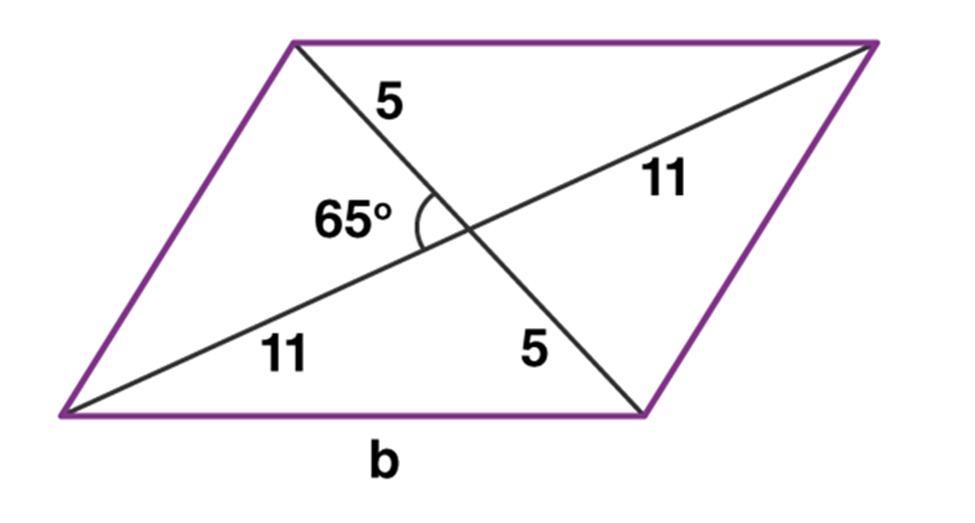
The angle opposite to the side b comes out to be 180 – 65 = 115°
We use the law of cosines to calculate the base of the parallelogram –
b² = 5² + 11² – 2(11)(5)cos(115°)
b² = 25 + 121 – 110(-0.422)
b² = 192.48
b = 13.87 cm.
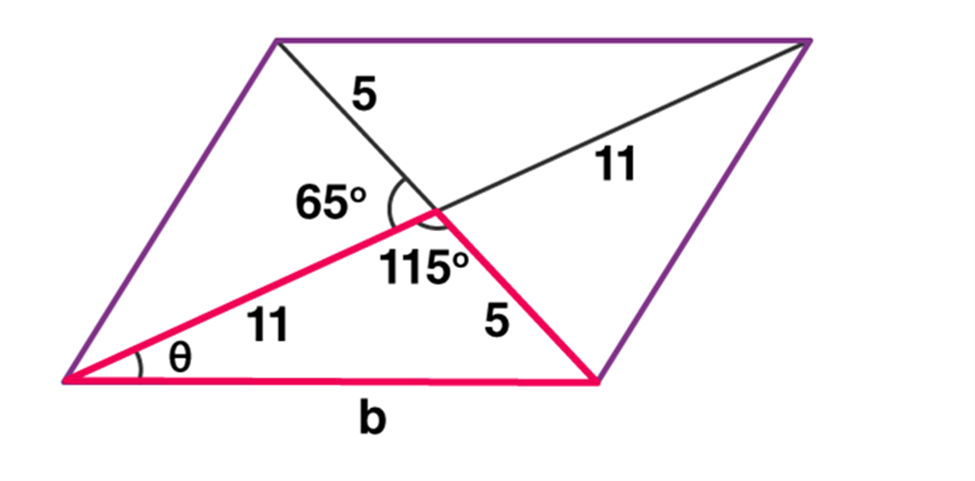
After finding the base, we need to calculate the height of the given parallelogram.
To find the height we have to calculate the value of θ, so we use sine law
5/sin(θ) = b/sin(115)
θ = 19.06
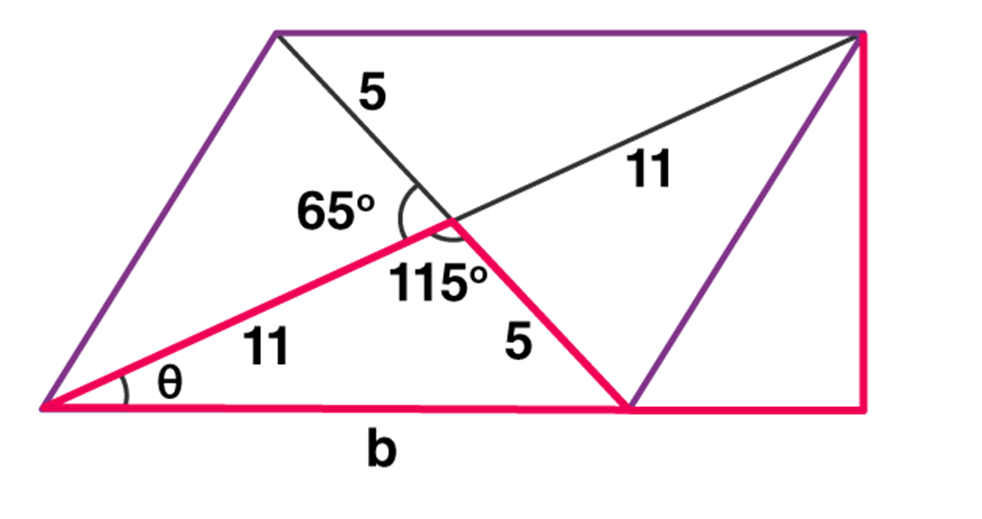
Now we extend the base and draw in the height of the figure and denote it as ‘h’.
The right-angled triangle (marked with a red line) has the Hypotenuse to be 22 cm and the Perpendicular to be h.
So
sin θ = h/22
h = 7.184 cm
Area = base × height
A = 13.87 × 7.184
A = 99.645 sq.cm
Another condition for a quadrilateral to be a parallelogram
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Another condition for a quadrilateral to be a parallelogram
Another Condition for a Quadrilateral to be a Parallelogram
Theorem 9: A quadrilateral is a parallelogram if a pair of the opposite side is equal and parallel.
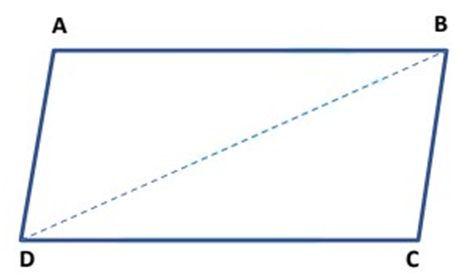
Given: A quadrilateral ABCD in which AB = CD and, AB ∥ CD.
To prove: Quadrilateral ABCD is a parallelogram.
Construction: Join BD.
Proof: Now, in ∆ BAD and ∆ DCB, we have
AB = CD (Given)
Since AB ∥ CD and transversal BD intersects at B and D, so alternate interior angles are equal.
⟹ ∠ CDB = ∠ ABD
BD = DB (Common)
Therefore, ∆ BAD ≅ ∆ DCB (By SAS criterion of congruence)
By using corresponding parts of congruent triangles
⟹ ∠ ADB = ∠ CBD
Now, line BD intersects AB and DC at B and D respectively, such that ∠ ADB = ∠ CBD
That is, alternate interior angles are equal.
∴ AD ∥ BC.
Thus, AB ∥ CD and AD ∥ BC.
Hence, quadrilateral ABCD is a parallelogram.
Example: In the figure, ABCD is a parallelogram and X, Y are the mid- points of sides AB and DC respectively. Show that quadrilateral DXBY is a parallelogram.
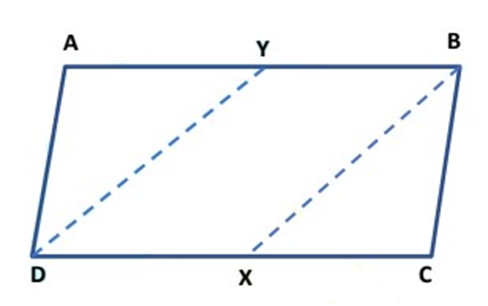
Given: ABCD is a parallelogram in which X and Y are the mid-points of AB and DC respectively.
To prove: Quadrilateral DXBY is a parallelogram.
Construction: Join DX and BX.
Proof: Since X and Y are the mid-points of DC and AB respectively.
∴ YB =
But, AB = DC [∵ ABCD is a parallelogram]
⟹ ![]() AB =
AB = ![]() DC
DC
⟹ YB = DX. [From(I)] ............. (II)
Also, AB ∥ DC [∵ ABCD is a parallelogram]
Another condition for a quadrilateral to be a parallelogram
Another Condition for a Quadrilateral to be a Parallelogram
Another Condition for a Quadrilateral to be a Parallelogram
Theorem 9: A quadrilateral is a parallelogram if a pair of the opposite side is equal and parallel.
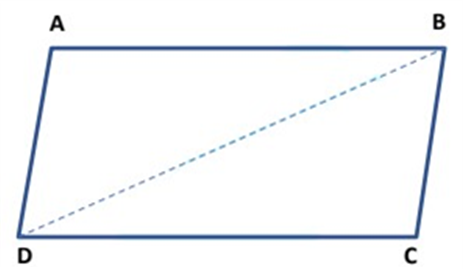
Given: A quadrilateral ABCD in which AB = CD and, AB ∥ CD.
To prove: Quadrilateral ABCD is a parallelogram.
Construction: Join BD.
Proof: Now, in ∆ BAD and ∆ DCB, we have
AB = CD (Given)
Since AB ∥ CD and transversal BD intersects at B and D, so alternate interior angles are equal.
⟹ ∠ CDB = ∠ ABD
BD = DB (Common)
Therefore, ∆ BAD ≅ ∆ DCB (By SAS-criterion of congruence)
By using corresponding parts of congruent triangles
⟹ ∠ ADB = ∠ CBD
Now, line BD intersects AB and DC at B and D respectively, such that ∠ ADB = ∠ CBD
That is, alternate interior angles are equal.
∴ AD ∥ BC.
Thus, AB ∥ CD and AD ∥ BC.
Hence, quadrilateral ABCD is a parallelogram.
Example: In the figure, ABCD is a parallelogram and X, Y are the mid- points of sides AB and DC respectively. Show that quadrilateral DXBY is a parallelogram.
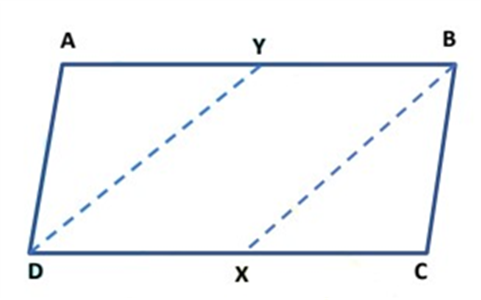
Given: ABCD is a parallelogram in which X and Y are the mid-points of AB and DC respectively.
To prove: Quadrilateral DXBY is a parallelogram.
Construction: Join DX and BX.
Proof: Since X and Y are the mid-points of DC and AB respectively.
∴ YB =
But, AB = DC [∵ ABCD is a parallelogram]
⟹  AB =
AB =  DC
DC
⟹ YB = DX. [From(I)] ............. (II)
Also, AB ∥ DC [∵ ABCD is a parallelogram]
∴ YB ∥ DX ............. (III)
Since a quadrilateral is a parallelogram if a pair of the opposite side is equal and parallel.
From (II) & (III), we get Quadrilateral DXBY is a parallelogram.
The Mid-Point Theorem
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
The Mid-Point Theorem
geometry is one of the significant and essential branches of mathematics. This field deals with the geometrical problems and figures which are based on their properties. One of the important theorems in the field of geometry that deals with the properties of triangles are called the Mid-Point Theorem.
The theory of the midpoint theorem is used in coordinate geometry stating that the midpoint of the line segment is an average of the endpoints. Both the ‘x’ and the ‘y’ coordinates must be known for solving an equation using this theorem. The Mid-Point Theorem is also useful in the fields of calculus and algebra.
MidPoint Theorem Statement
The midpoint theorem states that “The line segment in a triangle joining the midpoint of two sides of the triangle is said to be parallel to its third side and is also half of the length of the third side.”
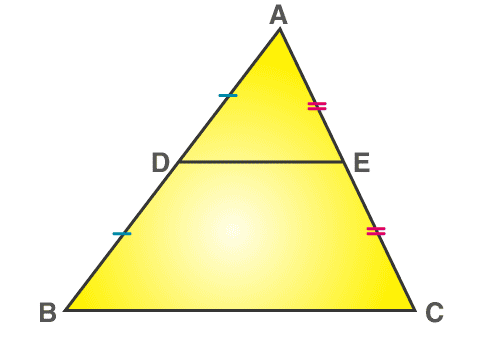
MidPoint Theorem Proof
If the line segment adjoins the midpoints of any of the sides of a triangle, then the line segment is said to be parallel to all the remaining sides, and it measures about half of the remaining sides.
Consider the triangle ABC, as shown in the above figure,
Let E and D be the midpoints of the sides AC and AB. Then the line DE is said to be parallel to the side BC, whereas the side DE is half of the side BC; i.e.
DE = (1/2 * BC).
Now consider the below figure,
Construction- Extend the line segment DE and produce it to F such that, EF = DE.
In triangle ADE and CFE,
EC = AE —– (given)
∠CEF = ∠AED (vertically opposite angles)
∠DAE = ∠ECF (alternate angles)
By ASA congruence criterion,
△ CFE ≅ △ ADE
Therefore,
∠CFE = ∠ADE {by c.p.c.t.}
∠FCE= ∠DAE {by c.p.c.t.}
and CF = AD {by c.p.c.t.}
∠CFE and ∠ADE are the alternate interior angles.
Assume CF and AB as two lines that are intersected by the transversal DF.
In a similar way, ∠FCE and ∠DAE are the alternate interior angles.
Assume CF and AB are the two lines that are intersected by the transversal AC.
Therefore, CF ∥ AB
So, CF ∥ BD
and CF = BD {since BD = AD, it is proved that CF = AD}
Thus, BDFC forms a parallelogram.
By the properties of a parallelogram, we can write
BC ∥ DF
and BC = DF
BC ∥ DE
and DE = (1/2 * BC).
Hence, the midpoint theorem is proved.
MidPoint Theorem Formula
In Coordinate Geometry, the midpoint theorem refers to the midpoint of the line segment. It defines the coordinate points of the midpoint of the line segment and can be found by taking the average of the coordinates of the given endpoints. The midpoint formula is used to determine the midpoint between the two given points.
If P1(x1, y1) and P2(x2, y2) are the coordinates of two given endpoints, then the midpoint formula is given as:
Midpoint = [(x1 + x2)/2, (y1 + y2)/2]
The converse of the MidPoint Theorem
The converse of the midpoint theorem states that ” if a line is drawn through the midpoint of one side of a triangle, and parallel to the other side, it bisects the third side”.
Midpoint Theorem Example
The example is given below to understand the midpoint theorem.
Example:
In triangle ABC, the midpoints of BC, CA, AB are D, E, and F, respectively. Find the value of EF, if the value of BC = 14 cm
Solution:
Given: BC = 14 cm
If F is the midpoint of AB and E is the midpoint of AC, then using the midpoint theorem:
EF = 1/2 (BC)
Substituting the value of BC,
EF = (1/2) × 14
EF = 7 cm
Therefore, the value of EF = 7cm.
80,202
The Mid-Point Theorem can also be proved using triangles. Suppose two lines are drawn parallel to the x and the y-axis which begin at endpoints and are connected through the midpoint, then the segment passes through the angle between them resulting in two similar triangles. This relation of these triangles forms the Mid-Point Theorem.
The Mid-Point Theorem
The Mid-Point Theorem
geometry is one among the significant and essential branches of mathematics. This field deals with the geometrical problems and figures which are based on their properties. One of the important theorems in the field of geometry that deals with the properties of triangles are called the Mid- Point Theorem.
The theory of midpoint theorem is used in coordinate geometry stating that the midpoint of the line segment is an average of the endpoints. Both the ‘x’ and the ‘y’ coordinates must be known for solving an equation using this theorem. The Mid- Point Theorem is also useful in the fields of calculus and algebra.
The midpoint theorem states that “The line segment in a triangle joining the midpoint of two sides of the triangle is said to be parallel to its third side and is also half of the length of the third side.”
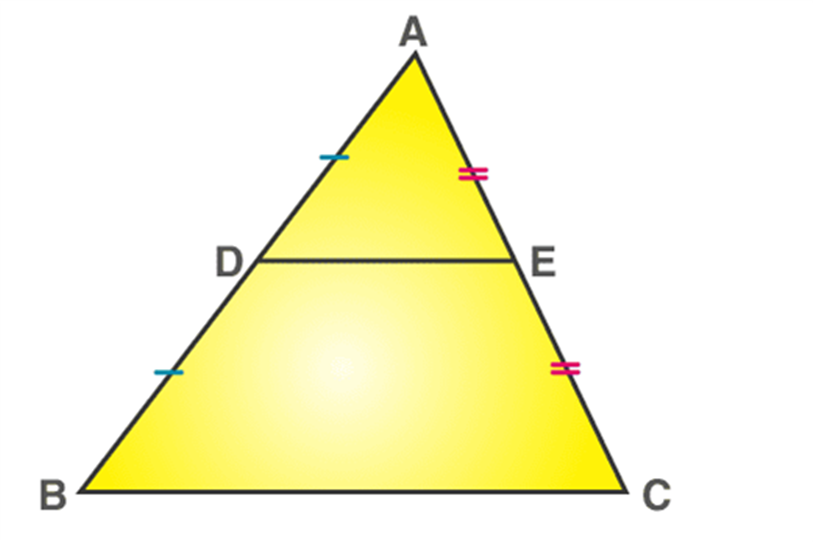
If the line segment adjoins midpoints of any of the sides of a triangle, then the line segment is said to be parallel to all the remaining sides, and it measures about half of the remaining sides.
Consider the triangle ABC, as shown in the above figure,
Let E and D be the midpoints of the sides AC and AB. Then the line DE is said to be parallel to the side BC, whereas the side DE is half of the side BC; i.e.
DE = (1/2 * BC).
Now consider the below figure,
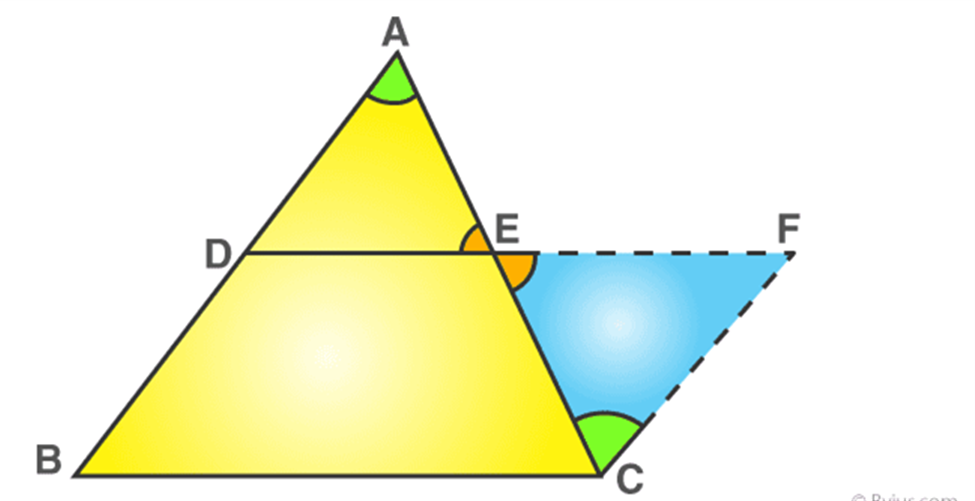
Construction- Extend the line segment DE and produce it to F such that, EF = DE.
In triangle ADE and CFE,
EC = AE —– (given)
∠CEF = ∠AED (vertically opposite angles)
∠DAE = ∠ECF (alternate angles)
By ASA congruence criterion,
△ CFE ≅ △ ADE
Therefore,
∠CFE = ∠ADE {by c.p.c.t.}
∠FCE= ∠DAE {by c.p.c.t.}
and CF = AD {by c.p.c.t.}
∠CFE and ∠ADE are the alternate interior angles.
Assume CF and AB as two lines which are intersected by the transversal DF.
In a similar way, ∠FCE and ∠DAE are the alternate interior angles.
Assume CF and AB are the two lines which are intersected by the transversal AC.
Therefore, CF ∥ AB
So, CF ∥ BD
and CF = BD {since BD = AD, it is proved that CF = AD}
Thus, BDFC forms a parallelogram.
By the properties of a parallelogram, we can write
BC ∥ DF
and BC = DF
BC ∥ DE
and DE = (1/2 * BC).
Hence, the midpoint theorem is proved.
MidPoint Theorem Formula
In Coordinate Geometry, the midpoint theorem refers to the midpoint of the line segment. It defines the coordinate points of the midpoint of the line segment and can be found by taking the average of the coordinates of the given endpoints. The midpoint formula is used to determine the midpoint between the two given points.
If P1(x1, y1) and P2(x2, y2) are the coordinates of two given endpoints, then the midpoint formula is given as:
Midpoint = [(x1 + x2)/2, (y1 + y2)/2]
The converse of MidPoint Theorem
The converse of the midpoint theorem states that ” if a line is drawn through the midpoint of one side of a triangle, and parallel to the other side, it bisects the third side”.
Midpoint Theorem Example
The example is given below to understand the midpoint theorem.
Example:
In triangle ABC, the midpoints of BC, CA, AB are D, E, and F, respectively. Find the value of EF, if the value of BC = 14 cm
Solution:
Given: BC = 14 cm
If F is the midpoint of AB and E is the midpoint of AC, then using the midpoint theorem:
EF = 1/2 (BC)
Substituting the value of BC,
EF = (1/2) × 14
EF = 7 cm
Therefore, the value of EF = 7cm.
80,202
The Mid- Point Theorem can also be proved using triangles. Suppose two lines are drawn parallel to the x and the y-axis which begin at endpoints and connected through the midpoint, then the segment passes through the angle between them resulting in two similar triangles. This relation of these triangles forms the Mid- Point Theorem.
Parallelograms on the same base and between the same parallels
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Parallelograms on the same base and between the same parallels
Parallelograms on the same base and between the same parallels are explained here in this article with the help of the theorem.
Theorem: - A parallelogram on the same base and between the same parallels are equal in area.
Proof:
Consider two parallelograms ABCD and EFCD on the same base DC and the same parallels AF and DC, as shown in the figure.
To prove: ar (ABCD) = ar (EFCD)
It means that we need to prove the area of parallelogram ABCD is equal to the area of a parallelogram EFCD.
Consider the triangles ADE and BCF,
∠ DAE = ∠ CBF [Corresponding angles from AD || BC and transversal AF] …(1)
∠ AED = ∠ BFC [Corresponding angles from ED || FC and transversal AF] …(2)
By using the angle sum property of a triangle, we can write:
∠ ADE = ∠ BCF ….(3)
Also, from the opposite sides of a parallelogram ABCD, we can write:
AD = BC ….(4)
Using the equations (1), (3), and (4) and by Angle-Side-Angle (ASA) rule,
∆ ADE ≅ ∆ BCF
Therefore, the area of triangle ADE is equal to the area of a triangle BCF. (As congruent figures have equal area)
(i.e) ar (ADE) = ar (BCF) …(5)
Thus, the ar (ABCD) = ar (ADE) + ar (EDCB)
ar (ABCD) = ar (BCF) + ar (EDCB) (using equation (5))
ar (ABCD) = ar (EFCD)
Thus, the area of parallelogram ABCD is equal to the area of parallelogram EFCD.
Hence, a parallelogram on the same base and between the same parallels are equal in area, is proved.
Example - Now, let us solve the below problem with the help of the theorem.
Question: Consider a parallelogram ABCD and EFCD is a rectangle. Also, AL is perpendicular to DC.
Prove that:
- ar (ABCD) = ar (EFCD)
- ar (ABCD) = DC × AL
Solution:
Given that ABCD is a parallelogram, and EFCD is a rectangle.
To prove : ar (ABCD) = ar (EFCD)
A rectangle is also a parallelogram, and by using the theorem “parallelogram on the same base and between the same parallels are equal in the area”, we can write
ar (ABCD) = ar (EFCD)
Hence proved.
To prove: ar (ABCD) = DC × AL
By using ar (ABCD) = ar (EFCD)
ar (ABCD) = DC × FC (As, the area of a rectangle = Length × Breadth) …(1)
Also given that AL ⊥ DC, we can say AFCL is also a rectangle.
Therefore, AL = FC …(2)
From (1) and (2), we can get ar (ABCD) = DC × AL
Hence, proved.
Practice Problems
Solve the following problems:
- The points P and Q lie on the sides DC and AD respectively of a parallelogram ABCD. Prove that ar (APB) = ar (BQC)
- In the figure given below, PQRS and ABRS are parallelograms. “X” is the point on the side BR.
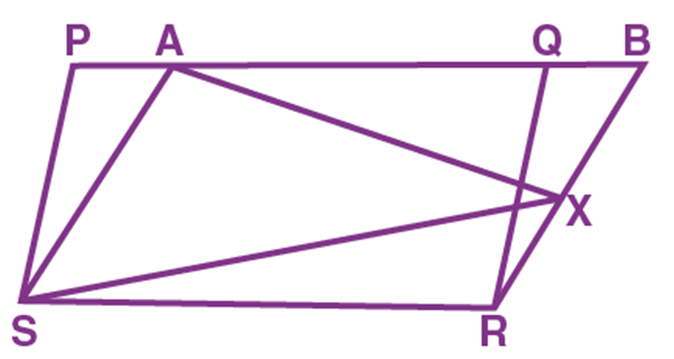
Prove that:
(1) ar (PQRS) = ar (ABRS)
(2) ar (AX S) = ½ ar (PQRS)
Parallelograms on the same base and between the same parallels
Parallelograms on the same base and between the same parallels
Parallelograms on the same base and between the same parallels are explained here in this article with the help of the theorem.
Theorem:
A parallelogram on the same base and between the same parallels are equal in area.
Proof:

Consider two parallelograms ABCD and EFCD on the same base DC and the same parallels AF and DC, as shown in the figure.
To prove: ar (ABCD) = ar (EFCD)
It means that we need to prove the area of parallelogram ABCD is equal to the area of a parallelogram EFCD.
Consider the triangles ADE and BCF,
∠ DAE = ∠ CBF [Corresponding angles from AD || BC and transversal AF] …(1)
∠ AED = ∠ BFC [Corresponding angles from ED || FC and transversal AF] …(2)
By using the angle sum property of a triangle, we can write:
∠ ADE = ∠ BCF ….(3)
Also, from the opposite sides of a parallelogram ABCD, we can write:
AD = BC ….(4)
Using the equations (1), (3), and (4) and by Angle-Side-Angle (ASA) rule,
∆ ADE ≅ ∆ BCF
Therefore, the area of triangle ADE is equal to the area of a triangle BCF. (As congruent figures have equal area)
(i.e) ar (ADE) = ar (BCF) …(5)
Thus, the ar (ABCD) = ar (ADE) + ar (EDCB)
ar (ABCD) = ar (BCF) + ar (EDCB) (using equation (5))
ar (ABCD) = ar (EFCD)
Thus, the area of parallelogram ABCD is equal to the area of parallelogram EFCD.
Hence, a parallelogram on the same base and between the same parallels are equal in area, is proved.
Example
Now, let us solve the below problem with the help of the theorem.
Question:
Consider a parallelogram ABCD and EFCD is a rectangle. Also, AL is perpendicular to DC.
Prove that:
- ar (ABCD) = ar (EFCD)
- ar (ABCD) = DC × AL
Solution:
Given that ABCD is a parallelogram, and EFCD is a rectangle.
To prove : ar (ABCD) = ar (EFCD)
A rectangle is also a parallelogram, and by using the theorem “parallelogram on the same base and between the same parallels are equal in the area”, we can write
ar (ABCD) = ar (EFCD)
Hence proved.
To prove: ar (ABCD) = DC × AL
By using ar (ABCD) = ar (EFCD)
ar (ABCD) = DC × FC (As, the area of a rectangle = Length × Breadth) …(1)
Also given that AL ⊥ DC, we can say AFCL is also a rectangle.
Therefore, AL = FC …(2)
From (1) and (2), we can get
ar (ABCD) = DC × AL
Hence, proved.
Practice Problems
Solve the following problems:
- The point P and Q lie on the sides DC and AD respectively of a parallelogram ABCD. Prove that ar (APB) = ar (BQC)
- In the figure given below, PQRS and ABRS are parallelograms. “X” is the point on the side BR.
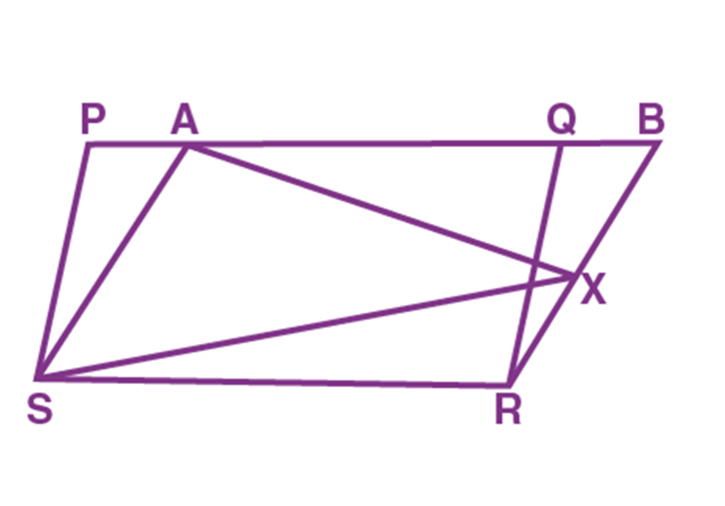
Prove that:
(1) ar (PQRS) = ar (ABRS)
(2) ar (AX S) = ½ ar (PQRS)
Triangles on the same base and between the same parallels
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Triangles on the same base and between the same parallels
Triangles on the same base and between the same parallels are explained here in this article using the theorem with a solved example.
Theorem: Two triangles on the same base and between the same parallels are equal in area.
Proof - Consider a parallelogram ABCD and AC be its diagonals as shown in the figure.
Assume that AN is perpendicular to DC.
We know that the diagonal of a parallelogram divides the parallelogram into two congruent triangles, we can write,
∆ ADC ≅ ∆ CBA
If the triangles are congruent, they have equal areas.
Thus, the area of a triangle ADC is equal to the area of a triangle CBA.
(i.e) ar (ADC) = ar (CBA)
Therefore, we can write
ar (ADC) = ½ ar (ABCD)
ar (ADC) = ½ (DC×AN)
Therefore, the area of the triangle = ½ × Base DC × Corresponding Altitude AN.
From the above formula, we can observe that two triangles with the same base (or equal bases) and equal areas will have equal corresponding altitudes.
In order to have an equal corresponding altitude, the triangles must lie between the same parallels.
Hence, two triangles on the same base and between the same parallels are equal in area.
The converse of this Theorem: Two triangles having the same base (or equal bases) and equal areas lie between the same parallels.
Example - Now, let us understand this theorem with the help of an example.
Question: Prove that the median of a triangle divides it into two triangles of equal areas.
Solution: Consider a triangle ABC and AD to be one of its diagonals.
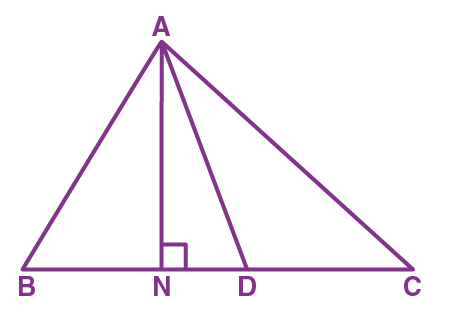
Now, we have to prove that,
ar (ABD) = ar (ACD).
Now, draw the line AN perpendicular to BC.
Therefore, the area of triangle ABD becomes,
ar(ABD) = ½ × base × altitude (of ∆ ABD)
In a triangle ABD, the base is BD and the altitude is AN.
Therefore, ar(ABD) = ½ (BD×AN)
As, BD = CD, the above mentioned equation can be written as:
ar(ABD) = ½ (CD×AN)
ar(ABD) = ½ × base × altitude (of ∆ ACD)
ar(ABD) = ar(ACD)
Hence, the median of a triangle divides it into two triangles of equal areas, which is proved.
Practice Problems
Solve the following problems.
- Prove that the diagonals of a parallelogram divide the parallelogram into four triangles of equal areas.
- E is the midpoint of median AD of a triangle ABC as shown in the figure. prove that ar (ABE) = ar (ACE).
Triangles on the same base and between the same parallels
Triangles on the same base and between the same parallels
Triangles on the same base and between the same parallels are explained here in this article using the theorem with a solved example.
Theorem:
Two triangles on the same base and between the same parallels are equal in area.
Proof
Consider a parallelogram ABCD and AC be its diagonals as shown in the figure.
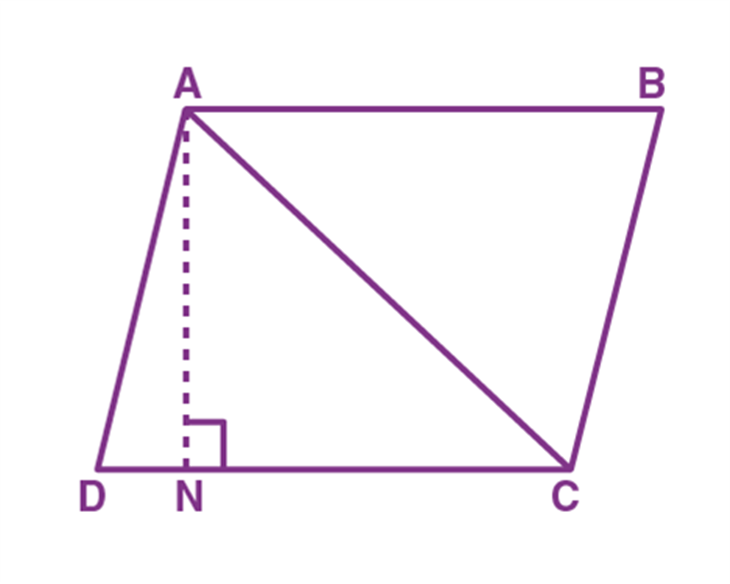
Assume that AN is perpendicular to DC.
We know that the diagonal of a parallelogram divides the parallelogram into two congruent triangles, we can write,
∆ ADC ≅ ∆ CBA
If the triangles are congruent, they have equal areas.
Thus, the area of triangle ADC is equal to the area of a triangle CBA.
(i.e) ar (ADC) = ar (CBA)
Therefore, we can write
ar (ADC) = ½ ar (ABCD)
ar (ADC) = ½ (DC×AN)
Therefore, the area of the triangle = ½ × Base DC × Corresponding Altitude AN.
From the above formula, we can observe that two triangles with the same base (or equal bases) and equal areas will have equal corresponding altitudes.
In order to have an equal corresponding altitude, the triangles must lie between the same parallels.
Hence, two triangles on the same base and between the same parallels are equal in area.
Converse of this Theorem:
Two triangles having the same base (or equal bases) and equal areas lie between the same parallels.
Example
Now, let us understand this theorem with the help of an example.
Question:
Prove that the median of a triangle divides it into two triangles of equal areas.
Solution:
Consider a triangle ABC and AD be the one of its diagonals.
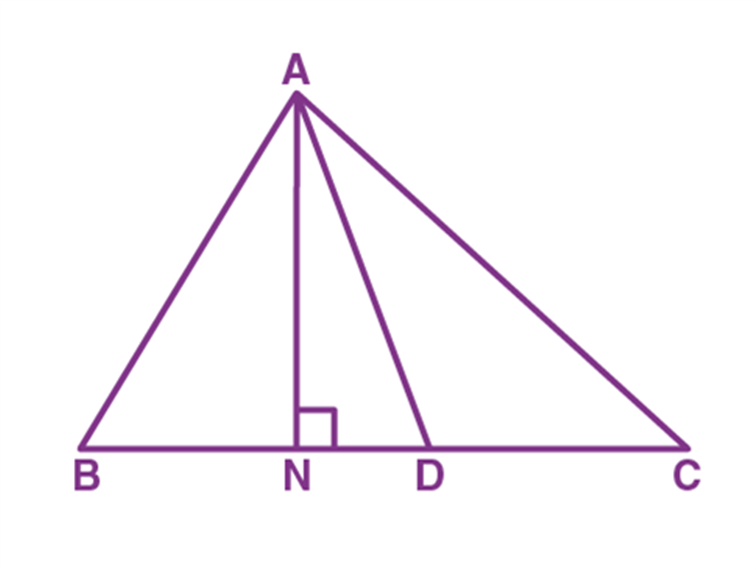
Now, we have to prove that,
ar (ABD) = ar (ACD).
Now, draw the line AN perpendicular to BC.
Therefore, the area of triangle ABD becomes,
ar(ABD) = ½ × base × altitude (of ∆ ABD)
In a triangle ABD, the base is BD and altitude is AN.
Therefore, ar(ABD) = ½ (BD×AN)
As, BD = CD, the above mentioned equation can be written as:
ar(ABD) = ½ (CD×AN)
ar(ABD) = ½ × base × altitude (of ∆ ACD)
ar(ABD) = ar(ACD)
Hence, the median of a triangle divides it into two triangles of equal areas, is proved.
Practice Problems
Solve the following problems.
- Prove that the diagonals of a parallelogram divides the parallelogram into four triangles of equal areas.
- E is the midpoint of median AD of a triangle ABC as shown in the figure. prove that ar (ABE) = ar (ACE).
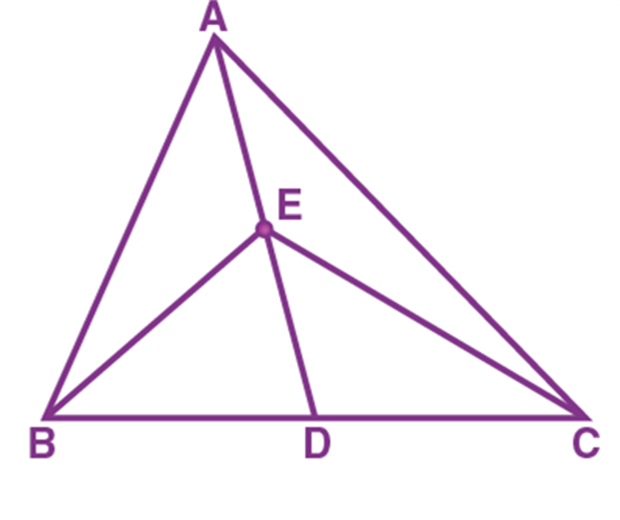
Angle subtended by a Chord at a Point
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Angle Subtended by a Chord at a Point
In Mathematics, a circle is a two-dimensional geometrical figure, where all the points on the surface of a circle are equidistant from the center point called the radius. The chord of a circle is the line segment that joins two points on the circumference of a circle. If you draw two or more equal chords of a circle and determine the angles subtended by them at the center, you will observe that the angles subtended by them at the center are equal. In this article, we will learn the theorems related to the angle subtended by a chord at a point in detail.
Angle Subtended by a Chord at a Point – Theorem
Theorem: Equal chords of a circle subtend equal angles at the center.
Proof - Consider a circle and draw two equal chords AB and CD of a circle with center “O” as shown in the figure.
To prove: ∠ AOB = ∠ COD.
From the triangles, AOB and COD, we get
OA = OC (Radii of a circle)
OB = OD (Radii of a circle)
AB = CD (Equal chords)
By, using Side-Side-Side (SSS Rule), we can write:
∆ AOB ≅ ∆ COD
As the triangles are congruent, the angles should be of equal measurement.
Therefore, ∠ AOB = ∠ COD [Using Corresponding parts of the congruent triangle (CPCT)]
Hence, the theorem “Equal chords of a circle subtend equal angles at the center” is proved.
Converse Theorem
If the angles subtended by the chords of a circle at the center are equal, then the chords are equal.
In the converse theorem, if ∠AOB is equal to ∠COD, we need to prove that the chord AB = CD.
This can be again proved with the help of CPCT and SSS rules.
Angle subtended by a Chord at a Point
Angle Subtended by a Chord at a Point
In Mathematics, a circle is a two-dimensional geometrical figure, where all the points on the surface of a circle are equidistant from the center point called the radius. The chord of a circle is the line segment that joins two points on the circumference of a circle. If you draw two or more equal chords of a circle and determine the angles subtended by them at the center, you will observe that the angles subtended by them at the center are equal. In this article, we will learn the theorems related to the angle subtended by a chord at a point in detail.
Angle Subtended by a Chord at a Point – Theorem
Theorem: Equal chords of a circle subtend equal angles at the center.
Proof
Consider a circle and draw two equal chords AB and CD of a circle with center “O” as shown in the figure.
To prove: ∠ AOB = ∠ COD.
From the triangles, AOB and COD, we get
OA = OC (Radii of a circle)
OB = OD (Radii of a circle)
AB = CD (Equal chords)
By, using Side-Side-Side (SSS Rule), we can write:
∆ AOB ≅ ∆ COD
As the triangles are congruent, the angles should be of equal measurement.
Therefore, ∠ AOB = ∠ COD [Using Corresponding parts of the congruent triangle (CPCT)]
Hence, the theorem “Equal chords of a circle subtend equal angles at the center” is proved.
Converse Theorem
If the angles subtended by the chords of a circle at the center are equal, then the chords are equal.
In the converse theorem, if ∠AOB is equal to ∠COD, we need to prove that the chord AB = CD.
This can be again proved with the help of CPCT and SSS rules.
Perpendicular from the centre to a Chord
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Perpendicular from the Centre to a Chord
In Mathematics, a chord is a line segment that joins two points on the circumference of a circle. We know that the longest chord of a circle is a diameter that passes through the center of a circle. In this article, we will discuss the theorem related to the perpendicular from the center to a circle and its proof, and the converse of this theorem in detail.
Perpendicular from the Centre to a Chord – Theorem and Proof
Theorem: The perpendicular from the center of a circle to a chord bisects the chord.
Proof: Consider a circle with the center “O”.
AB is a chord such that the line OX is perpendicular to the chord AB.
(i.e) OX ⊥ AB
Now, we need to prove: AX = BX
To prove AX = BX, consider two triangles OAX and OBX.
∠OXA = ∠OXB (∠X = 90°)
OX = OX (Common side)
OA = OB (Radii)
By using the RHS rule, we can prove that the triangle OAX is congruent to OBX.
Therefore,
∆OAX ≅ ∆OBX
Hence, we can say that AX = BX ( Using CPCT)
Thus, the perpendicular from the center of a circle to a chord bisects the chord, is proved.
The Converse of this Theorem:
The line drawn through the center of a circle to bisect a chord is perpendicular to the chord
Proof: Consider the same figure, as given above.
Assume that AB is the chord of a circle with a center “O”.
The center “O” is joined to the midpoint “X” of the chord AB.
Now, we need to prove OX ⊥ AB.
Join OA and OB, and the two triangles formed are OAX and OAB.
Here, OA = OB (Radii)
OX = OX (Common side)
AX = BX (As, X is the midpoint of AB)
Therefore, we can say that ∆OAX ≅ ∆OBX.
Thus, by using the RHS rule, we get
∠OMA = ∠OMB = 90°
This proves that the line drawn through the center of a circle to bisect a chord is perpendicular to the chord.
Hence, the converse of this theorem is proved.
Perpendicular from the centre to a Chord
Perpendicular from the Centre to a Chord
In Mathematics, a chord is a line segment that joins two points on the circumference of a circle. We know that the longest chord of a circle is a diameter that passes through the centre of a circle. In this article, we will discuss the theorem related to the perpendicular from the centre to a circle and its proof, and the converse of this theorem in detail.
Perpendicular from the Centre to a Chord – Theorem and Proof
Theorem:
The perpendicular from the centre of a circle to a chord bisects the chord.
Proof:
Consider a circle with centre “O”.
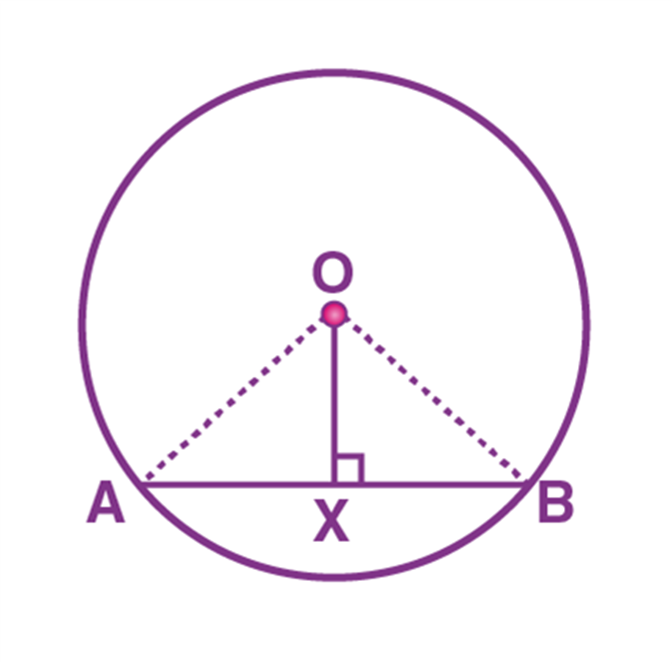
AB is a chord such that the line OX is perpendicular to the chord AB.
(i.e) OX ⊥ AB
Now, we need to prove: AX = BX
To prove AX = BX, consider two triangles OAX and OBX.
∠OXA = ∠OXB (∠X = 90°)
OX = OX (Common side)
OA = OB (Radii)
By using the RHS rule, we can prove that the triangle OAX is congruent to OBX.
Therefore,
∆OAX ≅ ∆OBX
Hence, we can say that AX = BX ( Using CPCT)
Thus, the perpendicular from the centre of a circle to a chord bisects the chord, is proved.
The Converse of this Theorem:
The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord
Proof:
Consider the same figure, as given above.
Assume that AB is the chord of a circle with centre “O”.
The centre “O” is joined to the midpoint “X” of the chord AB.
Now, we need to prove OX ⊥ AB.
Join OA and OB, and the two triangles formed are OAX and OAB.
Here,
OA = OB (Radii)
OX = OX (Common side)
AX = BX (As, X is the midpoint of AB)
Therefore, we can say that ∆OAX ≅ ∆OBX.
Thus, by using the RHS rule, we get
∠OMA = ∠OMB = 90°
This proves that the line drawn through the centre of a circle to bisect a chord is perpendicular to the chord.
Hence, the converse of this theorem is proved.
Circle through three points
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Circle through three points
To draw a straight line, the minimum number of points required is two. That means we can draw a straight line with the given two points. How many minimum points are sufficient to draw a unique circle? Is it possible to draw a circle passing through 3 points? In how many ways can we draw a circle that passes through three points? Well, let’s try to find answers to all these queries.
Learn: Circle Definition
Before drawing a circle passing through 3 points, let’s have a look at the circles that have been drawn through one and two points respectively.
Circle Passing Through a Point
Let us consider a point and try to draw a circle passing through that point.
As given in the figure, through a single point P, we can draw infinite circles passing through it.
Circle Passing Through Two Points
Now, let us take two points, P and Q and see what happens?
Again we see that an infinite number of circles passing through points P and Q can be drawn.
Circle Passing Through Three Points (Collinear or Non-Collinear)
Let us now take 3 points. For a circle passing through 3 points, two cases can arise.
- Three points can be collinear
- Three points can be non-collinear
Let us study both cases individually.
Case 1: A circle passing through 3 points: Points are collinear
Consider three points, P, Q and R, which are collinear.
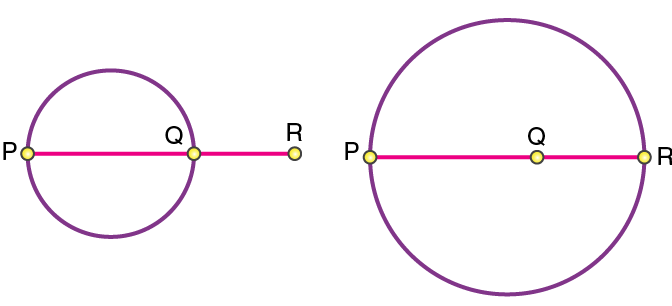
If three points are collinear, any one of the points either lies outside the circle or inside it. Therefore, a circle passing through 3 points, where the points are collinear, is not possible.
Case 2: A circle passing through 3 points: Points are non-collinear
To draw a circle passing through three non-collinear points, we need to locate the center of a circle passing through 3 points and its radius. Follow the steps given below to understand how we can draw a circle in this case.
Step 1: Take three points P, Q, R and join the points as shown below:
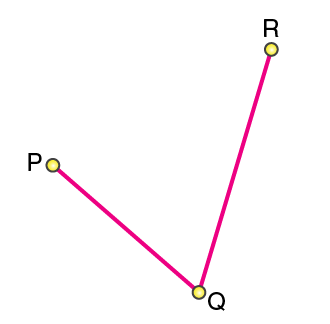
Step 2: Draw perpendicular bisectors of PQ and RQ. Let the bisectors AB and CD meet at O such that the point O is called the center of the circle.
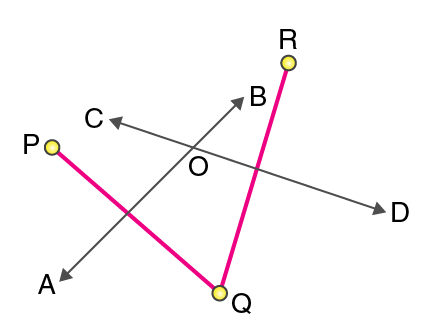
Step 3: Draw a circle with O as the center and radius OP or OQ or OR. We get a circle passing through 3 points P, Q, and R.

It is observed that only a unique circle will pass through all three points. It can be stated as a theorem and the proof is explained as follows.
It is observed that only a unique circle will pass through all three points. It can be stated as a theorem, and the proof of this is explained below.
Given:
Three non-collinear points P, Q and R
To prove:
Only one circle can be drawn through P, Q and R
Construction:
Join PQ and QR.
Draw the perpendicular bisectors of PQ and QR such that these perpendiculars intersect each other at O.
Proof:
|
S. No |
Statement |
Reason |
|
1 |
OP = OQ |
Every point on the perpendicular bisector of a line segment is equidistant from the endpoints of the line segment. |
|
2 |
OQ = OR |
Every point on the perpendicular bisector of a line segment is equidistant from the endpoints of the line segment. |
|
3 |
OP = OQ = OR |
From (i) and (ii) |
|
4 |
O is equidistant from P, Q and R |
|
If a circle is drawn with O as center and OP as radius, then it will also pass through Q and R.
O is the only point that is equidistant from P, Q and R as the perpendicular bisectors of PQ and QR intersect at O only.
Thus, O is the center of the circle to be drawn.
OP, OQ and OR will be radii of the circle.
From the above, it follows that a unique circle passing through 3 points can be drawn given that the points are non-collinear.
Till now, you learned how to draw a circle passing through 3 non-collinear points. Now, you will learn how to find the equation of a circle passing through 3 points. For this, we need to take three non-collinear points.
Circle Equation Passing Through 3 Points
Let’s derive the equation of the circle passing through the 3 points formula.
Let P(x1, y1), Q(x2, y2) and R(x3, y3) be the coordinates of three non-collinear points.
We know that,
The general form of equation of a circle is: x2 + y2 + 2gx + 2fy + c = 0….(1)
Now, we need to substitute the given points P, Q and R in this equation and simplify to get the value of g, f and c.
Substituting P(x1, y1) in equ(1),
x12 + y12 + 2gx1 + 2fy1 + c = 0….(2)
x22 + y22 + 2gx2 + 2fy2 + c = 0….(3)
x32 + y32 + 2gx3 + 2fy3 + c = 0….(4)
From (2) we get,
2gx1 = -x12 – y12 – 2fy1 – c….(5)
Again from (2) we get,
c = -x12 – y12 – 2gx1 – 2fy1….(6)
From (4) we get,
2fy3 = -x32 – y32 – 2gx3 – c….(7)
Now, subtracting (3) from (2),
2g(x1 – x2) = (x22 -x12) + (y22 – y12) + 2f (y2 – y1)….(8)
Substituting (6) in (7),
2fy3 = -x32 – y32 – 2gx3 + x12 + y12 + 2gx1 + 2fy1….(9)
Now, substituting equ(8), i.e. 2g in equ(9),
2f = [(x12 – x32)(x1 – x2) + (y12 – y32 )(x1 – x2) + (x22 – x12)(x1 – x3) + (y22 – y12)(x1 – x3)] / [(y3 – y1)(x1 – x2) – (y2 – y1)(x1 – x3)]
Similarly, we can get 2g as:
2g = [(x12 – x32)(y1 – x2) + (y12 – y32)(y1 – y2) + (x22 – x12)(y1 – y3) + (y22 – y12)(y1 – y3)] / [(x3 – x1)(y1 – y2) – (x2 – x1)(y1 – y3)]
Using these 2g and 2f values we can get the value of c.
Thus, by substituting g, f and c in (1) we will get the equation of the circle passing through the given three points.
Solved Example
Question: What is the equation of the circle passing through the points A(2, 0), B(-2, 0) and C(0, 2)?
Solution: Consider the general equation of circle:
x2 + y2 + 2gx + 2fy + c = 0….(i)
Substituting A(2, 0) in (i),
(2)2 + (0)2 + 2g(2) + 2f(0) + c = 0
4 + 4g + c = 0….(ii)
Substituting B(-2, 0) in (i),
(-2)2 + (0)2 + 2g(-2) + 2f(0) + c = 0
4 – 4g + c = 0….(iii)
Substituting C(0, 2) in (i),
(0)2 + (2)2 + 2g(0) + 2f(2) + c = 0
4 + 4f + c = 0….(iv)
Adding (ii) and (iii),
4 + 4g + c + 4 – 4g + c = 0
2c + 8 = 0
2c = -8
c = -4
Substituting c = -4 in (ii),
4 + 4g – 4 = 0
4g = 0
g = 0
Substituting c = -4 in (iv),
4 + 4f – 4 = 0
4f = 0
f = 0
Now, substituting the values of g, f and c in (i),
x2 + y2 + 2(0)x + 2(0)y + (-4) = 0
x2 + y2 – 4 = 0
Or
x2 + y2 = 4
This is the equation of the circle passing through the given three points A, B and C
Circle through three points
Circle through three points
To draw a straight line, the minimum number of points required is two. That means we can draw a straight line with the given two points. How many minimum points are sufficient to draw a unique circle? Is it possible to draw a circle passing through 3 points? In how many ways can we draw a circle that passes through three points? Well, let’s try to find answers to all these queries.
Learn: Circle Definition
Before drawing a circle passing through 3 points, let’s have a look at the circles that have been drawn through one and two points respectively.
Circle Passing Through a Point
Let us consider a point and try to draw a circle passing through that point.
As given in the figure, through a single point P, we can draw infinite circles passing through it.
Circle Passing Through Two Points
Now, let us take two points, P and Q and see what happens?
Again we see that an infinite number of circles passing through points P and Q can be drawn.
Circle Passing Through Three Points (Collinear or Non-Collinear)
Let us now take 3 points. For a circle passing through 3 points, two cases can arise.
- Three points can be collinear
- Three points can be non-collinear
Let us study both cases individually.
Case 1: A circle passing through 3 points: Points are collinear
Consider three points, P, Q and R, which are collinear.
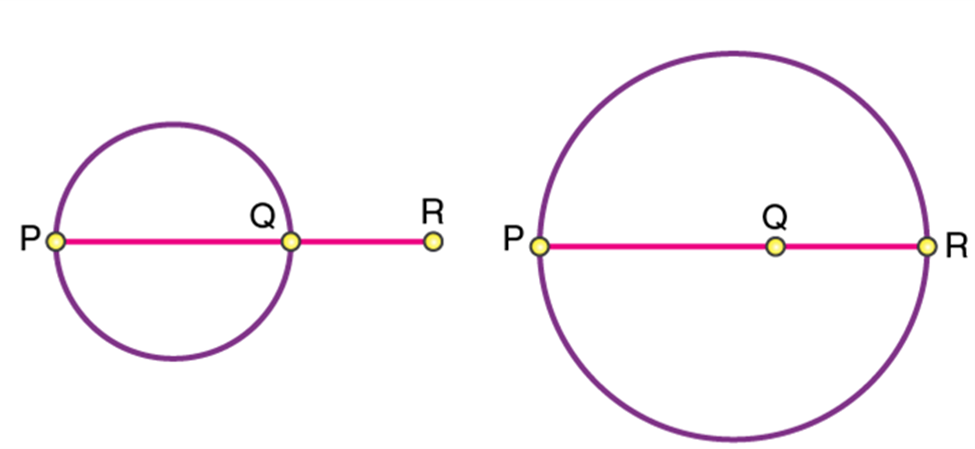
If three points are collinear, any one of the points either lie outside the circle or inside it. Therefore, a circle passing through 3 points, where the points are collinear, is not possible.
Case 2: A circle passing through 3 points: Points are non-collinear
To draw a circle passing through three non-collinear points, we need to locate the centre of a circle passing through 3 points and its radius. Follow the steps given below to understand how we can draw a circle in this case.
Step 1: Take three points P, Q, R and join the points as shown below:
Step 2: Draw perpendicular bisectors of PQ and RQ. Let the bisectors AB and CD meet at O such that the point O is called the centre of the circle.
Step 3: Draw a circle with O as the centre and radius OP or OQ or OR. We get a circle passing through 3 points P, Q, and R.
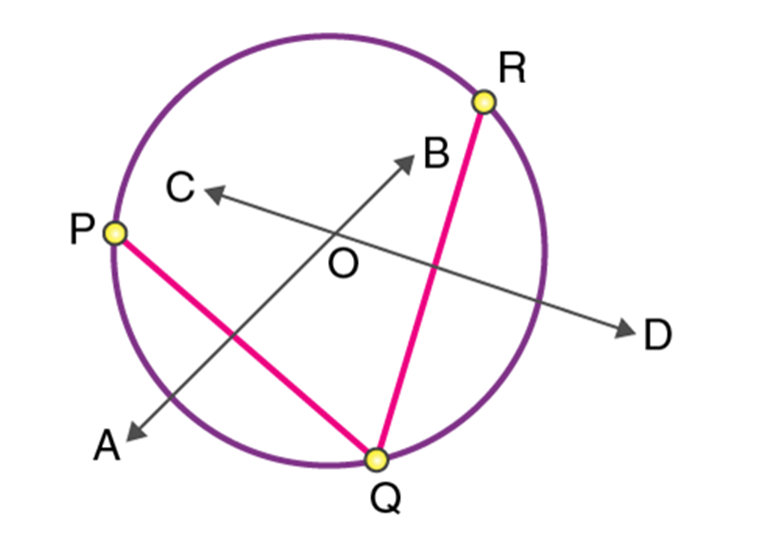
It is observed that only a unique circle will pass through all three points. It can be stated as a theorem and the proof is explained as follows.
It is observed that only a unique circle will pass through all three points. It can be stated as a theorem, and the proof of this is explained below.
Given:
Three non-collinear points P, Q and R
To prove:
Only one circle can be drawn through P, Q and R
Construction:
Join PQ and QR.
Draw the perpendicular bisectors of PQ and QR such that these perpendiculars intersect each other at O.
Proof:
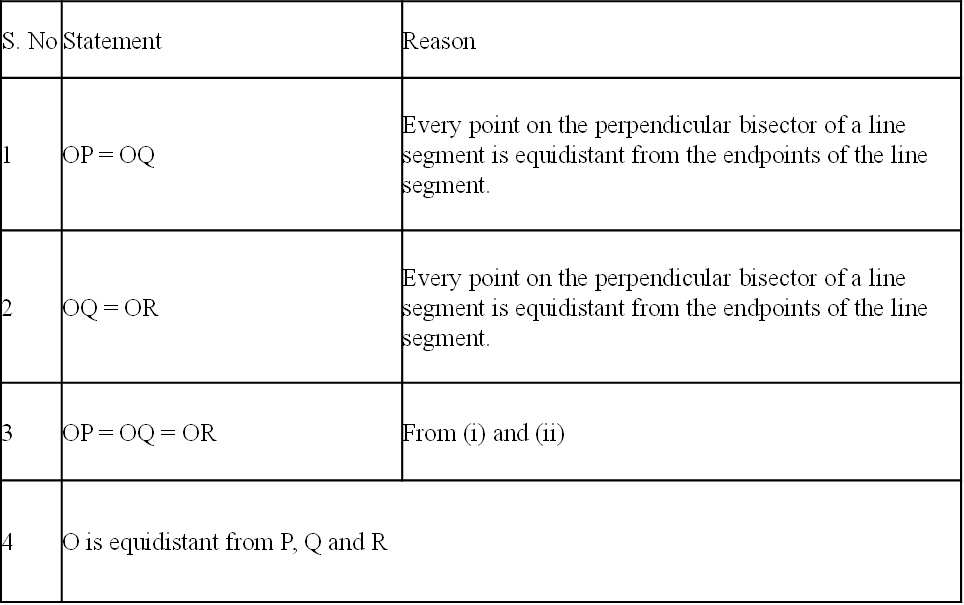
If a circle is drawn with O as centre and OP as radius, then it will also pass through Q and R.
O is the only point which is equidistant from P, Q and R as the perpendicular bisectors of PQ and QR intersect at O only.
Thus, O is the centre of the circle to be drawn.
OP, OQ and OR will be radii of the circle.
From above it follows that a unique circle passing through 3 points can be drawn given that the points are non-collinear.
Till now, you learned how to draw a circle passing through 3 non-collinear points. Now, you will learn how to find the equation of a circle passing through 3 points. For this we need to take three non-collinear points.
Circle Equation Passing Through 3 Points
Let’s derive the equation of the circle passing through the 3 points formula.
Let P(x1, y1), Q(x2, y2) and R(x3, y3) be the coordinates of three non-collinear points.
We know that,
The general form of equation of a circle is: x2 + y2 + 2gx + 2fy + c = 0….(1)
Now, we need to substitute the given points P, Q and R in this equation and simplify to get the value of g, f and c.
Substituting P(x1, y1) in equ(1),
x12 + y12 + 2gx1 + 2fy1 + c = 0….(2)
x22 + y22 + 2gx2 + 2fy2 + c = 0….(3)
x32 + y32 + 2gx3 + 2fy3 + c = 0….(4)
From (2) we get,
2gx1 = -x12 – y12 – 2fy1 – c….(5)
Again from (2) we get,
c = -x12 – y12 – 2gx1 – 2fy1….(6)
From (4) we get,
2fy3 = -x32 – y32 – 2gx3 – c….(7)
Now, subtracting (3) from (2),
2g(x1 – x2) = (x22 -x12) + (y22 – y12) + 2f (y2 – y1)….(8)
Substituting (6) in (7),
2fy3 = -x32 – y32 – 2gx3 + x12 + y12 + 2gx1 + 2fy1….(9)
Now, substituting equ(8), i.e. 2g in equ(9),
2f = [(x12 – x32)(x1 – x2) + (y12 – y32 )(x1 – x2) + (x22 – x12)(x1 – x3) + (y22 – y12)(x1 – x3)] / [(y3 – y1)(x1 – x2) – (y2 – y1)(x1 – x3)]
Similarly, we can get 2g as:
2g = [(x12 – x32)(y1 – x2) + (y12 – y32)(y1 – y2) + (x22 – x12)(y1 – y3) + (y22 – y12)(y1 – y3)] / [(x3 – x1)(y1 – y2) – (x2 – x1)(y1 – y3)]
Using these 2g and 2f values we can get the value of c.
Thus, by substituting g, f and c in (1) we will get the equation of the circle passing through the given three points.
Solved Example
Question:
What is the equation of the circle passing through the points A(2, 0), B(-2, 0) and C(0, 2)?
Solution:
Consider the general equation of circle:
x2 + y2 + 2gx + 2fy + c = 0….(i)
Substituting A(2, 0) in (i),
(2)2 + (0)2 + 2g(2) + 2f(0) + c = 0
4 + 4g + c = 0….(ii)
Substituting B(-2, 0) in (i),
(-2)2 + (0)2 + 2g(-2) + 2f(0) + c = 0
4 – 4g + c = 0….(iii)
Substituting C(0, 2) in (i),
(0)2 + (2)2 + 2g(0) + 2f(2) + c = 0
4 + 4f + c = 0….(iv)
Adding (ii) and (iii),
4 + 4g + c + 4 – 4g + c = 0
2c + 8 = 0
2c = -8
c = -4
Substituting c = -4 in (ii),
4 + 4g – 4 = 0
4g = 0
g = 0
Substituting c = -4 in (iv),
4 + 4f – 4 = 0
4f = 0
f = 0
Now, substituting the values of g, f and c in (i),
x2 + y2 + 2(0)x + 2(0)y + (-4) = 0
x2 + y2 – 4 = 0
Or
x2 + y2 = 4
This is the equation of the circle passing through the given three points A, B and C
Angle subtended by an arc of a circle
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
We know that the endpoints of a chord other than the diameter of a circle divide it into two arcs, namely the major arc and the minor arc. If we take two equal chords, we can say that equal chords make congruent arcs and conversely, congruent arcs make equal chords of a circle. In this article, we will discuss the theorem related to the angle subtended by an arc of a circle and its proof with a complete explanation.
Angle Subtended by an Arc of a Circle – Theorem and Proof
Theorem: The angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.
Proof: Consider a circle with center “O”. Here the arc PQ of the circle subtends angle POQ at Centre O and ∠PAQ at a point A on the remaining part of the circle.
To prove: ∠POQ = 2∠PAQ.
To prove this, join AO and extend it to point B.
There are two general cases while proving this theorem.
Case 1:
Consider a triangle APO,
Here, OA = OP (Radii)
Since, the angles opposite to the equal sides are equal,
∠OPA = ∠OAP …(1)
Also, by using the exterior angle property (exterior angle is the sum of interior opposite angles),
We can write,
∠BOP = ∠OAP + ∠OPA
By using (1),
∠BOP = ∠OAP + ∠OAP
∠BOP = 2∠OAP… (2)
Similarly, consider another triangle AQO,
OA = OQ (Radii)
As the angles opposite to the equal sides are equal,
∠OQA = ∠OAQ … (3)
Similarly, by using the exterior angle property, we get
∠BOQ = ∠OAQ + ∠OQA
∠BOQ = ∠OAQ + ∠OAQ (using (3))
∠BOQ = 2∠OAQ …(4)
Adding (2) and (4) we get,
∠BOP + ∠BOQ = 2∠OAP + 2∠OAQ
∠POQ = 2(∠OAP + ∠OAQ)
∠POQ = 2∠PAQ.
Hence, case (1) is proved.
Case 2:
To prove ∠POQ = 2∠PAQ for this case, we can follow the steps as same as for case (1). But while adding (2) and (4), we have to follow the below steps.
∠BOP + ∠BOQ = 2∠OAP + 2∠OAQ
Reflex angle ∠POQ = 2(∠OAP + ∠OAQ) (Since, PQ is a Major arc)
Reflex angle ∠POQ = 2∠PAQ.
Hence, proved.
Theorem: Angle subtended by a diameter/ semicircle on any point of a circle is 90°
Consider a circle with center “O” and PQ be its diameter, subtending ∠PAQ at a point A on the circle.
Now, we need to prove that ∠PAQ = 90°.
Here, POQ is a straight line that passes through the center “O” of the circle.
Therefore, the angle subtended by arc PQ at O is
∠POQ = 180° (Since, POQ is a straight line) ….(5)
Now, by using the theorem, “The angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle”, we can write
∠POQ = 2 ∠PAQ
∠PAQ = ∠POQ/2
By using (5),
∠PAQ = 180°/2
∠PAQ = 90°
Therefore, the angle subtended by a diameter/ semicircle on any point of a circle is 90°.
Hence, proved.
Angle subtended by an arc of a circle
Angle Subtended by an Arc of a Circle
We know that the end points of a chord other than the diameter of a circle divides it into two arcs, namely the major arc and the minor arc. If we take two equal chords, we can say that equal chords make congruent arcs and conversely, congruent arcs make equal chords of a circle. In this article, we will discuss the theorem related to the angle subtended by an arc of a circle and its proof with complete explanation.
Angle Subtended by an Arc of a Circle – Theorem and Proof
Theorem:
The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
Proof:
Consider a circle with centre “O”. Here the arc PQ of the circle subtends angle POQ at Centre O and ∠PAQ at a point A on the remaining part of the circle.
To prove: ∠POQ = 2∠PAQ.
To prove this, join AO and extend it to point B.
There are two general cases while proving this theorem.
Case 1:
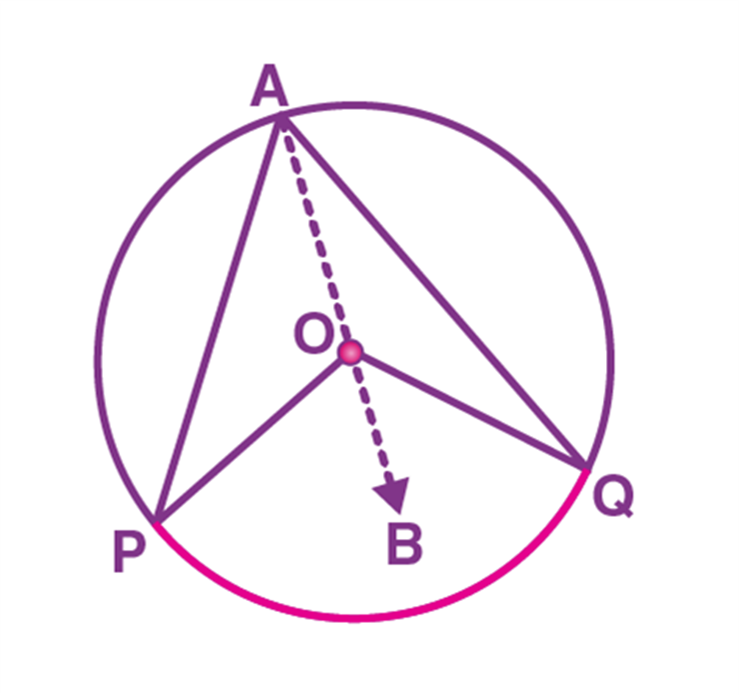
Consider a triangle APO,
Here, OA = OP (Radii)
Since, the angles opposite to the equal sides are equal,
∠OPA = ∠OAP …(1)
Also, by using the exterior angle property (exterior angle is the sum of interior opposite angles),
We can write,
∠BOP = ∠OAP + ∠OPA
By using (1),
∠BOP = ∠OAP + ∠OAP
∠BOP = 2∠OAP… (2)
Similarly, consider another triangle AQO,
OA = OQ (Radii)
As the angles opposite to the equal sides are equal,
∠OQA = ∠OAQ … (3)
Similarly, by using the exterior angle property, we get
∠BOQ = ∠OAQ + ∠OQA
∠BOQ = ∠OAQ + ∠OAQ (using (3))
∠BOQ = 2∠OAQ …(4)
Adding (2) and (4) we get,
∠BOP + ∠BOQ = 2∠OAP + 2∠OAQ
∠POQ = 2(∠OAP + ∠OAQ)
∠POQ = 2∠PAQ.
Hence, case (1) is proved.
Case 2:
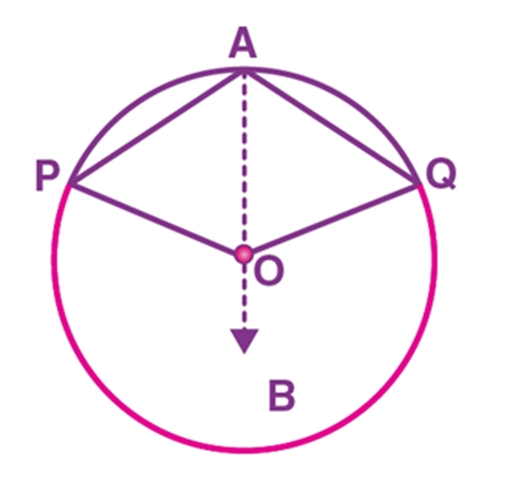
To prove ∠POQ = 2∠PAQ for this case, we can follow the steps as same as for case (1). But while adding (2) and (4), we have to follow the below steps.
∠BOP + ∠BOQ = 2∠OAP + 2∠OAQ
Reflex angle ∠POQ = 2(∠OAP + ∠OAQ) (Since, PQ is a Major arc)
Reflex angle ∠POQ = 2∠PAQ.
Hence, proved.
Theorem: Angle subtended by a diameter/ semicircle on any point of a circle is 90°
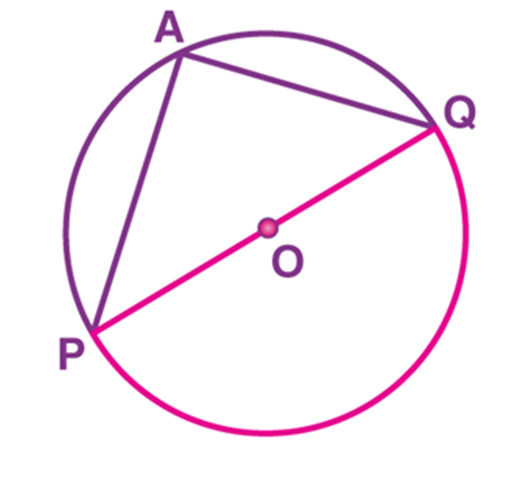
Consider a circle with centre “O” and PQ be its diameter, subtending ∠PAQ at a point A on the circle.
Now, we need to prove that ∠PAQ = 90°.
Here, POQ is a straight line that passes through the centre “O” of the circle.
Therefore, the angle subtended by arc PQ at O is
∠POQ = 180° (Since, POQ is a straight line) ….(5)
Now, by using the theorem, “The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle”, we can write
∠POQ = 2 ∠PAQ
∠PAQ = ∠POQ/2
By using (5),
∠PAQ = 180°/2
∠PAQ = 90°
Therefore, the angle subtended by a diameter/ semicircle on any point of a circle is 90°.
Hence, proved.
Cyclic Quadrilaterals
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Cyclic Quadrilateral
A cyclic quadrilateral is a quadrilateral that has all its four vertices lying on a circle. It is also sometimes called inscribed quadrilateral. The circle which consists of all the vertices of any polygon on its circumference is known as the circumcircle or circumscribed circle.
A quadrilateral is a 4 sided polygon bounded by 4 finite line segments. The word ‘quadrilateral’ is composed of two Latin words, Quadri meaning ‘four ‘and latus meaning ‘side’. It is a two-dimensional figure having four sides (or edges) and four vertices. A circle is the locus of all points in a plane that are equidistant from a fixed point.
If all the four vertices of a quadrilateral ABCD lie on the circumference of the circle, then ABCD is a cyclic quadrilateral. In other words, if any four points on the circumference of a circle are joined, they form the vertices of a cyclic quadrilateral. It can be visualized as a quadrilateral that is inscribed in a circle, i.e. all four vertices of the quadrilateral lie on the circumference of the circle.
Cyclic Quadrilateral Definition
The definition states that a quadrilateral that is circumscribed in a circle is called a cyclic quadrilateral. It means that all the four vertices of the quadrilateral lie in the circumference of the circle. Let us understand with a diagram.
In the figure given below, the quadrilateral ABCD is cyclic.
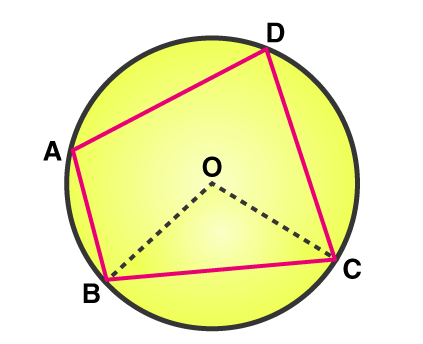
Let us do an activity. Take a circle and choose any 4 points on the circumference of the circle. Join these points to form a quadrilateral. Now measure the angles formed at the vertices of the cyclic quadrilateral. It is noted that the sum of the angles formed at the vertices is always 360o and the sum of angles formed at the opposite vertices is always supplementary.
Cyclic Quadrilateral Angles
The sum of the opposite angles of a cyclic quadrilateral is supplementary.
Let ∠A, ∠B, ∠C and ∠D are the four angles of an inscribed quadrilateral. Then,
∠A + ∠C = 180°
∠B + ∠D = 180°
Therefore, an inscribed quadrilateral also meets the angle sum property of a quadrilateral, according to which, the sum of all the angles equals 360 degrees. Hence,
∠A + ∠B + ∠C + ∠D= 360°
Radius of Cyclic Quadrilateral
If a, b, c and d are the successive sides of a cyclic quadrilateral, and s is the semi perimeter, then the radius is given by,
Diagonals of Cyclic Quadrilaterals
Suppose a,b,c and d are the sides of a cyclic quadrilateral and p & q are the diagonals, then we can find the diagonals of it using the below given formulas:
Area of Cyclic Quadrilateral
If a,b,c and d are the sides of an inscribed quadrilateral, then its area is given by:
Where s is the semiperimeter.
s = ½(a+b+c+d)
Cyclic Quadrilateral Theorems
There are two important theorems that prove the cyclic quadrilateral.
Theorem 1 - In a cyclic quadrilateral, the sum of either pair of opposite angles is supplementary.
Proof: Let us now try to prove this theorem.
Given: Acyclic quadrilateral ABCD inscribed in a circle with center O.
Construction: Join the vertices A and C with center O.
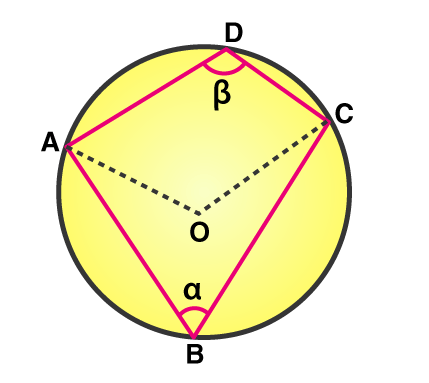
The converse of this theorem is also true, which states that if opposite angles of a quadrilateral are supplementary, then the quadrilateral is cyclic.
Theorem 2 - The ratio between the diagonals and the sides can be defined and is known as the Cyclic quadrilateral theorem. If there’s a quadrilateral that is inscribed in a circle, then the product of the diagonals is equal to the sum of the product of its two pairs of opposite sides.
If PQRS is a cyclic quadrilateral, PQ and RS, and QR and PS are opposite sides. PR and QS are the diagonals.
(PQ x RS) + ( QR x PS) = PR x QS
Properties of Cyclic Quadrilateral
• In a cyclic quadrilateral, the sum of a pair of opposite angles is 1800(supplementary).
• If the sum of two opposite angles is supplementary, then it’s a cyclic quadrilateral.
• The area of a cyclic quadrilateral is where a, b, c, and d are the four sides of the quadrilateral.
• The four vertices of a cyclic quadrilateral lie on the circumference of the circle.
• To get a rectangle or a parallelogram, just join the midpoints of the four sides in order.
• If PQRS is a cyclic quadrilateral, then ∠SPR = ∠SQR, ∠QPR = ∠QSR, ∠PQS = ∠PRS, ∠QRP = ∠QSP.
• If T is the point of intersection of the two diagonals, PT X TR = QT X TS.
• The exterior angle formed if any one side of the cyclic quadrilateral produced is equal to the interior angle opposite to it.
• In a given cyclic quadrilateral, d1 / d2 = sum of the product of opposite sides, which shares the diagonals endpoints.
• If it is a cyclic quadrilateral, then the perpendicular bisectors will be concurrent compulsorily.
• In a cyclic quadrilateral, the four perpendicular bisectors of the given four sides meet at the center O.
Problems and Solutions
Question: Find the value of angle D of a cyclic quadrilateral, if angle B is 60o.
Solution:
If ABCD is a cyclic quadrilateral, so the sum of a pair of two opposite angles will be 180°.
∠B + ∠ D = 180°
60° + ∠D = 180°
∠D = 180° – 60°
∠D = 120°
The value of angle D is 120°.
Question: Find the value of angle D of a cyclic quadrilateral, if angle B is 80°.
Solution:
If ABCD is a cyclic quadrilateral, so the sum of a pair of two opposite angles will be 180°.
∠B + ∠ D = 180°
80° + ∠D = 180°
∠D = 180° – 80°
∠D = 100°
The value of angle D is 100°.
Cyclic Quadrilaterals
Cyclic Quadrilateral
A cyclic quadrilateral is a quadrilateral which has all its four vertices lying on a circle. It is also sometimes called inscribed quadrilateral. The circle which consists of all the vertices of any polygon on its circumference is known as the circumcircle or circumscribed circle.
A quadrilateral is a 4 sided polygon bounded by 4 finite line segments. The word ‘quadrilateral’ is composed of two Latin words, Quadri meaning ‘four ‘and latus meaning ‘side’. It is a two-dimensional figure having four sides (or edges) and four vertices. A circle is the locus of all points in a plane which are equidistant from a fixed point.
If all the four vertices of a quadrilateral ABCD lie on the circumference of the circle, then ABCD is a cyclic quadrilateral. In other words, if any four points on the circumference of a circle are joined, they form the vertices of a cyclic quadrilateral. It can be visualized as a quadrilateral which is inscribed in a circle, i.e. all four vertices of the quadrilateral lie on the circumference of the circle.
Cyclic Quadrilateral Definition
The definition states that a quadrilateral which is circumscribed in a circle is called a cyclic quadrilateral. It means that all the four vertices of quadrilateral lie in the circumference of the circle. Let us understand with a diagram.
In the figure given below, the quadrilateral ABCD is cyclic.
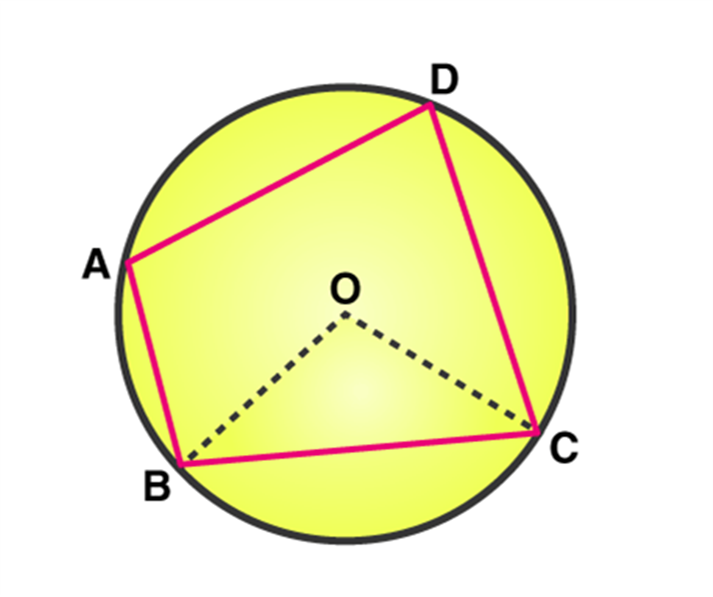
Let us do an activity. Take a circle and choose any 4 points on the circumference of the circle. Join these points to form a quadrilateral. Now measure the angles formed at the vertices of the cyclic quadrilateral. It is noted that the sum of the angles formed at the vertices is always 360o and the sum of angles formed at the opposite vertices is always supplementary.
Cyclic Quadrilateral Angles
The sum of the opposite angles of a cyclic quadrilateral is supplementary.
Let ∠A, ∠B, ∠C and ∠D are the four angles of an inscribed quadrilateral. Then,
∠A + ∠C = 180°
∠B + ∠D = 180°
Therefore, an inscribed quadrilateral also meets the angle sum property of a quadrilateral, according to which, the sum of all the angles equals 360 degrees. Hence,
∠A + ∠B + ∠C + ∠D= 360°
Radius of Cyclic Quadrilateral
If a, b, c and d are the successive sides of a cyclic quadrilateral, and s is the semi perimeter, then the radius is given by,
Diagonals of Cyclic Quadrilaterals
Suppose a,b,c and d are the sides of a cyclic quadrilateral and p & q are the diagonals, then we can find the diagonals of it using the below given formulas:
If a,b,c and d are the sides of a inscribed quadrialteral, then its area is given by:
Where s is the semiperimeter.
s = ½(a+b+c+d)
Cyclic Quadrilateral Theorems
There are two important theorems which prove the cyclic quadrilateral.
Theorem 1
In a cyclic quadrilateral, the sum of either pair of opposite angles is supplementary.
Proof: Let us now try to prove this theorem.
Given: A cyclic quadrilateral ABCD inscribed in a circle with center O.
Construction: Join the vertices A and C with center O.
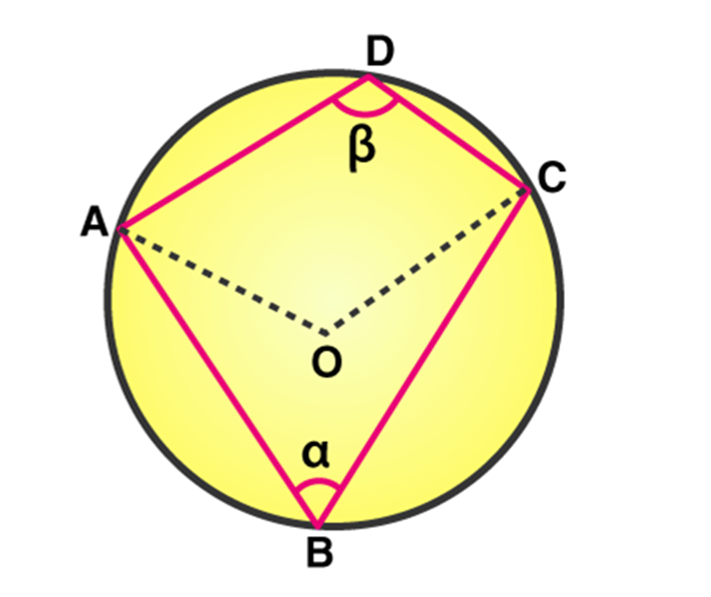
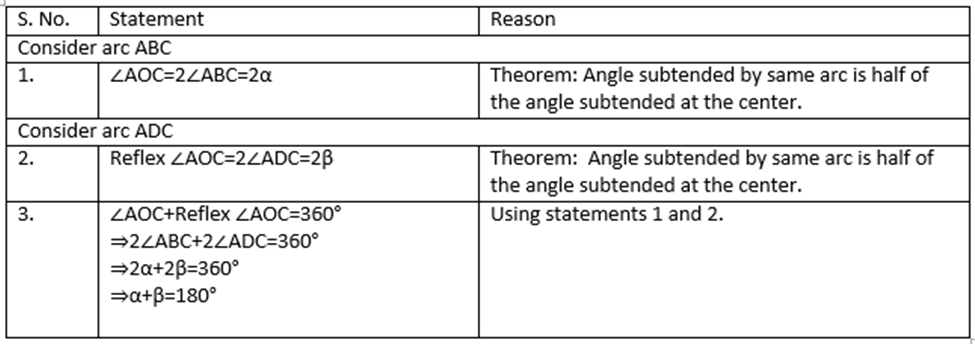
The converse of this theorem is also true, which states that if opposite angles of a quadrilateral are supplementary, then the quadrilateral is cyclic.
Theorem 2
The ratio between the diagonals and the sides can be defined and is known as Cyclic quadrilateral theorem. If there’s a quadrilateral which is inscribed in a circle, then the product of the diagonals is equal to the sum of the product of its two pairs of opposite sides.
If PQRS is a cyclic quadrilateral, PQ and RS, and QR and PS are opposite sides. PR and QS are the diagonals.
(PQ x RS) + ( QR x PS) = PR x QS
Properties of Cyclic Quadrilateral
|
|
where a, b, c, and d are the four sides of the quadrilateral. |
|
|
|
|
|
|
|
|
Problems and Solutions
Question: Find the value of angle D of a cyclic quadrilateral, if angle B is 60o.
Solution:
If ABCD is a cyclic quadrilateral, so the sum of a pair of two opposite angles will be 180°.
∠B + ∠ D = 180°
60° + ∠D = 180°
∠D = 180° – 60°
∠D = 120°
The value of angle D is 120°.
Question: Find the value of angle D of a cyclic quadrilateral, if angle B is 80°.
Solution:
If ABCD is a cyclic quadrilateral, so the sum of a pair of two opposite angles will be 180°.
∠B + ∠ D = 180°
80° + ∠D = 180°
∠D = 180° – 80°
∠D = 100°
The value of angle D is 100°.
You should practise more examples using cyclic quadrilateral formulas to understand the concept better.
Equal Chords and their distances from the centre
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
In Mathematics, a chord is the line segment that joins two points on the circumference of a circle. In general, a circle can have infinitely many chords. The distance of the line from a point is defined as the perpendicular distance from a point to a line. If you draw infinite chords to a circle, the longer chord is close to the center of the circle, than the smaller chord of a circle. In this article, we will discuss the theorem and proof related to the equal chords and their distance from the center and also its converse theorem in detail.
Equal Chords and their Distance from the Centre – Theorem and Proof
Theorem: Equal chords of a circle (or of congruent circles) are equidistant from the center (or centers).
Proof: Consider a circle with “O”.
AB and CD are the equal chords of a circle.
(i.e) AB = CD
The line OX is perpendicular to the chord AB and OY is perpendicular to the chord CD.
We have to prove OX = OY.
Also, the line OX is perpendicular to AB.
As the perpendicular from the center of the circle to a chord, bisects the chord, we can write it as
AX = BX = AB/2 …(1)
Similarly, the line OY is perpendicular to CD,
CY = DY = CD/2 ….(2) [Since, the perpendicular from the center of the circle to a chord, bisects the chord)
Given that, AB = CD
AB/2 = CD/2
Therefore, AX = CY …(3) [Using (1) and (2)]
Now, by using the triangles AOX and COY,
∠ OXA = ∠ OYC (Both are 90°)
OA = OC (Radii)
AX = CY (From equation (3))
From the RHS rule, we can write it as
∆ AOX ≅ ∆ COY
Hence, we can conclude that OX = OY (Using CPCT)
Therefore, the theorem “equal chords of a circle (or of congruent circles) are equidistant from the center (or centers)”, is proved.
Converse of this Theorem
The converse of the above-mentioned theorem is “chords equidistant from the center of a circle are equal in length”.
Example
Question: Two intersecting chords of a circle make equal angles with the diameter that passes through their point of intersection. Prove that the chords are equal.
Solution: Given that AB and CD are the two chords of a circle with a center “O” and it intersects at the point “E” as shown in the figure.
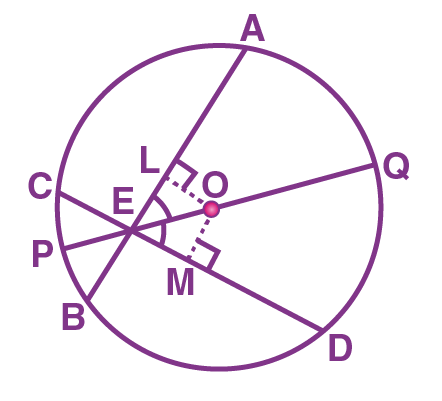
PQ is the diameter of a circle (longest chord of a circle), that passes through the point of intersection E, such that it makes an angle ∠ AEQ = ∠ DEQ.
Now, we need to prove that AB = CD.
Now, draw the perpendicular OL to the chord AB and the perpendicular line OM to the chord CD.
By using the angle sum property of a triangle, we can write it as:
∠ LOE = 180° – 90° – ∠ LEO
∠ LOE = 90° – ∠ LEO
= 90° – ∠ AEQ = 90° – ∠ DEQ
= 90° – ∠ MEO = ∠ MOE
Therefore,
∠ LOE = ∠ MOE
From the triangles, OLE and OME, we observe that
∠ LOE = ∠ MOE
Also, ∠ LEO = ∠ MEO
EO = EO (Common side)
Therefore, we will say that the triangles OLE and OME are congruent with each other.
(i.e) ∆ OLE ≅ ∆ OME
Thus, by using the CPCT rule,
OL = OM
By using equal chords and their distance from the center theorem, we can say,
AB = CD.
So, the chords AB and CD are equal.
Hence, proved.
Practice Problems
Solve the following problems.
- Find the length of the common chord, if two circles of radii 5 cm and 3 cm intersect at two points and the distance between the centers is 4 cm.
- The two equal chords of a circle intersect within a circle. Prove that the segments of one chord are equal to the corresponding segments of the other chord.
Equal Chords and their distances from the centre
Equal Chords and their distances from the centre
In Mathematics, a chord is the line segment which joins two points on the circumference of a circle. In general, a circle can have infinitely many chords. The distance of the line from a point is defined as the perpendicular distance from a point to a line. If you draw infinite chords to a circle, the longer chord is close to the centre of the circle, than the smaller chord of a circle. In this article, we will discuss the theorem and proof related to the equal chords and their distance from the centre and also its converse theorem in detail.
Equal Chords and their Distance from the Centre – Theorem and Proof
Theorem:
Equal chords of a circle (or of congruent circles) are equidistant from the centre (or centres).
Proof:
Consider a circle with “O”.
AB and CD are the equal chords of a circle.
(i.e) AB = CD
The line OX is perpendicular to the chord AB and OY is perpendicular to the chord CD.
We have to prove OX = OY.
Also, the line OX is perpendicular to AB.
As the perpendicular from the centre of the circle to a chord, bisects the chord, we can write it as
AX = BX = AB/2 …(1)
Similarly, the line OY is perpendicular to CD,
CY = DY = CD/2 ….(2) [Since, the perpendicular from the centre of the circle to a chord, bisects the chord)
Given that, AB = CD
AB/2 = CD/2
Therefore, AX = CY …(3) [Using (1) and (2)]
Now, by using the triangles AOX and COY,
∠ OXA = ∠ OYC (Both are 90°)
OA = OC (Radii)
AX = CY (From equation (3))
From the RHS rule, we can write it as
∆ AOX ≅ ∆ COY
Hence, we can conclude that OX = OY (Using CPCT)
Therefore, the theorem “equal chords of a circle (or of congruent circles) are equidistant from the centre (or centres)”, is proved.
Converse of this Theorem
The converse of the above-mentioned theorem is “chords equidistant from the centre of a circle are equal in length”.
Example
Question:
Two intersecting chords of a circle make equal angles with the diameter that passes through their point of intersection. Prove that the chords are equal.
Solution:
Given that AB and CD are the two chords of a circle with centre “O” and it intersects at the point “E” as shown in the figure.
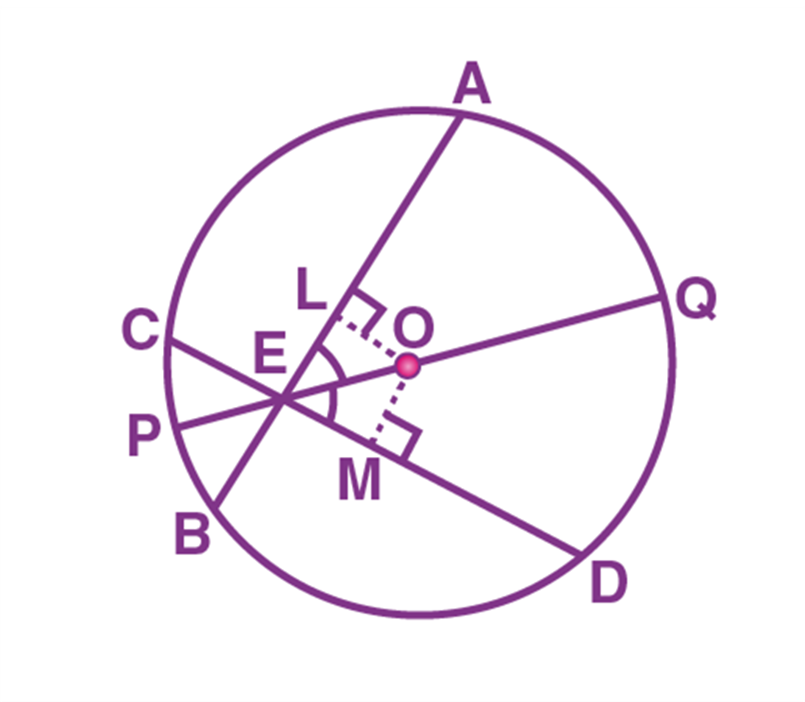
PQ is the diameter of a circle (longest chord of a circle), that passes through the point of intersection E, such that it makes an angle ∠ AEQ = ∠ DEQ.
Now, we need to prove that AB = CD.
Now, draw the perpendicular OL to the chord AB and the perpendicular line OM to the chord CD.
By using the angle sum property of a triangle, we can write it as:
∠ LOE = 180° – 90° – ∠ LEO
∠ LOE = 90° – ∠ LEO
= 90° – ∠ AEQ = 90° – ∠ DEQ
= 90° – ∠ MEO = ∠ MOE
Therefore,
∠ LOE = ∠ MOE
From the triangles, OLE and OME, we observe that
∠ LOE = ∠ MOE
Also, ∠ LEO = ∠ MEO
EO = EO (Common side)
Therefore, we will say that the triangles OLE and OME are congruent to each other.
(i.e) ∆ OLE ≅ ∆ OME
Thus, by using the CPCT rule,
OL = OM
By using equal chords and their distance from the centre theorem, we can say,
AB = CD.
So, the chords AB and CD are equal.
Hence, proved.
Practice Problems
Solve the following problems.
- Find the length of the common chord, if two circles of radii 5 cm and 3 cm intersect at two points and the distance between the centres is 4 cm.
- The two equal chords of a circle intersect within a circle. Prove that the segments of one chord are equal to the corresponding segments of the other chord.
Some construction of triangles
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Constructing Triangles
Constructing triangles will include the construction of different triangles using a protractor, a compass and a ruler. A triangle is a three-sided polygon. It has three sides, three vertices and three angles. Construction of triangles is easy when the measurements are given to us based on different properties such as SSS, SAS and ASA.
Let us learn here to construct a triangle with given measurements. Also, learn to draw triangles of some special cases.
How to Construct Triangles?
To construct a triangle one should know these properties and rules:
- All three sides are given (SSS – Side side side)
- Two sides and included angle are given (SAS – Side angle side)
- Two angles and the included side is given (ASA – Angle side angle)
- The measure of the hypotenuse and a side is given in the right triangle (RHS – Right angle hypotenuse side)
For constructing triangles from given data, we generally make use of the given congruency conditions and construct the required triangle.
Constructing triangle With SSS Property
When the length of three sides of the triangle is given, then follow the below steps to construct the required triangle.
- Draw a line segment AB, of length equal to the longest side of the triangle
- Now using a compass and ruler take the measure of the second side and draw an arc
- Again take the measure of the third side and cut the previous arc at a point C
- Now join the endpoints of the line segment to point C and get the required triangle ABC
Constructing triangle with SAS Property
When the length of the two sides and the angle included between them are given, then use the following steps to construct the triangle.
- Draw a line segment AB, of length equal to the longest side of the triangle, using a ruler
- Put the center of the protractor on one end of a line segment (say A) and measure the given angle. Join the points and construct a ray, such that the ray is nearer to the line segment AB
- Take the measure of another given side of the triangle using a compass and a ruler
- Put the compass at point A and cut the ray at another point, C
- Now join the other end of the line segment, i.e., B to the point C
- Hence, the triangle ABC is constructed
Constructing triangle with ASA Property
When the measures of two angles and the side included between them are given of a triangle, then it is said to be ASA congruency. Follow the given steps to draw a triangle with ASA property.
- Draw a line segment AB, of length equal to the given side of the triangle, using a ruler
- At one endpoint of a line segment (say A) measure one of the given angles and draw a ray AR
- At another endpoint of a line segment (i.e., B) measure the other angle using a protractor and draw the ray BQ, such that it cuts the previous ray at a point P
- Join the previous point P, with both the endpoints A and B of the line segment AB, to get the required triangle
Construction triangle with RHS Property
When the hypotenuse side and any one of the other two sides of a right triangle are given, then it is RHS property. Follow the given steps to draw a triangle with RHS property.
- Draw the line segment AB, equal to the measure of the hypotenuse side
- At one endpoint, say A, of line-segment measure the angle equal to 90 degrees and draw a ray, AR
- Measure the length of another given side and draw an arc to cut the ray AR at a point P
- Now join the points P and B to get the required right triangle
Special Cases of Constructing Triangles
There are a few special cases of constructing triangles that are discussed here.
Construction of Triangles – Case 1
Given the base of a triangle, its base angle and the sum of the other two sides
For constructing ∆ABC such that base BC, base angle ∠B and the sum of the other two sides, i.e. AB + AC are given, the following steps of construction are followed:
Steps of Construction of a Triangle
Step 1. Draw the base BC of ∆ABC as given and construct ∠XBC of the given measure at B as shown.
Step 2. Keeping the compass at point B cut an arc from the ray BX such that its length equals AB + AC at point P and join it to C as shown in the figure.
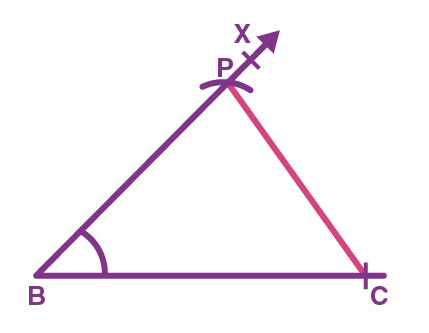
Step 3. Now measure ∠BPC and from C, draw an angle equal to ∠BPC as shown in the figure.
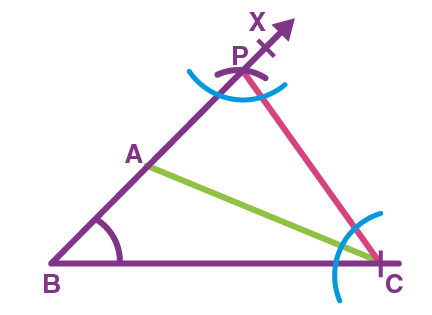
∆ABC is the required triangle. This can be proved as follows:
Base BC and ∠B are drawn as given. Now in ∆ACP,
|
Sl.No |
Statement |
Reason |
|
1 |
∠ACP = ∠APC |
By Construction |
|
2 |
AC = AP |
∆ACP is isosceles |
|
3 |
AB = BP – AP = BP – AC |
From Statement 2 |
|
4 |
AB + AC = BP |
Proved |
Construction of Triangles – Case 2
Given the base of a triangle, its base angle and the difference between the other two sides
For constructing ∆ABC such that base BC, base angle∠B and difference of the other two sides, i.e. AB – AC or AC-AB is given, then for constructing triangles such as these two cases can arise:
- AB > AC
- AC > AB
The following steps of construction are followed for the two cases:
Steps of Construction if AB > AC:
Step 1. Draw the base BC of ∆ABC as given and construct ∠XBC of the required measure at B as shown.
Step 2. From the ray, BX cut an arc equal to AB – AC at point P and join it to C as shown
Step 3. Draw the perpendicular bisector of PC and let it intersect BX at point A as shown:
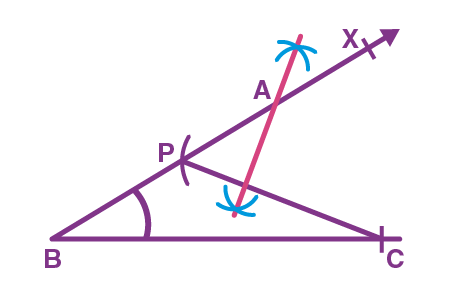
Step 4. Join AC, ∆ABC is the required triangle.
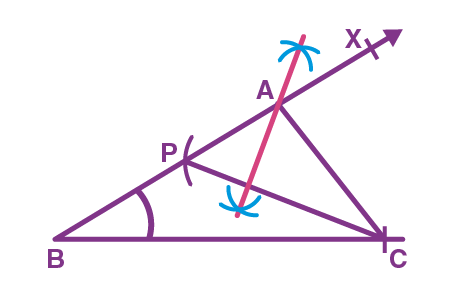
Steps of Construction if AC > AB:
Step 1. Draw the base BC of ∆ABC as given and construct ∠XBC of the required measure at B as shown.
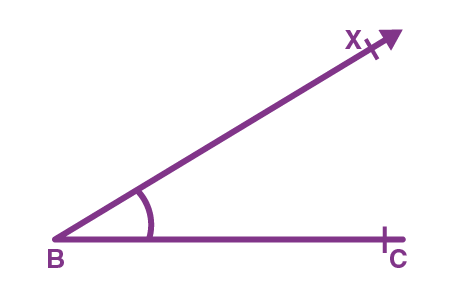
Step 2. On the ray, BX cut an arc equal to AB – AC at point P and join it to C. In this case, P will lie on the opposite side to the ray BX. Draw the perpendicular bisector of PC and let it intersect BX at point A as shown
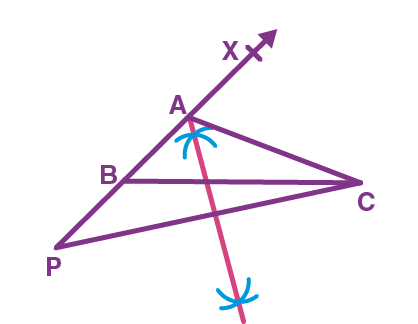
Step 3. Join the points A and C, and hence ∆ABC is the required triangle.
Some construction of triangles
Constructing Triangles
Constructing triangles will include the construction of different triangles using a protractor, a compass and a ruler. A triangle is a three-sided polygon. It has three sides, three vertices and three angles. Construction of triangles is easy when the measurements are given to us based on different properties such as SSS, SAS and ASA.
Let us learn here to construct a triangle with given measurements. Also, learn to draw triangles of some special cases.
How to Construct Triangles?
To construct a triangle one should know these properties and rules:
- All three sides are given (SSS – Side side side)
- Two sides and included angle are given (SAS – Side angle side)
- Two angles and the included side is given (ASA – Angle side angle)
- The measure of the hypotenuse and a side is given in the right triangle (RHS – Right angle hypotenuse side)
For constructing triangles from given data, we generally make use of the given congruency conditions and construct the required triangle.
Constructing triangle With SSS Property
When the length of three sides of the triangle is given, then follow the below steps to construct the required triangle.
- Draw a line segment AB, of length equal to the longest side of the triangle
- Now using a compass and ruler take the measure of the second side and draw an arc
- Again take the measure of the third side and cut the previous arc at a point C
- Now join the endpoints of the line segment to point C and get the required triangle ABC
Constructing triangle with SAS Property
When the length of two sides and the angle included between them are given, then use the following steps to construct the triangle.
- Draw a line segment AB, of length equal to the longest side of the triangle, using a ruler
- Put the center of protractor on one end of a line segment (say A) and measure the given angle. Join the points and construct a ray, such that the ray is nearer to the line segment AB
- Take the measure of another given side of the triangle using a compass and a ruler
- Put the compass at point A and cut the ray at another point, C
- Now join the other end of the line segment, i.e., B to the point C
- Hence, the triangle ABC is constructed
Constructing triangle with ASA Property
When the measures of two angles and the side included between them are given of a triangle, then it is said to be ASA congruency. Follow the given steps to draw a triangle with ASA property.
- Draw a line segment AB, of length equal to the given side of the triangle, using a ruler
- At one endpoint of line segment (say A) measure one of the given angles and draw a ray AR
- At another endpoint of line segment (i.e.,B) measure the other angle using a protractor and draw the ray BQ, such that it cuts the previous ray at a point P
- Join the previous point P, with both the endpoints A and B of the line segment AB, to get the required triangle
Construction triangle with RHS Property
When the hypotenuse side and any one of the other two sides of right triangle are given, then it is RHS property. Follow the given steps to draw a triangle with RHS property.
- Draw the line segment AB, equal to the measure of hypotenuse side
- At one endpoint, say A, of line-segment measure the angle equal to 90 degrees and draw a ray, AR
- Measure the length of another given side and draw an arc to cut the ray AR at a point P
- Now join the point P and B to get the required right triangle
Special Cases of Constructing Triangles
There are few special cases of constructing triangles that are discussed here.
Construction of Triangles – Case 1
Given the base of a triangle, its base angle and the sum of other two sides
For constructing ∆ABC such that base BC, base angle ∠B and the sum of other two sides, i.e. AB + AC are given, the following steps of construction is followed:
Steps of Construction of a Triangle
Step 1. Draw the base BC of ∆ABC as given and construct ∠XBC of the given measure at B as shown.
Step 2. Keeping the compass at point B cut an arc from the ray BX such that its length equals AB + AC at point P and join it to C as shown in the figure.
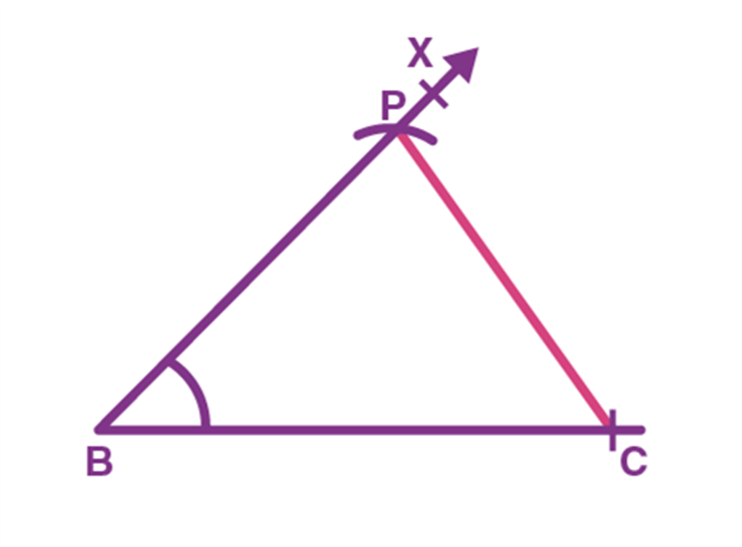
Step 3. Now measure ∠BPC and from C, draw an angle equal to ∠BPC as shown in the figure.
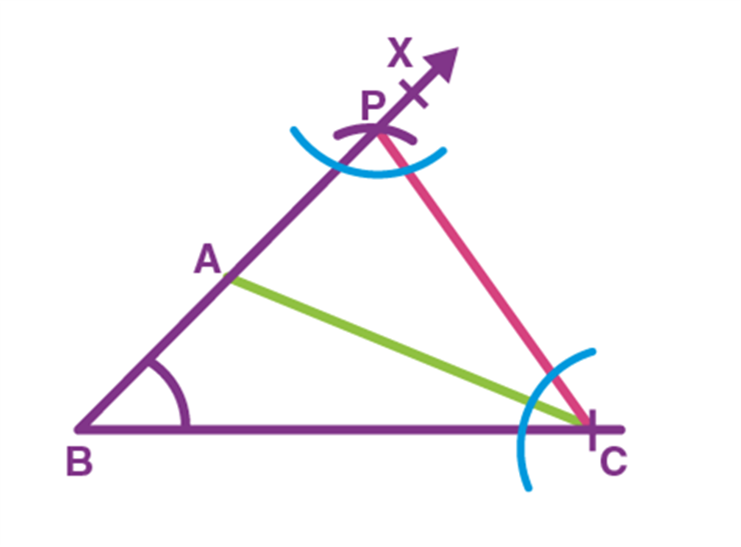
∆ABC is the required triangle. This can be proved as follows:
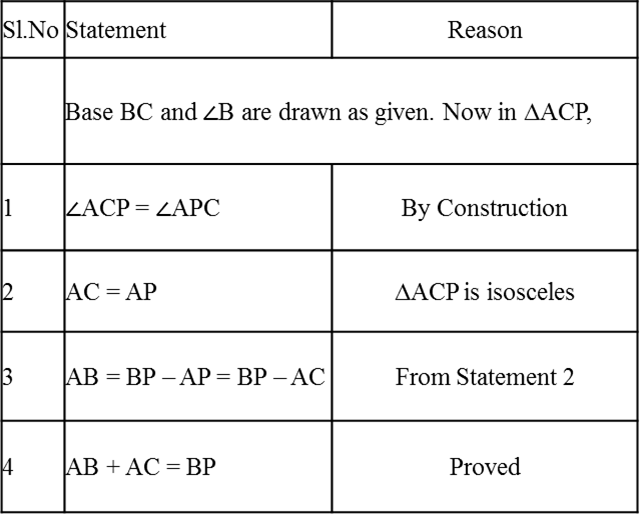
Construction of Triangles – Case 2
Given the base of a triangle, its base angle and the difference between the other two sides
For constructing ∆ABC such that base BC, base angle∠B and difference of the other two sides, i.e. AB – AC or AC-AB is given, then for constructing triangles such as these two cases can arise:
- AB > AC
- AC > AB
The following steps of construction are followed for the two cases:
Steps of Construction if AB > AC:
Step 1. Draw the base BC of ∆ABC as given and construct ∠XBC of the required measure at B as shown.
Step 2. From the ray, BX cut an arc equal to AB – AC at point P and join it to C as shown
Step 3. Draw the perpendicular bisector of PC and let it intersect BX at point A as shown:
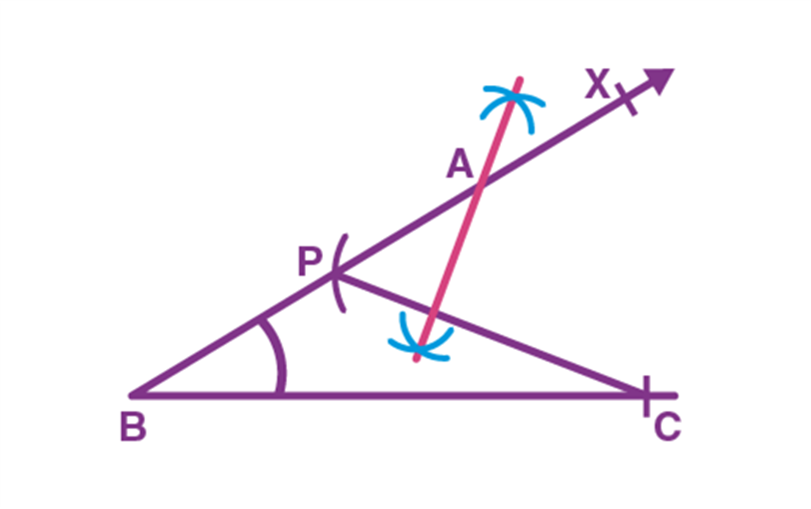
Step 4. Join AC, ∆ABC is the required triangle.
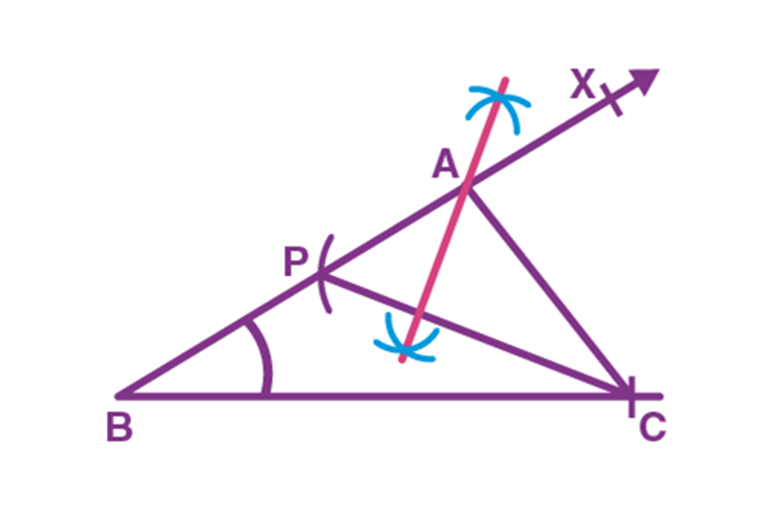
Steps of Construction if AC > AB:
Step 1. Draw the base BC of ∆ABC as given and construct ∠XBC of the required measure at B as shown.
Step 2. On the ray BX cut an arc equal to AB – AC at point P and join it to C. In this case P will lie on the opposite side to the ray BX. Draw the perpendicular bisector of PC and let it intersect BX at point A as shown
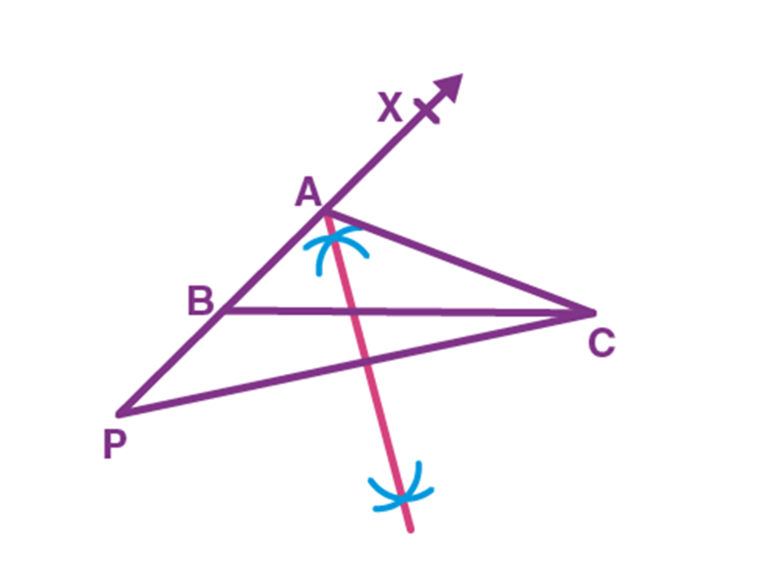
Step 3. Join the points A and C, and hence ∆ABC is the required triangle.

 ABCD CLASSES
ABCD CLASSES