Lines and Angles

Lines And Angles are the basic shapes in geometry. Lines are figures that are made up of infinite points extending indefinitely in both directions. Lines are straight and have negligible depth or width. There are a variety of lines you will learn about, such as perpendicular lines, intersecting lines, transversal lines, etc. An angle is a figure in which two rays emerge from a common point. You may also come across alternate and corresponding angles in this field.  Geometry shapes and their properties are the most practical branch of mathematics. Mostly this concept has been taught in Class 7 and Class 9.

Definition of Lines and Angles

As we have discussed, both lines and angles form the base for any shape in geometry. We cannot draw a two-dimensional to three-dimensional shape without using lines and angles. Thus, it is very necessary to learn the definitions of both terms.

Here, the basic definitions and properties of lines and also for angles are given. It will give the students a basic knowledge of these geometrical terms.

What are Lines?

A line is a straight one-dimensional figure, that extends in the opposite directions infinitely. A line can be horizontal or vertical. It can be drawn from left to right or top to bottom.

What are Angles?

Angles are the shape that is formed when the endpoints of two rays meet at a single point. They are measured in degrees (°) or radians. A complete rotation is equal to an angle of 360 degrees. It is represented by the symbol ‘∠’.

Types of Lines and Angles

There are various types of lines and angles in geometry based on the measurements and different scenarios. Let us learn here all those lines and angles along with their definitions.

Types of Lines

Lines are basically categorized as:

• Line segment
• Ray

Based on concepts or operations performed on lines, they are;

• Parallel Lines
• Perpendicular Lines
• Transversal

Line Segment - A line segment is a part of a line with two end-points. It is the shortest distance between two points and has a fixed length.

Ray - A ray is a part of a line, which has a starting point and extends infinitely in one direction.

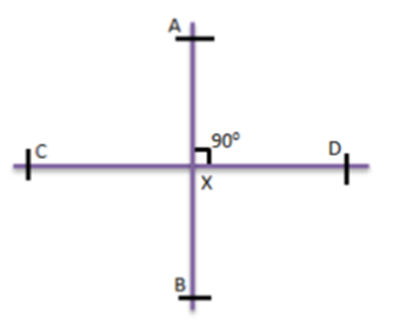
Perpendicular Lines - When two lines form a right angle with each other, by meeting at a single point, are called perpendicular lines. In the figure, you can see, lines AB and CD are perpendicular to each other.

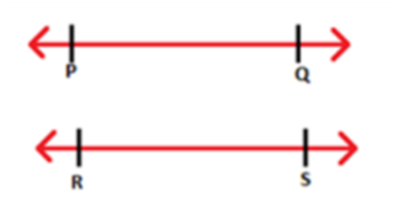
Parallel Lines - Two lines are said to be parallel when they do not meet at any point in a plane or which do not intersects each other. In the figure, lines PQ and RS are parallel to each other.

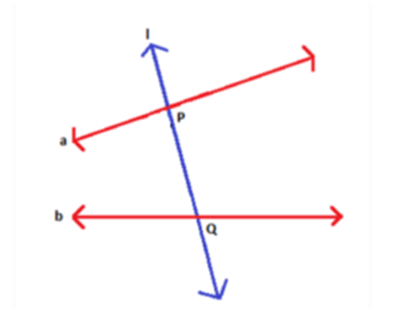
Transversal Line - When a line intersects two lines at distinct points, it is called a transversal. In the figure, a transversal l is intersecting two lines at point P and Q.

Types of Angles

Angles are basically classified as:

• Acute Angle(<90°)
• Right Angle(=90°)
• Obtuse Angle(>90°)
• Straight Angle(=180°)

And based on the relation between two angles, conceptual wise, they are;

• Supplementary Angles
• Complementary Angles
• Adjacent Angles
• Vertically Opposite Angles

Acute Angle

If the inclination between the arms is less than a right angle, it is called an acute angle.

Obtuse Angle

If the inclination between the arms is more than a right angle, it is called an obtuse angle.

Right Angle

If the arms form an angle of 90 degrees between them, it is called a right angle.

Straight Angle

If the arms form an angle of 180 degrees between them, it is called a straight angle.

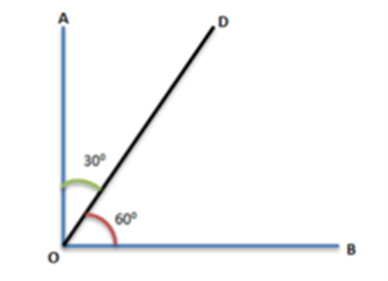
Complementary Angles

Two angles that sum up to 90 degrees are called complementary angles.

Supplementary Angles - Two angles that sum up to 180 degrees are called supplementary angles.

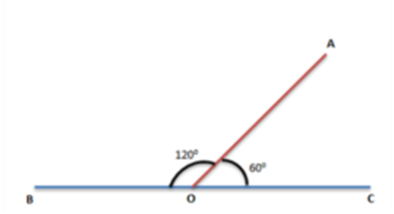
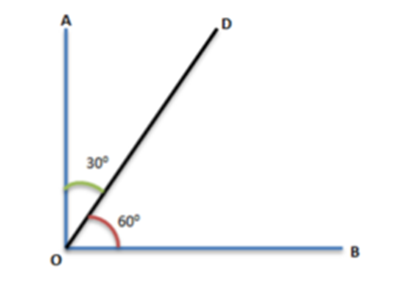
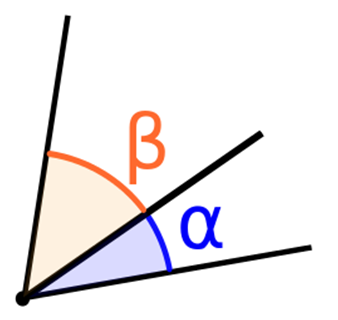
Adjacent Angles - Two angles that have a common side and a common vertex are called adjacent angles. In the following figure, ∠α and ∠β are adjacent angles.

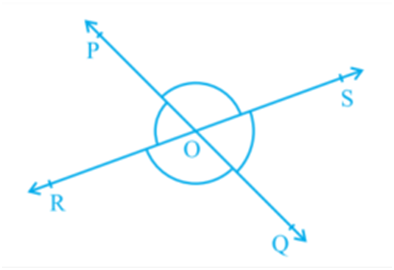
Vertically Opposite Angles - Two angles which are formed, opposite to each other, when two lines intersect at a common point or vertex, are called vertically opposite angles. In the figure, given below;

∠POR = ∠SOQ and ∠POS = ∠ROQ

Properties of Lines and Angles

Similar to other shapes and sizes in geometry, lines and angles also have their own properties. Let us see what are they.

Properties of Lines

• Collinear points are a set of three or more points that lie on the same line.
• The points which do not lie on the same line are called non-collinear points.

Note: Three points can be either collinear or non-collinear, but not both together at the same time.

Properties of Angles

• An angle is a figure in which two rays emerge from a common point. This point is called the vertex of the angle and the two rays forming the angle are called its arms or sides.
• An angle that is greater than 180 degrees but less than 360 degrees is called a reflex angle.
• If two adjacent angles add up to 180 degrees, they form a linear pair of angles. In the following figure, ∠a and ∠b form a linear pair.

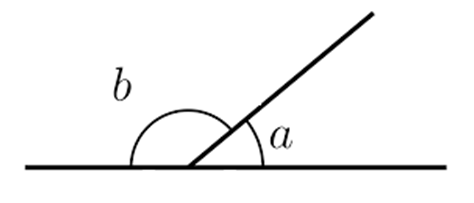
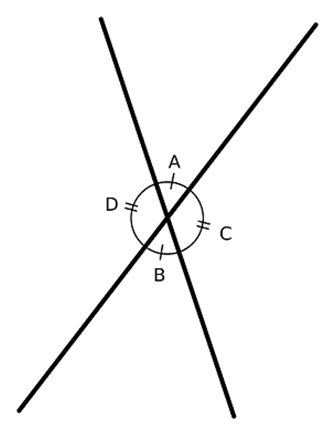
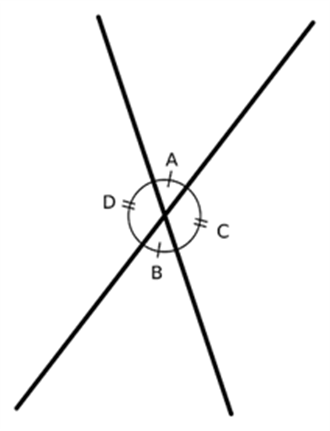
• When two lines intersect each other, the two opposite pairs of angles formed are called vertically opposite angles. In the following figure, ∠A and ∠B are vertically opposite angles. Another pair is ∠C and ∠D.

What are the five types of Angles?

The five types of angles are:

1. Acute Angle
2. Right Angle
3. Obtuse Angle
4. Straight Angle
5. Reflex Angle

What are the properties of Lines and Angles?

If two parallel lines are intersected by a transversal then:

• Its vertically opposite angles are always equal
• Its corresponding angles are equal
• Its alternate exterior and interior angles are equal

What are Lines and its types?

Lines are figures that are made up of infinite points extending indefinitely in both directions. The types of lines are:

1. Horizontal lines
2. Vertical lines
3. Parallel lines
4. Perpendicular lines

Chapter 6  -  Lines and Angles

Lines And Angles are the basic shapes in geometry. Lines are figures that are made up of infinite points extending indefinitely in both directions. Lines are straight and have negligible depth or width. There are a variety of lines you will learn about, such as perpendicular lines, intersecting lines, transversal lines, etc. An angle is a figure in which two rays emerge from a common point. You may also come across alternate and corresponding angles in this field.  Geometry shapes and their properties are the most practical branch of mathematics. Mostly this concept has been taught in Class 7 and Class 9.

Definition of Lines and Angles

As we have discussed, both lines and angles form the base for any shape in geometry. We cannot draw a two-dimensional to three-dimensional shape without using lines and angles. Thus, it is very necessary to learn the definitions of both terms.

Here, the basic definitions and properties of lines and also for angles are given. It will give the students a basic knowledge of these geometrical terms.

What are Lines?

A line is a straight one-dimensional figure, that extends in the opposite directions infinitely. A line can be horizontal or vertical. It can be drawn from left to right or top to bottom.

What are Angles?

Angles are the shape that is formed when the endpoints of two rays meet at a single point. They are measured in degrees (°) or radians. A complete rotation is equal to an angle of 360 degrees. It is represented by the symbol ‘∠’.

Types of Lines and Angles

There are various types of lines and angles in geometry based on the measurements and different scenarios. Let us learn here all those lines and angles along with their definitions.

Types of Lines

Lines are basically categorized as:

• Line segment
• Ray

Based on concepts or operations performed on lines, they are;

• Parallel Lines
• Perpendicular Lines
• Transversal

Line Segment

A line segment is a part of a line with two end-points. It is the shortest distance between two points and has a fixed length.

Ray

A ray is a part of a line, which has a starting point and extends infinitely in one direction.

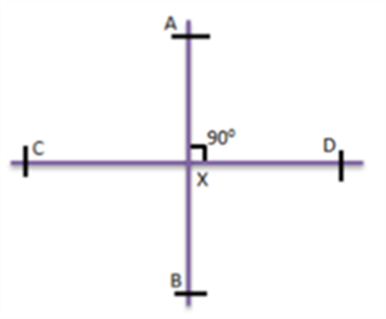
Perpendicular Lines

When two lines form a right angle with each other, by meeting at a single point, are called perpendicular lines. In the figure, you can see, lines AB and CD are perpendicular to each other.

Parallel Lines

Two lines are said to be parallel when they do not meet at any point in a plane or which do not intersects each other. In the figure, lines PQ and RS are parallel to each other.

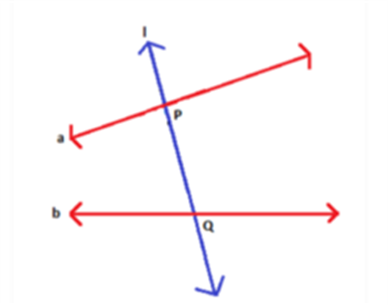
Transversal Line

When a line intersects two lines at distinct points, it is called a transversal. In the figure, a transversal l is intersecting two lines at point P and Q.

Types of Angles

Angles are basically classified as:

• Acute Angle(<90°)
• Right Angle(=90°)
• Obtuse Angle(>90°)
• Straight Angle(=180°)

And based on the relation between two angles, conceptual wise, they are;

• Supplementary Angles
• Complementary Angles
• Adjacent Angles
• Vertically Opposite Angles

Acute Angle

If the inclination between the arms is less than a right angle, it is called an acute angle.

Obtuse Angle

If the inclination between the arms is more than a right angle, it is called an obtuse angle.

Right Angle

If the arms form an angle of 90 degrees between them, it is called a right angle.

Straight Angle

If the arms form an angle of 180 degrees between them, it is called a straight angle.

Complementary Angles

Two angles which sum up to 90 degrees are called complementary angles.

Supplementary Angles

Two angles which sum up to 180 degrees are called supplementary angles.

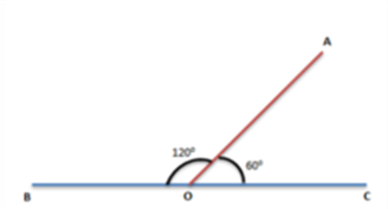
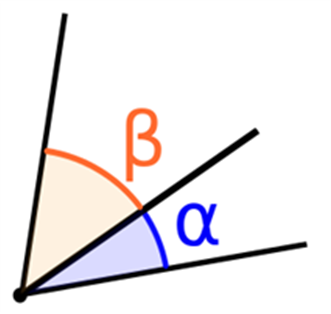
Adjacent Angles

Two angles which have a common side and a common vertex are called adjacent angles. In the following figure, ∠α and ∠β are adjacent angles.

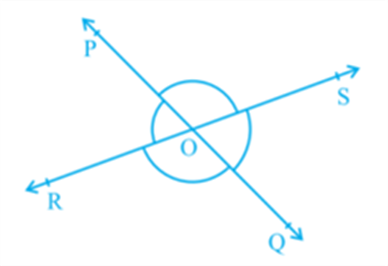
Vertically Opposite Angles

Two angles which are formed, opposite to each other, when two lines intersect at a common point or vertex, are called vertically opposite angles. In the figure, given below;

∠POR = ∠SOQ and ∠POS = ∠ROQ

Video Lesson on Lines

For More Information On Lines, Watch The Below Video:

10,432

Video Lessons on Types and Parts of Angles

Types of angles

1,36,490

Parts of Angles

14,976

Properties of Lines and Angles

Similar to other shapes and sizes in geometry, lines and angles also have their own properties. Let us see what are they.

Properties of Lines

• Collinear points are a set of three or more points which lie on the same line.
• The points which do not lie on the same line are called non-collinear points.

Note: Three points can be either collinear or non-collinear, but not both together at the same time.

Properties of Angles

• An angle is a figure in which two rays emerge from a common point. This point is called the vertex of the angle and the two rays forming the angle are called its arms or sides.
• An angle which is greater than 180 degrees but less than 360 degrees is called a reflex angle.
• If two adjacent angles add up to 180 degrees, they form a linear pair of angles. In the following figure, ∠a and ∠b form a linear pair.

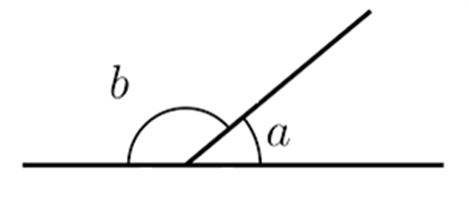
• When two lines intersect each other, the two opposite pairs of angles formed are called vertically opposite angles. In the following figure, ∠A and ∠B are vertically opposite angles. Another pair is ∠C and ∠D.

What are the five types of Angles?

The five types of angles are:

1. Acute Angle
2. Right Angle
3. Obtuse Angle
4. Straight Angle
5. Reflex Angle

What are the properties of Lines and Angles?

If two parallel lines are intersected by a transversal then:

• Its vertically opposite angles are always equal
• Its corresponding angles are equal
• Its alternate exterior and interior angles are equal

What are Lines and its types?

Lines are figures that are made up of infinite points extending indefinitely in both directions. The types of lines are:

1. Horizontal lines
2. Vertical lines
3. Parallel lines
4. Perpendicular lines

Intersecting Lines And Non-intersecting Lines

Before talking about what intersecting lines and non-intersecting lines are, let us recall the basic definition of a line. In geometry, a line is something that is made up of infinite points extending indefinitely in both directions. It is straight and has negligible depth or width.  It is illustrated by little arrows on the two sides. A line has no ends. In case, if the line has an endpoint, then it is called a line segment.

Any two points can be taken and a line can be drawn which passes through them and extends in both directions. For example, the line in the figure above is denoted by

.In this article, you will learn about two types of lines:

• Intersecting lines
• Non-intersecting lines

Intersecting Lines

Two or more lines which share exactly one common point are called intersecting lines. This common point exists on all these lines and is called the point of intersection.  It is to be noted that:

• The intersecting lines meet at one, and only one point, no matter at what angle they meet.
• No two straight lines can meet at more than one point.
• The lines that meet at more than one point are not straight lines. At least one of them is a curve.

Let us take a few examples.

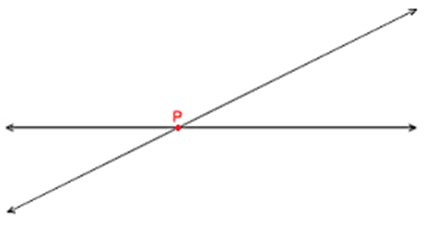
Consider these lines. They are two intersecting lines. The point of intersection is P.

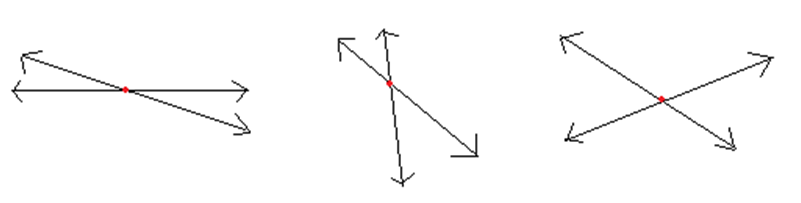
The figure above also shows intersecting lines at different angles.

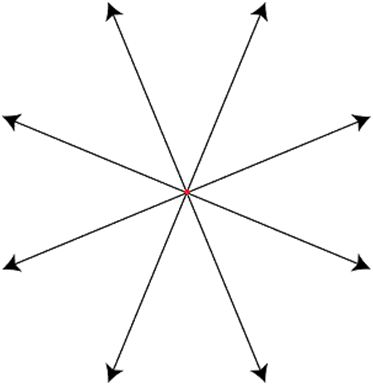
The figure shows an example of 4 intersecting lines.

Non-intersecting Lines

Two or more lines that do not intersect each other are called non-intersecting lines. It is to be noted that:

• Non-intersecting lines can never meet.
• They are also known as the parallel lines.
• They are always at the same distance from one another. This is called the distance between two parallel lines.

The figures above show non-intersecting or parallel lines.

 

Intersecting Lines And Non-intersecting Lines

Before talking about what intersecting lines and non-intersecting lines are, let us recall the basic definition of a line. In geometry, a line is something that is made up of infinite points extending indefinitely in both directions. It is straight and has negligible depth or width.  It is illustrated by little arrows on the two sides. A line has no ends. In case, if the line has an endpoint, then it is called a line segment.

Any two points can be taken and a line can be drawn which passes through them and extends in both directions. For example, the line in the figure above is denoted by

In this article, you will learn about two types of lines:

• Intersecting lines
• Non-intersecting lines

Intersecting Lines

Two or more lines which share exactly one common point are called intersecting lines. This common point exists on all these lines and is called the point of intersection.  It is to be noted that:

• The intersecting lines meet at one, and only one point, no matter at what angle they meet.
• No two straight lines can meet at more than one point.
• The lines that meet at more than one point are not straight lines. At least one of them is a curve.

Let us take a few examples.

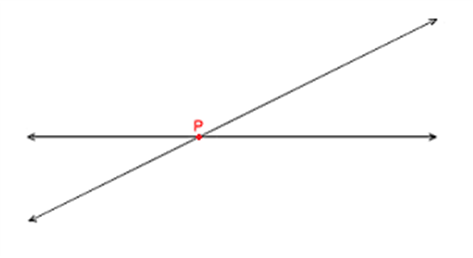
Consider these lines. They are two intersecting lines. The point of intersection is P.

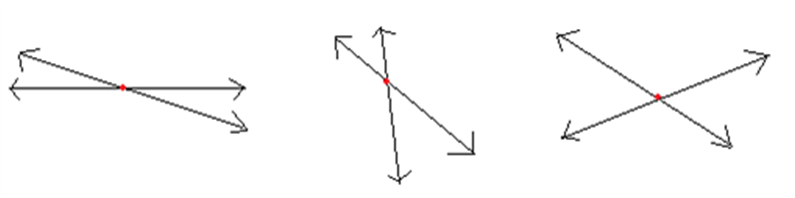
The figure above also shows intersecting lines at different angles.

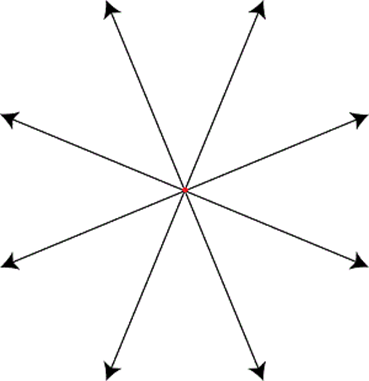
The figure shows an example of 4 intersecting lines.

8,288

Non-intersecting Lines

Two or more lines that do not intersect each other are called non-intersecting lines. It is to be noted that:

• Non-intersecting lines can never meet.
• They are also known as the parallel lines.
• They are always at the same distance from one another. This is called the distance between two parallel lines.

The figures above show non-intersecting or parallel lines.

Linear Pair Of Angles

Linear pair of angles are formed when two lines intersect each other at a single point. The angles are said to be linear if they are adjacent to each other after the intersection of the two lines. The sum of angles of a linear pair is always equal to 180°. Such angles are also known as supplementary angles. The adjacent angles are the angles which have a common vertex. Hence, here as well the linear angles have a common vertex. Also, there will be a common arm which represents both the angles. A real-life example of a linear pair is a ladder which is placed against a wall, forms linear angles at the ground.

Linearity represents one which is straight. So here also, linear angles are the one which is formed into a straight line. The pair of adjacent angles here are constructed on a line segment, but not all adjacent angles are linear. Hence, we can also say, that linear pair of angles is the adjacent angles whose non-common arms are basically opposite rays.

Explanation for Linear Pair of Angles

When the angle between the two lines is 180°, they form a straight angle. A straight angle is just another way to represent a straight line. A straight line can be visualized as a circle with an infinite radius. A line segment is any portion of a line which has two endpoints. Also, a portion of any line with only one endpoint is called a ray. A line segment with A and B as two endpoints is represented as

The figure shown below represents a line segment AB and the two arrows at the end indicate a line.

If a point O is taken anywhere on the line segment AB as shown, then the angle between the two line segments AO and OB is a straight angle i.e. 180°.

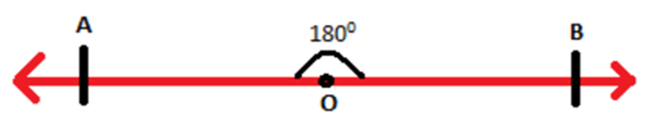
Consider a ray stand on the line segment as shown:

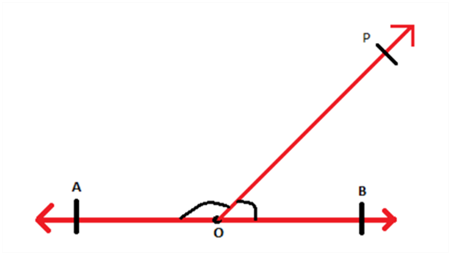
The angles which are formed at O are ∠POB and ∠POA. It is known that the angle between the two line segments AO and OB is 180°. therefore, the angles ∠POB and ∠POA add up to 180°.

Thus, ∠POB + ∠POA = ∠AOB = 180°

∠POB and ∠POA are adjacent to each other and when the sum of adjacent angles is 180° then such angles form linear pair of angles.

The above discussion can be stated as an axiom.

Axioms

Axiom 1: If a ray stands on a line then the adjacent angles form a linear pair of angles.

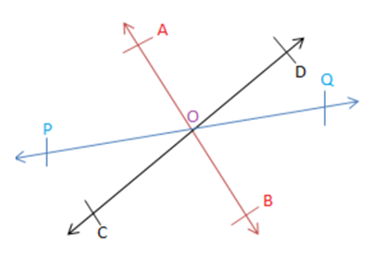
In the figure above, all the line segments pass through the point O as shown. As the ray OA lies on the line segment CD, angles ∠AOD and ∠AOC form a linear pair. Similarly, ∠QOD and ∠POD form a linear pair and so on.

The converse of the stated axiom is also true, which can also be stated as the following axiom.

Axiom 2: If two angles form a linear pair, then uncommon arms of both the angles form a straight line.

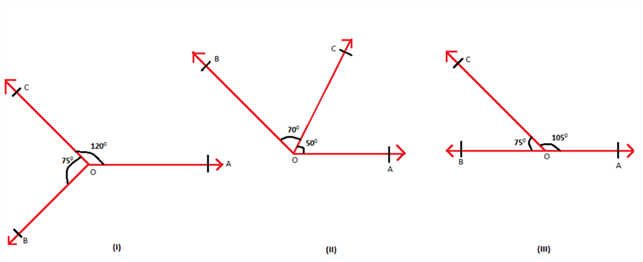
Figure 3 Adjacent angles with different measures

In the figure shown above, only the last one represents a linear pair, as the sum of the adjacent angles is 180°. Therefore, AB represents a line. The other two pairs of angles are adjacent but they do not form a linear pair. They do not form a straight line.

The two axioms mentioned above form the Linear Pair Axioms and are very helpful in solving various mathematical problems.

Example

Suppose two angles ∠AOC and ∠ BOC form a linear pair at point O in a line segment AB. If the difference between the two angles is 60°. Then find both the angles.

Solution: Given, ∠AOC and ∠ BOC form a linear pair

So, ∠AOC + ∠ BOC =180° ………(1)

Also given,

∠AOC – ∠ BOC = 60° ………(2)

Adding eq. 1 and 2, we get;

2∠AOC = 180° + 60° = 240°

∠AOC = 240°/2 = 120°

Now putting the value of ∠AOC in equation 1, we get;

∠BOC = 180° – ∠AOC = 180° – 120°

∠BOC = 60°

Linear Pair Of Angles

Linear pair of angles are formed when two lines intersect each other at a single point. The angles are said to be linear if they are adjacent to each other after the intersection of the two lines. The sum of angles of a linear pair is always equal to 180°. Such angles are also known as supplementary angles. The adjacent angles are the angles which have a common vertex. Hence, here as well the linear angles have a common vertex. Also, there will be a common arm which represents both the angles. A real-life example of a linear pair is a ladder which is placed against a wall, forms linear angles at the ground.

Linearity represents one which is straight. So here also, linear angles are the one which is formed into a straight line. The pair of adjacent angles here are constructed on a line segment, but not all adjacent angles are linear. Hence, we can also say, that linear pair of angles is the adjacent angles whose non-common arms are basically opposite rays.

Explanation for Linear Pair of Angles

When the angle between the two lines is 180°, they form a straight angle. A straight angle is just another way to represent a straight line. A straight line can be visualized as a circle with an infinite radius. A line segment is any portion of a line which has two endpoints. Also, a portion of any line with only one endpoint is called a ray. A line segment with A and B as two endpoints is represented as

. The figure shown below represents a line segment AB and the two arrows at the end indicate a line.

If a point O is taken anywhere on the line segment AB as shown, then the angle between the two line segments AO and OB is a straight angle i.e. 180°.

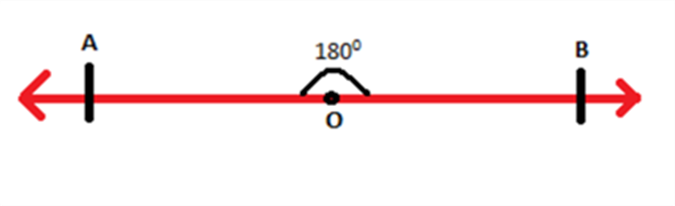
Consider a ray

stand on the line segment

as shown:

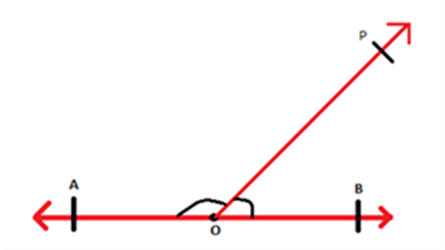
The angles which are formed at O are ∠POB and ∠POA. It is known that the angle between the two line segments AO and OB is 180°. therefore, the angles ∠POB and ∠POA add up to 180°.

Thus, ∠POB + ∠POA = ∠AOB = 180°

∠POB and ∠POA are adjacent to each other and when the sum of adjacent angles is 180° then such angles form linear pair of angles.

The above discussion can be stated as an axiom.

Axioms

Axiom 1: If a ray stands on a line then the adjacent angles form a linear pair of angles.

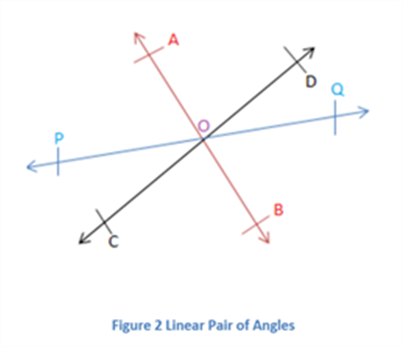
In the figure above, all the line segments pass through the point O as shown. As the ray OA lies on the line segment CD, angles ∠AOD and ∠AOC form a linear pair. Similarly, ∠QOD and ∠POD form a linear pair and so on.

The converse of the stated axiom is also true, which can also be stated as the following axiom.

Axiom 2: If two angles form a linear pair, then uncommon arms of both the angles form a straight line.

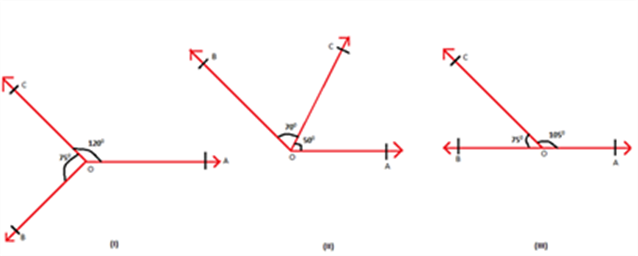
Figure 3 Adjacent angles with different measures

In the figure shown above, only the last one represents a linear pair, as the sum of the adjacent angles is 180°. Therefore, AB represents a line. The other two pairs of angles are adjacent but they do not form a linear pair. They do not form a straight line.

The two axioms mentioned above form the Linear Pair Axioms and are very helpful in solving various mathematical problems.

Example

Suppose two angles ∠AOC and ∠ BOC form a linear pair at point O in a line segment AB. If the difference between the two angles is 60°. Then find both the angles.

Solution: Given, ∠AOC and ∠ BOC form a linear pair

So, ∠AOC + ∠ BOC =180° ………(1)

Also given,

∠AOC – ∠ BOC = 60° ………(2)

Adding eq. 1 and 2, we get;

2∠AOC = 180° + 60° = 240°

∠AOC = 240°/2 = 120°

Now putting the value of ∠AOC in equation 1, we get;

∠BOC = 180° – ∠AOC = 180° – 120°

∠BOC = 60°

Parallel Lines & Transversal

In geometry, lines are classified into several types such as parallel, perpendicular, intersecting and non-intersecting lines, etc. For non-intersecting lines, we can draw a special line called transversal that intersects these lines at different points. In this article, you will learn about parallel lines, transversals and angle relationships with these lines along with suitable images and examples.

Parallel lines - Two lines are said to be parallel when they do not intersect each other. We can also say that two lines that run along and meet at infinity are called parallel lines.

Transversals - When a line intersects two lines at distinct points, it is called a transversal. In the below figure, line l intersects a and b at two distinct points, P and Q. Therefore, line l is the transversal line.

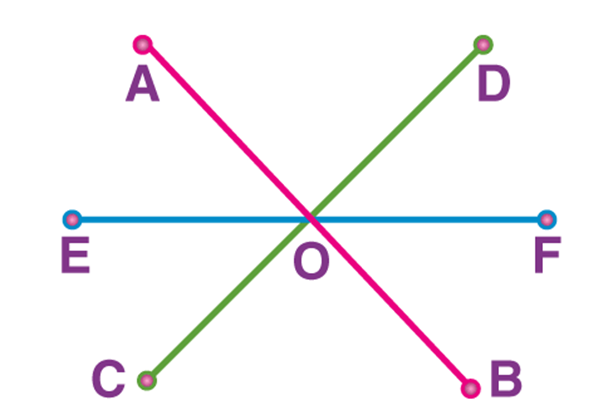
In the figure below, the line EF is not a transversal even if it intersects two lines AB and CD at O because it does not cut both lines at two distinct points. For a line to be transversal, it must cross two or more lines at separate points.

Angle Relationship Between the Parallel Lines and Transversal

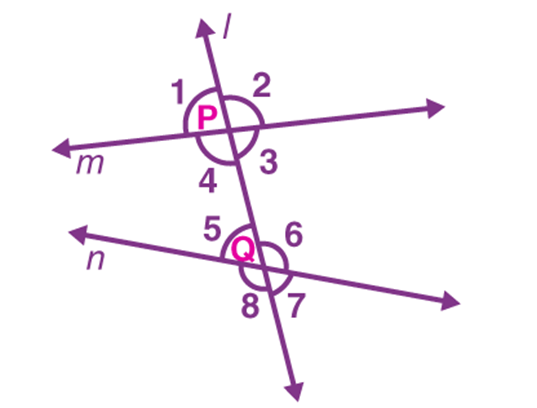
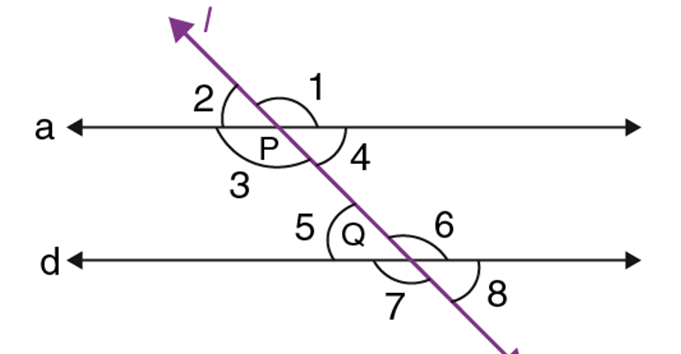
Various angle pairs are formed when a transversal intersects two or more parallel lines. Let us quickly recapitulate the angle relationships for the parallel lines cut by a transversal. Let a and d be two parallel lines intersected by the transversal l at the points P and Q, as shown in the figure below.

Now, we can write different pairs of angles and their corresponding relationships.

Corresponding Angles:

Corresponding angles are the angles which are formed in matching corners or corresponding corners with the transversal when two parallel lines and the transversal. 

∠1 and ∠6

∠4 and ∠8

∠2 and ∠5 

∠3 and ∠7

Also, if a transversal intersects two parallel lines, then each pair of corresponding angles is equal. Thus,

∠1 = ∠6

∠4 = ∠8

∠2 = ∠5 

∠3 = ∠7

Alternate interior angles:

Alternate interior angles are the angles formed when a transversal intersects two coplanar lines.

∠4 and ∠5 

∠3 and ∠6

However, if a transversal intersects two parallel lines, then each pair of alternate interior angles is equal.

∠4 = ∠5

∠3 = ∠6

Alternate exterior angles:

Alternate exterior angles are the pair of angles that are formed on the outer side of two lines but on the opposite side of the transversal. 

∠1 and ∠7 

∠2 and ∠8

If two parallel lines are cut by a transversal, then the resulting alternate exterior angles are congruent.

∠1 = ∠7 

∠2 = ∠8

Interior angles on the same side of the transversal:

Interior angles on the same side of the transversal are also referred to as consecutive interior angles or allied angles or co-interior angles.

∠3 and ∠5 

∠4 and ∠6

If a transversal intersects two parallel lines, then each pair of interior angles on the same side of the transversal is supplementary, i.e. they add up to 180°.

∠3 + ∠5 = 180°

∠4 + ∠6 = 180°

Vertically opposite angles

When two lines intersect each other, then the opposite angles, formed due to intersection, are called vertical angles or vertically opposite angles. Also, a pair of vertical angles are always congruent.

So,

∠1 = ∠3

∠2 = ∠4

∠7 = ∠6

∠8 = ∠5

The summary of angle relationships of parallel lines and transversal as given in the above figure is tabulated below:

Pair of angles formed	Angle relationships
Pairs of Corresponding angles	∠1 = ∠6, ∠4 = ∠8, ∠2 = ∠5, ∠3 = ∠7
Pairs of Alternate interior angles	∠4 = ∠5, ∠3 = ∠6
Pairs of Alternate exterior angles	∠1 = ∠7, ∠2 = ∠8
Pairs of Interior angles on the same side of the transversal	∠3 + ∠5 = 180°, ∠4 + ∠6 = 180°
Pairs of Vertically opposite angles	∠1 = ∠3, ∠2 = ∠4, ∠7 = ∠6, ∠8 = ∠5

Now, the question arises: how can we deduce if two lines are parallel or not? Is there any condition that demonstrates the parallel nature of two or more lines? Consider this situation.

His teacher asked Alan to draw two parallel lines. With the help of his set squares and ruler, he drew a straight line segment AB and then placed the set square on this line and drew two line segments XY and PQ, by changing the position of the set squares as shown.

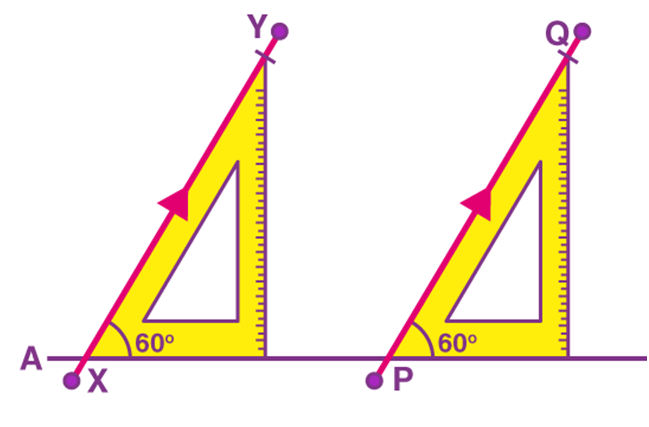
He claimed that XY and PQ are parallel. Can you tell how? It’s simply right. The line segment AB serves as the transversal to XY and PQ, and angle X and angle Y are corresponding angles in this case which are in equal measure. Therefore, XY and PQ are parallel line segments.

Parallel Lines & Transversal

In geometry, lines are classified into several types such as parallel, perpendicular, intersecting and non-intersecting lines, etc. For non-intersecting lines, we can draw a special line called transversal that intersects these lines at different points. In this article, you will learn about parallel lines, transversals and angle relationships with these lines along with suitable images and examples.

Parallel lines

Two lines are said to be parallel when they do not intersect each other. We can also say that two lines that run along and meet at infinity are called parallel lines.

Transversals

When a line intersects two lines at distinct points, it is called a transversal. In the below figure, line l intersects a and b at two distinct points, P and Q. Therefore, line l is the transversal line.

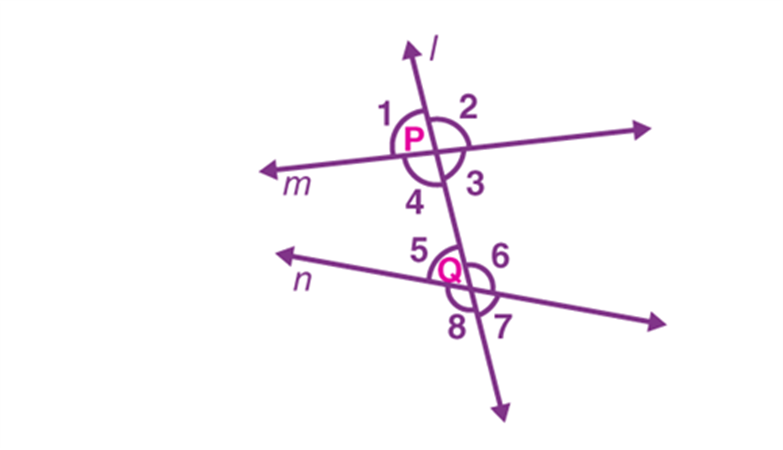
In the figure below, the line EF is not a transversal even if it intersects two lines AB and CD at O because it does not cut both lines at two distinct points. For a line to be transversal, it must cross two or more lines at separate points.

Angle Relationship Between the Parallel Lines and Transversal

Various angle pairs are formed when a transversal intersects two or more parallel lines. Let us quickly recapitulate the angle relationships for the parallel lines cut by a transversal. Let a and d be two parallel lines intersected by the transversal l at the points P and Q, as shown in the figure below.

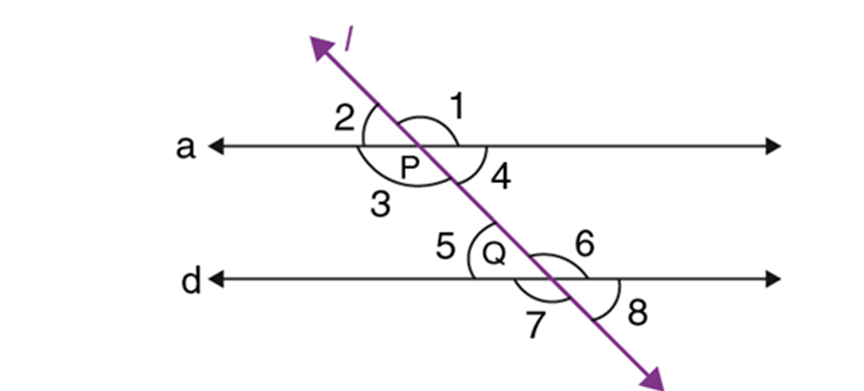
Now, we can write different pairs of angles and their corresponding relationships.

Corresponding Angles:

Corresponding angles are the angles which are formed in matching corners or corresponding corners with the transversal when two parallel lines and the transversal. 

∠1 and ∠6

∠4 and ∠8

∠2 and ∠5 

∠3 and ∠7

Also, if a transversal intersects two parallel lines, then each pair of corresponding angles is equal. Thus,

∠1 = ∠6

∠4 = ∠8

∠2 = ∠5 

∠3 = ∠7

Alternate interior angles:

Alternate interior angles are the angles formed when a transversal intersects two coplanar lines.

∠4 and ∠5 

∠3 and ∠6

However, if a transversal intersects two parallel lines, then each pair of alternate interior angles is equal.

∠4 = ∠5

∠3 = ∠6

Alternate exterior angles:

Alternate exterior angles are the pair of angles that are formed on the outer side of two lines but on the opposite side of the transversal. 

∠1 and ∠7 

∠2 and ∠8

If two parallel lines are cut by a transversal, then the resulting alternate exterior angles are congruent.

∠1 = ∠7 

∠2 = ∠8

Interior angles on the same side of the transversal:

Interior angles on the same side of the transversal are also referred to as consecutive interior angles or allied angles or co-interior angles.

∠3 and ∠5 

∠4 and ∠6

If a transversal intersects two parallel lines, then each pair of interior angles on the same side of the transversal is supplementary, i.e. they add up to 180°.

∠3 + ∠5 = 180°

∠4 + ∠6 = 180°

Vertically opposite angles

When two lines intersect each other, then the opposite angles, formed due to intersection, are called vertical angles or vertically opposite angles. Also, a pair of vertical angles are always congruent.

So,

∠1 = ∠3

∠2 = ∠4

∠7 = ∠6

∠8 = ∠5

The summary of angle relationships of parallel lines and transversal as given in the above figure is tabulated below:

Now, the question arises: how can we deduce if two lines are parallel or not? Is there any condition that demonstrates the parallel nature of two or more lines? Consider this situation.

His teacher asked Alan to draw two parallel lines. With the help of his set squares and ruler, he drew a straight line segment AB and then placed the set square on this line and drew two line segments XY and PQ, by changing the position of the set squares as shown.

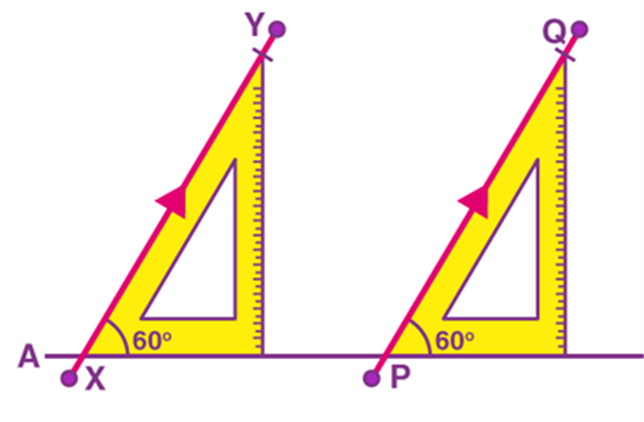
He claimed that XY and PQ are parallel. Can you tell how? It’s simply right. The line segment AB serves as the transversal to XY and PQ, and angle X and angle Y are corresponding angles in this case which are in equal measure. Therefore, XY and PQ are parallel line segments.

Solved Example

Question:

Observe the figure given below:

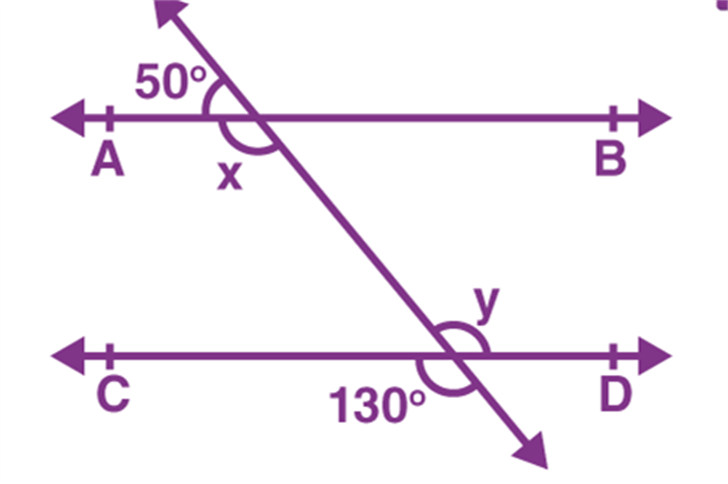
Find the missing angles.

Solution:

In the given figure, AB and CD are parallel lines and these are cut by a transversal line at two different points.

Here, x and 130° are the pair of corresponding angles.

So, x = 130°

Also, y and 130° are vertically opposite angles.

Thus, y = 130°

Lines Parallel to the Same Line

In Geometry, a line is defined as a one-dimensional geometric figure that extends infinitely in both directions. A line has no thickness. A line is generally made up of an infinite number of points. In this article, we will discuss the lines parallel to the same line and the theorem related to it with many solved examples.

What is Meant by Lines Parallel to the Same Line?

Theorem: Lines that are parallel to the same line are parallel to each other.

It means that if two lines are parallel to the same line, then they will be parallel to each other. Now, let us check this theorem with the help of the below figure.

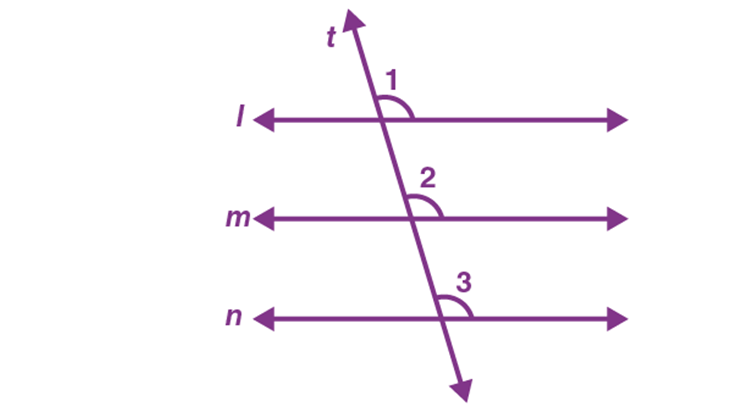
From the given figure, we can say that line m is parallel to line l and line n is parallel to line l. (i.e) line m || line l and line n || line l. Also, “t” is the transversal for the lines l, m and n.

Therefore, we can say that ∠1 = ∠2 and ∠1 = ∠3. (By corresponding angles axioms).

So, we can also say that ∠2 and ∠3 are corresponding and they are equal to each other.

Thus, ∠2 = ∠3

By using the converse of corresponding angle axioms, we conclude that line m is parallel to line n. (i.e) Line m || Line n.

Note: This property can be extended to more than two lines also.

Lines Parallel to the Same Line

In Geometry, a line is defined as a one-dimensional geometric figure that extends infinitely in both directions. A line has no thickness. A line is generally made up of an infinite number of points. In this article, we will discuss the lines parallel to the same line and the theorem related to it with many solved examples.

What is Meant by Lines Parallel to the Same Line?

Theorem: Lines that are parallel to the same line are parallel to each other.

It means that if two lines are parallel to the same line, then they will be parallel to each other. Now, let us check this theorem with the help of the below figure.

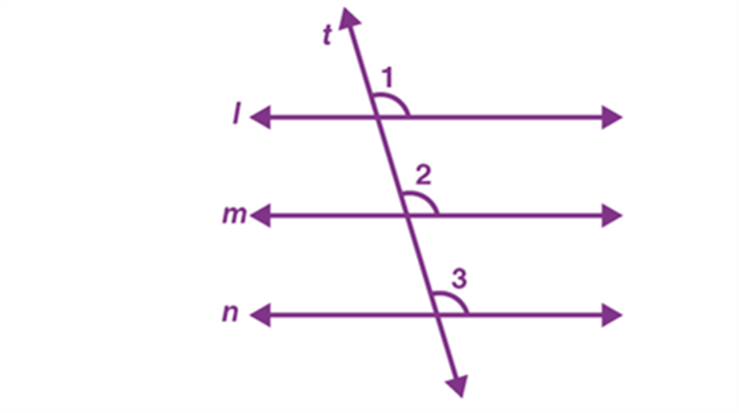
From the given figure, we can say that line m is parallel to line l and line n is parallel to line l. (i.e) line m || line l and line n || line l. Also, “t” is the transversal for the lines l, m and n.

Therefore, we can say that ∠1 = ∠2 and ∠1 = ∠3. (By corresponding angles axioms).

So, we can also say that ∠2 and ∠3 are corresponding and they are equal to each other.

Thus, ∠2 = ∠3

By using the converse of corresponding angle axioms, we conclude that line m is parallel to line n.

(i.e) Line m || Line n.

Note: This property can be extended to more than two lines also.

Solved Example

Example:

From the given figure, AB is parallel to CD and CD is parallel to EF.

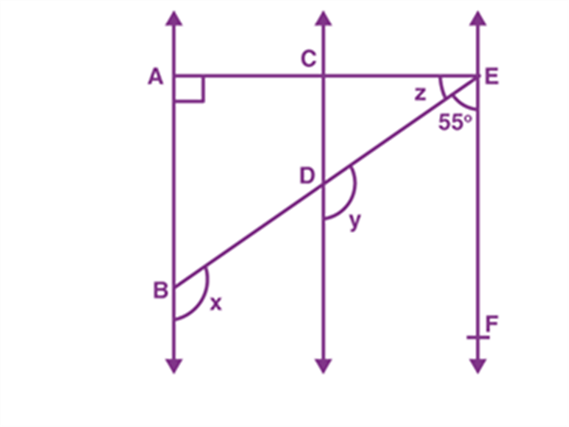
Also, given that EA is perpendicular to AB. Find the values of x, y and z, if ∠BEF = 55°.

Solution:

Given that AB|| CD, CD || EF, EA ⊥ AB, and ∠BEF = 55°.

Therefore, y+ 55° = 180° (Interior angles on the same side of transversal ED)

Hence, y = 180°-55°= 125°

By using the corresponding angles axiom, AB || CD, we can say that x = y.

Therefore, the value of x= 125°.

Since, AB || CD and CD || EF, therefore AB || EF.

So, we can write: ∠ FEA + ∠ EAB = 180° (Interior angles on the same side of transversal EA)

55° + z + 90° = 180°

z = 180° – 90° – 55°

z = 180° – 145°

z = 35°

Therefore, the values of x, y and z are 125°, 125° and 35°, respectively.

Practice Problems

Solve the following problems:

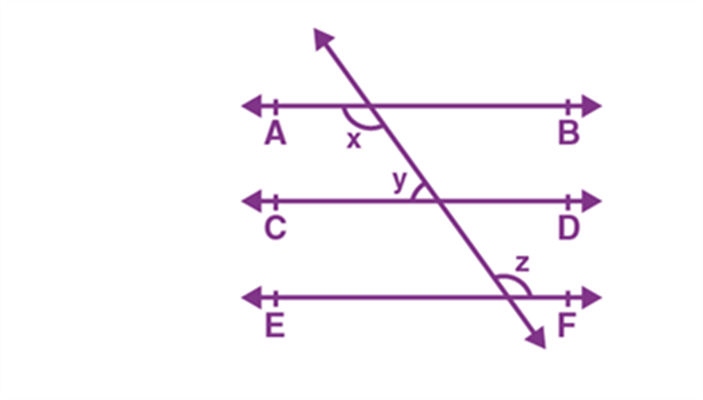
1. From the given figure, AB ||CD and CD || EF and y:z = 3:7. Find the value of x.

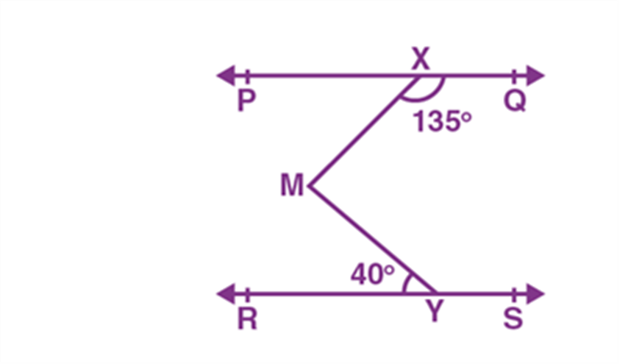
2. From the given figure, if PQ || RS and ∠MXQ = 135° and ∠MYR = 40°, then find the value of ∠XMY.

Angle Sum Property Of A Triangle

A triangle is the smallest polygon which has three sides and three interior angles. In this article, we are going to discuss the angle sum property and the exterior angle theorem of a triangle with its statement and proof in detail.

Angle Sum Property of a Triangle Theorem

In the given triangle, ∆ABC, AB, BC, and CA represent three sides. A, B and C are the three vertices and ∠ABC, ∠BCA and ∠CAB are three interior angles of ∆ABC.

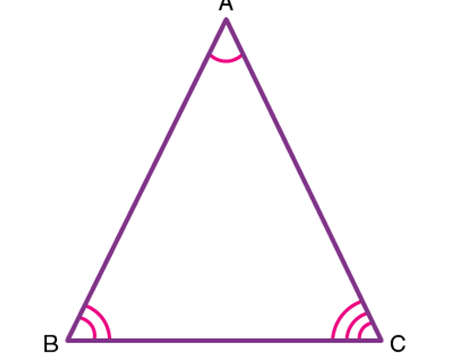
Theorem 1: Angle sum property of triangle states that the sum of interior angles of a triangle is 180°.

Proof: - Consider a ∆ABC, as shown in the figure below. To prove the above property of triangles, draw a line parallel to the side BC of the given triangle.

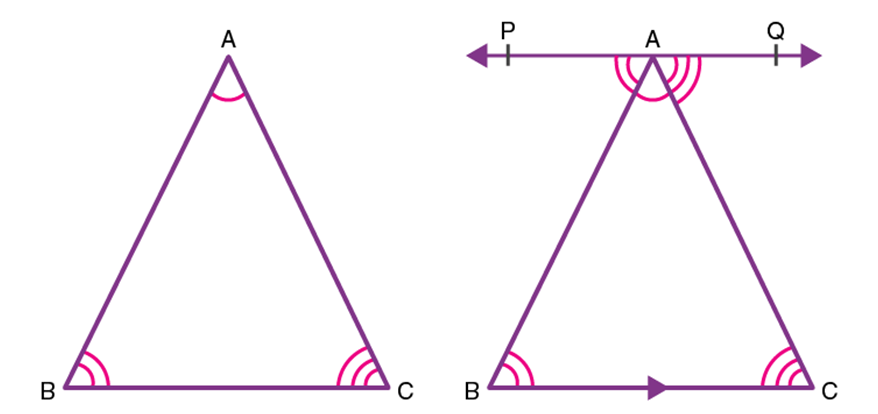
Since PQ is a straight line, it can be concluded that:

∠PAB + ∠BAC + ∠QAC = 180°  ………(1)

Since PQ||BC and AB, AC are transversals,

Therefore, ∠QAC = ∠ACB (a pair of alternate angle)

Also, ∠PAB = ∠CBA (a pair of alternate angle)

Substituting the value of ∠QAC and∠PAB in equation (1),

∠ACB + ∠BAC + ∠CBA= 180°

Thus, the sum of the interior angles of a triangle is 180°.

Exterior Angle Property of a Triangle Theorem

Theorem 2: If any side of a triangle is extended, then the exterior angle so formed is the sum of the two opposite interior angles of the triangle.

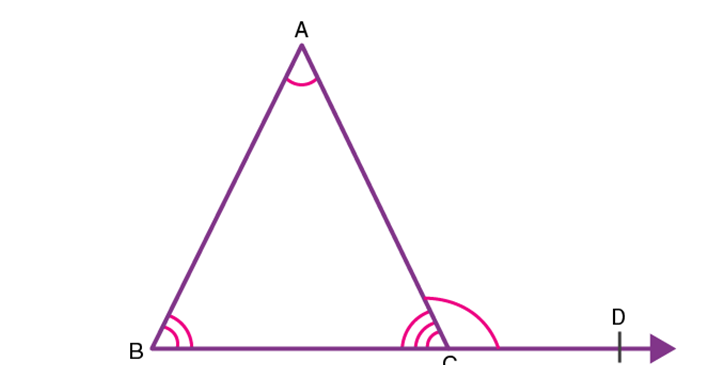
In the given figure, the side BC of ∆ABC is extended. The exterior angle ∠ACD so formed is the sum of measures of ∠ABC and ∠CAB.

Proof: - From figure 3, ∠ACB and ∠ACD form a linear pair since they represent the adjacent angles on a straight line.

Thus, ∠ACB + ∠ACD = 180°  ……….(2)

Also, from the angle sum property, it follows that:

∠ACB + ∠BAC + ∠CBA = 180° ……….(3)

From equation (2) and (3) it follows that:

∠ACD = ∠BAC + ∠CBA

This property can also be proved using the concept of parallel lines as follows:

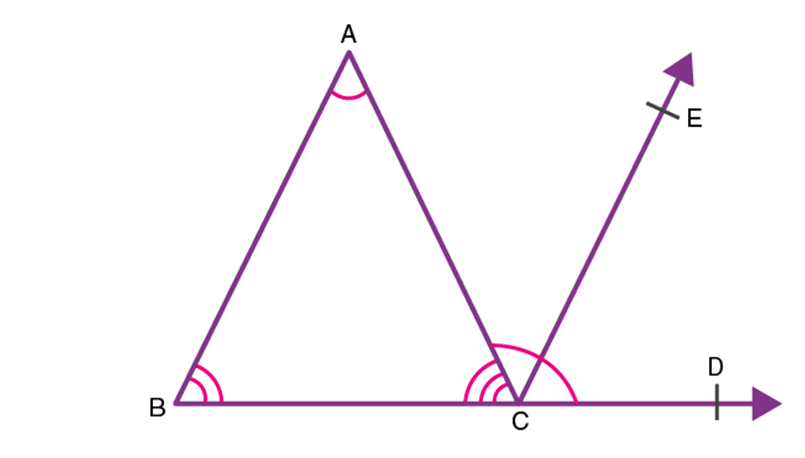
In the given figure, the side BC of ∆ABC is extended. A line parallel to the side AB is drawn, then: Since and is the transversal,

∠CAB = ∠ACE   ………(4) (Pair of alternate angles)

Also, and  is the transversal

Therefore, ∠ABC = ∠ECD  ……….(5) (Corresponding angles)

We have, ∠ACB + ∠BAC + ∠CBA = 180° ………(6)

Since the sum of angles on a straight line is 180°

Therefore, ∠ACB + ∠ACE + ∠ECD = 180° ………(7)

Since, ∠ACE + ∠ECD = ∠ACD(From figure 4)

Substituting this value in equation (7);

∠ACB + ∠ACD = 180° ………(8)

From the equations (6) and (8) it follows that,

∠ACD = ∠BAC + ∠CBA

Hence, it can be seen that the exterior angle of a triangle equals the sum of its opposite interior angles.

Angle Sum Property Of A Triangle

A triangle is the smallest polygon which has three sides and three interior angles. In this article, we are going to discuss the angle sum property and the exterior angle theorem of a triangle with its statement and proof in detail.

Angle Sum Property of a Triangle Theorem

In the given triangle, ∆ABC, AB, BC, and CA represent three sides. A, B and C are the three vertices and ∠ABC, ∠BCA and ∠CAB are three interior angles of ∆ABC.

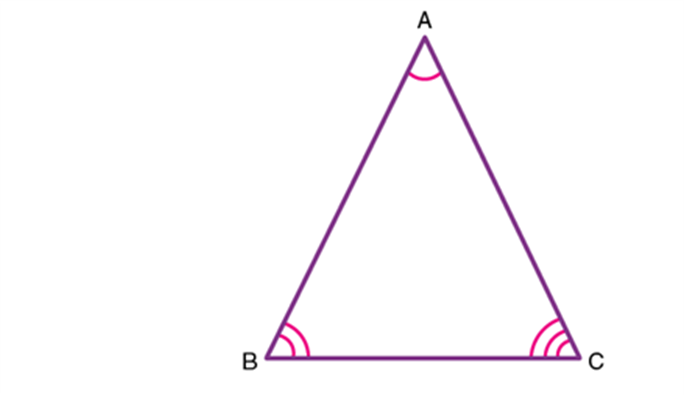
Theorem 1: Angle sum property of triangle states that the sum of interior angles of a triangle is 180°.

Proof: 

Consider a ∆ABC, as shown in the figure below. To prove the above property of triangles, draw a line

parallel to the side BC of the given triangle.

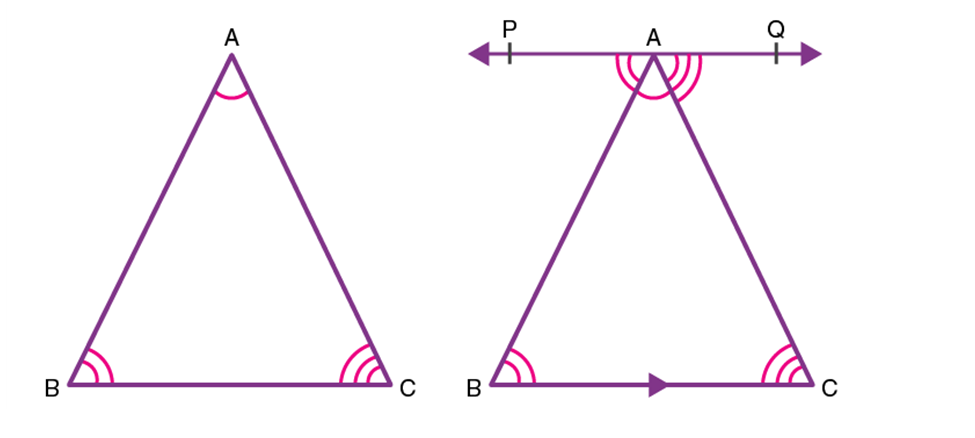
Since PQ is a straight line, it can be concluded that:

∠PAB + ∠BAC + ∠QAC = 180°  ………(1)

Since PQ||BC and AB, AC are transversals,

Therefore, ∠QAC = ∠ACB (a pair of alternate angle)

Also, ∠PAB = ∠CBA (a pair of alternate angle)

Substituting the value of ∠QAC and∠PAB in equation (1),

∠ACB + ∠BAC + ∠CBA= 180°

Thus, the sum of the interior angles of a triangle is 180°.

Exterior Angle Property of a Triangle Theorem

Theorem 2: If any side of a triangle is extended, then the exterior angle so formed is the sum of the two opposite interior angles of the triangle.

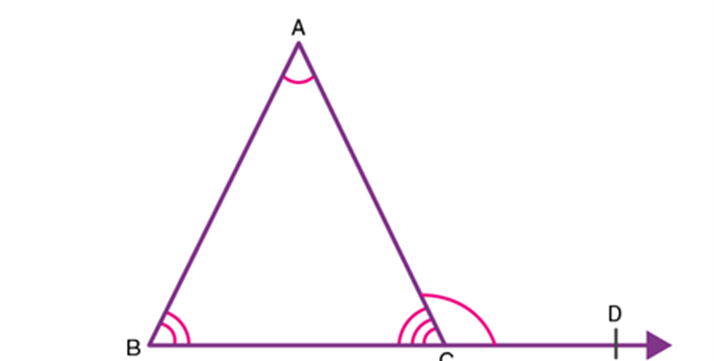
In the given figure, the side BC of ∆ABC is extended. The exterior angle ∠ACD so formed is the sum of measures of ∠ABC and ∠CAB.

Proof:

From figure 3, ∠ACB and ∠ACD form a linear pair since they represent the adjacent angles on a straight line.

Thus, ∠ACB + ∠ACD = 180°  ……….(2)

Also, from the angle sum property, it follows that:

∠ACB + ∠BAC + ∠CBA = 180° ……….(3)

From equation (2) and (3) it follows that:

∠ACD = ∠BAC + ∠CBA

This property can also be proved using the concept of parallel lines as follows:

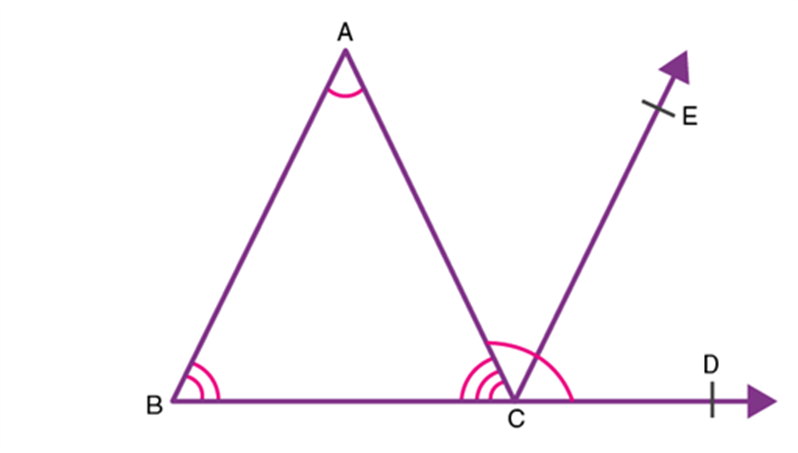
In the given figure, side BC of ∆ABC is extended. A line

 parallel to the side AB is drawn, then: Since

and

is the transversal,

∠CAB = ∠ACE   ………(4) (Pair of alternate angles)

Also, 

and

 is the transversal

Therefore, ∠ABC = ∠ECD  ……….(5) (Corresponding angles)

We have, ∠ACB + ∠BAC + ∠CBA = 180° ………(6)

Since the sum of angles on a straight line is 180°

Therefore, ∠ACB + ∠ACE + ∠ECD = 180° ………(7)

Since, ∠ACE + ∠ECD = ∠ACD(From figure 4)

Substituting this value in equation (7);

∠ACB + ∠ACD = 180° ………(8)

From the equations (6) and (8) it follows that,

∠ACD = ∠BAC + ∠CBA

Hence, it can be seen that the exterior angle of a triangle equals the sum of its opposite interior angles.

12,333