Angle sum property of a quadrilateral
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Quadrilateral: Angle Sum Property
Before talking about the quadrilaterals angle sum property, let us recall what angles and quadrilateral is. The angle is formed when two line segment joins at a single point. An angle is measured in degrees (°). Quadrilateral angles are the angles formed inside the shape of a quadrilateral. The quadrilateral is four-sided polygon that can have or not have equal sides. It is a closed figure in two-dimension and has non-curved sides. A quadrilateral is a polygon that has 4 vertices and 4 sides enclosing 4 angles and the sum of all the angles is 360°. When we draw draw the diagonals to the quadrilateral, it forms two triangles. Both these triangles have an angle sum of 180°. Therefore, the total angle sum of the quadrilateral is 360°. Angle sum is one of the properties of quadrilaterals. In this article, w will learn the rules of angle sum property.
Angle Sum Property of a Quadrilateral
According to the angle sum property of a Quadrilateral, the sum of all the four interior angles is 360 degrees.
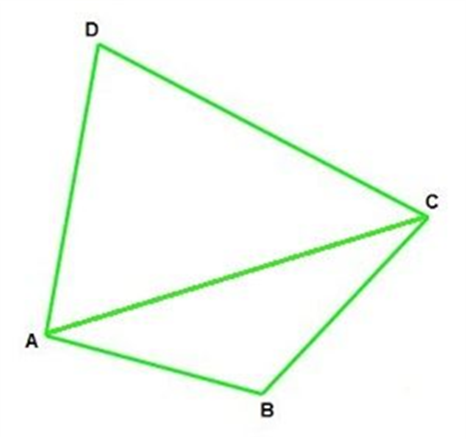
Proof: In the quadrilateral ABCD,
- ∠ABC, ∠BCD, ∠CDA, and ∠DAB are the internal angles.
- AC is a diagonal
- AC divides the quadrilateral into two triangles, ∆ABC and ∆ADC
We have learned that the sum of internal angles of a quadrilateral is 360°, that is, ∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°.
let’s prove that the sum of all the four angles of a quadrilateral is 360 degrees.
- We know that the sum of angles in a triangle is 180°.
- Now consider triangle ADC,
∠D + ∠DAC + ∠DCA = 180° (Sum of angles in a triangle)
- Now consider triangle ABC,
∠B + ∠BAC + ∠BCA = 180° (Sum of angles in a triangle)
- On adding both the equations obtained above we have,
(∠D + ∠DAC + ∠DCA) + (∠B + ∠BAC + ∠BCA) = 180° + 180°
∠D + (∠DAC + ∠BAC) + (∠BCA + ∠DCA) + ∠B = 360°
- We see that (∠DAC + ∠BAC) = ∠DAB and (∠BCA + ∠DCA) = ∠BCD.
- Replacing them we have,
∠D + ∠DAB + ∠BCD + ∠B = 360°
- That is,
∠D + ∠A + ∠C + ∠B = 360°.
Or, the sum of angles of a quadrilateral is 360°. This is the angle sum property of quadrilaterals.
Quadrilateral Angles
A quadrilateral has 4 angles. The sum of its interior angles is 360 degrees. We can find the angles of a quadrilateral if we know 3 angles or 2 angles or 1 angle and 4 lengths of the quadrilateral. In the image given below, a Trapezoid (also a type of Quadrilateral) is shown.
The sum of all the angles ∠A +∠B + ∠C + ∠D = 360°
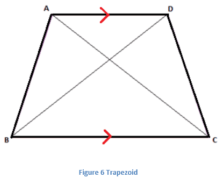
In the case of square and rectangle, the value of all the angles is 90 degrees. Hence, ∠A = ∠B = ∠C = ∠D = 90°
A quadrilateral, in general, has sides of different lengths and angles of different measures. However, squares, rectangles, etc. are special types of quadrilaterals with some of their sides and angles being equal.
Do the Opposite side in a Quadrilateral equals 180 Degrees?
There is no relationship between the opposite side and the angle measures of a quadrilateral. To prove this, the scalene trapezium has the side length of different measure, which does not have opposite angles of 180 degrees. But in case of some cyclic quadrilateral, such as square, isosceles trapezium, rectangle, the opposite angles are supplementary angles. It means that the angles add up to 180 degrees. One pair of opposite quadrilateral angles are equal in the kite and two pair of the opposite angles are equal in the quadrilateral such as rhombus and parallelogram. It means that the sum of the quadrilateral angles is equal to 360 degrees, but it is not necessary that the opposite angles in the quadrilateral should be of 180 degrees.
Types of Quadrilaterals
There are basically five types of quadrilaterals. They are;
- Parallelogram: Which has opposite sides as equal and parallel to each other.
- Rectangle: Which has equal opposite sides but all the angles are at 90 degrees.
- Square: Which all its four sides as equal and angles at 90 degrees.
- Rhombus: Its a parallelogram with all its sides as equal and its diagonals bisects each other at 90 degrees.
- Trapezium: Which has only one pair of sides as parallel and the sides may not be equal to each other.
Example
1. Find the fourth angle of a quadrilateral whose angles are 90°, 45° and 60°.
Solution: By the angle sum property we know;
Sum of all the interior angles of a quadrilateral = 360°
Let the unknown angle be x So,
90° + 45° + 60° + x = 360°
195° + x = 360°
x = 360° – 195°
x = 165°
Angle sum property of a quadrilateral
Chapter 8 - Quadrilaterals
Quadrilateral: Angle Sum Property
Before talking about the quadrilaterals angle sum property, let us recall what angles and quadrilateral is. The angle is formed when two line segment joins at a single point. An angle is measured in degrees (°). Quadrilateral angles are the angles formed inside the shape of a quadrilateral. The quadrilateral is four-sided polygon which can have or not have equal sides. It is a closed figure in two-dimension and has non-curved sides. A quadrilateral is a polygon which has 4 vertices and 4 sides enclosing 4 angles and the sum of all the angles is 360°. When we draw a draw the diagonals to the quadrilateral, it forms two triangles. Both these triangles have an angle sum of 180°. Therefore, the total angle sum of the quadrilateral is 360°. Angle sum is one of the properties of quadrilaterals. In this article, w will learn the rules of angle sum property.
Angle Sum Property of a Quadrilateral
According to the angle sum property of a Quadrilateral, the sum of all the four interior angles is 360 degrees.
Proof: In the quadrilateral ABCD,
- ∠ABC, ∠BCD, ∠CDA, and ∠DAB are the internal angles.
- AC is a diagonal
- AC divides the quadrilateral into two triangles, ∆ABC and ∆ADC
We have learned that the sum of internal angles of a quadrilateral is 360°, that is, ∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°.
let’s prove that the sum of all the four angles of a quadrilateral is 360 degrees.
- We know that the sum of angles in a triangle is 180°.
- Now consider triangle ADC,
∠D + ∠DAC + ∠DCA = 180° (Sum of angles in a triangle)
- Now consider triangle ABC,
∠B + ∠BAC + ∠BCA = 180° (Sum of angles in a triangle)
- On adding both the equations obtained above we have,
(∠D + ∠DAC + ∠DCA) + (∠B + ∠BAC + ∠BCA) = 180° + 180°
∠D + (∠DAC + ∠BAC) + (∠BCA + ∠DCA) + ∠B = 360°
- We see that (∠DAC + ∠BAC) = ∠DAB and (∠BCA + ∠DCA) = ∠BCD.
- Replacing them we have,
∠D + ∠DAB + ∠BCD + ∠B = 360°
- That is,
∠D + ∠A + ∠C + ∠B = 360°.
Or, the sum of angles of a quadrilateral is 360°. This is the angle sum property of quadrilaterals.
Quadrilateral Angles
A quadrilateral has 4 angles. The sum of its interior angles is 360 degrees. We can find the angles of a quadrilateral if we know 3 angles or 2 angles or 1 angle and 4 lengths of the quadrilateral. In the image given below, a Trapezoid (also a type of Quadrilateral) is shown.
The sum of all the angles ∠A +∠B + ∠C + ∠D = 360°
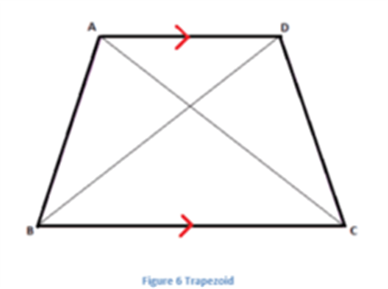
In the case of square and rectangle, the value of all the angles is 90 degrees. Hence,
∠A = ∠B = ∠C = ∠D = 90°
A quadrilateral, in general, has sides of different lengths and angles of different measures. However, squares, rectangles, etc. are special types of quadrilaterals with some of their sides and angles being equal.
Do the Opposite side in a Quadrilateral equals 180 Degrees?
There is no relationship between the opposite side and the angle measures of a quadrilateral. To prove this, the scalene trapezium has the side length of different measure, which does not have opposite angles of 180 degrees. But in case of some cyclic quadrilateral, such as square, isosceles trapezium, rectangle, the opposite angles are supplementary angles. It means that the angles add up to 180 degrees. One pair of opposite quadrilateral angles are equal in the kite and two pair of the opposite angles are equal in the quadrilateral such as rhombus and parallelogram. It means that the sum of the quadrilateral angles is equal to 360 degrees, but it is not necessary that the opposite angles in the quadrilateral should be of 180 degrees.
Types of Quadrilaterals
There are basically five types of quadrilaterals. They are;
- Parallelogram: Which has opposite sides as equal and parallel to each other.
- Rectangle: Which has equal opposite sides but all the angles are at 90 degrees.
- Square: Which all its four sides as equal and angles at 90 degrees.
- Rhombus: Its a parallelogram with all its sides as equal and its diagonals bisects each other at 90 degrees.
- Trapezium: Which has only one pair of sides as parallel and the sides may not be equal to each other.
Example
1. Find the fourth angle of a quadrilateral whose angles are 90°, 45° and 60°.
Solution: By the angle sum property we know;
Sum of all the interior angles of a quadrilateral = 360°
Let the unknown angle be x
So,
90° + 45° + 60° + x = 360°
195° + x = 360°
x = 360° – 195°
x = 165°
Types of Quadrilaterals
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Types of Quadrilaterals
Before talking about the types of quadrilaterals, let us recall what a quadrilateral is. A quadrilateral is a polygon that has the following properties
- 4 vertices and 4 sides enclosing 4 angles.
- The sum of all interior angles of a quadrilateral is 360 degrees.
- We can also derive the sum of interior angle from the formula of polygon i.e. (n -2) × 180, where n is equal to the number of sides of the polygon
A quadrilateral, in general, has sides of different lengths and angles of different measures. However, squares, rectangles, etc. are special types of quadrilaterals with some of their sides and angles being equal. This is the reason that the area of a quadrilateral depends on which type of quadrilateral it is. In this article, we will discuss the special types of quadrilaterals and their basic properties.
Different Types of Quadrilaterals
There are six basic types of quadrilaterals. They are:
- Trapezium
- Parallelogram
- Rectangle
- Rhombus
- Square
- Kite
Trapezium - It is a quadrilateral with one pair of opposite parallel sides. In the trapezium, ABCD, side AB is parallel to side CD.
Parallelogram - It is a quadrilateral with two pairs of parallel sides. The opposite sides are parallel and equal in length. The opposite angles are equal in measure. In the parallelogram, ABCD, side AB is parallel to side CD and side AD is parallel to side BC.
Also, the two diagonals formed to intersect each other at the midpoints. As in the figure given below, E is the point where both the diagonals meet. So
Length AE = EC, & Length BE = ED
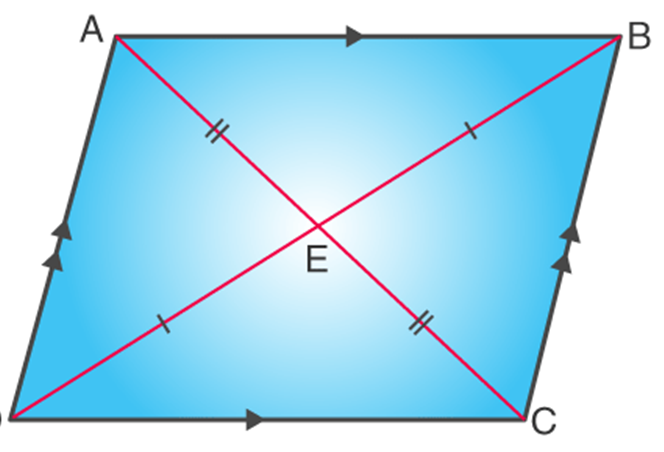
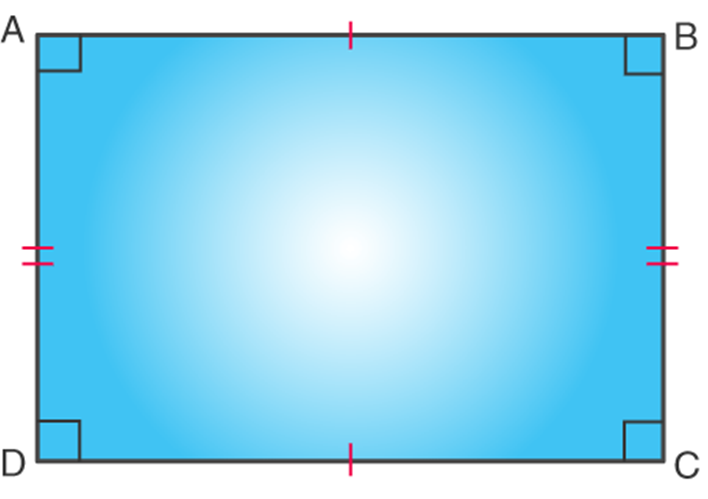
Rectangle - It is a quadrilateral with all the 4 angles of equal measure, that is, each of them is 90°. Both the pairs of opposite sides are parallel and equal in length.
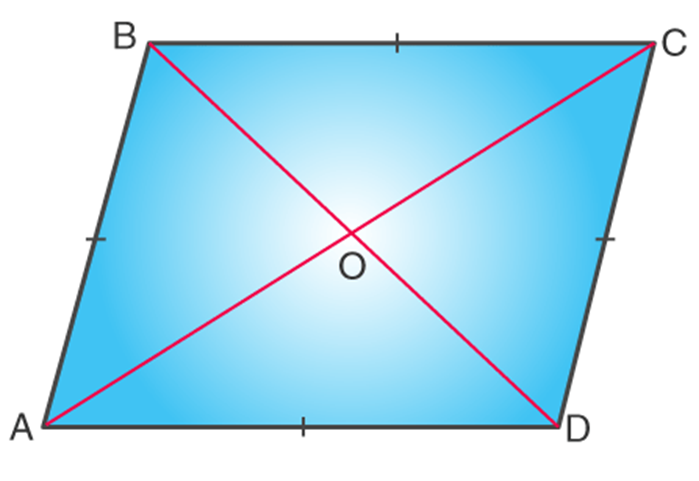
Rhombus - It is a quadrilateral with all four sides having equal lengths. The Opposite sides of a rhombus are parallel and opposite angles are equal.
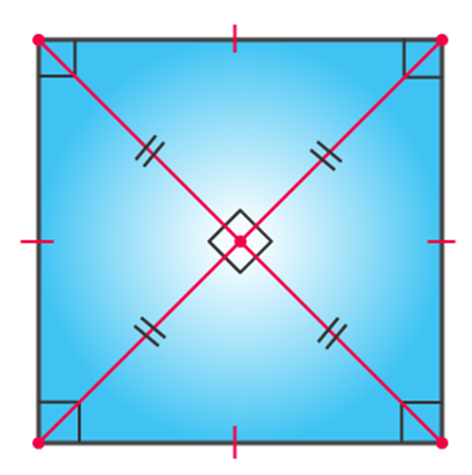
Square - It is a quadrilateral in which all the sides and angles are equal. Every angle is a right angle (i.e. 90° each). The pairs of opposite sides are parallel to each other.
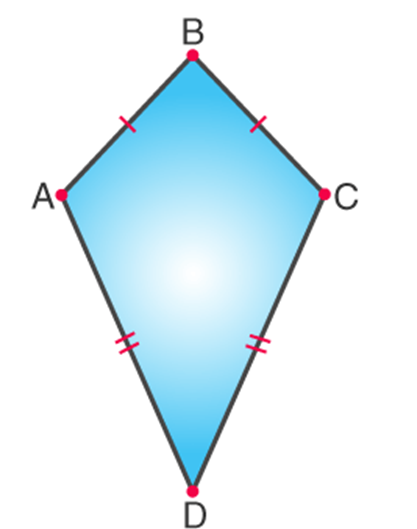
Kite - It is a quadrilateral that has 2 pairs of equal-length sides and these sides are adjacent to each other.
Some points about quadrilaterals to be kept in mind are:
- Square, rectangle, and rhombus are types of parallelograms.
- A square is a rectangle as well as a rhombus.
- Rectangle and rhombus are not a square.
- A parallelogram is a trapezium.
- A trapezium is not a parallelogram.
- Kite is not a parallelogram.
Types of Quadrilaterals
Types of Quadrilaterals
Before talking about the types of quadrilaterals, let us recall what a quadrilateral is. A quadrilateral is a polygon which has the following properties
- 4 vertices and 4 sides enclosing 4 angles.
- The sum of all interior angles of a quadrilateral is 360 degrees.
- We can also derive the sum of interior angle from the formula of polygon i.e. (n -2) × 180, where n is equal to the number of sides of the polygon
A quadrilateral, in general, has sides of different lengths and angles of different measures. However, squares, rectangles, etc. are special types of quadrilaterals with some of their sides and angles being equal. This is the reason that the area of quadrilateral depends on which type of quadrilateral it is. In this article, we will discuss the special types of quadrilaterals and their basic properties.
Different Types of Quadrilaterals
There are six basic types of quadrilaterals. They are:
- Trapezium
- Parallelogram
- Rectangle
- Rhombus
- Square
- Kite
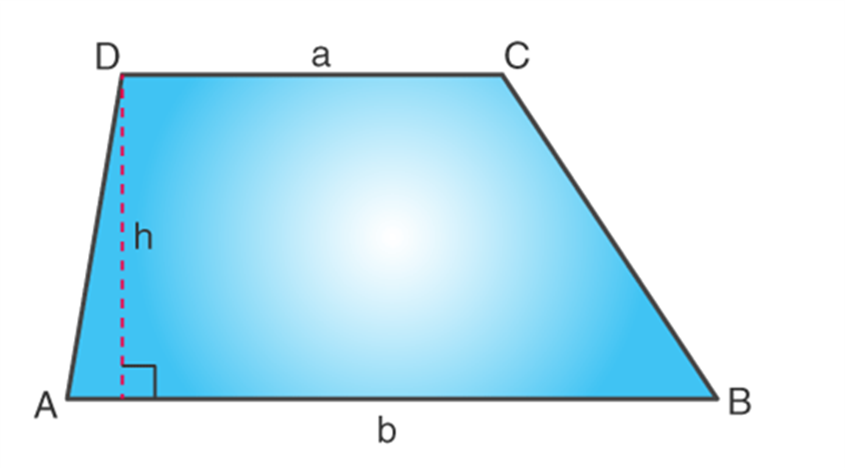
Trapezium
It is a quadrilateral with one pair of opposite parallel sides. In the trapezium, ABCD, side AB is parallel to side CD.
Parallelogram
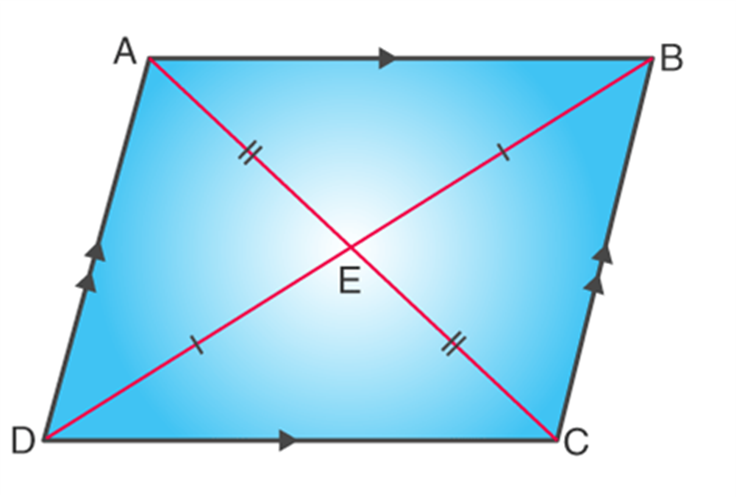
It is a quadrilateral with two pairs of parallel sides. The opposite sides are parallel and equal in length. The opposite angles are equal in measure. In the parallelogram, ABCD, side AB is parallel to side CD and side AD is parallel to side BC.
Also, the two diagonals formed to intersect each other at the midpoints. As in the figure given below, E is the point where both the diagonals meet. So
Length AE = EC, & Length BE = ED
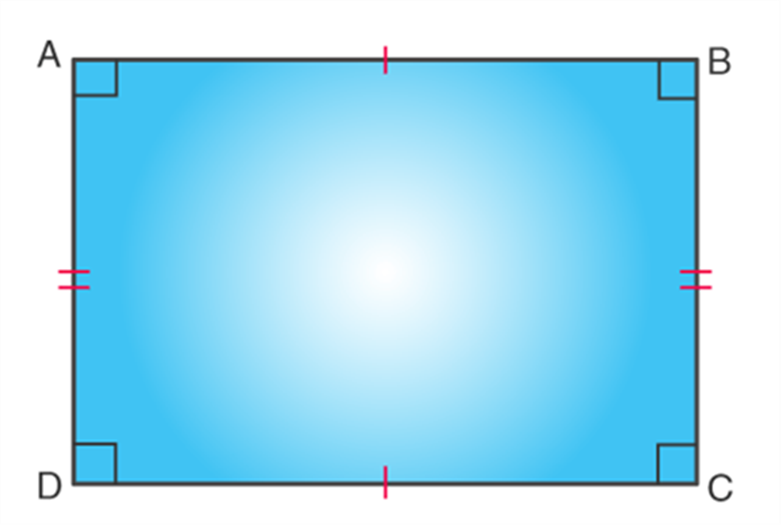
Rectangle
It is a quadrilateral with all the 4 angles of equal measure, that is, each of them is 90°. Both the pairs of opposite sides are parallel and equal in length.
Rhombus
It is a quadrilateral with all the four sides having equal lengths. The Opposite sides of a rhombus are parallel and opposite angles are equal.
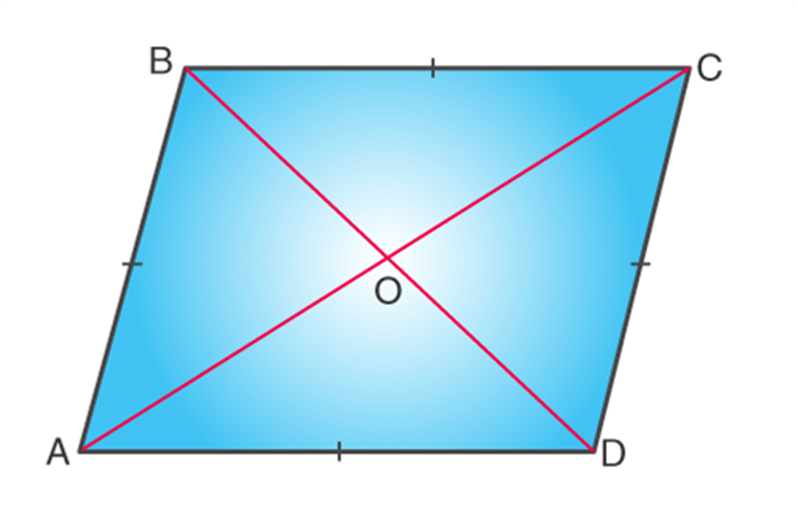
Square
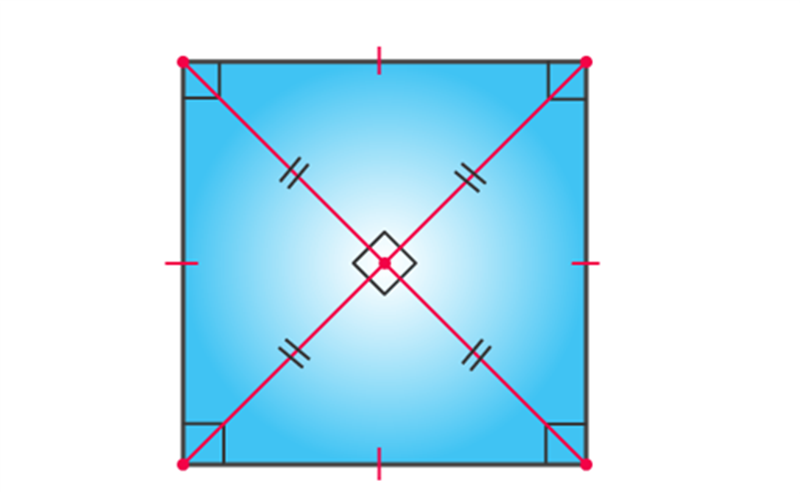
It is a quadrilateral in which all the sides and angles are equal. Every angle is a right angle (i.e. 90° each). The pairs of opposite sides are parallel to each other.
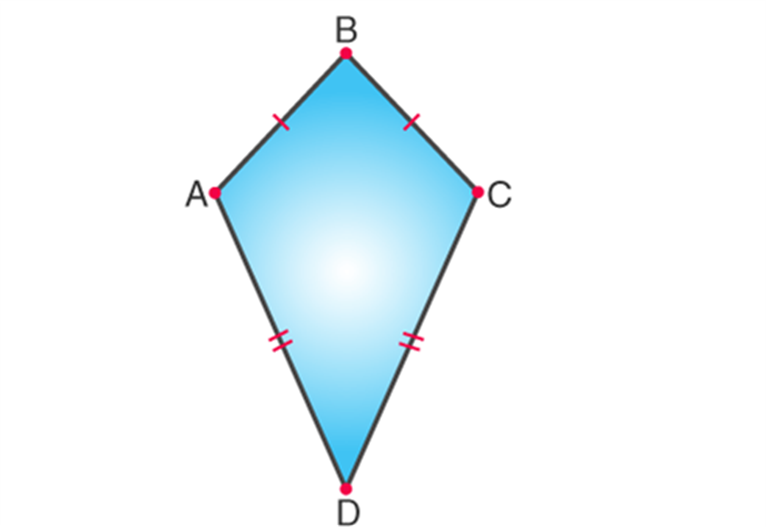
Kite
It is a quadrilateral that has 2 pairs of equal-length sides and these sides are adjacent to each other.
Some points about quadrilaterals to be kept in mind are:
- Square, rectangle, and rhombus are types of parallelograms.
- A square is a rectangle as well as a rhombus.
- Rectangle and rhombus are not a square.
- A parallelogram is a trapezium.
- A trapezium is not a parallelogram.
- Kite is not a parallelogram.
Properties of a Parallelogram
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Properties of a Parallelogram
A parallelogram is a two-dimensional geometrical shape, whose sides are parallel to each other. It is a type of polygon having four sides (also called quadrilateral), where the pair of parallel sides are equal in length. The Sum of adjacent angles of a parallelogram is equal to 180 degrees. In geometry, you must have learned about many 2D shapes and sizes such as circles, squares, rectangles, rhombus, etc. All of these shapes have a different set of properties. Also, the area and perimeter formulas of these shapes vary from each other and are used to solve many problems. Let us learn here the definition, formulas and properties of a parallelogram.
Parallelogram Definition
A parallelogram is a quadrilateral with two pairs of parallel sides. The opposite sides of a parallelogram are equal in length, and the opposite angles are equal in measure. Also, the interior angles on the same side of the transversal are supplementary. Sum of all the interior angles equals 360 degrees.
A three-dimensional shape that has its faces in a parallelogram shape, is called a parallelepiped. The area of the parallelogram depends on the base (one of its parallel sides) and the height (altitude drawn from top to bottom) of it. The perimeter of a parallelogram depends on the length of its four sides.
A square and a rectangle are two shapes that have similar properties to a parallelogram.
Rhombus: If all the sides of a parallelogram are congruent or equal to each other, then it is a rhombus.
If there is one parallel side and the other two sides are non-parallel, then it is a trapezium.
See the figure below:
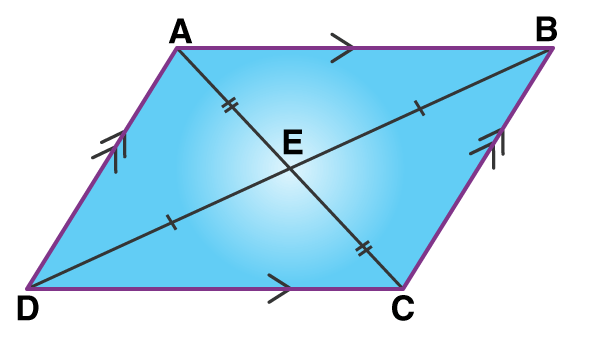
In the figure above, you can see, ABCD is a parallelogram, where AB || CD and AD || BC.
Also, AB = CD and AD = BC
And, ∠A = ∠C & ∠B = ∠D
Also, ∠A & ∠D are supplementary angles because these interior angles lie on the same side of the transversal. In the same way, ∠B & ∠C are supplementary angles.
Therefore,
∠A + ∠D = 180
∠B + ∠C = 180
|
Facts:
|
Shape of Parellelogram
A parallelogram is a two-dimensional shape. It has four sides, in which two pairs of sides are parallel. Also, the parallel sides are equal in length. If the length of the parallel sides is not equal in measurement, then the shape is not a parallelogram. Similarly, the opposite interior angles of parallelogram should always be equal. Otherwise, it is not a parallelogram.
Special Parallelograms
Square and Rectangle: A square and a rectangle are two shapes that have similar properties to a parallelogram. Both have their opposite sides equal and parallel to each other. Diagonals of both shapes bisect each other.
Rhombus: If all the sides of a parallelogram are congruent or equal to each other, then it is a rhombus.
Rhomboid: A special case of a parallelogram that has its opposite sides parallel to each other but adjacent sides are of unequal lengths. Also, the angles are equal to 90 degrees.
Trapezium: If there is one parallel side and the other two sides are non-parallel, then it is a trapezium.
Angles of Parallelogram
A parallelogram is a flat 2d shape that has four angles. The opposite interior angles are equal. The angles on the same side of the transversal are supplementary, which means they add up to 180 degrees. Hence, the sum of the interior angles of a parallelogram is 360 degrees.
Properties of Parallelogram
If a quadrilateral has a pair of parallel opposite sides, then it’s a special polygon called Parallelogram. The properties of a parallelogram are as follows:
- The opposite sides are parallel and congruent
- The opposite angles are congruent
- The consecutive angles are supplementary
- If any one of the angles is a right angle, then all the other angles will be at the right angle
- The two diagonals bisect each other
- Each diagonal bisects the parallelogram into two congruent triangles
- The Sum of squares of all the sides of a parallelogram is equal to the sum of squares of its diagonals. It is also called parallelogram law
Formulas (Area & Perimeter)
The formula for the area and perimeter of a parallelogram is covered here in this section. Students can use these formulas and solve problems based on them.
Area of Parallelogram
Area of a parallelogram is the region occupied by it in a two-dimensional plane. Below is the formula to find the parallelogram area:
Area = Base × Height
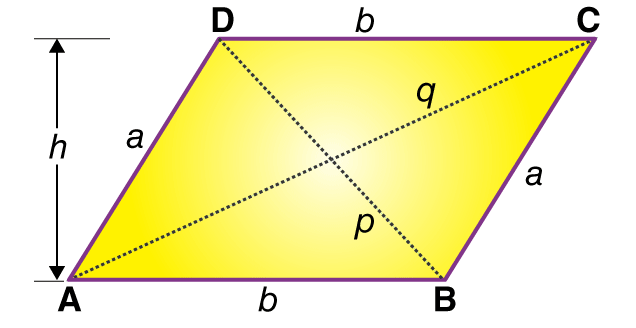
In the above figure, ||gramABCD, Area is given by;
|
Area = a b sin A = b a sin B |
where a is the slant length of the side of ||gramABCD and b is the base.
Check here: Area of a Parallelogram Formula
Perimeter of Parallelogram
The perimeter of any shape is the total distance covered around the shape or the total length of any shape. Similarly, the perimeter of a parallelogram is the total distance of the boundaries of the parallelogram. To calculate the perimeter value, we have to know the values of its length and breadth. The parallelogram has its opposite sides equal in length. Therefore, the formula to calculate the perimeter is written as;
|
Perimeter = 2 (a+b) units |
Where a and b are the length of the sides of the parallelogram.
Types of Parallelogram
There are mainly four types of Parallelogram, depending on various factors. The factors which distinguish between all of these different types of parallelograms are angles, sides etc.
- In a parallelogram, say PQRS
- If PQ = QR = RS = SP are the equal sides, then it’s a rhombus. All the properties are the same for rhombus as for parallelogram.
- Other two special types of a parallelogram are:
- Rectangle
- Square
Is Square a Parallelogram?
Square could be considered as a parallelogram since the opposite sides are parallel to each other, and the diagonals of the square bisect each other.
Is Rectangle a Parallelogram?
Yes, a rectangle is also a parallelogram, because it satisfies the conditions or meets the properties of a parallelogram such as the opposite sides are parallel and diagonals bisect each other.
Parallelogram Theorems
Theorem 1: Parallelograms on the same base and between the same parallel sides are equal in area.
Proof: Two parallelograms ABCD and ABEF, on the same base DC and between the same parallel line AB and FC.
To prove that area (ABCD) = area (ABEF).
Proof:
Consider the figure given below:
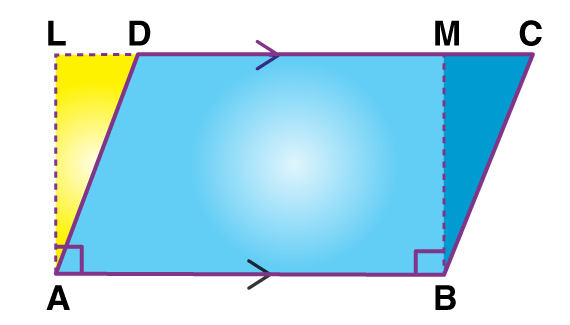
Parallelogram ABCD and rectangle ABML are on the same base and between the same parallels AB and LC.
area of parallelogram ABCD = area of parallelogram ABML
We know that area of a rectangle = length x breadth.
Therefore, area of parallelogram ABCD = AB x AL
Hence, the area of a parallelogram is the product of any base of it and the corresponding altitude.
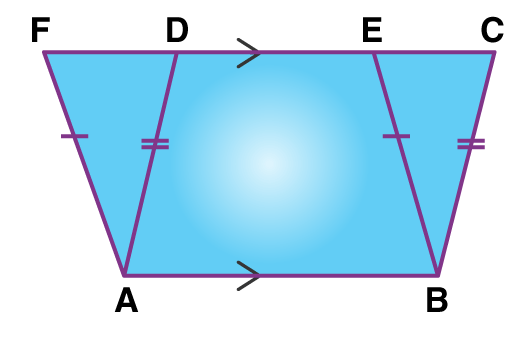
In ∆ADF and ∆BCE,
AD=BC (∴ABCD is a parallelogram ∴ AD=BC)
AF=BE (∴ABEF is a parallelogram ∴AF=BE)
∠ADF=∠BCE (Corresponding Angles)
∠AFD=∠BEC (Corresponding Angles)
∠DAF =∠CBE (Angle Sum Property)
∆ADE ≅ ∆BCF (From SAS-rule)
Area(ADF) = Area(BCE) (By congruence area axiom)
Area(ABCD)=Area(ABED) + Area(BCE)
Area(ABCD)=Area(ABED)+Area(ADF)
Area(ABCD)=Area(ABEF)
Hence, the area of parallelograms on the same base and between the same parallel sides is equal.
Corollary
A parallelogram and a rectangle on the same base and between the same parallels are equal in area.
Proof: Since a rectangle is also a parallelogram so, the result is a direct consequence of the above theorem.
Theorem: The area of a parallelogram is the product of its base and the corresponding altitude.
Given: In a parallelogram ABCD, AB is the base.
To prove that Area(||gmABCD) = AB×AL
Construction: Complete the rectangle ALMB by Drawing BM perpendicular to CD.
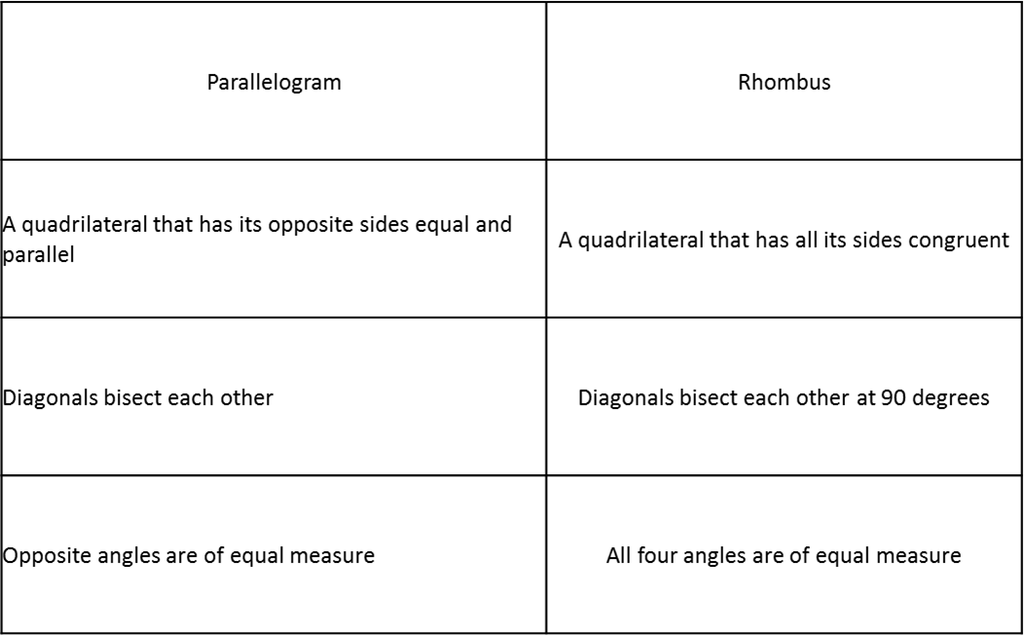
Difference Between Parallelogram and Rhombus
|
Parallelogram |
Rhombus |
|
A quadrilateral that has its opposite sides equal and parallel |
A quadrilateral that has all its sides congruent |
|
Diagonals bisect each other |
Diagonals bisect each other at 90 degrees |
|
Opposite angles are of equal measure |
All four angles are of equal measure |
Examples on Parallelogram
|
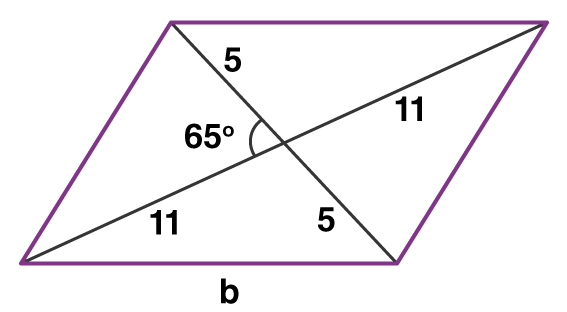
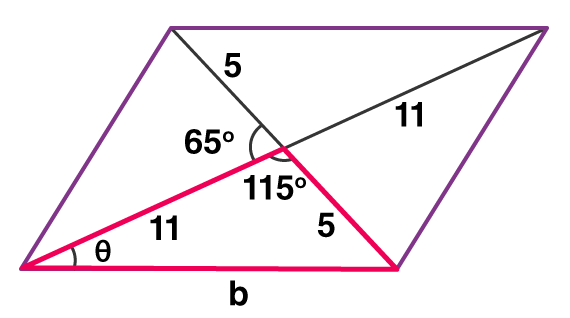
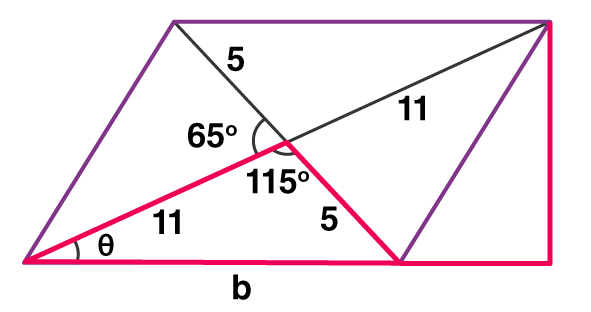
Example 1: Find the area of a parallelogram whose base is 5 cm and height is 8 cm. Solution-: Given, Base = 5 cm and Height = 8 cm. We know, Area = Base x Height Area = 5 × 8 Area = 40 Sq.cm Example 2: Find the area of a parallelogram having a length of diagonals to be 10 and 22 cm and an intersecting angle to be 65 degrees. Solution: We know that the diagonals of a parallelogram bisect each other. Hence, the length of half the diagonal will be 5 and 11 cm.
The angle opposite to the side b comes out to be 180 – 65 = 115° We use the law of cosines to calculate the base of the parallelogram – b² = 5² + 11² – 2(11)(5)cos(115°) b² = 25 + 121 – 110(-0.422) b² = 192.48 b = 13.87 cm.
After finding the base, we need to calculate the height of the given parallelogram. To find the height we have to calculate the value of θ, so we use sine law 5/sin(θ) = b/sin(115)
Now we extend the base and draw in the height of the figure and denote it as ‘h’. The right-angled triangle (marked with a red line) has the Hypotenuse to be 22 cm and the Perpendicular to be h. So sin θ = h/22 h = 7.184 cm Area = base × height A = 13.87 × 7.184 A = 99.645 sq.cm |
Properties of a Parallelogram
Properties of a Parallelogram
A parallelogram is a two-dimensional geometrical shape, whose sides are parallel to each other. It is a type of polygon having four sides (also called quadrilateral), where the pair of parallel sides are equal in length. The Sum of adjacent angles of a parallelogram is equal to 180 degrees. In geometry, you must have learned about many 2D shapes and sizes such as circle, square, rectangle, rhombus, etc. All of these shapes have a different set of properties. Also, the area and perimeter formulas of these shapes vary from each other and are used to solve many problems. Let us learn here the definition, formulas and properties of a parallelogram.
Parallelogram Definition
A parallelogram is a quadrilateral with two pairs of parallel sides. The opposite sides of a parallelogram are equal in length, and the opposite angles are equal in measure. Also, the interior angles on the same side of the transversal are supplementary. Sum of all the interior angles equals 360 degrees.
A three-dimensional shape that has its faces in parallelogram shape, is called a parallelepiped. The area of parallelogram depends on the base (one of its parallel sides) and height (altitude drawn from top to bottom) of it. The perimeter of a parallelogram depends on the length of its four sides.
A square and a rectangle are two shapes which have similar properties of a parallelogram.
Rhombus: If all the sides of a parallelogram are congruent or equal to each other, then it is a rhombus.
If there is one parallel side and the other two sides are non-parallel, then it is a trapezium.
See the figure below:
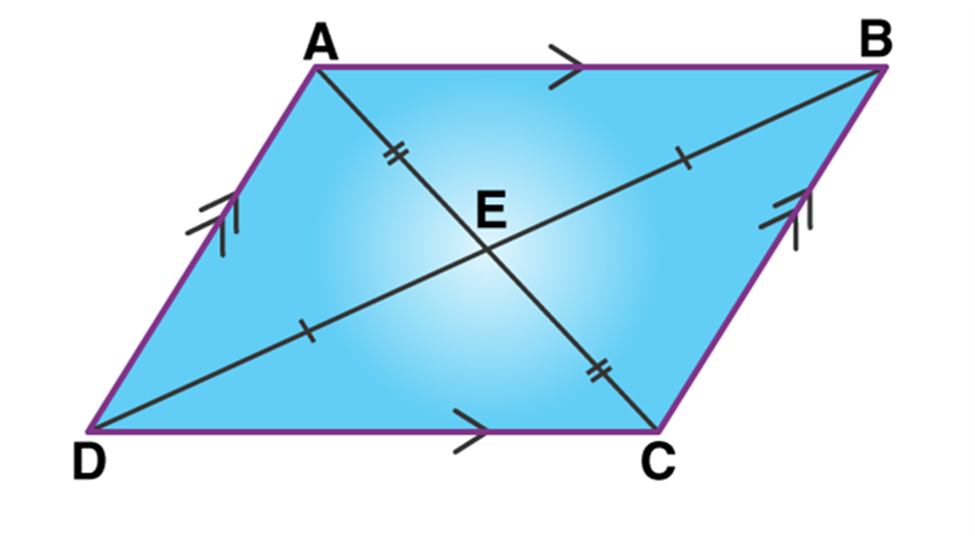
In the figure above, you can see, ABCD is a parallelogram, where AB || CD and AD || BC.
Also, AB = CD and AD = BC
And, ∠A = ∠C & ∠B = ∠D
Also, ∠A & ∠D are supplementary angles because these interior angles lie on the same side of the transversal. In the same way, ∠B & ∠C are supplementary angles.
Therefore,
∠A + ∠D = 180
∠B + ∠C = 180
Facts:
- Number of sides = 4
- Number of vertices = 4
- Mutually Parallel sides = 2 (in pair)
- Area = Base x Height
- Perimeter = 2 (Sum of adjacent sides length)
- Type of polygon = Quadrilateral
Shape of Parellelogram
A parallelogram is a two-dimensional shape. It has four sides, in which two pairs of sides are parallel. Also, the parallel sides are equal in length. If the length of the parallel sides is not equal in measurement, then the shape is not a parallelogram. Similarly, the opposite interior angles of parallelogram should always be equal. Otherwise, it is not a parallelogram.
Special Parallelograms
Square and Rectangle: A square and a rectangle are two shapes which have similar properties of a parallelogram. Both have their opposite sides equal and parallel to each other. Diagonals of both shapes bisect each other.
Rhombus: If all the sides of a parallelogram are congruent or equal to each other, then it is a rhombus.
Rhomboid: A special case of a parallelogram that has its opposite sides parallel to each other but adjacent sides are of unequal lengths. Also, the angles are equal to 90 degrees.
Trapezium: If there is one parallel side and the other two sides are non-parallel, then it is a trapezium.
Angles of Parallelogram
A parallelogram is a flat 2d shape which has four angles. The opposite interior angles are equal. The angles on the same side of the transversal are supplementary, that means they add up to 180 degrees. Hence, the sum of the interior angles of a parallelogram is 360 degrees.
Properties of Parallelogram
If a quadrilateral has a pair of parallel opposite sides, then it’s a special polygon called Parallelogram. The properties of a parallelogram are as follows:
- The opposite sides are parallel and congruent
- The opposite angles are congruent
- The consecutive angles are supplementary
- If any one of the angles is a right angle, then all the other angles will be at right angle
- The two diagonals bisect each other
- Each diagonal bisects the parallelogram into two congruent triangles
- The Sum of square of all the sides of parallelogram is equal to the sum of square of its diagonals. It is also called parallelogram law
Formulas (Area & Perimeter)
The formula for the area and perimeter of a parallelogram is covered here in this section. Students can use these formulas and solve problems based on them.
Area of Parallelogram
Area of a parallelogram is the region occupied by it in a two-dimensional plane. Below is the formula to find the parallelogram area:
Area = Base × Height
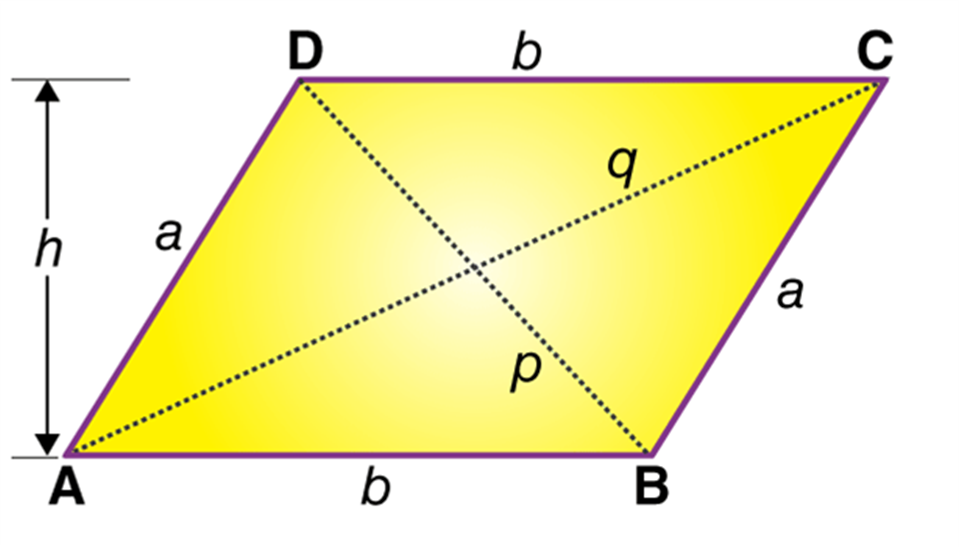
In the above figure, ||gramABCD, Area is given by;
Area = a b sin A = b a sin B
where a is the slant length of the side of ||gramABCD and b is the base.
Check here: Area of a Parallelogram Formula
Perimeter of Parallelogram
The perimeter of any shape is the total distance covered around the shape or the total length of any shape. Similarly, the perimeter of a parallelogram is the total distance of the boundaries of the parallelogram. To calculate the perimeter value, we have to know the values of its length and breadth. The parallelogram has its opposite sides equal in length. Therefore, the formula to calculate the perimeter is written as;
Perimeter = 2 (a+b) units
Where a and b are the length of the sides of the parallelogram.
Types of Parallelogram
There are mainly four types of Parallelogram, depending on various factors. The factors which distinguish between all of these different types of parallelogram are angles, sides etc.
- In a parallelogram, say PQRS
- If PQ = QR = RS = SP are the equal sides, then it’s a rhombus. All the properties are the same for rhombus as for parallelogram.
- Other two special types of a parallelogram are:
- Rectangle
- Square
Is Square a Parallelogram?
Square could be considered as a parallelogram since the opposite sides are parallel to each other, and the diagonals of the square bisect each other.
Is Rectangle a Parallelogram?
Yes, a rectangle is also a parallelogram, because it satisfies the conditions or meets the properties of parallelogram such as the opposite sides are parallel and diagonals bisect each other.
Parallelogram Theorems
Theorem 1: Parallelograms on the same base and between the same parallel sides are equal in area.
Proof: Two parallelograms ABCD and ABEF, on the same base DC and between the same parallel line AB and FC.
To prove that area (ABCD) = area (ABEF).
Proof:
Consider the figure given below:
Parallelogram ABCD and rectangle ABML are on the same base and between the same parallels AB and LC.
area of parallelogram ABCD = area of parallelogram ABML
We know that area of a rectangle = length x breadth.
Therefore, area of parallelogram ABCD = AB x AL
Hence, the area of a parallelogram is the product of any base of it and the corresponding altitude.
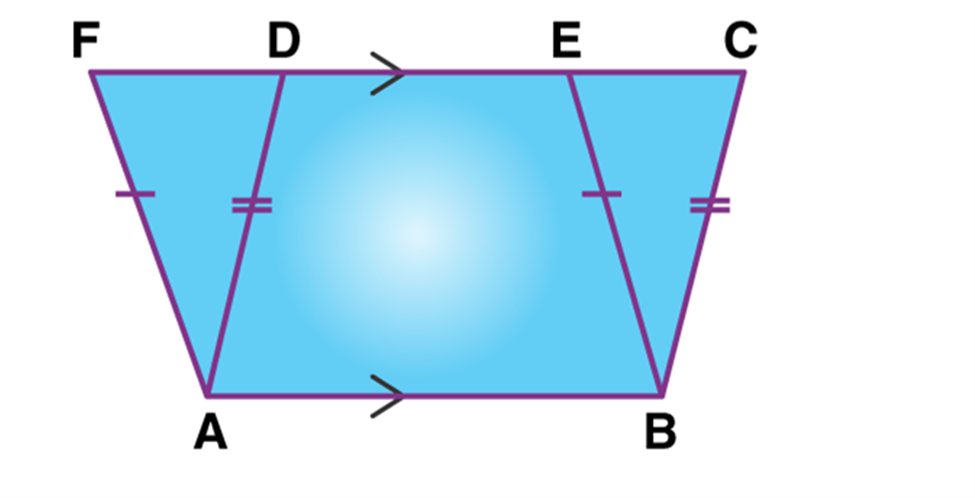
In ∆ADF and ∆BCE,
AD=BC (∴ABCD is a parallelogram ∴ AD=BC)
AF=BE (∴ABEF is a parallelogram ∴AF=BE)
∠ADF=∠BCE (Corresponding Angles)
∠AFD=∠BEC (Corresponding Angles)
∠DAF =∠CBE (Angle Sum Property)
∆ADE ≅ ∆BCF (From SAS-rule)
Area(ADF) = Area(BCE) (By congruence area axiom)
Area(ABCD)=Area(ABED) + Area(BCE)
Area(ABCD)=Area(ABED)+Area(ADF)
Area(ABCD)=Area(ABEF)
Hence, the area of parallelograms on the same base and between the same parallel sides is equal.
Corollary
A parallelogram and a rectangle on the same base and between the same parallels are equal in area.
Proof: Since a rectangle is also a parallelogram so, the result is a direct consequence of the above theorem.
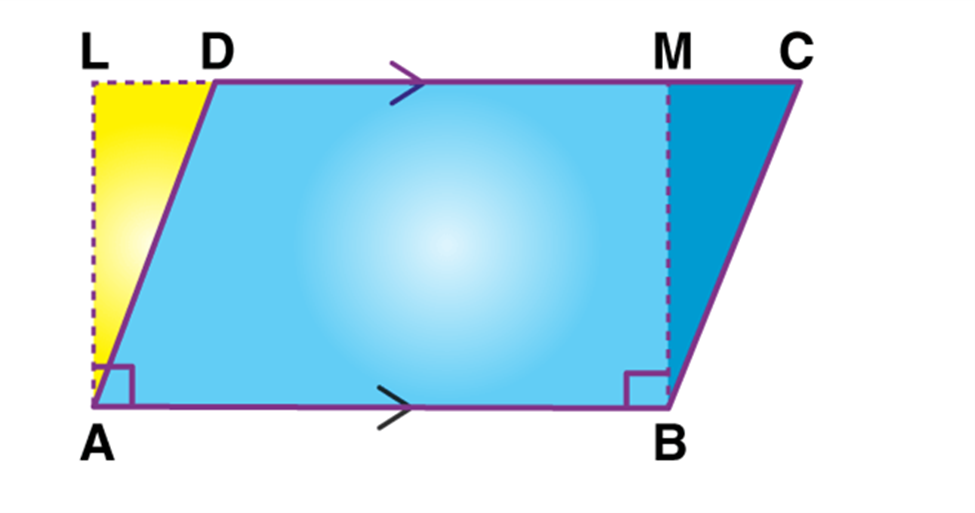
Theorem: The area of a parallelogram is the product of its base and the corresponding altitude.
Given: In a parallelogram ABCD, AB is the base.
To prove that Area(||gmABCD) = AB×AL
Construction: Complete the rectangle ALMB by Drawing BM perpendicular to CD.
Difference Between Parallelogram and Rhombus
Examples on Parallelogram
Example 1:
Find the area of a parallelogram whose base is 5 cm and height is 8 cm.
Solution-:
Given, Base = 5 cm and Height = 8 cm.
We know, Area = Base x Height
Area = 5 × 8
Area = 40 Sq.cm
Example 2:
Find the area of a parallelogram having a length of diagonals to be 10 and 22 cm and an intersecting angle to be 65 degrees.
Solution:
We know that the diagonals of a parallelogram bisect each other. Hence, the length of half the diagonal will be 5 and 11 cm.
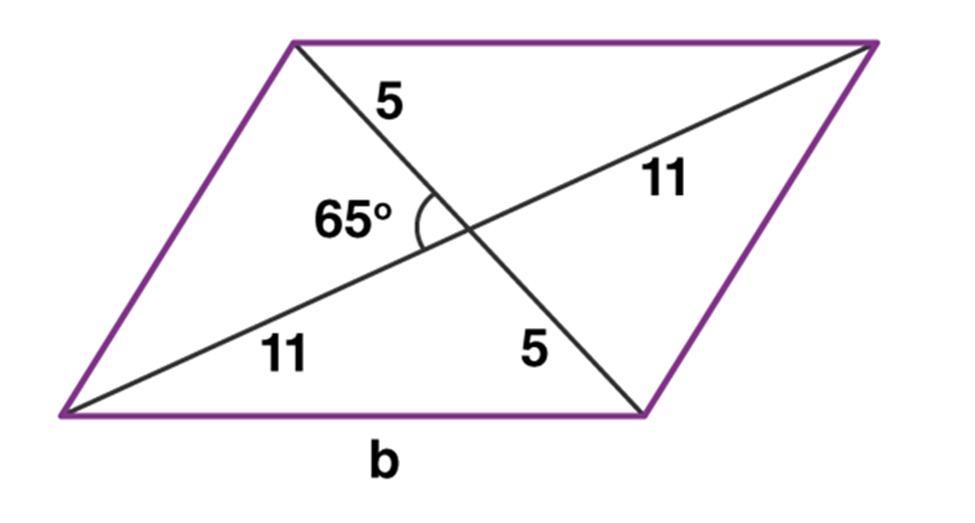
The angle opposite to the side b comes out to be 180 – 65 = 115°
We use the law of cosines to calculate the base of the parallelogram –
b² = 5² + 11² – 2(11)(5)cos(115°)
b² = 25 + 121 – 110(-0.422)
b² = 192.48
b = 13.87 cm.
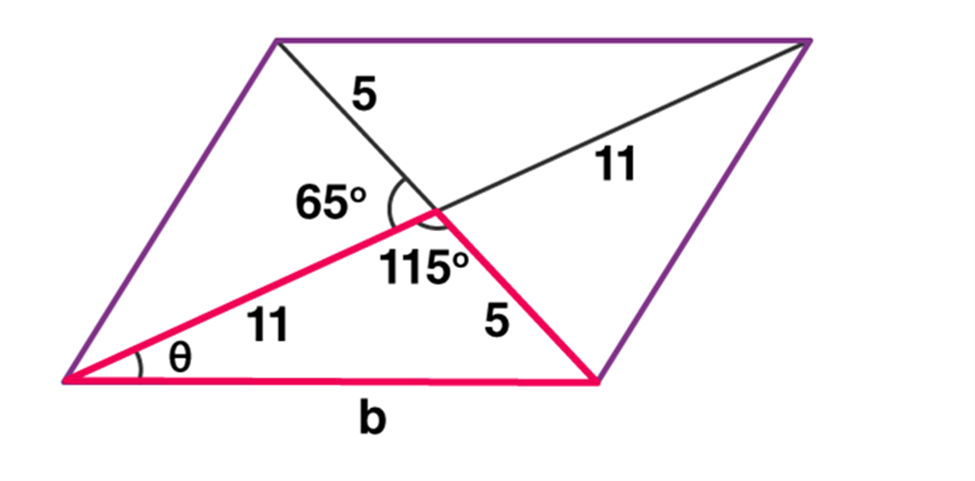
After finding the base, we need to calculate the height of the given parallelogram.
To find the height we have to calculate the value of θ, so we use sine law
5/sin(θ) = b/sin(115)
θ = 19.06
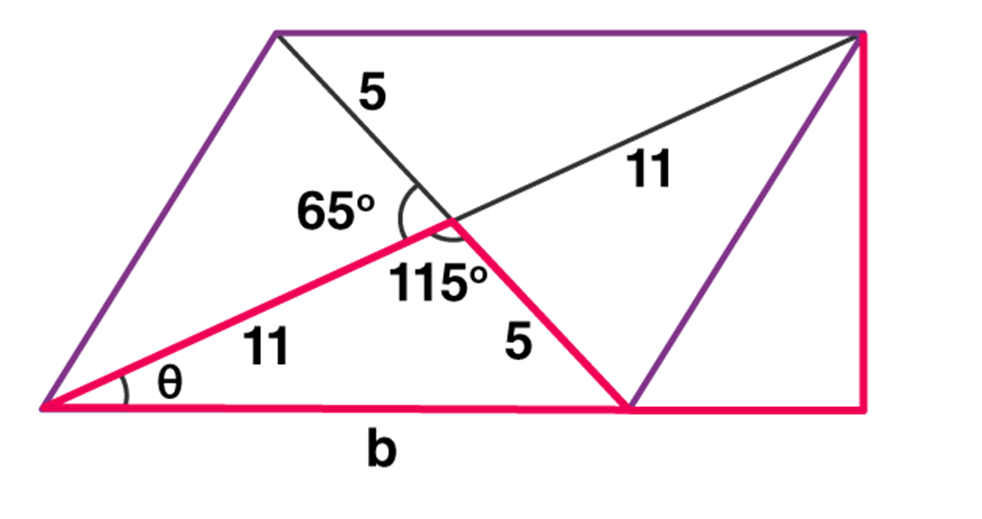
Now we extend the base and draw in the height of the figure and denote it as ‘h’.
The right-angled triangle (marked with a red line) has the Hypotenuse to be 22 cm and the Perpendicular to be h.
So
sin θ = h/22
h = 7.184 cm
Area = base × height
A = 13.87 × 7.184
A = 99.645 sq.cm
Another condition for a quadrilateral to be a parallelogram
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Another condition for a quadrilateral to be a parallelogram
Another Condition for a Quadrilateral to be a Parallelogram
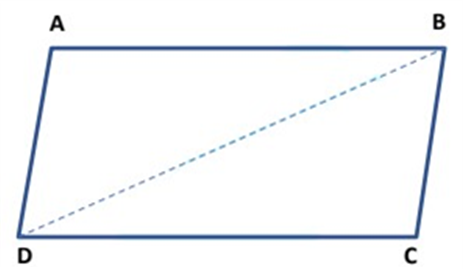
Theorem 9: A quadrilateral is a parallelogram if a pair of the opposite side is equal and parallel.
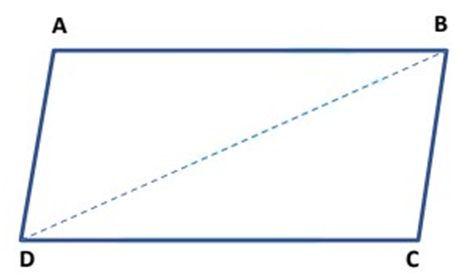
Given: A quadrilateral ABCD in which AB = CD and, AB ∥ CD.
To prove: Quadrilateral ABCD is a parallelogram.
Construction: Join BD.
Proof: Now, in ∆ BAD and ∆ DCB, we have
AB = CD (Given)
Since AB ∥ CD and transversal BD intersects at B and D, so alternate interior angles are equal.
⟹ ∠ CDB = ∠ ABD
BD = DB (Common)
Therefore, ∆ BAD ≅ ∆ DCB (By SAS criterion of congruence)
By using corresponding parts of congruent triangles
⟹ ∠ ADB = ∠ CBD
Now, line BD intersects AB and DC at B and D respectively, such that ∠ ADB = ∠ CBD
That is, alternate interior angles are equal.
∴ AD ∥ BC.
Thus, AB ∥ CD and AD ∥ BC.
Hence, quadrilateral ABCD is a parallelogram.
Example: In the figure, ABCD is a parallelogram and X, Y are the mid- points of sides AB and DC respectively. Show that quadrilateral DXBY is a parallelogram.
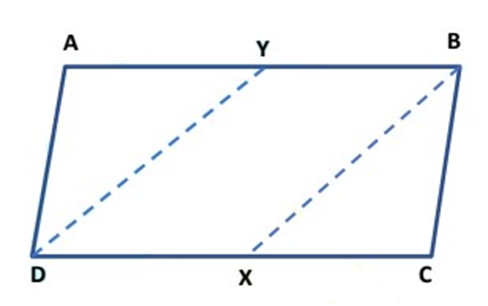
Given: ABCD is a parallelogram in which X and Y are the mid-points of AB and DC respectively.
To prove: Quadrilateral DXBY is a parallelogram.
Construction: Join DX and BX.
Proof: Since X and Y are the mid-points of DC and AB respectively.
∴ YB =
But, AB = DC [∵ ABCD is a parallelogram]
⟹ ![]() AB =
AB = ![]() DC
DC
⟹ YB = DX. [From(I)] ............. (II)
Also, AB ∥ DC [∵ ABCD is a parallelogram]
Another condition for a quadrilateral to be a parallelogram
Another Condition for a Quadrilateral to be a Parallelogram
Another Condition for a Quadrilateral to be a Parallelogram
Theorem 9: A quadrilateral is a parallelogram if a pair of the opposite side is equal and parallel.
Given: A quadrilateral ABCD in which AB = CD and, AB ∥ CD.
To prove: Quadrilateral ABCD is a parallelogram.
Construction: Join BD.
Proof: Now, in ∆ BAD and ∆ DCB, we have
AB = CD (Given)
Since AB ∥ CD and transversal BD intersects at B and D, so alternate interior angles are equal.
⟹ ∠ CDB = ∠ ABD
BD = DB (Common)
Therefore, ∆ BAD ≅ ∆ DCB (By SAS-criterion of congruence)
By using corresponding parts of congruent triangles
⟹ ∠ ADB = ∠ CBD
Now, line BD intersects AB and DC at B and D respectively, such that ∠ ADB = ∠ CBD
That is, alternate interior angles are equal.
∴ AD ∥ BC.
Thus, AB ∥ CD and AD ∥ BC.
Hence, quadrilateral ABCD is a parallelogram.
Example: In the figure, ABCD is a parallelogram and X, Y are the mid- points of sides AB and DC respectively. Show that quadrilateral DXBY is a parallelogram.
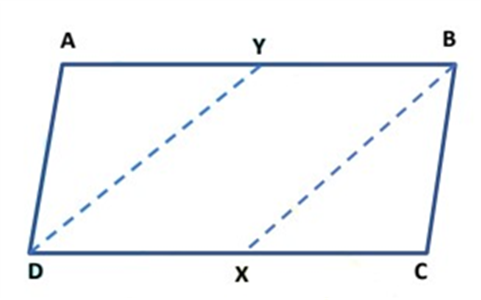
Given: ABCD is a parallelogram in which X and Y are the mid-points of AB and DC respectively.
To prove: Quadrilateral DXBY is a parallelogram.
Construction: Join DX and BX.
Proof: Since X and Y are the mid-points of DC and AB respectively.
∴ YB =
But, AB = DC [∵ ABCD is a parallelogram]
⟹  AB =
AB =  DC
DC
⟹ YB = DX. [From(I)] ............. (II)
Also, AB ∥ DC [∵ ABCD is a parallelogram]
∴ YB ∥ DX ............. (III)
Since a quadrilateral is a parallelogram if a pair of the opposite side is equal and parallel.
From (II) & (III), we get Quadrilateral DXBY is a parallelogram.
The Mid-Point Theorem
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
The Mid-Point Theorem
geometry is one of the significant and essential branches of mathematics. This field deals with the geometrical problems and figures which are based on their properties. One of the important theorems in the field of geometry that deals with the properties of triangles are called the Mid-Point Theorem.
The theory of the midpoint theorem is used in coordinate geometry stating that the midpoint of the line segment is an average of the endpoints. Both the ‘x’ and the ‘y’ coordinates must be known for solving an equation using this theorem. The Mid-Point Theorem is also useful in the fields of calculus and algebra.
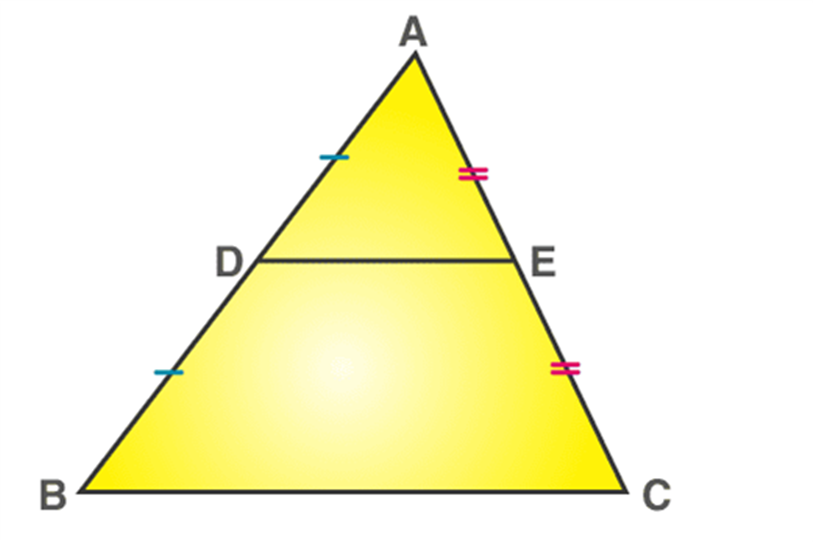
MidPoint Theorem Statement
The midpoint theorem states that “The line segment in a triangle joining the midpoint of two sides of the triangle is said to be parallel to its third side and is also half of the length of the third side.”
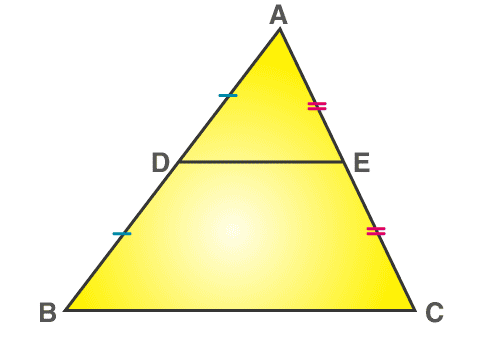
MidPoint Theorem Proof
If the line segment adjoins the midpoints of any of the sides of a triangle, then the line segment is said to be parallel to all the remaining sides, and it measures about half of the remaining sides.
Consider the triangle ABC, as shown in the above figure,
Let E and D be the midpoints of the sides AC and AB. Then the line DE is said to be parallel to the side BC, whereas the side DE is half of the side BC; i.e.
DE = (1/2 * BC).
Now consider the below figure,
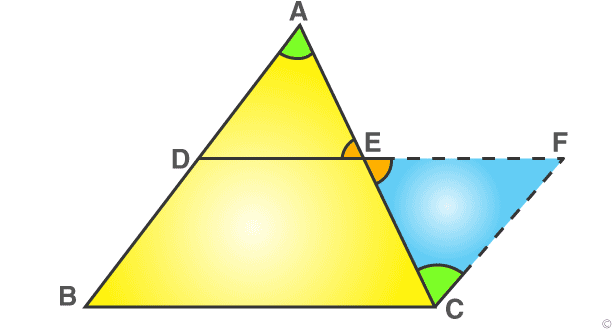
Construction- Extend the line segment DE and produce it to F such that, EF = DE.
In triangle ADE and CFE,
EC = AE —– (given)
∠CEF = ∠AED (vertically opposite angles)
∠DAE = ∠ECF (alternate angles)
By ASA congruence criterion,
△ CFE ≅ △ ADE
Therefore,
∠CFE = ∠ADE {by c.p.c.t.}
∠FCE= ∠DAE {by c.p.c.t.}
and CF = AD {by c.p.c.t.}
∠CFE and ∠ADE are the alternate interior angles.
Assume CF and AB as two lines that are intersected by the transversal DF.
In a similar way, ∠FCE and ∠DAE are the alternate interior angles.
Assume CF and AB are the two lines that are intersected by the transversal AC.
Therefore, CF ∥ AB
So, CF ∥ BD
and CF = BD {since BD = AD, it is proved that CF = AD}
Thus, BDFC forms a parallelogram.
By the properties of a parallelogram, we can write
BC ∥ DF
and BC = DF
BC ∥ DE
and DE = (1/2 * BC).
Hence, the midpoint theorem is proved.
MidPoint Theorem Formula
In Coordinate Geometry, the midpoint theorem refers to the midpoint of the line segment. It defines the coordinate points of the midpoint of the line segment and can be found by taking the average of the coordinates of the given endpoints. The midpoint formula is used to determine the midpoint between the two given points.
If P1(x1, y1) and P2(x2, y2) are the coordinates of two given endpoints, then the midpoint formula is given as:
Midpoint = [(x1 + x2)/2, (y1 + y2)/2]
The converse of the MidPoint Theorem
The converse of the midpoint theorem states that ” if a line is drawn through the midpoint of one side of a triangle, and parallel to the other side, it bisects the third side”.
Midpoint Theorem Example
The example is given below to understand the midpoint theorem.
Example:
In triangle ABC, the midpoints of BC, CA, AB are D, E, and F, respectively. Find the value of EF, if the value of BC = 14 cm
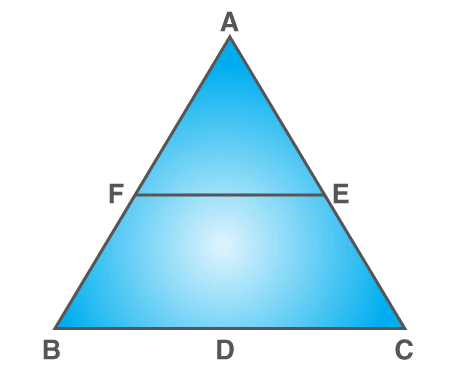
Solution:
Given: BC = 14 cm
If F is the midpoint of AB and E is the midpoint of AC, then using the midpoint theorem:
EF = 1/2 (BC)
Substituting the value of BC,
EF = (1/2) × 14
EF = 7 cm
Therefore, the value of EF = 7cm.
80,202
The Mid-Point Theorem can also be proved using triangles. Suppose two lines are drawn parallel to the x and the y-axis which begin at endpoints and are connected through the midpoint, then the segment passes through the angle between them resulting in two similar triangles. This relation of these triangles forms the Mid-Point Theorem.
The Mid-Point Theorem
The Mid-Point Theorem
geometry is one among the significant and essential branches of mathematics. This field deals with the geometrical problems and figures which are based on their properties. One of the important theorems in the field of geometry that deals with the properties of triangles are called the Mid- Point Theorem.
The theory of midpoint theorem is used in coordinate geometry stating that the midpoint of the line segment is an average of the endpoints. Both the ‘x’ and the ‘y’ coordinates must be known for solving an equation using this theorem. The Mid- Point Theorem is also useful in the fields of calculus and algebra.
The midpoint theorem states that “The line segment in a triangle joining the midpoint of two sides of the triangle is said to be parallel to its third side and is also half of the length of the third side.”
If the line segment adjoins midpoints of any of the sides of a triangle, then the line segment is said to be parallel to all the remaining sides, and it measures about half of the remaining sides.
Consider the triangle ABC, as shown in the above figure,
Let E and D be the midpoints of the sides AC and AB. Then the line DE is said to be parallel to the side BC, whereas the side DE is half of the side BC; i.e.
DE = (1/2 * BC).
Now consider the below figure,
Construction- Extend the line segment DE and produce it to F such that, EF = DE.
In triangle ADE and CFE,
EC = AE —– (given)
∠CEF = ∠AED (vertically opposite angles)
∠DAE = ∠ECF (alternate angles)
By ASA congruence criterion,
△ CFE ≅ △ ADE
Therefore,
∠CFE = ∠ADE {by c.p.c.t.}
∠FCE= ∠DAE {by c.p.c.t.}
and CF = AD {by c.p.c.t.}
∠CFE and ∠ADE are the alternate interior angles.
Assume CF and AB as two lines which are intersected by the transversal DF.
In a similar way, ∠FCE and ∠DAE are the alternate interior angles.
Assume CF and AB are the two lines which are intersected by the transversal AC.
Therefore, CF ∥ AB
So, CF ∥ BD
and CF = BD {since BD = AD, it is proved that CF = AD}
Thus, BDFC forms a parallelogram.
By the properties of a parallelogram, we can write
BC ∥ DF
and BC = DF
BC ∥ DE
and DE = (1/2 * BC).
Hence, the midpoint theorem is proved.
MidPoint Theorem Formula
In Coordinate Geometry, the midpoint theorem refers to the midpoint of the line segment. It defines the coordinate points of the midpoint of the line segment and can be found by taking the average of the coordinates of the given endpoints. The midpoint formula is used to determine the midpoint between the two given points.
If P1(x1, y1) and P2(x2, y2) are the coordinates of two given endpoints, then the midpoint formula is given as:
Midpoint = [(x1 + x2)/2, (y1 + y2)/2]
The converse of MidPoint Theorem
The converse of the midpoint theorem states that ” if a line is drawn through the midpoint of one side of a triangle, and parallel to the other side, it bisects the third side”.
Midpoint Theorem Example
The example is given below to understand the midpoint theorem.
Example:
In triangle ABC, the midpoints of BC, CA, AB are D, E, and F, respectively. Find the value of EF, if the value of BC = 14 cm
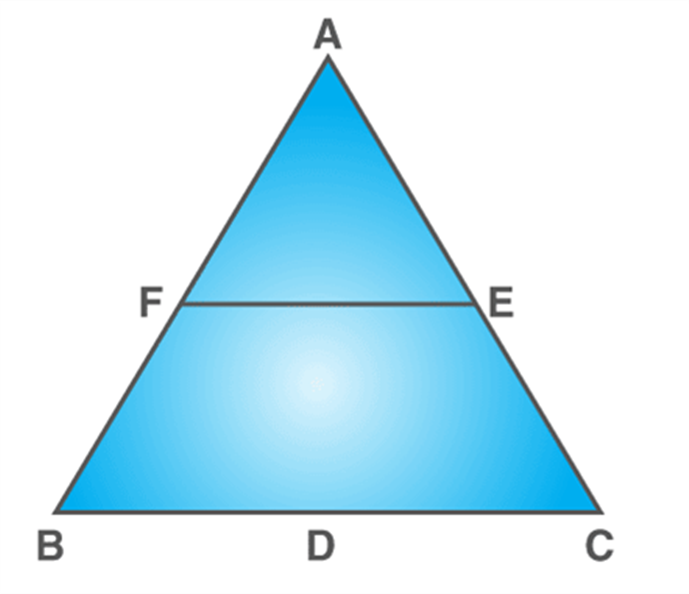
Solution:
Given: BC = 14 cm
If F is the midpoint of AB and E is the midpoint of AC, then using the midpoint theorem:
EF = 1/2 (BC)
Substituting the value of BC,
EF = (1/2) × 14
EF = 7 cm
Therefore, the value of EF = 7cm.
80,202
The Mid- Point Theorem can also be proved using triangles. Suppose two lines are drawn parallel to the x and the y-axis which begin at endpoints and connected through the midpoint, then the segment passes through the angle between them resulting in two similar triangles. This relation of these triangles forms the Mid- Point Theorem.

 ABCD CLASSES
ABCD CLASSES