Perpendicular from the Centre to a Chord

In Mathematics, a chord is a line segment that joins two points on the circumference of a circle. We know that the longest chord of a circle is a diameter that passes through the centre of a circle. In this article, we will discuss the theorem related to the perpendicular from the centre to a circle and its proof, and the converse of this theorem in detail.

Perpendicular from the Centre to a Chord – Theorem and Proof

Theorem:

The perpendicular from the centre of a circle to a chord bisects the chord.

Proof:

Consider a circle with centre “O”.

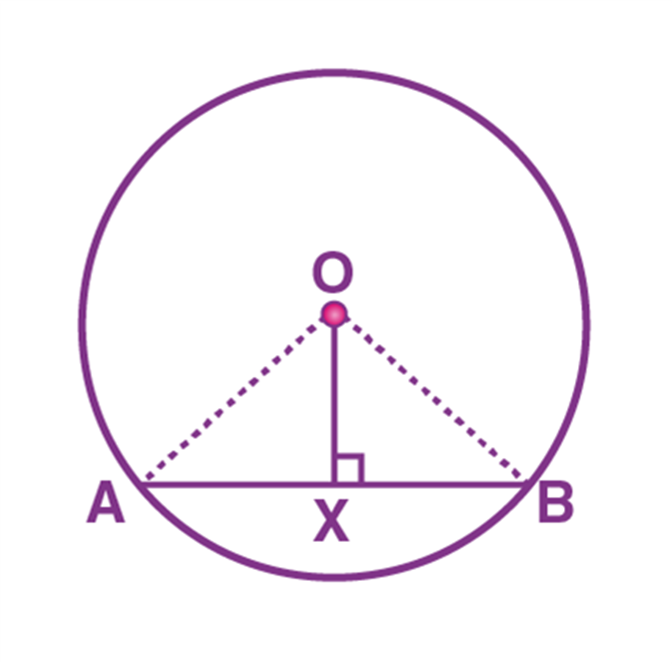
AB is a chord such that the line OX is perpendicular to the chord AB.

(i.e) OX ⊥ AB

Now, we need to prove: AX = BX

To prove AX = BX, consider two triangles OAX and OBX.

∠OXA = ∠OXB (∠X = 90°)

OX = OX (Common side)

OA = OB (Radii)

By using the RHS rule, we can prove that the triangle OAX is congruent to OBX.

Therefore,

∆OAX ≅ ∆OBX

Hence, we can say that AX = BX ( Using CPCT)

Thus, the perpendicular from the centre of a circle to a chord bisects the chord, is proved.

The Converse of this Theorem:

The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord

Proof:

Consider the same figure, as given above.

Assume that AB is the chord of a circle with centre “O”.

The centre “O” is joined to the midpoint “X” of the chord AB.

Now, we need to prove OX ⊥ AB.

Join OA and OB, and the two triangles formed are OAX and OAB.

Here,

OA = OB (Radii)

OX = OX (Common side)

AX = BX (As, X is the midpoint of AB)

Therefore, we can say that ∆OAX ≅ ∆OBX.

Thus, by using the RHS rule, we get

∠OMA = ∠OMB = 90°

This proves that the line drawn through the centre of a circle to bisect a chord is perpendicular to the chord.

Hence, the converse of this theorem is proved.