Angle subtended by an arc of a circle

We know that the endpoints of a chord other than the diameter of a circle divide it into two arcs, namely the major arc and the minor arc. If we take two equal chords, we can say that equal chords make congruent arcs and conversely, congruent arcs make equal chords of a circle. In this article, we will discuss the theorem related to the angle subtended by an arc of a circle and its proof with a complete explanation.

Angle Subtended by an Arc of a Circle – Theorem and Proof

Theorem: The angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.

Proof: Consider a circle with center “O”. Here the arc PQ of the circle subtends angle POQ at Centre O and ∠PAQ at a point A on the remaining part of the circle.

To prove: ∠POQ = 2∠PAQ.

To prove this, join AO and extend it to point B.

There are two general cases while proving this theorem.

Case 1:

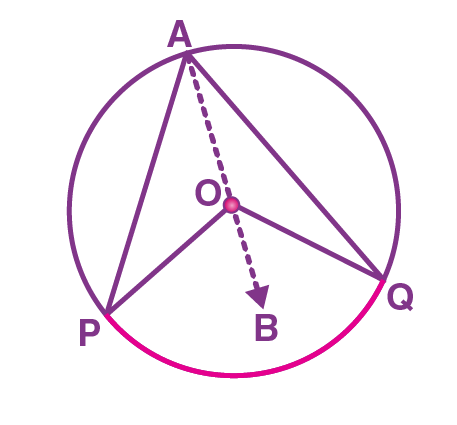
Consider a triangle APO,

Here, OA = OP (Radii)

Since, the angles opposite to the equal sides are equal,

∠OPA = ∠OAP …(1)

Also, by using the exterior angle property (exterior angle is the sum of interior opposite angles),

We can write,

∠BOP = ∠OAP + ∠OPA

By using (1),

∠BOP = ∠OAP + ∠OAP

∠BOP = 2∠OAP… (2)

Similarly, consider another triangle AQO,

OA = OQ (Radii)

As the angles opposite to the equal sides are equal,

∠OQA = ∠OAQ … (3)

Similarly, by using the exterior angle property, we get

∠BOQ = ∠OAQ + ∠OQA

∠BOQ = ∠OAQ + ∠OAQ (using (3))

∠BOQ = 2∠OAQ …(4)

Adding (2) and (4) we get,

∠BOP + ∠BOQ = 2∠OAP + 2∠OAQ

∠POQ = 2(∠OAP + ∠OAQ)

∠POQ = 2∠PAQ.

Hence, case (1) is proved.

Case 2:

 

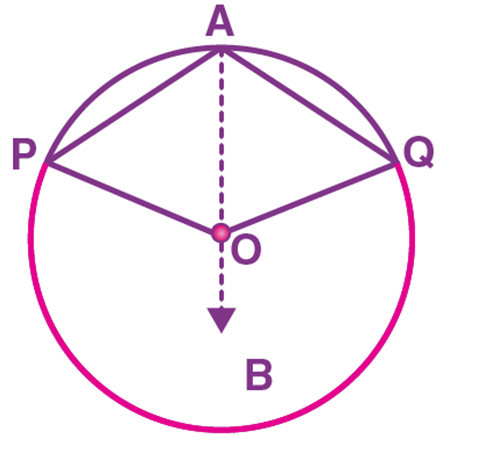
To prove ∠POQ = 2∠PAQ for this case, we can follow the steps as same as for case (1). But while adding (2) and (4), we have to follow the below steps.

∠BOP + ∠BOQ = 2∠OAP + 2∠OAQ

Reflex angle ∠POQ = 2(∠OAP + ∠OAQ) (Since, PQ is a Major arc)

Reflex angle ∠POQ = 2∠PAQ.

Hence, proved.

Theorem: Angle subtended by a diameter/ semicircle on any point of a circle is 90°

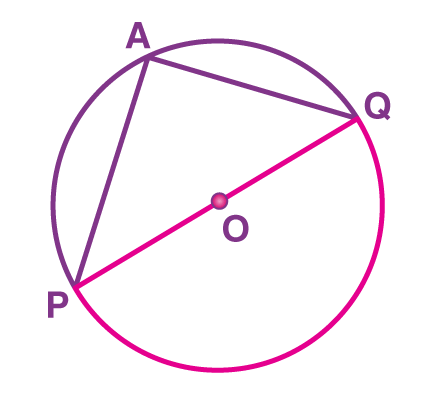
Consider a circle with center “O” and PQ be its diameter, subtending ∠PAQ at a point A on the circle.

Now, we need to prove that ∠PAQ = 90°.

Here, POQ is a straight line that passes through the center “O” of the circle.

Therefore, the angle subtended by arc PQ at O is

∠POQ = 180° (Since, POQ is a straight line) ….(5)

Now, by using the theorem, “The angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle”, we can write

∠POQ = 2 ∠PAQ

∠PAQ = ∠POQ/2

By using (5),

∠PAQ = 180°/2

∠PAQ = 90°

Therefore, the angle subtended by a diameter/ semicircle on any point of a circle is 90°.

Hence, proved.