Equal Chords and their distances from the centre

Equal Chords and their distances from the centre

In Mathematics, a chord is the line segment which joins two points on the circumference of a circle. In general, a circle can have infinitely many chords. The distance of the line from a point is defined as the perpendicular distance from a point to a line. If you draw infinite chords to a circle, the longer chord is close to the centre of the circle, than the smaller chord of a circle. In this article, we will discuss the theorem and proof related to the equal chords and their distance from the centre and also its converse theorem in detail.

Equal Chords and their Distance from the Centre – Theorem and Proof

Theorem:

Equal chords of a circle (or of congruent circles) are equidistant from the centre (or centres).

Proof:

Consider a circle with “O”.

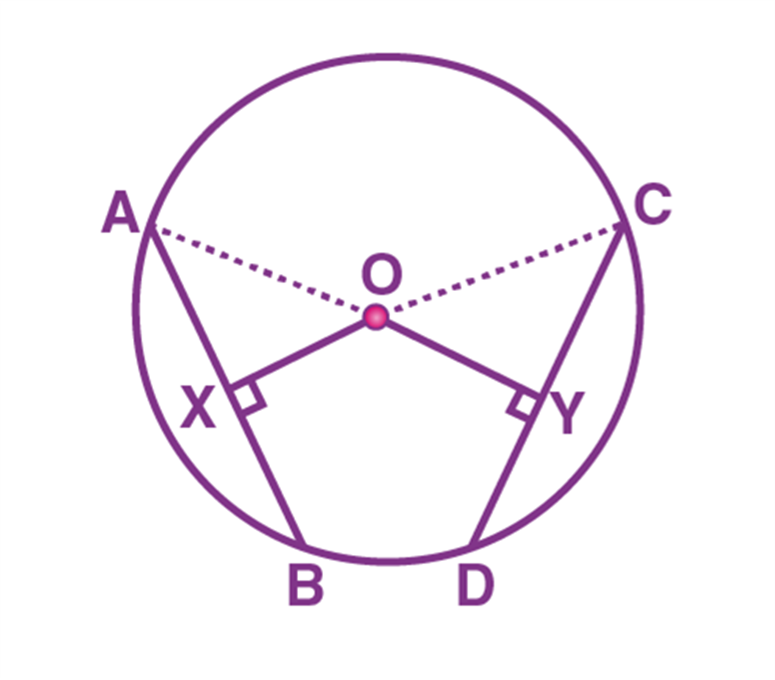
AB and CD are the equal chords of a circle.

(i.e) AB = CD

The line OX is perpendicular to the chord AB and OY is perpendicular to the chord CD.

We have to prove OX = OY.

Also, the line OX is perpendicular to AB.

As the perpendicular from the centre of the circle to a chord, bisects the chord, we can write it as

AX = BX = AB/2 …(1)

Similarly, the line OY is perpendicular to CD,

CY = DY = CD/2 ….(2) [Since, the perpendicular from the centre of the circle to a chord, bisects the chord)

Given that, AB = CD

AB/2 = CD/2

Therefore, AX = CY …(3) [Using (1) and (2)]

Now, by using the triangles AOX and COY,

∠ OXA = ∠ OYC (Both are 90°)

OA = OC (Radii)

AX = CY (From equation (3))

From the RHS rule, we can write it as

∆ AOX ≅ ∆ COY

Hence, we can conclude that OX = OY (Using CPCT)

Therefore, the theorem “equal chords of a circle (or of congruent circles) are equidistant from the centre (or centres)”, is proved.

Converse of this Theorem

The converse of the above-mentioned theorem is “chords equidistant from the centre of a circle are equal in length”.

Example

Question:

Two intersecting chords of a circle make equal angles with the diameter that passes through their point of intersection. Prove that the chords are equal.

Solution:

Given that AB and CD are the two chords of a circle with centre “O” and it intersects at the point “E” as shown in the figure.

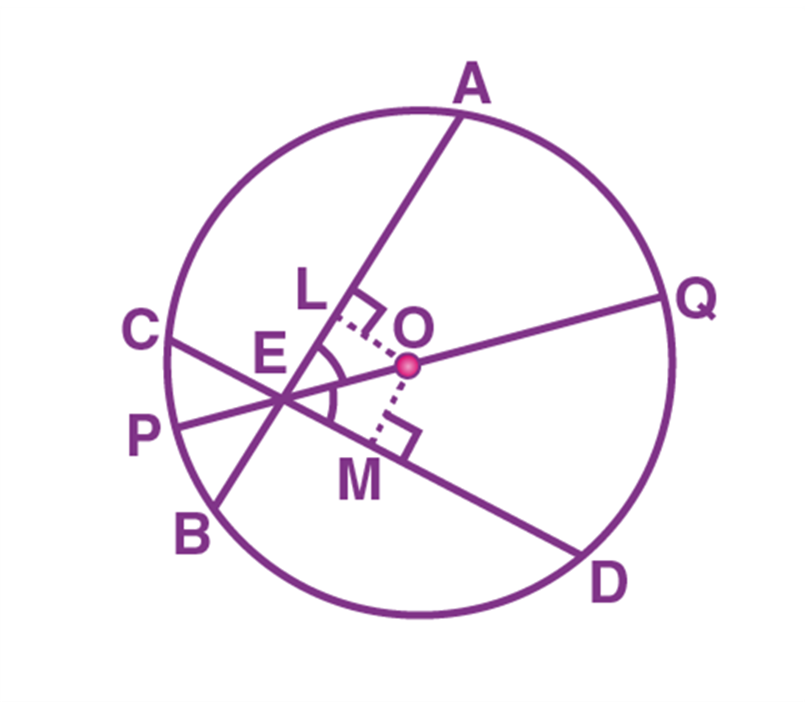
PQ is the diameter of a circle (longest chord of a circle), that passes through the point of intersection E, such that it makes an angle ∠ AEQ = ∠ DEQ.

Now, we need to prove that AB = CD.

Now, draw the perpendicular OL to the chord AB and the perpendicular line OM to the chord CD.

By using the angle sum property of a triangle, we can write it as:

∠ LOE = 180° – 90° – ∠ LEO

∠ LOE = 90° – ∠ LEO

= 90° – ∠ AEQ = 90° – ∠ DEQ

= 90° – ∠ MEO = ∠ MOE

Therefore,

∠ LOE = ∠ MOE

From the triangles, OLE and OME, we observe that

∠ LOE = ∠ MOE

Also, ∠ LEO = ∠ MEO

EO = EO (Common side)

Therefore, we will say that the triangles OLE and OME are congruent to each other.

(i.e) ∆ OLE ≅ ∆ OME

Thus, by using the CPCT rule,

OL = OM

By using equal chords and their distance from the centre theorem, we can say,

AB = CD.

So, the chords AB and CD are equal.

Hence, proved.

Practice Problems

Solve the following problems.

1. Find the length of the common chord, if two circles of radii 5 cm and 3 cm intersect at two points and the distance between the centres is 4 cm.
2. The two equal chords of a circle intersect within a circle. Prove that the segments of one chord are equal to the corresponding segments of the other chord.