Congruence of Triangles
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Congruence of Triangles
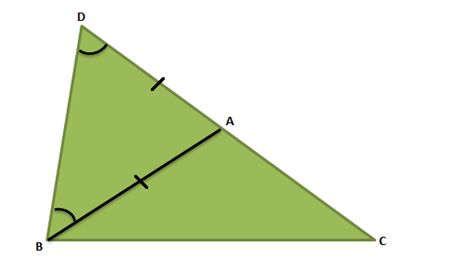
Congruence of triangles: Two triangles are said to be congruent if all three corresponding sides are equal and all the three corresponding angles are equal in measure. These triangles can be slides, rotated, flipped and turned to be looked identical. If repositioned, they coincide with each other. The symbol of congruence is’ ≅’.
The corresponding sides and angles of congruent triangles are equal. There are basically four congruency rules that proves if two triangles are congruent. But it is necessary to find all six dimensions. Hence, the congruence of triangles can be evaluated by knowing only three values out of six. The meaning of congruence in Maths is when two figures are similar to each other based on their shape and size. Also, learn about Congruent Figures here.
Congruence is the term used to define an object and its mirror image. Two objects or shapes are said to be congruent if they superimpose on each other. Their shape and dimensions are the same. In the case of geometric figures, line segments with the same length are congruent and angles with the same measure are congruent.
|
Conditions for Congruence of Triangles:
|
CPCT is the term, we come across when we learn about the congruent triangle. Let’s see the condition for triangles to be congruent with proof.
Congruent meaning in Maths
The meaning of congruent in Maths is addressed to those figures and shapes that can be repositioned or flipped to coincide with the other shapes. These shapes can be reflected to coincide with similar shapes.
Two shapes are congruent if they have the same shape and size. We can also say if two shapes are congruent, then the mirror image of one shape is same as the other.
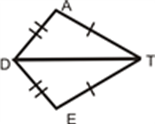
Congruent Triangles
A polygon made of three line segments forming three angles is known as a Triangle.
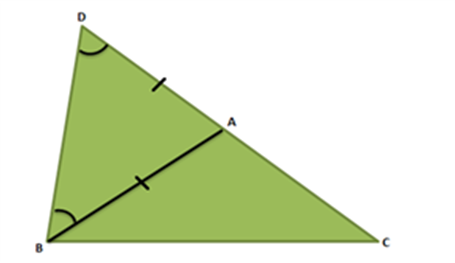
Two triangles are said to be congruent if their sides have the same length and angles have same measure. Thus, two triangles can be superimposed side to side and angle to angle.
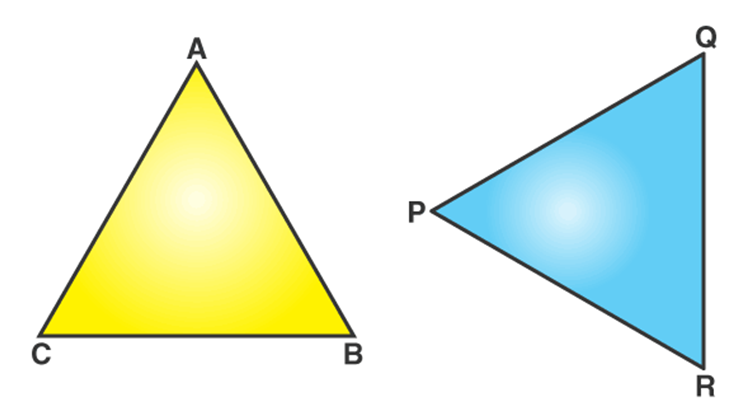
In the above figure, Δ ABC and Δ PQR are congruent triangles. This means,
Vertices: A and P, B and Q, and C and R are the same.
Sides: AB=PQ, QR= BC and AC=PR;
Angles: ∠A = ∠P, ∠B = ∠Q, and ∠C = ∠R.
Congruent triangles are triangles having corresponding sides and angles to be equal. Congruence is denoted by the symbol “≅”. They have the same area and the same perimeter.
CPCT Full Form - CPCT is the term we come across when we learn about the congruent triangle. CPCT means “Corresponding Parts of Congruent Triangles”. As we know that the corresponding parts of congruent triangles are equal. While dealing with the concepts related to triangles and solving questions, we often make use of the abbreviation cpct in short words instead of full form.
CPCT Rules in Maths
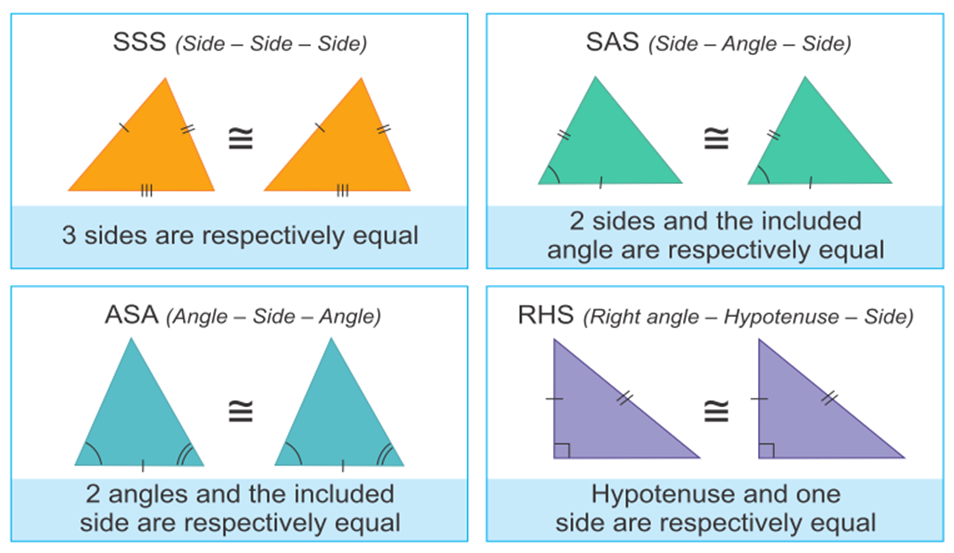
The full form of CPCT is Corresponding parts of Congruent triangles. Congruence can be predicted without actually measuring the sides and angles of a triangle. Different rules of congruency are as follows.
- SSS (Side-Side-Side)
- SAS (Side-Angle-Side)
- ASA (Angle-Side-Angle)
- AAS (Angle-Angle-Side)
- RHS (Right angle-Hypotenuse-Side)
Let us learn them all in detail.
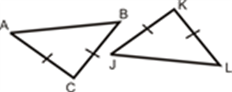
SSS (Side-Side-Side)
If all the three sides of one triangle are equivalent to the corresponding three sides of the second triangle, then the two triangles are said to be congruent by SSS rule.
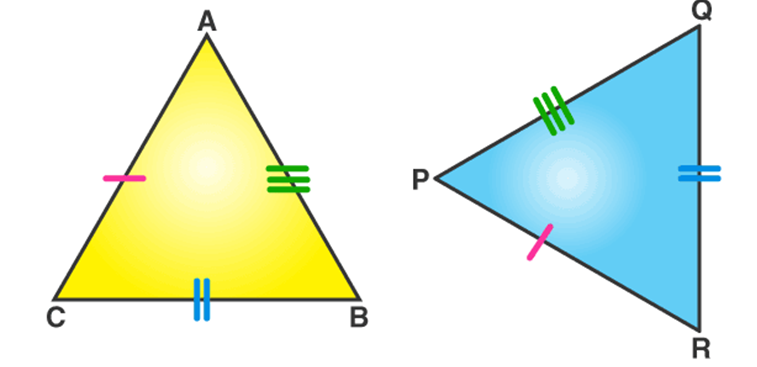
In the above-given figure, AB= PQ, QR= BC and AC=PR, hence Δ ABC ≅ Δ PQR.
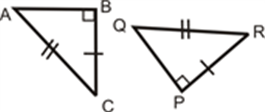
SAS (Side-Angle-Side)
If any two sides and the angle included between the sides of one triangle are equivalent to the corresponding two sides and the angle between the sides of the second triangle, then the two triangles are said to be congruent by SAS rule.
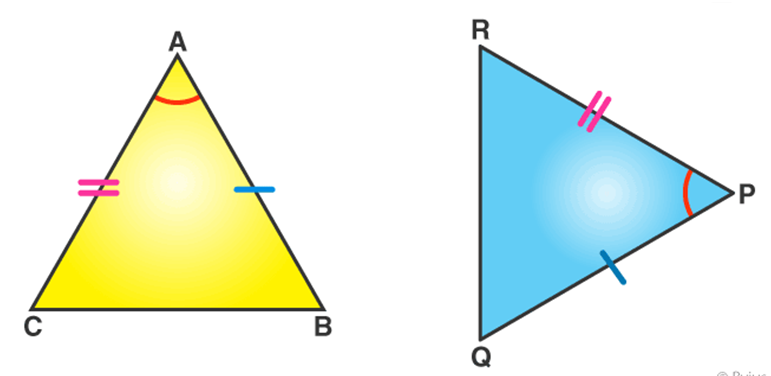
In above given figure, sides AB= PQ, AC=PR and angle between AC and AB equal to angle between PR and PQ i.e. ∠A = ∠P. Hence, Δ ABC ≅ Δ PQR.
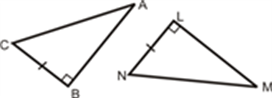
ASA (Angle-Side- Angle)
If any two angles and the side included between the angles of one triangle are equivalent to the corresponding two angles and side included between the angles of the second triangle, then the two triangles are said to be congruent by ASA rule.
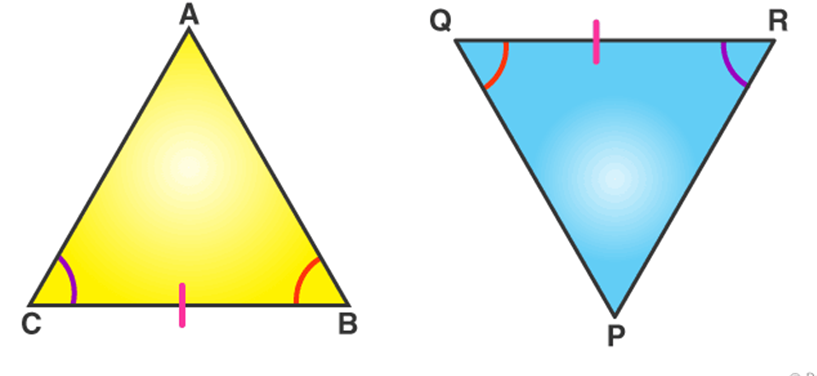
In above given figure, ∠ B = ∠ Q, ∠ C = ∠ R and sides between ∠B and ∠C , ∠Q and ∠ R are equal to each other i.e. BC= QR. Hence, Δ ABC ≅ Δ PQR.
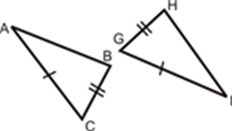
AAS (Angle-Angle-Side) [Application of ASA]
AAS stands for Angle-angle-side. When two angles and a non-included side of a triangle are equal to the corresponding angles and sides of another triangle, then the triangles are said to be congruent.
AAS congruency can be proved in easy steps. Suppose we have two triangles ABC and DEF, where,
∠B = ∠E [Corresponding sides] ∠C = ∠F [Corresponding sides] And
AC = DF [Adjacent sides]
By angle sum property of triangle, we know that;
∠A + ∠B + ∠C = 180 ………(1)
∠D + ∠E + ∠F = 180 ……….(2)
From equation 1 and 2 we can say;
∠A + ∠B + ∠C = ∠D + ∠E + ∠F
∠A + ∠E + ∠F = ∠D + ∠E + ∠F [Since, ∠B = ∠E and ∠C = ∠F] ∠A = ∠D
Hence, in triangle ABC and DEF,
∠A = ∠D
AC = DF
∠C = ∠F
Hence, by ASA congruency,
Δ ABC ≅ Δ DEF
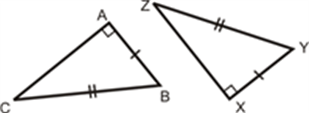
RHS (Right angle- Hypotenuse-Side)
If the hypotenuse and a side of a right- angled triangle is equivalent to the hypotenuse and a side of the second right- angled triangle, then the two right triangles are said to be congruent by RHS rule.
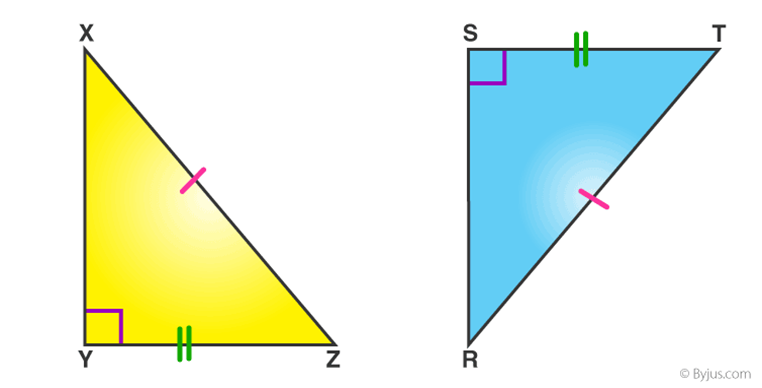
In above figure, hypotenuse XZ = RT and side YZ=ST, hence triangle XYZ ≅ triangle RST.
Congruence of Triangles
Chapter 7 - Triangles
Congruence of Triangles
Congruence of triangles: Two triangles are said to be congruent if all three corresponding sides are equal and all the three corresponding angles are equal in measure. These triangles can be slides, rotated, flipped and turned to be looked identical. If repositioned, they coincide with each other. The symbol of congruence is’ ≅’.
The corresponding sides and angles of congruent triangles are equal. There are basically four congruency rules that proves if two triangles are congruent. But it is necessary to find all six dimensions. Hence, the congruence of triangles can be evaluated by knowing only three values out of six. The meaning of congruence in Maths is when two figures are similar to each other based on their shape and size. Also, learn about Congruent Figures here.
Congruence is the term used to define an object and its mirror image. Two objects or shapes are said to be congruent if they superimpose on each other. Their shape and dimensions are the same. In the case of geometric figures, line segments with the same length are congruent and angles with the same measure are congruent.
|
Conditions for Congruence of Triangles: |
CPCT is the term, we come across when we learn about the congruent triangle. Let’s see the condition for triangles to be congruent with proof.
Congruent meaning in Maths
The meaning of congruent in Maths is addressed to those figures and shapes that can be repositioned or flipped to coincide with the other shapes. These shapes can be reflected to coincide with similar shapes.
Two shapes are congruent if they have the same shape and size. We can also say if two shapes are congruent, then the mirror image of one shape is same as the other.
Congruent Triangles
A polygon made of three line segments forming three angles is known as a Triangle.
Two triangles are said to be congruent if their sides have the same length and angles have same measure. Thus, two triangles can be superimposed side to side and angle to angle.
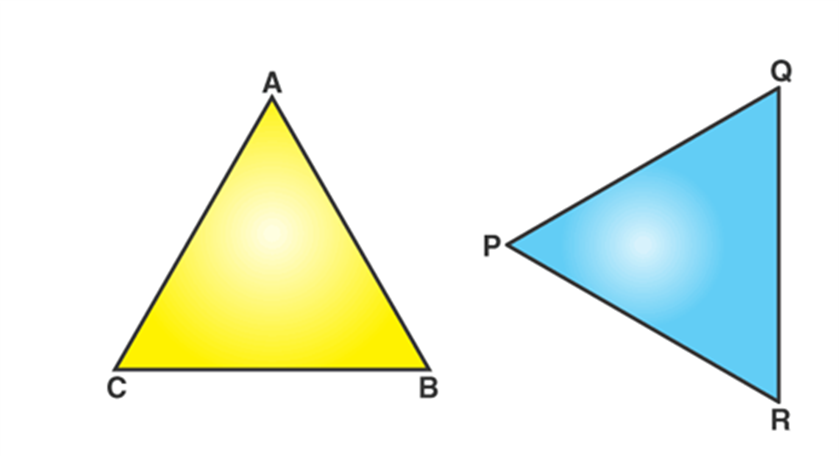
In the above figure, Δ ABC and Δ PQR are congruent triangles. This means,
Vertices: A and P, B and Q, and C and R are the same.
Sides: AB=PQ, QR= BC and AC=PR;
Angles: ∠A = ∠P, ∠B = ∠Q, and ∠C = ∠R.
Congruent triangles are triangles having corresponding sides and angles to be equal. Congruence is denoted by the symbol “≅”. They have the same area and the same perimeter.
7,728
CPCT Full Form
CPCT is the term we come across when we learn about the congruent triangle. CPCT means “Corresponding Parts of Congruent Triangles”. As we know that the corresponding parts of congruent triangles are equal. While dealing with the concepts related to triangles and solving questions, we often make use of the abbreviation cpct in short words instead of full form.
CPCT Rules in Maths
The full form of CPCT is Corresponding parts of Congruent triangles. Congruence can be predicted without actually measuring the sides and angles of a triangle. Different rules of congruency are as follows.
- SSS (Side-Side-Side)
- SAS (Side-Angle-Side)
- ASA (Angle-Side-Angle)
- AAS (Angle-Angle-Side)
- RHS (Right angle-Hypotenuse-Side)
Let us learn them all in detail.
SSS (Side-Side-Side)
If all the three sides of one triangle are equivalent to the corresponding three sides of the second triangle, then the two triangles are said to be congruent by SSS rule.
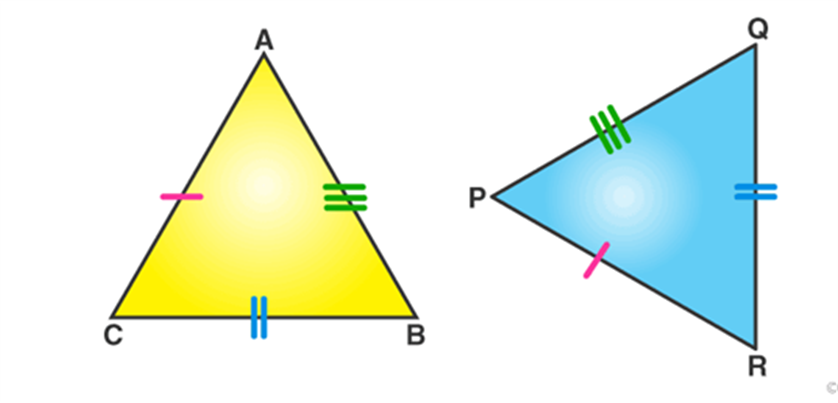
In the above-given figure, AB= PQ, QR= BC and AC=PR, hence Δ ABC ≅ Δ PQR.
SAS (Side-Angle-Side)
If any two sides and the angle included between the sides of one triangle are equivalent to the corresponding two sides and the angle between the sides of the second triangle, then the two triangles are said to be congruent by SAS rule.
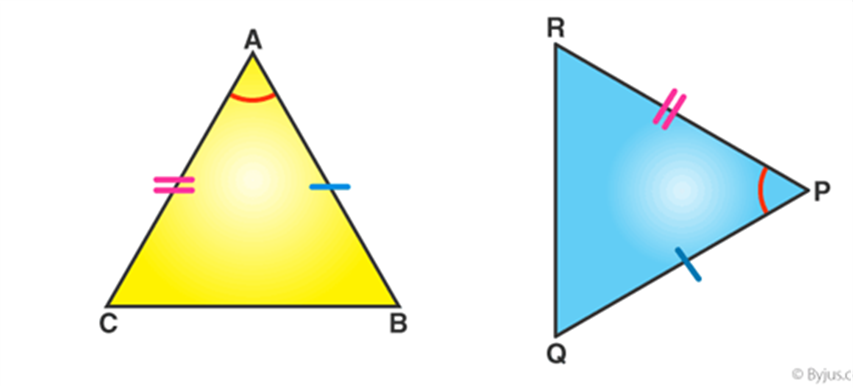
In above given figure, sides AB= PQ, AC=PR and angle between AC and AB equal to angle between PR and PQ i.e. ∠A = ∠P. Hence, Δ ABC ≅ Δ PQR.
ASA (Angle-Side- Angle)
If any two angles and the side included between the angles of one triangle are equivalent to the corresponding two angles and side included between the angles of the second triangle, then the two triangles are said to be congruent by ASA rule.
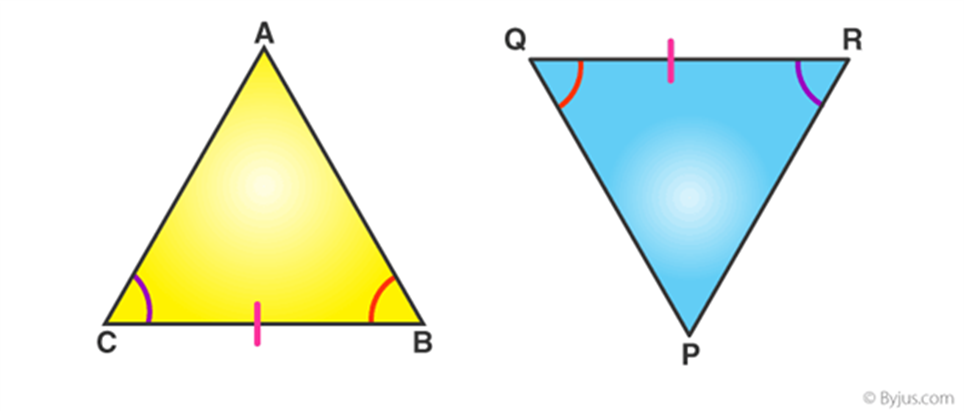
In above given figure, ∠ B = ∠ Q, ∠ C = ∠ R and sides between ∠B and ∠C , ∠Q and ∠ R are equal to each other i.e. BC= QR. Hence, Δ ABC ≅ Δ PQR.
For More Information On SAS And ASA Congruency Rules, Watch The Below Video:
10,184
AAS (Angle-Angle-Side) [Application of ASA]
AAS stands for Angle-angle-side. When two angles and a non-included side of a triangle are equal to the corresponding angles and sides of another triangle, then the triangles are said to be congruent.
AAS congruency can be proved in easy steps. Suppose we have two triangles ABC and DEF, where,
∠B = ∠E [Corresponding sides] ∠C = ∠F [Corresponding sides] And
AC = DF [Adjacent sides]
By angle sum property of triangle, we know that;
∠A + ∠B + ∠C = 180 ………(1)
∠D + ∠E + ∠F = 180 ……….(2)
From equation 1 and 2 we can say;
∠A + ∠B + ∠C = ∠D + ∠E + ∠F
∠A + ∠E + ∠F = ∠D + ∠E + ∠F [Since, ∠B = ∠E and ∠C = ∠F] ∠A = ∠D
Hence, in triangle ABC and DEF,
∠A = ∠D
AC = DF
∠C = ∠F
Hence, by ASA congruency,
Δ ABC ≅ Δ DEF
RHS (Right angle- Hypotenuse-Side)
If the hypotenuse and a side of a right- angled triangle is equivalent to the hypotenuse and a side of the second right- angled triangle, then the two right triangles are said to be congruent by RHS rule.
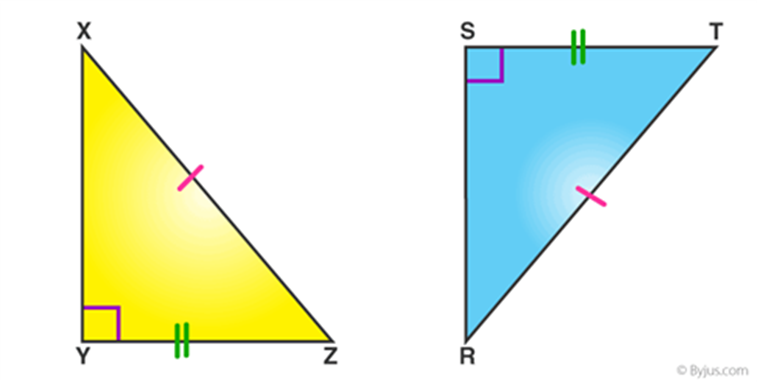
In above figure, hypotenuse XZ = RT and side YZ=ST, hence triangle XYZ ≅ triangle RST.
Solved Example
|
Let’s Work Out:
Solution: We are required to prove ∠BEA = ∠BEC = 90° and AE = EC.Consider ∆ABD and ∆CBD,AB = BC (Given)AD = CD (Given) BD = BD (Common) Therefore, ∆ABD ≅ ∆CBD (By SSS congruency) ∠ABD = ∠CBD (CPCTC) Now, consider ∆ABE and ∆CBE, AB = BC (Given) ∠ABD = ∠CBD (Proved above) BE = BE (Common) Therefore, ∆ABE≅ ∆CBE (By SAS congruency) ∠BEA = ∠BEC (CPCTC) And ∠BEA +∠BEC = 180° (Linear pair) 2∠BEA = 180° (∠BEA = ∠BEC) ∠BEA = 180°/2 = 90° = ∠BEC AE = EC (CPCTC) Hence, BD is a perpendicular bisector of AC. Example 2: In a Δ ABC, if AB = AC and ∠ B = 70°, find ∠ A. Solution: Given: In a Δ ABC, AB = AC and ∠B = 70° ∠ B = ∠ C [Angles opposite to equal sides are equal] Therefore, ∠ B = ∠ C = 70° Sum of angles in a triangle = 180° ∠ A + ∠ B + ∠ C = 180° ∠ A + 70° + 70° = 180° ∠ A = 180° – 140° ∠ A = 40° |
Criteria for congruence of triangles
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Criteria For Congruent Triangles
Congruent triangles are triangles that have the same size and shape. This means that the corresponding sides are equal and the corresponding angles are equal.
Congruent Triangles do not have to be in the same orientation or position. They only have to be identical in size and shape.
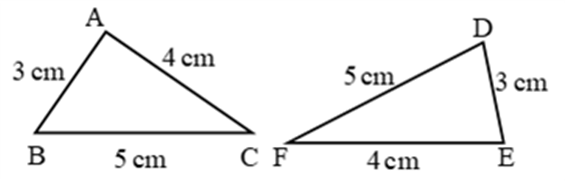
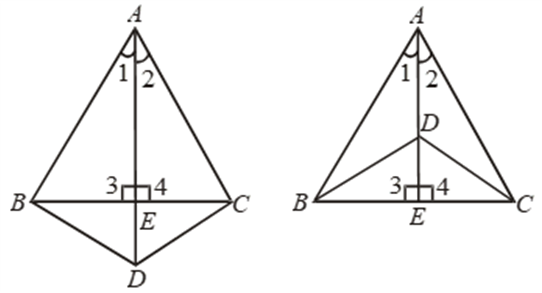
1. SSS (Side Side Side) Congruence Criteria (Condition):
Two triangles are congruent, if three sides of one triangle are equal to the corresponding three sides of the other triangle.
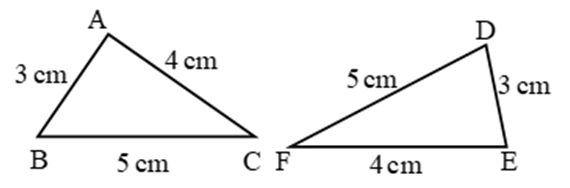
∴ By SSS criteria ∆ABC ∆EDF
∴ ∠A = ∠E, ∠B = ∠D, ∠C = ∠F (c.p.c.t.)
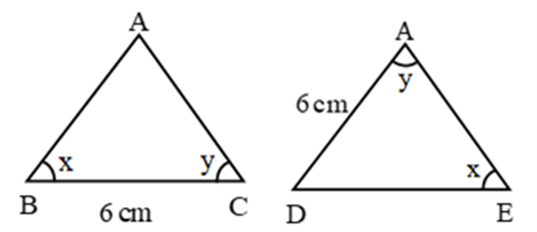
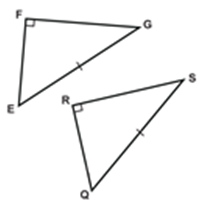
2. ASA (Angle Side Angle) Congruence Criteria (Condition):
Two triangles are congruent, if two angles and the included side of one is equal to the corresponding angles and side of the other.
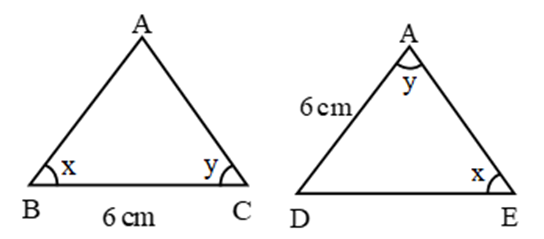
∴ By ASA criteria ∆ABC ≅ ∆DEF
∴ ∠A = ∠D, AB = DE, AC = DF (c.p.c.t.)
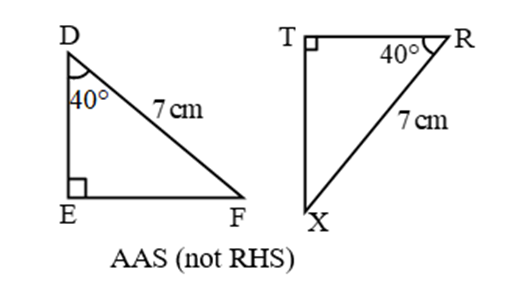
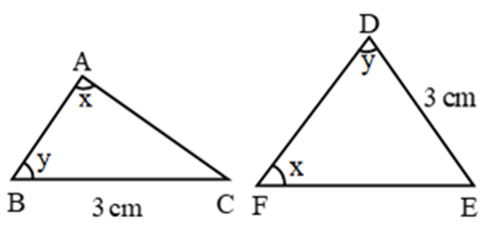
3. AAS (Angle Angle Side) Congruence Criteria (Condition):
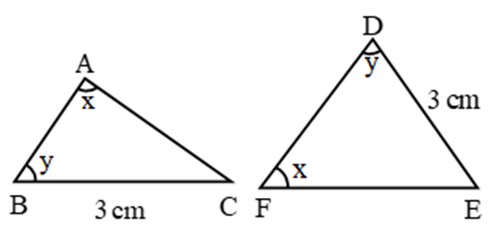
∴ By AAS, ∆ABC ≅ ∆FDE
∴ ∠C = ∠E, AB = FD, AC = FE (c.p.c.t.)
4. SAS (Side Angle Side) Congruence Criteria (Condition):
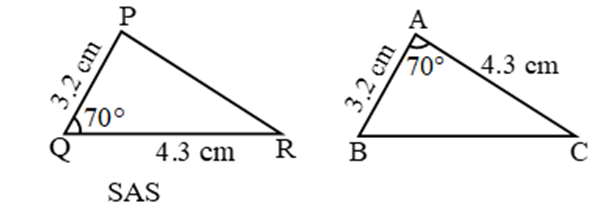
When two sides and the included angle of one triangle is equal to the corresponding sides and the included angle of another triangle, the two triangles are congruent. This, condition of congruence is known as side-angle-side congruence. In short we write SAS condition.
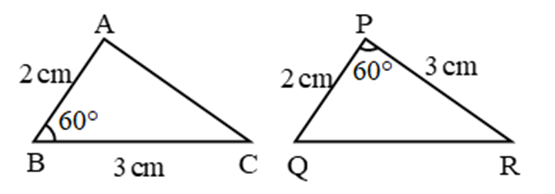
By SAS, ∆ABC ≅ ∆QPR
∴ ∠A = ∠Q, ∠C = ∠R, AC = QR (c.p.c.t.)
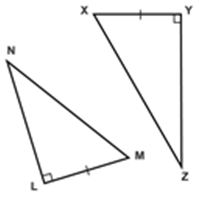
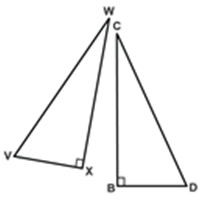
5. RHS (Right Hypotenuse Side) Congruence Criteria (Condition):
Two right triangles are congruent, if the hypotenuse and one side of one triangle are respectively equal to the hypotenuse and a side of the other triangle.
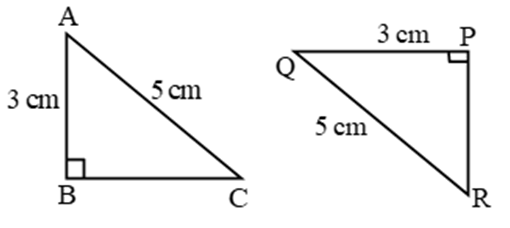
∴ By RHS, ∆ABC ≅ ∆QPR
∴ ∠A = ∠Q, ∠C = ∠R, BC = PR (c.p.c.t.)
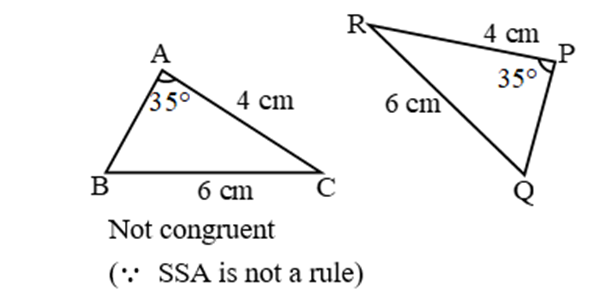
Example 1:
Example 2:
Example 3:
Example 4:
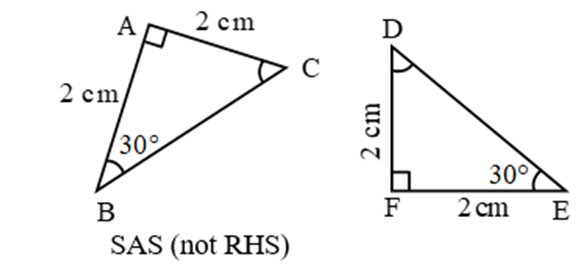
Theorem 1: If two angles and the included side of one triangle are equal to two angles and the included side of other triangle, then both triangles are congruent.
Proof:
Given: ∆ABC and ∆DEF in which
∠ABC = ∠DEF, ∠ACB = ∠DFE and BC = EF.
To Prove: ∆ABC ≅ ∆DEF.
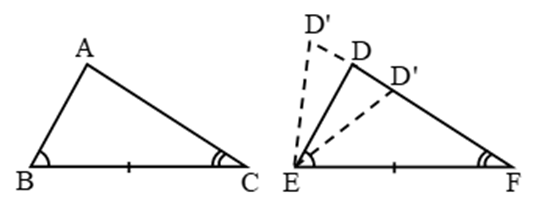
Proof:
Case I:
Let AC = DF.
In this case, AC = DF, BC = EF and ∠C = ∠F.
∴ ∆ABC ≅ ∆DEF (SAS-criteria)
Case II:
If possible, let AC ≠ DF.
Then, construct D’ F = AC. Join D’ E.
Now, in ∆ABC and ∆D’EF, we have AC = D’F, BC = EF and ∠C = ∠F.
∴ ∆ABC ∆D’EF (SAS-criteria)
∴ ∠ABC = ∠D’EF (c.p.c.t)
But, ∠ABC = ∠DEF (given)
∴ ∠D’EF = ∠DEF.
This is possible only when D and D’ coincide.
∴ ∆ABC ≅ ∆DEF.
Theorem 2: Two right-angled triangles are congruent if one side and the hypotenuse of the one are respectively equal to the corresponding side and the hypotenuse of the other. (i.e. RHS)
Given: Two right-angled triangles ∆ABC & ∆DEF in which ∠B = ∠E = 90°, BC = EF and AC = DF.
To Prove: ∆ABC ≅ ∆DEF.
Construction: Produce DE to G such that
GE = AB. Join GF.
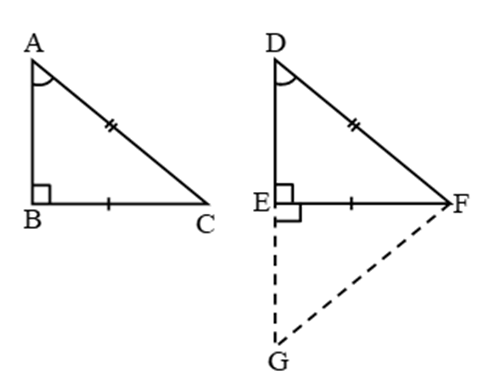
Proof: In ∆ABC and ∆GEF, we have:
AB = GE (construction),
BC = EF (given),
∠B = ∠FEG = 90°
⇒ ∆ABC ∆GEF (SAS-criteria)
⇒ ∠A = ∠G and AC = GF (c.p.c.t.)
Now, AC = GF and AC = DF ⇒GF = DF
⇒ ∠G = ∠D ⇒ ∠A = ∠D [∵ ∠G = ∠A]
Now, ∠A = ∠D, ∠B = ∠E ⇒ 3rd ∠C = 3rd ∠F.
Thus, in ∆ABC and ∆DEF, we have:
BC = EF, AC = DF and ∠C = ∠F.
∴ ∆ABC ≅ ∆DEF (SAS-criteria).
Criteria For Congruent Triangles Example Problems With Solutions
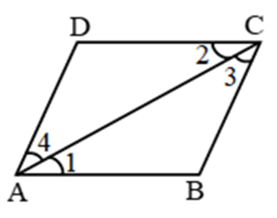
Example 1: Prove that diagonal of a parallelogram divides it into two congruent triangles.
Solution: Let ABCD is a parallelogram and AC is a diagonal.
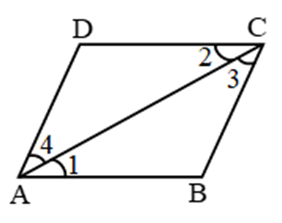
(By SSS): In ∆ABC and ∆ADC
AB = CD (opp. sides of ||gm)
BC = AD (opp. sides of ||gm)
AC = AC (common)
∴ By SSS, ∆ABC ≅ ∆CDA proved
{other results : ∠1 = ∠2, ∠3 = ∠4, ∠B = ∠D (c.p.c.t.)}
(By ASA): In ∆ABC and ∆ADC
∠1 = ∠2 (alternate)
AC = AC (common)
∠3 = ∠4 (alternate)
∴ By ASA, ∆ABC ≅ ∆CDA
{other results: ∠B = ∠D, AB = CD, BC = AD (c.p.c.t.)}
(By AAS): In ∆ABC and ∆ADC
∠1 = ∠2 (alternate)
∠3 = ∠4 (alternate)
BC = AD (opp. sides)
∴ ∆ABC ≅ ∆CDA
{other results : AB = CD, ∠B = ∠D, AC = AC (c.p.c.t.)}
(By SAS): In ∆ABC and ∆ADC
AB = CD (opp. sides of ||gm)
∠1 = ∠2 (alternate)
AC = AC (common)
∴ ∆ABC ≅ ∆CDA
{other results: ∠3 = ∠4, BC = AD, ∠B = ∠D (c.p.c.t.)
We can not use ‘RHS’ for this proof.
Note: ASS or SSA criteria for congruency is not valid.
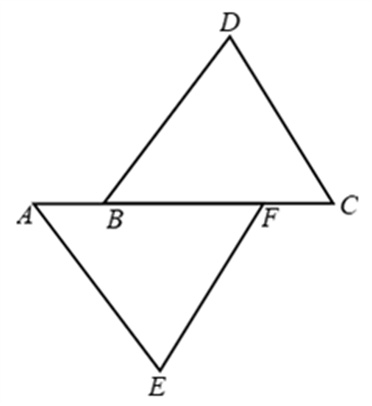
Example 2: In Fig. it is given that AB = CF, EF = BD and ∠AFE = ∠DBC. Prove that ∆AFE ∆CBD.
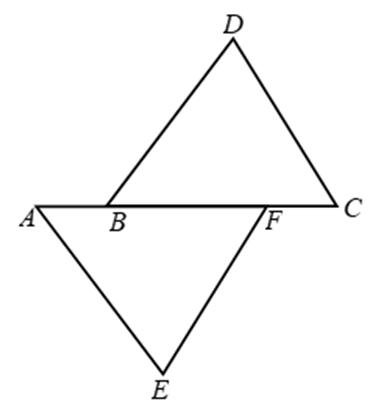
Solution: We have, AB = CF
⇒ AB + BF = CF + BF
⇒ AF = CB …. (i)
In ∆s AFE and CBD, we have AF = CB [From (i)]
∠AFE = ∠DBC [Given]
and EF = BD [Given]
So, by SAS criterion of congruence, we have ∆AFE ≅ ∆CBD
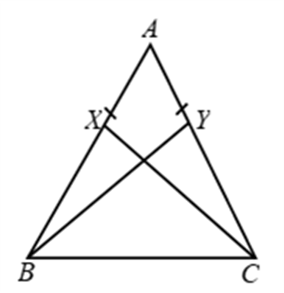
Example 3: In Fig. X and Y are two points on equal sides AB and AC of a ∆ABC such that AX = AY. Prove that XC = YB.
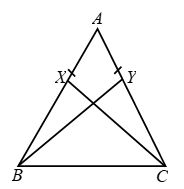
Solution: In ∆s AXC and AYB, we have
AX = AY [Given]
∠A = ∠A [Common angle]
AC = AB [Given]
So, by SAS criterion of congruene
∆AXC ≅ ∆AYB ⇒ XC = YB (c.p.c.t.)
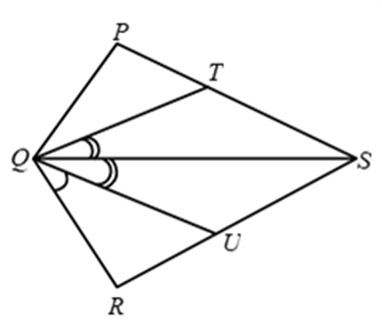
Example 4: In Fig. PQRS is a quadrilateral and T and U are respectively points on PS and RS such PQ = RQ, ∠PQT = ∠RQU and ∠TQS = ∠UQS. Prove that QT = QU.
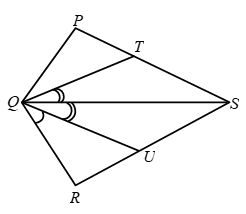
Solution: We have, ∠PQT = ∠RQU
and, ∠TQS = ∠UQS
∴ ∠PQT + ∠TQS = ∠RQU + ∠UQS
⇒ ∠PQS = ∠RQS …. (i)
Thus, in triangles PQS and RQS, we have
PQ = RQ [Given]
∠PQS = ∠RQS [From (i)]
and, QS = QS [Common side]
Therefore, by SAS congruence criterion, we have
∆PQS ≅ ∆RQS
⇒ ∠QPS = ∠QRS (c.p.c.t.)
⇒ ∠QPT = ∠QRU …. (ii)
Now, consider triangles QPT and QRS. In these two triangles, we have
QP = QR [Given]
∠PQT = ∠RQU [Given]
∠QPT = ∠QRU [From (ii)]
Therefore, by ASA congruence criterion, we get
∆QPT ≅ ∆QRU ⇒ QT = QU.
Example 5: In Fig. PS = QR and ∠SPQ = ∠RQP.
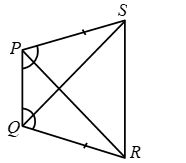
Prove that PR = QS and ∠QPR = ∠PQS.
Solution: In ∆SPQ and ∆RQP, we have
PS = QR [Given]
∠SPQ = ∠RQP [Given]
PQ = PQ [Common]
Therefore, by SAS criterion of congruence, we have
∆SPQ ∆RQP ⇒ SQ = RP and ∠QPR = ∠PQS
Example 6: ∆ABC is an isosceles triangle with AB = AC. Side BA is produced to D such that
AB = AD. Prove that ∠BCD is a right angle.
Solution: Given : A ∆ABC such that AB = AC. Side BA is produced to D such that AB = AD.
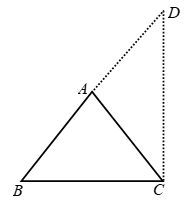
Construction : Join CD.
To prove : ∠BCD = 90º
Proof : In ∆ABC, we have AB = AC
⇒ ∠ACB = ∠ABC …(i) [∵ Angles opp. to equal sides are equal]
Now, AB = AD [Given]
∴ AD = AC [∴ AB = AC]
Thus, in ∆ADC, we have AD = AC
⇒ ∠ACD = ∠ADC …(ii)
[∵ Angles opp. to equal sides are equal]
Adding (i) and (ii), we get
∠ACB + ∠ACD = ∠ABC + ∠ADC
⇒ ∠BCD = ∠ABC + ∠BDC
[∵ ∠ADC = ∠BDC, ∠ABC = ∠DBC]
⇒ ∠BCD + ∠BCD = ∠DBC + ∠BCD + ∠BDC
[adding ∠BCD on both sides ]
⇒ 2 ∠BCD = 180º
[∵ Sum of the angles of a ∆ is 180º]
Hence, ∠BCD is a right angle.
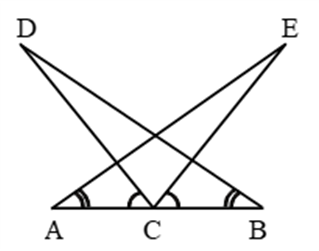
Example 7: In Fig. AC = BC, ∠DCA = ∠ECB and ∠DBC = ∠EAC.
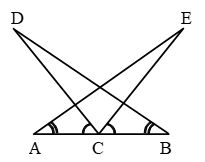
Prove that triangles DBC and EAC are congruent, and hence DC = EC.
Solution: We have, ∠DCA = ∠ECB
⇒ ∠DCA + ∠ECD = ∠ECB + ∠ECD
⇒ ∠ECA = ∠DCB …. (i)
Now, in ∆s DBC and EAC, we have
∠DCB = ∠ECA [From (i)]
BC = AC [Given]
and ∠DBC = ∠EAC [Given]
So, by ASA criterion of congruence
∆DBC ≅ ∠EAS ⇒ DC = EC (c.p.c.t.)
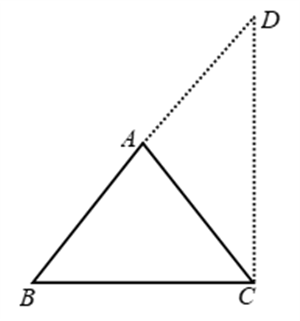
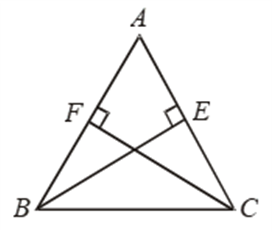
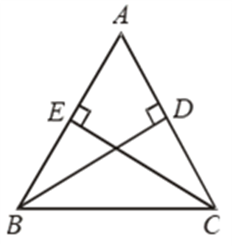
Example 8: If the altitudes from two vertices of a triangle to the opposite sides are equal, prove that the triangle is isosceles.
Solution: Given: A ∆ABC in which altitudes BE and CF from B and C respectively on AC and AB are equal.
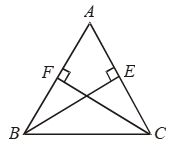
To prove: ∆ABC is isosceles i.e. AB = AC
Proof: In ∆s ABC and ACF, we have
∠AEB = ∠AFC [Each equal to 90º]
∠BAE = ∠CAF [Common angle]
and, BE = CF [Given]
So, by AAS criterion of congruence, we have
∆ABE ≅ ∆ACF
⇒ AB = AC [∵ Corresponding parts of congruent triangles are equal]
Hence, ∆ABC is isosceles.
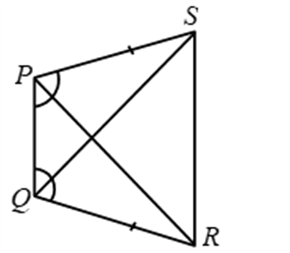
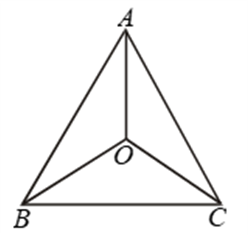
Example 9: In ∆ABC, AB = AC and the bisectors of angles B and C intersect at point O. Prove that BO = CO and the ray AO is the bisector of angle BAC.
Solution: In ∆ABC, we have AB = AC
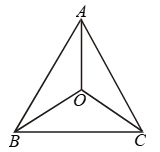

Now, in ∆ABO and ∆ACO, we have
AB = AC [Given]
∠OBC = ∠OCB [From (i)]
OB = OC [From (ii)]
So, by SAS criterion of congruence
∆ABO ≅ ∆ACO ⇒ ∠BAO = ∠CAO
[∵ Corresponding parts of congruent triangles are equal]
⇒ AO is the bisector of ∠BAC.
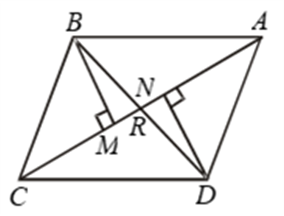
Example 10: In Fig. BM and DN are both perpendicular to the segments AC and BM = DN.
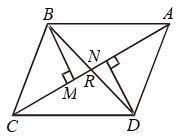
Prove that AC bisects BD.
Solution: In ∆s BMR and DNR, we have
∠BMR = ∠DNR
[Each equal to 90º ∵ BM ⊥ AC and DN ⊥ AC]
∠BRM = ∠DRN [Vert. opp. angles]
and, BM = DN [Given]
So, by AAS criterion of congruence
∆BMR ≅ ∆DNR ⇒ BR = DR
[∵ Corresponding parts of congruent triangles are equal]
⇒ R is the mid-point of BD.
Hence, AC bisects BD.
Example 11: In Fig. BD and CE are two altitudes of a ∆ABC such that BD = CE.
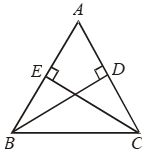
Prove that ∆ABC is isolceles.
Solution: In ∆ABD and ∆ACE, we have
∠ADB = ∠AEC = 90º [Given]
∠BAD = ∠CAE [Common]
and, BD = CE [Given]
So, by AAS congruence criterion, we have
∆ABD ≅ ∆ACE
⇒ AB = AC [∵ Corresponding parts of congruent triangles are equal]
Hence, ∆ABC is isosceles.
Example 12: If two isosceles triangles have a common base, the line joining their vertices bisects them at right angles.
Solution: Given: Two isosceles triangles ABC and DBC having the common base BC such that AB = AC and DB = DC.
To prove: AD (or AD produced) bisects BC at right angle.
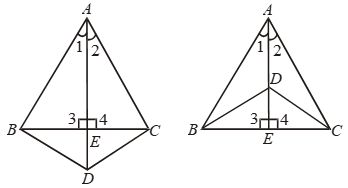
Proof : In ∆s ABD and ACD, we have
AB = AC [Given]
BD = CD [Given]
AD = AD [Common side]
So, by SSS criterion of congruence
∆ABD ≅ ∆ACD
⇒ ∠1 = ∠2 …. (i)
[∵ Corresponding parts of congruent triangles are equal]
Now, in ∆s ABE and ACE, we have
AB = AC [Given]
∠1 = ∠2 [From (i)]
and, AE = AE [Commoni side]
So, by SAS criterion of congruence,
∆ABE ≅ ∆ACE ⇒ BE = CE
[∵ Corresponding parts of congruent triangles are equal]
and, ∠3 = ∠4
But, ∠3 + ∠4 = 180º
[∵ Sum of the angles of a linear pair is 180º]
⇒ 2 ∠3 = 180º [∵ ∠3 = ∠4]
⇒ ∠3 = 90º
∴ ∠3 = ∠4 = 90º
Hence, AD bisects BC at right angles.
Example 13: AD, BE and CF, the altitudes of ∆ABC are equal. Prove that ∆ABC is an equilateral triangle
Solution: In right triangles BCE and BFC, we have
Hyp. BC = Hyp. BC
BE = CF [Given]
So, by RHS criterion of congruence,
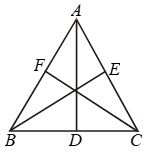
∆BCE ∆BFC.
⇒ ∠B = ∠C [∵ Corresponding parts of congruent triangles are equal]
⇒ AC = AB …. (i)
[∵ Sides opposite to equal angles are equal]
Similarly, ∆ABD ≅ ∆ABE ⇒ ∠B =∠A
[Corresponding parts of congruent triangles are equal]
⇒ AC = BC …. (ii)
[Sides opposite to equal angles are equal]
From (i) and (ii), we get AB = BC = AC
Hence, ∆ABC is an equilateral triangle.
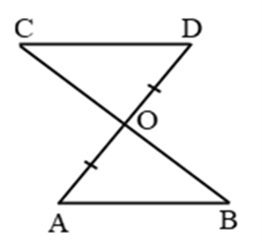
Example 14: In Fig. AD = BC and BD = CA.
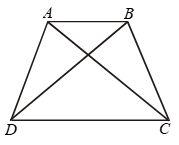
Prove that ∠ADB = ∠BCA and ∠DAB = ∠CBA.
Solution: In triangles ABD and ABC, we have
AD = BC [Given]
BD = CA [Given]
and AB = AB [Common]
So, by SSS congruence criterion, we have
∆ABD ∠CBA ⇒ ∠DAB = ∠ABC
[∵ Corresponding parts of congruent triangles are equal] ⇒ ∠DAB = ∠CBA
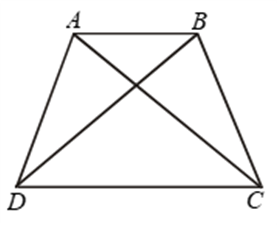
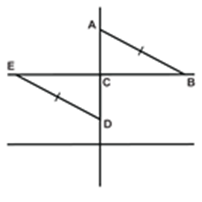
Example 15: Line-segment AB is parallel to another line-segment CD. O is the mid-point of AD (see figure). Show that (i) ∆AOB ≅ ∆DOC (ii) O is also the mid point of BC.
Solution: (i) Consider ∆AOB and ∆DOC ∠ABO = ∠DCO
(Alternate angles as AB || CD and BC is the transversal)
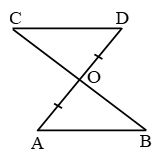
∠AOB = ∠DOC (Vertically opposite angles)
OA = OD (Given)
Therefore, ∆AOB ≅ ∆DOC (AAS rule)
(ii) OB = OC (c.p.c.t.)
So, O is the mid-point of BC.
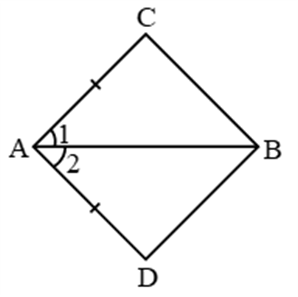
Example 16: In quadrilateral ABCD, AC = AD and AB bisects ∠A. Show that ∆ABC ∆ABD. What can you say about BC and BD ?
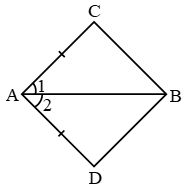
Solution: In ∆ABC & ∆ABD
AB = AB (common)
∠1 = ∠2 {∵ AB is bisector of ∠A}
AC = AD (Given)
∴ By SAS, ∆ABC ≅ ∆ABD Proved
also BC = BD (c.p.c.t.)
Example 17: AD and BC are equal perpendiculars to a line segment AB. Show that CD bisects AB.
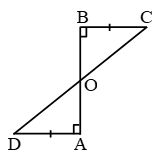
Solution: To show CD bisect AB i.e. AO = OB
∴ in ∆OAD and ∆OBC
∠O = ∠O (vertically opposite angles)
∠A = ∠B = 90° (Given)
AD = BC (Given)
∴ By AAS, ∆OAD ≅ ∆OBC
∴ OA = OB (c.p.c.t.)
∴ CD, bisects AB. Proved
Example 18: Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendicular from B to the arms of ∠A (see figure). Show that
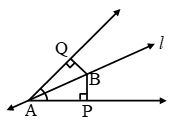
(i) ∆APB ≅ ∆AQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.
Solution: (i) In ∆APB and ∆AQB
∠P = ∠Q = 90° (Given)
∠PAB = ∠QAB (Given that ‘l’ bisect ∠A)
AB = AB (Common)
∴ By AAS, ∆APB ≅ ∆AQB. Proved
(ii) BP = BQ (c.p.c.t.) Proved.
Example 19: In given figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.
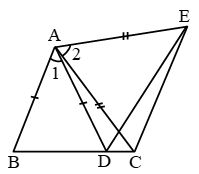
Solution: In ∆ABC and ∆ADE
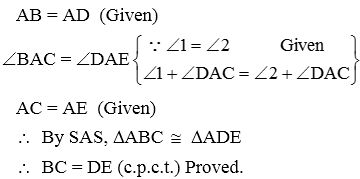
Example 20: In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that:
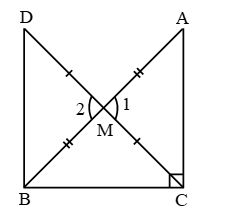
(i) ∆AMC ≅ ∆BMD
(ii) ∠DBC is a right angle
(iii) ∆DBC ≅ ∆ACB
(iv) CM = AB
Solution: (i) In ∆AMC and ∆BMD
AM = MB (M is mid point of AB)
∠1 = ∠2 (vertically opposite angles)
CM = MD (given)
∴ By SAS, ∆AMC ≅ ∆MBD Proved.
(ii) ∠ACM = ∠MDB (c.p.c.t. of (i))
These are alternate angles
∴ DB || AC
So ∠DBC + ∠ACB = 180°
(Cointerior angles)
⇒ ∠DBC + 90° = 180°
⇒ ∠DBC = 90° Proved.
(iii) In ∆DBC & ∆ACB
BC = BC ( common)
∠DBC = ∠ACB = 90°
DB = AC (c.p.c.t. of part (i))
∴ By SAS, ∆DBC ≅ ∆ACB. Proved
(iv) DC = AB (c.p.c.t. of part (iii))
But CM = DC (given)
∴ CM = AB Proved.
Criteria for congruence of triangles
Criteria For Congruent Triangles
Congruent triangles are triangles that have the same size and shape. This means that the corresponding sides are equal and the corresponding angles are equal.
Congruent Triangles do not have to be in the same orientation or position. They only have to be identical in size and shape.
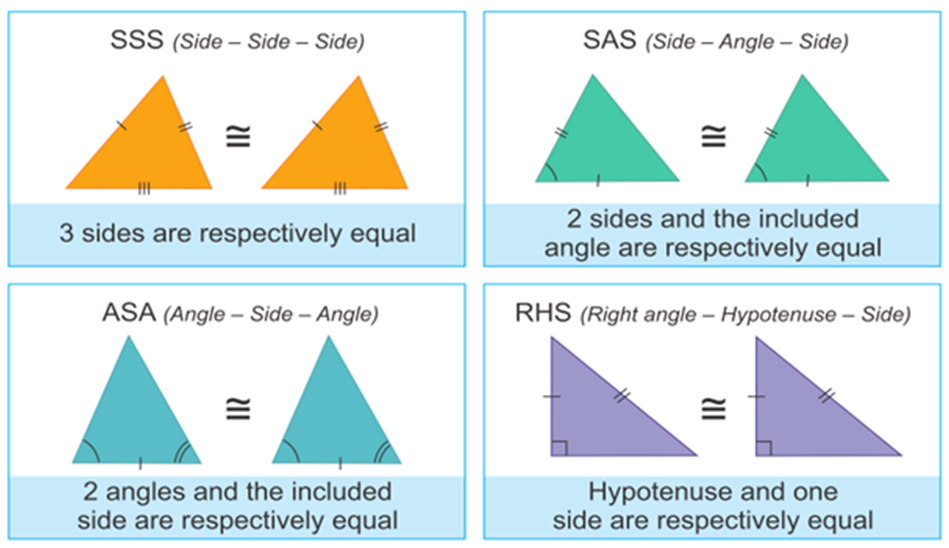
SSS (Side Side Side) Congruence Criteria (Condition):
Two triangles are congruent, if three sides of one triangle are equal to the corresponding three sides of the other triangle.
∴ By SSS criteria ∆ABC ∆EDF
∴ ∠A = ∠E, ∠B = ∠D, ∠C = ∠F (c.p.c.t.)
ASA (Angle Side Angle) Congruence Criteria (Condition):
Two triangles are congruent, if two angles and the included side of one is equal to the corresponding angles and side of the other.
∴ By ASA criteria ∆ABC ≅ ∆DEF
∴ ∠A = ∠D, AB = DE, AC = DF (c.p.c.t.)
AAS (Angle Angle Side) Congruence Criteria (Condition):
∴ By AAS, ∆ABC ≅ ∆FDE
∴ ∠C = ∠E, AB = FD, AC = FE (c.p.c.t.)
SAS (Side Angle Side) Congruence Criteria (Condition):
When two sides and the included angle of one triangle is equal to the corresponding sides and the included angle of another triangle, the two triangles are congruent. This, condition of congruence is known as side-angle-side congruence. In short we write SAS condition.
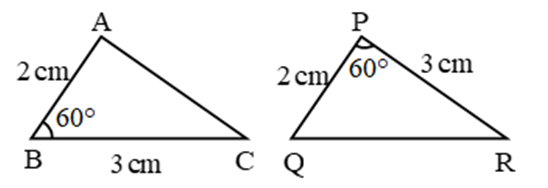
By SAS, ∆ABC ≅ ∆QPR
∴ ∠A = ∠Q, ∠C = ∠R, AC = QR (c.p.c.t.)
RHS (Right Hypotenuse Side) Congruence Criteria (Condition):
Two right triangles are congruent, if the hypotenuse and one side of one triangle are respectively equal to the hypotenuse and a side of the other triangle.
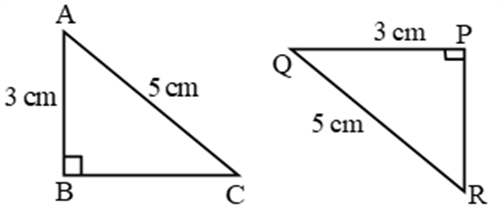
∴ By RHS, ∆ABC ≅ ∆QPR
∴ ∠A = ∠Q, ∠C = ∠R, BC = PR (c.p.c.t.)
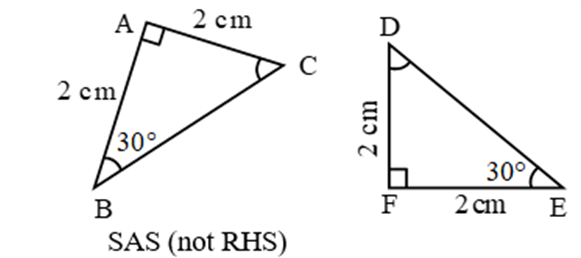
Example 1:
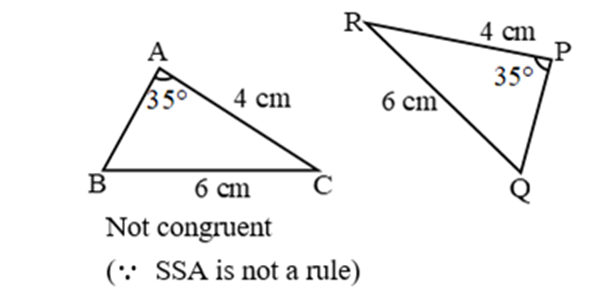
Example 2:
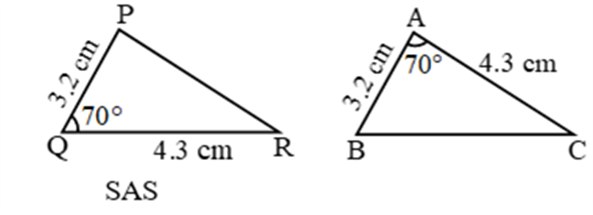
Example 3:
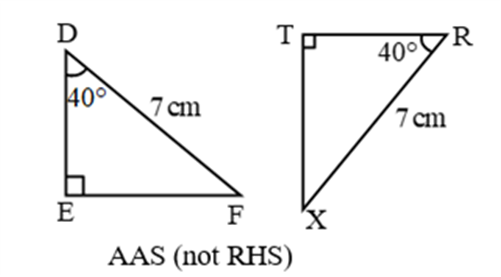
Example 4:
Theorem 1: If two angles and the included side of one triangle are equal to two angles and the included side of other triangle, then both triangles are congruent.
Proof:
Given: ∆ABC and ∆DEF in which
∠ABC = ∠DEF, ∠ACB = ∠DFE and BC = EF.
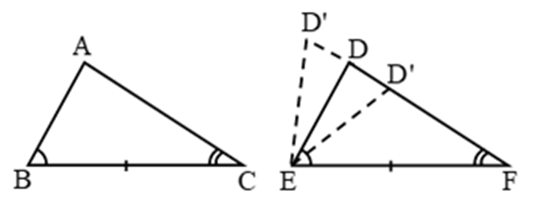
To Prove: ∆ABC ≅ ∆DEF.
Proof:
Case I:
Let AC = DF.
In this case, AC = DF, BC = EF and ∠C = ∠F.
∴ ∆ABC ≅ ∆DEF (SAS-criteria)
Case II:
If possible, let AC ≠ DF.
Then, construct D’ F = AC. Join D’ E.
Now, in ∆ABC and ∆D’EF, we have AC = D’F, BC = EF and ∠C = ∠F.
∴ ∆ABC ∆D’EF (SAS-criteria)
∴ ∠ABC = ∠D’EF (c.p.c.t)
But, ∠ABC = ∠DEF (given)
∴ ∠D’EF = ∠DEF.
This is possible only when D and D’ coincide.
∴ ∆ABC ≅ ∆DEF.
Theorem 2: Two right-angled triangles are congruent if one side and the hypotenuse of the one are respectively equal to the corresponding side and the hypotenuse of the other. (i.e. RHS)
Given: Two right-angled triangles ∆ABC & ∆DEF in which ∠B = ∠E = 90°, BC = EF and AC = DF.
To Prove: ∆ABC ≅ ∆DEF.
Construction: Produce DE to G such that
GE = AB. Join GF.
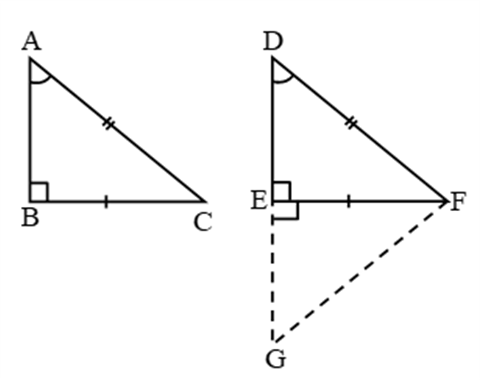
Proof: In ∆ABC and ∆GEF, we have:
AB = GE (construction),
BC = EF (given),
∠B = ∠FEG = 90°
⇒ ∆ABC ∆GEF (SAS-criteria)
⇒ ∠A = ∠G and AC = GF (c.p.c.t.)
Now, AC = GF and AC = DF ⇒GF = DF
⇒ ∠G = ∠D ⇒ ∠A = ∠D [∵ ∠G = ∠A]
Now, ∠A = ∠D, ∠B = ∠E ⇒ 3rd ∠C = 3rd ∠F.
Thus, in ∆ABC and ∆DEF, we have:
BC = EF, AC = DF and ∠C = ∠F.
∴ ∆ABC ≅ ∆DEF (SAS-criteria).
Criteria For Congruent Triangles Example Problems With Solutions
Example 1: Prove that diagonal of a parallelogram divides it into two congruent triangles.
Solution: Let ABCD is a parallelogram and AC is a diagonal.
(By SSS): In ∆ABC and ∆ADC
AB = CD (opp. sides of ||gm)
BC = AD (opp. sides of ||gm)
AC = AC (common)
∴ By SSS, ∆ABC ≅ ∆CDA proved
{other results : ∠1 = ∠2, ∠3 = ∠4, ∠B = ∠D (c.p.c.t.)}
(By ASA): In ∆ABC and ∆ADC
∠1 = ∠2 (alternate)
AC = AC (common)
∠3 = ∠4 (alternate)
∴ By ASA, ∆ABC ≅ ∆CDA
{other results: ∠B = ∠D, AB = CD, BC = AD (c.p.c.t.)}
(By AAS): In ∆ABC and ∆ADC
∠1 = ∠2 (alternate)
∠3 = ∠4 (alternate)
BC = AD (opp. sides)
∴ ∆ABC ≅ ∆CDA
{other results : AB = CD, ∠B = ∠D, AC = AC (c.p.c.t.)}
(By SAS): In ∆ABC and ∆ADC
AB = CD (opp. sides of ||gm)
∠1 = ∠2 (alternate)
AC = AC (common)
∴ ∆ABC ≅ ∆CDA
{other results: ∠3 = ∠4, BC = AD, ∠B = ∠D (c.p.c.t.)
We can not use ‘RHS’ for this proof.
Note: ASS or SSA criteria for congruency is not valid.
Example 2: In Fig. it is given that AB = CF, EF = BD and ∠AFE = ∠DBC. Prove that ∆AFE ∆CBD.
Solution: We have, AB = CF
⇒ AB + BF = CF + BF
⇒ AF = CB …. (i)
In ∆s AFE and CBD, we have
AF = CB [From (i)]
∠AFE = ∠DBC [Given]
and EF = BD [Given]
So, by SAS criterion of congruence, we have
∆AFE ≅ ∆CBD
Example 3: In Fig. X and Y are two points on equal sides AB and AC of a ∆ABC such that AX = AY. Prove that XC = YB.
Solution: In ∆s AXC and AYB, we have
AX = AY [Given]
∠A = ∠A [Common angle]
AC = AB [Given]
So, by SAS criterion of congruene
∆AXC ≅ ∆AYB
⇒ XC = YB (c.p.c.t.)
Example 4: In Fig. PQRS is a quadrilateral and T and U are respectively points on PS and RS such PQ = RQ, ∠PQT = ∠RQU and ∠TQS = ∠UQS. Prove that QT = QU.
Solution: We have,
∠PQT = ∠RQU
and, ∠TQS = ∠UQS
∴ ∠PQT + ∠TQS = ∠RQU + ∠UQS
⇒ ∠PQS = ∠RQS …. (i)
Thus, in triangles PQS and RQS, we have
PQ = RQ [Given]
∠PQS = ∠RQS [From (i)]
and, QS = QS [Common side]
Therefore, by SAS congruence criterion, we have
∆PQS ≅ ∆RQS
⇒ ∠QPS = ∠QRS (c.p.c.t.)
⇒ ∠QPT = ∠QRU …. (ii)
Now, consider triangles QPT and QRS. In these two triangles, we have
QP = QR [Given]
∠PQT = ∠RQU [Given]
∠QPT = ∠QRU [From (ii)]
Therefore, by ASA congruence criterion, we get
∆QPT ≅ ∆QRU
⇒ QT = QU.
Example 5: In Fig. PS = QR and ∠SPQ = ∠RQP.
Prove that PR = QS and ∠QPR = ∠PQS.
Solution: In ∆SPQ and ∆RQP, we have
PS = QR [Given]
∠SPQ = ∠RQP [Given]
PQ = PQ [Common]
Therefore, by SAS criterion of congruence, we have
∆SPQ ∆RQP ⇒ SQ = RP and
∠QPR = ∠PQS
Example 6: ∆ABC is an isosceles triangle with AB = AC. Side BA is produced to D such that
AB = AD. Prove that ∠BCD is a right angle.
Solution: Given : A ∆ABC such that AB = AC. Side BA is produced to D such that AB = AD.
Construction : Join CD.
To prove : ∠BCD = 90º
Proof : In ∆ABC, we have AB = AC
⇒ ∠ACB = ∠ABC …(i) [∵ Angles opp. to equal sides are equal]
Now, AB = AD [Given]
∴ AD = AC [∴ AB = AC]
Thus, in ∆ADC, we have
AD = AC
⇒ ∠ACD = ∠ADC …(ii)
[∵ Angles opp. to equal sides are equal]
Adding (i) and (ii), we get
∠ACB + ∠ACD = ∠ABC + ∠ADC
⇒ ∠BCD = ∠ABC + ∠BDC
[∵ ∠ADC = ∠BDC, ∠ABC = ∠DBC]
⇒ ∠BCD + ∠BCD = ∠DBC + ∠BCD + ∠BDC
[adding ∠BCD on both sides ]
⇒ 2 ∠BCD = 180º
[∵ Sum of the angles of a ∆ is 180º]
Hence, ∠BCD is a right angle.
Example 7: In Fig. AC = BC, ∠DCA = ∠ECB and ∠DBC = ∠EAC.
Prove that triangles DBC and EAC are congruent, and hence DC = EC.
Solution: We have,
∠DCA = ∠ECB
⇒ ∠DCA + ∠ECD = ∠ECB + ∠ECD
⇒ ∠ECA = ∠DCB …. (i)
Now, in ∆s DBC and EAC, we have
∠DCB = ∠ECA [From (i)]
BC = AC [Given]
and ∠DBC = ∠EAC [Given]
So, by ASA criterion of congruence
∆DBC ≅ ∠EAS
⇒ DC = EC (c.p.c.t.)
Example 8: If the altitudes from two vertices of a triangle to the opposite sides are equal, prove that the triangle is isosceles.
Solution: Given: A ∆ABC in which altitudes BE and CF from B and C respectively on AC and AB are equal.
To prove: ∆ABC is isoceles i.e. AB = AC
Proof: In ∆s ABC and ACF, we have
∠AEB = ∠AFC [Each equal to 90º]
∠BAE = ∠CAF [Common angle]
and, BE = CF [Given]
So, by AAS criterion of congurence, we have
∆ABE ≅ ∆ACF
⇒ AB = AC [∵ Corresopnding parts of congruent triangles are equal]
Hence, ∆ABC is isosceles.
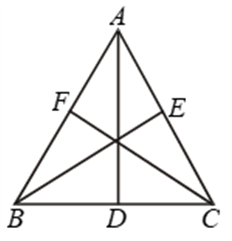
Example 9: In ∆ABC, AB = AC and the bisectors of angles B and C intersect at point O. Prove that BO = CO and the ray AO is the bisector of angle BAC.
Solution: In ∆ABC, we have
AB = AC
Now, in ∆ABO and ∆ACO, we have
AB = AC [Given]
∠OBC = ∠OCB [From (i)]
OB = OC [From (ii)]
So, by SAS criterion of congruence
∆ABO ≅ ∆ACO
⇒ ∠BAO = ∠CAO
[∵ Corresponding parts of congruent triangles are equal]
⇒ AO is the bisector of ∠BAC.
Example 10: In Fig. BM and DN are both perpendiculars to the segments AC and BM = DN.
Prove that AC bisects BD.
Solution: In ∆s BMR and DNR, we have
∠BMR = ∠DNR
[Each equal to 90º ∵ BM ⊥ AC and DN ⊥ AC]
∠BRM = ∠DRN [Vert. opp. angles]
and, BM = DN [Given]
So, by AAS criterion of congruence
∆BMR ≅ ∆DNR
⇒ BR = DR
[∵ Corresponding parts of congruent triangles are equal]
⇒ R is the mid-point of BD.
Hence, AC bisects BD.
Example 11: In Fig. BD and CE are two altitudes of a ∆ABC such that BD = CE.
Prove that ∆ABC is isolceles.
Solution: In ∆ABD and ∆ACE, we have
∠ADB = ∠AEC = 90º [Given]
∠BAD = ∠CAE [Common]
and, BD = CE [Given]
So, by AAS congruence criterion, we have
∆ABD ≅ ∆ACE
⇒ AB = AC [∵ Corresponding parts of congruent triangles are equal]
Hence, ∆ABC is isosceles.
Example 12: If two isosceles triangles have a common base, the line joining their vertices bisects them at right angles.
Solution: Given: Two isosceles triangles ABC and DBC having the common base BC such that AB = AC and DB = DC.
To prove: AD (or AD produced) bisects BC at right angle.
Proof : In ∆s ABD and ACD, we have
AB = AC [Given]
BD = CD [Given]
AD = AD [Common side]
So, by SSS criterion of congruence
∆ABD ≅ ∆ACD
⇒ ∠1 = ∠2 …. (i)
[∵ Corresponding parts of congruent triangles are equal]
Now, in ∆s ABE and ACE, we have
AB = AC [Given]
∠1 = ∠2 [From (i)]
and, AE = AE [Commoni side]
So, by SAS criterion of congruence,
∆ABE ≅ ∆ACE
⇒ BE = CE
[∵ Corresponding parts of congruent triangles are equal]
and, ∠3 = ∠4
But, ∠3 + ∠4 = 180º
[∵ Sum of the angles of a linear pair is 180º]
⇒ 2 ∠3 = 180º [∵ ∠3 = ∠4]
⇒ ∠3 = 90º
∴ ∠3 = ∠4 = 90º
Hence, AD bisects BC at right angles.
Example 13: AD, BE and CF, the altitudes of ∆ABC are equal. Prove that ∆ABC is an equilateral triangle
Solution: In right triangles BCE and BFC, we have
Hyp. BC = Hyp. BC
BE = CF [Given]
So, by RHS criterion of congruence,
∆BCE ∆BFC.
⇒ ∠B = ∠C [∵ Corresponding parts of congruent triangles are equal]
⇒ AC = AB …. (i)
[∵ Sides opposite to equal angles are equal]
Similarly, ∆ABD ≅ ∆ABE
⇒ ∠B =∠A
[Corresponding parts of congruent triangles are equal]
⇒ AC = BC …. (ii)
[Sides opposite to equal angles are equal]
From (i) and (ii), we get
AB = BC = AC
Hence, ∆ABC is an equilateral triangle.
Example 14: In Fig. AD = BC and BD = CA.
Prove that ∠ADB = ∠BCA and
∠DAB = ∠CBA.
Solution: In triangles ABD and ABC, we have
AD = BC [Given]
BD = CA [Given]
and AB = AB [Common]
So, by SSS congruence criterion, we have
∆ABD ∠CBA ⇒ ∠DAB = ∠ABC
[∵ Corresponding parts of congruent triangles are equal]
⇒ ∠DAB = ∠CBA
Example 15: Line-segment AB is parallel to another line-segment CD. O is the mid-point of AD (see figure). Show that (i) ∆AOB ≅ ∆DOC (ii) O is also the mid point of BC.
Solution: (i) Consider ∆AOB and ∆DOC
∠ABO = ∠DCO
(Alternate angles as AB || CD and BC is the transversal)
∠AOB = ∠DOC (Vertically opposite angles)
OA = OD (Given)
Therefore, ∆AOB ≅ ∆DOC (AAS rule)
(ii) OB = OC (c.p.c.t.)
So, O is the mid-point of BC.
Example 16: In quadrilateral ABCD, AC = AD and AB bisects ∠A. Show that ∆ABC ∆ABD. What can you say about BC and BD ?
Solution: In ∆ABC & ∆ABD
AB = AB (common)
∠1 = ∠2 {∵ AB is bisector of ∠A}
AC = AD (Given)
∴ By SAS, ∆ABC ≅ ∆ABD Proved
also BC = BD (c.p.c.t.)
Example 17: AD and BC are equal perpendiculars to a line segment AB. Show that CD bisects AB.
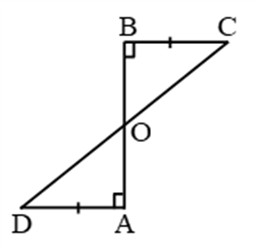
Solution: To show CD bisect AB i.e. AO = OB
∴ in ∆OAD and ∆OBC
∠O = ∠O (vertically opposite angles)
∠A = ∠B = 90° (Given)
AD = BC (Given)
∴ By AAS, ∆OAD ≅ ∆OBC
∴ OA = OB (c.p.c.t.)
∴ CD, bisects AB. Proved
Example 18: Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that
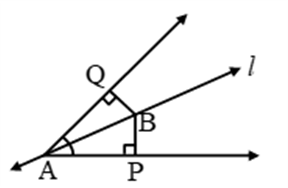
(i) ∆APB ≅ ∆AQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.
Solution: (i) In ∆APB and ∆AQB
∠P = ∠Q = 90° (Given)
∠PAB = ∠QAB (Given that ‘l’ bisect ∠A)
AB = AB (Common)
∴ By AAS, ∆APB ≅ ∆AQB. Proved
(ii) BP = BQ (c.p.c.t.) Proved.
Example 19: In given figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.
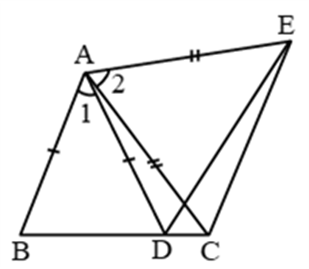
Solution: In ∆ABC and ∆ADE

Example 20: In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that:
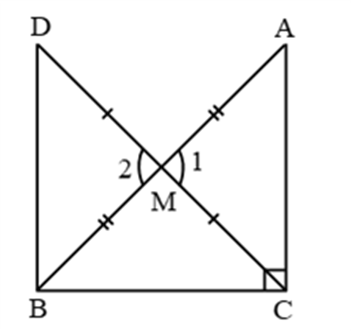
(i) ∆AMC ≅ ∆BMD
(ii) ∠DBC is a right angle
(iii) ∆DBC ≅ ∆ACB
(iv) CM = AB
Solution: (i) In ∆AMC and ∆BMD
AM = MB (M is mid point of AB)
∠1 = ∠2 (vertically opposite angles)
CM = MD (given)
∴ By SAS, ∆AMC ≅ ∆MBD Proved.
(ii) ∠ACM = ∠MDB (c.p.c.t. of (i))
These are alternate angles
∴ DB || AC
So ∠DBC + ∠ACB = 180°
(Cointerior angles)
⇒ ∠DBC + 90° = 180°
⇒ ∠DBC = 90° Proved.
(iii) In ∆DBC & ∆ACB
BC = BC ( common)
∠DBC = ∠ACB = 90°
DB = AC (c.p.c.t. of part (i))
∴ By SAS, ∆DBC ≅ ∆ACB. Proved
(iv) DC = AB (c.p.c.t. of part (iii))
But CM = DC (given)
∴ CM = AB Proved.
Some properties of a triangle
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Properties of Triangle
All the properties of a triangle are based on its sides and angles. By the definition of triangle, we know that, it is a closed polygon that consists of three sides and three vertices. Also, the sum of all three internal angles of a triangle equal to 180°.
Depending upon the length of sides and measure of angles, the triangles are classified into different types of triangles. Triangle is an important concept which is taught in most of the classes like Class 7, Class 8, Class 9, Class 10 and in Class 11. You will learn the properties of triangles here along with its definitions, types and its significance in Maths.
In the beginning, we start from understanding the shape of triangles, its types and properties, theorems based on it such as Pythagoras theorem, etc. In higher classes, we deal with trigonometry, where the right-angled triangle is the base of the concept. Let us learn here some of the fundamentals of the triangle by knowing its properties.
Types of Triangle
|
Based on the Sides |
Based on the Angles |
|
Scalene Triangle |
Acute angled Triangle |
|
Isosceles Triangle |
Right angle Triangle |
|
Equilateral Triangle |
Obtuse-angled Triangle |
So before, discussing the properties of triangles, let us discuss types of triangles given above.
Scalene Triangle: All the sides and angles are unequal.
Isosceles Triangle: It has two equal sides. Also, the angles opposite these equal sides are equal.
Equilateral Triangle: All the sides are equal and all the three angles equal to 60°.
Acute Angled Triangle: A triangle having all its angles less than 90°.
Right Angled Triangle: A triangle having one of the three angles exactly 90°.
Obtuse Angled Triangle: A triangle having one of the three angles more than 90°.
Triangle Properties
The properties of the triangle are:
- The sum of all the angles of a triangle (of all types) is equal to 180°.
- The sum of the length of the two sides of a triangle is greater than the length of the third side.
- In the same way, the difference between the two sides of a triangle is less than the length of the third side.
- The side opposite the greater angle is the longest side of all the three sides of a triangle.
- The exterior angle of a triangle is always equal to the sum of the interior opposite angles. This property of a triangle is called an exterior angle property.
- Two triangles are said to be similar if the corresponding angles of both triangles are congruent and the lengths of their sides are proportional.
- Area of a triangle = ½ × Base × Height
- The perimeter of a triangle = sum of all its three sides
Triangle Formula
- Area of a triangle is the region occupied by a triangle in a two-dimensional plane. The dimension of the area is square units. The formula for area is given by;
Area = 1/2 x Base x Height
- The perimeter of a triangle is the length of the outer boundary of a triangle. To find the perimeter of a triangle we need to add the length of the sides of the triangle.
P = a + b + c
- Semi-perimeter of a triangle is half of the perimeter of the triangle. It is represented by s.
s = (a + b + c)/2
where a, b and c are the sides of the triangle.
- By Heron’s formula, the area of the triangle is given by:
A = √[s(s – a)(s – b)(s – c)]
where ‘s’ is the semi-perimeter of the triangle.
- By the Pythagorean theorem, the hypotenuse of a right-angled triangle can be calculated by the formula:
Hypotenuse2 = Base2 + Perpendicular2
Solved Examples
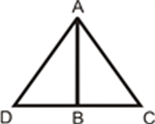
Example 1: If an equilateral triangle has lengths of sides as 5 cm and perpendicular is drawn from the vertex to the base of the triangle, then find its area and perimeter.
Solution: Given, side of the equilateral triangle, say AB = BC = CD = 5 cm
If we draw a perpendicular from the vertex of an equilateral triangle, A to the base at point O, it divides the base into two equal sides.
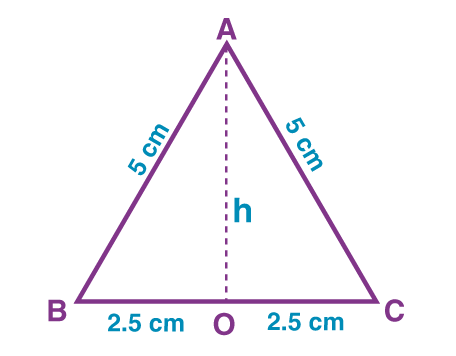
Such that, BO = OC = 2.5 cm
Now, the area of triangle = ½ × Base × Height
To find the height of the triangle, AOB, we have to use Pythagoras theorem.
That is, Hypotenuse2 = Base2 + Perpendicular2
Or Perpendicular =
Therefore, OA =
Or OA =
OA =
Area of triangle ABC = ½ × BC × OA
= ½ × 5 ×
= 2.5 × 4.33
Area of triangle ABC = 10.825 cm2
Perimeter of triangle ABC = sum of all its three sides
= 5 + 5 + 5 cm
= 15 cm
Example 2: If the sides of a triangle are given by 3 cm, 4 cm and 5 cm, where the base is 4cm and the altitude of the triangle is 3.2 cm, then find the area and perimeter of the triangle.
Solution: Let the given sides of the triangle be:
a = 3 cm, b = 4 cm and c = 5 cm
Altitude is the height of the triangle = 3.2 cm
By the formula of area of the triangle, we know;
Area = 1/2 x base x height
A = (1/2) x 4 x 3.2
A = 6.4 sq.cm.
Now, the perimeter of the triangle is given by;
P = a + b + c
P = 3 + 4 + 5
P = 12 cm.
Some properties of a triangle
Properties of Triangle
All the properties of a triangle are based on its sides and angles. By the definition of triangle, we know that, it is a closed polygon that consists of three sides and three vertices. Also, the sum of all three internal angles of a triangle equal to 180°.
Depending upon the length of sides and measure of angles, the triangles are classified into different types of triangles. Triangle is an important concept which is taught in most of the classes like Class 7, Class 8, Class 9, Class 10 and in Class 11. You will learn the properties of triangles here along with its definitions, types and its significance in Maths.
In the beginning, we start from understanding the shape of triangles, its types and properties, theorems based on it such as Pythagoras theorem, etc. In higher classes, we deal with trigonometry, where the right-angled triangle is the base of the concept. Let us learn here some of the fundamentals of the triangle by knowing its properties.
Types of Triangle
|
Based on the Sides |
Based on the Angles |
|
Scalene Triangle |
Acute angled Triangle |
|
Isosceles Triangle |
Right angle Triangle |
|
Equilateral Triangle |
Obtuse-angled Triangle |
So before, discussing the properties of triangles, let us discuss types of triangles given above.
Scalene Triangle: All the sides and angles are unequal.
Isosceles Triangle: It has two equal sides. Also, the angles opposite these equal sides are equal.
Equilateral Triangle: All the sides are equal and all the three angles equal to 60°.
Acute Angled Triangle: A triangle having all its angles less than 90°.
Right Angled Triangle: A triangle having one of the three angles exactly 90°.
Obtuse Angled Triangle: A triangle having one of the three angles more than 90°.
Triangle Properties
The properties of the triangle are:
- The sum of all the angles of a triangle (of all types) is equal to 180°.
- The sum of the length of the two sides of a triangle is greater than the length of the third side.
- In the same way, the difference between the two sides of a triangle is less than the length of the third side.
- The side opposite the greater angle is the longest side of all the three sides of a triangle.
- The exterior angle of a triangle is always equal to the sum of the interior opposite angles. This property of a triangle is called an exterior angle property.
- Two triangles are said to be similar if their corresponding angles of both triangles are congruent and the lengths of their sides are proportional.
- Area of a triangle = ½ × Base × Height
- The perimeter of a triangle = sum of all its three sides
Triangle Formula
- Area of a triangle is the region occupied by a triangle in a two-dimensional plane. The dimension of the area is square units. The formula for area is given by;
Area = 1/2 x Base x Height
- The perimeter of a triangle is the length of the outer boundary of a triangle. To find the perimeter of a triangle we need to add the length of the sides of the triangle.
P = a + b + c
- Semi-perimeter of a triangle is half of the perimeter of the triangle. It is represented by s.
s = (a + b + c)/2
where a, b and c are the sides of the triangle.
- By Heron’s formula, the area of the triangle is given by:
A = √[s(s – a)(s – b)(s – c)]
where ‘s’ is the semi-perimeter of the triangle.
- By the Pythagorean theorem, the hypotenuse of a right-angled triangle can be calculated by the formula:
Hypotenuse2 = Base2 + Perpendicular2
Solved Examples
Example 1: If an equilateral triangle has lengths of sides as 5 cm and perpendicular is drawn from the vertex to the base of the triangle, then find its area and perimeter.
Solution: Given, side of the equilateral triangle, say AB = BC = CD = 5 cm
If we draw a perpendicular from the vertex of an equilateral triangle, A to the base at point O, it divides the base into two equal sides.
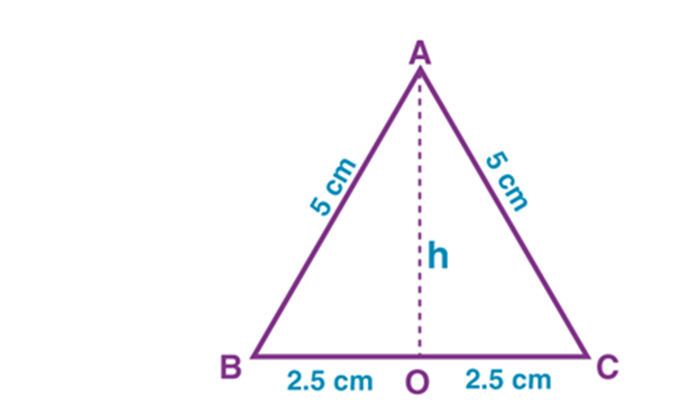
Such that, BO = OC = 2.5 cm
Now, the area of triangle = ½ × Base × Height
To find the height of the triangle, AOB, we have to use Pythagoras theorem.
That is, Hypotenuse2 = Base2 + Perpendicular2
Or Perpendicular =
Therefore, OA =
Or OA =
OA =
Area of triangle ABC = ½ × BC × OA
= ½ × 5 ×
= 2.5 × 4.33
Area of triangle ABC = 10.825 cm2
Perimeter of triangle ABC = sum of all its three sides
= 5 + 5 + 5 cm
= 15 cm
Example 2: If the sides of a triangle are given by 3 cm, 4 cm and 5 cm, where the base is 4cm and the altitude of the triangle is 3.2 cm, then find the area and perimeter of the triangle.
Solution: Let the given sides of the triangle be:
a = 3 cm, b = 4 cm and c = 5 cm
Altitude is the height of the triangle = 3.2 cm
By the formula of area of the triangle, we know;
Area = 1/2 x base x height
A = (1/2) x 4 x 3.2
A = 6.4 sq.cm.
Now, the perimeter of the triangle is given by;
P = a + b + c
P = 3 + 4 + 5
P = 12 cm.
Some more criteria for Congruence of Triangles
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Some More Criteria for Congruence of Triangles
Theorem 4 - SSS Congruence Rule
SSS Triangle Congruence
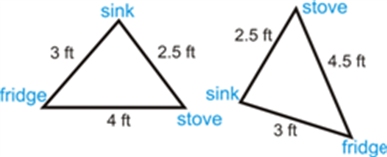
What if your parents were remodeling their kitchen so that measurements between the sink, refrigerator, and oven are in the picture at the left, below. Your neighbor’s kitchen has the measurements on the right, below. Are the two triangles congruent? After completing this Concept, you'll be able to determine whether or not two triangles are congruent given only their side lengths.
[Figure 1]
Side-Side-Side (SSS) Triangle Congruence Theorem: If three sides in one triangle are congruent to three sides in another triangle, then the triangles are congruent.
Now, we only need to show that all three sides in a triangle are congruent to the three sides in another triangle. We no longer have to show 3 sets of angles are congruent and 3 sets of sides are congruent in order to say that the two triangles are congruent.
Example A
Write a triangle congruence statement based on the diagram below:
[Figure 2]
From the tic marks, we know AB¯¯¯¯¯¯¯¯≅LM¯¯¯¯¯¯¯¯¯,AC¯¯¯¯¯¯¯¯≅LK¯¯¯¯¯¯¯¯,BC¯¯¯¯¯¯¯¯≅MK¯¯¯¯¯¯¯¯¯¯. Using the SSS Congruence rule we know the two triangles are congruent. Lining up the corresponding sides, we have △ABC≅△LMK.
Don’t forget ORDER MATTERS when writing triangle congruence statements. Here, we lined up the sides with one tic mark, then the sides with two tic marks, and finally the sides with three tic marks.
Example B
Write a two-column proof to show that the two triangles are congruent.
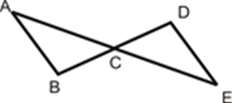
Given: AB¯¯¯¯¯¯¯¯≅DE¯¯¯¯¯¯¯¯
[Figure 3]
C is the midpoint of AE¯¯¯¯¯¯¯¯ and DB¯¯¯¯¯¯¯¯.
Prove: △ACB≅△ECD
|
Statement |
Reason |
|
1. AB¯¯¯¯¯¯¯¯≅DE¯¯¯¯¯¯¯¯ C is the midpoint of AE¯¯¯¯¯¯¯¯ and DB¯¯¯¯¯¯¯¯ |
Given |
|
2. AC¯¯¯¯¯¯¯¯≅CE¯¯¯¯¯¯¯¯,BC¯¯¯¯¯¯¯¯≅CD¯¯¯¯¯¯¯¯ |
Definition of a midpoint |
|
3. △ACB≅△ECD |
SSS Congruence rule |
Make sure that you clearly state the three sets of congruent sides BEFORE stating that the triangles are congruent.
Feel free to mark the picture with the information you are given as well as information that you can infer (vertical angles, information from parallel lines, midpoints, angle bisectors, right angles).
Concept Problem Revisited
From what we have learned in this section, the two triangles are not congruent because the distance from the fridge to the stove in your house is 4 feet and in your neighbor’s it is 4.5 ft. The SSS Congruence rule tells us that all three sides have to be congruent.
Vocabulary
Two figures are congruent if they have exactly the same size and shape. By definition, two triangles are congruent if the three corresponding angles and sides are congruent. The symbol ≅ means congruent. There are shortcuts for proving that triangles are congruent. The SSS Triangle Congruence Rule states that if three sides in one triangle are congruent to three sides in another triangle, then the triangles are congruent.
Theorem 5 - RHS Congruence Rule
HL Triangle Congruence
What if you were given two right triangles and provided with only the measure of their hypotenuses and one of their legs? How could you determine if the two right triangles were congruent? After completing this Concept, you'll be able to use the Hypotenuse-Leg (HL) shortcut to prove right triangles are congruent.
Guidance
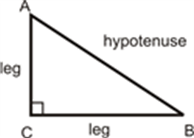
Recall that a right triangle has exactly one right angle. The two sides adjacent to the right angle are called legs and the side opposite the right angle is called the hypotenuse.
[Figure 13]
The Pythagorean Theorem says, for any right triangle, (leg)2+(leg)2=(hypotenuse)2. What this means is that if you are given two sides of a right triangle, you can always find the third. Therefore, if you know that two sides of a right triangle are congruent to two sides of another right triangle, you can conclude that third sides are also congruent.
RHS Congruence Theorem: If the hypotenuse and leg in one right triangle are congruent to the hypotenuse and leg in another right triangle, then the two triangles are congruent.
The markings in the picture are enough to say △ABC≅△XYZ.
[Figure 14]
Notice that this theorem is only used with a hypotenuse and a leg. If you know that the two legs of a right triangle are congruent to two legs of another triangle, the two triangles would be congruent by SAS, because the right angle would be between them.
Example A
What information would you need to prove that these two triangles are congruent using the RHS Congruence Theorem?
[Figure 15]
For RHS Congruence condition, we need the hypotenuses to be congruent. So, AC¯¯¯¯¯¯¯¯≅MN¯¯¯¯¯¯¯¯¯¯.
Example B
Determine if the triangles are congruent. If they are, write the congruence statement and which congruence postulate or theorem you used.
[Figure 16]
We know the two triangles are right triangles. The have one pair of legs that is congruent and their hypotenuses are congruent. This means that △ABC≅△RQP by RHS Congruence theorem.
Example C
Determine the additional piece of information needed to show the two triangles are congruent by RHS Congruence theorem.
[Figure 17]
We already know one pair of legs is congruent and that they are right triangles. The additional piece of information we need is that the two hypotenuses are congruent, UT¯¯¯¯¯¯¯≅FG¯¯¯¯¯¯¯¯.
Vocabulary
Two figures are congruent if they have exactly the same size and shape. By definition, two triangles are congruent if the three corresponding angles and sides are congruent. The symbol ≅ means congruent. There are shortcuts for proving that triangles are congruent. The RHS Congruence Theorem states that if the hypotenuse and leg in one right triangle are congruent to the hypotenuse and leg in another right triangle, then the two triangles are congruent. A right triangle has exactly one right (90∘) angle. The two sides adjacent to the right angle are called legs and the side opposite the right angle is called the hypotenuse.
Some more criteria for Congruence of Triangles
Some More Criteria for Congruence of Triangles
Theorem 4 - SSS Congruence Rule
SSS Triangle Congruence
What if your parents were remodeling their kitchen so that measurements between the sink, refrigerator, and oven are in the picture at the left, below. Your neighbor’s kitchen has the measurements on the right, below. Are the two triangles congruent? After completing this Concept, you'll be able to determine whether or not two triangles are congruent given only their side lengths.
[Figure 1]
Side-Side-Side (SSS) Triangle Congruence Theorem: If three sides in one triangle are congruent to three sides in another triangle, then the triangles are congruent.
Now, we only need to show that all three sides in a triangle are congruent to the three sides in another triangle. We no longer have to show 3 sets of angles are congruent and 3 sets of sides are congruent in order to say that the two triangles are congruent.
Example A
Write a triangle congruence statement based on the diagram below:
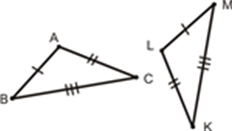
[Figure 2]
From the tic marks, we know AB¯¯¯¯¯¯¯¯≅LM¯¯¯¯¯¯¯¯¯,AC¯¯¯¯¯¯¯¯≅LK¯¯¯¯¯¯¯¯,BC¯¯¯¯¯¯¯¯≅MK¯¯¯¯¯¯¯¯¯¯. Using the SSS Congruence rule we know the two triangles are congruent. Lining up the corresponding sides, we have △ABC≅△LMK.
Don’t forget ORDER MATTERS when writing triangle congruence statements. Here, we lined up the sides with one tic mark, then the sides with two tic marks, and finally the sides with three tic marks.
Example B
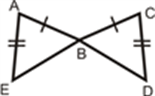
Write a two-column proof to show that the two triangles are congruent.
Given: AB¯¯¯¯¯¯¯¯≅DE¯¯¯¯¯¯¯¯
[Figure 3]
C is the midpoint of AE¯¯¯¯¯¯¯¯ and DB¯¯¯¯¯¯¯¯.
Prove: △ACB≅△ECD
Make sure that you clearly state the three sets of congruent sides BEFORE stating that the triangles are congruent.
Feel free to mark the picture with the information you are given as well as information that you can infer (vertical angles, information from parallel lines, midpoints, angle bisectors, right angles).
Concept Problem Revisited
From what we have learned in this section, the two triangles are not congruent because the distance from the fridge to the stove in your house is 4 feet and in your neighbor’s it is 4.5 ft. The SSS Congruence rule tells us that all three sides have to be congruent.
Vocabulary
Two figures are congruent if they have exactly the same size and shape. By definition, two triangles are congruent if the three corresponding angles and sides are congruent. The symbol ≅ means congruent. There are shortcuts for proving that triangles are congruent. The SSS Triangle Congruence Rule states that if three sides in one triangle are congruent to three sides in another triangle, then the triangles are congruent.
Guided Practice
1. Fill in the blanks in the proof below.
Given: AB¯¯¯¯¯¯¯¯≅DC¯¯¯¯¯¯¯¯, AC¯¯¯¯¯¯¯¯≅DB¯¯¯¯¯¯¯¯
Prove: △ABC≅△DCB
[Figure 4]
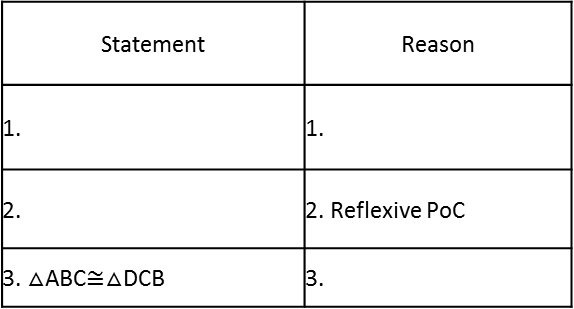
2. Is the pair of triangles congruent? If so, write the congruence statement and why.

[Figure 5]
Answers:
1
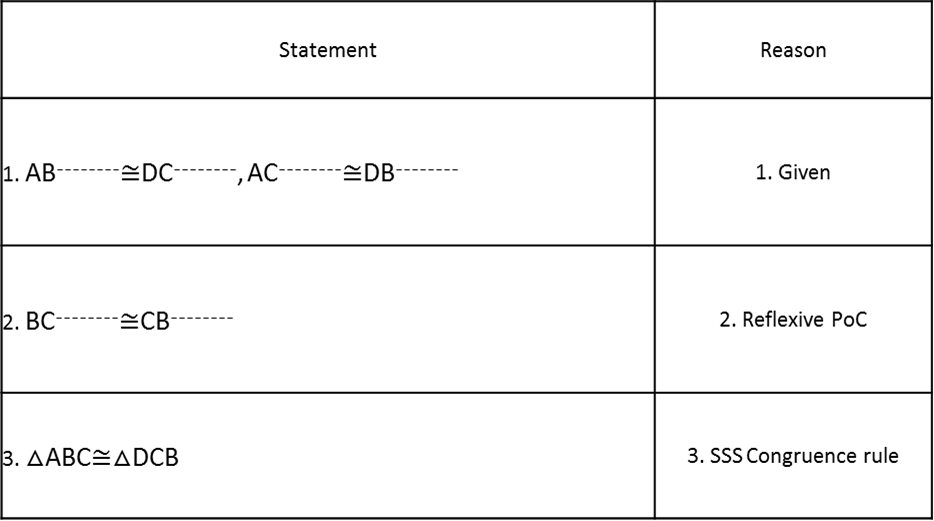
2. The triangles are congruent because they have three pairs of sides congruent. △DEF≅△IGH.
Practice
Are the pairs of triangles congruent? If so, write the congruence statement and why.
1
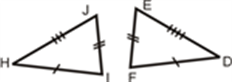
[Figure 6]
2.
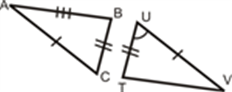
[Figure 7]
3.
[Figure 8]
4.
[Figure 9]
State the additional piece of information needed to show that each pair of triangles is congruent.
5. Use SSS
[Figure 10]
6. Use SSS
[Figure 11]
Fill in the blanks in the proofs below.
7. Given: B is the midpoint of DC¯¯¯¯¯¯¯¯, AD¯¯¯¯¯¯¯¯≅AC¯¯¯¯¯¯¯¯. Prove: △ABD≅△ABC
[Figure 12]

Theorem 5 - RHS Congruence Rule
HL Triangle Congruence
What if you were given two right triangles and provided with only the measure of their hypotenuses and one of their legs? How could you determine if the two right triangles were congruent? After completing this Concept, you'll be able to use the Hypotenuse-Leg (HL) shortcut to prove right triangles are congruent.
Guidance
Recall that a right triangle has exactly one right angle. The two sides adjacent to the right angle are called legs and the side opposite the right angle is called the hypotenuse.
[Figure 13]
The Pythagorean Theorem says, for any right triangle, (leg)2+(leg)2=(hypotenuse)2. What this means is that if you are given two sides of a right triangle, you can always find the third. Therefore, if you know that two sides of a right triangle are congruent to two sides of another right triangle, you can conclude that third sides are also congruent.
RHS Congruence Theorem: If the hypotenuse and leg in one right triangle are congruent to the hypotenuse and leg in another right triangle, then the two triangles are congruent.
The markings in the picture are enough to say △ABC≅△XYZ.
[Figure 14]
Notice that this theorem is only used with a hypotenuse and a leg. If you know that the two legs of a right triangle are congruent to two legs of another triangle, the two triangles would be congruent by SAS, because the right angle would be between them.
Example A
What information would you need to prove that these two triangles are congruent using the RHS Congruence Theorem?
[Figure 15]
For RHS Congruence condition, we need the hypotenuses to be congruent. So, AC¯¯¯¯¯¯¯¯≅MN¯¯¯¯¯¯¯¯¯¯.
Example B
Determine if the triangles are congruent. If they are, write the congruence statement and which congruence postulate or theorem you used.
[Figure 16]
We know the two triangles are right triangles. The have one pair of legs that is congruent and their hypotenuses are congruent. This means that △ABC≅△RQP by RHS Congruence theorem.
Example C
Determine the additional piece of information needed to show the two triangles are congruent by RHS Congruence theorem.
[Figure 17]
We already know one pair of legs is congruent and that they are right triangles. The additional piece of information we need is that the two hypotenuses are congruent, UT¯¯¯¯¯¯¯≅FG¯¯¯¯¯¯¯¯.
Watch this video for help with the examples above.
Vocabulary
Two figures are congruent if they have exactly the same size and shape. By definition, two triangles are congruent if the three corresponding angles and sides are congruent. The symbol ≅ means congruent. There are shortcuts for proving that triangles are congruent. The RHS Congruence Theorem states that if the hypotenuse and leg in one right triangle are congruent to the hypotenuse and leg in another right triangle, then the two triangles are congruent. A right triangle has exactly one right (90∘) angle. The two sides adjacent to the right angle are called legs and the side opposite the right angle is called the hypotenuse.
Guided Practice
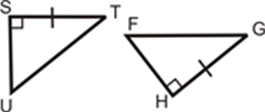
1. Determine if the triangles are congruent. If they are, write the congruence statement and which congruence postulate or theorem you used.
[Figure 18]
2. Fill in the blanks in the proof below.
Given:
SV¯¯¯¯¯¯¯⊥WU¯¯¯¯¯¯¯¯¯
T is the midpoint of SV¯¯¯¯¯¯¯ and WU¯¯¯¯¯¯¯¯¯
Prove: WS¯¯¯¯¯¯¯¯¯≅UV¯¯¯¯¯¯¯¯
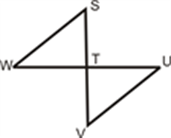
[Figure 19]

3. If two right triangles have congruent hypotenuses and one pair of non-right angles that are congruent, are the two right triangles definitively congruent?
Answers:
1. All we know is that two pairs of sides are congruent. Since we do not know if these are right triangles, we cannot use RHS Congruence theorem. We do not know if these triangles are congruent.
2
Note that even though these were right triangles, we did not use the RHS congruence theorem because we were not originally given that the two hypotenuses were congruent. The SAS congruence shortcut was quicker in this case.
3. Yes, by the AAS Congruence shortcut. One pair of congruent angles is the right angles, and another pair is given. The congruent pair of sides are the hypotenuses that are congruent. Note that just like in #2, even though the triangles are right triangles, it is possible to use a congruence shortcut other than RHS Congruence theorem to prove the triangles are congruent.
Practice
Using the RHS Congruence Theorem, what information do you need to prove the two triangles are congruent?
1.
[Figure 20]
2.
[Figure 21]
3.
[Figure 22]
The triangles are formed by two parallel lines cut by a perpendicular transversal. C is the midpoint of AD¯¯¯¯¯¯¯¯. Complete the proof to show the two triangles are congruent.
[Figure 23]
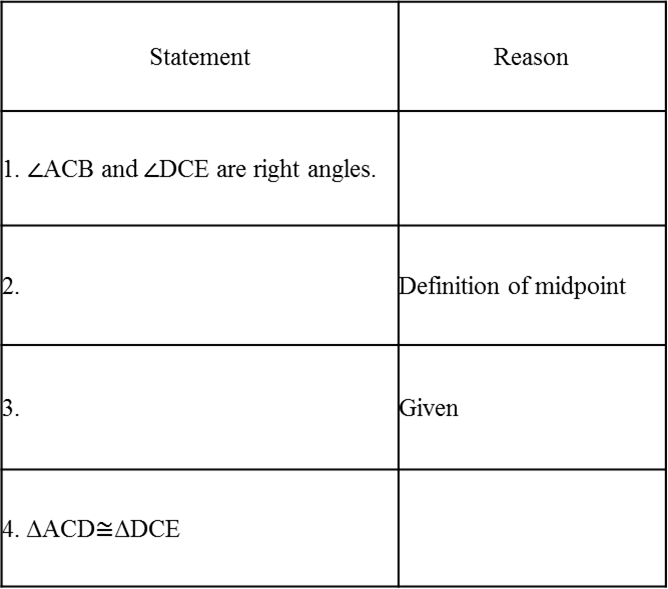
Based on the following details, are the two right triangles definitively congruent?
4. The hypotenuses of two right triangles are congruent.
5. Both sets of legs in the two right triangles are congruent.
6. One set of legs are congruent in the two right triangles.
7. The hypotenuses and one pair of legs are congruent in the two right triangles.
8. One of the non right angles of the two right triangles is congruent.
9. All of the angles of the two right triangles are congruent.
10. All of the sides of the two right triangles are congruent.
11. Both triangles have one leg that is twice the length of the other.
Inequalities in Triangle
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Triangle Inequality Theorem
According to triangle inequality theorem, for any given triangle, the sum of two sides of a triangle is always greater than the third side. A polygon bounded by three line segments is known as the Triangle. It is the smallest possible polygon. A triangle has three sides, three vertices, and three interior angles. The types of triangles are based on its angle measure and length of the sides. The inequality theorem is applicable for all types triangles such as equilateral, isosceles and scalene. Now let us learn this theorem in details with its proof.
Triangle Inequality Theorem Proof
The triangle inequality theorem describes the relationship between the three sides of a triangle. According to this theorem, for any triangle, the sum of lengths of two sides is always greater than the third side. In other words, this theorem specifies that the shortest distance between two distinct points is always a straight line.
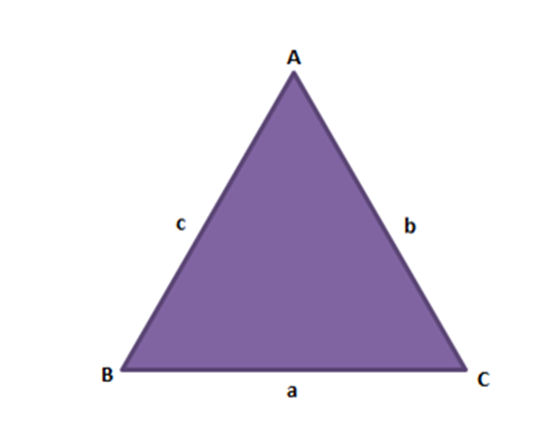
Consider a ∆ABC as shown below, with a, b and c as the side lengths.
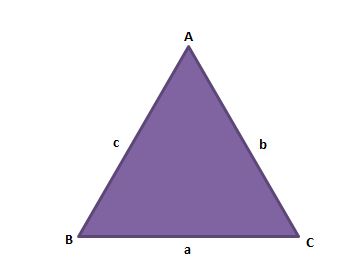
The triangle inequality theorem states that:
a < b + c,
b < a + c,
c < a + b
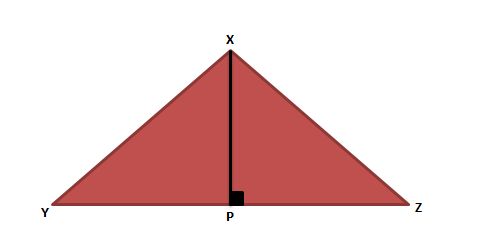
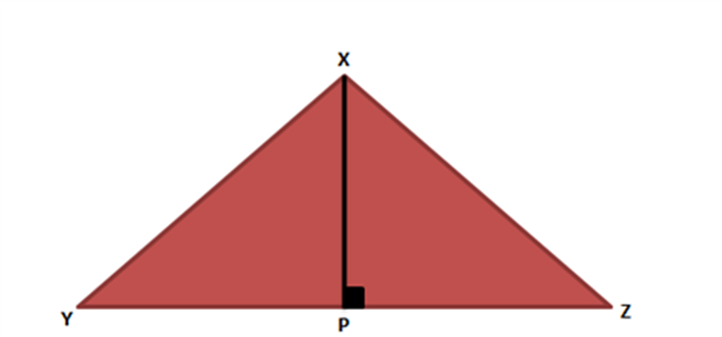
In any triangle, the shortest distance from any vertex to the opposite side is the Perpendicular. In figure below, XP is the shortest line segment from vertex X to side YZ.
Let us prove the theorem now for a triangle ABC.
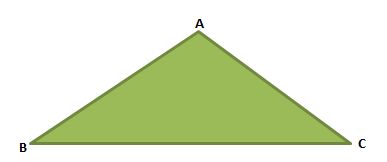
Triangle ABC
To Prove: |BC|< |AB| + |AC|
Construction: Consider a ∆ABC. Extend the side AC to a point D such that AD = AB as shown in the fig. below.
Proof of triangle inequality theorem
|
S.No |
Statement |
Reason |
|
1. |
|CD|= |AC| + |AD| |
From figure 3 |
|
2. |
|CD|= |AC| + |AB| |
AB = AD, ∆ADB is an isosceles triangle |
|
3. |
∠DBA <∠DBC |
Since ∠DBC = ∠DBA+∠ABD |
|
4. |
∠ADB<∠DBC |
∆ADB is an isosceles triangle and ∠ADB = ∠DBA |
|
5. |
|BC|<|CD| |
Side opposite to greater angle is larger |
|
6. |
|BC|<|AC| + |AB| |
From statements 3 and 4 |
Thus, we can conclude that the sum of two sides of a triangle is greater than the third side.
Example Problems
Q.1. If 4cm, 8cm and 2cm are the measures of three lines segment. Can it be used to draw a triangle?
Solution: The triangle is formed by three line segments 4cm, 8cm and 2cm, then it should satisfy the inequality theorem.
Hence, let us check if the sum of two sides is greater than the third side.
4 + 8 > 2 ⇒ 12 > 2 ⇒ True
8 + 2 > 4 ⇒ 10 > 4 ⇒ True
4 + 2 > 8 ⇒ 6 > 8 ⇒ False
Therefore, the sides of the triangle do not satisfy the inequality theorem. So, we cannot construct a triangle with these three line segments.
Q.2: Could a triangle have side length as 6cm, 7cm and 5cm?
Solution: If 6cm, 7cm and 5cm are the sides of the triangle, then they should satisfy the inequality theorem.
Hence,
6 + 7 > 5 ⇒ 13 > 5 ⇒ True
7 + 5 > 6 ⇒ 12 > 6 ⇒ True
6 + 5 > 7 ⇒ 11 > 7 ⇒ True
All the three conditions are satisfied, therefore a triangle could have side length as 6cm, 7cm and 5cm
Q.3: If the two sides of a triangle are 2 and 7. Find all the possible lengths of the third side.
Solution: To find the possible values of the third side of the triangle we can use the formula:
A difference of two sides< Unknown side < Sum of the two sides
7 -2 < x < 7 + 2
5 < x <9
There could be any value for the third side between 5 and 9.
Inequalities in Triangle
Triangle Inequality Theorem
According to triangle inequality theorem, for any given triangle, the sum of two sides of a triangle is always greater than the third side. A polygon bounded by three line-segments is known as the Triangle. It is the smallest possible polygon. A triangle has three sides, three vertices, and three interior angles. The types of triangles are based on its angle measure and length of the sides. The inequality theorem is applicable for all types triangles such as equilateral, isosceles and scalene. Now let us learn this theorem in details with its proof.
Triangle Inequality Theorem Proof
The triangle inequality theorem describes the relationship between the three sides of a triangle. According to this theorem, for any triangle, the sum of lengths of two sides is always greater than the third side. In other words, this theorem specifies that the shortest distance between two distinct points is always a straight line.
Consider a ∆ABC as shown below, with a, b and c as the side lengths.
The triangle inequality theorem states that:
a < b + c,
b < a + c,
c < a + b
In any triangle, the shortest distance from any vertex to the opposite side is the Perpendicular. In figure below, XP is the shortest line segment from vertex X to side YZ.
Let us prove the theorem now for a triangle ABC.
Triangle ABC
To Prove: |BC|< |AB| + |AC|
Construction: Consider a ∆ABC. Extend the side AC to a point D such that AD = AB as shown in the fig. below.
Proof of triangle inequality theorem
|
S.No |
Statement |
Reason |
|
1. |
|CD|= |AC| + |AD| |
From figure 3 |
|
2. |
|CD|= |AC| + |AB| |
AB = AD, ∆ADB is an isosceles triangle |
|
3. |
∠DBA <∠DBC |
Since ∠DBC = ∠DBA+∠ABD |
|
4. |
∠ADB<∠DBC |
∆ADB is an isosceles triangle and ∠ADB = ∠DBA |
|
5. |
|BC|<|CD| |
Side opposite to greater angle is larger |
|
6. |
|BC|<|AC| + |AB| |
From statements 3 and 4 |
Thus, we can conclude that the sum of two sides of a triangle is greater than the third side.
Example Problems
Q.1. If 4cm, 8cm and 2cm are the measures of three lines segment. Can it be used to draw a triangle?
Solution: The triangle is formed by three line segments 4cm, 8cm and 2cm, then it should satisfy the inequality theorem.
Hence, let us check if the sum of two sides is greater than the third side.
4 + 8 > 2 ⇒ 12 > 2 ⇒ True
8 + 2 > 4 ⇒ 10 > 4 ⇒ True
4 + 2 > 8 ⇒ 6 > 8 ⇒ False
Therefore, the sides of the triangle do not satisfy the inequality theorem. So, we cannot construct a triangle with these three line-segments.
Q.2: Could a triangle have side length as 6cm, 7cm and 5cm?
Solution: If 6cm, 7cm and 5cm are the sides of the triangle, then they should satisfy inequality theorem.
Hence,
6 + 7 > 5 ⇒ 13 > 5 ⇒ True
7 + 5 > 6 ⇒ 12 > 6 ⇒ True
6 + 5 > 7 ⇒ 11 > 7 ⇒ True
All the three conditions are satisfied, therefore a triangle could have side length as 6cm, 7cm and 5cm
Q.3: If the two sides of a triangle are 2 and 7. Find all the possible lengths of the third side.
Solution: To find the possible values of the third side of the triangle we can use the formula:
A difference of two sides< Unknown side < Sum of the two sides
7 -2 < x < 7 + 2
5 < x <9
There could be any value for the third side between 5 and 9.

 ABCD CLASSES
ABCD CLASSES